Fenêtres pour l'analyse spectrale

1. Introduction

L'analyse spectrale d'un signal s(t) se fait sur une durée T, correspondant par exemple à la durée de l'enregistrement du signal. On considère par convention que la fonction s(t) est définie sur $[-T/2,T/2]$. L'analyse spectrale repose sur la transformée de Fourier, qui par définition s'applique à une fonction définie sur $-]\infty,+\infty[$. L'analyse spectrale de s(t) consiste à calculer la transformée de Fourier de :

$$u\left(t\right)=s\left(t\right)w\left(t\right)\text{(1)}$$

où $w\left(t\right)$ est une fonction de fenêtrage (ou plus simplement fenêtre) définie sur $]-\infty,+\infty[$ mais non nulle seulement sur l'intervalle $[-T/2,T/2]$. La fonction u(t) est bien définie sur $]-\infty,+\infty[$ mais elle est nulle en dehors de l'intervalle $[-T/2,T/2]$.

D'après le théorème de convolution, la transformée de Fourier (TF) de u(t) est le produit de convolution de la TF de s(t) et de la TF de w(t). On est donc amené à s'intéresser à la TF de la fenêtre w(t). La résolution fréquentielle de l'analyse spectrale est essentiellement déterminée par la durée T mais la forme de la fenêtre a aussi une influence sur le spectre et notamment sur la possibilité de résoudre deux raies très voisines.

L'analyse spectrale d'un signal échantillonné ([1]) repose sur la transformée de Fourier à temps discret (TFTD) et sur la transformée de Fourier discrète (TFD).

Ce document montre les propriétés de différentes fenêtres. On verra en particulier comment la TFD permet d'obtenir une approximation de la TF d'une fenêtre. La méthode exposée est de première importance car elle s'applique également pour obtenir la TF du signal s(t).

2. Transformée de Fourier discrète

Rappelons tout d'abord la définition de la transformée de Fourier (TF). Par convention, on note par une majuscule la TF d'un signal dont la fonction est notée par une minuscule. La transformée de Fourier est une fonction de la fréquence $f$ ou bien de la pulsation $\omega =2\pi f$. Dans ce document, on exprime la TF comme fonction de la fréquence. La TF de u(t) est définie par :

$$U\left(f\right)={\int }_{-\infty }^{+\infty }u\left(t\right)exp(-j2\pi ft)dt\text{(2)}$$

Si la fonction u(t) est à valeurs réelles (hypothèse que l'on fera pour la suite), on a :

$$U(-f)=U{\left(f\right)}^{*}\text{(3)}$$

où ${\left[z\right]}^{*}$ désigne le complexe conjugé de $z$.

Un signal échantillonné avec la période d'échantillonnage T_e est défini par :

$$\begin{array}{ccc}\hfill & t_q=q{T}_e\hfill & \hfill \text{(4)}\\ \hfill & u_q=u\left(t_q\right)\hfill & \hfill \text{(5)}\end{array}$$

où q est un nombre entier (relatif). Le signal u_q est qualifié de signal numérique ou bien de signal à temps discret. L'approximation de l'intégrale $\mathrm{(2)}$ par la formule des rectangles s'écrit :

$$U\left(f\right)\approx \sum _{q=-\infty }^{\infty }{T}_e{u}_{q}exp(-j2\pi fq{T}_e)\text{(6)}$$

La transformée de Fourier à temps discret (TFTD) est définie par :

$$U_{T_e}\left(f\right)=\sum _{q=-\infty }^{\infty }{u}_{q}exp(-j2\pi fq{T}_e)\text{(7)}$$

La TFTD constitue une approximation de la TF, d'autant meilleure que la période d'échantillonnage est petite :

$$\underset{T_e\to 0}{lim}{T}_e{U}_{T_e}\left(f\right)=U\left(f\right)\text{(8)}$$

Bien évidemment, le calcul numérique d'une TFTD est impossible car le nombre de terme de la somme est infini, à moins que la fonction u(t) soit à support borné, ce qui est précisément le cas de la fonction u(t) définie par $\mathrm{(1)}$. Sur l'intervalle de largeur T, la fonction u(t) comporte N échantillons, que l'on suppose pair. Posons alors :

$$t_k=-\frac{T}{2}+k\frac{T}{N}\text{(9)}$$

avec $k=0,1,\dots N-1$.

Les échantillons sont donc indexés par k et on bien sûr $q=k-\frac{N}{2}$. L'approximation $\mathrm{(6)}$ s'écrit alors :

$$U\left(f\right)\approx \sum _{k=0}^{N-1}{T}_e{u}_{k}exp(-j2\pi fk{T}_e)exp\left(j2\pi f\frac{N{T}_e}{2}\right)\text{(10)}$$

Sachant que $T=N{T}_e$, on obtient :

$$U\left(f\right)\approx \frac{T}{N}exp\left(j\pi fT\right)\sum _{k=0}^{N-1}{u}_{k}exp(-j2\pi fk\frac{T}{N})\text{(11)}$$

Posons :

$$U_{T,N}\left(f\right)=\frac{T}{N}exp\left(j\pi fT\right)\sum _{k=0}^{N-1}{u}_{k}exp(-j2\pi fk\frac{T}{N})\text{(12)}$$

qui constitue l'approximation de la TF pour un signal comportant N échantillons. Dans un premier temps, on limite le calcul de l'approximation de la TF aux fréquences définies par :

$$f_n=\frac{n}{T}\text{(13)}$$

où n est un nombre entier. On a pour ces fréquences :

$$U_{T,N}\left(f_n\right)=\frac{T}{N}exp\left(j\pi n\right)\sum _{k=0}^{N-1}{u}_{k}exp(-j2\pi k\frac{n}{N})\text{(14)}$$

La transformée de Fourier discrète est définie par :

$$U_n^{tfd}=\frac{1}{N}\sum _{k=0}^{N-1}{u}_{k}exp(-j2\pi k\frac{n}{N})\text{(15)}$$

Il est important de faire la disctinction entre la TFTD et la TFD :

• La transformée de Fourier à temps discret (TFTD), définie par $\mathrm{(7)}$, est définie pour une fréquence réelle quelconque.
• La transformée de Fourier discrète (TFD), définie par $\mathrm{(15)}$, est définie seulement pour les fréquences $f_n=\frac{n}{T}$.

Autrement dit, dans la TFTD, seul le temps est discret, alors que dans la TFD, le temps et la fréquence sont discrets.

D'après ce qui précède, on a :

$$U\left(f_n\right)\approx Texp\left(j\pi n\right)U_n^{tfd}\text{(16)}$$

Si nous faisons en plus les deux hypothèses suivantes :

• la transformée de Fourier U(f) est à support borné : il existe une fréquence f_m telle que pour |f|>f_m on ait U(f)=0,
• la fréquence d'échantillonnage vérifie f_e>2f_m (condition de Nyquist-Shannon),

alors la TFDT est exactement égale à la TF sur l'intervalle de fréquences [-f_e/2,f_e/2] :

$$U\left(f_n\right)=Texp\left(j\pi n\right)U_n^{tfd}\text{(17)}$$

La TFD possède deux propriétés importantes. La première est la périodicité :

$$U_{n+N}^{tfd}=U_n^{tfd}\text{(18)}$$

Il résulte de la périodicité que le calcul de la TFD se limite à :

$$n=0,1,\dots N-1\text{(19)}$$

La TFD peut être vue comme une application qui à N nombres réels u_k associe les N nombres complexes $U_n^{tfd}$ pour $n=0,1,\dots N-1$. Le calcul numérique de la TFD de N nombres consiste donc à calculer N sommes, chacun comportant N termes. La complexité temporelle de ce calcul est donc en principe $O\left(N^2\right)$. Si N est une puissance de 2, l'algorithme de Transformée de Fourier rapide permet de faire le calcul avec une complexité $O\left(Nln\left(N\right)\right)$ (cet algorithme devrait s'appeler transformée de Fourier discrète rapide).

Dans la mesure où les valeurs de u(t) sont réelles, la TFD possède une autre propriété importante :

$$U_{N-n}^{tfd}={\left[U_n^{tfd}\right]}^{*}\text{(20)}$$

Remarque : dans la définition de la TFD (relation $\mathrm{(15)}$) le facteur $\frac{1}{N}$ est parfois omis. C'est le cas pour la fonction numpy.fft.fft.

La TFD permet, grace à la relation $\mathrm{(17)}$, d'obtenir une approximation de la TF de u(t), mais seulement pour les fréquences $f_n=\frac{n}{T}$. Il est possible d'obtenir la TFTD, ou du moins une approximation de la TFTD, qui est plus proche de la TF car elle est définie pour toute fréquence. La TFTD correspond à la limite de la TFD lorsque $T\to \infty$. Pour s'approcher de la TFTD, il suffit donc d'augmenter la durée T au delà de la largeur de la fenêtre $w\left(t\right)$, voire même beaucoup plus grande que cette largeur. Il suffit pour cela de compléter le signal échantillonné et fenêtré par des zéros. C'est la méthode de remplissage par des zéros (zero padding). Si N désigne la longueur du signal échantillonné, on complète par des zéros de manière à obtenir un signal à N' échantillons auquel on applique la TFD. N' doit être une puissance de 2 de manière à pouvoir faire le calcul avec l'algorithme de transformée de Fourier rapide. La résolution fréquentielle obtenue est :

$$\Delta f=\frac{1}{N\text{'}{T}_e}=\frac{N}{N\text{'}}\frac{1}{T}\text{(21)}$$

Un rapport $\frac{N\text{'}}{N}$ de 5 à 10 permet d'obtenir en général une très bonne approximation de la TFTD, c'est-à-dire un spectre pour une fréquence continue (non discrète).

Pour résumer, cette méthode du remplissage par des zéros a un double intérêt :

• Si N n'est pas une puissance de 2, il est aisé de choisi N'>N égal à une puissance de 2.
• Plus N' est grand, plus le spectre obtenu se rapproche de celui obtenu par la transformée de Fourier à temps discret.

Bien évidemment, l'augmentation de T ne change rien au fait que la période d'échantillonnage T_e est finie (non nulle). Pour cette raison, le spectre du signal échantillonné est périodique, de période $f_e=\frac{1}{T_e}$ (la fréquence d'échantillonnage).

Si N' est assez grand, une simple interpolation linéaire entre les points (ce que fait la fonction matplotlib.pyplot.plot) permet d'obtenir une bonne représentation graphique de la TFDT, donc de la TF.

Remarque : il arrive fréquemment que le nombre d'échantillons N enregistrés dans une expérience ne soit pas une puissance de 2. Ce serait une erreur de chercher à réduire N pour obtenir une puissance de 2. En effet, cette méthode consisterait soit à ne garder qu'une partie des échantillons (en nombre égal à une puissance de 2), soit à procéder à une réduction de la fréquence d'échantillonnage afin de garder la durée T inchangée. Ces deux méthodes sont mauvaises, la première parce qu'elle réduit la durée analysée, la seconde parce qu'elle réduit la fréquence d'échantillonnage (qui normalement est choisie de manière judicieuse par l'expérimentateur). La bonne méthode consiste à compléter le signal échantillonné par des zéros afin d'obtenir un nombre N' d'échantillons puissance de 2. Cette méthode ne change ni la fréquence d'échantillonnage, ni la durée analysée. On aura même intérêt à ajouter un très grand nombre de zéros afin à obtenir une bonne représentation de la TFTD.

3. Fenêtre rectangulaire

La fenêtre la plus simple est la fenêtre rectangulaire, définie par :

$$\begin{array}{cc}\hfill & w_r\left(t\right)=1pourt\in [-\frac{T}{2},\frac{T}{2}]\hfill \\ \hfill & w_r\left(t\right)=0pour\left|t\right|>\frac{T}{2}\hfill \end{array}$$

C'est le fenêtrage qui se fait par défaut lorsque les échantillons sont obtenus par une expérience de durée T.

Considérons sa transformée de Fourier :

$$W_r\left(f\right)={\int }_{-\infty }^{+\infty }{w}_r\left(t\right)exp(-j2\pi ft)dt={\int }_{-\frac{T}{2}}^{\frac{T}{2}}exp(-j2\pi ft)dt\text{(22)}$$

Cette intégrale se calcule aisément, on obtient :

$$W_r\left(f\right)=T\frac{sin\left(\pi fT\right)}{\pi fT}=Tsinc\left(fT\right)\text{(23)}$$

où sinc désigne la fonction sinus cardinal.

Les valeurs de cette TF sont réelles mais certaines sont négatives. Pour obtenir une représentation graphique indépendante de T, nous pouvons tracer $\frac{W_r\left(f\right)}{T}$ en fonction de $fT$ :

import numpy as np
from matplotlib.pyplot import *
figure(figsize=(16,6))
x = np.linspace(-100,100,10000)
Wr = np.sinc(x)
plot(x,Wr)
xlim(-20,20)
grid()
xlabel("fT",fontsize=16)
ylabel(r"$W_r(f)/T$",fontsize=16)
			 

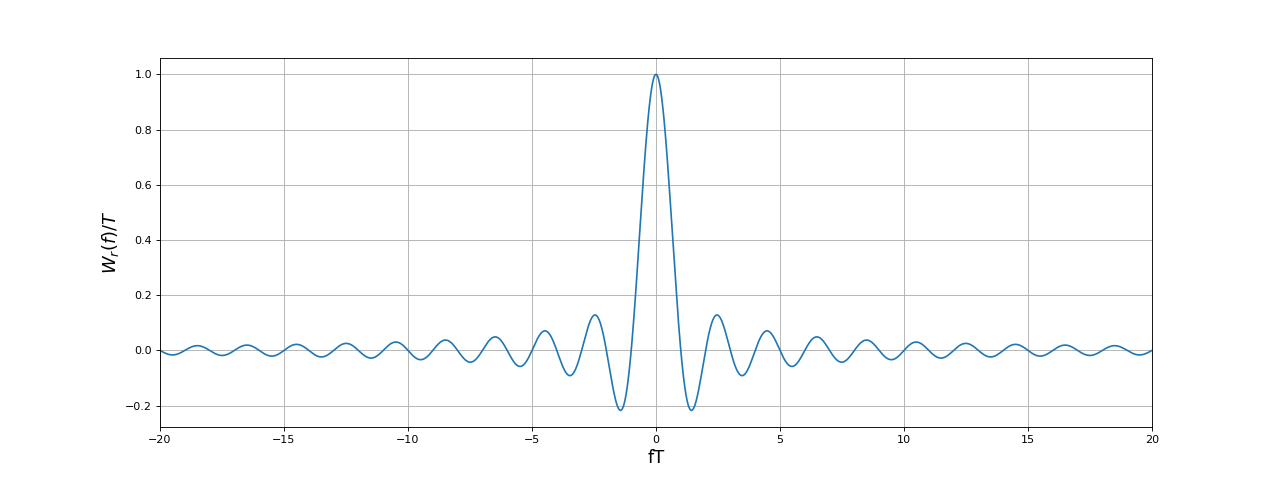fig1.pdf

Le plus souvent, on représente le module de la TF :

import numpy as np
from matplotlib.pyplot import *
figure(figsize=(16,6))
plot(x,np.absolute(Wr))
xlim(-20,20)
grid()
xlabel("fT",fontsize=16)
ylabel(r"$|W_r(f)|/T$",fontsize=16)
			 

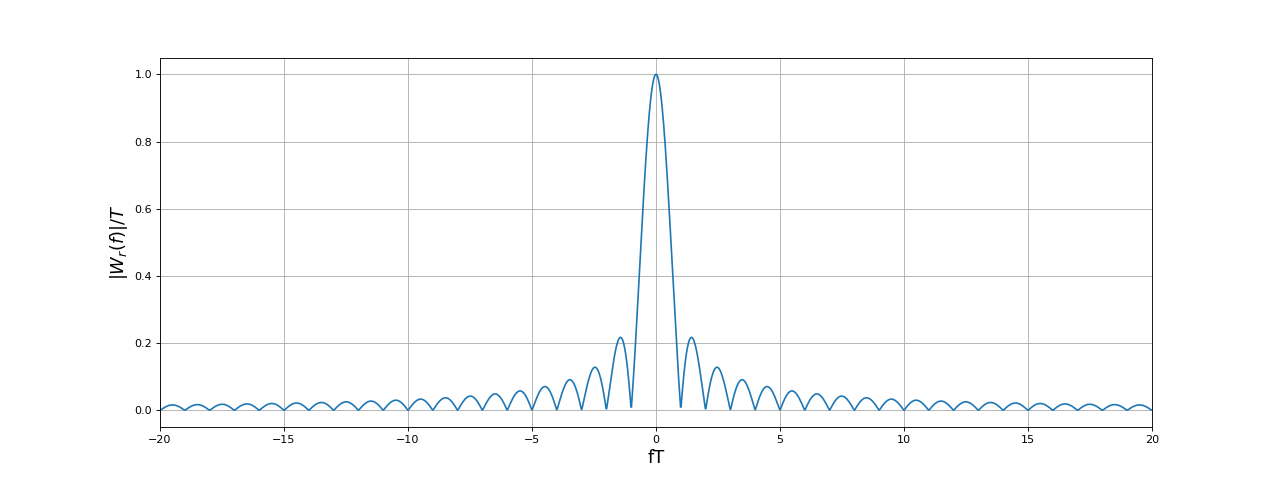fig2.pdf

Comme déjà mentionné, il s'agit d'une fonction paire car le signal (ici la fonction de fenêtrage) est à valeurs réelles.

Le lobe principal de la TF a une largeur :

$$\Delta f=\frac{2}{T}\text{(24)}$$

Ce lobe principal a donc une largeur inversement proportionnelle à la durée de la fenêtre. Pour apprécier la hauteur des lobes secondaires, il est préférable de tracer le spectre en décibel :

import numpy as np
from matplotlib.pyplot import *
figure(figsize=(16,6))
plot(x,20*np.log10(np.absolute(Wr)))
grid()
xlabel("fT",fontsize=16)
ylabel(r"$20\,ln(W_r(f)/T)$",fontsize=16)
xlim(-20,20)
ylim(-50,0)
			 

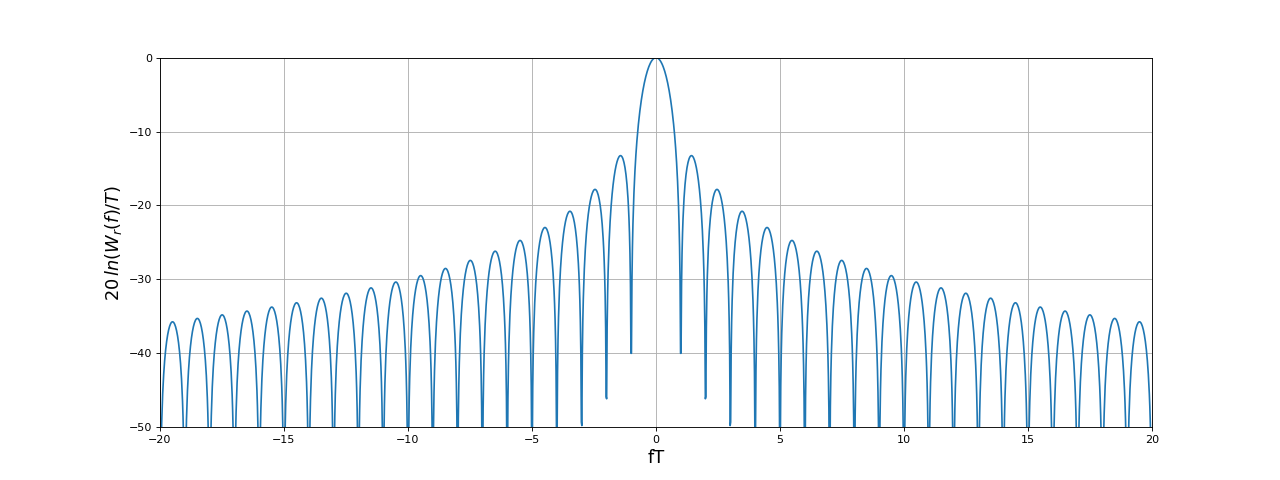fig3.pdf

La fenêtre rectangulaire est caractérisée par des lobes secondaires relativement hauts. Il faut aller jusqu'au troisième lobe pour descendre en dessous de -20 dB par rapport au maximum.

Voyons à présent comment la TFD permet d'obtenir une approximation de la TF de la fenêtre rectangulaire. On doit calculer la TFD d'un signal défini par N échantillons tous égaux à 1 :

from numpy.fft import fft
N = 1000
w = np.ones(N)
tfd = 1/N*fft(w)
			 

Il fait remarquer que la fonction numpy.fft.fft fonctionne pour une taille de tableau quelconque. L'algorithme implémenté par cette fonction consiste à appliquer la FFT tant que la taille du tableau est divisible par 2 puis à terminer par un calcul direct de la TFD. Par exemple, si le tableau contient 100 éléments, on se ramène au calcul de deux TFD à 50 éléments, puis à 4 TFD à 25 éléments. Puisque 25 est impair, le calcul d'une TFD à 25 éléments doit se faire de manière directe, c'est-à-dire par calcul direct des 25 sommes définissant la TFD (chacune comportant 25 termes). Pour que le calcul soit optimisé, il est donc important que N soit une puissance de 2.

Pour représenter graphiquement le spectre, il faut définir les fréquences associées à la TFD : $f_n=\frac{n}{T}$. Comme ci-dessus, nous allons en fait utiliser la fréquence réduite définie par $x_n=f_{n}T=n$.

freq_red = np.arange(N)	 
			 

Pour obtenir l'approximation de $W_r\left(f\right)/T$, on applique la relation $\mathrm{(17)}$ :

tf_approx = np.exp(1j*np.pi*freq_red)*tfd
			 

Il faut remarquer que le facteur $exp\left(j\pi n\right)$ ne change rien au module.

Voici le tracé de l'approximation de la TF obtenue par la TFD (sous forme de points) superposé au tracé de la TF :

import numpy as np
from matplotlib.pyplot import *
figure(figsize=(16,6))
plot(x,np.absolute(Wr))
plot(freq_red,np.absolute(tf_approx),'r.')
grid()
xlabel("fT",fontsize=16)
ylabel(r"$W_r(f)/T$",fontsize=16)
xlim(0,20)
			 

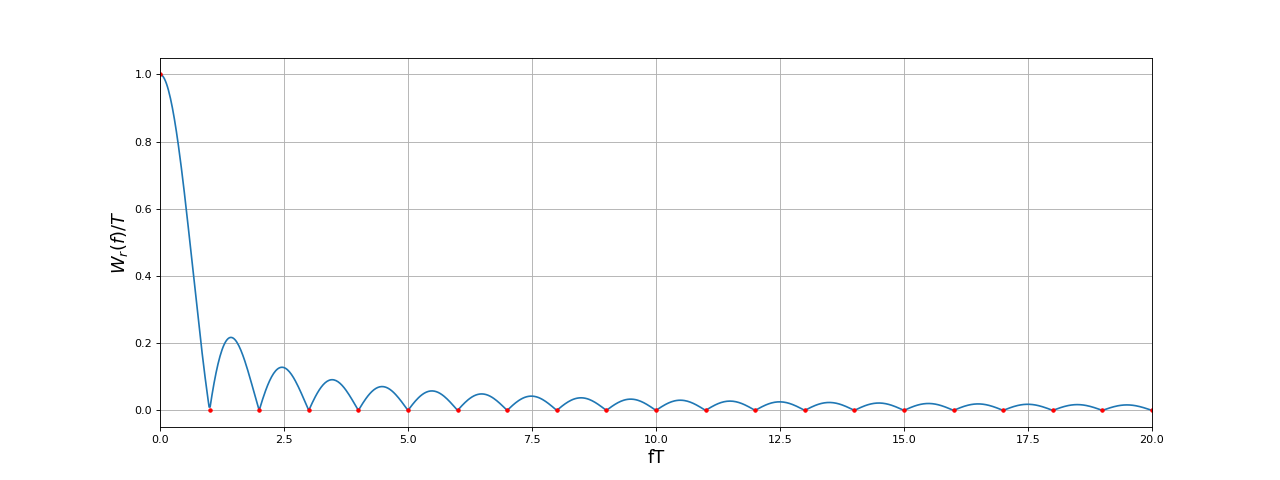fig4.pdf

Comme on le voit, la TFD appliquée aux échantillons limités à la fenêtre elle-même donne une approximation de la TF très grossière car elle ne permet pas de reconstituer la courbe avec ses lobes. Cela n'a rien d'étonnant, puisque le signal échantillonné considéré n'est qu'une partie de la fonction de fenêtrage. Nous avons volontairement commencé par cet exemple car c'est précisément de qu'il se passe lorsqu'on applique la TFD à un signal échantillonné limité à une durée T sans le compléter par des zéros. Pour améliorer le résultat, il faut compléter par des zéros, ce qui revient simplement à définir le signal échantillonné sur une durée beaucoup plus grande que la largeur de la fenêtre (T). Le signal complété par des zéros comporte N' échantillons (de préférence une puissance de 2). Les fréquences de la TFD sont espacées de $\frac{1}{N\text{'}{T}_e}=\frac{N}{N\text{'}T}$ soit un espacement de $\frac{N}{N\text{'}}$ exprimé en fréquence réduite (fréquence mutlipliée par T). Nous ajoutons des zéros à gauche et à droite, de manière garder une fonction paire. Si on s'intéresse seulement au module de la TF, on peut ajouter les zéros à droite seulement.

Np = 2**12
w_p = np.zeros(Np)
i = (N-Np)//2
w_p[i:i+N] = w
tfd_p = 1/N*fft(w_p)
freq_red_p = np.arange(Np)*N/Np
figure(figsize=(16,6))
plot(freq_red_p,np.absolute(tfd_p),'r.')
plot(x,np.absolute(Wr))
xlim(0,20)
xlabel("fT",fontsize=16)
ylabel(r"$W_r(f)/T$",fontsize=16)
grid()
			  

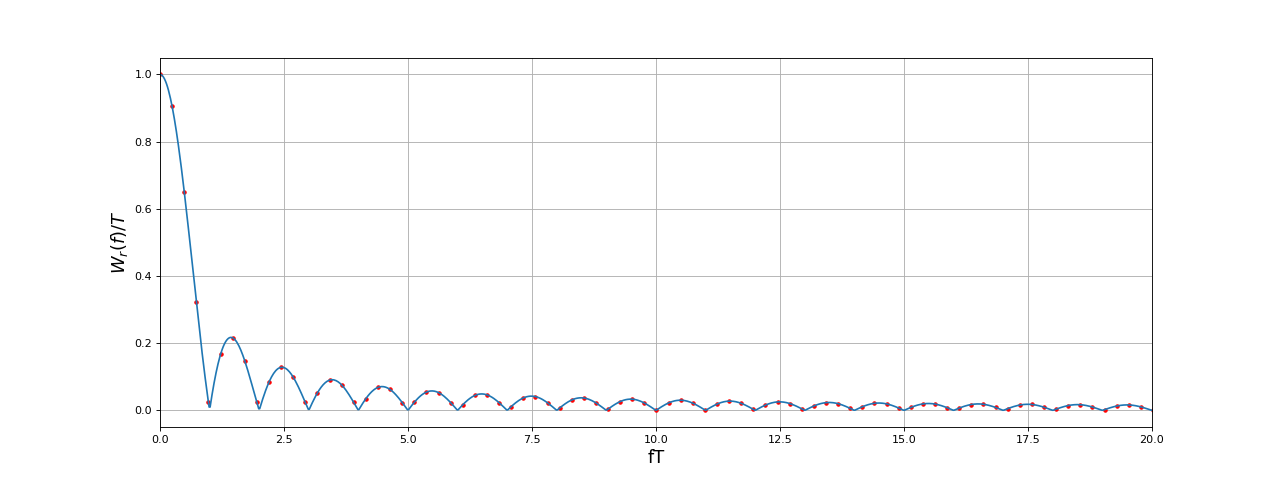fig5.pdf

Voici la totalité de la TFD :

figure(figsize=(20,6))
plot(freq_red_p,np.absolute(tfd_p),'r-')
xlim(0,N)
xlabel("fT",fontsize=16)
ylabel(r"$W_r(f)/T$",fontsize=16)
grid()
			  

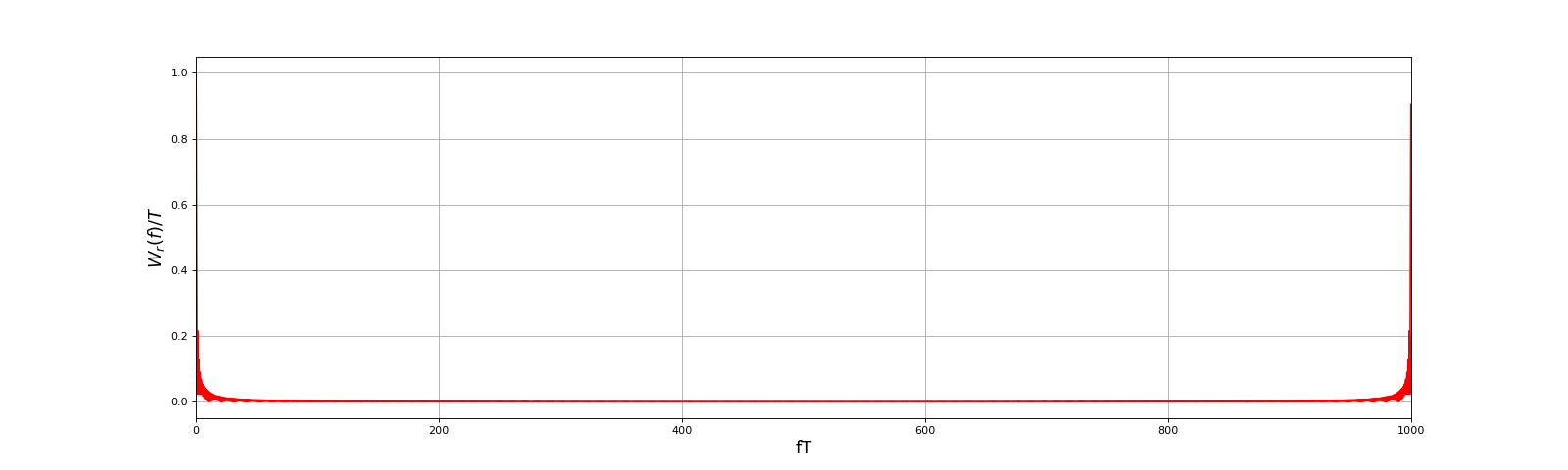fig6.pdf

Le spectre de la TFD s'étend de la fréquence nulle à la fréquence d'échantillonnage, qui s'écrit en fréquence réduite : $x_e=f_{e}T=N$. La première moitié de ce spectre, pour des fréquences de 0 à N/2, correspond à la TF. La seconde moitié, pour des fréquence de N/2 à N correspond, d'après la propriété de périodicité de la TFD, aux fréquence négatives de la TF. Pour un signal à valeurs réelles, la proriété $\mathrm{(3)}$ de la TF (et la propriété équivalente $\mathrm{(20)}$ de la TFD) implique que le spectre est une fonction paire et qu'il n'est donc pas nécessaire de le représenter pour les fréquences négatives.

L'ajout de zéro permet, comme expliqué plus haut, d'obtenir une approximation satisfaisante de la TFTD à partir de la TF, ce qui finalement nous permet d'obtenir une bonne approximation de la TF. Voyons le résultat avec un N' 100 fois plus grand :

Np = 2**14
w_p = np.zeros(Np)
i = (N-Np)//2
w_p[i:i+N] = w
tfd_p = 1/N*fft(w_p)
freq_red_p = np.arange(Np)*N/Np
figure(figsize=(16,6))
plot(freq_red_p,np.absolute(tfd_p),'r.')
plot(x,np.absolute(Wr))
xlim(0,20)
xlabel("fT",fontsize=16)
ylabel(r"$W_r(f)/T$",fontsize=16)
grid()
			  

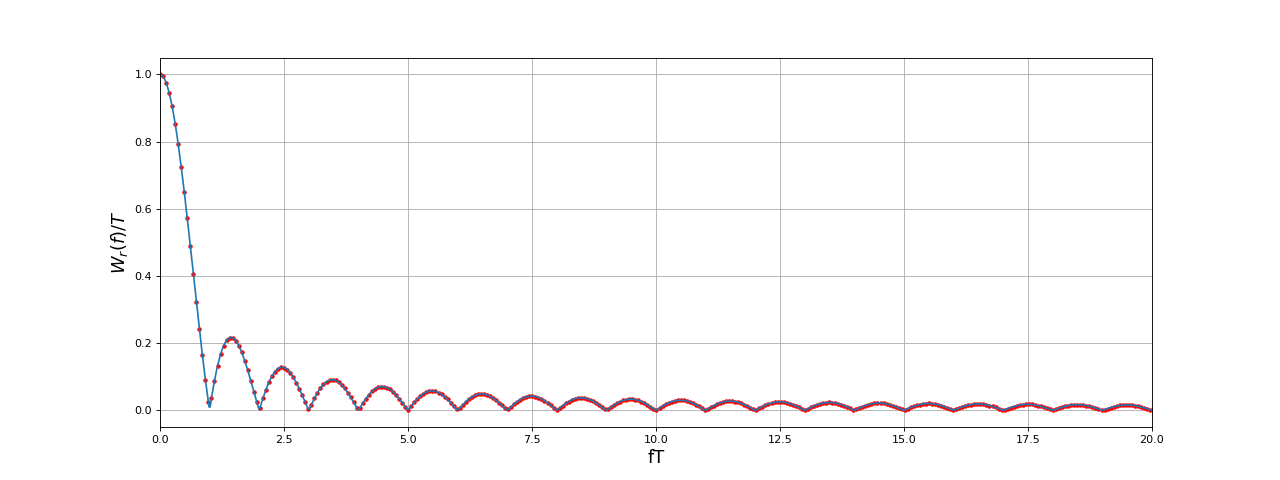fig7.pdf

Comme prévu, plus on ajoute de zéros, c'est-à-dire plus la durée $T\text{'}=N\text{'}{T}_e$ est grande, plus on s'approche de la TFTD et plus on s'approche de la TF (pour les fréquences inférieures à $f_e/2$).

4. Fenêtres de Hamming

La fenêtre de Hamming généralisée est définie par :

$$w_h\left(t\right)=w_r\left(t\right)(\alpha -(1-\alpha )cos(\frac{2\pi }{T}(t+\frac{T}{2})\left)\right)=w_r\left(t\right)(\alpha +(1-\alpha )cos(\frac{2\pi }{T}t\left)\right)\text{(25)}$$

où $w_r\left(t\right)$ est la fenêtre rectangulaire de largeur T étudiée ci-dessus.

En particulier la fenêtre de Hamming est obtenue pour α=0,54 et la fenêtre de Hann pour α=0,5. La fonction scipy.signal.windows.general_hamming renvoie un échantillonnage à N points de cette fenêtre. Voici par exemple la fenêtre de Hamming :

from scipy.signal.windows import general_hamming
N = 1000
alpha = 0.54
w = general_hamming(N,alpha)
t = np.arange(N)/N-0.5

figure(figsize=(8,6))
title('Hamming')
plot(t,w)
grid()
xlabel(r"$\frac{t}{T}$",fontsize=16)
ylabel(r"$w_h$",fontsize=16)
ylim(0,1)
			

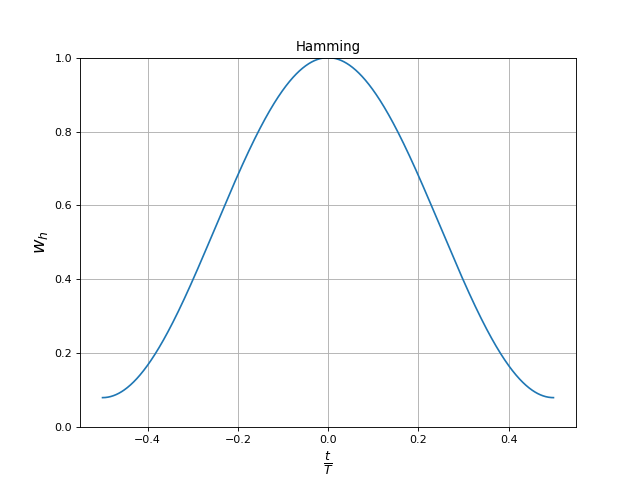fig8.pdf

Pour calculer la transformée de Fourier (TF) de la fenêtre de Hamming généralisée, considérons tout d'abord la TF du cosinus :

$$\begin{array}{cc}\hfill {\int }_{-\frac{T}{2}}^{\frac{T}{2}}cos\left(\frac{2\pi }{T}t\right)exp(-j2\pi ft)dt& ={\int }_{-\frac{T}{2}}^{\frac{T}{2}}\frac{1}{2}\left(exp\right(j\frac{2\pi }{T}t)+exp(-j\frac{2\pi }{T}t\left)\right)exp(-j2\pi ft)dt\hfill \\ \hfill & =\frac{T}{2}(sinc(1-fT)+sinc(1+fT))\hfill \end{array}$$

La TF de la fenêtre de Hamming généralisée s'en déduit :

$$W_h\left(f\right)=\alpha Tsinc\left(fT\right)+(1-\alpha )\frac{T}{2}(sinc(1-fT)+sinc(1+fT))\text{(26)}$$

On trace $\frac{W_h\left(f\right)}{T}$ en fonction de $f{T}^{}$ :

figure(figsize=(16,6))
title('Hamming')
alpha = 0.54
x = np.linspace(-100,100,10000)
Wh = alpha*np.sinc(x)+(1-alpha)/2*(np.sinc(1-x)+np.sinc(1+x))
plot(x,np.absolute(Wh))
xlim(-20,20)
grid()
xlabel("fT",fontsize=16)
ylabel(r"$W_h(f)/T$",fontsize=16)
			 

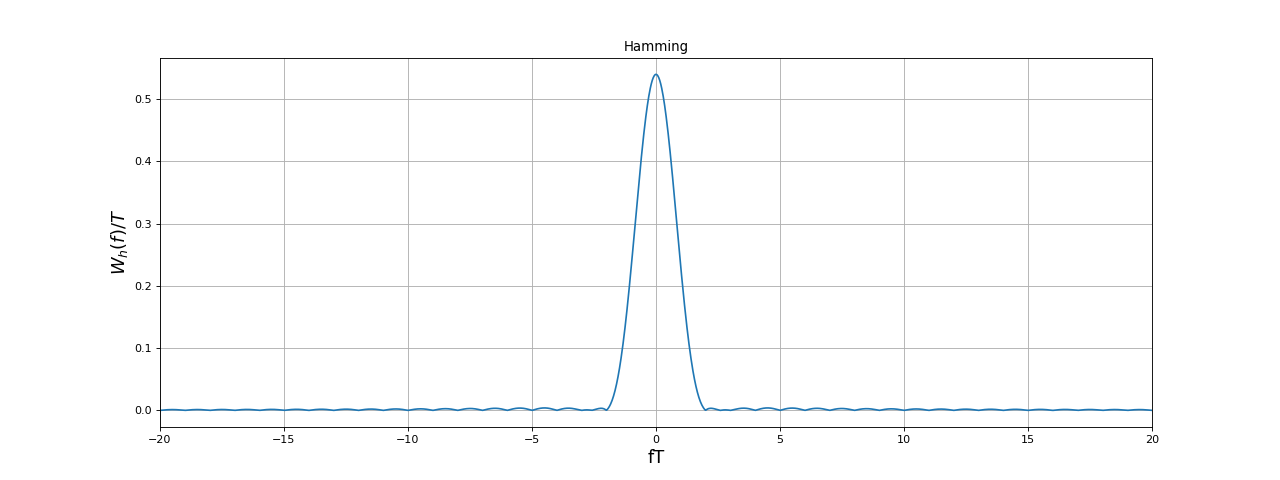fig9.pdf

figure(figsize=(16,6))
title('Hamming')
Wh_max = Wh.max()
plot(x,20*np.log10(np.absolute(Wh/Wh_max)))
xlim(-20,20)
ylim(-100,0)
grid()
xlabel("fT",fontsize=16)
ylabel(r"$W_h(f)/T$",fontsize=16)
ylim(-100,0)
			 

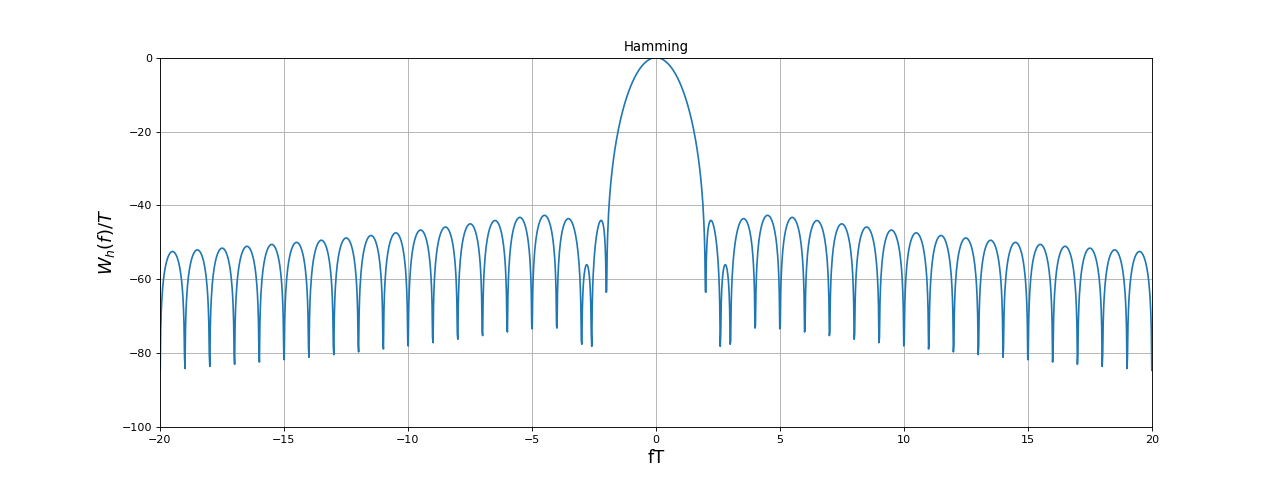fig10.pdf

Le lobe principal de la TF de la fenêtre de Hamming est beaucoup plus large que celui de la fenêtre rectangulaire mais les autres lobes sont beaucoup plus faibles puisqu'ils sont à moins de -40 dB par rapport au maximum.

Pour calculer une approximation de la TF par TFD, on procède comme pour la fenêtre rectangulaire, en ajoutant des zéros :

Np = 2**15
w_p = np.zeros(Np)
i = (N-Np)//2
w_p[i:i+N] = w
tfd_p = 1/N*fft(w_p)
freq_red_p = np.arange(Np)*N/Np
figure(figsize=(16,6))
title('Hamming')
plot(freq_red_p,20*np.log10(np.absolute(tfd_p)),'r.')
plot(x,20*np.log10(np.absolute(Wh)))
xlim(0,20)
ylim(-100,0)
xlabel("fT",fontsize=16)
ylabel(r"$W_h(f)/T$",fontsize=16)
grid()
			  

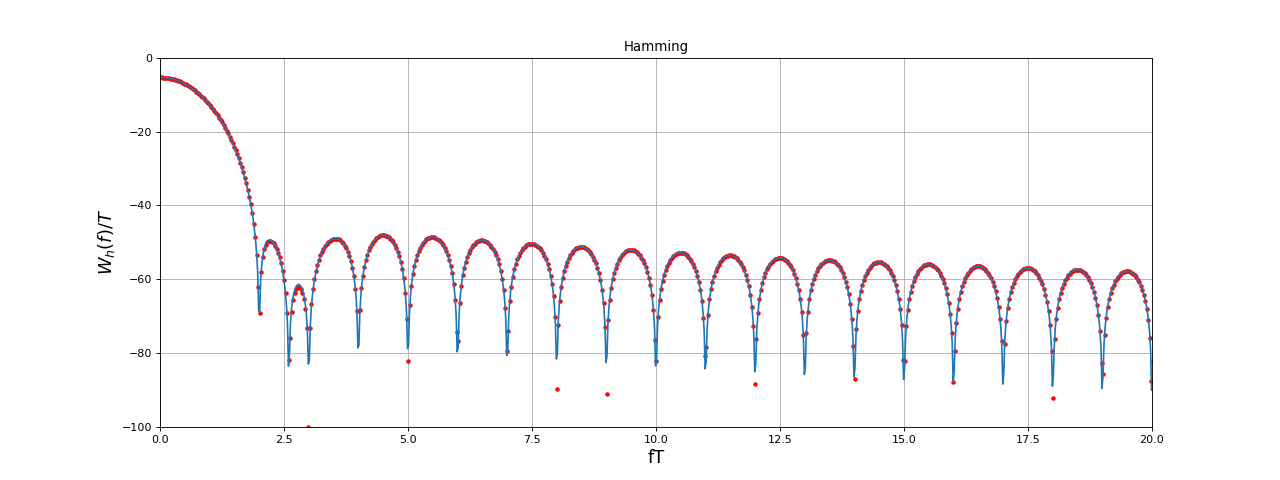fig11.pdf

Voici la fenêtre de Hann (α=0,5) :

from scipy.signal.windows import general_hamming
N = 1000
alpha = 0.5
w = general_hamming(N,alpha)
t = np.arange(N)/N-0.5

figure(figsize=(8,6))
title('Hann')
plot(t,w)
grid()
xlabel(r"$\frac{t}{T}$",fontsize=16)
ylabel(r"$w_h$",fontsize=16)
ylim(0,1)
			

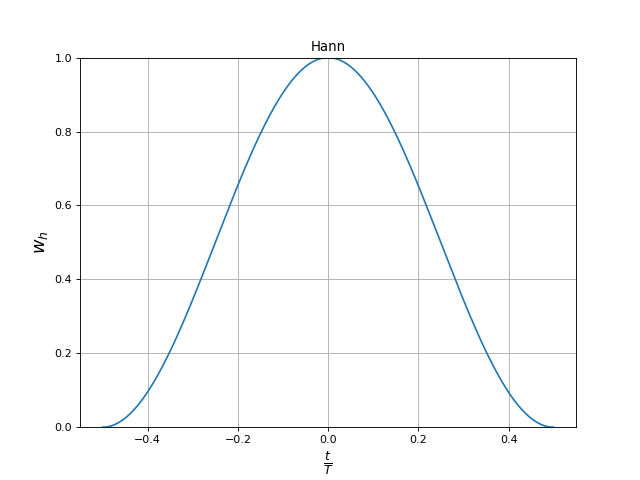fig12.pdf

et sa transformée de Fourier :

figure(figsize=(16,6))
title('Hann')
x = np.linspace(-100,100,10000)
Whh = alpha*np.sinc(x)+(1-alpha)/2*(np.sinc(1-x)+np.sinc(1+x))
plot(x,np.absolute(Whh))
xlim(-20,20)
grid()
xlabel("fT",fontsize=16)
ylabel(r"$W_h(f)/T$",fontsize=16)
			 

fig13.pdf

figure(figsize=(16,6))
title('Hann')
Whh_max = Whh.max()
plot(x,20*np.log10(np.absolute(Whh/Whh_max)))
xlim(-20,20)
ylim(-100,0)
grid()
xlabel("fT",fontsize=16)
ylabel(r"$W_{hh}(f)/T$",fontsize=16)
ylim(-100,0)
			 

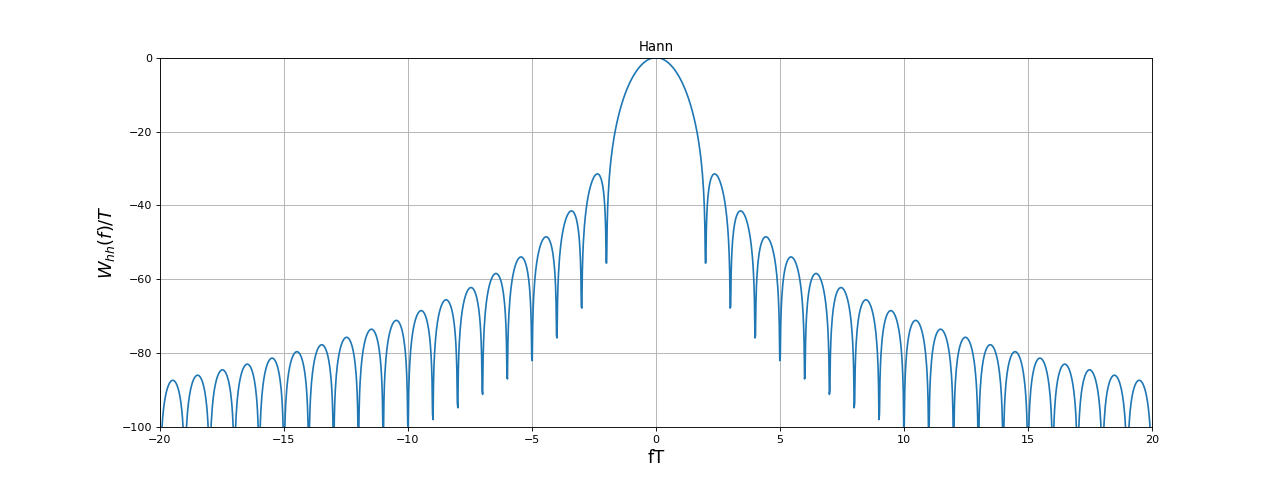fig14.pdf

Il est intéressant de comparer les fenêtres rectangulaire, Hamming et Hann :

figure(figsize=(16,6))
plot(x,20*np.log10(np.absolute(Wr)),label='Rectangulaire')
plot(x,20*np.log10(np.absolute(Wh/Wh_max)),label='Hamming')
plot(x,20*np.log10(np.absolute(Whh/Whh_max)),label='Hann')
xlim(-20,20)
ylim(-100,0)
grid()
xlabel("fT",fontsize=16)
ylabel(r"$W_{hh}(f)/T$",fontsize=16)
ylim(-100,0)
legend(loc='upper right')
			 

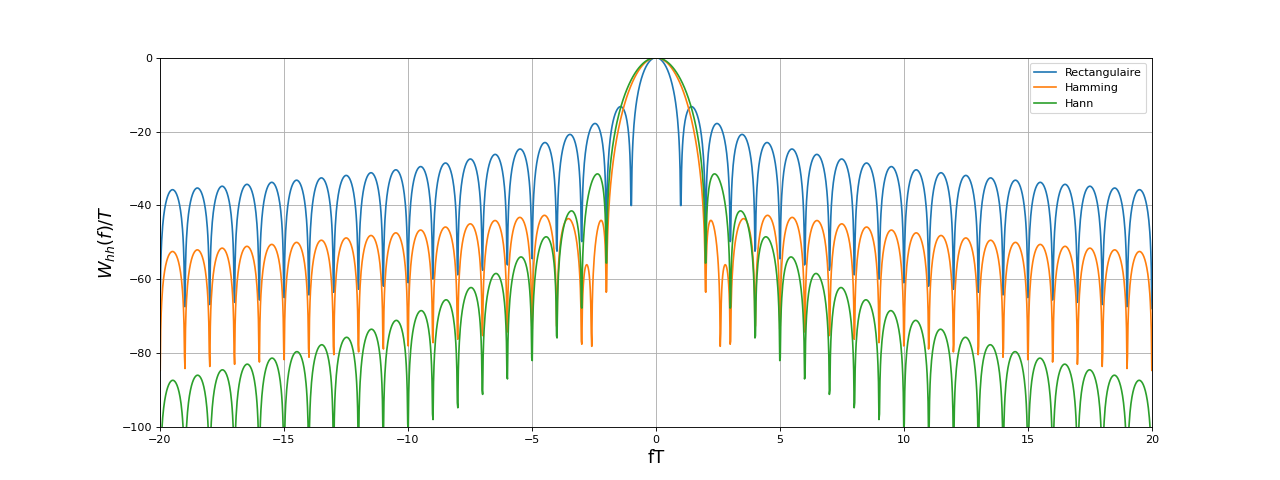fig15.pdf

La fenêtre rectangulaire a le lobe principal le moins large mais ses lobes secondaires sont très intenses. La fenêtre rectangulaire est très bien pour l'analyse spectrale des signaux périodiques, pour lesquels les fréquences des harmoniques sont très distantes. En revanche, elle peut poser problème quand le spectre contient deux raies très voisines, en particulier une raie faible au voisinage d'une raie intense. La fenêtre de Hamming a un lobe principal deux fois plus grand mais ses lobes secondaires sont beaucoup plus faibles car ils sont tous en dessous de -40 dB. La fenêtre de Hann présente la plus forte décroissance de la hauteur des lobes secondaires mais son premier lobe secondaire est plus haut que celui de la fenêtre de Hamming.

Par ailleurs, la hauteur du maximum (lobe principal) est différente pour les trois fenêtres. Cette hauteur doit être prise en compte pour l'estimation de la hauteur des raies dans l'analyse spectrale.

print(Wr.max())
--> 0.9998354818101798

print(Wh.max())
--> 0.5399571664110703

print(Whh.max())
--> 0.499967747680713

Les hauteurs exactes sont respectivement pour les fenêtres rectangulaire, Hamming et Hann : 1, 0,54 et 0,50.

5. Fenêtre de Blackman

La fenêtre de Blackman est définie par :

$$w_b\left(t\right)=w_r\left(t\right)({\alpha }_1+{\alpha }_{2}cos(\frac{2\pi }{T}(t+\frac{T}{2}))+{\alpha }_{3}cos(\frac{4\pi }{T}(t+\frac{T}{2})\left)\right)\text{(27)}$$

avec :

$$\begin{array}{cc}\hfill & {\alpha }_1=0,42\hfill \\ \hfill & {\alpha }_2=-0,5\hfill \\ \hfill & {\alpha }_3=0,08\hfill \end{array}$$

La fenêtre peut aussi s'écrire :

$$w_b\left(t\right)=w_r\left(t\right)({\alpha }_1-{\alpha }_{2}cos(\frac{2\pi }{T}t)+{\alpha }_{3}cos(\frac{4\pi }{T}t\left)\right)\text{(28)}$$

Sa transformée de Fourier est :

$$W_b\left(f\right)={\alpha }_{1}Tsinc\left(fT\right)-\frac{1}{2}T{\alpha }_2(sinc(1-fT)+sinc(1+fT))+\frac{1}{2}T{\alpha }_3(sinc\left((2-fT)\right)+sinc\left((2+fT)\right))\text{(29)}$$

from scipy.signal.windows import blackman
N = 1000
w = blackman(N)
t = np.arange(N)/N-0.5
figure(figsize=(8,6))
title('Blackman')
plot(t,w)
grid()
xlabel(r"$\frac{t}{T}$",fontsize=16)
ylabel(r"$w_h$",fontsize=16)
ylim(0,1)
			

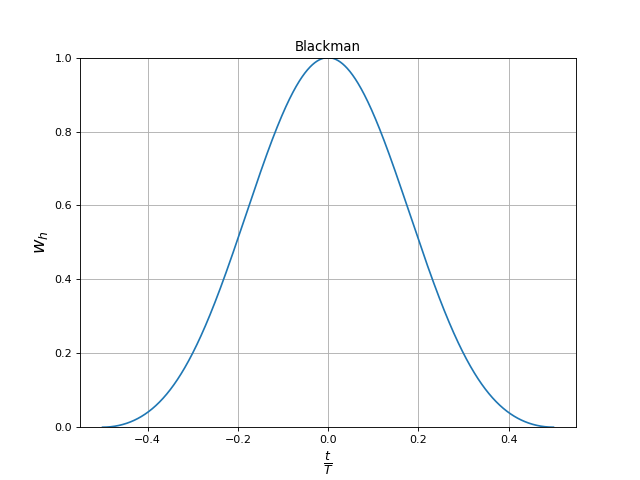fig16.pdf

figure(figsize=(16,6))
title('Blackman')
alpha1 = 0.42
alpha2 = -0.5
alpha3 = 0.08
x = np.linspace(-100,100,10000)
Wb = alpha1*np.sinc(x)-alpha2/2*(np.sinc(1-x)+np.sinc(1+x))+alpha3/2*(np.sinc((2-x))+np.sinc((2+x)))
plot(x,np.absolute(Wb))
xlim(-20,20)
grid()
xlabel("fT",fontsize=16)
ylabel(r"$W_h(f)/T$",fontsize=16)
			 

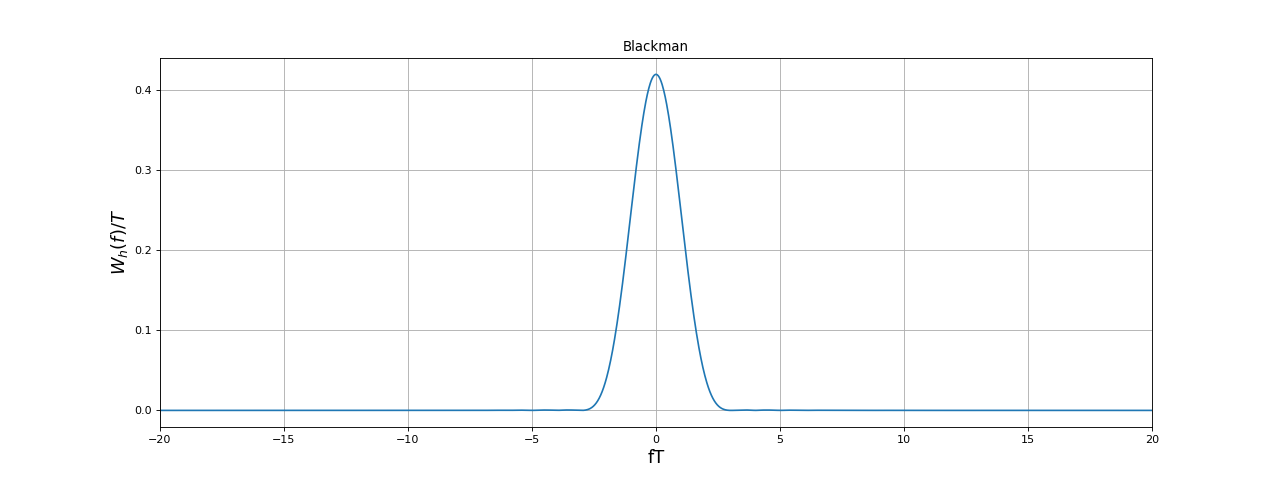fig17.pdf

figure(figsize=(16,6))
title('Blackman')
Wb_max = Wb.max()
plot(x,20*np.log10(np.absolute(Wb/Wb_max)))
xlim(-20,20)
ylim(-100,0)
grid()
xlabel("fT",fontsize=16)
ylabel(r"$W_{hh}(f)/T$",fontsize=16)
ylim(-100,0)
			 

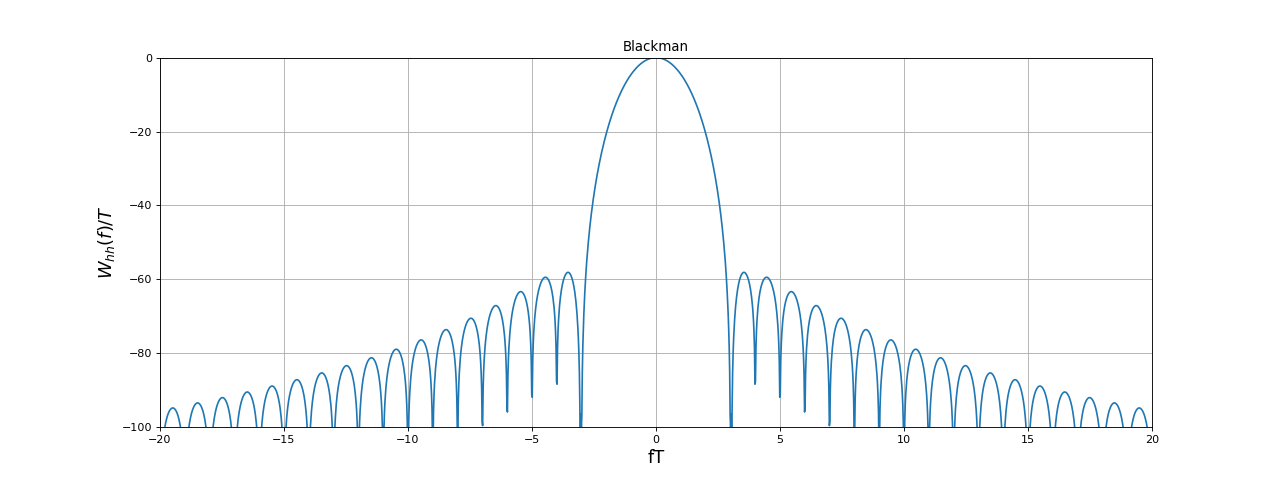fig18.pdf

Voici le calcul de sa TF par TFD :

Np = 2**15
w_p = np.zeros(Np)
i = (N-Np)//2
w_p[i:i+N] = w
tfd_p = 1/N*fft(w_p)
freq_red_p = np.arange(Np)*N/Np
figure(figsize=(16,6))
title('Blackman')
plot(freq_red_p,20*np.log10(np.absolute(tfd_p)),'r.')
plot(x,20*np.log10(np.absolute(Wb)))
xlim(0,20)
ylim(-120,0)
xlabel("fT",fontsize=16)
ylabel(r"$W_b(f)/T$",fontsize=16)
grid()
			  

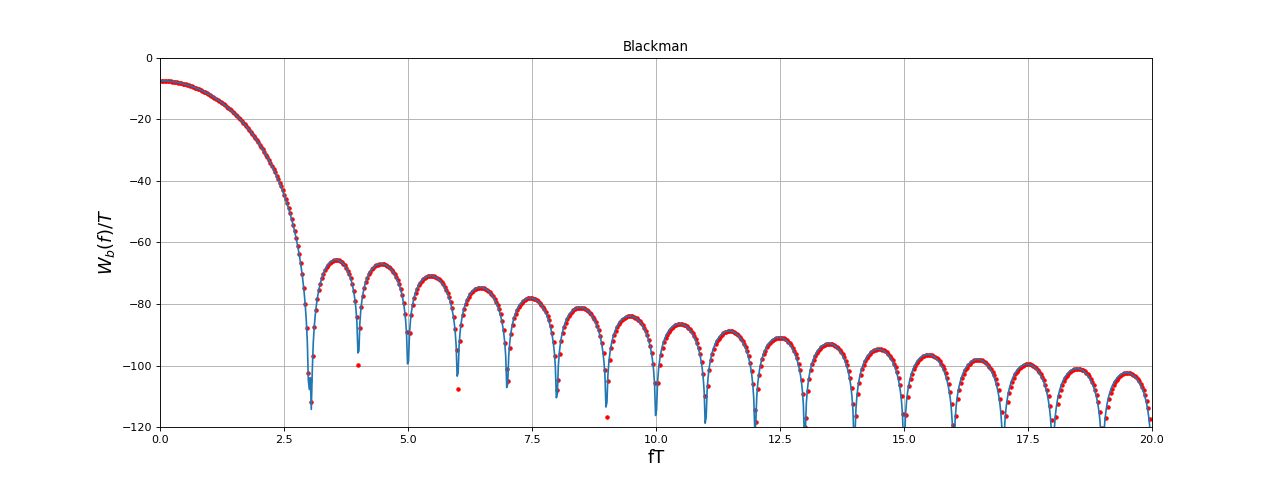fig19.pdf

Voici une comparaison des quatre fenêtres :

figure(figsize=(16,6))
plot(x,20*np.log10(np.absolute(Wr)),label='Rectangulaire')
plot(x,20*np.log10(np.absolute(Wh/Wh_max)),label='Hamming')
plot(x,20*np.log10(np.absolute(Whh/Whh_max)),label='Hann')
plot(x,20*np.log10(np.absolute(Wb/Wb_max)),label='Blackman')
xlim(-20,20)
ylim(-100,0)
grid()
xlabel("fT",fontsize=16)
ylabel(r"$W_{hh}(f)/T$",fontsize=16)
ylim(-100,0)
legend(loc='upper right')
			 

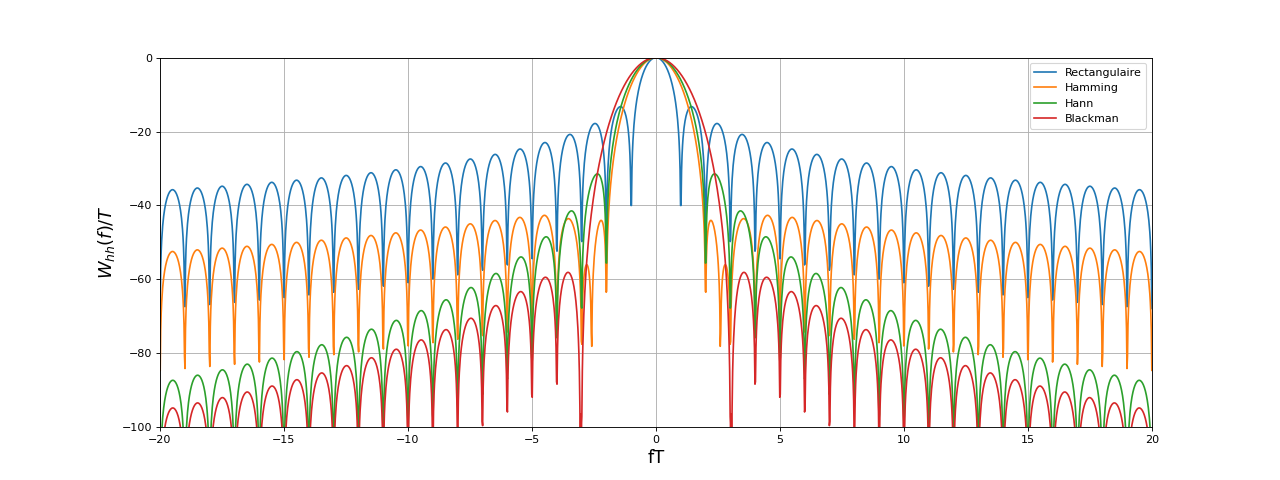fig20.pdf

et le maximum de la TF de la fenêtre de Blackman :

print(Wb.max())
--> 0.41997890901492774

La fenêtre de Blackman a des lobes secondaires très faibles mais son lobe principal est très large. Le maximum est le coefficient ${\alpha }_1$ : sa valeur exacte est donc 0,42.