Thermodynamique statistique

1.a. Micro et macro-états

Un système thermodynamique est un système comportant un nombre de constituants élémentaires très grand, en pratique de l'ordre du nombre d'Avogadro.

Nous allons raisonner sur un exemple particulier : un gaz parfait monoatomique, que l'on modélisera par N atomes ponctuels, occupant un volume V fermé et formant un système isolé d'énergie E. On suppose que ces atomes obéissent aux lois de Newton de la mécanique (gaz parfait classique). Chaque atome a donc une trajectoire : on peut à tout instant définir sa position dans l'espace et sa vitesse. Pour un gaz parfait, l'énergie est la somme des énergies cinétiques des atomes :

$$E=\sum _{i=1}^N\frac{1}{2}m{\overrightarrow{v}}_i^2=\sum _{i=1}^N\frac{{\overrightarrow{p}}_i^2}{2m}\text{(1)}$$

L'état d'un atome à un instant donné est entièrement défini par sa position (x,y,z) et sa quantité de mouvement (p_x,p_y,p_z). Il peut être représenté par un point dans un espace à 6 dimensions, appelé espace des phases. En mécanique classique, toute position ou toute vitesse est a priori possible. Néanmoins, il peut être utile de diviser l'espace des phases en petits volumes. La figure suivante montre le principe d'une telle subdivision pour une particule se déplaçant sur un seul axe :

Figure pleine page

Pour la particule représentée par le point, on attribue un état discret correspondant à la case occupée. La discrétisation de l'espace des phases est un moyen de faire des calculs statistiques, mais il correspond aussi à une réalité physique dans le cadre de la mécanique quantique.

On procède de la même manière pour l'espace à 6 dimensions représentant l'état d'une particule. La distance Δx définissant l'intervalle de position doit être d'échelle mésoscopique. Un volume mésoscopique est petit à l'échelle macroscopique, mais comporte tout de même un très grand nombre d'atomes. Pour un gaz à pression atmosphérique, un cube de 1 μm de côté est un volume mésoscopique. L'échelle mésoscopique est donc la plus petite échelle qui permette de définir des grandeurs thermodynamiques, comme la densité ou la température.

On appelle micro-état l'état du système à un instant donné. Dans le cas présent, un micro-état est défini par les 6N variables que sont les positions et les vitesses des particules. Un microétat est donc représenté par un point dans un espace des phases à 6N dimensions. Cet espace peut être aussi discrétisé, c'est-à-dire divisé en cellules élémentaires à 6N dimensions. Dans ce cas, le micro-état est défini par la cellule occupée.

On appelle macro-état (ou état thermodynamique), l'état du gaz tel qu'il est observé à l'échelle macroscopique. Dans le cas présent, si le gaz est à l'équilibre, le macro-état est simplement défini par l'énergie E et le volume V.

D'une manière générale, un macro-état est défini par un petit nombre de variables, alors qu'un micro-état est défini par un nombre de variables extrêmement grand. L'objectif de la thermodynamique statistique est d'expliquer les observations macroscopiques à partir des micro-états.

Pour revenir au modèle du gaz parfait, on remarque que l'énergie d'interaction entre les atomes est négligée. Cela ne signifie par qu'il n'y a pas d'interactions entre les atomes. Il y a bien des interactions, sous forme de collisions, qui permettent au gaz d'atteindre un état d'équilibre thermodynamique, mais elles ont une contribution négligeable à l'énergie totale. C'est toujours en ce sens qu'on entend l'hypothèse de particules indépendantes.

1.b. Approche probabiliste

Pour un macro-état donné, le système passe sans arrêt d'un micro-état à un autre à cause du mouvement des atomes. Pour un gaz à température ambiante, le nombre de micro-états parcourus pendant une seconde est même extrêmement grand (on peut en principe les dénombrer grace à la discrétisation). La thermodynamique statistique repose sur une première hypothèse, appelée hypothèse ergodique :

Dans le cas présent, il s'agit de tous les microétats pour lesquels les atomes sont dans le volume V et ont l'énergie E.

Dans la réalité, un gaz est effectivement ergodique, même si le temps de parcours dépend beaucoup du volume.

Une fois cette hypothèse faite, on adopte une approche probabiliste, qui a été inventée par Boltzmann (physicien autrichien 1844-1906), et développée par Gibbs (physicien américain 1839-1903). Cette approche consiste à considérer les micro-états du système de manière probabiliste, sans se préoccuper de la dynamique, c'est-à-dire de la manière dont le système passe d'un micro-état à un autre. L'hypothèse fondamentale est la suivante :

Dans notre exemple, cela signifie que le système a la même probabilité de se trouver dans toutes les cellules de l'espace des phases. On définit alors Ω(N,V,E) le nombre de micro-états qui obéissent aux contraintes imposées au système (volume et énergie fixés). Il s'agit bien évidemment d'un nombre extrêmement grand. Boltzmann a défini l'entropie statistique par :

$$S=kln\left(\Omega \right)\text{(2)}$$

Pour un système isolé en évolution, l'accroissement de l'entropie (second principe de la thermodynamique) correspond à une augmentation du nombre de micro-états accessibles, ce que l'on désigne souvent par augmentation du désordre moléculaire. Dans ce cours d'introduction, nous n'allons pas utiliser directement l'entropie. Nous la mentionnons ici en raison de sa grande importance. C'est l'entropie qui permet de relier l'approche probabiliste aux grandeurs thermodynamiques classiques.

2.a. Atmosphère isotherme

Dans le gaz parfait considéré ci-dessus, il est possible de définir une densité locale n (nombre d'atomes par unité de volume), en se plaçant à l'échelle mésocopique. Lorsque le gaz n'est soumis à aucune force extérieure, cette densité est uniforme, égale à :

$$n=\frac{N}{V}\text{(3)}$$

Pour voir comment la densité est modifiée en présence d'un champ de force, considérons le cas du champ de pesanteur (uniforme). Le modèle utilisé est celui de l'atmosphère isotherme (l'atmosphère réelle n'est pas du tout isotherme). En raison de la pesanteur, la pression du gaz (parfait) dépend de l'altitude z. Considérons une couche de gaz mésoscopique comprise entre les altitudes z et z+dz, d'aire A. La figure suivante représente les trois forces qui agissent sur cette portion de gaz (ρ est la masse volumique).

Figure pleine page

L'équilibre mécanique s'écrit :

$$P\left(z\right)-P(z+dz)=\rho gdz\text{(4)}$$

On introduit la densité locale n et la masse m d'une molécule :

$$\rho =mn\text{(5)}$$

ce qui conduit à l'équation différentielle :

$$dP=-mngdz\text{(6)}$$

L'équation d'état du gaz parfait s'écrit :

$$P=n\frac{R}{N_a}T=nkT\text{(7)}$$

où $k=1,38\cdot 10^{-23}J\cdot K^{-1}$ est la constante de Boltzmann. On a donc l'équation différentielle pour la densité :

$$\frac{dn}{n}=-\frac{mgdz}{kT}\text{(8)}$$

Si le gaz est à l'équilibre thermique (atmosphère isotherme), l'intégration de cette équation donne :

$$n\left(z\right)=n\left(0\right)e^{-\frac{mgz}{kT}}\text{(9)}$$

L'argument de l'exponentielle est l'opposé du rapport de l'énergie potentielle d'un atome sur l'énergie thermique kT.

2.b. Probabilité d'un l'état d'une particule

En l'absence de champ de force, un atome du gaz parfait a la même probabilité de se trouver dans tous les points du volume (dans toutes les cases de l'espace discrétisé). Il n'en est plus de même en présence d'un champ de force extérieur. La densité obtenue dans le modèle de l'atmosphère isotherme nous suggère de définir la densité de probabilité par :

$$f\left(z\right)=C{e}^{-\frac{mgz}{kT}}\text{(10)}$$

La probabilité pour un atome d'être entre z et z+dz est f(z)dz.

Le facteur exponentiel de cette expression est le facteur de Boltzmann. Il est caractéristique des systèmes en équilibre thermique à la température T.

La constante C est déterminée en écrivant la normalisation de la probabilité : la somme de toutes les probabilités doit être égale à 1. Pour une densité de probabilité, on écrit :

$${\int }_0^{H}f\left(z\right)dz=1\text{(11)}$$

où H est la hauteur du volume V.

Cette relation se généralise à une particule dans un système dont la température est T. On suppose que les états de la particule sont dénombrables. Pour l'atome du gaz parfait, on y parvient en utilisant la discrétisation de l'espace des phases. On peut alors exprimer la probabilité pour qu'une particule soit dans un état donné. On désigne par la lettre α un état donné de la particule, par exemple une cellule de l'espace des phases à 6 dimensions. La loi de distribution de Boltzmann est la suivante :

La constante C se détermine en écrivant que la somme des probabilités sur tous les états de la particule est égale à 1 :

$$\sum _{\alpha }{p}_{\alpha }=1\text{(13)}$$

Cette loi de probabilité est appelée distribution de Boltzmann. Si N est le nombre de particules du système, le nombre moyen de particules dans un état donné est :

$$n_{\alpha }=N{p}_{\alpha }\text{(14)}$$

Pour une justification de cette distribution, voir Distribution de Boltzmann (complément hors programme). Voir aussi Simulation de Monte-Carlo d'un système à énergie constante.

Il faut bien faire attention à comprendre cette expression comme la probabilité pour la particule d'être dans un état donné, et non pas d'avoir une énergie donnée. En effet, il arrive fréquemment que plusieurs états aient la même énergie. C'est le cas dans le modèle de gaz parfait considéré plus haut. Par exemple, pour une particule se déplaçant dans un espace à une dimension sans force extérieure, tous les états de même quantité de mouvement ont la même énergie.

Figure pleine page

Un niveau d'énergie auquel correspondent plusieurs états est appelé niveau d'énergie dégénéré. Dans cet exemple, le nombre d'états pour chaque niveau d'énergie est indépendant de ce niveau, donc la distribution des niveaux d'énergie vérifie aussi la distribution de Boltzmann (seule la constante C change). Ce n'est plus le cas si l'on considère les états représentés sur la figure suivante :

Figure pleine page

À énergie constante, un niveau d'énergie dégénéré a une probabilité plus forte qu'un niveau non dégénéré.

Pour reprendre l'exemple de la particule dans l'espace à une dimension, on remarque que l'introduction d'une énergie potentielle de la forme -mgx modifie l'énergie des états en fonction de leur position x. Ce phénomène est appelé levée de dégénérescence.

La probabilité de la distribution de Boltzmann décroît exponentiellement avec l'énergie. Cela signifie que les états de plus faible énergie sont les plus probables. Plus la température est élevée, moins la décroissance est rapide.

Comparons les probabilités de deux états :

$$\frac{p_{\alpha }}{p_{\beta }}=e^{-\frac{E_{\alpha }-E_{\beta }}{kT}}=e^{-\frac{\epsilon }{kT}}\text{(15)}$$

L'état d'énergie le plus faible est toujours le plus probable, mais l'écart se réduit si l'on augmente la température. Plus précisément, si kT<ε, l'état de plus faible énergie est beaucoup plus probable. Si $kT\gg \epsilon$, les deux états ont des probabilités très voisines.

2.c. Système en équilibre avec un thermostat

La distribution de Boltzmann se généralise à un système quelconque en équilibre thermique avec un thermostat (ou source de chaleur) de température T. Ce type de système n'est pas isolé, puisqu'il échange de l'énergie avec le thermostat. A priori, son énergie totale E n'est donc pas constante. Désignons par la lettre μ un micro-état de ce système. La probabilité de ce micro-état s'écrit :

$$p_{\mu }=C{e}^{-\frac{E_{\alpha }}{kT}}\text{(16)}$$

où E_μ est l'énergie du système pour ce micro-état. La constante est déterminée en écrivant la somme sur tous les micro-états :

$$\sum _{\mu }{p}_{\mu }=1\text{(17)}$$

La particule considérée précédemment n'est qu'un cas particulier, car la particule est en équilibre thermique avec le reste du système qui constitue un thermostat (s'il est assez grand).

La précaution signalée plus haut sur les niveaux d'énergies dégénérés est très importante dans le cas général, car les niveaux d'énergie d'un système comportant plusieurs particules sont toujours dégénérés, et le nombre d'états dépend fortement du niveau d'énergie. Pour un système à N particules, il augmente en gros comme E^N. Lorsque N est grand, l'augmentation avec l'énergie du nombre d'état correspondant est donc très rapide. La probabilité pour que le système ait une énergie E est :

$$p\left(E\right)=C\Omega \left(E\right)e^{-\frac{E}{kT}}\text{(18)}$$

où Ω(E) est le nombre de micro-états ayant l'énergie E.

2.d. Calculs statistiques

Soit une grandeur physique X_μ qui dépend du micro-état. La distribution de Boltzmann permet de calculer la valeur moyenne de cette grandeur (c'est-à-dire son espérance) :

$$\overline{X}=\frac{\sum _{\mu }{X}_{\mu }{e}^{-\frac{E_{\mu }}{kT}}}{\sum _{\mu }{e}^{-\frac{E_{\mu }}{kT}}}\text{(19)}$$

Par exemple, la valeur moyenne de l'énergie du système est :

$$\overline{E}=\frac{\sum _{\mu }{E}_{\mu }{e}^{-\frac{E_{\mu }}{kT}}}{\sum _{\mu }{e}^{-\frac{E_{\mu }}{kT}}}\text{(20)}$$

Un autre grandeur importante est la variance, qui indique la dispersion des valeurs autour de la valeur moyenne. La variance est la moyenne du carré de l'écart entre X et sa valeur moyenne :

$$var\left(X\right)=\overline{{(X-\overline{X})}^2}\text{(21)}$$

L'expression de la variance se développe :

$$var\left(X\right)=\overline{X^2}+{\overline{X}}^2-2\overline{X}\overline{X}=\overline{X^2}-{\overline{X}}^2\text{(22)}$$

Comme la valeur moyenne est en général déjà connue, on calcule la variance à l'aide de la valeur moyenne du carré de X.

On appelle écart quadratique moyen (ou écart-type), la racine carrée de la variance :

$$\Delta X=\sqrt{var\left(X\right)}\text{(23)}$$

L'écart-type peut être comparé directement à la valeur moyenne, et donne une information sur la dispersion des valeurs autour de la moyenne. Si le rapport

$$\frac{\Delta E}{\overline{E}}\text{(24)}$$

est faible alors l'énergie du système reste très probablement très proche de sa valeur moyenne. On verra plus loin que c'est le cas lorsque le nombre de particules est grand. Pour une particule individuelle, l'écart-type est du même ordre que la moyenne, ce qui indique une très forte dispersion.

Les calculs statistiques sont facilités en posant :

$$\begin{array}{ccc}\hfill & \beta =\frac{1}{kT}\hfill & \hfill \text{(25)}\\ \hfill & Z=\sum _{\mu }{e}^{-\beta E_{\mu }}\hfill & \hfill \text{(26)}\end{array}$$

Z est la fonction de partition du système. Si l'on dispose d'une expression de Z, on peut faire tous les calculs statistiques. Par exemple :

$$\overline{E}=-{\left(\frac{\partial lnZ}{\partial \beta }\right)}_{N,V}\text{(27)}$$

En dérivant deux fois la fonction de partition par rapport à β, on obtient la variance de l'énergie :

$${\left(\frac{{\partial }^{2}lnZ}{\partial {\beta }^2}\right)}_{N,V}=\overline{E^2}-{\overline{E}}^2={\left(\Delta E\right)}^2\text{(28)}$$

On a donc :

$${\left(\Delta E\right)}^2=-{\left(\frac{\partial \overline{E}}{\partial \beta }\right)}_{N,V}\text{(29)}$$

Cette expression peut s'écrire en introduisant la capacité thermique à volume constante :

$$\overline{E}=C_{v}T=\frac{C_v}{k\beta }\text{(30)}$$

Le calcul conduit à

$${\left(\Delta E\right)}^2=k{T}^2{C}_v\text{(31)}$$

Ainsi la variance est proportionnelle à la capacité thermique à volume constant. Le rapport entre l'écart-type et la valeur moyenne est alors :

$$\frac{\Delta E}{\overline{E}}=\frac{\sqrt{k{T}^2{C}_v}}{\overline{E}}\text{(32)}$$

L'énergie moyenne et la capacité thermique sont deux grandeurs extensives proportionnelles à N. On en déduit la loi d'échelle :

$$\frac{\Delta E}{\overline{E}}=\sqrt{\frac{k}{C_v}}\simeq O\left(\frac{1}{\sqrt{N}}\right)\text{(33)}$$

L'écart-type relatif est donc d'autant plus faible que le système est grand. Pour un système thermodynamique macroscopique, cet écart relatif est extrêmement faible, ce qui signifie que l'énergie du système reste très probablement très proche de son énergie moyenne. Ainsi un système thermodynamique en équilibre avec un thermostat est similaire à un système isolé d'énergie constante (tant qu'il reste à l'équilibre).

3.a. Définition

On considère un système formé de N particules indépendantes et discernables. Pour chaque particule, il y a M états possibles, numérotés de 0 à M-1. À chaque état m est associée une énergie ε_m. Pour simplifier, on suppose que ces niveaux d'énergie sont régulièrement espacés, et on note ε le quantum d'énergie.

Un exemple physique de système de ce type est un cristal, dont chaque atome est modélisé par un oscillateur harmonique. On démontre en mécanique quantique que l'énergie de l'état m d'un oscillateur harmonique est :

$${\epsilon }_m=(m+\frac{1}{2})\hslash \omega \text{(34)}$$

On suppose ici que tous ces oscillateurs sont indépendants, ce qui n'est pas exact dans un cristal réel.

Le modèle de gaz parfait évoqué plus haut peut aussi être représenté de cette manière, dans la mesure où son espace des phases est discrétisé.

La figure suivante montre les niveaux d'énergie de quelques particules du système. Les niveaux d'énergie sont non dégénérés.

Figure pleine page

Les particules sont indépendantes dans le sens où l'énergie d'interaction entre les particules est négligeable devant l'énergie des particules. Il y a tout de même des petites interactions entre particules qui permettent au système d'atteindre l'équilibre thermodynamique. Par exemple, pour un gaz parfait, il y a des collisions entre molécules qui permettent d'atteindre l'équilibre, bien que l'énergie potentielle d'interaction soit négligeable.

3.b. Moyenne et écart-type de l'énergie d'une particule

La probabilité que la particule soit dans l'état m est :

$$p_m=\frac{e^{-\frac{{\epsilon }_m}{kT}}}{\sum _{m\text{'}=0}^{M-1}{e}^{-\frac{{\epsilon }_{m\text{'}}}{kT}}}\text{(35)}$$

L'énergie moyenne d'une particule est donc :

$$\overline{e}=\frac{\sum _{m=0}^{M-1}{\epsilon }_m{e}^{-\frac{{\epsilon }_m}{kT}}}{\sum _{m=0}^{M-1}{e}^{-\frac{{\epsilon }_m}{kT}}}\text{(36)}$$

Lorsque les niveaux d'énergie sont équidistants, la fonction de partition d'une particule se calcule aisément en introduisant l'espacement ε des niveaux d'énergie :

$$z=\sum _{m=0}^{M-1}{e}^{-\beta ({\epsilon }_0+m\epsilon )}=e^{-\beta {\epsilon }_0}\sum _{m=0}^{M-1}{\left(e^{-\beta \epsilon }\right)}^m=e^{-\beta {\epsilon }_0}\frac{1-e^{-\beta M\epsilon }}{1-e^{-\beta \epsilon }}\text{(37)}$$

On en déduit l'énergie moyenne d'une particule :

$$\overline{e}={\epsilon }_0+\frac{\epsilon }{e^{\beta \epsilon }-1}-\frac{M\epsilon }{e^{\beta M\epsilon }-1}\text{(38)}$$

Lorsque le nombre de niveaux d'énergie est assez grand et kT faible par rapport au dernier niveau, on peut simplifier ce résultat en considérant la limite $M\to \infty$, ce qui élimine le dernier terme.

La variance est :

$${\left(\Delta e\right)}^2=\frac{{\epsilon }^2{e}^{\beta \epsilon }}{{(e^{\beta \epsilon }-1)}^2}-\frac{{\left(M\epsilon \right)}^2{e}^{\beta M\epsilon }}{{(e^{\beta M\epsilon }-1)}^2}\text{(39)}$$

Pour tracer l'énergie moyenne en fonction de la température, on adopte les valeurs k=1 et ε=1. Le premier niveau est choisi nul (il suffit de l'ajouter à la valeur moyenne). L'écart type est représenté sous forme de barres d'erreur.

On commence par le cas où le nombre d'états M est très grand :

from matplotlib.pyplot import *
import numpy


def moy_e(M,T):
    return 1.0/(numpy.exp(1.0/T)-1)-M/(numpy.exp(M/T)-1)
    
def var_e(M,T):
    return numpy.exp(1.0/T)/(numpy.exp(1.0/T)-1)**2\
           -M**2*numpy.exp(-M/T)/(1-numpy.exp(-M/T))**2
    
def ecart_e(M,T):
    return numpy.sqrt(var_e(M,T))
    
def Cv(M,T):
    return var_e(M,T)/T**2
    
T = numpy.linspace(0.01,5,200)
figure()
M=1000
e1 = moy_e(M,T)
de1 = ecart_e(M,T)
plot(T,e1)
errorbar(T,e1,yerr=de1/2,fmt=None)
xlabel("T")
ylabel("e")
grid()
                     

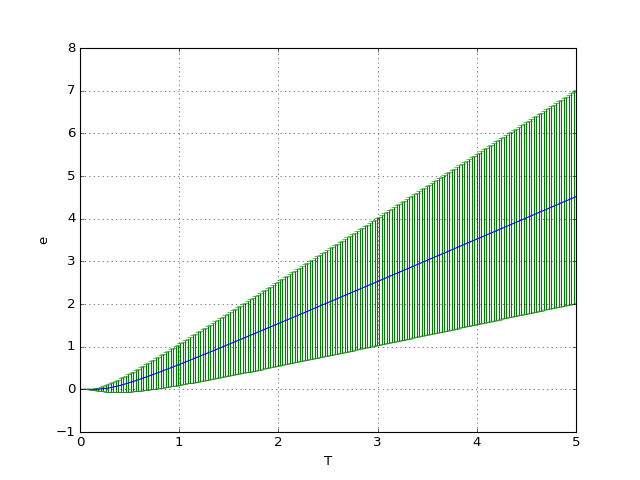figA.pdf

Lorsque l'énergie thermique kT est petite par rapport à la différence ε, la probabilité est négligeable pour les états $m\ge 1$, et donc l'énergie moyenne est égale à ε₀ et la variance est nulle. Si au contraire l'énergie thermique est grande devant l'écart entre deux niveaux d'énergie consécutifs, des états différents peuvent être occupés et la variance est grande.

Voyons le tracé de la capacité thermique :

cv1 = Cv(M,T)
figure()
plot(T,cv1)
xlabel("T")
ylabel("Cv")
grid()
                     

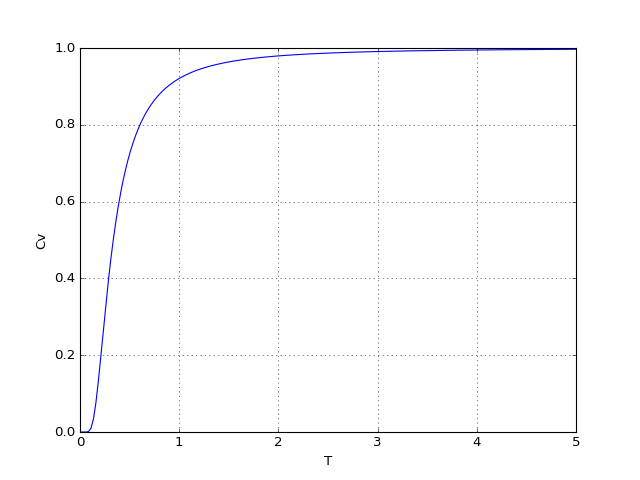figB.pdf

Voyons ce qu'on obtient pour un nombre de niveaux d'énergie limité, c'est-à-dire lorsque le dernier niveau d'énergie peut être occupé dans la gamme de température considérée. Dans l'exemple ci-dessous, il y a seulement 4 niveaux d'énergie.

M=4
T = numpy.linspace(0.01,10,200)
figure()
e1 = moy_e(M,T)
de1 = ecart_e(M,T)
plot(T,e1)
errorbar(T,e1,yerr=de1/2,fmt=None)
xlabel("T")
ylabel("e")
grid()
                      

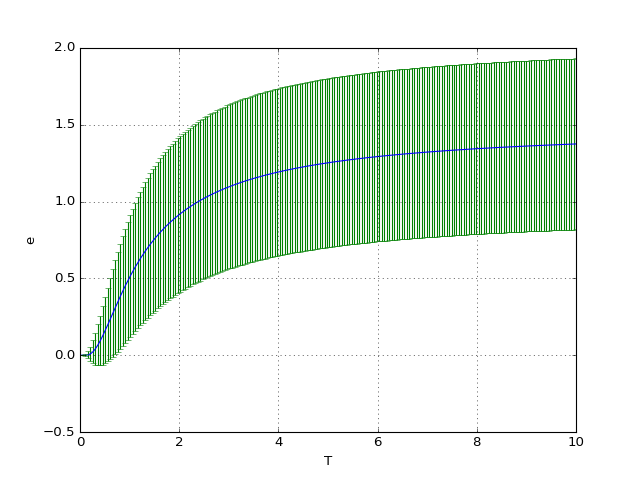figC.pdf

À haute température, tous les états des particules sont équiprobables. L'énergie moyenne tend vers la moitié de l'énergie maximale.

cv1 = Cv(M,T)
figure()
plot(T,cv1)
xlabel("T")
ylabel("Cv")
grid()
                     

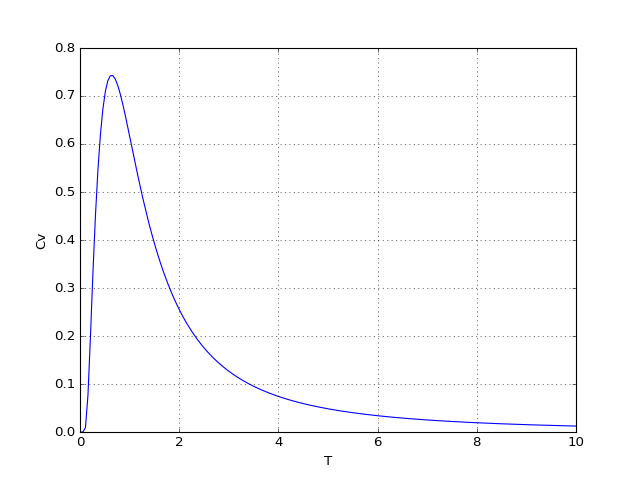figD.pdf

3.c. Moyenne et écart-type de l'énergie du système

Considérons à présent le système en entier, comportant N particules. Pour une énergie E donnée, il y a plusieurs micro-états qui ont cette énergie, et même un très grand nombre si N est grand. La valeur moyenne de l'énergie du système s'écrit :

$$\overline{E}=\frac{\sum _{\mu }{E}_{\mu }{e}^{-\beta E_{\mu }}}{\sum _{\mu }{e}^{-\beta E_{\mu }}}=-{\left(\frac{\partial lnZ}{\partial \beta }\right)}_{N,V}\text{(40)}$$

Pour écrire la fonction de partition Z, il faut considérer une somme sur tous les micro-états, c'est-à-dire une somme multiple sur les nombres m_i de toutes les particules :

$$Z=\sum _{m_1,m_2,m_2,...m_N}{e}^{-\beta (m_1\epsilon +m_2\epsilon +...)}\text{(41)}$$

En écrivant la somme sous cette forme, on a utilisé implicitement le fait que les particules sont discernables. Pour un système quantique, les particules identiques sont indiscernables et la somme doit être calculée différemment. On voit que la fonction de partition se factorise de la manière suivante :

$$Z=\left(\sum _{m_1=0}^{M-1}{e}^{-\beta m_1\epsilon }\right)\left(\sum _{m_2=0}^{M-1}{e}^{-\beta m_2\epsilon }\right)....\text{(42)}$$

La fonction de partition du système est simplement le produit des fonctions de partition des particules. Cette propriété vient du fait que les particules sont indépendantes. Puisque toutes les particules sont identiques, on a finalement :

$$Z=z^N\text{(43)}$$

L'énergie moyenne est :

$$\overline{E}=-\frac{\partial lnZ}{\partial \beta }=-N\frac{\partial lnz}{\partial \beta }=N\overline{e}\text{(44)}$$

Pour des particules indépendantes, l'énergie moyenne est donc égale au nombre de particules multipliée par l'énergie moyenne d'une particule.

La variance est :

$$\Delta E^2=-{\left(\frac{\partial \overline{E}}{\partial \beta }\right)}_{N,V}=N\Delta e^2\text{(45)}$$

La variance pour le système est donc égale à la variance pour une particule multipliée par N. On en déduit le rapport de l'écart quadratique moyen sur la moyenne :

$$\frac{\Delta E}{\overline{E}}=\frac{1}{\sqrt{N}}\frac{\Delta e}{\overline{e}}\text{(46)}$$

L'écart relatif diminue comme l'inverse de la racine carrée du nombre de particules. Ce résultat n'est d'ailleurs pas spécifique à la distribution de Boltzmann. Il s'applique de manière générale à N variables aléatoires indépendantes.

Pour un système thermodynamique, où N est de l'ordre du nombre d'Avogadro, l'écart relatif est infime. Autrement dit, l'énergie du système en équilibre avec un thermostat est pratiquement constante. À l'équilibre, un système isolé est pratiquement identique à un système à température constante. D'une manière générale, les grandeurs physiques ont une très faible variance dans un système thermodynamique à l'équilibre.

La simulation de Monte-Carlo Distribution de Boltzmann : particules indépendantes montre des tirages aléatoires pour ce système à N particules.

3.d. Système à deux niveaux

On considère le cas particulier d'un système à deux niveaux, c'est-à-dire dont les particules ont deux niveaux d'énergie (M=2). De nombreux systèmes quantiques peuvent être modélisés, au moins en première approximation, par un système à deux niveaux. Un exemple est un modèle du paramagnétisme, consistant à attribuer à chaque particule (par exemple les atomes d'un cristal) un spin 1/2. Dans un champ magnétique $\overrightarrow{B}=B{\overrightarrow{u}}_z$, la composante du moment magnétique de ces atomes sur z ne peut prendre que deux valeurs +μ et -μ (voir expérience de Stern et Gerlach). Chaque particule a donc deux états, l'un d'énergie ε₀=-μB, l'autre d'énergie ε₁=+μB.

Un système à M niveaux non régulièrement espacés (comme un atome) peut éventuellement être modélisé par un système à deux niveaux lorsque ses deux premiers niveaux ont une énergie beaucoup plus basse que le troisième. Si la température n'est pas suffisante pour peupler le troisième niveau, on peut considérer seulement les deux premiers.

On peut appliquer les résultats déjà établis pour M quelconque, mais il est instructif de refaire les calculs. Par convention, on pose ε₀=0. Le second niveau d'énergie est donc ε₁=ε. La probabilité des deux états est :

$$\begin{array}{ccc}\hfill & p_0=\frac{1}{1+e^{-\beta \epsilon }}\hfill & \hfill \text{(47)}\\ \hfill & p_1=\frac{e^{-\beta \epsilon }}{1+e^{-\beta \epsilon }}\hfill & \hfill \text{(48)}\end{array}$$

L'énergie moyenne des particules est :

$$\overline{e}=\frac{\epsilon e^{-\beta \epsilon }}{1+e^{-\beta \epsilon }}\text{(49)}$$

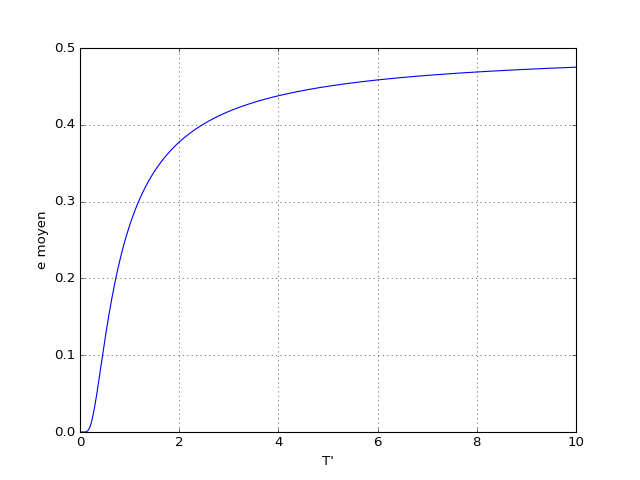
Voyons la courbe en fonction de T. La température sans dimensions utilisée pour les figures est définie par T'=kT/ε.

                    
def e(T):
    x = numpy.exp(-1.0/T)
    return x/(1+x)
        
figure()
T = numpy.linspace(0,10,500)
plot(T,e(T))
xlabel("T'")
ylabel("e moyen")
grid()
                    

figE.pdf

On peut distinguer deux comportements limites. À haute température ($kT\gg \epsilon$) les deux états sont équiprobables. Il y a autant de particules dans un état que dans l'autre et donc :

$$\overline{e}\to \frac{1}{2}\text{(50)}$$

À basse température ($kT<\epsilon$), le premier niveau est beaucoup plus peuplé que le second et

$$\overline{e}=\epsilon e^{-\beta \epsilon }\text{(51)}$$

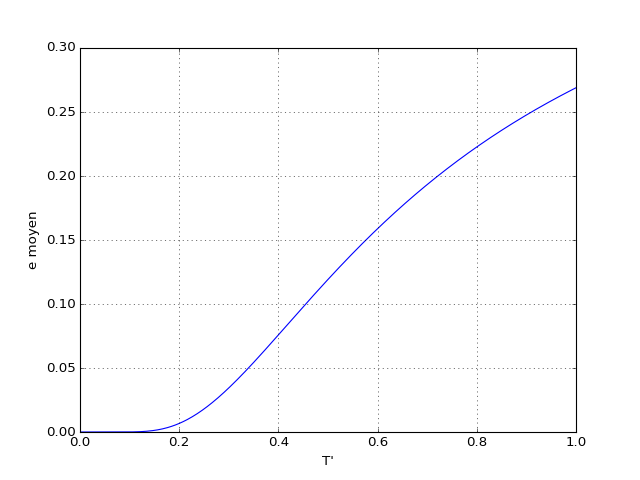
Voyons la courbe à basse température :

figure()
T = numpy.linspace(0,1,500)
plot(T,e(T))
xlabel("T'")
ylabel("e moyen")
grid()
                     

figF.pdf

À très basse température ($kT\ll \epsilon$), seul le niveau de basse énergie est peuplé, car la probabilité pour une particule d'être dans l'autre état est négligeable.

L'énergie moyenne du système est :

$$\overline{E}=N\overline{e}\text{(52)}$$

Calculons sa capacité thermique :

$$C_v=\frac{d\overline{E}}{dT}=\frac{d\overline{E}}{d\beta }\frac{d\beta }{dT}=-\frac{1}{k{T}^2}\frac{d\overline{E}}{d\beta }\text{(53)}$$

On peut sans difficulté faire ce calcul, mais considérons plutôt les deux cas limites. À basse température, on obtient :

$$C_v=\frac{N{\epsilon }^2}{k{T}^2}{e}^{-\frac{\epsilon }{kT}}\text{(54)}$$

La capacité est pratiquement nulle lorsque $kT\ll \epsilon$. La variance est :

$$\Delta E^2=k{T}^2{C}_v=N{\epsilon }^2{e}^{-\beta \epsilon }\text{(55)}$$

On retrouve l'évolution de l'écart-type moyen avec le nombre de particules :

$$\frac{\Delta E}{\overline{E}}=\frac{1}{\sqrt{N}}{e}^{\frac{\beta \epsilon }{2}}\text{(56)}$$

Lorsque N est très grand, l'énergie totale du système a une très faible probabilité de s'éloigner de sa valeur moyenne. Pour un système ergodique, cela signifie que les fluctuations temporelles de l'énergie sont très faibles.

À haute température, l'énergie tend vers une valeur constante donc la capacité thermique tend vers zéro.

4.a. Gaz parfait monoatomique classique

On reprend le modèle de gaz parfait monoatomique défini plus haut. L'énergie d'un atome se limite à son énergie cinétique de translation :

$$e=\frac{p^2}{2m}=\frac{p_x^2+p_y^2+p_z^2}{2m}\text{(57)}$$

où l'on a introduit les composantes de la quantité de mouvement sur trois axes.

Le modèle de gaz parfait classique (dans le sens de non quantique) consiste à considérer que cette énergie cinétique varie de manière continue. Cela revient à faire tendre ε vers zéro. On remplace donc les cellules de l'espace des phases par des volumes infinitésimaux. Dans ce cas, on utilise une densité de probabilité. La probabibilité pour une particule d'avoir une quantité de mouvement dans l'intervalle (p_x,p_x+dp_x),(p_y,p_y+dp_y),(p_z,p_z+dp_z) est :

$$f(p_x,p_y,p_z)d{p}_{x}d{p}_{y}d{p}_z=C{e}^{-\beta \frac{p_x^2+p_y^2+p_z^2}{2m}}d{p}_{x}d{p}_{y}d{p}_z\text{(58)}$$

La condition de normalisation s'écrit :

$$\int f(p_x,p_y,p_z)d{p}_{x}d{p}_{y}d{p}_z=1\text{(59)}$$

Il s'agit d'une intégrale triple, les composantes des quantités de mouvement variant de moins l'infini à plus l'infini. On remarque que cette intégrale ce factorise en trois intégrales identiques :

$$z={\int }_{-\infty }^{\infty }{e}^{-\beta \frac{p_x^2}{2m}}d{p}_x\text{(60)}$$

Considérons la moyenne de l'énergie cinétique pour un degré de liberté, par exemple l'énergie cinétique pour l'axe x :

$$\overline{\frac{p_x^2}{2m}}=C\int \frac{p_x^2}{2m}{e}^{-\beta \frac{p_x^2+p_y^2+p_z^2}{2m}}d{p}_{x}d{p}_{y}d{p}_z\text{(61)}$$

En développant l'exponentielle, l'intégrale se factorise en trois intégrales indépendantes. On obtient finalement :

$$\overline{\frac{p_x^2}{2m}}=-\frac{\partial lnz}{\partial \beta }\text{(62)}$$

En faisant le changement de variable $u={\beta }^{\frac{1}{2}}{p}_x$ on obtient :

$$z={\beta }^{-\frac{1}{2}}{\int }_{-\infty }^{\infty }{e}^{-\frac{u^2}{2m}}du\text{(63)}$$

ce qui conduit à :

$$\overline{\frac{p_x^2}{2m}}=\frac{1}{2}{\beta }^{-1}=\frac{1}{2}kT\text{(64)}$$

L'énergie cinétique moyenne d'un atome est donc 3/2kT. On en déduit l'énergie du gaz

$$E=\frac{3}{2}NkT\text{(65)}$$

puis sa capacité thermique :

$$C_v=\frac{3}{2}Nk\text{(66)}$$

En introduisant le nombre de moles, on retrouve la capacité molaire classique 3/2R.

4.b. Théorème d'équipartition de l'énergie

Le résultat précédent se généralise à toute forme d'énergie qui est quadratique par rapport à un degré de liberté.

Considérons comme exemple un gaz parfait formé de molécules diatomiques. L'énergie d'une molécule comporte son énergie cinétique de translation et son énergie cinétique de rotation. Pour la rotation, il y a deux degrés de libertés, car il faut deux angles pour définir la position d'une molécule diatomique dans l'espace (il y a invariance par rotation autour de son axe). Les degrés de liberté de rotation sont quadratiques par rapport à la vitesse angulaire. Par exemple, pour la rotation autour d'un axe fixe :

$$e_{rot}=\frac{1}{2}I{\omega }^2\text{(67)}$$

où I est le moment d'inertie de la molécule autour de l'axe de rotation. Dans ce cas, il y a deux dimensions supplémentaires dans l'espace des phases, correspondant à l'angle et à la vitesse angulaire.

Pour un gaz parfait diatomique, il y a donc 5 degrés de liberté à énergie quadratique par molécule. Le théorème d'équipartition de l'énergie nous donne alors l'énergie moyenne par molécule :

$$\overline{e}=\frac{5}{2}kT\text{(68)}$$

On en déduit la capacité molaire 5/2R d'un gaz parfait diatomique classique.

4.c. Modèle classique des solides

Dans un solide, les atomes (ou les ions) du réseau cristallin ont une position moyenne fixe mais vibrent légèrement autour de cette position sous l'effet des forces exercées par les atomes voisins. Comme les déplacements sont faibles (par rapport aux distances interatomiques), on peut appliquer un modèle classique avec des forces de rappel linéaires. En première approximation, on peut considérer que chaque atome constitue un oscillateur harmonique indépendant. Soit K₀ le coefficient de raideur, qui relie le déplacement à la force. L'énergie pour cet oscillateur est la somme d'une énergie cinétique de translation et d'une énergie potentielle élastique :

$$e=\frac{p_x^2}{2m}+\frac{1}{2}{K}_0{x}^2\text{(69)}$$

Pour l'axe x, il y a en fait deux degrés de liberté (on raisonne dans l'espace des phases), un pour la quantité de mouvement, l'autre pour la position. On a ici un exemple d'une énergie qui dépend de deux variables. Les niveaux d'énergie sont donc dégénérés. Puisque les deux formes d'énergie sont quadratiques par rapport au degré de liberté correspondant, la moyenne est :

$$\overline{e}=kT\text{(70)}$$

Pour les trois dimensions de l'espace, cela fait une énergie moyenne 3kT, d'où l'on déduit la capacité thermique molaire du solide :

$$C_{vm}=3R=24,9J\cdot mo{l}^{-1}\cdot K^{-1}\text{(71)}$$

C'est la loi de Dulong et Petit, qui a été constatée expérimentalement bien avant le développement de la thermodynamique statistique. En fait, ce résultat n'est valable qu'à haute température (en gros au dessus de 300 K). Lorsque la température décroît, la capacité thermique diminue. Cette propriété ne peut être expliquée que par un modèle quantique, introduit par Einstein en 1907, qui s'est appuyé pour cela sur les découvertes de Planck à propos du rayonnement du corps noir. Le modèle de particules indépendantes à énergies discrètes conduit en effet (voir courbes plus haut) à une capacité thermique tendant vers zéro à basse température. Cela vient du fait que, à très basse température, seul le niveau de plus basse énergie est peuplé. L'énergie du solide devient alors indépendante de la température. En reprenant l'hypothèse de Planck sur la quantification de l'énergie, Einstein a montré que les courbes de capacité thermique en fonction de la température pouvaient s'expliquer par l'introduction d'un quantum d'énergie :

$$\epsilon =\hslash \omega \text{(72)}$$

La pulsation de l'oscillateur est reliée aux paramètres classiques par :

$$\omega =\sqrt{\frac{K_0}{m}}\text{(73)}$$

C'est effectivement le résultat qui est obtenu pour un oscillateur harmonique en mécanique quantique : les niveaux d'énergie sont discrets, avec un espacement constant entre deux niveaux consécutifs.