Distribution de Boltzmann : échantillonnage
1. Introduction
Ce document est une introduction à l'utilisation de la distribution de Boltzmann en physique statistique. On verra son application à un système de particules indépendantes à spectre d'énergie discret. On verra aussi comment faire un échantillonnage selon cette distribution dans une simulation de Monte-Carlo, que l'on fera pour le système de particules indépendantes.
2. Distribution de Boltzmann
2.a. Probabilités des micro-états
On considère un système comportant N particules, en équilibre thermique avec un thermostat de température T. L'énergie E de ce système peut varier en raison des échanges avec le thermostat. On appelle micro-état la donnée de toutes les variables microscopiques (positions et vitesses des particules, nombres quantiques, etc) qui définissent complètement l'état de ces particules. On note μ un micro-état particulier. L'approche statistique consiste à attribuer une probabilité à ces micro-états, sans se préoccuper de la manière dont le système passe d'un micro-état à un autre. Lorsque le système est en équilibre avec un thermostat, ces micro-états obéissent à la distribution de Boltzmann (ou distribution canonique). La probabilité d'un micro-état particulier est :
où Eμ est l'énergie du micro-état et k la constante de Boltzmann. La constante C est obtenue en écrivant que la somme des probabilités de tous les micro-états est égale à 1 :
On obtient finalement :
La distribution de Boltzmann s'applique à un système à l'équilibre avec un thermostat quelque soit sa taille. Il peut s'agir d'une seule molécule dans un gaz, d'un groupe de plusieurs molécules, ou bien d'un système thermodynamique contenant un nombre N de particules très grand.
On voit qu'un micro-état est d'autant plus probable que son énergie est basse. On a bien souvent besoin de comparer la probabilité de deux micro-états :
Lorsque kT est petit devant la différence d'énergie, la probabilité de l'état de plus faible énergie est beaucoup plus grande que l'autre. Lorsque kT est grand devant la différence d'énergie, les deux probabilités sont pratiquement égales.
À une énergie E donnée correspond en général plusieurs micro-états (si N>1). On dit que ce niveau d'énergie est dégénéré. Lorsque N est grand, le nombre de micro-états est de l'ordre de Ω(N,E)=EN, qui est une fonction très rapidement croissante de l'énergie (l'énergie est supposée positive). Les états de faible énergie sont plus probables mais leur nombre est beaucoup plus faible que ceux de plus grande énergie. La probabilité pour que le système ait une énergie E est proportionnelle à la fois à la probabilité d'un micro-état ayant cette énergie et au nombre de micro-états de cette énergie :
où Ω(E) est le nombre de micro-états ayant l'énergie E.
C'est seulement dans le cas d'un niveau d'énergie non dégénéré que Ω(E)=1. Cela montre qu'il faut bien distinguer probabilité d'un micro-état et probabilité d'une énergie.
2.b. Calculs statistiques
Soit une grandeur physique Xμ qui dépend du micro-état. La distribution de Boltzmann permet de calculer la valeur moyenne de cette grandeur (que les mathématiciens appellent l'espérance) :
Par exemple, la valeur moyenne de l'énergie du système est :
Un autre grandeur importante est la variance, qui indique la dispersion des valeurs autour de la valeur moyenne. La variance est la moyenne du carré de l'écart entre X et sa valeur moyenne :
L'expression de la variance se développe :
Comme la valeur moyenne est en général déjà connue, on calcule la variance à l'aide de la valeur moyenne du carré de X.
On appelle écart quadratique moyen (ou écart-type), la racine carrée de la variance :
L'écart-type peut être comparé directement à la valeur moyenne, et donne une information sur la dispersion des valeurs autour de la moyenne. Si le rapport
est faible, cela signifie que l'énergie du système reste très probablement très proche de sa valeur moyenne. On verra plus loin que c'est le cas lorsque le nombre de particules est grand. Pour une particule individuelle, l'écart-type est du même ordre que la moyenne, ce qui indique une très forte dispersion.
Les calculs statistiques sont facilités en posant :
Z est la fonction de partition du système. Si l'on dispose d'une expression de Z, on peut faire tous les calculs statistiques. Par exemple :
On peut montrer que la variance de l'énergie s'écrit :
Ainsi la variance est proportionnelle à la capacité thermique à volume constant. Le rapport entre l'écart-type et la valeur moyenne est alors :
L'énergie moyenne et la capacité thermique sont deux grandeurs extensives proportionnelles à N. On en déduit la loi d'échelle :
L'écart-type relatif est donc d'autant plus faible que le système est grand. Pour un système thermodynamique macroscopique, cet écart relatif est extrêmement faible, ce qui signifie que l'énergie du système reste très probablement très proche de son énergie moyenne. Ainsi un système thermodynamique en équilibre avec un thermostat est similaire à un système isolé d'énergie constante (tant qu'il reste à l'équilibre).
2.c. Ergodicité
Un système physique réel est dit ergodique si tous les micro-états sont effectivement occupés par le système au cours du temps (en suivant la distribution de Boltzmann). Ce balayage des micro-états se fait avec un temps caractéristique τ, qui dépend beaucoup du système considéré et surtout de sa taille. Lorsqu'un système est ergodique, la moyenne temporelle d'une grandeur sur la durée τ coïncide avec la moyenne statistique définie plus haut. Expérimentalement, on mesure une moyenne temporelle et non pas une moyenne statistique. On peut donc dire que la validité de l'approche statistique suppose que l'ergodicité soit vérifiée sur une durée de l'ordre du temps de réponse des capteurs utilisés.
En pratique, il n'est pas nécessaire que l'ergodicité soit vérifiée à l'échelle macroscopique pour que l'approche statistique soit valable. Par exemple, pour un volume liquide de l'ordre du litre, il faut un temps très long à une molécule pour parcourir toutes les positions du récipient. Néanmoins la physique statistique s'applique bien à ce type de système, car l'ergodicité est vérifiée à l'échelle mésoscopique.
3. Système à particules indépendantes
3.a. Définition du système
On considère un système formé de N particules indépendantes et discernables. Pour chaque particule, il y a M états possibles, numérotés de 0 à M-1. À chaque état m est associée une énergie εm. Pour simplifier, on suppose que ces niveaux d'énergie sont régulièrement espacés, et on note ε le quantum d'énergie.
Un exemple physique de système de ce type est un cristal, dont chaque atome est modélisé par un oscillateur harmonique. On démontre en mécanique quantique que l'énergie de l'état m d'un oscillateur harmonique est :
On suppose ici que tous ces oscillateurs sont indépendants, ce qui n'est pas exact dans un cristal réel.
La figure suivante montre les niveaux d'énergie de quelques particules du système. Il est important de bien noter qu'à chaque niveau d'énergie correspond un et un seul état de la particule. On dit que ces niveaux d'énergie sont non dégénérés.
Figure pleine pageLes particules sont indépendantes dans le sens où l'énergie d'interaction entre les particules est négligeable devant l'énergie des particules. Il y a tout de même des petites interactions entre particules qui permettent au système d'atteindre l'équilibre thermodynamique. Par exemple, pour un gaz parfait, il y a des collisions entre molécules qui permettent d'atteindre l'équilibre, bien que l'énergie potentielle d'interaction soit négligeable.
3.b. Distribution des états d'une particule
La distribution de Boltzmann s'applique tout à fait à une particule, car le reste du système se comporte comme un thermostat vis à vis de cette particule. La probabilité que la particule soit dans l'état m est :
L'énergie moyenne d'une particule est donc :
Lorsque les niveaux d'énergie sont équidistants, la fonction de partition d'une particule se calcule aisément en introduisant l'espacement ε des niveaux d'énergie :
On en déduit l'énergie moyenne d'une particule :
Lorsque le nombre de niveaux d'énergie est assez grand et kT faible par rapport au dernier niveau, on peut simplifier ce résultat en considérant la limite , ce qui élimine le dernier terme.
La variance est :
Pour tracer l'énergie moyenne en fonction de la température, on adopte les valeurs k=1 et ε=1. Le premier niveau est choisi nul (il suffit de l'ajouter à la valeur moyenne). L'écart type est représenté sous forme de barres d'erreur.
On commence par le cas où le nombre d'états M est très grand :
from matplotlib.pyplot import *
import numpy
def moy_e(M,T):
return 1.0/(numpy.exp(1.0/T)-1)-M/(numpy.exp(M/T)-1)
def var_e(M,T):
return numpy.exp(1.0/T)/(numpy.exp(1.0/T)-1)**2-M**2*numpy.exp(-M/T)/(1-numpy.exp(-M/T))**2
def ecart_e(M,T):
return numpy.sqrt(var_e(M,T))
def Cv(M,T):
return var_e(M,T)/T**2
T = numpy.linspace(0.01,5,100)
figure()
M=1000
e1 = moy_e(M,T)
de1 = ecart_e(M,T)
plot(T,e1)
errorbar(T,e1,yerr=de1/2,fmt=None)
xlabel("T")
ylabel("e")
grid()
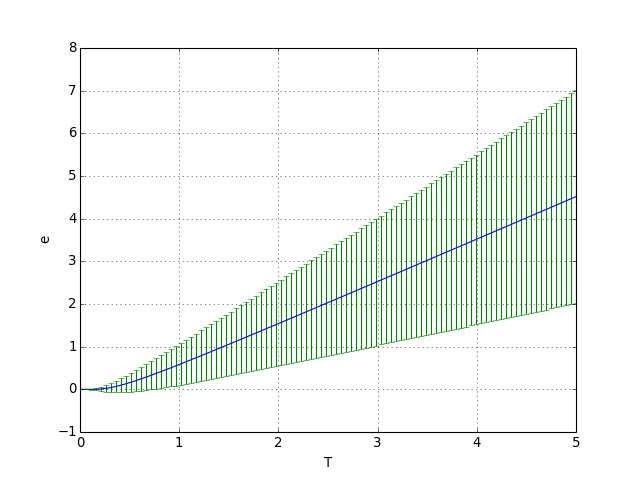 figA.pdf
figA.pdf
Lorsque l'énergie thermique kT est petite par rapport à la différence ε, la probabilité est négligeable pour les états , et donc l'énergie moyenne est égale à ε0 et la variance est nulle. Si au contraire l'énergie thermique est grande devant l'écart entre deux niveaux d'énergie consécutifs, un grand nombre d'états différents peuvent être occupés et la variance est très importante.
Voyons le tracé de la capacité thermique :
cv1 = Cv(M,T)
figure()
plot(T,cv1)
xlabel("T")
ylabel("Cv")
grid()
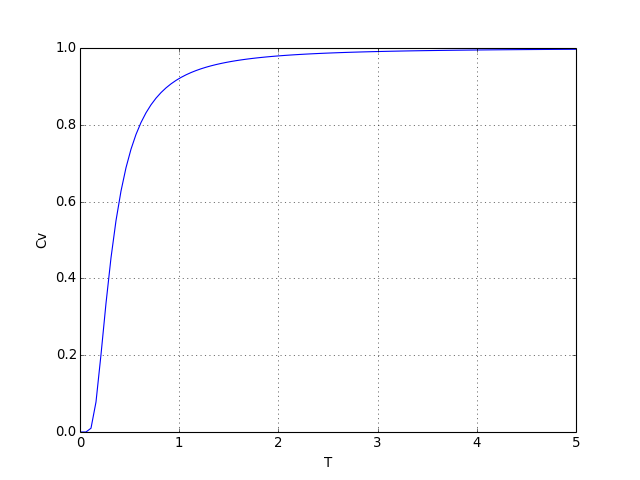 figB.pdf
figB.pdf
Voici ce qu'on obtient pour un nombre de niveaux d'énergie limité, c'est-à-dire lorsque le dernier niveau d'énergie peut être occupé dans la gamme de température considérée :
M=2
figure()
e1 = moy_e(M,T)
de1 = ecart_e(M,T)
plot(T,e1)
errorbar(T,e1,yerr=de1/2,fmt=None)
xlabel("T")
ylabel("e")
grid()
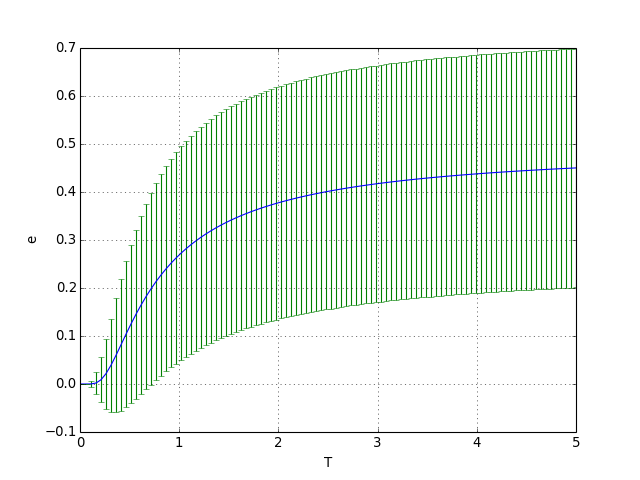 figC.pdf
figC.pdf
À haute température, tous les états des particules sont équiprobables. L'énergie moyenne tend vers la moitié de l'énergie maximale.
cv1 = Cv(M,T)
figure()
plot(T,cv1)
xlabel("T")
ylabel("Cv")
grid()
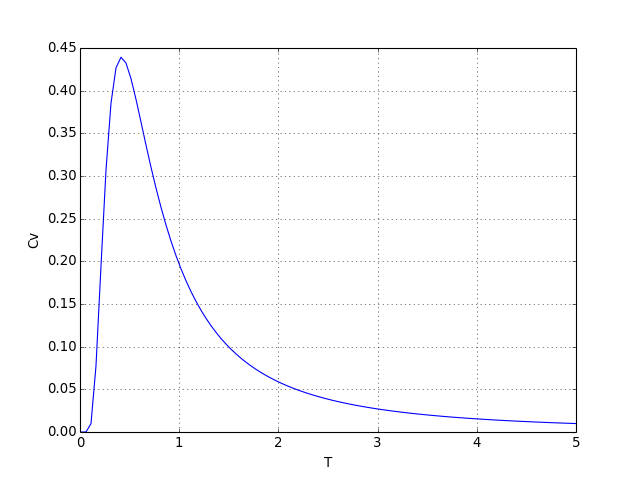 figD.pdf
figD.pdf
3.c. Distribution des états du système
Considérons à présent le système en entier, comportant N particules. Pour une énergie E donnée, il y a plusieurs micro-états qui ont cette énergie, et même un très grand nombre si N est grand. La valeur moyenne de l'énergie du système s'écrit :
Pour écrire la fonction de partition Z, il faut considérer une somme sur tous les micro-états, c'est-à-dire une somme multiple sur les nombres mi de toutes les particules :
En écrivant la somme sous cette forme, on a utilisé implicitement le fait que les particules sont discernables. Pour un système quantique, les particules identiques sont indiscernables et la somme doit être calculée différemment. On voit que la fonction de partition se factorise de la manière suivante :
La fonction de partition du système est simplement le produit des fonctions de partition des particules. Cette propriété vient du fait que les particules sont indépendantes. Puisque toutes les particules sont identiques, on a finalement :
L'énergie moyenne est :
Pour des particules indépendantes, l'énergie moyenne est donc égale au nombre de particules multipliée par l'énergie moyenne d'une particule.
La variance est :
La variance pour le système est donc égale à la variance pour une particule multipliée par N. On en déduit le rapport de l'écart quadratique moyen sur la moyenne :
L'écart relatif diminue comme l'inverse de la racine carrée du nombre de particules. Ce résultat n'est d'ailleurs pas spécifique à la distribution de Boltzmann. Il s'applique de manière générale à N variables aléatoires indépendantes.
Pour un système thermodynamique, où N est de l'ordre du nombre d'Avogadro, l'écart relatif est infime. Autrement dit, l'énergie du système en équilibre avec un thermostat est pratiquement constante. D'une manière générale, les grandeurs physiques ont une très faible variance dans un système thermodynamique à l'équilibre.
4. Méthodes de Monte-Carlo
4.a. Principe
Une méthode de Monte-Carlo consiste à générer aléatoirement des échantillons de micro-états du système de manière à effectuer des calculs statistiques, par exemple le calcul de la valeur moyenne de l'énergie et de sa variance.
Une première idée serait de générer un grand nombre d'états aléatoirement, avec la même probabilité pour tous les états, et de calculer la moyenne d'une grandeur X par :
Cette méthode est extrêmement inefficace (et même impraticable), car la très grande majorité des micro-états a une probabilité très faible dans la distribution de Boltzmann. Le nombre de micro-états que l'on peut générer au cours d'une simulation est infime par rapport au nombre de micro-états effectivement accessibles au système.
La solution consiste à générer des micro-états avec des probabilités vérifiant la distribution de Boltzmann. Supposons que l'on génère aléatoirement P micro-états répartis aléatoirement selon la distribution de Boltzmann. La probabilité de survenue d'un état pμ dans cet échantillonnage est précisément la probabilité de Boltzmann. La valeur moyenne d'une grandeur X s'écrit alors :
Pour générer des micro-états aléatoirement (on dit aussi échantillonner) en suivant la distribution de Boltzmann (ou toute autre distribution), nous allons voir deux méthodes : l'échantillonnage direct par la méthode du rejet et l'échantillonnage de Metropolis.
Nous allons effectuer une simulation de Monte-Carlo pour le système de particules indépendantes. Les résultats exacts ont été établis ci-dessus pour ce système, ce qui permettra de vérifier la pertinence de la simulation. Bien sûr, ce type de simulation a vraiment un intérêt lorsque le calcul statistique analytique n'est pas possible. C'est généralement le cas lorsque les particules interagissent entre elles.
Voir aussi la simulation Distribution de Boltzmann : particules indépendantes.
4.b. Méthode du rejet
Considérons le système de particules indépendantes étudié ci-dessus. Pour générer un état aléatoirement, on commence par choisir aléatoirement une particule parmis les N particules du système. Pour cette particule choisie, on doit attribuer un niveau d'énergie aléatoirement sachant que la probabilité d'avoir un niveau m est
La méthode du rejet ne nécessite pas la connaissance de la constante C. Il suffit de connaître la probabilité maximale, qui est ici égale à 1 si C=1. Représentons graphiquement la probabilité en fonction de m :
Figure pleine pageOn commence par faire un tirage aléatoire d'un nombre entier m compris en 0 et M-1. Ce nombre a une probabilité d'être accepté égale à .
La deuxième étape consiste à tirer un nombre aléatoire x réel (en fait un flottant) compris entre 0 et 1. Graphiquement, cela revient à attribuer une ordonnée au point représentatif. On voit ainsi que le point doit être rejeté si :
Sur la figure, les points rejetés sont noir, les points acceptés sont rouges. On voit immédiatement l'inconvénient de cette méthode : un grand nombre de rejets lorsque beaucoup d'états ont une faible probabilité. Dans la distribution de Boltzmann, cela concerne les états dont l'énergie est supérieure à kT.
Pour implémenter cette méthode, on définit une classe qui contient les différents tableaux nécessaires aux calculs. Le constructeur a pour arguments le nombre de particules et le nombre d'états. On définit des niveaux d'énergie qui pourront éventuellement avoir une répartition quelconque, même si la répartition par défaut est régulière. On définit un tableau pour le calcul de la moyenne de l'énergie des particules. Ce tableau contiendra la somme des énergies de chaque particule. Pour le calcul de la variance, on définit un tableau qui contiendra la somme de l'énergie au carré.
import numpy
import math
import random
class Particules:
def __init__(self,N,M):
self.N = N
self.M = M
self.etats_particules = numpy.zeros(N)
self.energies_particules = numpy.zeros(N)
self.niveaux_energie = numpy.arange(1,M+1)
self.sommes_energies = numpy.zeros(N)
self.somme_E = 0.0
self.sommes_energies_2 = numpy.zeros(N)
self.somme_E_2 = 0.0
self.compteur = 0
self.n_rejets = 0
La fonction suivante initialise les sommes utilisées pour le calcul des moyennes. Le compteur contiendra le nombre de valeurs ajoutées dans les sommes, qui sera utile pour le calcul final des moyennes.
def initialiser_sommes(self):
for k in range(self.N):
self.sommes_energies[k] = 0.0
self.sommes_energies_2[k] = 0.0
self.somme_E = 0.0
self.somme_E_2 = 0.0
self.compteur = 0
La fonction suivante génère un nouvel état en choisissant aléatoirement une particule et en appliquant la méthode du rejet pour choisir l'état de cette particule. Le nombre de rejets est comptabilisé.
def nouvel_etat(self):
k = random.randrange(self.N)
rejet = True
while rejet:
i = random.randrange(self.M)
e = self.niveaux_energie[i]
if random.random() < math.exp(-self.beta*e):
rejet = False
self.etats_particules[k] = i
self.energies_particules[k] = e
else:
self.n_rejets += 1
La fonction suivante met a jour les sommes :
def sommes(self):
for k in range(self.N):
e = self.energies_particules[k]
self.sommes_energies[k] += e
self.sommes_energies_2[k] += e*e
E = numpy.sum(self.energies_particules)
self.somme_E += E
self.somme_E_2 += E*E
self.compteur += 1
La fonction suivante effectue des itérations. Ses arguments sont :
- n1 : nombre de blocs d'itérations. Pour chaque bloc, les tableaux de sommes sont mis à jour.
- n2 : nombre d'itérations dans un bloc d'itérations. Ces itérations consiste à modifier l'état du système sans mettre à jour les sommes.
- T : température
- methode : directe ou metropolis
À chaque bloc de calcul, les valeurs moyennes et les écarts-types sont affichés, ainsi que l'écart-type divisé par la moyenne. Le taux de rejet est aussi affiché. La fonction renvoit la moyenne, l'écart-type de l'énergie du système, et le taux de rejet.
def iterations(self,n1,n2,T,methode="directe"):
self.n_rejets = 0
self.beta = 1.0/T
self.exp = math.exp(-self.beta)
if methode=="directe":
for i in range(n1):
for j in range(n2):
self.nouvel_etat()
self.sommes()
elif methode=="metropolis":
for i in range(n1):
for j in range(n2):
self.nouvel_etat_metropolis()
self.sommes()
moy_E = self.somme_E/self.compteur
var_E = self.somme_E_2/self.compteur-moy_E**2
ecart_E = math.sqrt(var_E)
print("Systeme : E = %f, dE = %f, dE/E = %f"%(moy_E,ecart_E,ecart_E/moy_E))
moyennes_energies = self.sommes_energies/self.compteur
moy_e = numpy.mean(moyennes_energies)
moyennes_energies_2 = self.sommes_energies_2/self.compteur
var_e = numpy.mean(moyennes_energies_2)-moy_e**2
ecart_e = math.sqrt(var_e)
print("Particule : e = %f, de = %f, de/e = %f"%(moy_e,ecart_e,ecart_e/moy_e))
taux_rejet = self.n_rejets*1.0/(n1*n2)
print("Taux de rejet : %f"%(taux_rejet))
return (moy_E,ecart_E,taux_rejet)
4.c. Méthode de Metropolis
Cette méthode d'échantillonnage doit son nom à l'auteur principal d'un article publié en 1953 ([1]), qui présentait une simulation de Monte-Carlo d'un modèle de sphères dures. Voir à ce sujet : Modèle des sphères dures à deux dimensions. L'algorithme de Metropolis est aujourd'hui très largement utilisé en physique statistique, et de manière plus générale dans les simulations de Monte-Carlo dans différents domaines (synthèse d'images, finance, simulations d'épidémies, etc). C'est un bon exemple d'une méthode inventée pour la physique qui s'est répandue dans différents domaines scientifiques.
Dans la méthode du rejet, les différents états du système sont générés sans aucune relation entre un état et le suivant. La méthode de Metropolis consiste à générer un état en partant du précédent. En terme technique, il s'agit de générer une chaîne de Markov d'états. La régle qui permet de passer d'un état au suivant doit être établie de manière à obtenir une chaîne d'états (lorsque le régime stationnaire est atteint) qui soient distribués selon la distribution choisie, en l'occurence la distribution de Maxwell. Pour une explication détaillée de la méthode de Metropolis, voir Algorithme de Metropolis.
Le passage d'un état à un autre se fait en deux étapes : une étape de sélection d'un nouvel état et une étape d'acceptation (ou de refus).
Figure pleine pagePour une distribution donnée, il y a plusieurs algorithmes de Metropolis. Nous allons en décrire un adapté au problème des particules indépendantes.
Pour la méthode de sélection d'un changement, on choisit une particule aléatoirement parmis les N particules (avec une probabilité uniforme), puis on choisit aléatoirement une variation d'énergie de cette particule de +1 ou de -1 (sauf si la transition n'est pas permise). Notons δe cette variation d'énergie.
Dans l'étape d'acceptation, on effectue les opérations suivantes :
- Si , le changement d'état de la particule est accepté.
- Si , on tire un nombre aléatoire réel x avec une probabilité uniforme sur l'intervalle [0,1]. Si alors le changement est accepté. Sinon le nouvel état est identique au précédent.
En cas de refus du changement d'état de la particule, le nouvel état est identique au précédent, et ce nouvel état est pris en compte dans les calculs statistiques. Il faut bien faire la distinction avec le refus de la méthode du rejet.
La fonction suivante, ajoutée à la classe déjà définie, implémente un changement d'état par la méthode de Metropolis. Le facteur est précalculé et stocké dans self.exp.
def nouvel_etat_metropolis(self):
k = random.randrange(self.N)
i = self.etats_particules[k]
delta_i = 0
if i==0:
delta_i = 1
elif i==self.M-1:
delta_i = -1
else:
if random.randint(1,2)==1:
delta_i = -1
else:
delta_i = 1
j = i+delta_i
dE = self.niveaux_energie[j]-self.niveaux_energie[i]
if dE <= 0.0:
self.etats_particules[k] = j
self.energies_particules[k] = self.niveaux_energie[j]
else:
if random.random() < self.exp:
self.etats_particules[k] = j
self.energies_particules[k] = self.niveaux_energie[j]
La méthode de Metropolis a un avantage considérable sur la méthode d'échantillonnage directe (par rejet) dès que le nombre d'états M est assez élevé pour que de nombreux états aient une probabilité d'occupation très faible. Dans de nombreuses situations, une méthode d'échantillonnage directe est tout simplement impossible car beaucoup trop coûteuse en calculs à cause du nombre trop important de rejets. C'est le cas du modèle des sphères dures, où il faut répartir des sphères aléatoirement dans l'espace sans qu'elles se chevauchent. Pour la méthode de Metropolis appliquée aux sphères dures voir la simulation Sphères dures 2D : Metropolis.
En revanche, la méthode de Metropolis présente un inconvénient : il faut effectuer un certain nombre de changements avant d'atteindre un régime permanent permettant de faire les calculs statistiques. Pendant le régime transitoire, les états générés ne sont pas encore distribués selon la distribution de Boltzmann. En pratique, le nombre d'itérations à faire pour atteindre le régime permanent peut être du même ordre que le nombre d'itérations utilisées pour les calculs statistiques. Il faut en général faire des tests pour vérifier que le régime permanent est bien atteint.
4.d. Simulations
from particules import Particules
Voyons tout d'abord la méthode d'échantillonnage directe.
On écrit une fonction qui calcule l'énergie moyenne du système pour différentes températures et on trace la courbe :
def courbe_T(N,M,nT,n1,n2):
particules = Particules(N,M)
T= numpy.arange(1,nT+1)*0.5
E = numpy.zeros(nT)
dE = numpy.zeros(nT)
rejet = numpy.zeros(nT)
for k in range(nT):
print("T = %f"%T[k])
(E[k],dE[k],rejet[k])=particules.iterations(n1,n2,T[k],"directe")
particules.initialiser_sommes()
figure()
subplot(211)
errorbar(T,E,yerr=dE,fmt=None)
plot(T,E,'o')
axis([0,numpy.max(T),0,numpy.max(E)*2])
xlabel("T")
ylabel("E")
grid()
subplot(212)
plot(T,rejet,'o')
xlabel('T')
ylabel('rejet')
grid()
Voici un exemple avec 10 particules et 10 niveaux d'énergie :
N=10
M=10
nT=20
n1=2000
n2=100
courbe_T(N,M,nT,n1,n2)
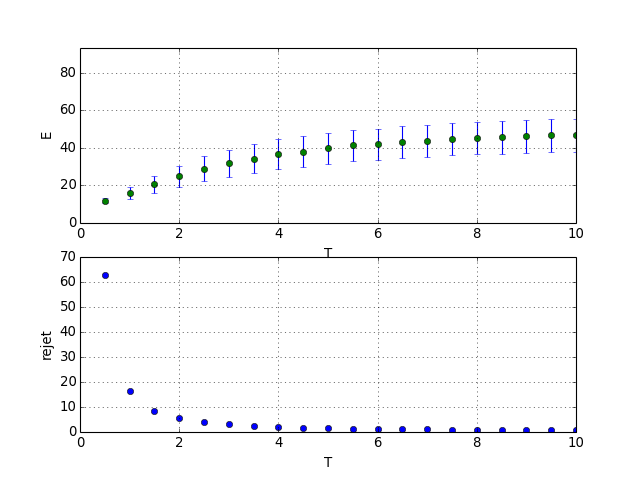 figE.pdf
figE.pdf
Pour les faibles températures, le taux de rejet est très grand. Un taux de rejet de 10 signifie qu'il faut en moyenne 10 tirages avant d'en obtenir un qui soit retenu.
La fonction suivante fait la même chose avec la méthode de Metropolis. Dans ce cas, des itérations doivent être effectuées avant de commencer le calcul des moyennes.
def courbe_T_metropolis(N,M,nT,n1,n2):
particules = Particules(N,M)
T= numpy.arange(1,nT+1)*0.5
E = numpy.zeros(nT)
dE = numpy.zeros(nT)
for k in range(nT):
print("T = %f"%T[k])
particules.iterations(n1,n2,T[k],"metropolis")
(E[k],dE[k],rejet)=particules.iterations(n1,n2,T[k],"metropolis")
particules.initialiser_sommes()
figure()
errorbar(T,E,yerr=dE,fmt=None)
plot(T,E,'o')
axis([0,numpy.max(T),0,numpy.max(E)*2])
xlabel("T")
ylabel("E")
grid()
courbe_T_metropolis(N,M,nT,n1,n2)
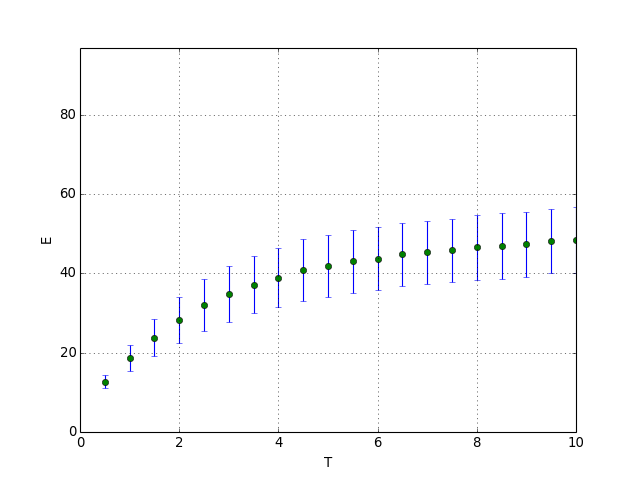 figF.pdf
figF.pdf