Pendule libre conservatif

1. Équations du mouvement

L'équation différentielle du mouvement d'un pendule pesant conservatif est :

$$\frac{d^2\theta }{d{t}^2}+{\omega }_0^{2}sin\left(\theta \right)=0$$

On introduit la vitesse angulaire :

$$\omega =\frac{d\theta }{dt}$$

On définit un système différentiel du premier ordre pour $\theta$ et $\omega$ :

$$\begin{array}{ccc}\hfill & \frac{d\theta }{dt}=\omega \hfill & \hfill \text{(1)}\\ \hfill & \frac{d\omega }{dt}=-{\omega }_0^{2}sin\left(\theta \right)\hfill & \hfill \text{(2)}\end{array}$$

L'espace à deux dimensions correspondant à l'angle et à la vitesse angulaire est appelé l'espace des phases.

L'intégrale première (énergie mécanique) est :

$$E=\frac{1}{2}(\frac{d\theta }{dt}{)}^2-{\omega }_0^{2}cos\left(\theta \right)$$

On peut à partir de cette expression définir la fonction Hamiltonien :

$$H(\theta ,\omega )=\frac{1}{2}{\omega }^2-{\omega }_0^{2}cos\left(\theta \right)$$

ce qui permet d'écrire le système différentiel précédent sous la forme générale suivante (équations de Hamilton) :

$$\begin{array}{ccc}\hfill & \frac{d\theta }{dt}=\frac{\partial H}{\partial \omega }\hfill & \hfill \text{(3)}\\ \hfill & \frac{d\omega }{dt}=-\frac{\partial H}{\partial \theta }\hfill & \hfill \text{(4)}\end{array}$$

2. Intégration numérique

L'intégration numérique consiste à obtenir des valeurs approchées de l'angle et de la vitesse angulaire pour des points régulièrement espacés sur un intervalle de temps donné. La méthode la plus simple pour calculer ces valeurs approchées est la méthode d'Euler explicite.

Dans cette partie, on voit comment effectuer une intégration numérique avec le module scipy.integrate.

import math
import numpy as np
from matplotlib.pyplot import *
import scipy.integrate
            

On pose par convention ${\omega }_0=2\pi$, ce qui permet d'avoir une période des petites oscillations égale à 1. Le système différentiel du premier ordre est défini sous forme d'une fonction de $y=[\theta ,\omega ]$ et du temps :

def equation(y,t):
    return [y[1],-(2*math.pi)**2*math.sin(y[0])]
            

On choisit le temps maximal du calcul (une centaine de périodes) et le temps d'échantillonnage (une fraction de période) :

tmax=100
te=0.01
            

Un tableau numpy comportant les échantillons de temps est créé :

t = np.arange(start=0,stop=tmax,step=te)
            

L'intégration numérique se fait avec la fonction scipy.integrate.odeint. Cette fonction utilise le solveur LSODA de la bibliothèque fortran ODEPACK. La méthode utilisée par ce solveur est une méthode à pas multiple et à ordre variable (la méthode d'Euler est à un pas et d'ordre 1).

Ce type de méthode numérique effectue une évaluation de l'erreur commise à chaque pas de calcul (passage de l'instant $t$ à $t+\Delta t$). Le pas $\Delta t$ est modifié en permanence (on parle d'adaptation du pas) de manière à maintenir l'erreur inférieure à :

$${\epsilon }_a+{\epsilon }_r\left|y\right|$$

où ${\epsilon }_a$ est la tolérance absolue, ${\epsilon }_r$ la tolérance relative et $\left|y\right|$ la norme des variables, qui est dans le cas présent :

$$\left|y\right|=\sqrt{{\theta }^2+{\omega }^2}$$

Plus les tolérances sont faibles, plus le calcul est précis, mais plus il est long. Les valeurs des tolérances sont déterminées empiriquement. On commence par ces valeurs :

atol=1e-8
rtol=1e-8
            

On prend pour condition initial un angle non nul assez grand (pour voir les effets non linéaires) et une vitesse angulaire nulle :

y0=[0.8*math.pi,0]
            

Enfin la fonction de calcul :

y = scipy.integrate.odeint(equation,y0,t,rtol=rtol,atol=atol)
            

Le résultat est un tableau numpy dont les lignes correspondent aux différents instants. Dans le cas présent, ce tableau a 2 colonnes. Pour récupérer les listes des angles et des vitesses angulaires, on effectue la transposée :

yt = y.transpose()
theta = yt[0]
omega = yt[1]
            

Voyons l'angle en fonction du temps sur quelques périodes :

figure(figsize=(10,4))
plot(t,theta)
xlabel('t')
ylabel('theta')
axis([0,10,-4,4])
            

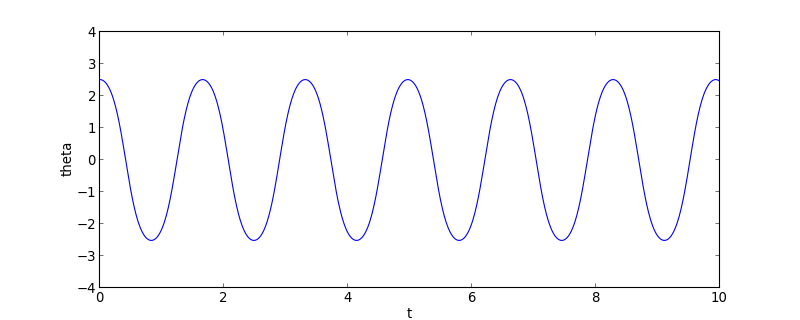figA.pdf

L'évolution à long terme apparaît sur le tracé dans l'espace des phases :

figure(figsize=(6,6))
plot(theta,omega/(2*math.pi))
xlabel('theta')
ylabel('omega')
axis([-4,4,-4,4])
        

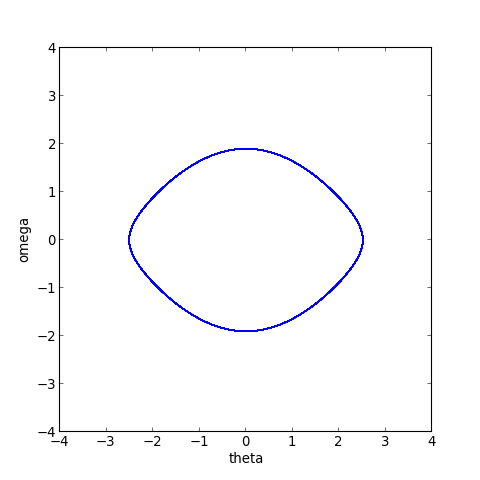figB.pdf

On voit sur cette représentation que la solution approchée reste périodique, comme il se doit.

Pour contrôler la stabilité du calcul numérique, une bonne méthode consiste à tracer l'énergie, qui doit rester constante au cours du temps pour un système conservatif :

energie = 0.5*np.power(omega,2)-(2*math.pi)**2*np.cos(theta)
figure(figsize=(12,4))
plot(t,energie)
xlabel('t')
ylabel('energie')
        

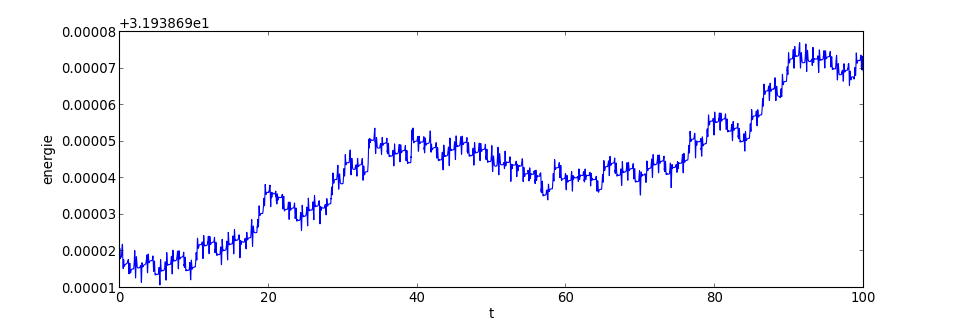figC.pdf

On voit sur ce graphique que l'erreur absolue sur l'énergie est de l'ordre de $8\cdot 10^{-5}$ au temps maximal, soit une erreur relative de $2\mathrm{.}5\cdot 10^{-6}$.

L'analyse spectrale du mouvement est effectuée avec la fonction numpy.fft.fft qui calcule la transformée de Fourier discrète des échantillons :

import numpy.fft
tfd = numpy.fft.fft(theta)
spectre=np.absolute(tfd)
        

On construit la liste des fréquences correspondantes, sachant que le pas des fréquences est l'inverse de la durée totale analysée :

n = theta.size
freq = np.zeros(n)
for k in range(n):
    freq[k] = 1.0/(te*n)*k
        

Enfin le tracé du spectre

figure(figsize=(12,4))
plot(freq,spectre)
xlabel('f')
ylabel('A')
axis([0,10,0,spectre.max()])
        

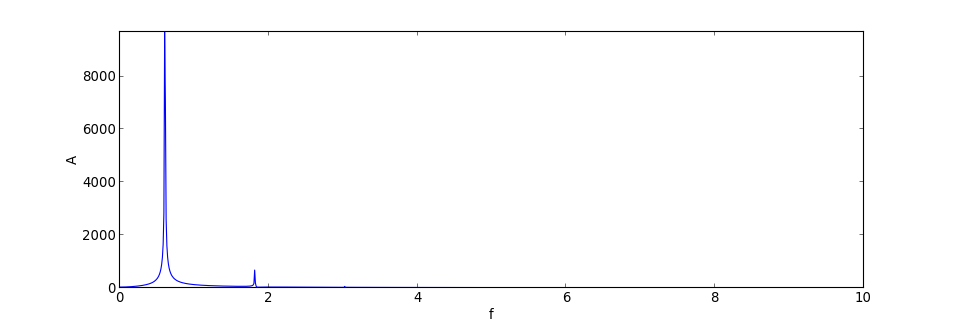figD.pdf

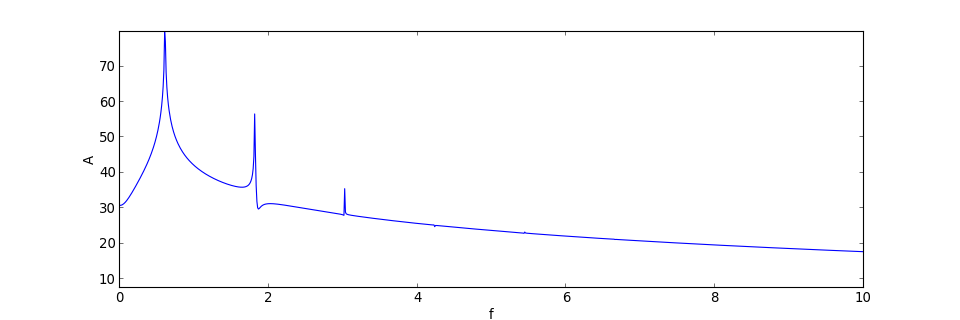
On voit que la fréquence est nettement inférieure à 1 et qu'il y a une harmonique de rang 3. Pour voir les harmoniques faibles, on trace le spectre en décibel :

spectre_db = 20*np.log10(spectre)
figure(figsize=(12,4))
plot(freq,spectre_db)
xlabel('f')
ylabel('A')
axis([0,10,spectre_db.min(),spectre_db.max()])
        

figE.pdf

On voit à présent l'harmonique de rang 5, dont l'amplitude est à environ -45 dB du fondamental.

Pour tester la stabilité de la méthode numérique, effectuons le calcul sur une durée beaucoup plus longue :

tmax=1000
t = np.arange(start=0,stop=tmax,step=te)
y = scipy.integrate.odeint(equation,y0,t,rtol=1e-8,atol=1e-8)
yt = y.transpose()
theta = yt[0]
omega = yt[1]
figure(figsize=(6,6))
plot(theta,omega/(2*math.pi))
xlabel('theta')
ylabel('omega')
axis([-4,4,-4,4])
        

figF.pdf

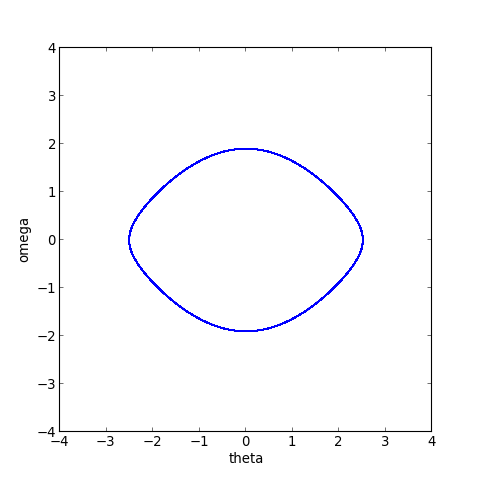
Sur le portrait de phase, tout se passe bien. Voyons l'énergie en fonction du temps :

energie = 0.5*np.power(omega,2)-(2*math.pi)**2*np.cos(theta)
figure(figsize=(12,4))
plot(t,energie)
xlabel('t')
ylabel('energie')
        

figG.pdf

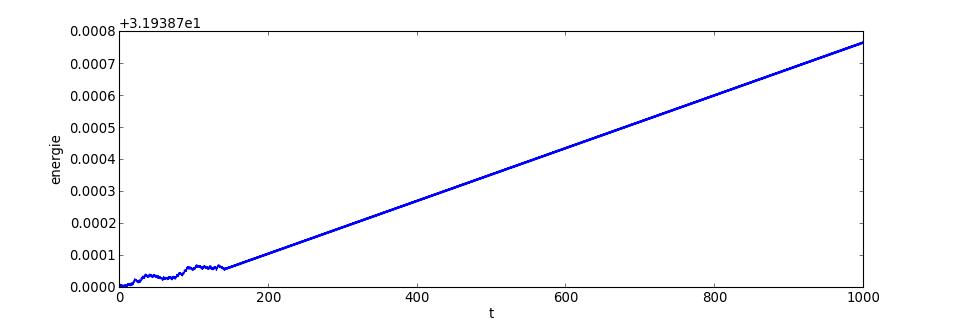
Bien que l'erreur sur l'énergie reste faible à l'instant maximal, on devine sur cette figure une augmentation sans fin de l'erreur lorsqu'on augmente le temps de calcul. Cela vient de l'instabilité de la méthode numérique utilisée vis à vis du système étudié. C'est pour cette raison que d'autres méthodes numériques (méthode de Stormer-Verlet) sont utilisées pour les simulations des systèmes conservatifs sur le long terme (dynamique moléculaire, système solaire, etc).

3. Période d'oscillation

Pour un angle initial ${\theta }_0$ et une vitesse angulaire initiale nulle, l'intégrale première fournit la vitesse angulaire en fonction de l'angle :

$$\frac{d\theta }{dt}=\sqrt{2{\omega }_0^2(cos\theta -cos{\theta }_0)}$$

Sachant que le mouvement est périodique, on en déduit la période sous forme d'une intégrale :

$$\frac{T}{4}={\int }_0^{{\theta }_0}\frac{d\theta }{\sqrt{2{\omega }_0^2(cos\theta -cos{\theta }_0)}}$$

Pour une valeur donnée de l'angle initial, l'intégrale peut être calculée numériquement avec la fonction scipy.integrate.quad :

theta0=0.8*math.pi
def f(theta):
    return 4.0/(math.sqrt(2*(2*math.pi)**2*(math.cos(theta)-math.cos(theta0))))
T = scipy.integrate.quad(f,0,theta0)
            

print(T)
--> (1.655096644746601, 1.2293956963560504e-09)

La première valeur est la valeur approchée de l'intégrale, la seconde une estimation de l'erreur absolue.

La fréquence correspondante :

f = 1.0/T[0]
            

print(f)
--> 0.6041943249501919