Méthode d'Euler explicite

1. Définition

Soit une équation différentielle pour la fonction y de la variable t de la forme suivante :

$$\frac{dy}{dt}=f(t,y\left(t\right))\text{(1)}$$

avec la condition initiale

$$y\left(0\right)=y_0\text{(2)}$$

La variable t sera appelée le temps. Dans le cas d'un système différentiel du premier ordre, y désigne une matrice colonne comportant les fonctions inconnues.

L'intégration numérique d'une équation de ce type consiste à calculer des valeurs approchées de y sur un intervalle [0,T]. Pour cela, on divise cet intervalle en N sous-intervalles de longueur h=T/N et on définit les instants :

$$t_n=nh\text{(3)}$$

où l'entier n varie de 0 à N. Dans la méthode d'Euler explicite, la valeur approchée à l'instant t_n+1 est obtenue à partir de la précédente par

$$y_{n+1}=y_n+hf(t_n,y_n)\text{(4)}$$

On définit l'erreur (globale) à l'instant t_n par :

$$e_n=|y\left(t_n\right)-y_n|\text{(5)}$$

Bien entendu, la résolution numérique n'a d'intérêt que si la solution exacte y(t) ne peut être déterminée. Aussi l'erreur ne peut être connue avec précision mais nous verrons qu'il est possible de savoir comment cette erreur dépend du pas h. Une autre question très importante est l'évolution de l'erreur e_n en fonction de n : c'est le problème de la stabilité.

Supposons que y(t_n) soit connu sans imprécision. On appelle erreur locale l'erreur introduite pour le calcul à l'instant suivant. La méthode d'Euler repose sur le développement de Taylor suivant :

$$y\left(t_{n+1}\right)\simeq y\left(t_n\right)+h\frac{dy}{dt}\left(t_n\right)\text{(6)}$$

dans lequel le terme négligé est d'ordre h². Pour cette raison, la méthode d'Euler est dite d'ordre 1. L'erreur locale est donc vraisemblablement proportionnelle à h², ce qui signifie qu'une réduction du pas h d'un facteur 2 réduit l'erreur locale d'un facteur 4.

2. Programmation avec scilab

Pour tester le fonctionnement, on considère l'équation différentielle de l'oscillateur harmonique, qui se met sous la forme d'un système différentiel du premier ordre :

$$\begin{array}{ccc}\hfill & \frac{d{y}_1}{dt}=y_2\hfill & \hfill \text{(7)}\\ \hfill & \frac{d{y}_2}{dt}=-4{\pi }^2{y}_1\hfill & \hfill \text{(8)}\end{array}$$

Le système différentiel est défini par une fonction :

function [dy]=oscillateur(t,y),
 dy(1)=y(2),
 dy(2)=-4*%pi^2*y(1),
endfunction 
   

La fonction suivante effectue le calcul de y_n+1 à partir de y_n :

function [y]=pasEuler(systeme,ne,h,t,yn),
   dy = systeme(t,yn);
   for e=1:ne,
    y(e) = yn(e)+h*dy(e)
   end;
endfunction
   
   

Pour stocker les valeurs obtenues sur l'intervalle [0,T], on utilise la convention de la fonction ode de scilab : les valeurs sont stockées dans une matrice dont chaque ligne correspond à une composante de y. La fonction suivante effectue le calcul complet, avec une condition initiale (instant 0) définie dans une matrice colonne.

function [mt,my]=euler(yi,T,N,systeme,ne),
   h = T/N;
   my = zeros(ne,N+1);
   mt = zeros(1,N+1);
   my(:,1)=yi;
   mt(1)=0;
   for k=1:N,
    my(:,k+1)=pasEuler(systeme,ne,h,mt(k),my(:,k));
    mt(k+1) = mt(k)+h;
   end;
endfunction
   

Voyons le fonctionnement avec le système défini plus haut :

yi=[1;0];
ne=2;
N=1000;
T=5;
[mt,my] = euler(yi,T,N,oscillateur,ne);
   

figA=scf();
plot2d(mt,my(1,:));
xtitle('','t','y(1)');
   

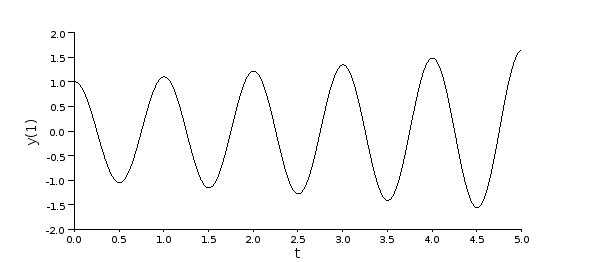figA.pdf

3. Étude de l'erreur

Pour l'exemple précédent, la solution exacte est connue. On peut donc tracer l'erreur en fonction du temps pour la fonction y₁ :

figB=scf();
plot2d(mt,abs(my(1,:)-cos(2*%pi*mt)));
xtitle('','t','erreur');
   

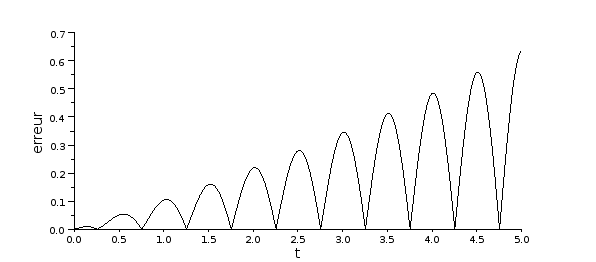figB.pdf

Le caractère oscillatoire de l'erreur montre qu'il ne faut pas se contenter d'étudier l'erreur pour une valeur fixée de t. Voyons comment évolue l'erreur si on réduit le pas d'un facteur 2 :

N=N*2;
[mt2,my2] = euler(yi,T,N,oscillateur,ne);
N=N*2;
[mt3,my3] = euler(yi,T,N,oscillateur,ne);
   

figC=scf();
plot2d(mt,abs(my(1,:)-cos(2*%pi*mt)),style=4);
plot2d(mt2,abs(my2(1,:)-cos(2*%pi*mt2)),style=5);
plot2d(mt3,abs(my3(1,:)-cos(2*%pi*mt3)),style=6);
xtitle('','t','erreur');
   

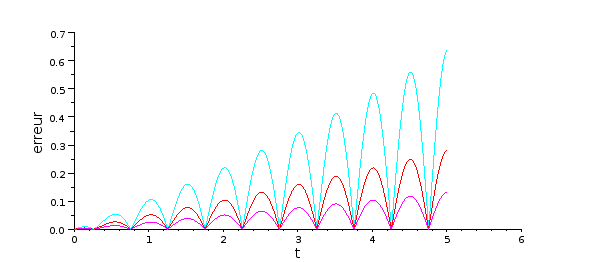figC.pdf

L'erreur est (à peu près) divisée par deux à chaque fois que le pas est réduit d'un facteur 2. Pour une méthode d'ordre 1, l'erreur globale est en effet proportionnelle à h. Bien entendu, la valeur effective de l'erreur dépend de l'équation différentielle, mais aussi de l'instant considéré comme on le voit sur cet exemple.

Pour étudier plus en détail l'évolution de l'erreur avec le pas, on peut la calculer à un instant où elle est maximale. La fonction suivante calcule seulement le point à l'instant T choisi :

function my=eulerEnd(yi,T,N,systeme,ne),
   y = yi;
   h = T/N;
   t = 0;
   for k=1:N,
    my = pasEuler(systeme,ne,h,t,y);
    y = my;
    t = t+h;
   end;
endfunction   
   

Voyons l'erreur en t=4.5 en fonction de h :

N=logspace(2,5,30);
e=N;
h=N;
k=size(N); k=k(2);
T=4.5;
for i=1:k,
 my = eulerEnd(yi,T,N(i),oscillateur,ne);
 e(i) = abs(my(1)-cos(2*%pi*T));
 h(i) = T/N(i);
end;
   

figD=scf();
plot2d(h,e,style=-5,logflag='ll');
xtitle('','h','erreur');
   

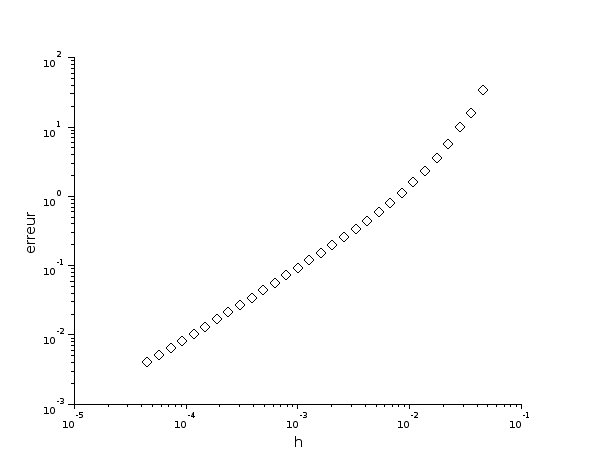figD.pdf

On constate sur cet exemple que l'erreur évolue proportionnellement à h seulement pour des valeurs assez petites.

4. Étude de la stabilité

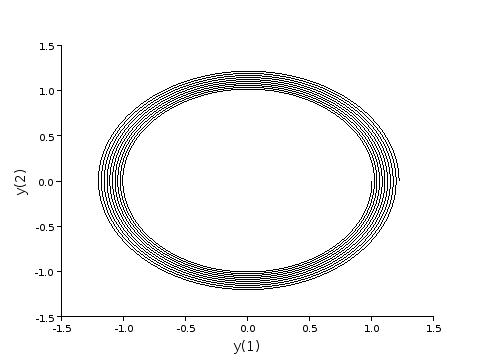
La méthode d'Euler est instable pour l'équation différentielle considérée ci-dessus (oscillateur harmonique) car le maximum local de l'erreur ne fait que croître avec le temps. Pour voir l'effet de cette instabilité on peut tracer la trajectoire dans l'espace des phases (ici plan) :

T=10;
N=10000;
[mt,my] = euler(yi,T,N,oscillateur,ne);
   

figE=scf();
plot2d(my(1,:),my(2,:)/(2*%pi));
xtitle('','y(1)','y(2)');
   

figE.pdf

L'instabilité se traduit par un éloignement progressif et sans borne de la courbe par rapport à la trajectoire fermée correspondant à la solution exacte (cercle de rayon 1).

L'étude théorique de la stabilité se fait en considérant l'équation différentielle linéaire suivante ([1]):

$$\frac{dy}{dt}=qy\left(t\right)\text{(9)}$$

où q est un nombre complexe. Ce type d'équation survient dans la résolution des systèmes différentiels linéaires. Pour la condition initiale y(0)=1, la solution est :

$$y\left(t\right)=exp\left(qt\right)\text{(10)}$$

Pour cette équation, la méthode d'Euler s'écrit :

$$y_{n+1}=(1+hq)y_n\text{(11)}$$

Les valeurs approchées obtenues par cette méthode sont donc :

$$y_n=y_0{(1+hq)}^n\text{(12)}$$

On pose z=hq. Le domaine de stabilité est défini comme le domaine du plan complexe où la suite précédente est bornée, c'est-à-dire :

$$|1+z|\le 1\text{(13)}$$

Il s'agit du disque de centre z=-1 et de rayon 1. Pour des points situés hors de ce disque et dont la partie réelle est négative, la méthode d'Euler conduit à une solution non bornée alors que la solution exacte tend vers zéro.

D'une manière plus générale, un système différentiel linéaire se met sous la forme matricielle suivante :

$$y\text{'}\left(t\right)=My\left(t\right)\text{(14)}$$

où M est une matrice carrée. L'étude de stabilité doit être faite pour chacune des valeurs propres q de la matrice M.

Voyons par exemple les valeurs propres pour l'équation de l'oscillateur harmonique :

M=[0,1;-4*%pi^2,0];
vp = spec(M);
   

%i*6.2831853 
-%i*6.2831853 

On en déduit que z=hq est en dehors du domaine de stabilité, pour ces deux valeurs propres et quelque soit la valeur de h (non nulle). La méthode d'Euler est donc toujours instable pour cet équation différentielle.

Voyons à présent l'équation différentielle d'un oscillateur harmonique amorti :

$$\begin{array}{ccc}\hfill & \frac{d{y}_1}{dt}=y_2\hfill & \hfill \text{(15)}\\ \hfill & \frac{d{y}_2}{dt}=-4{\pi }^2{y}_1-0\mathrm{.}1y_2\hfill & \hfill \text{(16)}\end{array}$$

Les valeurs propres sont :

M=[0,1;-4*%pi^2,-0.1];
vp = spec(M);
   

-0.05+%i*6.2829864 
-0.05-%i*6.2829864 

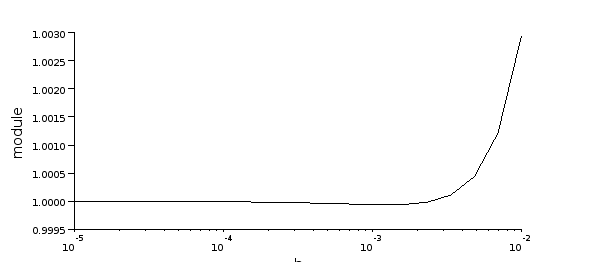
La condition de stabilité s'écrit donc

$$|1+(-0\mathrm{.}05\pm i2\pi )h|\le 1\text{(17)}$$

soit

$${(1-0\mathrm{.}05h)}^2+4{\pi }^2{h}^2\le 1\text{(18)}$$

n=20;
h=logspace(-5,-2,n);
m = h;
for i=1:n,
 m(i)=(1-0.05*h(i))^2+4*%pi^2*h(i)^2;
end;
   

figF=scf();
plot2d(h,m,logflag='ln');
xtitle('','h','module')
   

figF.pdf

La stabilité est donc obtenue pour des valeurs de h inférieures à environ 0.003. Pour le vérifier, on définit le système correspondant :

function [dy]=amorti(t,y),
 dy(1)=y(2),
 dy(2)=-4*%pi^2*y(1)-0.1*y(2),
endfunction
   

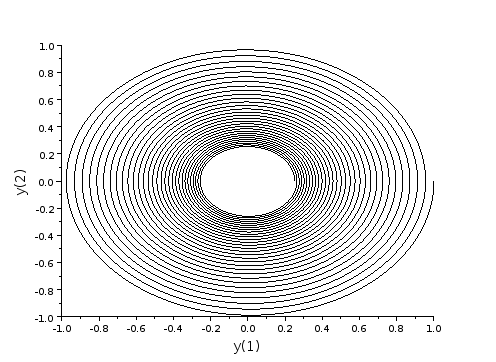
On intègre avec la méthode d'Euler puis on trace la trajectoire dans l'espace des phases :

T=30;
h=2e-4;
N=int(T/h);
ne=2;
yi=[1;0];
[mt1,my1] = euler(yi,T,N,amorti,ne);
   

figG=scf();
plot2d(my1(1,:),my1(2,:)/(2*%pi));
xtitle('','y(1)','y(2)');
   

figG.pdf

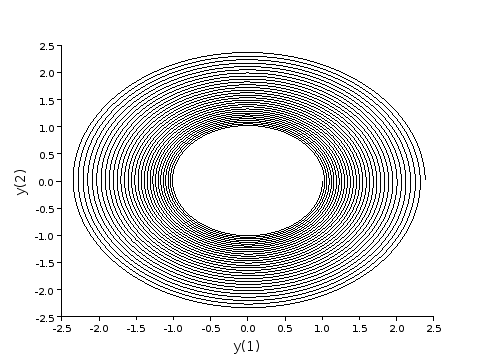
L'amplitude de l'oscillation est décroissante, comme prévu pour un oscillateur harmonique amorti. Voyons pour un pas en dehors du domaine de stabilité :

h=4e-3;
N=int(T/h);
ne=2;
yi=[1;0];
[mt2,my2] = euler(yi,T,N,amorti,ne);
   

figH=scf();
plot2d(my2(1,:),my2(2,:)/(2*%pi));
xtitle('','y(1)','y(2)');
   

figH.pdf

Cette fois-ci l'amplitude de l'oscillation augmente. L'instabilité se traduit ici par un comportement opposé à celui attendu.

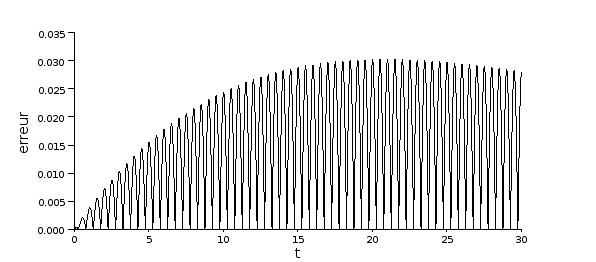
Pour finir, traçons l'erreur pour un pas h situé dans le domaine de stabilité :

s=size(mt1); s=s(2);
e=zeros(s);
for i=1:s,
 e(i) = abs(my1(1,i)-exp(-0.05*mt1(i))*(cos(2*%pi*mt1(i))+0.05/(2*%pi)*sin(2*%pi*mt1(i))));
end;
  

figJ=scf();
plot2d(mt1,e);
xtitle('','t','erreur');
  

figJ.pdf