Convertisseur continu-continu abaisseur
2.c. Équations différentielles
2.f. Résolution semi-analytique
3.c. Étude à rapport cyclique fixé
1. Introduction
Ce document étudie le fonctionnement d'un convertisseur continu-continu abaisseur de tension (ou convertisseur DC-DC buck). L'étude théorique et les simulations numériques sont faites en prenant en compte la résistance interne de la source et celle de la bobine.
La réalisation d'un convertisseur piloté par Arduino est aussi présentée, avec une régulation de la tension par un correcteur proportionnel-intégrale-dérivée.
Ce type de convertisseur est utilisé dans les alimentations à découpage. L'alimentation d'un moteur à courant continu fait aussi appel à un convertisseur abaisseur.
2. Étude théorique
2.a. Transistor MOSFET
Un convertisseur à découpage fonctionne avec un ou deux commutateurs commandés. Pour les applications de moyenne puissance, le transistor MOSFET est le plus employé.
Le transistor MOSFET comporte trois bornes : le drain (D), la source (S) et la grille (G). Lorsque la tension entre la grille et la source est supérieure à environ 10 V, un courant peut circuler du drain vers la source avec une résistance de l'ordre de 0,5 ohms et de la source vers le drain avec une résistance encore plus faible si la tension VD-VS est inférieure à -0,7 V. Dans la mesure où la résistance drain source est négligée, le schéma équivalent du transistor losque la grille est polarisée est donc un interrrupteur fermé, qui par définition laisse passer le courant dans les deux sens.
Lorsque la grille est au même potentiel que la source (ou que la différence de potentiel est inférieure à 10 V), aucun courant ne circule du drain vers la source mais la caractéristique drain-source est à-peu-près celle d'une diode, laissance passer un courant de la source vers le drain lorsque la tension VD-VS est inférieure à -0,7 V. Lorsque la grille n'est pas polarisée, le transitor est donc équivalent à une diode. Finalement, le transistor est approximativement équivalent à un interrupteur commandé par la tension grille-source en parallèle avec une diode orientée de la source vers le drain. Cette diode joue un rôle seulement lorsque la grille n'est pas polarisée.
Figure pleine page2.b. Schéma du convertisseur
Le convertisseur continu-continu élévateur de tension [1][2], dans sa version la plus simple (convertisseur non synchrone), comporte un transistor MOSFET (modélisé par une diode en parallèle avec un interrupteur) et une diode :
Figure pleine pageVe est la tension d'entrée, délivrée par la source d'énergie. R est la résistance de charge. Vs est la tension de sortie, c'est-à-dire la tension aux bornes de la résistance de charge. Ces deux tensions sont positives. Dans cette version, l'énergie ne peut circuler que de la source vers la charge.
Bien que ce ne soit pas toujours le cas en réalité, la tension Ve sera considérée comme parfaitement constante pour l'étude théorique. L'interrupteur est commandé avec une période de découpage T. Le rapport cyclique est : l'état 1 a une durée , l'état 2 a une durée . Dans l'état 1, la diode est bloquée et le courant d'intensité i(t) positive délivrée par la source de tension s'écoule vers la charge via la bobine de filtrage (auto-inductance L et résistance interne r). Remarquons que dans l'état 1, la source du transistor est pratiquement au potentiel Ve. Lorsque, partant de l'état 1, la tension de grille est annulée, ce courant ne peut plus circuler. Sa rapide décroissance provoque l'apparition d'une f.é.m. très forte aux bornes de l'auto-inductance qui rend la diode D conductrice (cette diode est souvent appelée diode de roue libre). Dans l'état 2, le potentiel de la source du transistor est donc très faible et en conséquence le transistor ne laisse passer aucun courant (ni dans un sens ni dans l'autre). Le rôle du condensateur est de filtrer le courant délivré par la source de tension afin qu'il varie le moins possible. Le rôle de la bobine est de filtrer la tension Vs afin qu'elle varie le moins possible. Bien évidemment, ce condensateur n'a aucun effet sur le fonctionnement du circuit lorsque la source est idéale (re=0). Si la source est un accumulateur, le condensateur permet de lisser les variations de tension dues à la résistance interne de celui-ci. Dans le cas d'une alimentation à découpage branchée sur le secteur, la source est en réalité un pont de redressement dont la tension de sortie est loin d'être constante (bien que de valeur moyenne positive) et le condensateur joue un rôle essentiel de lissage de cette tension. Les filtrages réalisés dans ce schéma sont du premier ordre mais il est possible d'améliorer le filtrage avec des filtres du deuxième ordre. En particulier, il est courant d'améliorer le filtrage en sortie en ajoutant un condensateur aux bornes de la charge (Amélioration du filtrage).
Nous considérons le convertisseur suivant (convertisseur synchrone), comportant deux transistors MOSFET :
Figure pleine pageCe circuit fonctionne comme le précédent à une différence près : le passage à l'état passant du transitor 2 dans le sens source-drain est commandé dès le début de l'état 2 (au même moment que l'ouverture de K1) au lieu de se faire dès que la tension source-drain dépassage la tension de seuil de la diode. Rappelons que, lorsque le transistor 2 est passant, sa diode drain-source peut être ignorée puisque le courant passe dans l'interrupteur fermé. Ce convertisseur est qualifié de synchrone car le passage du courant dans le commutateur 2 se fait de manière synchrone avec l'ouverture de K1. Dans l'état 2, l'énergie dissipée dans le transistor 2 est inférieure à celle dissipée dans la diode de roue libre du convertisseur non synchrone. Il s'en suit une meilleure efficacité du convertisseur synchrone. Une autre propriété intéressante de ce circuit est sa réversibilité : si la charge et la source sont inversées, on obtient un convertisseur continu-continu élévateur (ou convertisseur boost). Si le convertisseur est utilisé pour alimenter un moteur à courant continu et si la source est un accumulateur, le transfert d'énergie du moteur vers la source est possible (régénération).
Dans l'état 2, le courant i(t) est décroissant. Il peut devenir négatif car le transistor 2 est conducteur dans le sens drain-source. Dans le cas du convertisseur non synchrone, où une diode remplace ce transistor, le courant i(t) est toujours positif : dès qu'il s'annule, la diode devient bloquante et il reste nul jusqu'au passage à l'état 1.
Lorsque le convertisseur synchrone est étudié expérimentalement, il est possible de reproduire le comportement du convertisseur non synchrone en laissant le transistor 2 tout le temps ouvert (grille non polarisée) : la diode de roue libre est alors la diode source-drain du transistor.
2.c. Équations différentielles
Il y a deux courants à déterminer : ie(t) (courant sortant de la source) et i(t) (courant traversant la charge). Pour une tension Ve(t) quelconque, les deux équations différentielles couplées dans l'état 1 sont :
et dans l'état 2 :
Pour chacun des deux états, la condition initiale est fournie par deux conditions de continuité. La première est la continuité du courant dans L, c'est-à-dire la continuité de i(t). La seconde est la continuité de la tension aux bornes de C. Or cette tension est Ve-reie donc, si la tension Ve est une fonction continue, le courant ie(t) est aussi continu au moment du changement d'état. À l'instant initial de la simulation, la tension d'entrée passe de 0 à Ve, i=0 et, puisque le condensateur est déchargé, ie=Ve/re.
Lorsque la tension Ve est constante et si la résistance re est nulle (source idéale), il est aisé de déterminer la valeur moyenne de Vs sur une période. Pour ce faire, on utilise le fait que la moyenne de la tension aux bornes d'une auto-inductance est nulle (puisque cette tension est la dérivée temporelle d'une fonction périodique) et que le courant moyen dans une capacité est nul. Si l'on note les valeurs moyennes en majuscule, on a où V2 est la tension drain-source moyenne du transistor 2, qui s'obtient sans difficulté : . On obtient donc, pour une source idéale :
2.d. Résolution numérique
Le système différentiel peut être résolu numériquement. L'avantage de cette méthode est qu'elle peut s'adapter sans difficultés au cas où la tension Ve n'est pas constante.
La fonction suivante effectue la résolution numérique sur une période du découpage, pour une tension d'entrée constante :
import numpy as np
from matplotlib.pyplot import *
from scipy.integrate import odeint
def periode(L,r,C,re,R,T,alpha,Ve,t0,ie0,i0,N=100):
def systeme1(Y,t): # Y[0] : ie, Y[1] : i
dY0 = (Y[1]-Y[0])/(re*C)
dY1 = (Ve-re*Y[0]-(r+R)*Y[1])/L
return [dY0,dY1]
temps1 = np.linspace(t0,t0+T*alpha,N//2)
sol = odeint(systeme1,[ie0,i0],temps1,rtol=1e-4,atol=1e-4)
ie1 = sol[:,0]
i1 = sol[:,1]
def systeme2(Y,t):
dY0 = (-Y[0])/(re*C)
dY1 = (-(r+R)*Y[1])/L
return [dY0,dY1]
temps2 = np.linspace(t0+T*alpha,t0+T,N//2)
sol = odeint(systeme2,[ie1[-1],i1[-1]],temps2,rtol=1e-4,atol=1e-4)
ie2 = sol[:,0]
i2 = sol[:,1]
temps = np.concatenate((temps1,temps2))
ie = np.concatenate((ie1,ie2))
i = np.concatenate((i1,i2))
return temps,ie,i
La fonction suivante effectue le calcul pour P périodes :
def simulation(L,r,C,re,R,T,alpha,Ve,t0,ie0,i0,P,N=100):
tab_temps = np.zeros(N*P)
tab_ie = np.zeros(N*P)
tab_i = np.zeros(N*P)
k = 0
for p in range(P):
temps,ie,i = periode(L,r,C,re,R,T,alpha,Ve,t0,ie0,i0,N)
ie0 = ie[-1]
i0 = i[-1]
t0 += T
tab_temps[k:k+N] = temps
tab_ie[k:k+N] = ie
tab_i[k:k+N] = i
k += N
return tab_temps,tab_ie,tab_i
Voici un exemple de simulation, avec une fréquence de découpage de 20 kHz :
L = 0.5e-3
r = 1
C = 2000e-6
R = 10
Ve = 10
re = 1
alpha = 0.5
ie0 = Ve/re
i0 = 0
t0 = 0
T = 5e-5 # 20 kHz
P = 1500
temps,ie,i = simulation(L,r,C,re,R,T,alpha,Ve,t0,ie0,i0,P)
figure(figsize=(16,8))
subplot(211)
title(r"$V_e=10\ {\rm V},\ \alpha=0{,}5$",fontsize=16)
plot(temps,ie)
grid()
ylabel(r"$i_e\ (\rm A)$",fontsize=16)
subplot(212)
plot(temps,R*i)
grid()
xlabel("t (s)",fontsize=16)
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
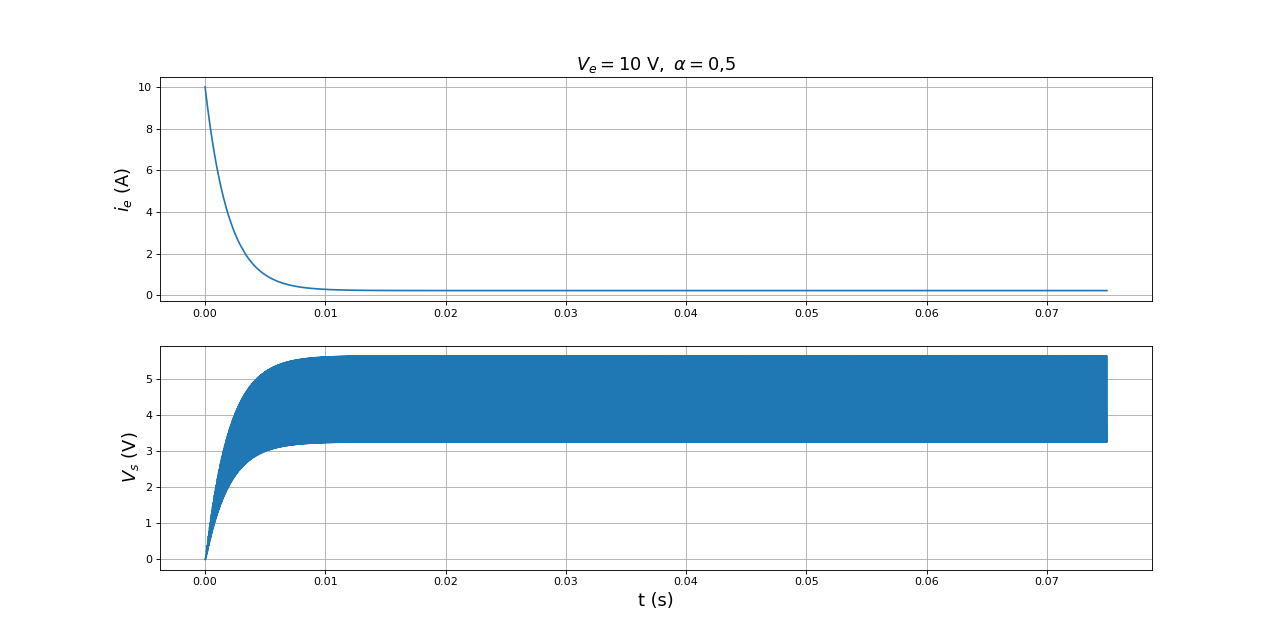 fig1.pdf
fig1.pdf
figure(figsize=(16,8))
subplot(211)
title(r"$V_e=10\ {\rm V},\ \alpha=0{,}5$",fontsize=16)
plot(temps,ie)
xlim(0.02,0.021)
ylim(0,0.5)
grid()
ylabel(r"$i_e\ (\rm A)$",fontsize=16)
subplot(212)
plot(temps,R*i)
xlim(0.02,0.021)
grid()
xlabel("t (s)",fontsize=16)
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
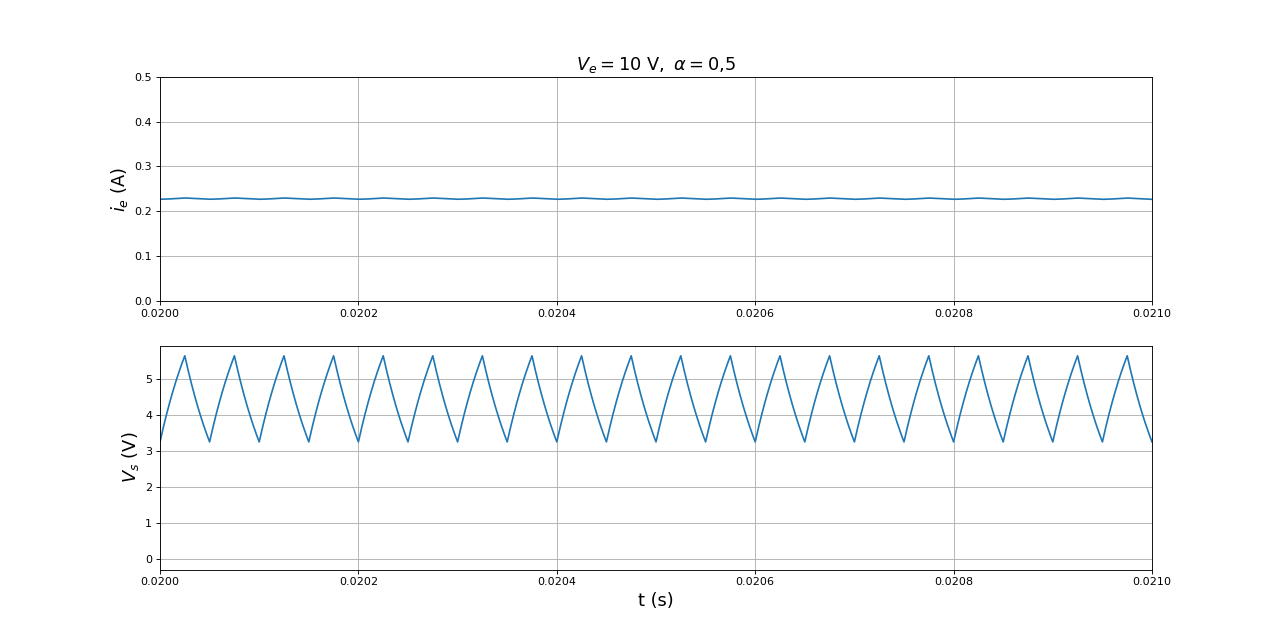 fig2.pdf
fig2.pdf
La fonction suivante calcule le taux d'ondulation d'une grandeur en régime permanent (le calcul se fait sur la seconde moitié du signal) :
def ondulation(x): N = len(x) x = x[N//2:N] return (x.max()-x.min())/x.mean() ondulVs = ondulation(R*i)
print(ondulVs) --> np.float64(0.5363748452985085)
Le taux d'ondulation de la tension de sortie est très grand. Ce résultat était prévisible puisque le temps de réponse du circuit RL est , deux fois plus grand que la période. Pour réduire l'ondulation sans changer le circuit, il faut soit réduire encore la résistance de charge (qui est déjà faible), soit augmenter la fréquence d'échantillonnage (qui est déjà grande).
2.e. Amélioration du filtrage
Un lissage beaucoup plus efficace de la tension de sortie est obtenu en ajoutant un condensateur en parallèle avec la charge :
Figure pleine pageDans le cas de l'alimentation d'un moteur à courant continu, ce type de filtrage est irréalisable puisque l'auto-inductance est celle du moteur. Cependant, la résistance R est nulle dans ce cas (il n'y a que la résistance du bobinage) donc le temps de réponse est plus petit.
Le filtre de sortie est à présent un filtre LC d'ordre 2. Il est intéressant d'étudier la réponse fréquentielle de ce filtre. Voici sa fonction de transfert en régime sinusoïdal :
Cs = 1000e-6
f = np.logspace(2,6,1000)
w = f*2*np.pi
H1 = R/(r+R+1j*L*w)
GdB1 = 20*np.log10(np.absolute(H1))
H2 = 1/(1+(r+1j*L*w)*(1/R+1j*Cs*w))
GdB2 = 20*np.log10(np.absolute(H2))
figure()
plot(f,GdB1,label="L")
plot(f,GdB2,label="LC")
legend(loc="upper right")
xscale('log')
grid()
xlabel("f (Hz)",fontsize=16)
ylabel("GdB",fontsize=16)
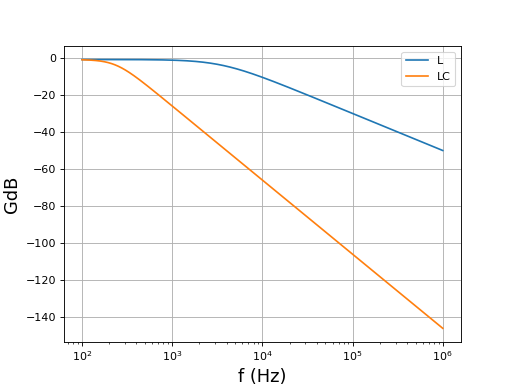 fig3.pdf
fig3.pdf
L'amélioration est considérable : pour une fréquence de découpage de 20 kHz, on a une atténuation d'environ 80 dB contre seulement 20 dB pour le premier filtre (la fréquence de coupure et abaissée et la pente est plus grande).
Pour un convertisseur idéal (r=re=0) l'analyse par valeur moyenne conduit à donc la tension en sortie ne dépend pas de la résistance de charge.
Les trois courants à déterminer sont ie(t),i2(t),i(t). Les deux premiers sont continus au moment du changement d'état. Le troisième l'est aussi en raison de la continuité de la tension aux bornes de Cs. Dans l'état 1, les équations différentielles sont :
et dans l'état 2 :
Pour la résolution numérique, il faut écrire explicitement le système différentiel du premier ordre. Le voici pour l'état 1 lorsque la tension Ve est constante :
et pour l'état 2 :
La relation pour une source idéale (re=0) reste valable puisque le courant moyen dans Cs est nul.
Voici la nouvelle fonction de calcul sur une période :
def periode(L,r,C,re,R,Cs,T,alpha,Ve,t0,ie0,i20,i0,N=100):
def systeme1(Y,t): # Y[0] : ie, Y[1] : i2, Y[2] : i
dY0 = (Y[2]-Y[0])/(re*C)
dY1 = (Ve-re*Y[0]-r*Y[1]-R*Y[2])/L
dY2 = (Y[1]-Y[2])/(Cs*R)
return [dY0,dY1,dY2]
temps1 = np.linspace(t0,t0+T*alpha,N//2)
sol = odeint(systeme1,[ie0,i20,i0],temps1,rtol=1e-4,atol=1e-4)
ie_1 = sol[:,0]
i2_1 = sol[:,1]
i_1 = sol[:,2]
def systeme2(Y,t):
dY0 = (-Y[0])/(re*C)
dY1 = (-r*Y[1]-R*Y[2])/L
dY2 = (Y[1]-Y[2])/(Cs*R)
return [dY0,dY1,dY2]
temps2 = np.linspace(t0+T*alpha,t0+T,N//2)
sol = odeint(systeme2,[ie_1[-1],i2_1[-1],i_1[-1]],temps2,rtol=1e-4,atol=1e-4)
ie_2 = sol[:,0]
i2_2 = sol[:,1]
i_2 = sol[:,2]
temps = np.concatenate((temps1,temps2))
ie = np.concatenate((ie_1,ie_2))
i2 = np.concatenate((i2_1,i2_2))
i = np.concatenate((i_1,i_2))
return temps,ie,i2,i
def simulation(L,r,C,re,R,Cs,T,alpha,Ve,t0,ie0,i20,i0,P,N=100):
tab_temps = np.zeros(N*P)
tab_ie = np.zeros(N*P)
tab_i2 = np.zeros(N*P)
tab_i = np.zeros(N*P)
k = 0
for p in range(P):
temps,ie,i2,i = periode(L,r,C,re,R,Cs,T,alpha,Ve,t0,ie0,i20,i0,N)
ie0 = ie[-1]
i20 = i2[-1]
i0 = i[-1]
t0 += T
tab_temps[k:k+N] = temps
tab_ie[k:k+N] = ie
tab_i2[k:k+N] = i2
tab_i[k:k+N] = i
k += N
return tab_temps,tab_ie,tab_i2,tab_i
Voici une simulation reprenant les valeurs précédentes :
L = 0.5e-3
r = 1
C = 2000e-6
R = 10
Cs = 1000e-6
Ve = 10
re = 1
alpha = 0.5
T = 5e-5 # 20 kHz
P = 1500
temps,ie,i2,i = simulation(L,r,C,re,R,Cs,T,alpha,Ve,0,Ve/re,0,0,P)
figure(figsize=(16,8))
subplot(211)
title(r"$V_e=10\ {\rm V},\ \alpha=0{,}5$",fontsize=16)
plot(temps,ie,label=r"$i_e$")
plot(temps,i2,label=r"$i_2$")
legend(loc="upper right")
grid()
ylabel(r"$i\ (\rm A)$",fontsize=16)
subplot(212)
plot(temps,R*i)
grid()
xlabel("t (s)",fontsize=16)
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
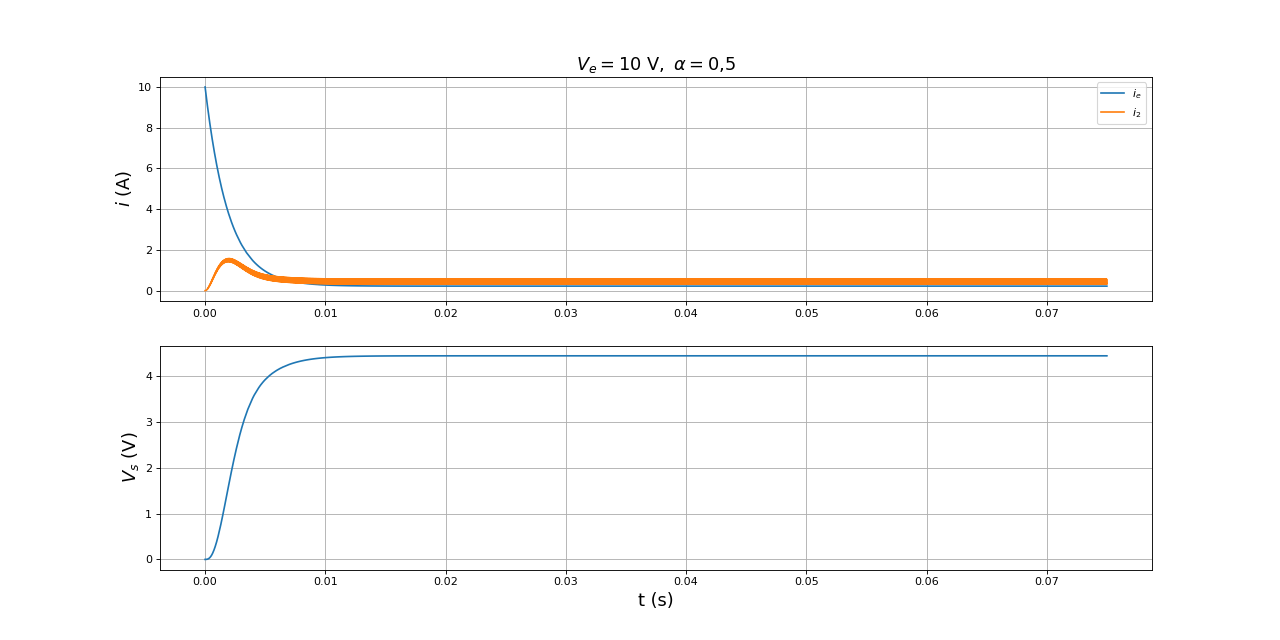 fig4.pdf
fig4.pdf
ondulVs = ondulation(R*i)
print(ondulVs) --> np.float64(0.0003400310008057523)
Comme prévu d'après la réponse fréquentielle, les ondulations sont extrêmement faibles. On peut se permettre d'augmenter la résistance de charge :
L = 0.5e-3
r = 1
C = 2000e-6
R = 200
Cs = 1000e-6
Ve = 10
re = 1
alpha = 0.5
T = 5e-5 # 20 kHz
P = 1500
temps,ie,i2,i = simulation(L,r,C,re,R,Cs,T,alpha,Ve,0,Ve/re,0,0,P)
figure(figsize=(16,8))
subplot(211)
title(r"$V_e=10\ {\rm V},\ \alpha=0{,}5$",fontsize=16)
plot(temps,ie,label=r"$i_e$")
plot(temps,i2,label=r"$i_2$")
legend(loc="upper right")
grid()
ylabel(r"$i\ (\rm A)$",fontsize=16)
subplot(212)
plot(temps,R*i)
grid()
xlabel("t (s)",fontsize=16)
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
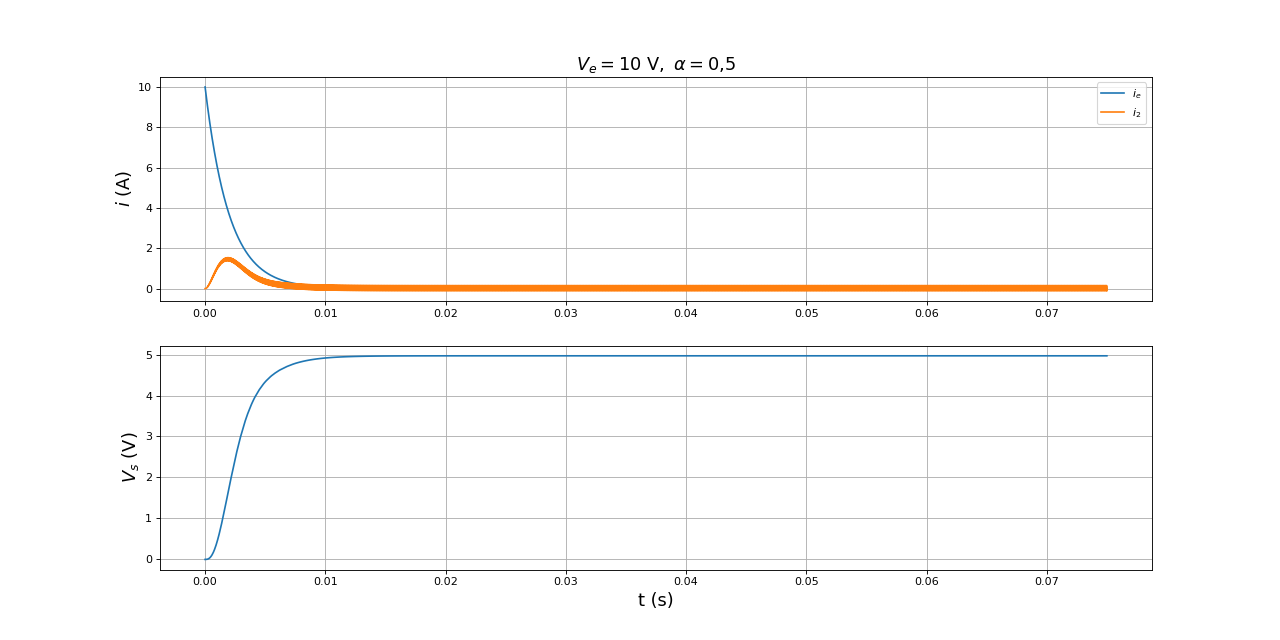 fig5.pdf
fig5.pdf
ondulVs = ondulation(R*i)
print(ondulVs) --> np.float64(0.0003115905460091685)
Voici un détail montrant les variations de courant en régime permanent :
figure(figsize=(16,6))
title(r"$V_e=10\ {\rm V},\ \alpha=0{,}5$",fontsize=16)
plot(temps,ie,label=r"$i_e$")
plot(temps,i2,label=r"$i_2$")
legend(loc="upper right")
grid()
ylabel(r"$i\ (\rm A)$",fontsize=16)
xlim(0.02,0.0202)
ylim(-0.2,0.2)
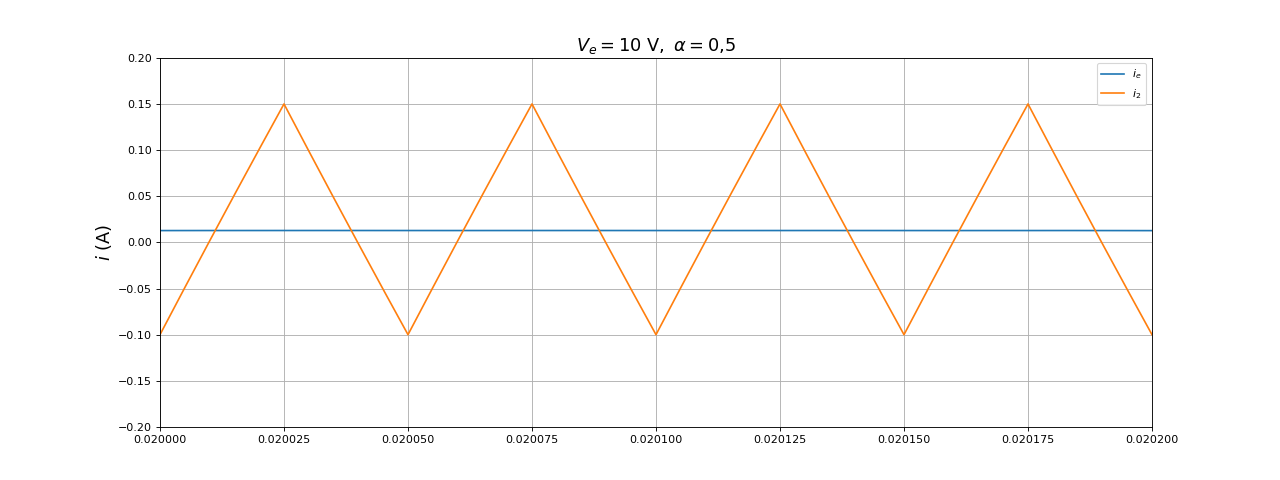 fig6.pdf
fig6.pdf
Au cours de l'état 2, le courant i2(t) décroît puis devient négatif. En effet, l'amplitude d'ondulation de ce courant ne dépend pas de la résistance de charge et le courant moyen décroît lorsque R augmente : il y a en conséquence un courant moyen minimal (égal à la moitié de l'amplitude d'ondulation) pour que i2(t) soit toujours positif. Pour le convertisseur synchrone considéré ici, ce courant négatif se réalise effectivement et ne pose pas de problème. En revanche, pour le convertisseur non synchrone (diode à la place du transistor 2), le courant reste égal à zéro après s'être annulé (car la diode devient bloquante). Le convertisseur est alors en mode de conduction discontinue, qui doit être évité [3].
2.f. Résolution semi-analytique
Pour chacun des deux états, le système différentiel peut être résolu analytiquement.
Introduisons la matrice colonne suivante :
Le système d'équations différentielles s'écrit :
Pour l'état 1, on a :
et pour l'état 2 :
La solution particulière constante Yp est obtenue par résolution du système AY=-B.
La solution générale de l'équation sans second membre, c'est-à-dire , est recherchée sous la forme , ce qui conduit à l'équation . Il s'agit donc de rechercher les valeurs propres et vecteurs propres complexes de la matrice A. Supposons qu'elle soit diagonalisable. La solution générale du système sans second membre s'écrit :
où sont les trois valeurs propres et des vecteurs propres correspondants.
La solution générale du système complet s'obtient en ajoutant la solution particulière constante :
Les constantes ca, cb et cc sont obtenues avec la condition de continuité de Y(t) à l'instant t=t0 (puisque les trois courants vérifient la continuité) :
La fonction suivante détermine la solution à partir des valeurs et vecteurs propres et de la solution particulière constante, pour une condition initiale donnée :
def solution(valProp,vectProp,Yp,t0,t1,Yp0,N):
Va = vectProp[:,0]
Vb = vectProp[:,1]
Vc = vectProp[:,2]
lamb_a = valProp[0]
lamb_b = valProp[1]
lamb_c = valProp[2]
ea = np.exp(lamb_a*t0)
eb = np.exp(lamb_b*t0)
ec = np.exp(lamb_c*t0)
D = np.array([[ea*Va[0],eb*Vb[0],ec*Vc[0]],[ea*Va[1],eb*Vb[1],ec*Vc[1]],[ea*Va[2],eb*Vb[2],ec*Vc[2]]])
E = np.array([Yp0[0]-Yp[0],Yp0[1]-Yp[1],Yp0[2]-Yp[2]])
C = solve(D,E)
t = np.linspace(t0,t1,N)
a_a = C[0]*np.exp(lamb_a*t)
a_b = C[1]*np.exp(lamb_b*t)
a_c = C[2]*np.exp(lamb_c*t)
Y0 = a_a*Va[0]+a_b*Vb[0]+a_c*Vc[0]+Yp[0]
Y1 = a_a*Va[1]+a_b*Vb[1]+a_c*Vc[1]+Yp[1]
Y2 = a_a*Va[2]+a_b*Vb[2]+a_c*Vc[2]+Yp[1]
return t,[Y0,Y1,Y2]
La fonction suivante effectue le calcul de ie,i2,i sur une période de découpage, en calculant la solution de l'état 1 puis celle de l'état 2 :
def periode2(valProp1,vectProp1,valProp2,vectProp2,Yp1,Yp2,T,alpha,Ve,t,ie0,i20,i0,N=100):
temps1,Y1 = solution(valProp1,vectProp1,Yp1,0,alpha*T,[ie0,i20,i0],int(alpha*N))
ie_1 = Y1[0]
i2_1 = Y1[1]
i_1 = Y1[2]
temps2,Y2 = solution(valProp2,vectProp2,Yp2,alpha*T,T,[ie_1[-1],i2_1[-1],i_1[-1]],N-int(alpha*N))
ie_2 = Y2[0]
i2_2 = Y2[1]
i_2 = Y2[2]
temps = np.concatenate((t+temps1,t+temps2))
ie = np.concatenate((ie_1,ie_2))
i2 = np.concatenate((i2_1,i2_2))
i = np.concatenate((i_1,i_2))
return temps,np.real(ie),np.real(i2),np.real(i)
La fonction suivante effectue le calcul complet pour un nombre P de périodes de découpage :
from numpy.linalg import solve,eig
def simulation2(L,r,C,re,R,Cs,T,alpha,Ve,t0,ie0,i20,i0,P,N=100):
tab_temps = np.zeros(N*P)
tab_ie = np.zeros(N*P)
tab_i2 = np.zeros(N*P)
tab_i = np.zeros(N*P)
A1 = np.array([[-1/(re*C),0,1/(re*C)],[-re/L,-r/L,-R/L],[0,1/(R*Cs),-1/(R*Cs)]])
B1 = np.array([0,Ve/L,0])
Yp1 = solve(A1,-B1)
valProp1, vectProp1 = eig(A1)
A2 = np.array([[-1/(re*C),0,0],[0,-r/L,-R/L],[0,1/(R*Cs),-1/(R*Cs)]])
B2 = np.array([0,0,0])
Yp2 = solve(A2,-B2)
valProp2, vectProp2 = eig(A2)
k = 0
t = t0
for p in range(P):
temps,ie,i2,i = periode2(valProp1,vectProp1,valProp2,vectProp2,Yp1,Yp2,T,alpha,Ve,t,ie0,i20,i0,N)
ie0 = ie[-1]
i20 = i2[-1]
i0 = i[-1]
t += T
tab_temps[k:k+N] = temps
tab_ie[k:k+N] = ie
tab_i2[k:k+N] = i2
tab_i[k:k+N] = i
k += N
return tab_temps,tab_ie,tab_i2,tab_i
Voici une simulation reprenant les valeurs précédentes :
L = 0.5e-3
r = 1
C = 2000e-6
R = 10
Cs = 1000e-6
Ve = 10
re = 1
alpha = 0.5
T = 5e-5 # 20 kHz
P = 1500
temps,ie,i2,i = simulation2(L,r,C,re,R,Cs,T,alpha,Ve,0,Ve/re,0,0,P)
figure(figsize=(16,8))
subplot(211)
title(r"$V_e=10\ {\rm V},\ \alpha=0{,}5$",fontsize=16)
plot(temps,ie)
grid()
ylabel(r"$i_e\ (\rm A)$",fontsize=16)
subplot(212)
plot(temps,R*i)
grid()
xlabel("t (s)",fontsize=16)
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
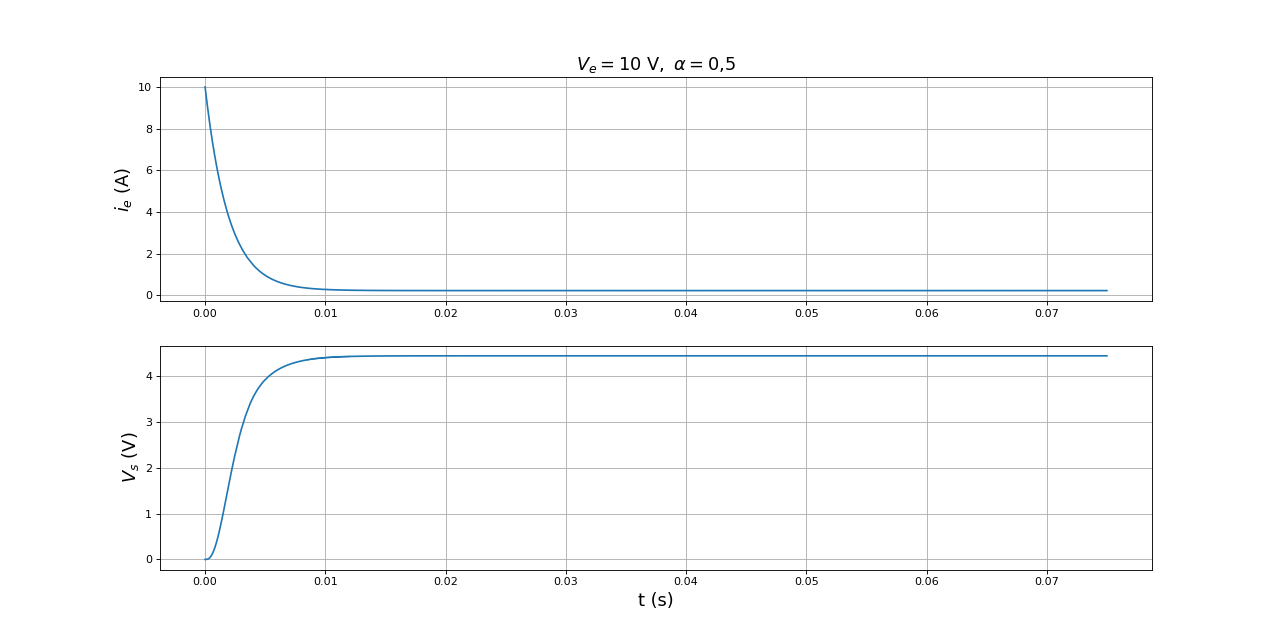 fig7.pdf
fig7.pdf
ondulVs = ondulation(R*i)
print(ondulVs) --> np.float64(0.0003437477346365556)
Voici le courant dans la bobine et le courant délivré par la source :
figure(figsize=(16,6))
plot(temps,ie,label="ie")
plot(temps,i2,label="i2")
grid()
xlabel("t (s)",fontsize=16)
ylabel("i (A)",fontsize=16)
legend(loc="upper right")
ylim(0,2)
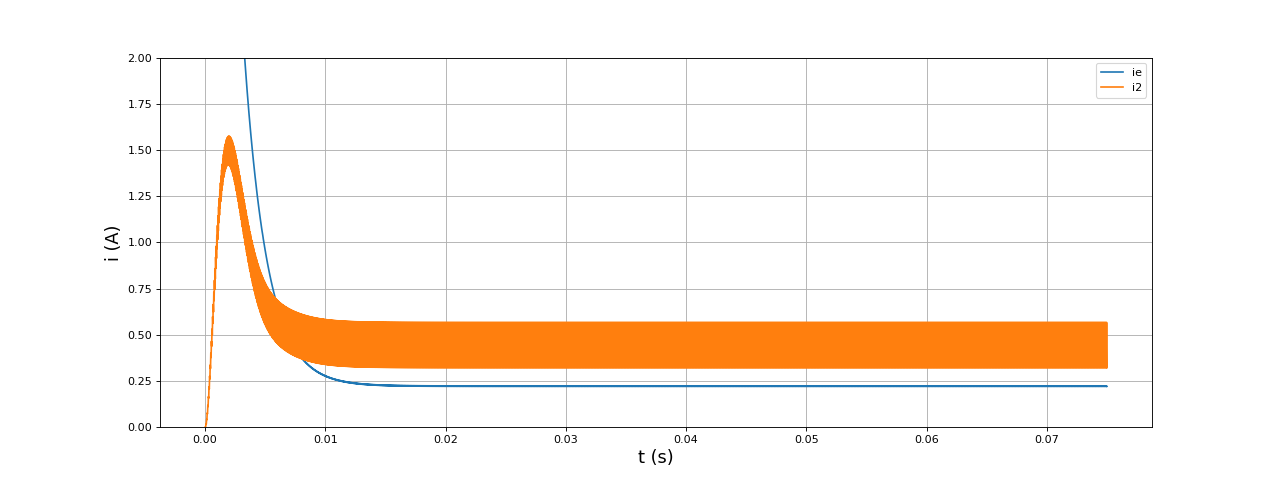 fig8.pdf
fig8.pdf
Le courant dans la bobine atteint une valeur très élevée au démarrage. En régime permanent, les ondulations de ce courant sont importantes. Elles sont absorbées par le condensateur, ce qui conduit à un courant dans la charge quasi constant.
Une autre simulation intéressante consiste, à partir du régime permanent, à changer le rapport cyclique :
L = 0.5e-3
r = 1
C = 2000e-6
R = 10
Cs = 1000e-6
Ve = 10
re = 1
T = 5e-5 # 20 kHz
P = 500
figure(figsize=(16,6))
alpha = 0.2
temps,ie,i2,i = simulation2(L,r,C,re,R,Cs,T,alpha,Ve,0,Ve/re,0,0,P)
plot(temps,R*i)
alpha = 0.8
temps,ie,i2,i = simulation2(L,r,C,re,R,Cs,T,alpha,Ve,temps[-1],ie[-1],i2[-1],i[-1],P)
plot(temps,R*i)
alpha = 0.2
temps,ie,i2,i = simulation2(L,r,C,re,R,Cs,T,alpha,Ve,temps[-1],ie[-1],i2[-1],i[-1],P)
plot(temps,R*i)
grid()
xlabel("t (s)",fontsize=16)
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
title(r"$V_e=10\ {\rm V},\ \alpha=0{,}2\rightarrow 0{,}8\rightarrow 0{,}2$",fontsize=16)
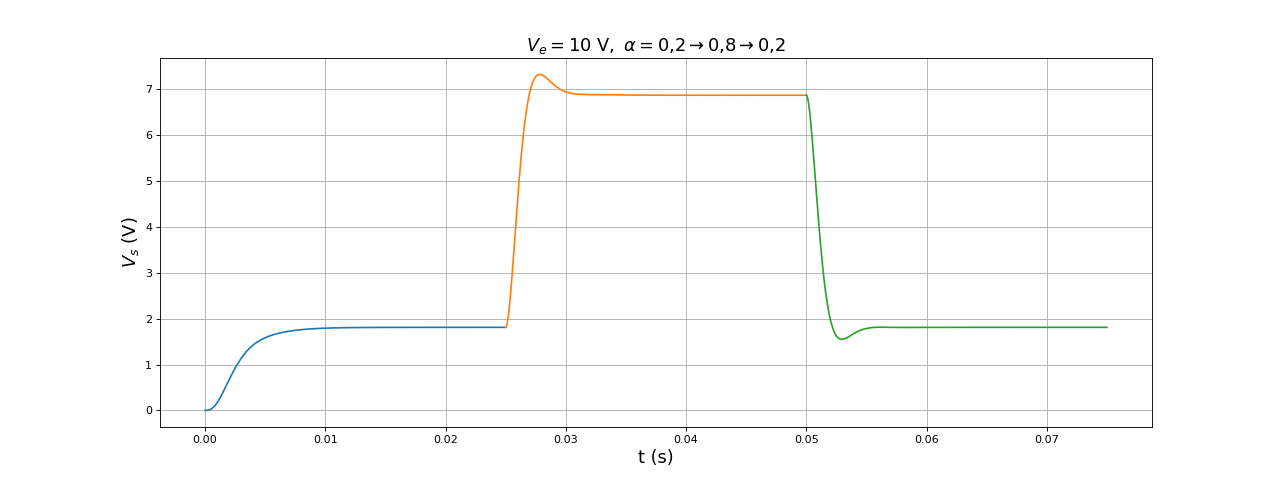 fig9.pdf
fig9.pdf
Cette courbe constitue la réponse du convertisseur à un échelon du rapport cyclique. Le temps de réponse est d'environ 5 ms.
2.g. Abaissement de tension
Voici le tracé du gain en tension en fonction du rapport cyclique, obtenu au moyen de la simulation semi-analytique (qui est plus efficace que la résolution numérique) :
gain = []
alpha = np.linspace(0.01,0.99,30)
L = 0.5e-3
r = 1
C = 2000e-6
R = 10
Cs = 1000e-6
Ve = 10
re = 1
T = 5e-5 # 20 kHz
P = 1500
for k in range(len(alpha)):
temps,ie,i2,i = simulation2(L,r,C,re,R,Cs,T,alpha[k],Ve,0,Ve/re,0,0,P)
Vs = R*i
N = len(Vs)
Vs = Vs[N//2:N]
gain.append(Vs.mean()/Ve)
figure(figsize=(8,6))
title(r"$R=10\,\rm\Omega$",fontsize=16)
plot(alpha,gain)
xlim(0,1)
ylim(0,1)
plot([0,1],[0,R/(R+r)],"k--")
grid()
xlabel(r"$\alpha$",fontsize=16)
ylabel(r"$\frac{Vs}{Ve}$",fontsize=16)
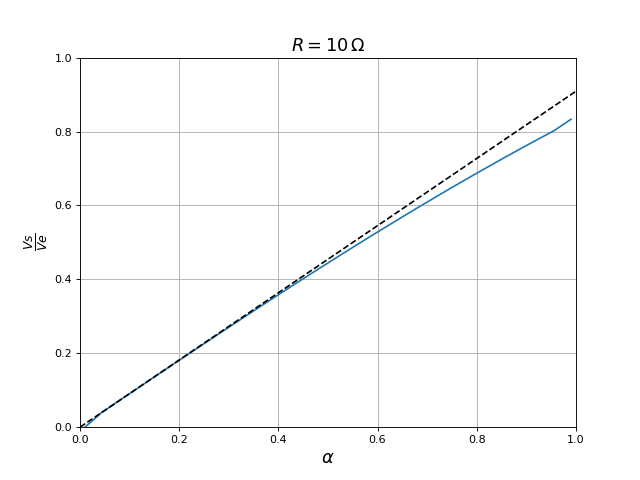 fig10.pdf
fig10.pdf
Le trait en pointillé représente le gain pour une source idéale. Pour cette résistance de charge, l'effet de la résistance de sortie de la source est important lorsque le rapport cyclique est proche de 1.
Voici la même courbe pour une résistance de charge 10 fois plus grande :
gain = []
alpha = np.linspace(0.01,0.99,30)
L = 0.5e-3
r = 1
C = 2000e-6
R = 100
Cs = 1000e-6
Ve = 10
re = 1
T = 5e-5 # 20 kHz
P = 1500
for k in range(len(alpha)):
temps,ie,i2,i = simulation2(L,r,C,re,R,Cs,T,alpha[k],Ve,0,Ve/re,0,0,P)
Vs = R*i
N = len(Vs)
Vs = Vs[N//2:N]
gain.append(Vs.mean()/Ve)
figure(figsize=(8,6))
title(r"$R=100\,\rm\Omega$",fontsize=16)
plot(alpha,gain)
xlim(0,1)
ylim(0,1)
plot([0,1],[0,R/(R+r)],"k--")
grid()
xlabel(r"$\alpha$",fontsize=16)
ylabel(r"$\frac{Vs}{Ve}$",fontsize=16)
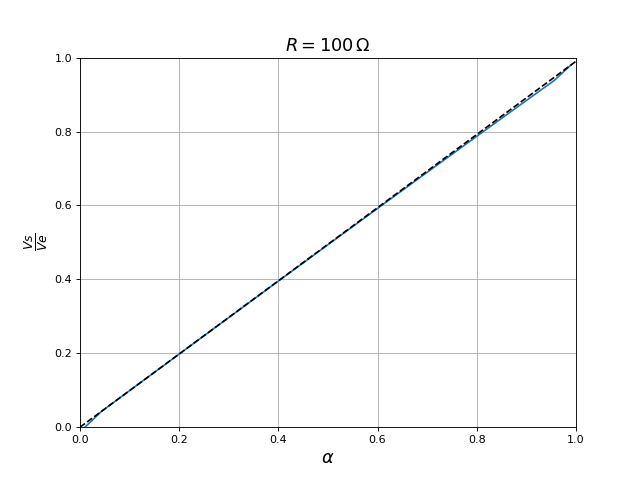 fig11.pdf
fig11.pdf
L'influence de re est négligeable lorsque la résistance de charge est assez grande, ce qui était prévisible puisque re est faible devant R.
Pour un rapport cyclique fixé, voici l'influence de la résistance r (résistance interne de la bobine) :
gain = []
r = np.logspace(-2,1,10)
alpha = 0.5
L = 0.5e-3
C = 2000e-6
R = 10
Cs = 1000e-6
Ve = 10
re = 1
T = 5e-5 # 20 kHz
P = 1500
for k in range(len(r)):
temps,ie,i2,i = simulation2(L,r[k],C,re,R,Cs,T,alpha,Ve,0,Ve/re,0,0,P)
Vs = R*i
N = len(Vs)
Vs = Vs[N//2:N]
gain.append(Vs.mean()/Ve)
figure(figsize=(8,6))
title(r"$\alpha=0,5$",fontsize=16)
plot(r,gain)
ylim(0,1)
xscale('log')
grid()
xlabel(r"$r\ (\rm\Omega)$",fontsize=16)
ylabel(r"$\frac{Vs}{Ve}$",fontsize=16)
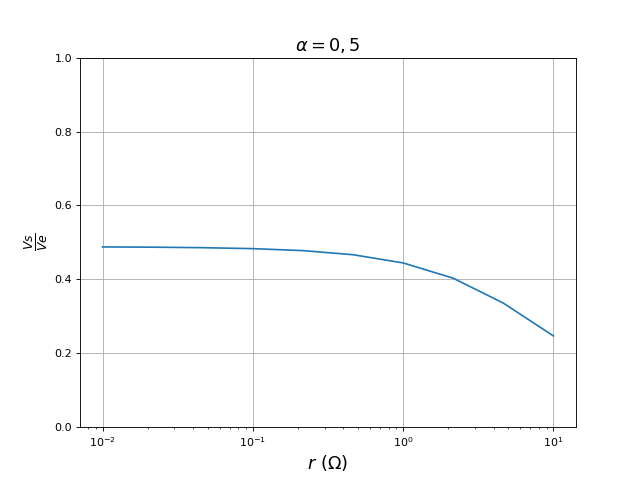 fig12.pdf
fig12.pdf
Pour un rapport cyclique fixé, voici l'influence de la résistance re (résistance de sortie de la source) :
gain = []
re = np.logspace(-2,1,10)
alpha = 0.5
L = 0.5e-3
r = 1
C = 2000e-6
R = 10
Cs = 1000e-6
Ve = 10
T = 5e-5 # 20 kHz
P = 1500
for k in range(len(re)):
temps,ie,i2,i = simulation2(L,r,C,re[k],R,Cs,T,alpha,Ve,0,Ve/re[k],0,0,P)
Vs = R*i
N = len(Vs)
Vs = Vs[N//2:N]
gain.append(Vs.mean()/Ve)
figure(figsize=(8,6))
title(r"$\alpha=0,5$",fontsize=16)
plot(re,gain)
ylim(0,1)
xscale('log')
grid()
xlabel(r"$r_e\ (\rm\Omega)$",fontsize=16)
ylabel(r"$\frac{V_s}{V_e}$",fontsize=16)
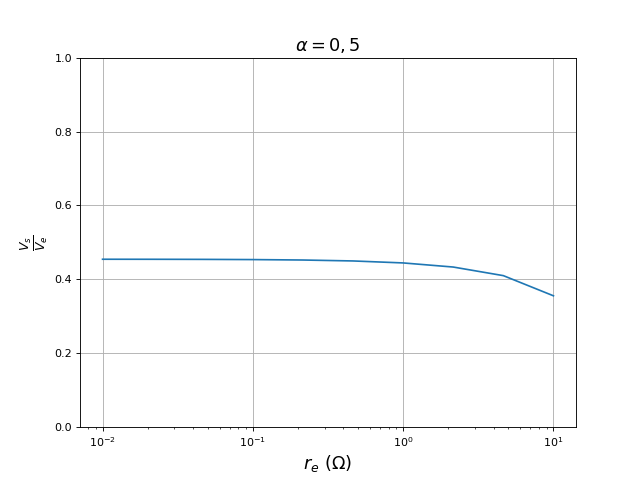 fig13.pdf
fig13.pdf
2.h. Rendement énergétique
Le rendement énergétique est le rapport de l'énergie moyenne dissipée dans la résistance de charge par l'énergie moyenne fournie par la source de tension.
def rendement(L,r,C,re,R,Cs,T,alpha,P): Ve = 1 temps,ie,i2,i = simulation2(L,r,C,re,R,Cs,T,alpha,Ve,0,Ve/re,0,0,P) Vs = R*i N = len(Vs) Vs = Vs[N//2:N] ie = ie[N//2:N] return (Vs**2).mean()/R/(Ve*ie).mean()
Voici le rendement en fonction du rapport cyclique :
rend = []
alpha = np.linspace(0.02,0.99,50)
L = 0.5e-3
r = 1
C = 2000e-6
R = 10
Cs = 1000e-6
Ve = 10
re = 1
T = 5e-5 # 20 kHz
P = 1500
for k in range(len(alpha)):
rend.append(rendement(L,r,C,re,R,Cs,T,alpha[k],P))
figure(figsize=(8,6))
title(r"$R=10\,\rm\Omega$",fontsize=16)
plot(alpha,rend)
xlim(0,1)
ylim(0,1)
grid()
xlabel(r"$\alpha$",fontsize=16)
ylabel(r"$\frac{P_c}{P_c}$",fontsize=16)
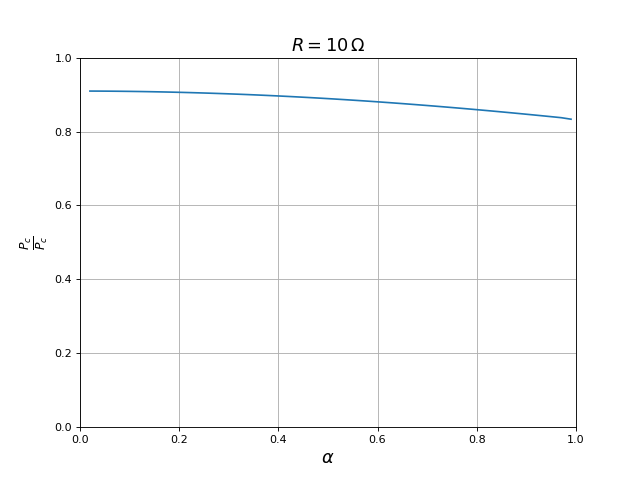 fig14.pdf
fig14.pdf
2.i. Simulation SPICE
Une simulation SPICE permet de faire intervenir un modèle plus réaliste des transistors, qui prend en compte la résistance drain-source lorsque le transistor est passant et la caractéristique de la diode source-drain.
Pour comparaison, on considère la simulation suivante par la méthode semi-analytique, à la fréquence de 10 kHz :
L = 0.5e-3
r = 1
C = 2000e-6
R = 10
Cs = 1000e-6
Ve = 10
re = 1
alpha = 0.5
T = 1e-4 # 10 kHz
P = 1500
temps,ie,i2,i = simulation2(L,r,C,re,R,Cs,T,alpha,Ve,0,Ve/re,0,0,P)
figure(figsize=(16,8))
subplot(311)
title(r"$V_e=10\ {\rm V},\ \alpha=0{,}5$",fontsize=16)
plot(temps,ie,label=r"$i_e$")
ylabel(r"$i_e\ (\rm A)$",fontsize=16)
grid()
subplot(312)
plot(temps,i2,label=r"$i_2$")
ylabel(r"$i_2\ (\rm A)$",fontsize=16)
grid()
ylim(0,2)
subplot(313)
plot(temps,R*i)
ylim(0,5)
grid()
xlabel("t (s)",fontsize=16)
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
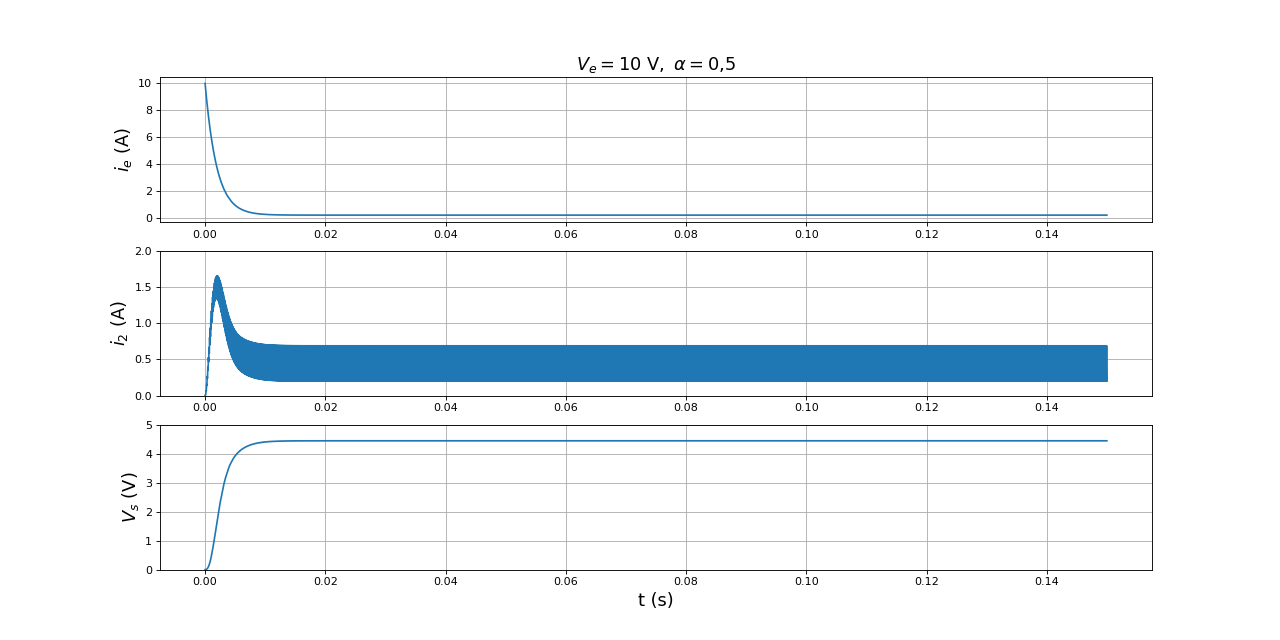 fig15.pdf
fig15.pdf
Voici une simulation effectuée avec LTSpice au moyen du modèle de transitor IPA50R500 (fourni par le fabriquant) :
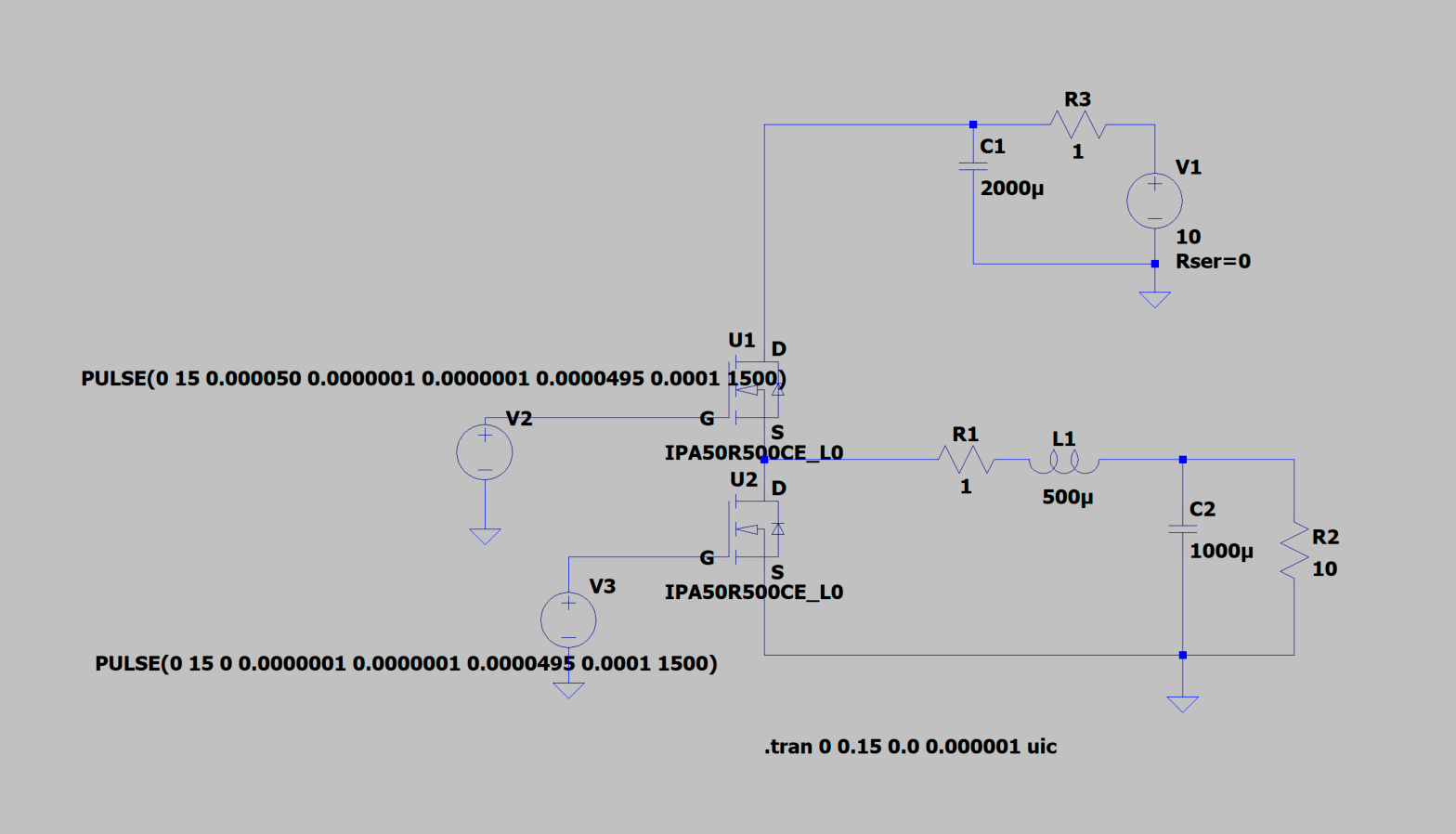
La commande de grille de chaque transistor est effectuée au moyen d'une source de tension qui délivre une tension carrée d'amplitude 15 V et de période 0,1 ms. Le rapport cyclique est 0,5. La tension carrée est générée par l'instruction PULSE. Le passage de la valeur 0 à la valeur 15 V se fait nécessairement sur une durée finie (paramètre Trise) car la simulation entièrement numérique réalisée par Spice n'accepte pas les discontinuités des sources de tension. Afin d'éviter un chevauchement des états haut des deux commandes (et en conséquence la conduction simultané des deux transistors), on doit réduire la durée de l'état haut (Ton) par rapport à la période.
La directive UIC ajoutée à la commande de simulation TRANS permet d'appliquer la condition initiale choisie par l'utilisateur : ici la tension initiale en sortie est nulle et le courant dans la bobine est nul.
[temps,Vs,i2,ie] = np.load("convertisseur-buck-1.npy")
i2 = -i2
figure(figsize=(16,8))
subplot(311)
title(r"$V_e=10\ {\rm V},\ \alpha=0{,}5$",fontsize=16)
plot(temps,ie,label=r"$i_e$")
ylabel(r"$i_e\ (\rm A)$",fontsize=16)
grid()
subplot(312)
plot(temps,i2,label=r"$i_2$")
ylabel(r"$i_2\ (\rm A)$",fontsize=16)
grid()
ylim(0,2)
subplot(313)
plot(temps,Vs)
ylim(0,5)
grid()
xlabel("t (s)",fontsize=16)
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
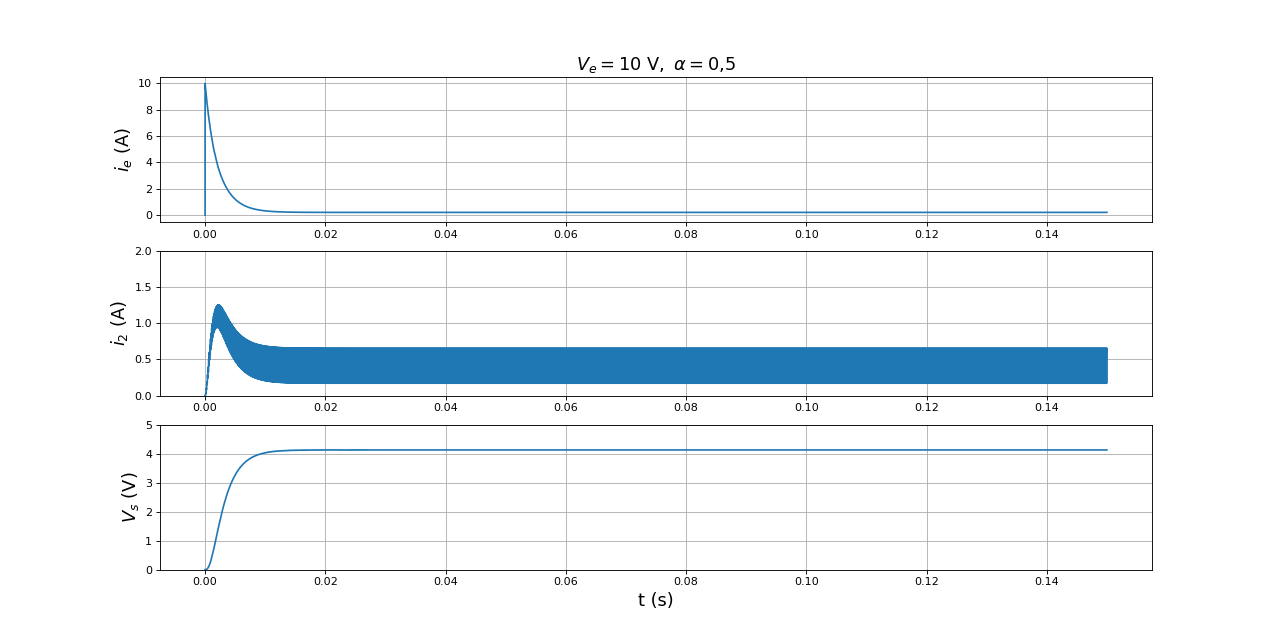 fig16.pdf
fig16.pdf
Le principal apport de la simulation Spice par rapport au modèle présenté ici est la prise en compte de la résistance drain-source des transistors lorsqu'ils sont passants. L'effet de cette résistance est de diminuer un peu la tension de sortie pour un rapport cyclique donné. Le rendement devrait aussi baisser un peu.
3. Étude expérimentale
3.a. Circuit
La bobine utilisée est un enroulement sur un tore en poude de fer (Wurth Electronik). Les mesures d'impédance sont réalisées avec l'Analog Discovery 2 et le logiciel Waveforms. Un amplificateur linéaire de puissance est utilisé et différentes amplitudes de la tension d'entrée sont choisies. Voici les parties réelle et imaginaire de l'impédance en fonction de la fréquence :
[f1,R1,X1] = np.loadtxt('impedance-bobine-500mV.csv',unpack=True,skiprows=31,delimiter=',')
[f2,R2,X2] = np.loadtxt('impedance-bobine-1V.csv',unpack=True,skiprows=31,delimiter=',')
[f3,R3,X3] = np.loadtxt('impedance-bobine-2V.csv',unpack=True,skiprows=31,delimiter=',')
[f4,R4,X4] = np.loadtxt('impedance-bobine-5V.csv',unpack=True,skiprows=31,delimiter=',')
figure(figsize=(12,8))
subplot(211)
plot(f1,R1,label='0.5 V')
plot(f2,R2,label='1 V')
plot(f3,R3,label='2 V')
plot(f4,R4,label='5 V')
grid()
xscale('log')
yscale('log')
ylabel(r"$R\ (\rm\Omega)$",fontsize=14)
legend(loc='upper left')
subplot(212)
plot(f1,X1,label='0.5 V')
plot(f2,X2,label='1 V')
plot(f3,X3,label='2 V')
plot(f4,X4,label='5 V')
grid()
xscale('log')
yscale('log')
ylabel(r"$X\ (\rm\Omega)$",fontsize=14)
legend(loc='upper left')
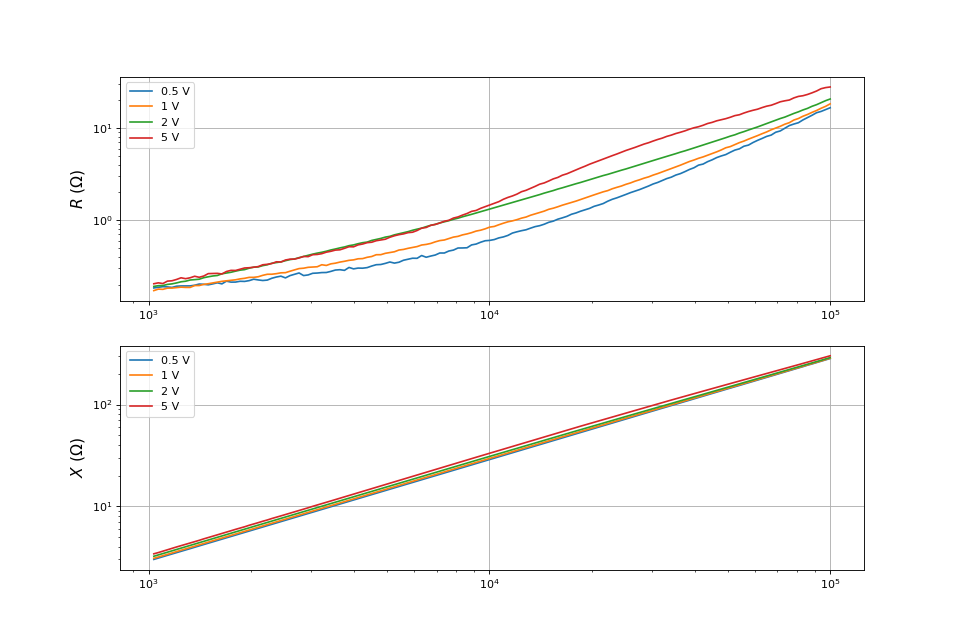 fig17.pdf
fig17.pdf
Voici les valeurs de l'auto-inductance déduites de la pente de la partie imaginaire de l'impédance :
p1 = np.polyfit(f1,X1,deg=1)
L1 = p1[0]/(2*np.pi)
p2 = np.polyfit(f2,X2,deg=1)
L2 = p2[0]/(2*np.pi)
p3 = np.polyfit(f3,X3,deg=1)
L3 = p3[0]/(2*np.pi)
p4 = np.polyfit(f4,X4,deg=1)
L4 = p4[0]/(2*np.pi)
print([L1,L2,L3,L4]) --> [np.float64(0.0004517477924609053), np.float64(0.00045523906672610454), np.float64(0.0004631525140633003), np.float64(0.0004880015319133242)]
L'auto-inductance augmente un peu avec l'intensité du courant (l'intensité est ici de 100 mA maximum). Les valeurs obtenues avec un RLC-mètre sont et à une fréquence de 10 kHz. Il s'agit de valeurs valables pour une intensité du courant faible (quelques dizaines mA). Pour une utilisation dans un circuit de forte puissance, il faut s'attendre à une valeur nettement plus grande de la résistance.
Comme le montrent les simulations ci-dessus, le courant dans la bobine a une valeur moyenne positive mais présente des ondulations non négligeables à la fréquence de découpage. Pour cette application, le noyau en poudre de fer n'est pas optimal à cause des courants induits dans le fer (un noyau en ferrite serait sans doute plus approprié). Dans les modèles, la résistance est constante alors qu'en réalité elle dépend de la fréquence. La valeur constante la plus pertinente est de l'ordre de 1 ohm car on peut supposer que les ondulations à la fréquence de découpage (10 kHz) imposent la valeur de la résistance, même si leur amplitude est relativement faible.
Voici le schéma du circuit complet, où la bobine est représentée par son auto-inductance et sa résistance en série :
Figure pleine pageLes deux transistors MOSFET sont pilotés par le IR2113, qui permet de piloter les deux séparément avec deux signaux de commande. Il existe aussi des pilotes permettant de commander les deux transistors en opposition avec un seul signal de commande (voir Transistors MOSFET de puissance), qui conviendraient très bien pour cette application. Les expériences décrites plus loin sont réalisées avec une alimentation stabilisée comme source en entrée.
Le potentiomètre permet de réduire la tension de sortie pour la ramener en dessous de 5 V afin d'être envoyée sur l'entrée A0 de l'Arduino pour numérisation.
La commande de grille des deux transistors nécessite une tension de 15 V que nous fournissons avec une alimentation séparée.
3.b. Programme Arduino
Ce programme tourne sur Arduino MEGA. Les signaux HIN et LIN sont générés par les deux sorties A et B du Timer 1, respectivement câblées sur D11 et D12. La programmation d'un Timer pour la génération de signaux PWM est expliqué dans Pilotage d'un pont L298. Le rapport cyclique est envoyé depuis un script Python selon le protocole de communication décrit dans Échanges de données avec un Arduino.
#define HIN 11 // transistor haut
#define LIN 12 // transistor bas
uint16_t diviseur[6] = {0,1,8,64,256,1024};
uint16_t icr;
uint16_t temps_mort = 0;
uint16_t ocra,ocrb;
float rapport;
// communication série
#define GET_DATA 10
#define SET_DATA 11
#define DATA_0_SIZE 4 // rapport cyclique (float)
#define DATA_1_SIZE 4 // Tension Vs
uint8_t data_0[DATA_0_SIZE];
uint8_t data_1[DATA_1_SIZE];
bool data_1_request = false;
bool data_1_ready = true;
// rapport cyclique du découpage
void set_rapport(float rapport) {
if (icr*rapport>temps_mort) {
ocra = icr*rapport-temps_mort;
ocrb = icr*rapport+temps_mort;
}
else {
ocra = icr*rapport;
ocrb = icr*rapport;
}
OCR1A = ocra;
OCR1B = ocrb;
}
//Timer 1 : OC1A : sortie D11, OC1B : sortie D12
void timer1_init(uint32_t period, float rapport) {
cli();
TCCR1A = (1 << COM1A1) | (1 << COM1B1) | (1 << COM1B0);
TCCR1B = (1 << WGM13);
icr = (F_CPU/1000000*period/2);
int d = 1;
while ((icr>0xFFFF)&&(d<5)) {
d++;
icr = (F_CPU/1000000*period/2/diviseur[d]);
}
TCCR1B |= d;
set_rapport(rapport);
TCNT1 = 0;
ICR1 = icr;
sei();
}
// traitement d'une donnée entrante
void set_data() {
char n;
while (Serial.available()<1) {};
n = Serial.read();
if (n==0) {
while (Serial.available()<DATA_0_SIZE) {};
Serial.readBytes(data_0,DATA_0_SIZE);
memcpy(&rapport,data_0,DATA_0_SIZE);
set_rapport(rapport);
}
}
void get_data() {
char n;
while (Serial.available()<1) {};
n = Serial.read();
if (n==1) data_1_request = true;
}
void send_data() {
if ((data_1_ready)&&(data_1_request)) {
data_1_request = false;
float Vs = analogRead(A0) *5.0/1024;
Serial.write((uint8_t *)&Vs,DATA_1_SIZE);
}
}
void read_serial() {
char com;
if (Serial.available()>0) {
com = Serial.read();
if (com==GET_DATA) get_data();
else if (com==SET_DATA) set_data();
}
}
void setup() {
Serial.begin(115200);
pinMode(HIN,OUTPUT);
pinMode(LIN,OUTPUT);
rapport = 0.3;
timer1_init(50,rapport); // fréquence 20 kHz
}
void loop() {
read_serial();
send_data();
delay(100);
}
Pour modifier le rapport cyclique, on utilise le script Arduino.py et le script suivant :
from Arduino import Arduino
ard = Arduino('COM3',[4,4])
RAPPORT = 0
TENSION = 1
while True:
r = input('?')
if r=='n': break
elif r=="v":
Vs = ard.read_float(TENSION)
print("Vs = %f"%Vs)
else:
rapport = float(r)
ard.write_float(RAPPORT,rapport)
ard.close()
On entre la valeur du rapport cyclique, ou la lettre v pour obtenir la tension Vs, ou la lettre n pour terminer.
3.c. Étude à rapport cyclique fixé
La fréquence de découpage est 20 kHz. La source est une alimentation stabilisée en tension, délivrant une tension Ve=5,0 V, et la résistance de charge R=100 Ω. Remarquons que l'emploie d'une alimentation stabilisée ne garantit pas que la tension qu'elle délivre soit parfaitement constante. La constance de la tension délivrée doit être vérifée à l'oscilloscope. Dans le cas présent, le condensateur de capacité C placé en entrée aide grandement à maintenir la stabilité de cette tension mais des variations restent possibles au moment des commutations. Voici, pour un rapport cyclique α=0,5, les signaux de commande des deux transistors K1,K2, et la tension Vs en sortie du convertisseur (aux bornes de la charge) :
[ta,K1,K2] = np.loadtxt("buck-DC5-PWM-r0,5-R100.txt",unpack=True,skiprows=1)
[tb,Vs] = np.loadtxt("buck-DC5-Vs-r0,5-R100.txt",unpack=True,skiprows=1)
figure(figsize=(16,6))
plot(ta,K1,label=r"$K_1$")
plot(ta,K2,label=r"$K_2$")
plot(tb,Vs,label=r"$V_s$")
xlabel("t (s)",fontsize=16)
ylabel("Volts",fontsize=16)
grid()
ylim(0,5)
legend(loc="upper right")
title(r"$\alpha=0{,}5,\ R=100\ {\rm \Omega}$",fontsize=16)
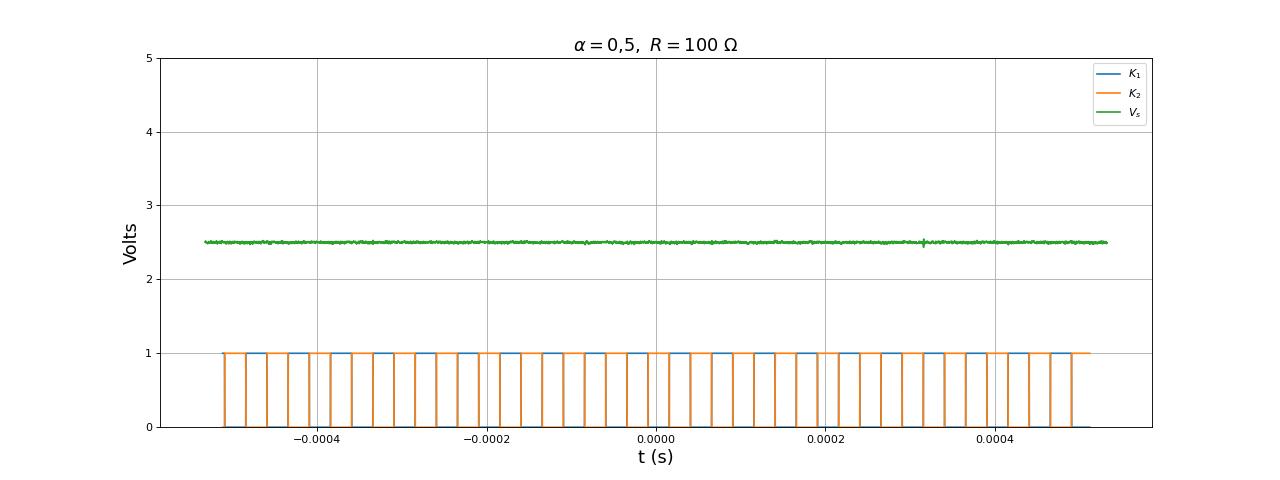 fig18.pdf
fig18.pdf
Voici les signaux pour un rapport cyclique α=0,1 :
[ta,K1,K2] = np.loadtxt("buck-DC5-PWM-r0,1-R100.txt",unpack=True,skiprows=1)
[tb,Vs] = np.loadtxt("buck-DC5-Vs-r0,1-R100.txt",unpack=True,skiprows=1)
figure(figsize=(16,6))
plot(ta,K1,label=r"$K_1$")
plot(ta,K2,label=r"$K_2$")
plot(tb,Vs,label=r"$V_s$")
xlabel("t (s)",fontsize=16)
ylabel("Volts",fontsize=16)
grid()
ylim(0,5)
legend(loc="upper right")
title(r"$\alpha=0{,}1,\ R=100\ {\rm \Omega}$",fontsize=16)
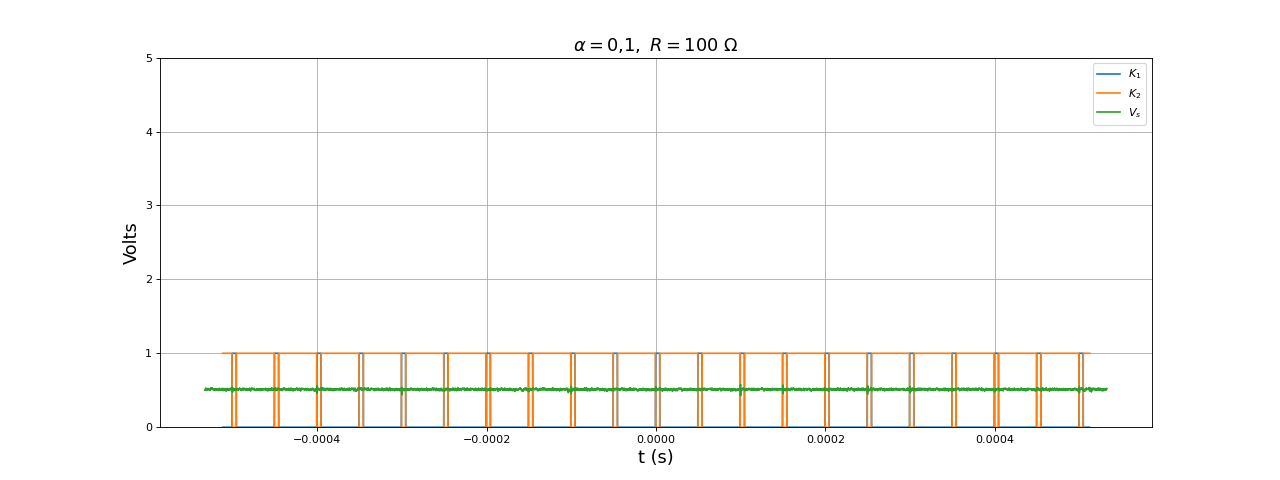 fig19.pdf
fig19.pdf
et pour un rapport cyclique α=0,9 :
[ta,K1,K2] = np.loadtxt("buck-DC5-PWM-r0,9-R100.txt",unpack=True,skiprows=1)
[tb,Vs] = np.loadtxt("buck-DC5-Vs-r0,9-R100.txt",unpack=True,skiprows=1)
figure(figsize=(16,6))
plot(ta,K1,label=r"$K_1$")
plot(ta,K2,label=r"$K_2$")
plot(tb,Vs,label=r"$V_s$")
xlabel("t (s)",fontsize=16)
ylabel("Volts",fontsize=16)
grid()
ylim(0,5)
legend(loc="upper right")
title(r"$\alpha=0{,}9,\ R=100\ {\rm \Omega}$",fontsize=16)
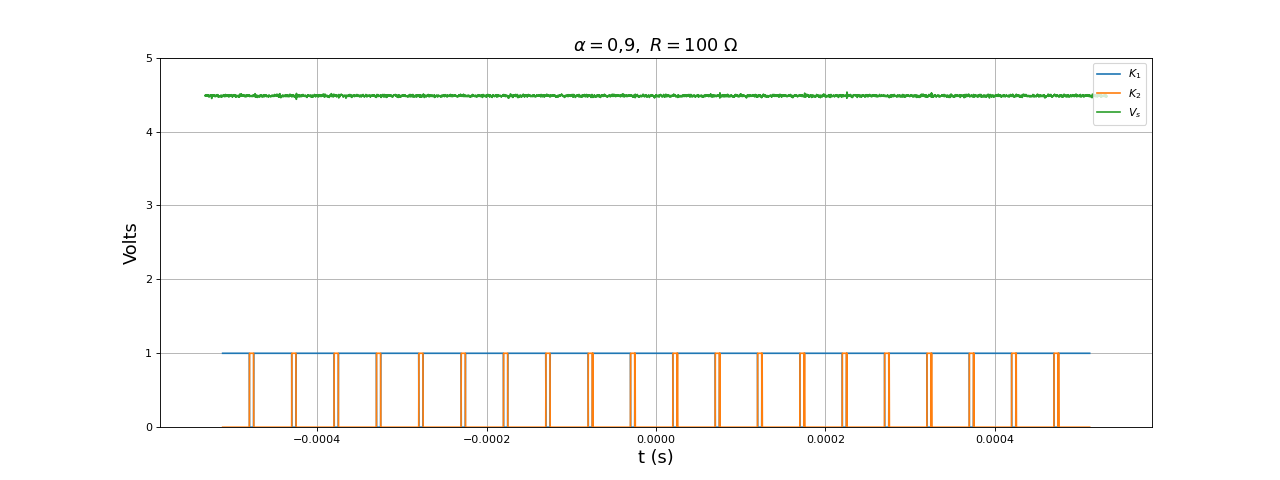 fig20.pdf
fig20.pdf
Pour différents rapports cycliques, on relève la tension Vs moyenne avec l'oscilloscope et la tension donnée par l'Arduino :
alpha = [0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,0.95,0.99]
Vs_moy = [0.51,1.007,1.504,2.000,2.498,2.994,3.489,3.987,4.483,4.732,4.931]
Vs_ard = [0.48,0.988,1.477,1.971,2.48,2.984,3.478,3.986,4.476,4.722,4.921]
figure(figsize=(8,6))
plot(alpha,Vs_moy,label="Vs oscillo")
plot(alpha,Vs_ard,label="Vs arduino")
grid()
xlabel(r"$\alpha$",fontsize=16)
ylabel("Volts",fontsize=16)
xlim(0,1)
ylim(0,5)
legend(loc="upper left")
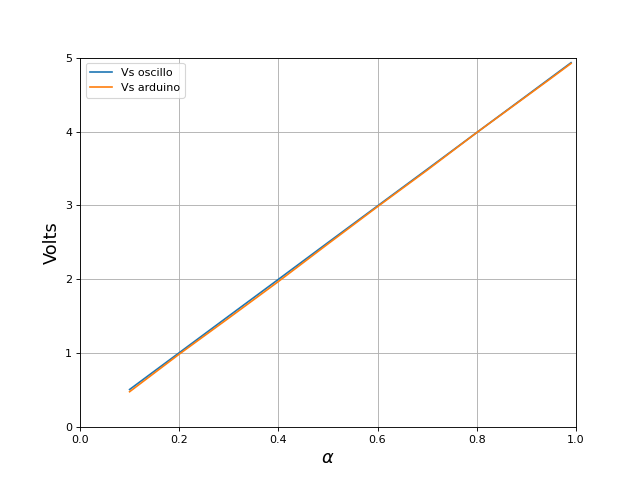 fig21.pdf
fig21.pdf
Afin de mesurer le courant ie(t), une résistance de R1=1 Ω est placée en série sur la sortie positive de l'alimentation. Voici la tension de sortie et la tension aux bornes de cette résistance :
[ta,K1,K2] = np.loadtxt("buck-DC5-PWM-Ve-ie-r0,5-R100.txt",unpack=True,skiprows=1)
[tb,Ve,ie] = np.loadtxt("buck-DC5-Ve-ie-r0,5-R100.txt",unpack=True,skiprows=1)
figure(figsize=(16,6))
subplot(211)
plot(ta,K1,label=r"$K_1$")
plot(ta,K2,label=r"$K_2$")
plot(tb,Ve,label=r"$V_e$")
grid()
ylim(0,6)
legend(loc="upper right")
title(r"$\alpha=0{,}5,\ R=100\ {\rm \Omega}$",fontsize=16)
subplot(212)
plot(tb,ie,label=r"$R_1i_e$")
grid()
xlabel("t (s)",fontsize=16)
ylabel(r"$i_e\ (\rm A)$",fontsize=16)
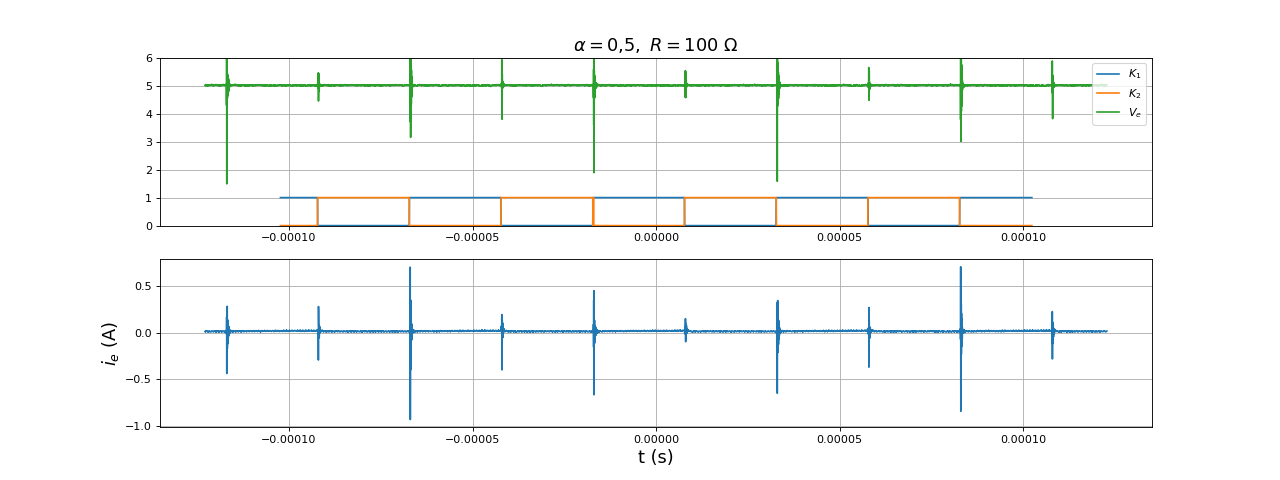 fig22.pdf
fig22.pdf
Le courant sortant de l'alimentation comporte des pics positifs et négatifs de très grande amplitude au moment de la commutation des transistors. Ces pics ont une répercution sur la tension Ve malgré la présence du condensateur. Bien qu'ils soient invisibles sur la tension de sortie du convertisseur, ils ont un effet négatif sur le rendement énergétique. Ils sont causés pas le léger retard entre la commande d'un transistor pour le rendre bloquant (abaissement de la tension de grille) et son changement d'état effectif. Au moment du passage de l'état 1 à l'état 2, le transistor 2 devient passant alors que le transistor 1 n'est pas encore passé à l'état bloquant. Au moment du passage de l'état 2 à l'état 1, le transistor 1 devient passant alors que le transistor 2 est encore passant. Afin de supprimer ces phases où les deux transistors sont passant simultanément (qui constituent un court-circuit pour l'alimentation), on introduit un temps mort entre la commande d'un transistor et celle de l'autre. Le temps mort est introduit sous la forme d'un décalage de OCA (signal de commande du transistor 1) et OCB (signal de commande du transistor 2), défini dans la variable temps_mort. La figure suivante montre comment les signaux de commande sont générés :
Figure pleine pageSi OCR1A=OCR1B, les signaux de commande changent d'état simultanément. Si OCR1A et légèrement abaissé et OCR1B légèrement augmenté, il apparaît un petit intervalle de temps où les deux commandes sont à zéro, ce qui doit permettre d'éliminer l'intervalle de temps où les deux transistors sont passants en même temps. Si la fréquence de découpage est de l'ordre de 10 kHz, le diviseur de fréquence d'horloge vaut 1 donc ICR=400. Une valeur de 1 pour temps_mort donne donc un décalage temporel de 2/400 de la période. Voici le résultat pour temps_mort = 5 :
[ta,K1,K2] = np.loadtxt("buck-DC5-PWM-Ve-ie-r0,5-R100-TM5.txt",unpack=True,skiprows=1)
[tb,Ve,ie] = np.loadtxt("buck-DC5-Ve-ie-r0,5-R100-TM5.txt",unpack=True,skiprows=1)
figure(figsize=(16,6))
subplot(211)
plot(ta,K1,label=r"$K_1$")
plot(ta,K2,label=r"$K_2$")
plot(tb,Ve,label=r"$V_e$")
grid()
ylim(0,6)
legend(loc="upper right")
title(r"$\alpha=0{,}5,\ R=100\ {\rm \Omega},\ TM=5$",fontsize=16)
subplot(212)
plot(tb,ie,label=r"$R_1i_e$")
grid()
xlabel("t (s)",fontsize=16)
ylabel(r"$i_e\ (\rm A)$",fontsize=16)
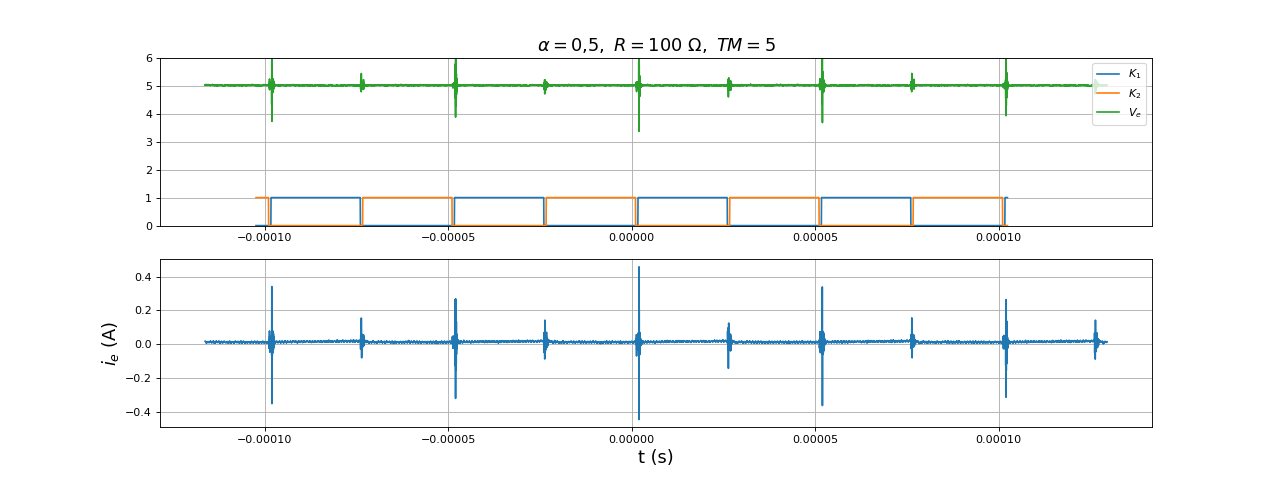 fig23.pdf
fig23.pdf
pour temps_mort = 10 :
[ta,K1,K2] = np.loadtxt("buck-DC5-PWM-Ve-ie-r0,5-R100-TM10.txt",unpack=True,skiprows=1)
[tb,Ve,ie] = np.loadtxt("buck-DC5-Ve-ie-r0,5-R100-TM10.txt",unpack=True,skiprows=1)
figure(figsize=(16,6))
subplot(211)
plot(ta,K1,label=r"$K_1$")
plot(ta,K2,label=r"$K_2$")
plot(tb,Ve,label=r"$V_e$")
grid()
ylim(0,6)
legend(loc="upper right")
title(r"$\alpha=0{,}5,\ R=100\ {\rm \Omega},\ TM=10$",fontsize=16)
subplot(212)
plot(tb,ie,label=r"$R_1i_e$")
grid()
xlabel("t (s)",fontsize=16)
ylabel(r"$i_e\ (\rm A)$",fontsize=16)
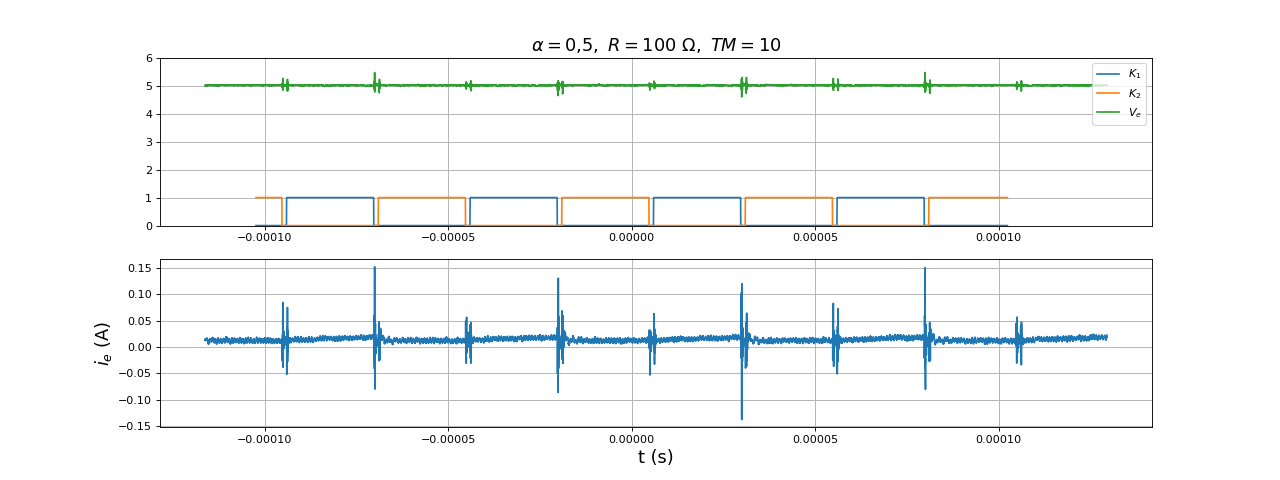 fig24.pdf
fig24.pdf
et pour temps_mort = 20 :
[ta,K1,K2] = np.loadtxt("buck-DC5-PWM-Ve-ie-r0,5-R100-TM20.txt",unpack=True,skiprows=1)
[tb,Ve,ie] = np.loadtxt("buck-DC5-Ve-ie-r0,5-R100-TM20.txt",unpack=True,skiprows=1)
figure(figsize=(16,6))
subplot(211)
plot(ta,K1,label=r"$K_1$")
plot(ta,K2,label=r"$K_2$")
plot(tb,Ve,label=r"$V_e$")
grid()
ylim(0,6)
legend(loc="upper right")
title(r"$\alpha=0{,}5,\ R=100\ {\rm \Omega},\ TM=20$",fontsize=16)
subplot(212)
plot(tb,ie,label=r"$R_1i_e$")
grid()
xlabel("t (s)",fontsize=16)
ylabel(r"$i_e\ (\rm A)$",fontsize=16)
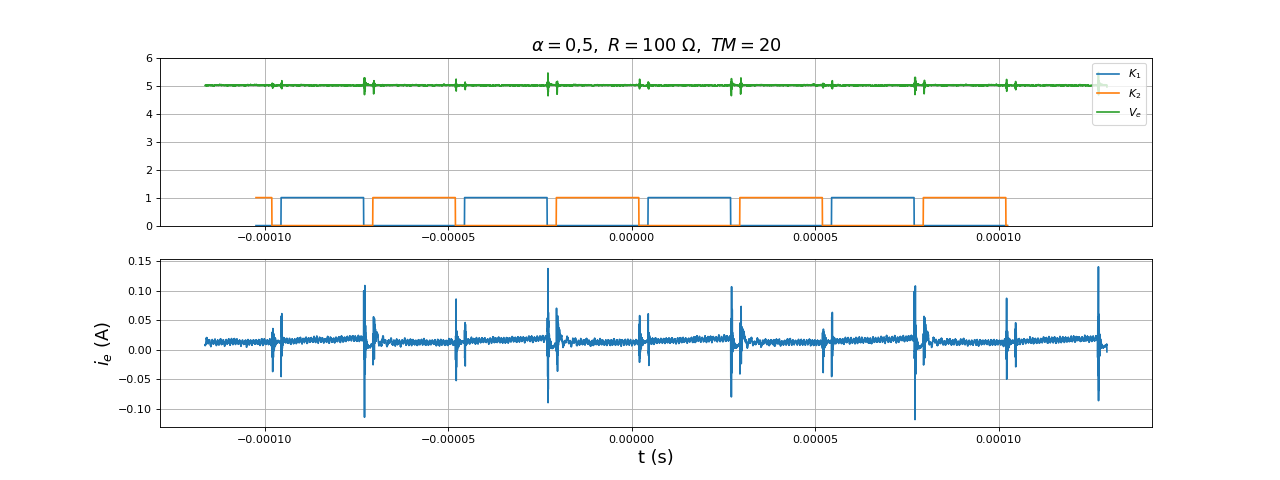 fig25.pdf
fig25.pdf
Nous optons pour temps_mort = 10. Voici la tension en sortie pour un rapport cylique de 0,5 :
[ta,K1,K2] = np.loadtxt("buck-DC5-PWM-Vs-ie-r0,5-R100-TM10.txt",unpack=True,skiprows=1)
[tb,Vs,ie] = np.loadtxt("buck-DC5-Vs-ie-r0,5-R100-TM10.txt",unpack=True,skiprows=1)
figure(figsize=(16,6))
plot(ta,K1,label=r"$K_1$")
plot(ta,K2,label=r"$K_2$")
plot(tb,Vs,label=r"$V_s$")
xlabel("t (s)",fontsize=16)
ylabel("Volts",fontsize=16)
grid()
ylim(0,5)
legend(loc="upper right")
title(r"$\alpha=0{,}5,\ R=100\ {\rm \Omega}$",fontsize=16)
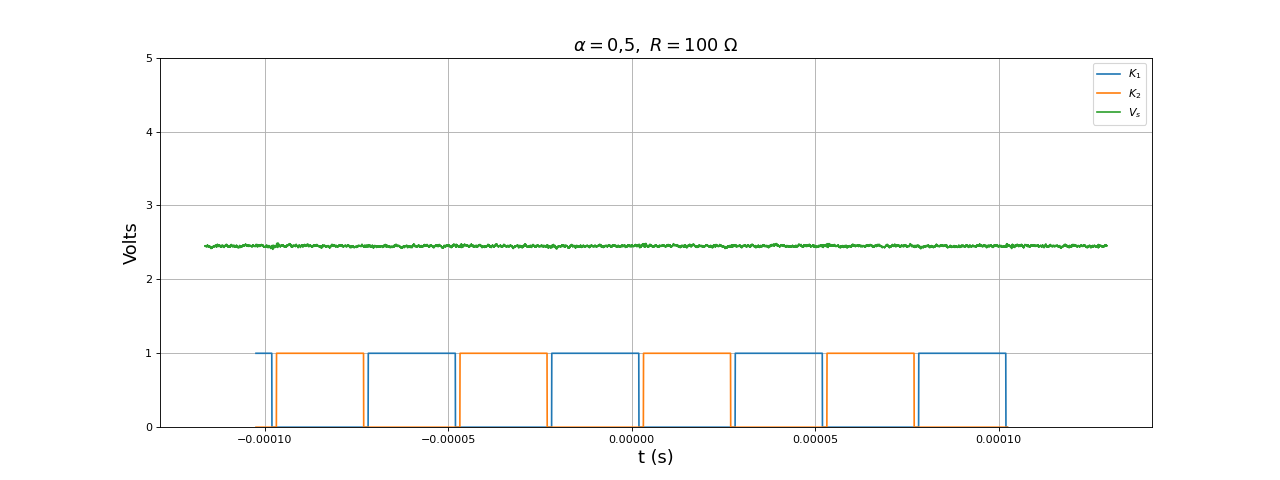 fig26.pdf
fig26.pdf
et pour un rapport cyclique de 0,99 :
[ta,K1,K2] = np.loadtxt("buck-DC5-PWM-Vs-ie-r0,99-R100-TM10.txt",unpack=True,skiprows=1)
[tb,Vs,ie] = np.loadtxt("buck-DC5-Vs-ie-r0,99-R100-TM10.txt",unpack=True,skiprows=1)
figure(figsize=(16,6))
plot(ta,K1,label=r"$K_1$")
plot(ta,K2,label=r"$K_2$")
plot(tb,Vs,label=r"$V_s$")
xlabel("t (s)",fontsize=16)
ylabel("Volts",fontsize=16)
grid()
ylim(0,5)
legend(loc="upper right")
title(r"$\alpha=0{,}99,\ R=100\ {\rm \Omega}$",fontsize=16)
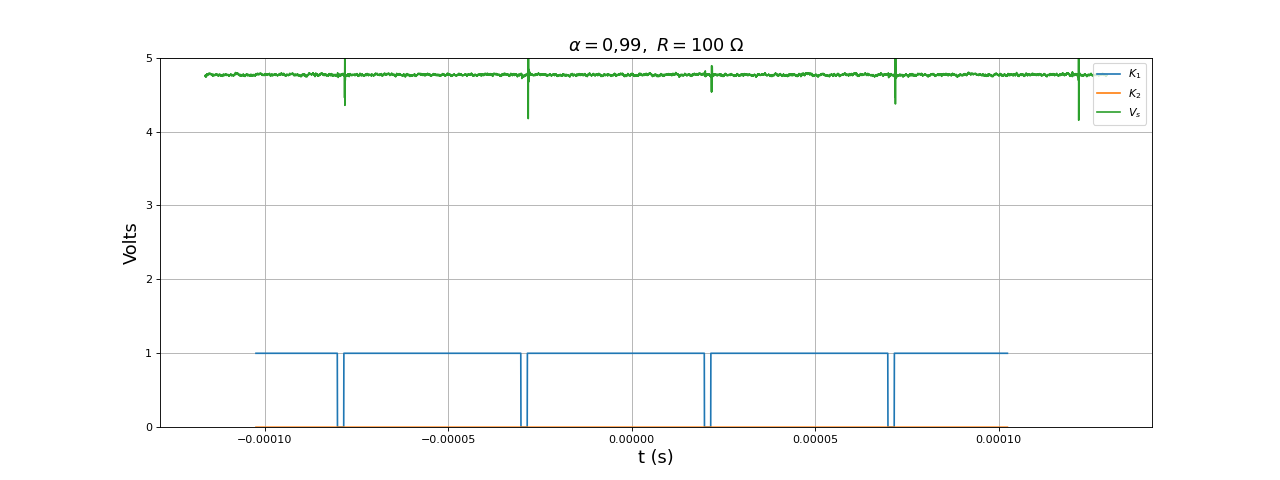 fig27.pdf
fig27.pdf
L'introduction du temps mort a un inconvénient : lorsque le rapport cyclique est très proche de 1, le transistor 2 reste tout le temps à l'état bloquant (interrupteur ouvert). Cela n'empêche pas le fonctionnement du convertisseur : on retrouve le fonctionnement du convertisseur non synchrone, où une diode est placée au lieu du transistor 2.
Pour mesurer la puissance délivrée par la source et calculer le rendement, nous comparons deux méthodes : la première consiste à calculer la puissance délivrée par la source comme la moyenne du produit Ve(t)ie(t) pour un enregistrement de 1 ms (8192 échantillons), la seconde en considérant que Ve est parfaitement constante (égale à 5 V). Voici cette comparaison, pour α=0,5 et α=0,8 :
[t,Ve,ie] = np.loadtxt("buck-DC5-Ve-ie-r0,5-R100-TM10-1ms.txt",unpack=True,skiprows=1)
Pe = (Ve*ie).mean()
Vs = 2.45
R = 100
Pc = Vs**2/R
rend1 = Pc/Pe
Ve = 5
rend2 = Pc/(Ve*ie.mean())
print([rend1,rend2]) --> [np.float64(0.8890724589238647), np.float64(0.890575337367482)]
[t,Ve,ie] = np.loadtxt("buck-DC5-Ve-ie-r0,8-R100-TM10-1ms.txt",unpack=True,skiprows=1)
Pe = (Ve*ie).mean()
Vs = 2.45
R = 100
Pc = Vs**2/R
rend1 = Pc/Pe
Ve = 5
rend2 = Pc/(Ve*ie.mean())
print([rend1,rend2]) --> [np.float64(0.39227930043866077), np.float64(0.3930926344924914)]
L'écart des valeurs de rendement obtenues par ces deux méthodes est assez faible pour qu'on puisse adopter la seconde méthode, plus simple à mettre en œuvre puisque la valeur moyenne de ie s'obtient directement sur l'oscilloscope. Autrement dit, les variations de la tension délivrée par l'alimentation sont négligeables.
alpha = [0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,0.95,0.99]
Vs_moy = [0.975,1.4719,1.9641,2.450,2.924,3.373,3.833,4.319,4.564,4.767]
ie = [2.21,5.31,9.29,13.96,19.01,24.47,30.96,38.8,43.21,47.1] # R1*ie en mV
ie = np.array(ie)
Vs_moy = np.array(Vs_moy)
Ve = 5.0
R = 100
figure(figsize=(8,6))
plot(alpha,Vs_moy/Ve,label="Gain")
plot(alpha,Vs_moy**2/R/(Ve*ie*1e-3),label=r"$\frac{P_c}{P_e}$")
xlim(0,1)
ylim(0,1)
grid()
xlabel(r"$\alpha$",fontsize=16)
legend(loc="upper left")
title(r"$R=100\ {\rm \Omega},\ TM=10$",fontsize=16)
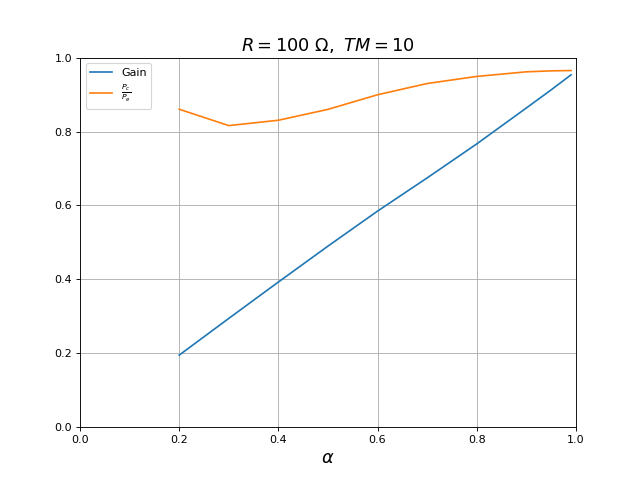 fig28.pdf
fig28.pdf
Le rendement est croissant avec le rapport cyclique (la valeur pour α=0,2 est probablement très incertaine), ce qui est la tendance inverse de celle obtenue par la simulation, mais celle-ci adopte un modèle de transistor idéal.
alpha = [0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,0.95,0.99]
Vs_moy = [1.006,1.501,1.996,2.488,2.981,3.470,3.958,4.445,4.686,4.879]
ie = [2.79,5.96,9.96,14.79,20,25.98,32.85,40.96,45.50,49.9] # R1*ie en mV
ie = np.array(ie)
Vs_moy = np.array(Vs_moy)
Ve = 5.0
R = 100
figure(figsize=(8,6))
plot(alpha,Vs_moy/Ve,label="Gain")
plot(alpha,Vs_moy**2/R/(Ve*ie*1e-3),label=r"$\frac{P_c}{P_e}$")
xlim(0,1)
ylim(0,1)
grid()
xlabel(r"$\alpha$",fontsize=16)
legend(loc="upper left")
title(r"$R=100\ {\rm \Omega},\ TM=0$",fontsize=16)
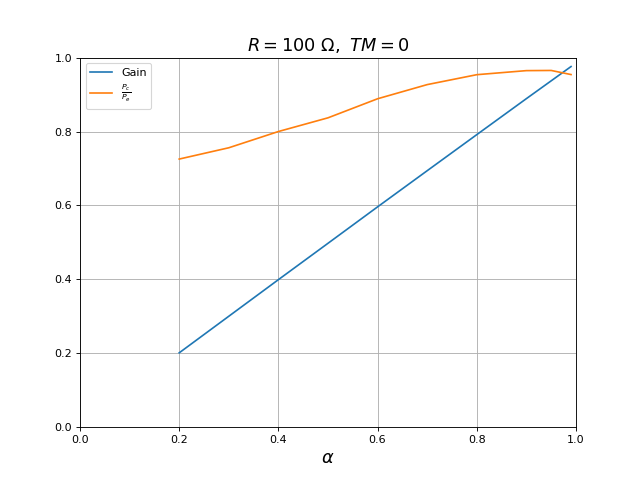 fig29.pdf
fig29.pdf
Voici les courbes pour le convertisseur non synchrone (transistor 2 remplacé par une diode) :
alpha = [0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,0.95,0.99]
Vs_moy = [1.577,2.1993,2.6748,3.0533,3.4304,3.573,3.8744,4.4112,4.6836,4.9227]
ie = [6.1363,11.55,16.58,20.955,26.066,27.96,32.16,40.56,45.35,49.36] # R1*ie en mV
ie = np.array(ie)
Vs_moy = np.array(Vs_moy)
Ve = 5.0
R = 100
figure(figsize=(8,6))
plot(alpha,Vs_moy/Ve,label="Gain")
plot(alpha,Vs_moy**2/R/(Ve*ie*1e-3),label=r"$\frac{P_c}{P_e}$")
xlim(0,1)
ylim(0,1)
grid()
xlabel(r"$\alpha$",fontsize=16)
legend(loc="upper left")
title(r"$R=100\ {\rm \Omega},\ TM=0,\ \rm{Non\ synchrone}$",fontsize=16)
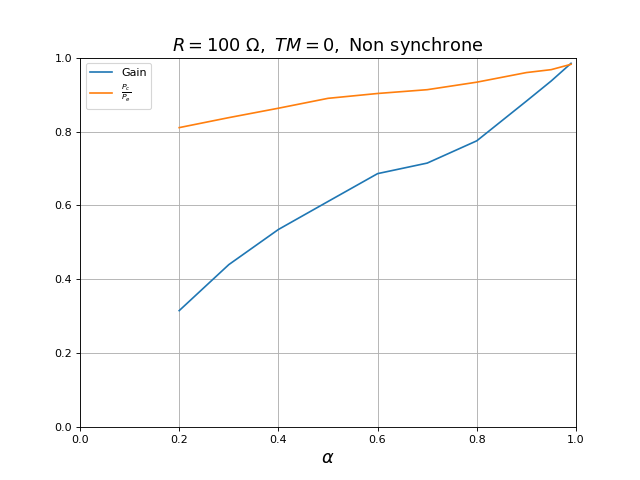 fig30.pdf
fig30.pdf
Pour le convertisseur non synchrone avec cette résistance de charge relativement grande, le gain n'est pas proportionnel au rapport cyclique : cela est vraisemblablement dû au fonctionnement en mode de conduction discontinu.
Voici le gain et le rendement pour une résistance de charge R=15 Ω :
alpha = [0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,0.95,0.99]
Vs_moy = [0.8383,1.3074,1.7741,2.2351,2.6885,3.1319,3.5636,3.9818,4.1886,4.3583]
ie = [10.59,24.92,45.92,73.03,105.51,143.72,187.08,235.54,261.82,283.88] # R1*ie en mV
ie = np.array(ie)
Vs_moy = np.array(Vs_moy)
Ve = 5.0
R = 15
figure(figsize=(8,6))
plot(alpha,Vs_moy/Ve,label="Gain")
plot(alpha,Vs_moy**2/R/(Ve*ie*1e-3),label=r"$\frac{P_c}{P_e}$")
xlim(0,1)
ylim(0,1)
grid()
xlabel(r"$\alpha$",fontsize=16)
legend(loc="upper left")
title(r"$R=15\ {\rm \Omega},\ TM=10$",fontsize=16)
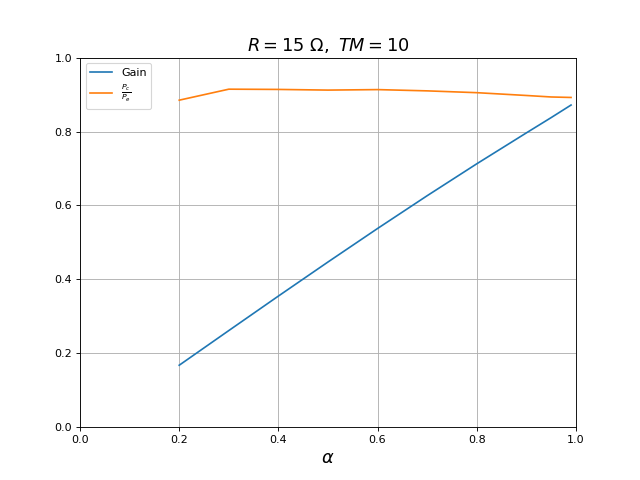 fig31.pdf
fig31.pdf
La baisse du gain est attribuable à la résistance de la bobine (relation ). On en déduit cette résistance : r=0,94 Ω. Cette valeur est plus faible que la valeur obtenue par mesure de l'impédance de la bobine en régime sinusoïdal à 20 kHz, ce qui n'est pas étonnant puisque la variation du courant dans cette résistance est ici beaucoup plus faible qu'en courant alternatif. Le rendement est plus élevé que pour le résistance de charge de 100 ohms, ce qui est étonnant puisque la résistance de la bobine augmente avec le courant.
Voici le gain et le rendement pour une résistance de charge R=15 Ω dans le cas du convertisseur non synchrone :
alpha = [0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,0.95,0.99]
Vs_moy = [0.58916,1.0892,1.6028,2.1155,2.619,3.1165,3.5975,4.0656,4.2919,4.4722]
ie = [8.66,23.15,44.74,73.03,107.61,148.00,193.66,244.84,271.71,298.36] # R1*ie en mV
ie = np.array(ie)
Vs_moy = np.array(Vs_moy)
Ve = 5.0
R = 100
figure(figsize=(8,6))
plot(alpha,Vs_moy/Ve,label="Gain")
plot(alpha,Vs_moy**2/R/(Ve*ie*1e-3),label=r"$\frac{P_c}{P_e}$")
xlim(0,1)
ylim(0,1)
grid()
xlabel(r"$\alpha$",fontsize=16)
legend(loc="upper left")
title(r"$R=15\ {\rm \Omega},\ TM=0,\ \rm{Non\ synchrone}$",fontsize=16)
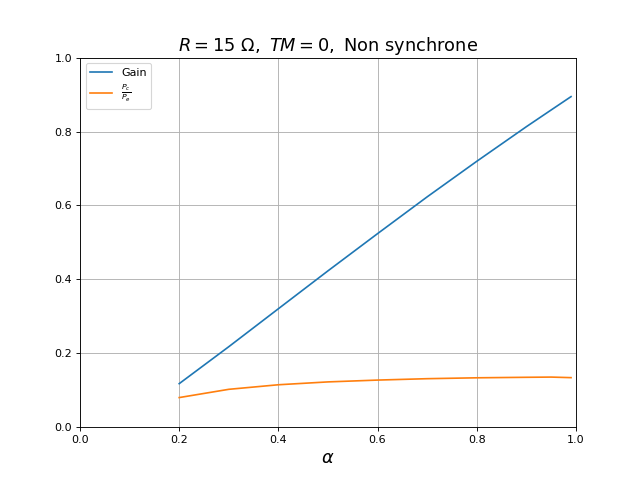 fig32.pdf
fig32.pdf
Pour cette résistance de charge plus petite, le convertisseur non synchrone a un comportement linéaire car il fonctionne en mode de conduction continu (la diode n'est jamais bloquante dans l'état 2). Le gain pour un rapport cyclique donné est plus bas que celui du convertisseur synchrone, le rendement énergétique est très faible.
3.d. Étude dynamique
Il s'agit de savoir comment le convertisseur réagit à un changement du rapport cyclique. La réponse à un échelon, c'est-à-dire à un changement instantané du rapport cyclique, est aisément obtenue. Voici la tension de sortie lorsque le rapport cyclique passe de 0,2 à 0,8 et réciproquement :
figure(figsize=(16,6))
[t,Vs] = np.loadtxt("buck-DC5-r0,2-0,8-Vs-R15.txt",skiprows=1,unpack=True)
plot(t,Vs,label=r"$\alpha=0,2\rightarrow 0,8$")
[t,Vs] = np.loadtxt("buck-DC5-r0,8-0,2-Vs-R15.txt",skiprows=1,unpack=True)
plot(t,Vs,label=r"$\alpha=0,8\rightarrow 0,2$")
grid()
ylim(0,6)
legend(loc="upper right")
xlabel("t (s)",fontsize=16)
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
title(r"$R=15\,{\rm\Omega}$",fontsize=16)
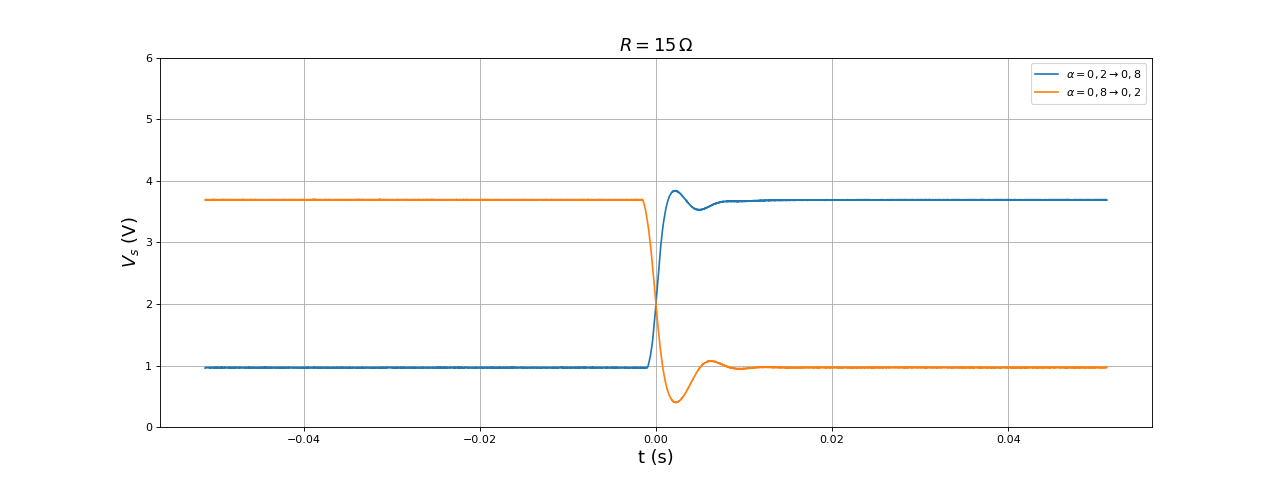 fig33.pdf
fig33.pdf
Le convertisseur se comporte de manière linéaire en régime stationnaire (quelle que soit la charge pour la version synchrone) puisque la tension de sortie est proportionnelle au rapport cyclique. La linéarité en régime dynamique n'est pas prouvée mais la forme de la réponse indicielle ci-dessus suggère cette hypothèse. On notera A(s) sa fonction de transfert (rapport de Vs sur en régime sinusoïdal permanent). La réponse indicielle présente un dépassement marquée et une oscillation rapidement amortie, ce qui suggère une fonction de transfert d'ordre 2. En comparaison, la réponse au changement de rapport cyclique obtenue par la simulation (Résolution semi-analytique) présente un dépassement immédiatement amorti (pas de passage en dessous de la valeur stationnaire après le dépassement). Le temps de réponse dans l'expérience est un peu plus grand que celui de la simulation.
3.e. Régulation de la tension de sortie : correcteur PID
La régulation de la tension de sortie par une boucle d'asservissement permet d'une part d'obtenir une tension de sortie choisie, d'autre part de la maintenir quasi constante malgré des variations de la tension d'entrée ou de la résistance de charge. Par exemple, dans le cas d'une alimentation régulée branchée sur le secteur, le convertisseur est précédé d'un redresseur et la tension d'entrée, bien que de valeur moyenne positive, présente des variations non négligeables à la fréquence de 100 Hz (deux fois 50 Hz à cause du redressement double alternance). Le système de régulation doit avoir un temps de réponse petit devant 10 ms afin d'être en mesure de maintenir la tension de sortie constante. Par ailleurs, la tension de sortie doit rester constante en cas de variation de la résistance de charge (nous ne traitons pas le cas des charges inductives ou capacitives). Nous avons vu que la résistance de charge est sans effet si le convertisseur est idéal. En réalité, l'effet sur la tension de sortie se manifeste lorsque la résistance de charge est inférieure à 10 fois la résistance interne du convertisseur (bobine et transistors).
La régulation se fait au moyen d'une rétroaction qui permet de maintenir la tension Vs à une valeur proche d'une valeur de consigne. Notons Vsc la tension commandée (ou tension consigne). La figure suivante représente le système complet avec la rétroaction permettant d'obtenir la tension commandée, dans l'hypothèse où la mesure de la tension Vs se fait avec un retard négligeable.
Figure pleine pageLe système électronique (convertisseur) a pour entrée le rapport cyclique et pour sortie la tension Vs. Le bloc C est généralement nommé correcteur car il corrige le sytème principal (bloc A).
La fonction de transfert du système bouclé est :
Le correcteur proportionnel est défini par :
donc et :
Remarquons que la tension en sortie est une fonction croissante du rapport cyclique donc Kp>0.
L'erreur étant , l'erreur relative est :
L'erreur en régime stationnaire (à fréquence nulle) est donc :
On conséquence, plus Kp est grand plus l'erreur est petite. Cependant, le système devient instable à partir d'une certaine valeur de Kp et on doit donc se contenter d'une erreur plus ou moins grande.
L'ajout d'un intégrateur dans le correcteur permet d'éliminer l'erreur en régime stationnaire. On obtient ainsi un correcteur proportionnel intégral (PI) :
donc :
et :
L'effet de l'intégrateur est d'apporter une correction proportionnelle à l'erreur cumulée dans le temps. En régime stationnaire, l'erreur s'annule mais l'erreur cumulée reste non nulle et permet justement via le terme intégral d'assurer l'erreur nulle.
Dans le cas présent Ki>0. L'erreur relative est :
L'erreur en régime stationnaire (s=0) est donc nulle. Cependant, la présence de l'intégrateur allonge le temps de réponse. Pour voir cela, supposons que le temps de réponse du convertisseur soit négligeable. On a alors et :
L'équation différentielle correspondante est :
Si , la réponse à un échelon se fait avec une exponentielle dont le temps caractéristique est :
alors que si Ki=0 (correcteur proportionnel), la réponse est instantanée. On voit cependant que le temps de réponse diminue lorsqu'on augmente Ki.
Lorsque la fonction de transfert A(s) est d'ordre 2 (c'est semble-t-il le cas pour le convertisseur étudié ici), la fonction H(s) est d'ordre 3 donc le système peut être instable si les paramètres sont mal réglés. L'ajout d'un terme dérivateur permet éventuellement d'améliorer la réponse, sous réserve que la mesure de Vs ne soit pas trop bruitée. On obtient ainsi un correcteur proportionnel-intégrale-dérivée (correcteur PID), défini par :
avec par exemple .
La fonction de transfert du correcteur PID est :
Une autre écriture, plus commode pour effectuer les réglages, consiste à introduire deux temps caractéristique Ti et Td et :
La tension Vs est échantillonnée avec une période Te. L'intégration numérique (voir Filtres intégrateur et dérivateur) est obtenue par le fitrage récursif suivant :
Si la tension de la source est supérieure à 5 V, la tension Vs doit être réduite avec un pont diviseur afin d'être numérisée par l'Arduino (tension maximale de 5 V).
Un microcontrôleur permet de réaliser l'asservissement. Le programme Arduino donné ci-dessous complète le précédent en y ajoutant les fonctions suivantes :
- Transmission de la tension de consigne (tensionVs) et des paramètres Ki,Kp,Kd.
- Interruption déclenchée périodiquement par le Timer 3 pour effectuer la numérisation de Vs sur l'entrée analogique A0.
- Dans la boucle loop, calcul de la correction PID et changement du rapport cyclique, à chaque fois qu'une nouvelle valeur de Vs est obtenue.
La numérisation de Vs est effectuée dans une interruption périodiquement déclenchée par le Timer 3, ce qui permet d'avoir une fréquence d'échantillonnage bien définie. Afin de contrôler la durée de mise à jour du rapport cyclique (ce temps doit être inférieur à la période d'échantillonnage), la sortie D3 est mise à 1 au début du traitement et à 0 à la fin.
#define HIN 11 // transistor haut
#define LIN 12 // transistor bas
#define CONTROL 3 // PE5
#define AREF 4.95 // tension sur AREF
#define DIVPOT 1 // rapport du potentiomètre
uint16_t diviseur[6] = {0,1,8,64,256,1024};
uint16_t icr;
uint16_t temps_mort = 0;
uint16_t ocra,ocrb;
float rapport;
// communication série
#define GET_DATA 10
#define SET_DATA 11
#define DATA_0_SIZE 4 // rapport cyclique (float)
#define DATA_1_SIZE 4 // Tension Vs
#define DATA_2_SIZE 4 // Kp
#define DATA_3_SIZE 4 // Ki
#define DATA_4_SIZE 4 // Kd
uint8_t data_0[DATA_0_SIZE];
uint8_t data_1[DATA_1_SIZE];
uint8_t data_2[DATA_2_SIZE];
uint8_t data_3[DATA_3_SIZE];
uint8_t data_4[DATA_4_SIZE];
bool data_1_request = false;
bool data_1_ready = true;
float tensionVs, integVs;
float lastVs,Vs;
float Kp = 0.1;
float Ki = 10;
float Kd = 1e-4;
uint8_t control = 0;
bool update = false;
uint16_t xA0;
float Te = 0.001;
// rapport cyclique du découpage
void set_rapport(float rapport) {
if (icr*rapport>temps_mort) {
ocra = icr*rapport-temps_mort;
ocrb = icr*rapport+temps_mort;
}
else {
ocra = icr*rapport;
ocrb = icr*rapport;
}
OCR1A = ocra;
OCR1B = ocrb;
}
//Timer 1 : OC1A : sortie D11, OC1B : sortie D12
void timer1_init(uint32_t period, float rapport) {
cli();
TCCR1A = (1 << COM1A1) | (1 << COM1B1) | (1 << COM1B0);
TCCR1B = (1 << WGM13);
icr = (F_CPU/1000000*period/2);
int d = 1;
while ((icr>0xFFFF)&&(d<5)) {
d++;
icr = (F_CPU/1000000*period/2/diviseur[d]);
}
TCCR1B |= d;
set_rapport(rapport);
TCNT1 = 0;
ICR1 = icr;
sei();
}
void timer3_init(uint32_t period) {
TCCR3A = 0;
TCCR3B = 0;
TCCR3B |= (1 << WGM32); // Waveform Generation mode 4 (CTC, OCRA,Immediate,MAX)
uint32_t top = (F_CPU/1000000*period);
int clock = 1;
while ((top>0xFFFF)&&(clock<5)) {
clock++;
top = (F_CPU/1000000*period/diviseur[clock]);
}
OCR3A = top;
OCR3B = top >> 1;
TIMSK3 = (1 << OCIE3B);
TCCR3B |= clock;
}
void adc_init() {
ADMUX = 0b01000000 | 0; // ADC0
ADCSRA = 0;
ADCSRA |= (1 << ADEN); // enable ADC
ADCSRA |= 7 ;
ADCSRB = 0;
}
ISR(TIMER3_COMPB_vect) {
ADCSRA |= 0b01000000; // start ADC
while (ADCSRA & 0b01000000);
xA0 = ADCL | (ADCH << 8);
update = true;
}
// traitement d'une donnée entrante
void set_data() {
char n;
while (Serial.available()<1) {};
n = Serial.read();
if (n==0) {
while (Serial.available()<DATA_0_SIZE) {};
Serial.readBytes(data_0,DATA_0_SIZE);
memcpy(&rapport,data_0,DATA_0_SIZE);
set_rapport(rapport);
}
else if (n==1) {
while (Serial.available()<DATA_1_SIZE) {};
Serial.readBytes(data_1,DATA_1_SIZE);
memcpy(&tensionVs,data_1,DATA_1_SIZE);
integVs = 0;
}
else if (n==2) {
while (Serial.available()<DATA_2_SIZE) {};
Serial.readBytes(data_2,DATA_2_SIZE);
memcpy(&Kp,data_2,DATA_2_SIZE);
}
else if (n==3) {
while (Serial.available()<DATA_3_SIZE) {};
Serial.readBytes(data_3,DATA_3_SIZE);
memcpy(&Ki,data_3,DATA_3_SIZE);
}
else if (n==4) {
while (Serial.available()<DATA_4_SIZE) {};
Serial.readBytes(data_4,DATA_4_SIZE);
memcpy(&Kd,data_4,DATA_4_SIZE);
}
}
void get_data() {
char n;
while (Serial.available()<1) {};
n = Serial.read();
if (n==1) data_1_request = true;
}
void send_data() {
if ((data_1_ready)&&(data_1_request)) {
data_1_request = false;
float Vs = xA0 *AREF/1024*DIVPOT;
Serial.write((uint8_t *)&Vs,DATA_1_SIZE);
}
}
void read_serial() {
char com;
if (Serial.available()>0) {
com = Serial.read();
if (com==GET_DATA) get_data();
else if (com==SET_DATA) set_data();
}
}
void setup() {
Serial.begin(115200);
pinMode(HIN,OUTPUT);
pinMode(LIN,OUTPUT);
pinMode(CONTROL,OUTPUT);
digitalWrite(CONTROL,LOW);
rapport = 0.5;
tensionVs = 0.0;
integVs = 0;
lastVs = 0.0;
timer1_init(50,rapport); // fréquence de découpage 20 kHz
adc_init();
timer3_init(500); // fréquence d'échantillonnage 2 kHz
}
void loop() {
read_serial();
send_data();
if ((tensionVs!=0.0)&&update) {
PORTE |= (1<<5); // digitalWrite(CONTROL,HIGH)
Vs = xA0 *AREF/1024*DIVPOT;
integVs += 0.5*Te*((tensionVs-Vs)+(tensionVs-lastVs));
rapport = 0.5+(tensionVs-Vs)*Kp+integVs*Ki-(Vs-lastVs)/Te*Kd ;
lastVs = Vs;
if (rapport > 0.99) rapport = 0.99;
else if (rapport < 0.1) rapport = 0.1;
set_rapport(rapport);
update = false;
PORTE &= ~(1<<5); // digitalWrite(CONTROL,LOW)
}
}
Le script Python suivant configure le correcteur PID (valeurs de Kp,Ti,Td) puis demande à l'utilisateur une tension de consigne. Initialement, le rapport cyclique est fixé à 0,5. La régulation démarre seulement lorsqu'une tension de consigne non nulle a été envoyée à l'Arduino.
from Arduino import Arduino
import time
ard = Arduino('COM4',[4,4,4,4,4])
time.sleep(1)
RAPPORT = 0
TENSION = 1
KP = 2
KI = 3
KD = 4
Kp = 0.01
Ti = 1e-3
Ki = Kp/Ti # ou bien Ki=0 pour enlever l'intégrateur
Td = 0
Kd = Kp*Td
ard.write_float(KP,Kp)
ard.write_float(KI,Ki)
ard.write_float(KD,Kd)
while True:
r = input('?')
if r=='n': break
elif r=="v":
Vs = ard.read_float(TENSION)
print("Vs = %f"%Vs)
else:
tension = float(r)
ard.write_float(TENSION,tension)
ard.close()
On commence par étudier le correcteur proportionnel seul (sans intégrateur ni dérivateur). La résistance de charge est de , la fréquence de découpage 20 kHz et la fréquence d'échantillonnage 2 kHz. Voici la tension en sortie et le signal de contrôle (sortie D3) pour une tension consigne de 1 V :
figure(figsize=(16,6))
[t,Vs,D3] = np.loadtxt("buck-DC5-Vs-D3-Kp0,1-R15.txt",skiprows=1,unpack=True)
plot(t,Vs,label=r"$V_s$")
plot(t,D3,label=r"D3")
grid()
ylim(0,6)
legend(loc="upper right")
xlabel("t (s)",fontsize=16)
ylabel(r"$V\ (\rm V)$",fontsize=16)
title(r"$R=15\,{\rm\Omega},\ K_p=0,1,\ K_i=0,\ K_d=0$",fontsize=16)
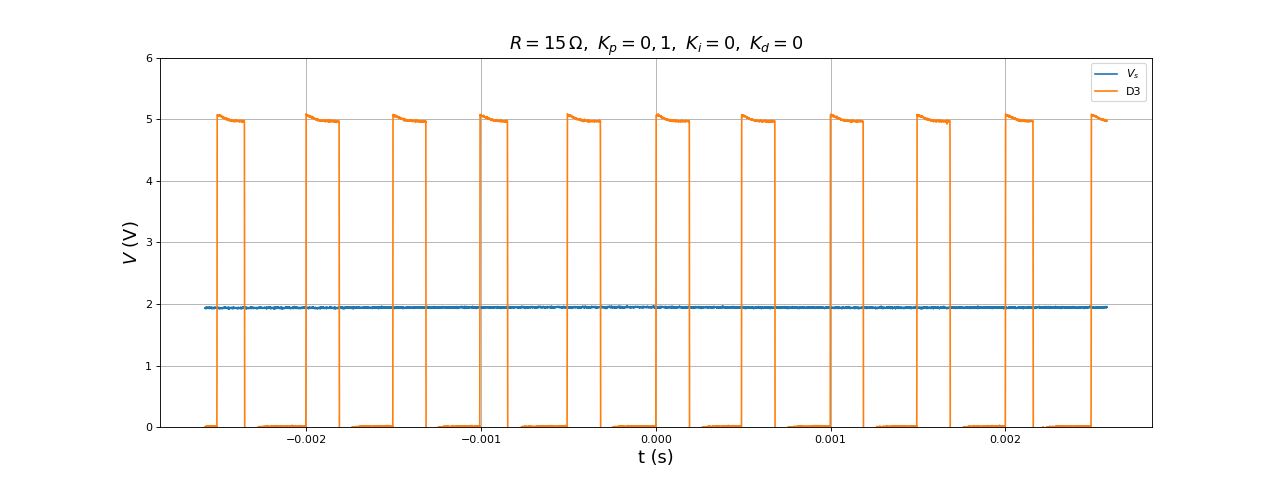 fig34.pdf
fig34.pdf
La durée du traitement (état haut de D3) est de 170 microsecondes, largement inférieur à la période d'échantillonnage. L'erreur est très grande : la tension en sortie vaut 2 V alors que la commande est 1 V. Augmentons Kp :
figure(figsize=(16,6))
[t,Vs] = np.loadtxt("buck-DC5-Vs-Kp0,4-R15.txt",skiprows=1,unpack=True)
plot(t,Vs,label=r"$V_s$")
grid()
ylim(0,6)
xlabel("t (s)",fontsize=16)
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
title(r"$R=15\,{\rm\Omega},\ K_p=0,4,\ K_i=0,\ T_d=0$",fontsize=16)
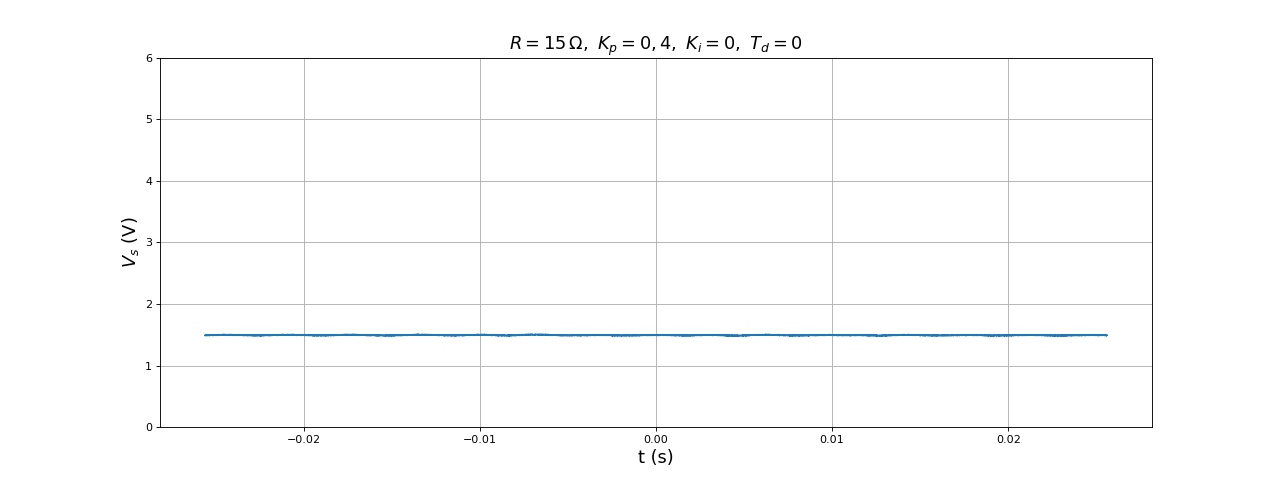 fig35.pdf
fig35.pdf
L'augmentation de Kp permet de réduire l'erreur mais celle-ci reste grande. On augmente encore Kp :
figure(figsize=(16,6))
[t,Vs] = np.loadtxt("buck-DC5-Vs-Kp0,5-R15.txt",skiprows=1,unpack=True)
plot(t,Vs,label=r"$V_s$")
grid()
ylim(0,6)
xlabel("t (s)",fontsize=16)
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
title(r"$R=15\,{\rm\Omega},\ K_p=0,5,\ K_i=0,\ T_d=0$",fontsize=16)
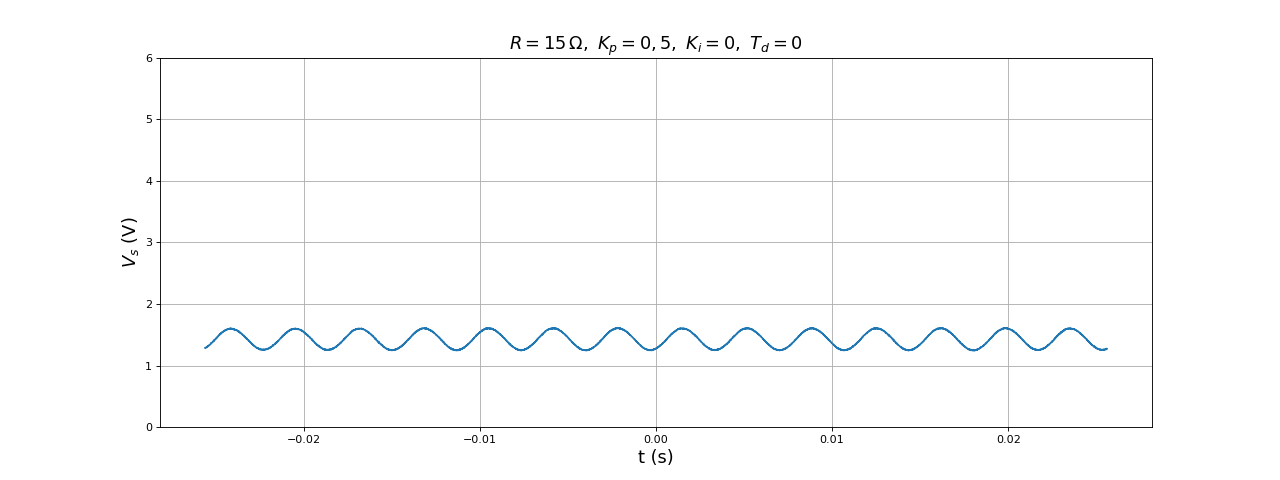 fig36.pdf
fig36.pdf
La sortie devient instable au dessus d'une certaine valeur de Kp, conformément à ce que prévoit la théorie pour un système de degré 2. L'instabilité se manifeste ici par une oscillation quasi sinusoïdale permamente, probablement à cause de phénomènes non linéaires non pris en compte dans la théorie (il est très improbable qu'on soit précisément en stabilité marginale). Pour la valeur Kp=0,3, voici la réponse indicielle, lorsque la consigne passe de 1 V à 4 V :
figure(figsize=(16,6))
[t,Vs] = np.loadtxt("buck-DC5-Vs-Kp0,3-R15-1-4V.txt",skiprows=1,unpack=True)
plot(t,Vs,label=r"$V_s$")
grid()
ylim(0,6)
xlim(-0.05,0.05)
xlabel("t (s)",fontsize=16)
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
title(r"$R=15\,{\rm\Omega},\ K_p=0,3,\ K_i=0,\ T_d=0$",fontsize=16)
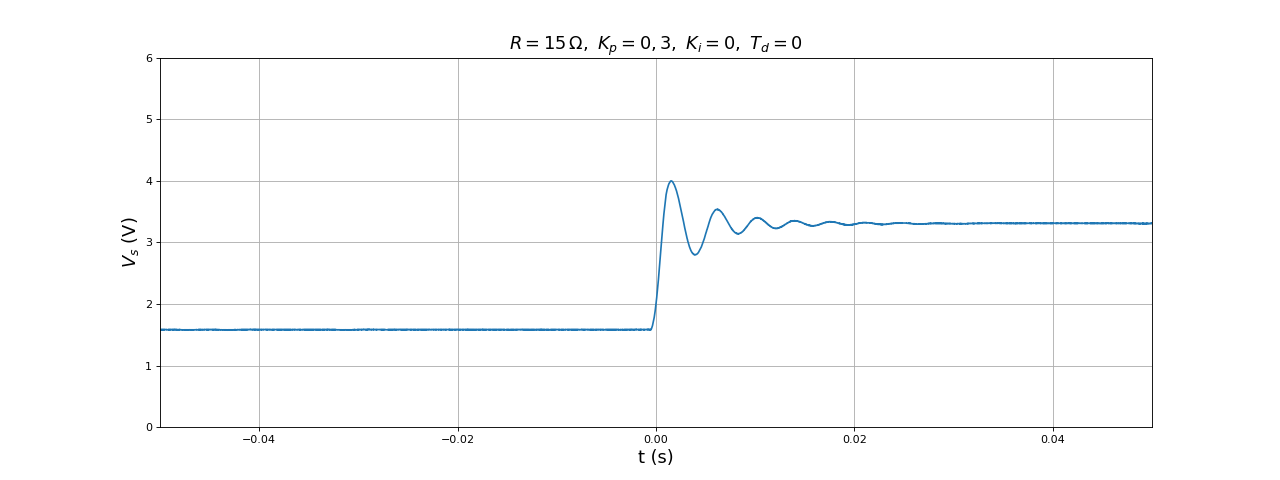 fig37.pdf
fig37.pdf
Si l'on compare cette réponse à celle du convertisseur (non asservi) obtenue plus haut (Étude dynamique), on voit que le correcteur proportionnel augmente le comportement oscillatoire amorti et allonge le temps de réponse, d'autant plus que Kp est grand. L'erreur reste grande avant que le comportement instable n'apparaisse. Le correcteur proportionnel seul ne peut suffire.
On ajoute à présent la correction intégrale, avec une valeur de Ti du même ordre de grandeur que le temps de réponse du système non asservi (10 ms).
figure(figsize=(16,6))
[t,Vs] = np.loadtxt("buck-DC5-Vs-Kp0,3-Ti0,01-R15-1-4V.txt",skiprows=1,unpack=True)
plot(t,Vs,label=r"$V_s$")
grid()
ylim(0,6)
xlim(-0.05,0.05)
xlabel("t (s)",fontsize=16)
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
title(r"$R=15\,{\rm\Omega},\ K_p=0,3,\ T_i=0,01,\ T_d=0$",fontsize=16)
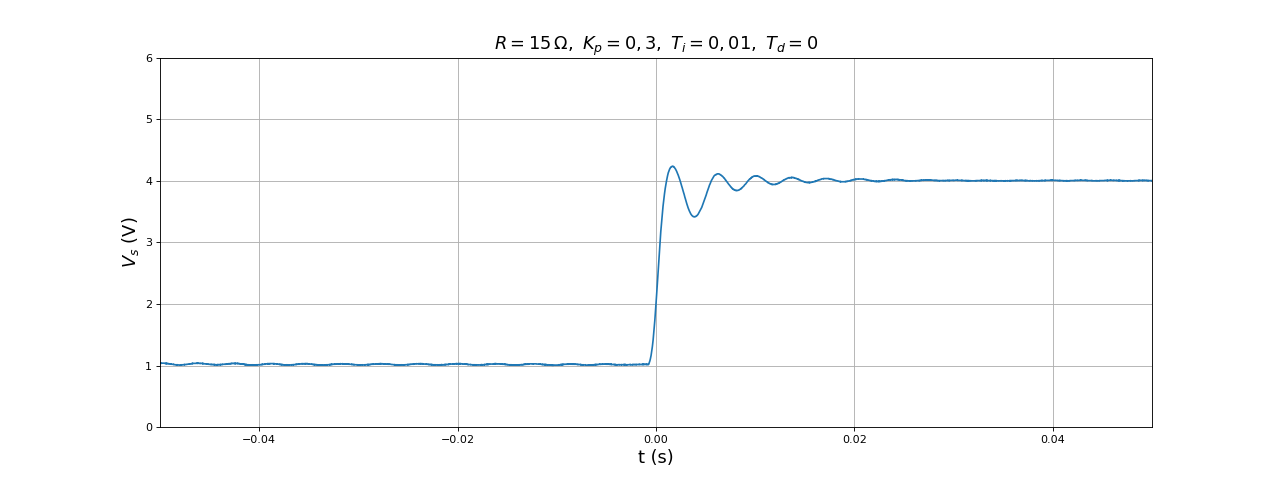 fig38.pdf
fig38.pdf
L'intégrateur permet d'éliminer complètement l'erreur. En régime permanent, il subsiste ici une petite oscillation. Comme le montre l'étude menée dans correcteur proportionnel-intégrale-dérivée, il faut abaisser Kp afin de diminuer le temps Ti en dessous duquel le système devient instable :
figure(figsize=(16,6))
[t,Vs] = np.loadtxt("buck-DC5-Vs-Kp0,1-Ti0,01-R15-1-4V.txt",skiprows=1,unpack=True)
plot(t,Vs,label=r"$V_s$")
grid()
ylim(0,6)
xlim(-0.05,0.05)
xlabel("t (s)",fontsize=16)
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
title(r"$R=15\,{\rm\Omega},\ K_p=0,1,\ T_i=0,01,\ T_d=0$",fontsize=16)
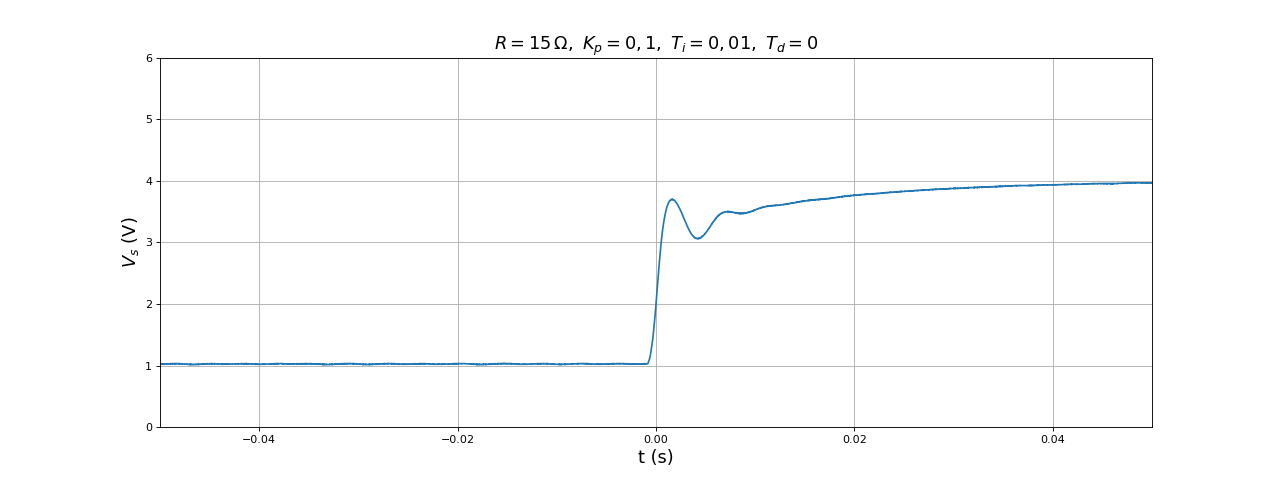 fig39.pdf
fig39.pdf
L'étude théorique montre qu'il existe une valeur optimale de Kp donnant le temps de réponse le plus court. Nous recherchons cette valeur par essais successifs.
figure(figsize=(16,6))
[t,Vs] = np.loadtxt("buck-DC5-Vs-Kp0,25-Ti0,01-R15-1-4V.txt",skiprows=1,unpack=True)
plot(t,Vs,label=r"$V_s$")
grid()
ylim(0,6)
xlim(-0.05,0.05)
xlabel("t (s)",fontsize=16)
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
title(r"$R=15\,{\rm\Omega},\ K_p=0,25,\ T_i=0,01,\ T_d=0$",fontsize=16)
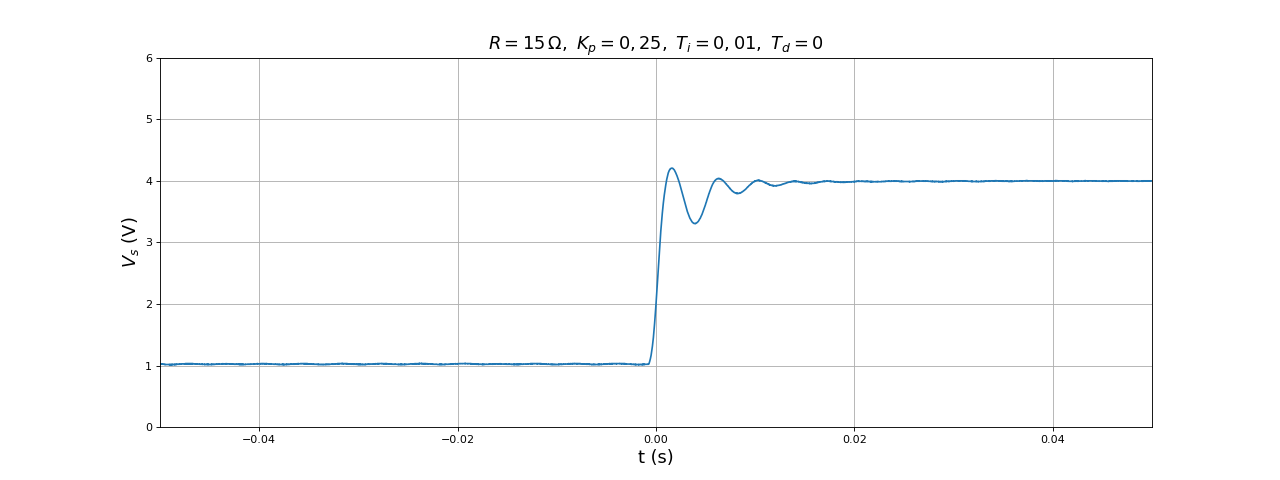 fig40.pdf
fig40.pdf
Pour la valeur de Ti adoptée, nous obtenons la réponse la plus rapide pour le correcteur PI, avec un dépassement plutôt faible.
Pour finir, nous ajoutons le dérivateur dans le correcteur. Le temps Td doit reste assez petit pour garder la stabilité.
figure(figsize=(16,6))
[t,Vs] = np.loadtxt("buck-DC5-Vs-Kp0,25-Ti0,01-Td0,001-R15-1-4V.txt",skiprows=1,unpack=True)
plot(t,Vs,label=r"$V_s$")
grid()
ylim(0,6)
xlim(-0.05,0.05)
xlabel("t (s)",fontsize=16)
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
title(r"$R=15\,{\rm\Omega},\ K_p=0,25,\ T_i=0,01,\ T_d=0,001$",fontsize=16)
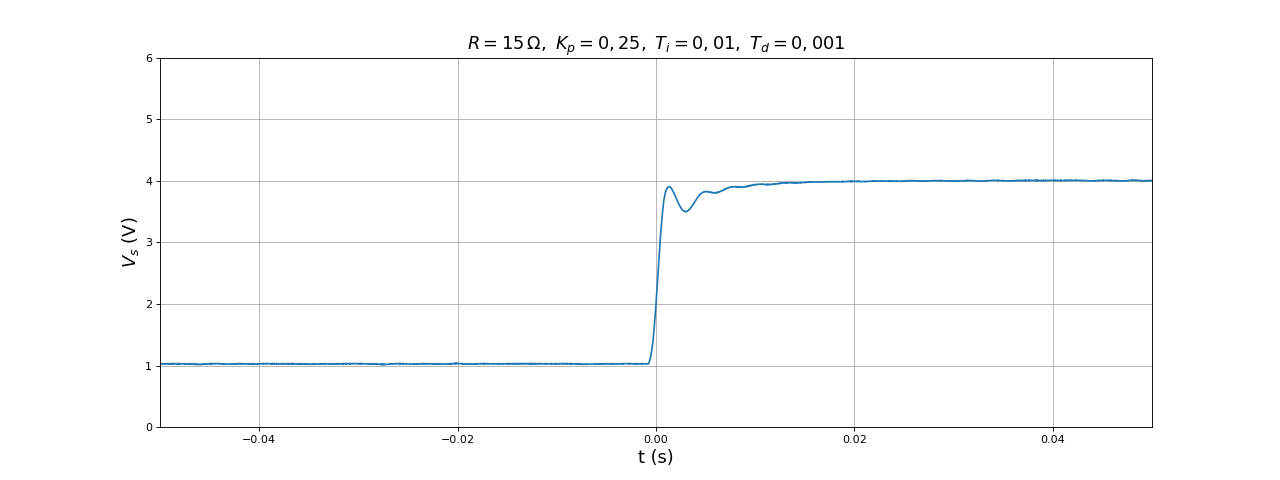 fig41.pdf
fig41.pdf
Le dérivateur permet d'éliminer le dépassement et de réduire le temps de réponse. D'après l'exemple traité dans correcteur proportionnel-intégrale-dérivée, il existe une valeur optimale de Td, que nous recherchons par essais successifs :
figure(figsize=(16,6))
[t,Vs] = np.loadtxt("buck-DC5-Vs-Kp0,25-Ti0,01-Td0,002-R15-1-4V.txt",skiprows=1,unpack=True)
plot(t,Vs,label=r"$V_s$")
grid()
ylim(0,6)
xlim(-0.05,0.05)
xlabel("t (s)",fontsize=16)
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
title(r"$R=15\,{\rm\Omega},\ K_p=0,25,\ T_i=0,01,\ T_d=0,002$",fontsize=16)
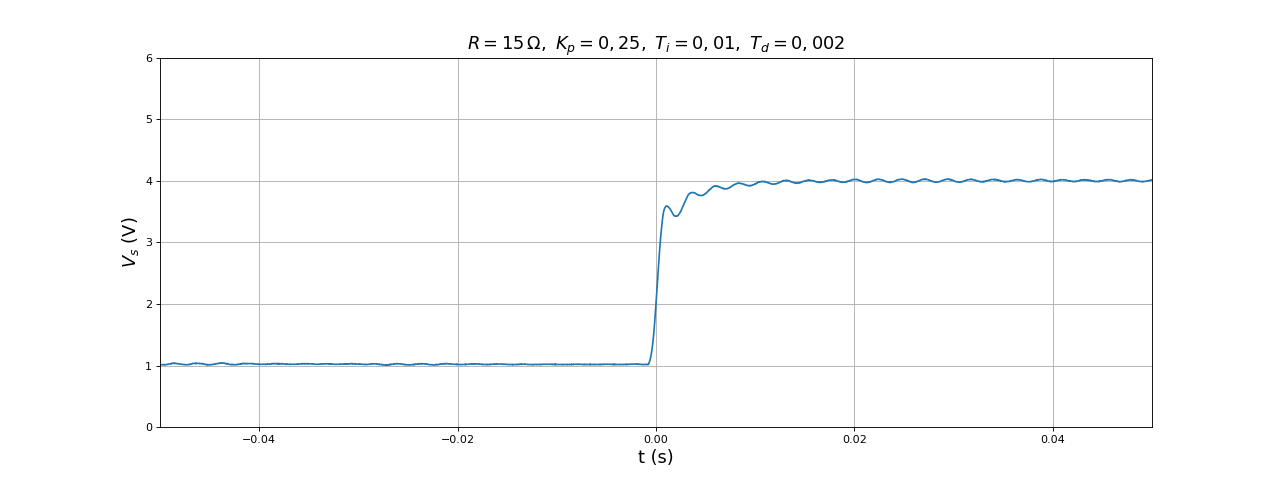 fig42.pdf
fig42.pdf
figure(figsize=(16,6))
[t,Vs] = np.loadtxt("buck-DC5-Vs-Kp0,25-Ti0,01-Td0,0015-R15-1-4V.txt",skiprows=1,unpack=True)
plot(t,Vs,label=r"$V_s$")
grid()
ylim(0,6)
xlim(-0.05,0.05)
xlabel("t (s)",fontsize=16)
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
title(r"$R=15\,{\rm\Omega},\ K_p=0,25,\ T_i=0,01,\ T_d=0,0015$",fontsize=16)
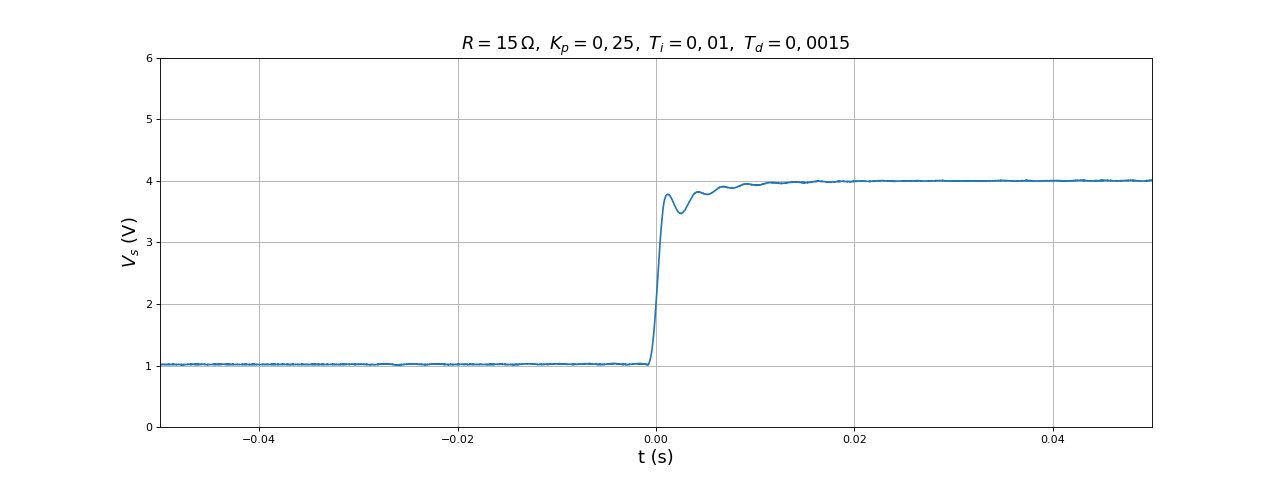 fig43.pdf
fig43.pdf
La première valeur (0,002) est un peu trop grande car elle conduit à une oscillation permamente. La seconde (0,0015) convient. Voici la réponse pour un échelon descendant :
figure(figsize=(16,6))
[t,Vs] = np.loadtxt("buck-DC5-Vs-Kp0,25-Ti0,01-Td0,0015-R15-4-1V.txt",skiprows=1,unpack=True)
plot(t,Vs,label=r"$V_s$")
grid()
ylim(0,6)
xlim(-0.05,0.05)
xlabel("t (s)",fontsize=16)
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
title(r"$R=15\,{\rm\Omega},\ K_p=0,25,\ T_i=0,01,\ T_d=0,0015$",fontsize=16)
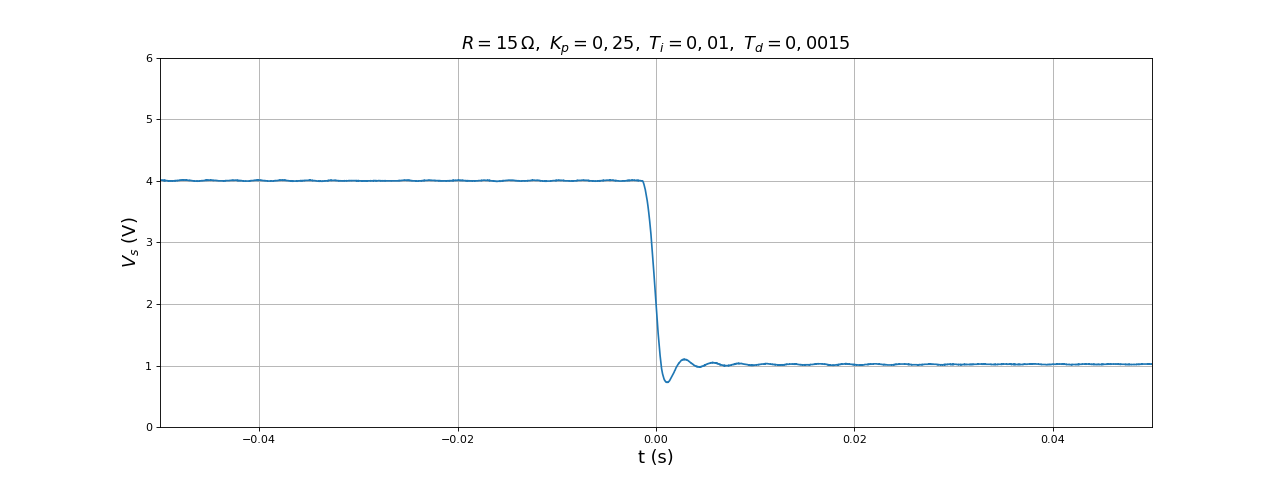 fig44.pdf
fig44.pdf
Pour l'échelon descendant, il y a un léger dépassement. Le temps de réponse obtenu est proche de celui du système non asservi et la convergence vers la valeur stationnaire se fait avec un dépassement modéré. Il faut aussi remarquer que la chaîne de mesure introduit un retard de 500 microsecondes (la période d'échantillonnage) qui n'est pas pris en compte dans l'étude théorique. Ce temps de retard est petit devant le temps de réponse mais peut-être pas négligeable (il peut en tout cas avoir un effet sur la condition de stabilité).
Notre procédure de réglage repose sur un choix initial de Ti. Une tentative d'amélioration pourrait consister à répéter la procédure pour d'autres valeurs de Ti. Nous adoptons une autre méthode, consistant à diminuer légèrement Ti de manière à réduire le temps de réponse sans introduire de dépassement :
figure(figsize=(16,6))
[t,Vs] = np.loadtxt("buck-DC5-Vs-Kp0,25-Ti0,009-Td0,0015-R15-1-4V.txt",skiprows=1,unpack=True)
plot(t,Vs)
[t,Vs] = np.loadtxt("buck-DC5-Vs-Kp0,25-Ti0,009-Td0,0015-R15-4-1V.txt",skiprows=1,unpack=True)
plot(t,Vs)
grid()
ylim(0,6)
xlim(-0.05,0.05)
xlabel("t (s)",fontsize=16)
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
title(r"$R=15\,{\rm\Omega},\ K_p=0,25,\ T_i=0,009,\ T_d=0,0015$",fontsize=16)
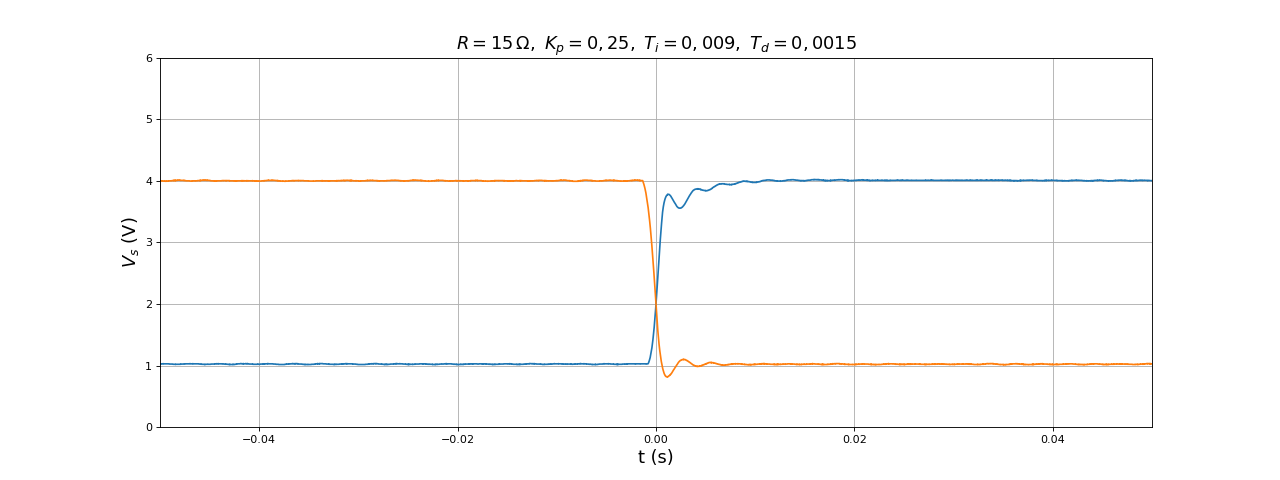 fig45.pdf
fig45.pdf
4. Utilisation d'un pont en H
4.a. Principe
On trouve dans le commerce des ponts en H (par exemple constitué de quatre transistors MOSFET) prévus pour l'alimentation des moteurs à courant continu. Il est possible d'utiliser la moitié du pont pour réaliser un convertisseur abaisseur. La figure suivante montre comme la sortie A du pont doit être reliée au filtre :
Figure pleine pageLe pont est constitué de deux bras de pont, le bras A avec sa sortie OUTA et le bras B avec sa sortie OUTB. Le plus souvent, la commande de ce type de pont se fait par trois entrées : ENABLE, IN1 et IN2. Lorsque ENABLE = 0, tous les transistors sont ouverts quel soit l'état de IN1 et IN2. Lorsque ENABLE = 1, IN1 pilote les transistors T2 et T3 alors que IN2 pilote les transistors T1 et T4, comme précisé sur la figure ci-dessus. Lorsqu'un moteur à courant continu est branché entre OUTA et OUTB, on choisit le sens du passage du courant avec IN1 et IN2 et on applique un signal PWM sur ENABLE pour appliquer une tension effective au moteur égale à la tension de la source Vs multipliée par le rapport cyclique. On peut aussi réaliser un frein moteur avec IN1=1 et IN2=1 ou bien une roue libre avec IN1=0 et IN2=0. Pour utiliser le bras de pont A dans un convertisseur continu-continu, il faut laisser ENABLE = 1 en permanence et appliquer deux signaux PWM complémentaires sur IN1 et IN2, c'est-à-dire dont les deux états sont (IN1=1,IN2=0) et (IN1=0,IN2=1). Il s'agit de la même commande que celle décrite plus haut (Programme Arduino) pour piloter les deux transistors MOSFET via le driver IR2113.
Certains ponts en H possèdent seulement deux entrées de commande, appelées le plus souvent PWM et DIR. Dans ce cas, la commande PWM est identique à la commande ENABLE et la commande DIR permet de choisir l'un des deux états donnés sur la figure ci-dessus. Avec ce type de commande, le pilotage du convertisseur se fait en laissant PWM=1 en permanence et en appliquant le signal PWM à l'entrée DIR. Remarquons que ce type de commande pour un moteur ne permet ni la roue libre ni le frein moteur.
4.b. Pilotage par Arduino
Cette partie montre comment générer deux signaux PWM complémentaires avec un Arduino MEGA. On utilise pour cela un des Timers 1,3 ou 4. Un Timer permet de générer des signaux PWM sur ses sorties OCA, OCB et OCC. Voici les bornes reliées à ces sorties sur l'Arduino MEGA :
- Timer 1 : OC1A (D11), OC1B (D12), OC1C (D13).
- Timer 3 : OC3A (D5), OC3B (D2), OC3B (D3).
- Timer 4 : OC4A (D6), OC4B (D7), OC4C (D8).
La figure suivante montre le fonctionnement de la génération des signaux complémentaires avec le Timer 1 sur ses sorties OC1A et OC1B :
Figure pleine pageLe compteur (registre TCNT1) est incrémenté à une cadence égale à la fréquence d'horloge (16 MHz) divisée par 1, 8, 64, 256 ou 1024 (diviseur d'horloge). Il est incrémenté jusqu'à la valeur contenue dans le registre ICR1 puis décrémenté jusqu'à zéro. Les sorties OC1A et OC1B sont générées à partir des seuils définis dans respectivement OCR1A (Output Compare Register) et OCR1B. La sortie OC1A est configurée avec le mode : clear OC1A on compare when up counting, la sortie OC1B avec le mode : set OC1B on compare match when up counting. Cela permet de générer deux signaux complémentaires. Le rapport cyclique de OC1B est le rapport OCR1A/ICR1.
La période T est déterminée par le diviseur d'horloge et par la valeur de ICR1. Pour obtenir une période donnée, on calcule ICR avec la formule suivante :
où f est la fréquence d'horloge (16 MHz), d le diviseur de cette fréquence. Il s'agit d'un compteur 16 bits donc ICR doit être inférieur à 0xFFFF. S'il ne l'est pas, on doit augmenter le diviseur d'horloge. La valeur la plus grande de ce dernier étant 1024, la période la plus grande pouvant être obtenue est de 8,39 secondes (environ). Le rapport cyclique est quantifié : le nombre de rapports cycliques possibles est le nombre de valeurs de OCR1A possibles, c'est-à-dire ICR1. Pour le convertisseur continu-continu étudié dans ce document, une période de découpage de 100 microsecondes convient bien. Le diviseur d=1 conduit à ICR1=800, ce qui conduit à une finesse de réglage du rapport cyclique satisfaisante pour la plupart des applications.
La fonction suivante permet de programmer le Timer 1 pour la génération de deux signaux complémentaires sur ses sorties OCA et OCB :
void timer1_init(uint32_t period, float rapport) {
uint16_t diviseur[6] = {0,1,8,64,256,1024};
TCCR1A = (1 << COM1B1) | (1 << COM1B0) | (1 << COM1A1); // Clear OC1A on compare match (set output to high level), Set OC1B on compare match (set output to low level)
TCCR1B = 1 << WGM13; // PWM, Phase and Frequency Correct
uint32_t icr = (F_CPU/1000000*period/2);
int clock = 1;
while ((icr>0xFFFF)&&(clock<5)) {
clock++;
icr = (F_CPU/1000000*period/2/diviseur[clock]);
}
uint16_t ocra = icr*(1.0-rapport); // rapport cyclique de OC1B
ICR1 = icr;
OCR1A = ocra;
OCR1B = ocra;
TCCR1B |= clock;
}
Pour la sortie OCA (D11), les bits COM1A0 et COM1A1 du registre TCCR1A sont mis à 1, ce qui permet d'obtenir le mode : Set OCnA/OCnB/OCnC on compare match (set output to high level). Pour la sortie OCB (D12), seul le bit COM1B1 est mis à 1, ce qui permet d'obtenir le mode : Clear OCnA/OCnB/OCnC on compare match (set output to low level). On obtient ainsi les deux signaux complémentaires. Le mode de génération de la forme d'onde (Waveform Generation Mode) se définit avec les 4 bits WGM13, WGM12, WGM11 et WGM10 (les deux premiers sont dans le registre TCCR1A, les deux derniers dans TCCR1B). Voici le tableau des différents modes :
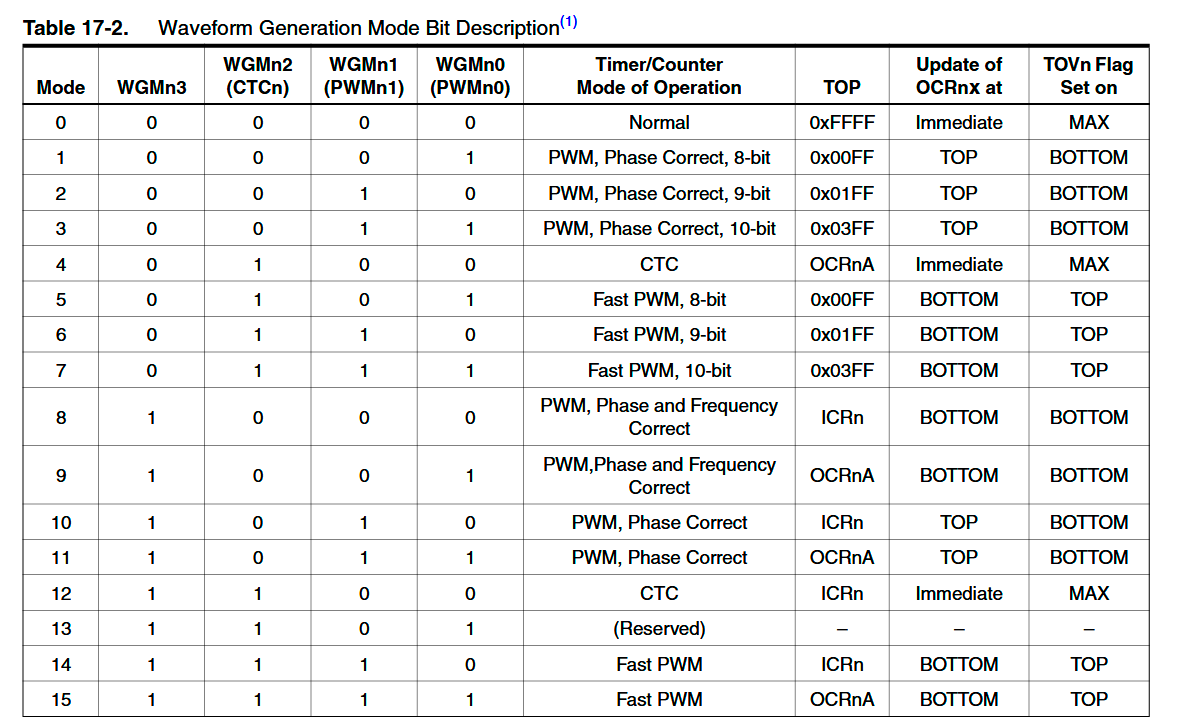
Dans le cas présent, nous avons opté pour le mode PWM, Phase and Frequency Correct.
Remarquons que rapport définit le rapport cyclique du signal généré sur OCA; celui généré sur OCB a bien évidemment le rapport cyclique 1-rapport (nous avons fait l'inverse dans le programme présenté plus haut). Si nous inversons la configuration des sorties OCA et OCB (dans le registre TCCR1A), la fonction devient :
void timer1_init(uint32_t period, float rapport) {
uint16_t diviseur[6] = {0,1,8,64,256,1024};
TCCR1A = (1 << COM1A1) | (1 << COM1A0) | (1 << COM1B1); // Set OC1A on compare match (set output to high level), Clear OC1B on compare match (set output to low level)
TCCR1B = 1 << WGM13;
uint32_t icr = (F_CPU/1000000*period/2);
int clock = 1;
while ((icr>0xFFFF)&&(clock<5)) {
clock++;
icr = (F_CPU/1000000*period/2/diviseur[clock]);
}
uint16_t ocra = icr*rapport; // rapport cyclique de OC1A
ICR1 = icr;
OCR1A = ocra;
OCR1B = ocra;
TCCR1B |= clock;
}
Si l'on souhaite utiliser la sortie OCC (D13) au lieu de OCB (D12), il suffit de remplacer la ligne OCR1B = ocra par OCR1C = ocra.
La transposition de la fonction pour la programmation d'un autre Timer, par exemple le Timer 3, se fait simplement en remplaçant l'indice 1 dans les noms de registre par l'indice 3 (il n'est pas nécessaire de le faire dans les noms de bits) :
void timer3_init(uint32_t period, float rapport) {
uint16_t diviseur[6] = {0,1,8,64,256,1024};
TCCR3A = (1 << COM1A1) | (1 << COM1A0) | (1 << COM1B1); // Set OC1A on compare match (set output to high level), Clear OC1B on compare match (set output to low level)
TCCR3B = 1 << WGM13; // PWM, Phase and Frequency Correct
uint32_t icr = (F_CPU/1000000*period/2);
int clock = 1;
while ((icr>0xFFFF)&&(clock<5)) {
clock++;
icr = (F_CPU/1000000*period/2/diviseur[clock]);
}
uint16_t ocra = icr*(1.0-rapport); // rapport cyclique de OC1B
ICR3 = icr;
OCR3A = ocra;
OCR3B = ocra;
TCCR3B |= clock;
}