Correcteur proportionnel-intégrale-dérivée

1. Introduction

2. Système d'ordre 1

2.a. Fonction de transfert et stabilité

2.b. Régime stationnaire

2.c. Réponse à un échelon

2.d. Simulation

3. Système d'ordre 2

3.a. Fonction de transfert et stabilité

3.b. Réponse à un échelon

3.c. Simulation

3.d. Calcul des pôles

3.e. Exemple

1. Introduction

On considère un système linéaire définie par sa fonction de transfert A(p) ( $p = j ω$ en régime sinusoïdal). Son entrée et sa sortie sont notées respectivement E et S. L'asservissement du système a pour objectif de rendre la sortie S la plus proche possible d'une valeur de consigne, notée S_c (la sortie est asservie à la consigne). La figure suivante montre le schéma général de la boucle d'asservissement avec un correcteur :

Figure pleine page

La rétroaction est constituée d'une chaîne de mesure, de fonction de transfert B(p), qui permet de mesurer la sortie S. L'erreur est $ε (p) = S_{c} - B (p) S (p)$ . En l'absence de correction, celle-ci est directement injectée dans l'entrée du système. L'objectif est que S soit le plus proche possible de S_c et, en cas de changement brusque de cette dernière, la sortie doit parvenir le plus rapidement possible à sa valeur stationnaire. Il est parfois possible de modifier A(p) et B(p) afin d'obtenir la réponse souhaitée mais cette approche est très limitée. Pour modifier la réponse du système asservi, on ajoute un correcteur, supposé linéaire et défini par sa fonction de transfert C(p). En présence du correcteur, E(p)=C(p)(S_c-B(p)S(p)).

La fonction de transfert du système asservi est :

H (p) = \frac{S}{S_{c}} = \frac{A (p) C (p)}{1 + A (p) B (p) C (p)} (1)

Le correcteur proportionnel-intégrale-dérivée (PID) est défini par la :

C (p) = K_{p} + \frac{K_{i}}{p} + K_{d} p (2)

c'est-à-dire, dans le domaine temporel :

E (t) = K_{p} ε (t) + K_{i} \int_{0}^{t} ε (t) d t + K_{d} \frac{d ε}{d t} (3)

Une autre écriture du correcteur PID est :

C (p) = K_{p} (1 + \frac{1}{T_{i} p} + T_{d} p) (4)

où les deux constantes positives T_i,T_d ont les dimensions d'un temps.

Ce document montre comment simuler la réponse temporelle d'un système asservi avec un correcteur PID et montre une procédure de réglage de ses paramètres. On suppose que le retard introduit par la chaîne de mesure est négligeable, c'est-à-dire que B(p)=1. On étudiera le cas d'un système A(p) d'ordre 1 et le cas d'un système d'ordre 2.

2. Système d'ordre 1

2.a. Fonction de transfert et stabilité

Le système considéré est du premier ordre, avec une pulsation de coupure $ω_{0} = \frac{1}{T}$ . Sa fonction de transfert est de la forme :

A (p) = \frac{A_{0}}{1 + \frac{p}{ω_{0}}} = \frac{A_{0}}{1 + T p} (5)

La fonction de transfert du système asservi (avec $B (p) = 1$ ) muni du correcteur PID est donc :

H (p) = \frac{A_{0} K_{p} (T_{d} p^{2} + p + \frac{1}{T_{i}})}{(A_{0} K_{p} T_{d} + T) p^{2} + (A_{0} K_{p} + 1) p + \frac{A_{0} K_{p}}{T_{i}}} (6)

Remarquons que A₀K_p est nécessairement positif (on se placera dans le cas où ces deux constantes sont positives) donc les coefficients de la fonction de transfert (de la fraction rationnelle) sont positifs.

L'équation différentielle se déduit de la fonction de transfert :

(A_{0} K_{p} T_{d} + T) \frac{d^{2} S}{d t^{2}} + (A_{0} K_{p} + 1) \frac{d S}{d t} + \frac{A_{0} K_{p}}{T_{i}} S = A_{0} K_{p} T_{d} \frac{d^{2} S_{c}}{d t^{2}} + A_{0} K_{p} \frac{d S_{c}}{d t} + \frac{A_{0} K_{p}}{T_{i}} S_{c} (7)

La solution générale de cette équation est la somme d'une solution particulière et de la solution générale de l'équation sans second membre. Cette dernière est une combinaison linéaire des solutions de la forme $S (t) = exp (p t)$ , où p est solution de :

(A_{0} K_{p} T_{d} + T) p^{2} + (A_{0} K_{p} + 1) p + \frac{A_{0} K_{p}}{T_{i}} = 0 (8)

Autrement dit, p est un pôle de la fonction de transfert. Le système est stable si la solution générale de l'équation sans second membre tend vers zéro lorsque t tend vers l'infini, c'est-à-dire si tous les pôles ont une partie réelle strictement négative. Une partie réelle nulle conduit à une oscillation sinusoïdale permanente, que l'on peut aussi considérer comme une instabilité. Les pôles sont les solutions de l'équation $a p^{2} + b p + c = 0$ , dont le discriminant est $Δ = b^{2} - 4 a c$ . Si $Δ > 0$ , les pôles sont :

\begin{matrix} p_{1} = \frac{- b + \sqrt{b^{2} - 4 a c}}{2 a} & (9) \\ p_{2} = \frac{- b - \sqrt{b^{2} - 4 a c}}{2 a} & (10) \end{matrix}

a, b et c sont positifs donc ces deux pôles réels sont négatifs.

Si $Δ < 0$ , les pôles sont :

\begin{matrix} p_{1} = \frac{- b + j \sqrt{4 a c - b^{2}}}{2 a} & (11) \\ p_{2} = \frac{- b - j \sqrt{4 a c - b^{2}}}{2 a} & (12) \end{matrix}

a et b sont positifs donc la partie réelle de ces pôles est négative.

Enfin dans le cas où $Δ = 0$ , le pôle double est un réel négatif.

Le système d'ordre 1 asservi avec le correcteur PID est donc toujours stable.

2.b. Régime stationnaire

Lorsque S_c est constante, la sortie S parvient à une valeur stationnaire déterminée par la valeur de la fonction de transfert à fréquence nulle. Si $1 / T_{i} \neq 0$ :

H (0) = 1 (13)

mais si le terme intégrateur est absent ( $1 / T_{i} = 0$ ) on a :

H (0) = \frac{A_{0} K_{p}}{1 + A_{0} K_{p}} = \frac{1}{1 + \frac{1}{A_{0} K_{p}}} (14)

Dans le premier cas l'erreur en régime stationnaire est nulle mais dans le second cas :

ε (0) = S_{c} (\frac{1}{1 + A_{0} K_{p}}) (15)

Conclusion : en l'absence de l'intégrateur, l'erreur en régime stationnaire est non nulle et cette erreur est d'autant plus petite que K_p est grand; en présence du terme intégrateur, l'erreur en régime stationnaire est nulle.

2.c. Réponse à un échelon

On considère un échelon de la commande S_c : pour t<=0 on a S_c=0 et pour t>0 on a S_c=S_c⁰.

Sans intégrateur

Sans intégrateur (1/T_i=0), la fonction de transfert s'écrit :

H (p) = \frac{A_{0} K_{p} (T_{d} p + 1)}{(A_{0} K_{p} T_{d} + T) p + (A_{0} K_{p} + 1)} (16)

donc l'équation différentielle est :

(A_{0} K_{p} T_{d} + T) \frac{d S}{d t} + (A_{0} K_{p} + 1) S = A_{0} K_{p} T_{d} \frac{d S_{c}}{d t} + A_{0} K_{p} S_{c} (17)

Le temps caractéristique est :

τ = \frac{A_{0} K_{p} T_{d} + T}{A_{0} K_{p} + 1} = \frac{A_{0} K_{d} + T}{A_{0} K_{p} + 1} (18)

et la réponse à l'échelon s'écrit :

S (t) = \frac{A_{0} K_{p} S_{c}^{0}}{1 + A_{0} K_{p}} + A_{1} e^{- \frac{t}{τ}} (19)

La sortie tend donc vers la valeur stationnaire de manière monotone (sans dépassement) avec un temps caractéristique d'autant plus petit que K_p est grand. Le dérivateur n'a pas d'intérêt dans ce cas puisqu'il ne fait qu'allonger le temps de réponse. En l'absence d'intégrateur, on utilise seulement le correcteur proportionnel, avec l'inconvénient d'une erreur en régime stationnaire mais qui se réduit si K_p est grand.

En conclusion, pour un système d'ordre 1, le correcteur proportionnel suffit et permet de réduire le temps de réponse. Si K_p est assez grand, l'erreur est négligeable.

Avec intégrateur

La fonction de transfert est $(6)$ et l'équation différentielle $(7)$ . La forme de la réponse est déterminée par le signe de $Δ$ et le temps de réponse est déterminé par la partie réelle des pôles. Le discriminant est :

Δ = {(1 + A_{0} K_{p})}^{2} - 4 \frac{A_{0} K_{p}}{T_{i}} (A_{0} K_{p} T_{d} + T) = {(1 + A_{0} K_{p})}^{2} - 4 A_{0} K_{i} (A_{0} K_{d} + T) (20)

Si K_i est suffisamment faible, Δ>0 donc la solution s'écrit :

S (t) = S_{c}^{0} + A_{1} e^{- \frac{t}{τ_{1}}} + A_{2} e^{- \frac{t}{τ_{2}}} (21)

avec $τ_{1} = 1 / p_{1}$ et $τ_{2} = 1 / p_{2}$ . La sortie tend vers la consigne de manière monotone avec un temps caractéristique égal au plus grand de $τ_{1}$ et $τ_{2}$ , qui est :

τ_{m a x} = τ_{2} = \frac{2 a}{b - \sqrt{Δ}} = \frac{2 (A_{0} K_{d} + T)}{A_{0} K_{p} + 1 - \sqrt{{(1 + A_{0} K_{p})}^{2} - 4 A_{0} K_{i} (A_{0} K_{d} + T)}} (22)

Cette durée diminue lorsque K_i augmente. L'effet de K_d n'est pas évident.

On constate que $τ_{2} > τ$ , ce qui montre que l'introduction de l'intégrateur ne fait que retarder la réponse. De plus, si K_i est assez grand, Δ devient négatif et des oscillations amorties apparaissent. Cela confirme que l'intégrateur n'a aucun intérêt pour un système d'ordre 1.

2.d. Simulation

On cherche à obtenir la réponse à un échelon avec le correcteur PID (K_i non nul). Pour un système d'ordre 1, la résolution analytique est aisée mais nous adoptons une méthode entièrement numérique, consistant à résoudre l'équation différentielle. On pose $y_{0} (t) = S (t)$ et $y_{1} (t) = \frac{d S}{d t}$ . Le système différentiel d'ordre 1 à résoudre est :

\begin{matrix} \frac{d y_{0}}{d t} = y_{1} & (23) \\ \frac{d y_{1}}{d t} = \frac{1}{A_{0} K_{p} T_{d} + T} (\frac{A_{0} K_{p}}{T_{i}} S_{c}^{0} - (A_{0} K_{p} + 1) y_{1} - \frac{A_{0} K_{p}}{T_{i}} y_{0}) & (24) \end{matrix}

Nous considérons par convention la condition initiale y₀(0)=0,y₁(0)=0, même si en réalité d'autres conditions initiales sont possibles.

La fonction suivante effectue l'intégration numérique de ce système. Les paramètres du correcteur à fournir sont K_p,T_i,T_d.

import numpy as np
from matplotlib.pyplot import *
from scipy.integrate import odeint

def reponsePIDordre1(A0,T,Kp,Ti,Td,tmax,N,rtol=1e-4,atol=1e-4):
	Sc0 = 1
	def systeme(Y,t):
		dY0 = Y[1]
		dY1 = 1/(A0*Kp*Td+T)*(A0*Kp/Ti*Sc0-(A0*Kp+1)*Y[1]-A0*Kp/Ti*Y[0])
		return [dY0,dY1]
	temps = np.linspace(0,tmax,N)
	sol = odeint(systeme,[0,0],temps,rtol=rtol,atol=atol)
	return temps,sol[:,0]

La fonction suivante permet de contrôler directement les constantes K_p,K_i,K_d :

def reponsePIDordre1_bis(A0,T,Kp,Kd,Ki,tmax,N,rtol=1e-4,atol=1e-4):
	return reponsePIDordre1(A0,T,Kp,Kp/Ki,Kd/Kp,tmax,N,rtol,atol)

La fonction suivante effectue la résolution pour le correcteur proportionnel seul :

def reponsePordre1(A0,T,Kp,tmax,N,rtol=1e-4,atol=1e-4):
	Sc0 = 1
	def systeme(Y,t):
		return 1/T*(A0*Kp*Sc0-(A0*Kp+1)*Y[0])
	temps = np.linspace(0,tmax,N)
	sol = odeint(systeme,[0],temps,rtol=rtol,atol=atol)
	return temps,sol[:,0]

On commence par étudier l'influence de T_i en l'absence de dérivateur (correcteur PI) :

T = 1
A0 = 1
Kp = 100
Td = 0
tmax=1
N=1000
figure(figsize=(16,6))
title("T = 1 s, Kp = 100")
Ti = 0.01
t,S = reponsePIDordre1(A0,T,Kp,Ti,Td,tmax,N)
plot(t,S,label=r"$T_i=0,01\,\rm s$")
Ti = 0.1
t,S = reponsePIDordre1(A0,T,Kp,Ti,Td,tmax,N)
plot(t,S,label=r"$T_i=0,1\,\rm s$")
Ti = 1
t,S = reponsePIDordre1(A0,T,Kp,Ti,Td,tmax,N)
plot(t,S,label=r"$T_i=1\,\rm s$")
grid()
t,S = reponsePordre1(A0,T,Kp,tmax,N)
plot(t,S,label=r"$T_i=\infty$")
grid()
xlabel("t (s)",fontsize=16)
ylabel(r"$\frac{S}{S_c^0}$",fontsize=16)
legend(loc="lower right")
grid()

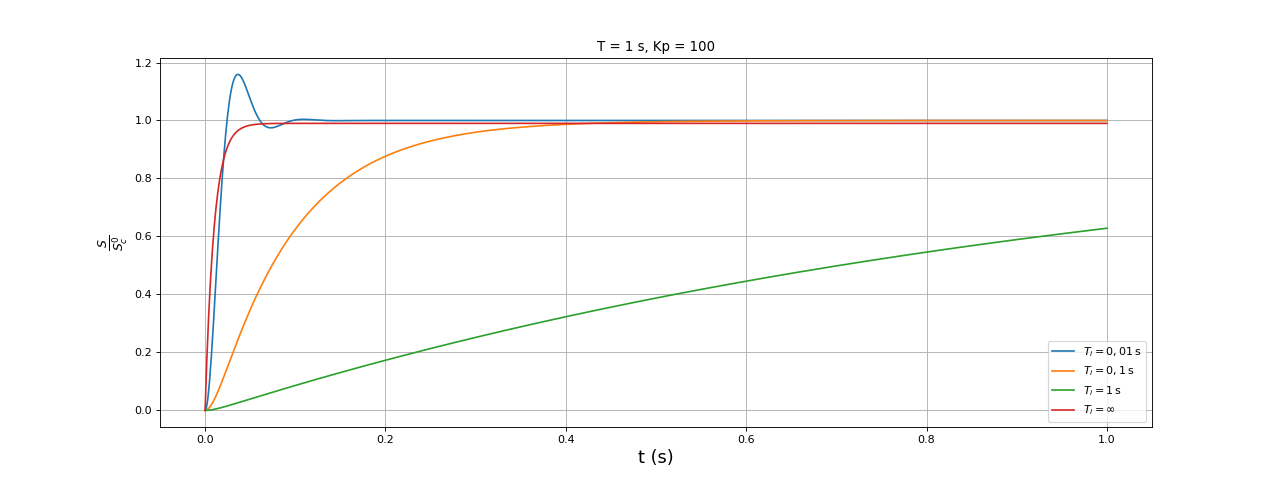fig1.pdf

Ces courbes confirment la conclusion énoncée plus haut : l'intégrateur ne fait que retarder la réponse ou introduit un dépassement avec une oscillation. Pour un système d'ordre 1, le correcteur proportionnel suffit, à condition de K_p soit assez grand pour que l'erreur soit négligeable.

Voyons l'effet du dérivateur :

T = 1
A0 = 1
Kp = 100
Td = 0.1
tmax=1
N=1000
figure(figsize=(16,6))
title("T = 1 s, Kp = 100")
Ti = 0.01
t,S = reponsePIDordre1(A0,T,Kp,Ti,Td,tmax,N)
plot(t,S,label=r"$T_i=0,01\,\rm s$")
Ti = 0.1
t,S = reponsePIDordre1(A0,T,Kp,Ti,Td,tmax,N)
plot(t,S,label=r"$T_i=0,1\,\rm s$")
Ti = 1
t,S = reponsePIDordre1(A0,T,Kp,Ti,Td,tmax,N)
plot(t,S,label=r"$T_i=1\,\rm s$")
grid()
t,S = reponsePordre1(A0,T,Kp,tmax,N)
plot(t,S,label=r"$T_i=\infty$")
grid()
xlabel("t (s)",fontsize=16)
ylabel(r"$\frac{S}{S_c^0}$",fontsize=16)
legend(loc="lower right")
grid()

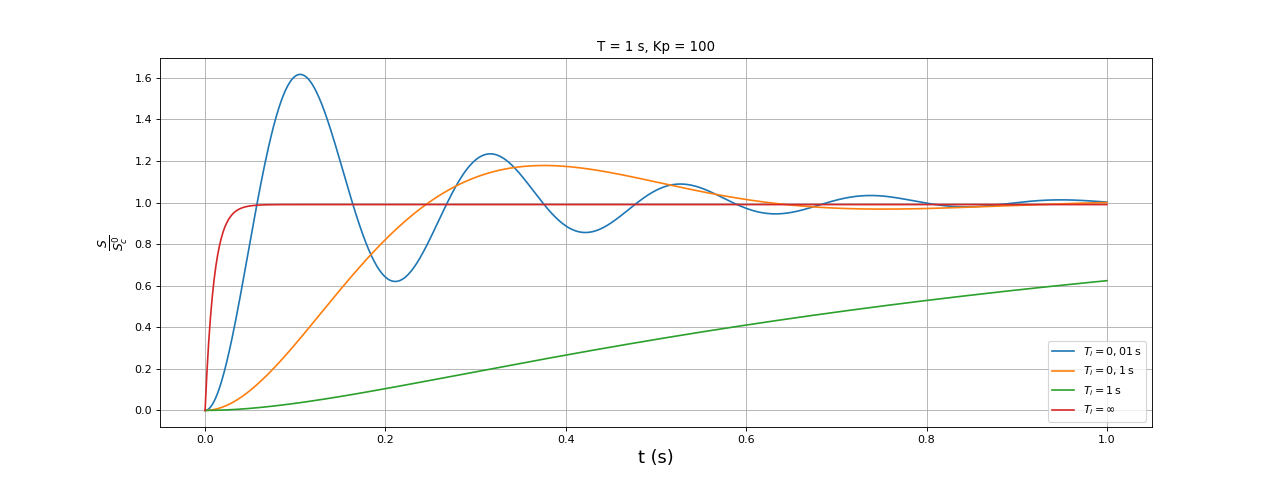fig2.pdf

Le dérivateur introduit un comportement oscillatoire (Δ<0) avec un dépassement très important, ce qui est évidemment néfaste.

3. Système d'ordre 2

3.a. Fonction de transfert et stabilité

La fonction de transfert du système est de la forme :

A (p) = \frac{A_{0}}{1 + 2 m \frac{p}{ω_{0}} + \frac{p^{2}}{ω_{0}^{2}}} = \frac{A_{0}}{1 + 2 m T p + T^{2} p^{2}} (25)

Si m>1, la réponse indicielle du système est de type amortie, si m<1 elle est de type oscillatoire amortie et si m=1 elle est de type critique.

La fonction de transfert du système asservi est :

H (p) = \frac{A_{0} K_{p} (T_{d} p^{2} + p + \frac{1}{T_{i}})}{T^{2} p^{3} + (2 m T + A_{0} K_{p} T_{d}) p^{2} + (1 + A_{0} K_{p}) p + \frac{A_{0} K_{p}}{T_{i}}} (26)

Dans le cas du correcteur proportionnel seul ( $T_{i} = \infty$ et $T_{d} = 0$ ), la fonction de transfert est :

H_{P} (p) = \frac{A_{0} K_{p}}{T^{2} p^{2} + 2 m T p + (1 + A_{0} K_{p})} (27)

Le système avec le correcteur proportionnel seul est toujours stable.

Dans le cas du correcteur PID complet, la stabilité est plus difficile à étudier puisqu'il faudrait connaître les pôles de la fonction de transfert. Le critère de Routh [1] permet de déterminer la stabilité au moyen d'opérations algébriques sur les coefficients du dénominateur.

\begin{matrix} T^{2} & 1 + A_{0} K_{p} \\ 2 m T + A_{0} K_{p} T_{d} & \frac{A_{0} K_{p}}{T_{i}} \\ \frac{(2 m T + A_{0} K_{p} T_{d}) (1 + A_{0} K_{p}) - \frac{T^{2} A_{0} K_{p}}{T_{i}}}{2 m T + A_{0} K_{p} T_{d}} & 0 \\ \frac{A_{0} K_{p}}{T_{i}} & 0 \end{matrix} (28)

Le système est stable si et seulement si tous les coefficients de la première colonne sont de même signe. Seul celui de la troisième ligne peut être négatif donc la condition de stabilité est :

(2 m T + A_{0} K_{p} T_{d}) (1 + A_{0} K_{p}) - \frac{T^{2} A_{0} K_{p}}{T_{i}} > 0 (29)

En conséquence, une valeur trop petite de T_i, c'est-à-dire trop grande de K_i, peut rendre le système instable.

3.b. Réponse à un échelon

Correcteur proportionnel

La valeur stationnaire de la sortie est déterminée par :

H_{P} (0) = \frac{A_{0} K_{p}}{1 + A_{0} K_{p}} (30)

qui est le même résultat que pour le système d'ordre 1 avec le correcteur proportionnel. L'erreur est donc d'autant plus petite que K_p est grand. Le discriminant de ce système d'ordre 2 s'écrit :

Δ = 4 m^{2} T^{2} - 4 T^{2} (1 + A_{0} K_{p}) = 4 (m^{2} - 1) T^{2} - 4 T^{2} A_{0} K_{p} (31)

Si m<1, la réponse est oscillatoire amortie (comme celle du système non asservi). Si m>1, une valeur trop grande de K_p est susceptible de conduire à $Δ < 0$ , c'est-à-dire à un comportement oscillatoire de la réponse indicielle.

En conclusion, une augmentation de K_p peut faire apparaître un comportement oscillatoire avant que l'erreur n'atteigne un niveau assez bas.

Correcteur PID

On a H(0)=1 donc l'erreur en régime stationnaire est nulle.

Il est difficile de mener une étude analytique de la réponse indicielle car celle-ci nécessite la connaissance de l'expression des pôles de la fonction de transfert (racines d'un polynôme de degré 3).

3.c. Simulation

La simulation consiste à résoudre numériquement les équations différentielles pour une consigne constante.

Pour le correcteur proportionnel, on pose $y_{0} (t) = S (t)$ et $y_{1} (t) = \frac{d S}{d t}$ et le système différentiel s'écrit :

\begin{matrix} \frac{d y_{0}}{d t} = y_{1} & (32) \\ \frac{d y_{1}}{d t} = \frac{1}{T^{2}} (A_{0} K_{p} S_{c}^{0} - 2 m T y_{1} - (1 + A_{0} K_{p}) y_{0}) & (33) \end{matrix}

La fonction suivante effectue la résolution pour le correcteur proportionnel seul :

def reponsePordre2(A0,T,m,Kp,tmax,N,rtol=1e-4,atol=1e-4):
	Sc0 = 1
	def systeme(Y,y):
		dY0 = Y[1]
		dY1 = 1/T**2*(A0*Kp*Sc0-2*m*T*Y[1]-(1+A0*Kp)*Y[0])
		return [dY0,dY1]
	temps = np.linspace(0,tmax,N)
	sol = odeint(systeme,[0,0],temps,rtol=rtol,atol=atol)
	return temps,sol[:,0]

Voyons l'effet du correcteur proportionnel lorsque m>1 (réponse amortie du système non asservi) :

T = 1 
m = 5
A0 = 1
tmax = 10
N = 1000
figure(figsize=(16,6))
title("T = 1, m=5")
Kp = 10
t,S = reponsePordre2(A0,T,m,Kp,tmax,N)
plot(t,S,label=r"$K_p=10$")
Kp = 20
t,S = reponsePordre2(A0,T,m,Kp,tmax,N)
plot(t,S,label=r"$K_p=20$")
Kp = 50
t,S = reponsePordre2(A0,T,m,Kp,tmax,N)
plot(t,S,label=r"$K_p=50$")
Kp = 100
t,S = reponsePordre2(A0,T,m,Kp,tmax,N)
plot(t,S,label=r"$K_p=100$")
xlabel("t (s)",fontsize=16)
ylabel(r"$\frac{S}{S_c^0}$",fontsize=16)
legend(loc="lower right")
grid()

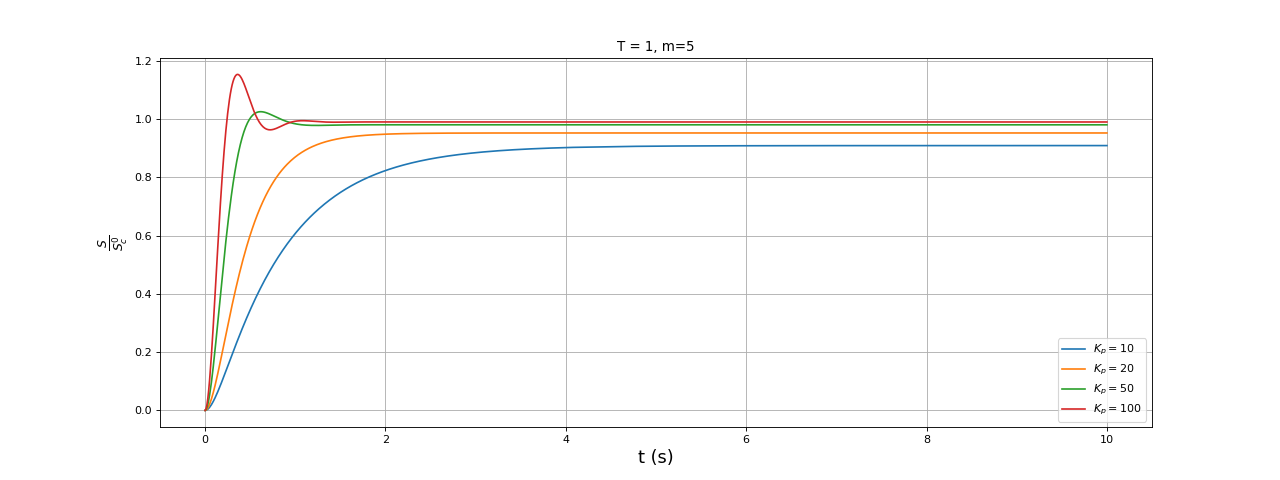fig3.pdf

Un valeur assez grande de K_p est nécessaire pour obtenir une erreur assez faible. Augmenter K_p permet de réduire le temps de réponse mais une valeur trop grande fait ressortir le comportement oscillatoire avec un dépassement important.

Voici l'effet du correcteur proportionnel lorsque m<1 (réponse non amortie du système non asservi) :

T = 1 
m = 0.5
A0 = 1
tmax = 20
N = 1000
figure(figsize=(16,6))
title("T = 1, m=0,5")
Kp = 10
t,S = reponsePordre2(A0,T,m,Kp,tmax,N)
plot(t,S,label=r"$K_p=10$")
Kp = 50
t,S = reponsePordre2(A0,T,m,Kp,tmax,N)
plot(t,S,label=r"$K_p=50$")
Kp = 100
t,S = reponsePordre2(A0,T,m,Kp,tmax,N)
plot(t,S,label=r"$K_p=100$")
xlabel("t (s)",fontsize=16)
ylabel(r"$\frac{S}{S_c^0}$",fontsize=16)
legend(loc="lower right")
grid()

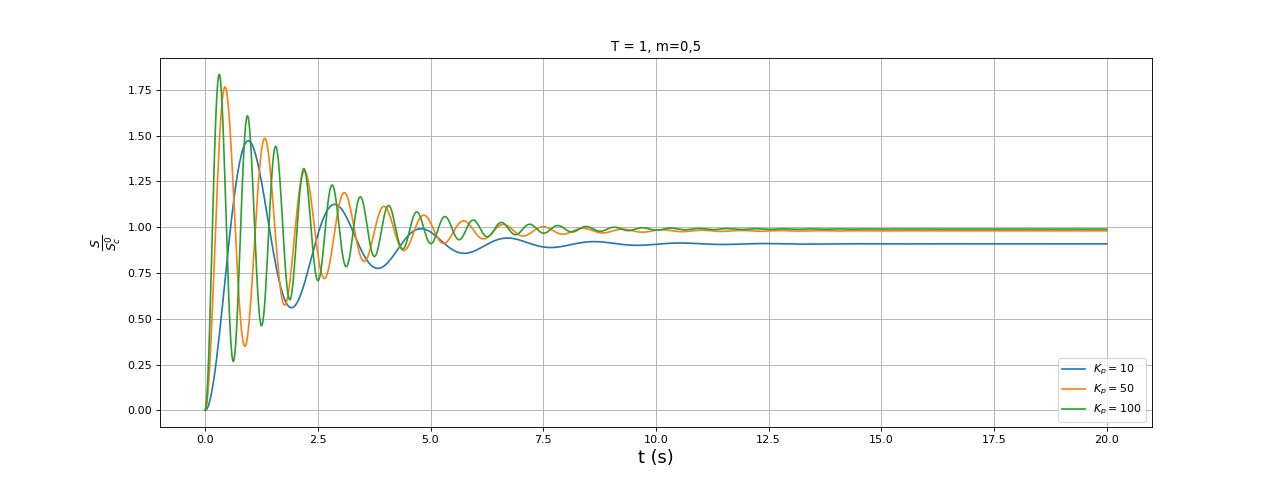fig4.pdf

Comme prévu, la réponse est toujours oscillatoire amortie. L'augmentation de K_p permet de réduire l'erreur mais ne change rien au temps de réponse tout en accentuant le dépassement.

Ces simulations montrent bien les limites du correcteur proportionnel dans le cas d'un système d'ordre 2, alors qu'il est tout à fait suffisant pour un système d'ordre 1.

Pour le correcteur PID, on pose $y_{0} (t) = S (t)$ , $y_{1} (t) = \frac{d S}{d t}$ et $y_{2} (t) = \frac{d^{2} S}{d t^{2}}$ . Le système différentiel pour une consigne constante est :

\begin{matrix} \frac{d y_{0}}{d t} = y_{1} & (34) \\ \frac{d y_{1}}{d t} = y_{2} & (35) \\ \frac{d y_{2}}{d t} = \frac{1}{T^{2}} (\frac{A_{0} K_{p}}{T_{i}} S_{c}^{0} - (2 m T + A_{0} K_{p} T_{d}) y_{2} - (1 + A_{0} K_{p}) y_{1} - \frac{A_{0} K_{p}}{T_{i}} y_{0}) & (36) \end{matrix}

La fonction suivante effectue la résolution pour le correcteur PID :

def reponsePIDordre2(A0,T,m,Kp,Ti,Td,tmax,N,rtol=1e-4,atol=1e-4):
	Sc0 = 1
	def systeme(Y,y):
		dY0 = Y[1]
		dY1 = Y[2]
		dY2 = 1/T**2*(A0*Kp*(Sc0-Y[0])/Ti-(2*m*T+A0*Kp*Td)*Y[2]-(1+A0*Kp)*Y[1])
		return [dY0,dY1,dY2]
	temps = np.linspace(0,tmax,N)
	sol = odeint(systeme,[0,0,0],temps,rtol=rtol,atol=atol)
	return temps,sol[:,0]

On commence par simuler la correction PI dans le cas m>1 en comparant au correcteur P :

T = 1 
m = 5
A0 = 1
tmax = 10
N = 1000
figure(figsize=(16,6))
title("T = 1, m=5")
Kp = 100
t,S = reponsePordre2(A0,T,m,Kp,tmax,N)
plot(t,S,label=r"$P : K_p=100$")
Kp = 100
Ti = 1
Td = 0
t,S = reponsePIDordre2(A0,T,m,Kp,Ti,Td,tmax,N)
plot(t,S,label=r"$PI : K_p=100,\ T_i=1$")
Ti = 0.5
t,S = reponsePIDordre2(A0,T,m,Kp,Ti,Td,tmax,N)
plot(t,S,label=r"$PI : K_p=100,\ T_i=0,5$")
Ti = 0.3
t,S = reponsePIDordre2(A0,T,m,Kp,Ti,Td,tmax,N)
plot(t,S,label=r"$PI : K_p=100,\ T_i=0,3$")
Ti = 0.1
t,S = reponsePIDordre2(A0,T,m,Kp,Ti,Td,tmax,N)
plot(t,S,label=r"$PI : K_p=100,\ T_i=0,1$")
xlabel("t (s)",fontsize=16)
ylabel(r"$\frac{S}{S_c^0}$",fontsize=16)
legend(loc="lower right")
grid()

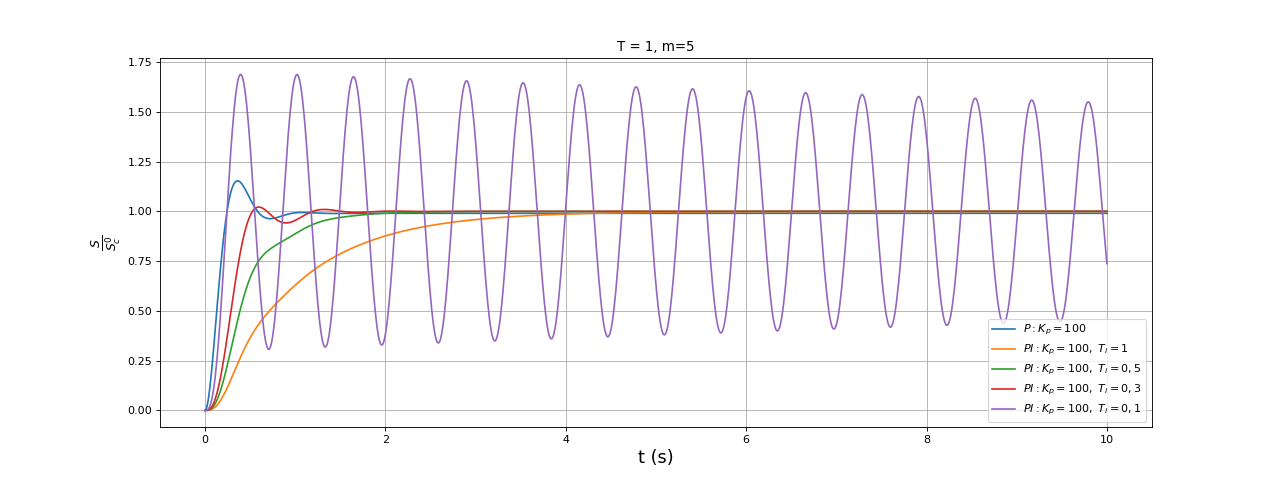fig5.pdf

La comparaison est faite avec un correcteur proportionnel dont le coefficient K_p est assez grand pour donner une erreur négligeable mais qui présente un dépassement important. Le terme intégral permet de converger vers la valeur stationnaire sans dépassement tout en ayant une erreur stationnaire nulle. Cependant, une valeur trop petite de T_i, c'est-à-dire trop grande de K_i, introduit un comportement oscillatoire amorti puis à un comportement oscillatoire très peu amorti s'il est trop faible. La théorie prévoit un comportement instable si T_i et trop petit :

T = 1 
m = 5
A0 = 1
tmax = 10
N = 1000
figure(figsize=(16,6))
title("T = 1, m=5")
Kp = 100
t,S = reponsePordre2(A0,T,m,Kp,tmax,N)
plot(t,S,label=r"$P : K_p=100$")
Kp = 100
Td = 0
Ti = 0.05
t,S = reponsePIDordre2(A0,T,m,Kp,Ti,Td,tmax,N)
plot(t,S,label=r"$PI : K_p=100,\ T_i=0,05$")
xlabel("t (s)",fontsize=16)
ylabel(r"$\frac{S}{S_c^0}$",fontsize=16)
legend(loc="lower right")
grid()

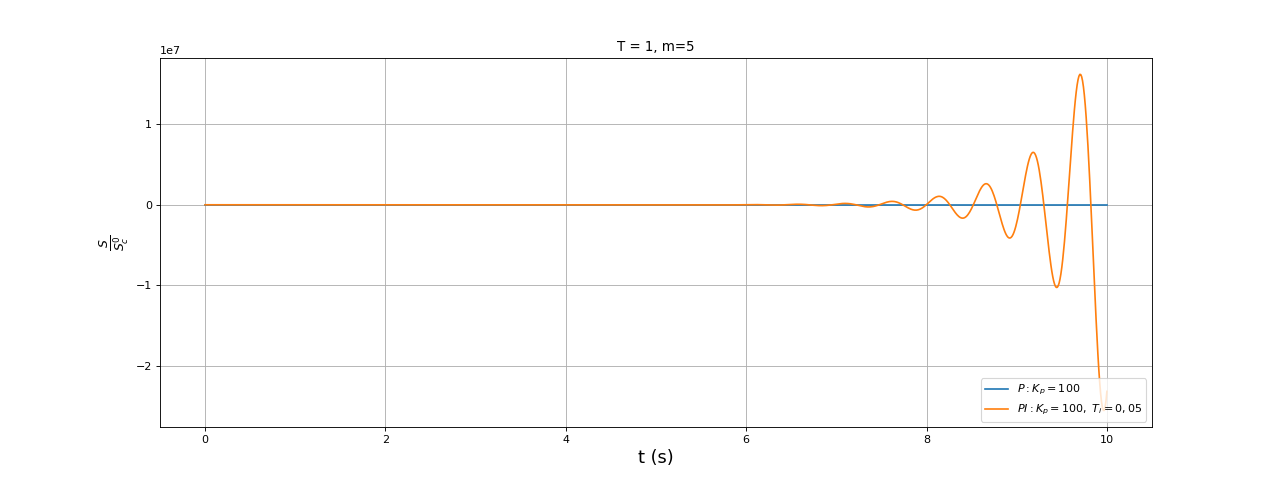fig6.pdf

Il semble que la diminution de T_i conduise dans un premier temps à une augmentation du temps d'amortissement des oscillations puis à un comportement instable dès que la condition $(29)$ n'est plus satisfaite. Ce comportement se comprend aisément : la partie réelle d'un pôle, d'abord négative, augmente (sa valeur absolue diminue) puis devient positive. Autrement dit, une instabilité est précédée par un régime oscillant dans lequel le temps d'amortissement tend vers l'infini. La fonction suivante calcule la valeur de T_i en dessous de laquelle le système est instable :

def Ti_limite(A0,T,m,Kp,Td):
	return (T**2*A0*Kp)/((2*m*T+A0*Kp*Td)*(1+A0*Kp))
T = 1 
m = 5
A0 = 1
Kp = 100
Ti_lim = Ti_limite(A0,T,m,Kp,Td)

print(Ti_lim)
--> 0.09900990099009901

La valeur 0,1 de la simulation ci-dessus était donc très proche de l'instabilité (comportement oscillatoire très peu amorti). Pour exactement cette valeur, on a un comportement oscillatoire permanent (stabilité marginale).

Voici à présent une simulation de la correction PI dans le cas m<1 :

T = 1 
m = 0.5
A0 = 1
Kp = 100
Td = 0
Ti_lim = Ti_limite(A0,T,m,Kp,Td)

print(Ti_lim)
--> 0.9900990099009901

La valeur limite de T_i est plus grande.

T = 1 
m = 0.5
A0 = 1
tmax = 10
N = 1000
figure(figsize=(16,6))
title("T = 1, m=0,5")
Kp = 100
t,S = reponsePordre2(A0,T,m,Kp,tmax,N)
plot(t,S,label=r"$P : K_p=100$")
Kp = 100
Ti = 5
Td = 0
t,S = reponsePIDordre2(A0,T,m,Kp,Ti,Td,tmax,N)
plot(t,S,label=r"$PI : K_p=100,\ T_i=5$")
Ti = 1
t,S = reponsePIDordre2(A0,T,m,Kp,Ti,Td,tmax,N)
plot(t,S,label=r"$PI : K_p=100,\ T_i=1$")
xlabel("t (s)",fontsize=16)
ylabel(r"$\frac{S}{S_c^0}$",fontsize=16)
legend(loc="lower right")
grid()

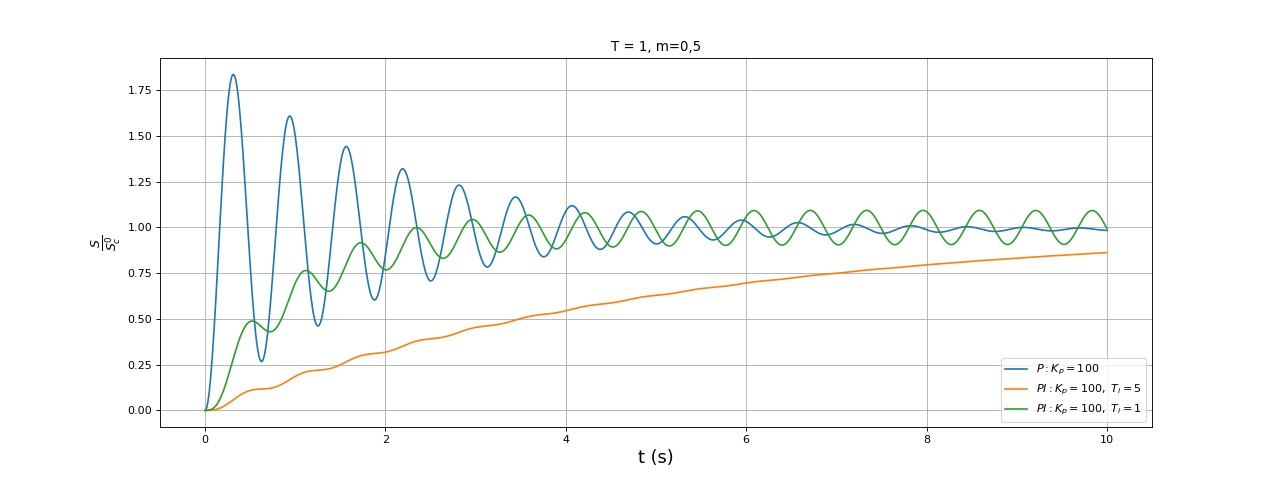fig7.pdf

L'intégrateur permet d'éliminer les oscillations (et le dépassement associé) mais au prix d'une augmentation du temps de réponse. Si T_i est trop petit, un comportement oscillatoire peut apparaître puis l'instabilité s'il passe en dessous de la valeur limite.

Pour étudier l'effet du dérivateur, nous reprenons les deux simulations précédentes en y ajoutant le dérivateur :

T = 1 
m = 5
A0 = 1
Kp = 100
Td = 1
Ti_lim = Ti_limite(A0,T,m,Kp,Td)

print(Ti_lim)
--> 0.009000900090009001

Le dérivateur permet de réduire la valeur limite de T_i, ce qui est une bonne chose.

T = 1 
m = 5
A0 = 1
tmax = 10
N = 1000
figure(figsize=(16,6))
title("T = 1, m=5")
Kp = 100
t,S = reponsePordre2(A0,T,m,Kp,tmax,N)
plot(t,S,label=r"$P : K_p=100$")
Kp = 100
Ti = 1
Td = 1
t,S = reponsePIDordre2(A0,T,m,Kp,Ti,Td,tmax,N)
plot(t,S,label=r"$PID : K_p=100,\ T_i=1,\ T_d=1$")
Ti = 0.5
t,S = reponsePIDordre2(A0,T,m,Kp,Ti,Td,tmax,N)
plot(t,S,label=r"$PID : K_p=100,\ T_i=0,5,\ T_d=1$")
Ti = 0.3
t,S = reponsePIDordre2(A0,T,m,Kp,Ti,Td,tmax,N)
plot(t,S,label=r"$PID : K_p=100,\ T_i=0,3,\ T_d=1$")
xlabel("t (s)",fontsize=16)
ylabel(r"$\frac{S}{S_c^0}$",fontsize=16)
legend(loc="lower right")
grid()

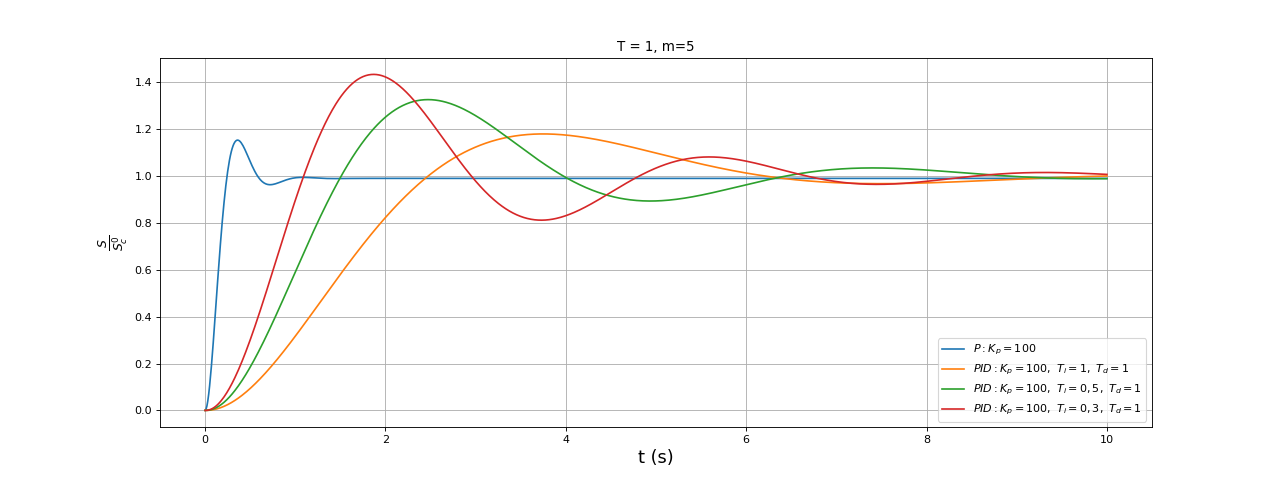fig8.pdf

Dans ce cas, le dérivateur n'apporte pas d'amélioration mais au contraire un plus grand dépassement.

T = 1 
m = 0.5
A0 = 1
Kp = 100
Td = 1
Ti_lim = Ti_limite(A0,T,m,Kp,Td)

print(Ti_lim)
--> 0.009802960494069209

La valeur limite de T_i est plus grande.

T = 1 
m = 0.5
A0 = 1
tmax = 10
N = 1000
figure(figsize=(16,6))
title("T = 1, m=0,5")
Kp = 100
t,S = reponsePordre2(A0,T,m,Kp,tmax,N)
plot(t,S,label=r"$P : K_p=100$")
Kp = 100
Ti = 5
Td = 1
t,S = reponsePIDordre2(A0,T,m,Kp,Ti,Td,tmax,N)
plot(t,S,label=r"$PID : K_p=100,\ T_i=5,\ T_d=1$")
Ti = 1
t,S = reponsePIDordre2(A0,T,m,Kp,Ti,Td,tmax,N)
plot(t,S,label=r"$PID : K_p=100,\ T_i=1,\ T_d=1$")
xlabel("t (s)",fontsize=16)
ylabel(r"$\frac{S}{S_c^0}$",fontsize=16)
legend(loc="lower right")
grid()

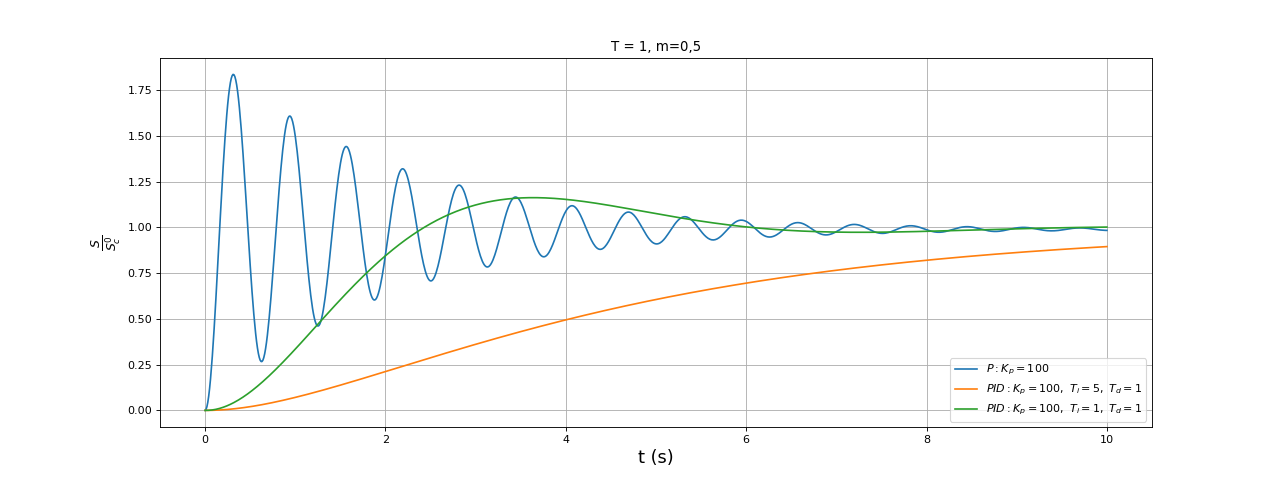fig9.pdf

Lorsque T_i=1, le dérivateur permet d'éliminer les oscillations faiblement amorties mais le dépassement reste. Dans le cas présent, l'intégrateur et le dérivateur permettent d'obtenir une réponse indicielle bien meilleure que le correcteur proportionnel seul : le dépassement est nettement plus faible et le temps de réponse un peu plus faible. On peut tenter de réduire encore T_i et T_d :

T = 1 
m = 0.5
A0 = 1
Kp = 100
Td = 0.5
Ti_lim = Ti_limite(A0,T,m,Kp,Td)

print(Ti_lim)
--> 0.01941370607649

T = 1 
m = 0.5
A0 = 1
tmax = 10
N = 1000
figure(figsize=(16,6))
title("T = 1, m=0,5")
Kp = 100
t,S = reponsePordre2(A0,T,m,Kp,tmax,N)
plot(t,S,label=r"$P : K_p=100$")
Kp = 100
Ti = 0.5
Td = 0.5
t,S = reponsePIDordre2(A0,T,m,Kp,Ti,Td,tmax,N)
plot(t,S,label=r"$PID : K_p=100,\ T_i=0,5,\ T_d=0,5$")
Ti = 0.2
Td = 0.2
t,S = reponsePIDordre2(A0,T,m,Kp,Ti,Td,tmax,N)
plot(t,S,label=r"$PID : K_p=100,\ T_i=0,2,\ T_d=0,2$")
Ti = 0.1
Td = 0.1
t,S = reponsePIDordre2(A0,T,m,Kp,Ti,Td,tmax,N)
plot(t,S,label=r"$PID : K_p=100,\ T_i=0,1,\ T_d=0,1$")
xlabel("t (s)",fontsize=16)
ylabel(r"$\frac{S}{S_c^0}$",fontsize=16)
legend(loc="lower right")
grid()

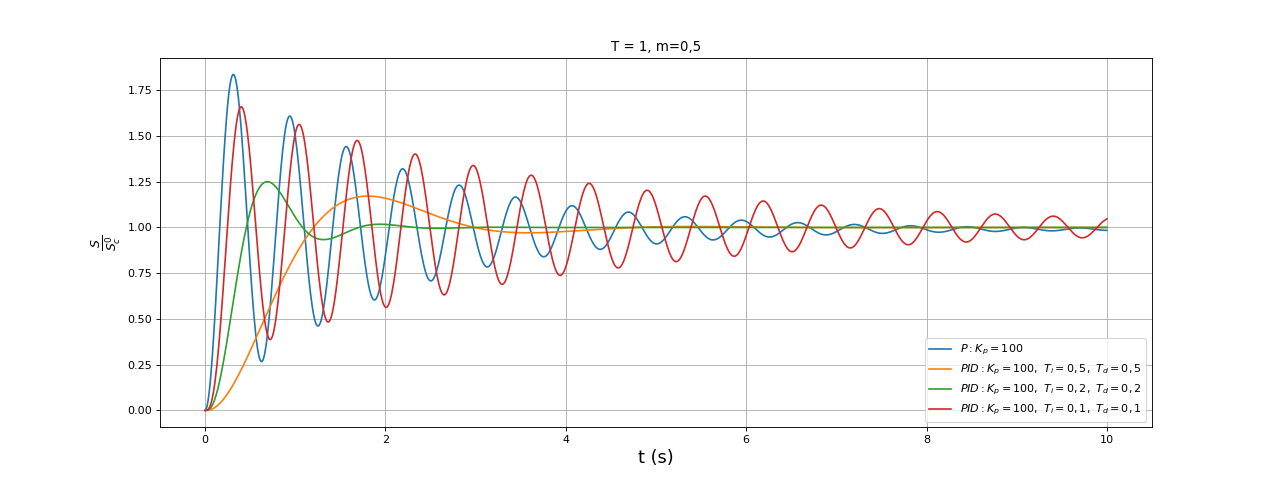fig10.pdf

Pour T_i=T_d=0,5, le dépassement est inchangé mais le temps de reponse et nettement réduit. Pour T_i=T_d=0,2 le temps de réponse se réduit encore mais le dépassement augmente. Pour T_i=T_d=0,5, la réponse se dégrade considérablement, sans doute parce qu'on s'approche de l'instabilité.

Pour conclure, cette simulation montre que le correcteur PID permet d'améliorer grandement la réponse d'un système dont la réponse indicielle sans asservissement est oscillatoire amortie.

3.d. Calcul des pôles

La décomposition de la fonction de transfert (fraction rationnelle) en éléments simples permet d'obtenir ses pôles. La fonction scipy.signal.residue effectue numériquement cette décomposition.

from scipy.signal import residue

def decompositionPIDordre2(A0,T,m,Kp,Ti,Td):
	b = [A0*Kp*Td,A0*Kp,A0*Kp/Ti]
	a = [T**2,2*m*T+A0*Kp*Td,1+A0*Kp,A0*Kp/Ti]
	return residue(b,a,tol=1e-4)

Voici un exemple, qui reprend les coefficients de la dernière simulation :

A0 = 1
T = 1
m = 0.5
Kp = 100
Ti = 0.2
Td = 0.2
[r,p,d] = decompositionPIDordre2(A0,T,m,Kp,Ti,Td)

Voici les résidus :

print(r)
--> array([ 0.72929871+0.62424818j,  0.72929871-0.62424818j,
       18.54140258+0.j        ])

et les pôles :

print(p)
--> array([ -2.12366127+5.03349166j,  -2.12366127-5.03349166j,
       -16.75267746+0.j        ])

La réponse indicielle s'écrit :

S (t) = 1 + a_{1} e^{p_{1} t} + a_{2} e^{p_{2} t} + a_{3} e^{p_{3} t} (37)

Les deux premiers pôles sont conjugués donc les constantes a₁ et a₂ le sont aussi et la somme des deux premières exponentielles est réelle. Le troisième pôle est réel. Si l'on reprend les conditions initiales nulles adoptées pour la simulation précédente, les trois constantes vérifient le système d'équations linéaire suivant :

\begin{matrix} a_{1} + a_{2} + a_{2} = - 1 \\ p_{1} a_{1} + p_{2} a_{2} + p_{3} a_{3} = 0 \\ p_{1}^{2} a_{1} + p_{2}^{2} a_{2} + p_{3}^{2} a_{3} = 0 \end{matrix}

Voici la résolution numérique de ce système :

from numpy.linalg import solve
A = np.array([[1,1,1],[p[0],p[1],p[2]],[p[0]**2,p[1]**2,p[2]**2]])
B = np.array([-1,0,0])
a = solve(A,B)

print(a)
--> array([-0.4376505+0.39216166j, -0.4376505-0.39216166j,
       -0.124699 +0.j        ])

Les deux premières constantes sont bien conjugées et la troisième est réelle (à l'erreur d'arrondi près). Voici le tracé de la réponse indicielle :

t = np.linspace(0,10,1000)
S = 1 + np.real(a[0]*np.exp(p[0]*t)+a[1]*np.exp(p[1]*t)+a[2]*np.exp(p[2]*t))
figure(figsize=(16,6))
plot(t,S)
xlabel("t (s)",fontsize=16)
ylabel(r"$\frac{S}{S_c^0}$",fontsize=16)
grid()

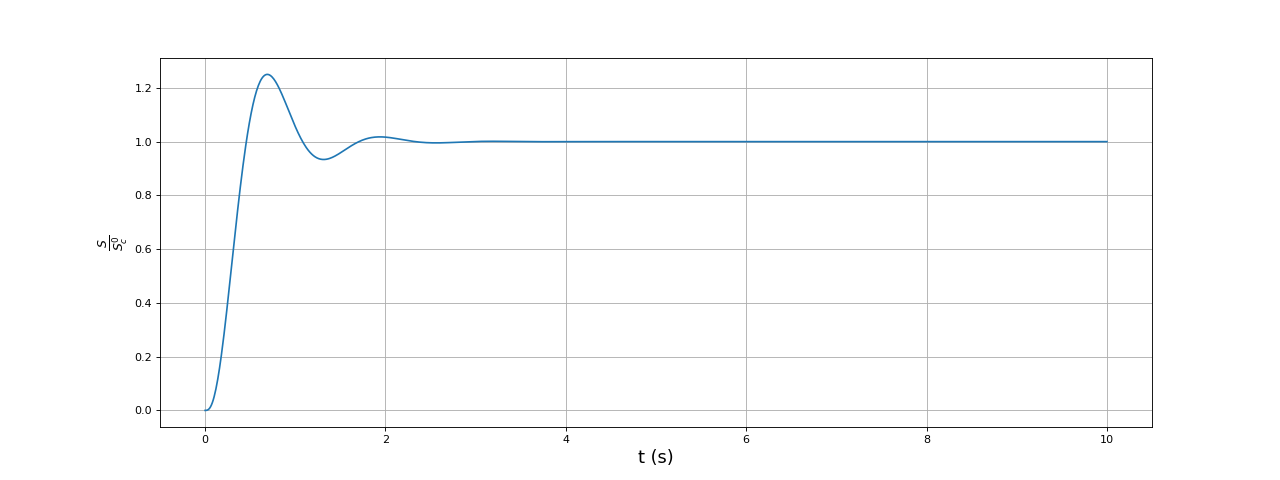fig11.pdf

Voici une fonction qui fait tous les calculs :

def reponsePIDordre2poles(A0,T,m,Kp,Ti,Td,tmax,N):
	[r,p,d] = decompositionPIDordre2(A0,T,m,Kp,Ti,Td)
	A = np.array([[1,1,1],[p[0],p[1],p[2]],[p[0]**2,p[1]**2,p[2]**2]])
	B = np.array([-1,0,0])
	a = solve(A,B)
	t = np.linspace(0,tmax,N)
	S = 1 + np.real(a[0]*np.exp(p[0]*t)+a[1]*np.exp(p[1]*t)+a[2]*np.exp(p[2]*t))
	return t,S

L'influence d'un paramètre peut être étudiée en traçant la partie réelle des pôles en fonction de ce paramètre. Voici par exemple l'influence de T_d à K_p et T_i fixés :

A0 = 1
T = 1
m = 0.5
Kp = 100
Ti = 0.2
Td = np.linspace(0.01,0.5,30)
figure()
title("Kp=100, Ti = 0,2")
style =  ["ro","b+","g."]
for k in range(len(Td)):
	[r,p,d] = decompositionPIDordre2(A0,T,m,Kp,Ti,Td[k])
	for i in range(3):
		plot(Td[k],-np.real(p[i]),style[i])
xlabel(r"$T_d$",fontsize=16)
ylabel("-Re(p)")

grid()

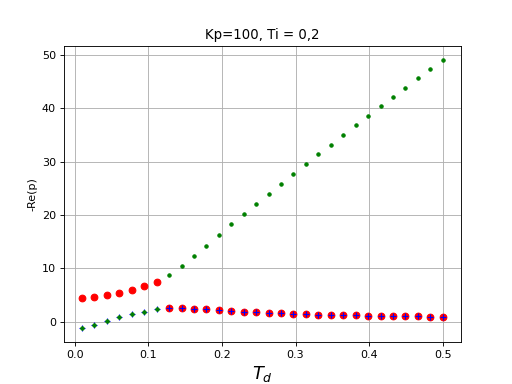fig12.pdf

Après avoir repéré le domaine où toutes les parties réelles sont négatives, on peut utiliser une échelle logarithmique pour l'opposée de la partie réelle :

yscale('log')

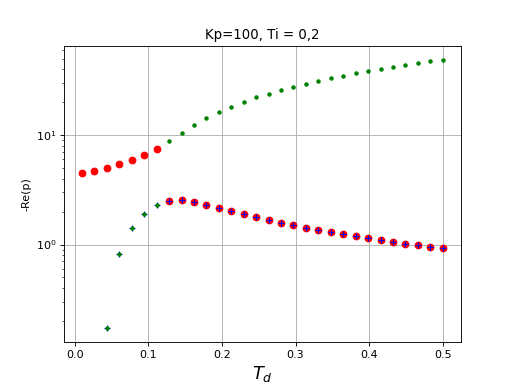fig13.pdf

Le temps de réponse est l'inverse de -Re(p) le plus petit. On a donc intérêt à choisir une valeur de T_d qui donne la plus petite valeur de -Re(p) la plus grande. Ici, il s'agit de 0,12. Cependant, la partie réelle ne donne aucune information sur le dépassement. Pour cela, il faut tracer la réponse indicielle pour différentes valeurs de T_d proches de la valeur optimale :

T = 1 
m = 0.5
A0 = 1
tmax = 10
N = 1000
figure(figsize=(16,6))
title("T = 1, m=0,5")
Kp = 100
t,S = reponsePordre2(A0,T,m,Kp,tmax,N)
plot(t,S,label=r"$P : K_p=100$")
Ti = 0.2
Td = 0.1
t,S = reponsePIDordre2poles(A0,T,m,Kp,Ti,Td,tmax,N)
plot(t,S,label=r"$PID : K_p=100,\ T_i=0,2,\ T_d=0,1$")
Ti = 0.2
Td = 0.12
t,S = reponsePIDordre2poles(A0,T,m,Kp,Ti,Td,tmax,N)
plot(t,S,label=r"$PID : K_p=100,\ T_i=0,2,\ T_d=0,12$")
Ti = 0.2
Td = 0.2
t,S = reponsePIDordre2poles(A0,T,m,Kp,Ti,Td,tmax,N)
plot(t,S,label=r"$PID : K_p=100,\ T_i=0,2,\ T_d=0,2$")
xlabel("t (s)",fontsize=16)
ylabel(r"$\frac{S}{S_c^0}$",fontsize=16)
legend(loc="lower right")
grid()

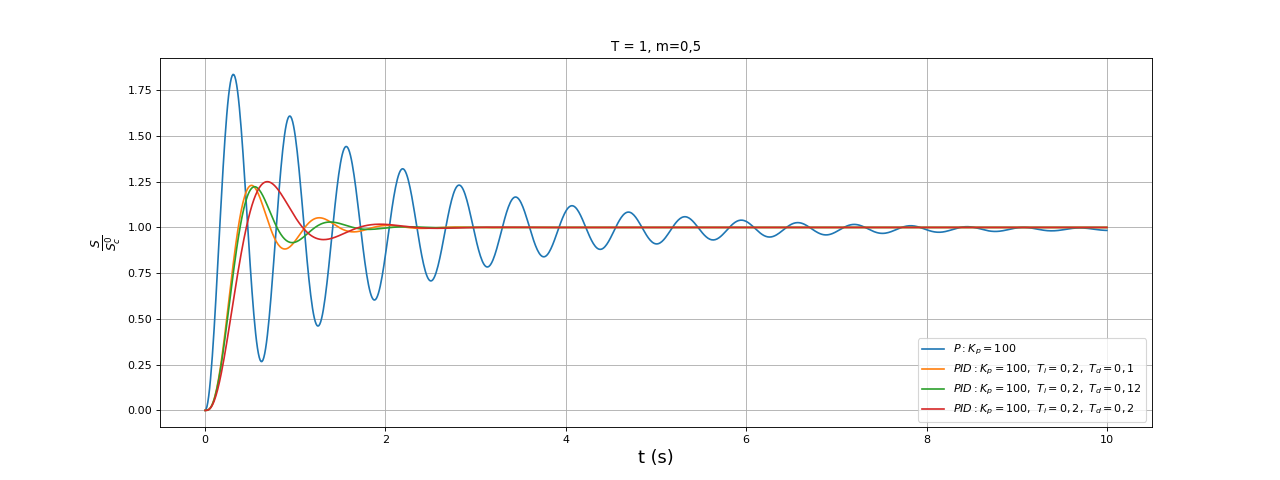fig14.pdf

Finalement, la meilleure réponse est obtenue avec T_d=0,1 car son dépassement est un peu plus faible. On remarque que cette valeur de T_i ne fonctionne pas sans le dérivateur puisque le système est instable si T_d est inférieur à 0,04 (environ). Conformément à la condition de stabilité $(29)$ , le dérivateur permet d'abaisser la valeur de T_i minimale. Autrement dit, le dérivateur permet de réaliser un intégrateur avec un temps de réponse plus petit.

3.e. Exemple

La fonction suivante calcule les pôles d'un système d'ordre 2 asservi avec un correcteur proportionnel :

def decompositionPordre2(A0,T,m,Kp):
	b = [A0*Kp]
	a = [T**2,2*m*T,1+A0*Kp]
	return residue(b,a,tol=1e-4)

et celle-ci renvoie la réponse indicielle :

def reponsePordre2poles(A0,T,m,Kp,tmax,N):
	[r,p,d] = decompositionPordre2(A0,T,m,Kp)
	A = np.array([[1,1],[p[0],p[1]]])
	B = np.array([-A0*Kp/(1+A0*Kp),0])
	a = solve(A,B)
	t = np.linspace(0,tmax,N)
	S = A0*Kp/(1+A0*Kp) + np.real(a[0]*np.exp(p[0]*t)+a[1]*np.exp(p[1]*t))
	return t,S

La fonction suivante renvoie la réponse indicielle d'un système d'ordre 2 (sans asservissement) :

def reponseOrdre2poles(A0,T,m,tmax,N):
	b = [A0]
	a = [T**2,2*m*T,1]
	[r,p,d] = residue(b,a,tol=1e-4)
	A = np.array([[1,1],[p[0],p[1]]])
	B = np.array([-1,0])
	a = solve(A,B)
	t = np.linspace(0,tmax,N)
	S = 1 + np.real(a[0]*np.exp(p[0]*t)+a[1]*np.exp(p[1]*t))
	return t,S

Nous cherchons à réaliser un asservissement pour un système supposé d'ordre 2 donc on connaît la réponse indicielle expérimentale. On commence par trouver les paramètres T et m qui permettent de reproduire au mieux cette réponse indicielle :

m=0.5
T = 1e-3
A0 = 1
tmax = 0.05
N = 1000
t,S = reponseOrdre2poles(A0,T,m,tmax,N)
figure(figsize=(16,6))
plot(t,S)
grid()
xlabel("t (s)",fontsize=16)
ylabel(r"$\frac{S}{A_0}$",fontsize=16)

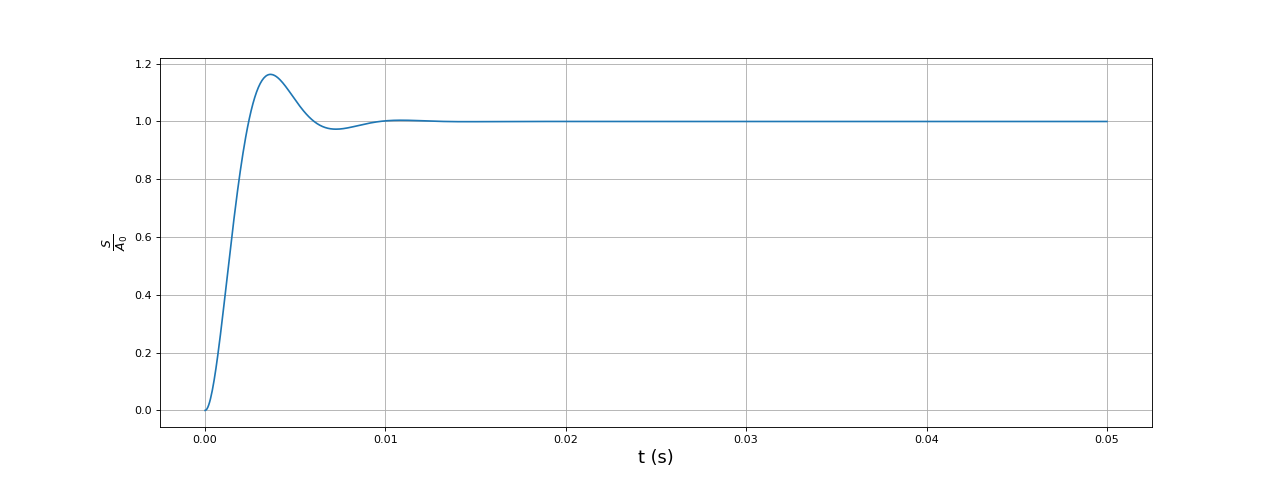fig15.pdf

On commence par étudier le correcteur proportionnel, sachant qu'une valeur de K_p grande est nécessaire pour obtenir une erreur faible :

tmax = 0.05
N = 1000
figure(figsize=(16,6))
title("T = 1e-3, m=0,5")
Kp = 10
t,S = reponsePordre2poles(A0,T,m,Kp,tmax,N)
plot(t,S,label=r"$P : K_p=10$")
Kp = 100
t,S = reponsePordre2poles(A0,T,m,Kp,tmax,N)
plot(t,S,label=r"$P : K_p=100$")
xlabel("t (s)",fontsize=16)
ylabel(r"$\frac{S}{S_c^0}$",fontsize=16)
legend(loc="lower right")
grid()

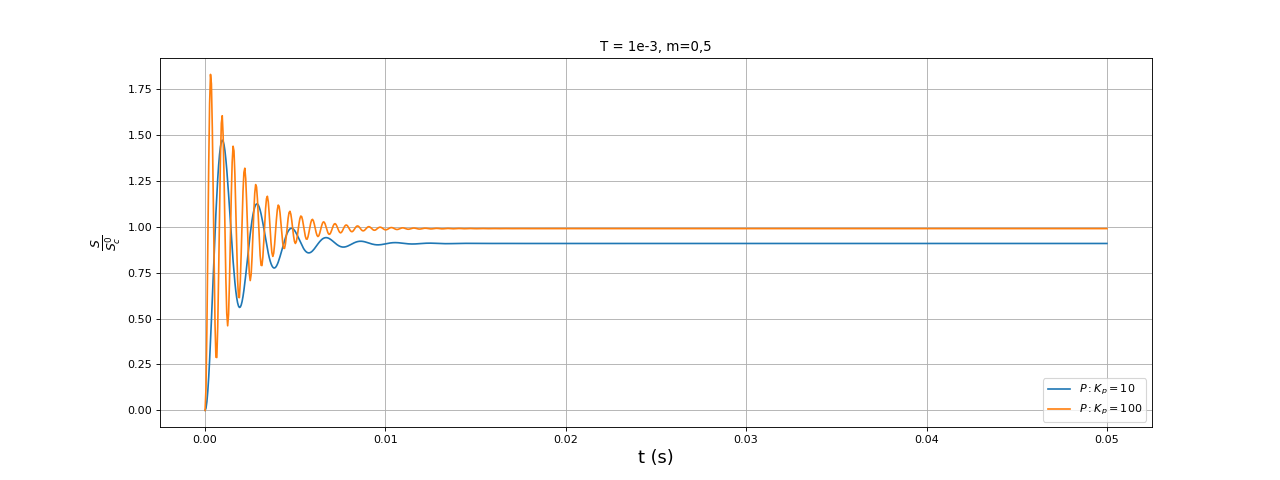fig16.pdf

L'inconvénient majeur du correcteur proportionnel est le fort dépassement de la réponse indicielle. On ajoute l'intégrateur et puisque celui-ci permet d'obtenir une erreur nulle, il est possible de réduire K_p. Il est intéressant de voir l'influence de ce dernier sur le temps T_i limite en dessous duquel le système est instable :

Kp = np.linspace(1,50,100)
Ti_lim = Ti_limite(A0,T,m,Kp,0)
figure(figsize=(12,6))
plot(Kp,Ti_lim)
grid()
xlabel(r"$K_p$",fontsize=16)
ylabel(r"$T_i\ (\rm min)$",fontsize=16)
yscale('log')

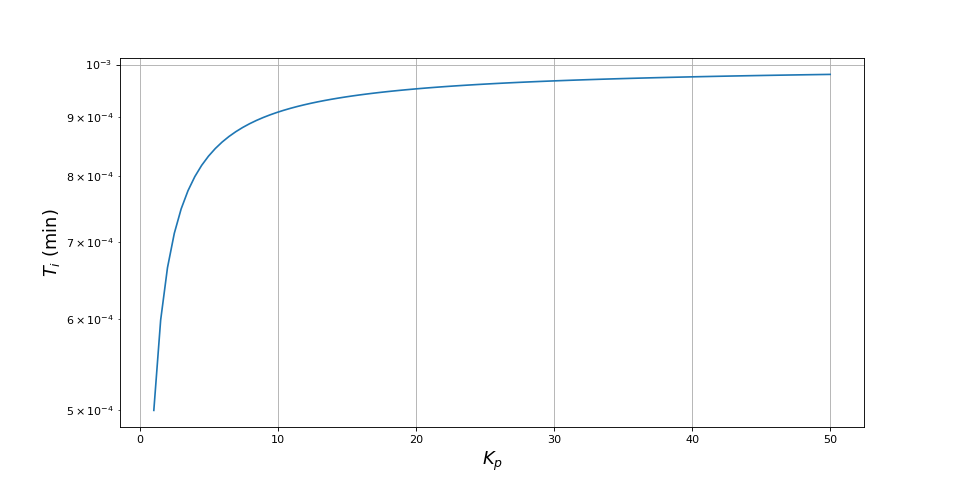fig17.pdf

Abaisser K_p permet d'adopter une valeur de T_i plus faible tout en restant dans le domaine de stabilité.

Pour une valeur de T_i donnée (dans le domaine de stabilité), voyons l'inluence de K_p sur la partie réelle des pôles :

Kp = np.logspace(-1,2,20)
Ti = 1e-3
Td = 0
figure()
title("Ti = 1e-3")
style =  ["ro","b+","g."]
for k in range(len(Kp)):
	[r,p,d] = decompositionPIDordre2(A0,T,m,Kp[k],Ti,0)
	for i in range(3):
		plot(Kp[k],-np.real(p[i]),style[i])
xlabel(r"$K_p$")
ylabel("-Re(p)")
yscale('log')
xscale('log')
grid()

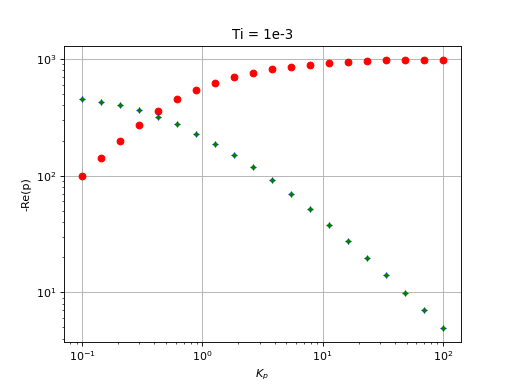fig18.pdf

La valeur optimale de K_p (pour cette valeur de T_i) est celle qui donne le plus petit de -Re(p) le plus grand. Il s'agit de K_p=0,5.

tmax = 0.05
N = 1000
figure(figsize=(16,6))
title("T = 1e-3, m=0,5")
Kp=0.1
Ti=1e-3
Td=0
t,S = reponsePIDordre2poles(A0,T,m,Kp,Ti,Td,tmax,N)
plot(t,S,label=r"$PI : K_p=0,1, T_i=1e-3$")
Kp=0.5
Ti=1e-3
Td=0
t,S = reponsePIDordre2poles(A0,T,m,Kp,Ti,Td,tmax,N)
plot(t,S,label=r"$PI : K_p=0,5, T_i=1e-3$")
Kp=1
Ti=1e-3
Td=0
t,S = reponsePIDordre2poles(A0,T,m,Kp,Ti,Td,tmax,N)
plot(t,S,label=r"$PI : K_p=1, T_i=1e-3$")
Kp=10
Ti=1e-3
Td=0
t,S = reponsePIDordre2poles(A0,T,m,Kp,Ti,Td,tmax,N)
plot(t,S,label=r"$PI : K_p=10, T_i=1e-3$")
xlabel("t (s)",fontsize=16)
ylabel(r"$\frac{S}{S_c^0}$",fontsize=16)
legend(loc="lower right")
grid()

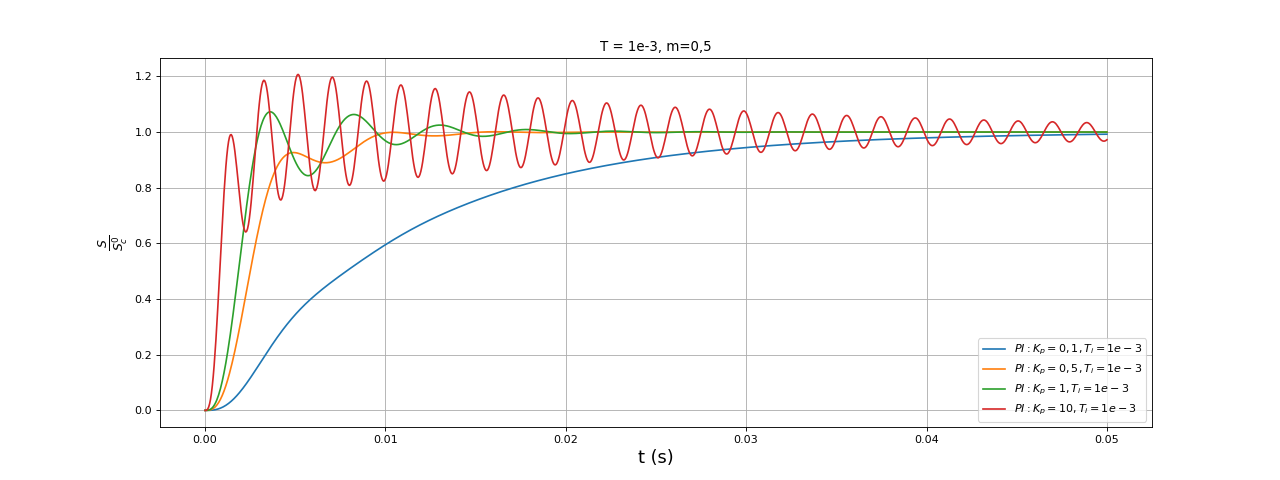fig19.pdf

La valeur K_p=0,5 est effectivement un bon choix : elle donne une réponse un peu plus lente que le correcteur proportionnel mais sans dépassement.

Pour K_p=0,5 et T_d=1e-3, on regarde l'influence du dérivateur :

Kp = 0.5
Ti = 1e-3
Td = np.logspace(-4,-2,100)
figure()
title("Kp = 0,5, Ti = 1e-3")
style =  ["ro","b+","g."]
for k in range(len(Td)):
	[r,p,d] = decompositionPIDordre2(A0,T,m,Kp,Ti,Td[k])
	for i in range(3):
		plot(Td[k],-np.real(p[i]),style[i])
xlabel(r"$T_d$")
ylabel("-Re(p)")
yscale('log')
xscale('log')
grid()

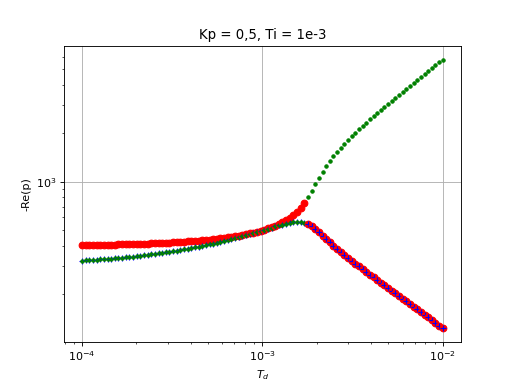fig20.pdf

La valeur optimale de T_d est environ 1.8e-3 :

tmax = 0.05
N = 1000
figure(figsize=(16,6))
title("T = 1e-3, m=0,5")
Kp=0.5
Ti=1e-3
Td=1.8e-3
t,S = reponsePIDordre2poles(A0,T,m,Kp,Ti,Td,tmax,N)
plot(t,S,label=r"$PI : K_p=0,5, T_i=1e-3, Td=1,8e-3$")
xlabel("t (s)",fontsize=16)
ylabel(r"$\frac{S}{S_c^0}$",fontsize=16)
legend(loc="lower right")
grid()

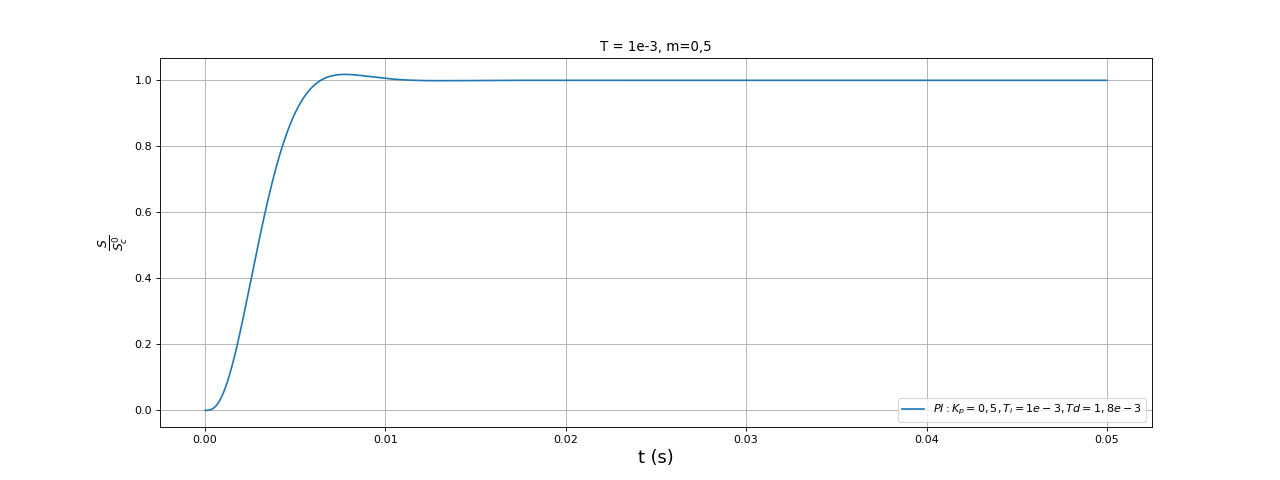fig21.pdf

On obtient une réponse indicielle très statisfaisante. Il ne s'agit peut-être pas de la solution optimale mais cette procédure de réglage avec calcul des pôles donne ici un bon résultat. En effet, le tracé de la partie réelle des pôles en fonction d'un paramètre du correcteur permet de trouver rapidement la valeur optimale de ce paramètre, les deux autres étant fixés.

La procédure d'ajustement mise en œuvre dans cet exemple est la suivante :

Choisir une valeur de T_i proche du temps de réponse du système non asservi.
Pour cette valeur, déterminer la valeur optimale de K_p, c'est-à-dire celle qui donne le temps de réponse le plus petit.
Ajouter le dérivateur et déterminer la valeur optimale de T_d (qui est proche de T_i) qui donne le temps de réponse le plus petit.

Il s'agit d'un problème d'optimisation à trois paramètres donc il existe évidemment d'autres manières d'ajuster les paramètres.

Références

[1] Y. Granjon, Automatique, (Dunod, 2015)