Condensateur

1. Introduction

Cette page présente la résolution du problème du condensateur plan par la méthode numérique des éléments finis. Le problème résolu est bidimensionnel, en géométrie rectiligne puis axisymétrique.

L'objectif est de calculer le champ électrique créé par un condensateur constitué de deux plaques parallèles. On calculera aussi la capacité du condensateur afin de la comparer à celle obtenue au moyen du modèle de condensateur plan infini.

Nous faisons la résolution par éléments finis avec le logiciel libre Finite Element Method Magnetic, au moyen de l'interface pour Python (pyfemm), qui permet de piloter le logiciel depuis un script Python (le logiciel doit être installé). Ce script permet de définir une géométrie complexe dépendant d'un ou de plusieurs paramètres et d'obtenir des tracés de champ sur des courbes particulières. Les commandes de l'interface Python sont des répliques des opérations que l'on effectue lorsqu'on utilise directement l'interface utilisateur. Il faut donc bien se familiariser avec cette interface avant d'aborder l'écriture des scripts Python.

Le logiciel FEMM permet d'effectuer la résolution numérique d'un problème d'électrostatique (ou de magnétostatique ou de diffusion thermique) par la méthode des éléments finis. Il résout les problèmes bidimensionnels, en géométrie plane ou axisymétrique. Contrairement au logiciel FreeFEM, dont l'utilisation pour un problème d'électrostatique est exposée dans Équation de Poisson : méthode des éléments finis, le logiciel FEMM peut être utilisé sans aucune connaissance sur la méthode des éléments finis ni même des équations de l'électrostatique. Le système électrostatique est en effet défini directement par ses caractéristiques physiques.

2. Condensateur semi-infini

2.a. Définition

Le condensateur est constitué de deux plaques de largeur L infinies dans la direction z :

Figure pleine page

La distance entre les deux faces internes est notée d et l'épaisseur des plaques est notée e. On note V(x,y) le potentiel électrique de ce problème bidimensionnel. L'équation de Laplace à deux dimensions est :

\frac{\partial^{2} V}{\partial x^{2}} + \frac{\partial^{2} V}{\partial y^{2}} = 0 (1)

Le champ électrique est calculé par dérivation du potentiel ( $\vec{E} = - \vec{g r a d} V$ ) puis la densité de charge sur la surface d'un plaque est calculée au moyen du théorème de Coulomb :

σ = ε_{0} \vec{E} \cdot \vec{n} (2)

où $\vec{n}$ est le vecteur normal sortant du conducteur. La quantité de charge portée par une des plaques (par unité de longueur) est calculée par intégration sur sa surface de la densité de charge, qui est en fait une intégrale sur le contour C du conducteur dans le plan XY :

Q = \int_{C} σ d ℓ (3)

avec $d ℓ = d x$ ou $d ℓ = d y$ suivant l'orientation du côté du contour. La charge par unité de longueur portée par la plaque de potentiel U/2 s'écrit :

Q = \int_{- L / 2}^{L / 2} (σ (- d / 2, y) + σ (- d / 2 - e, y)) d y + \int_{- d / 2 - e}^{- d / 2} (σ (x, - L / 2) + σ (x, L / 2)) d x (4)

On obtient ainsi la capacité par unité de longueur : $C = \frac{Q}{U}$ .

Une autre manière de calculer la capacité consiste à calculer l'énergie électrique dans tout le domaine :

\frac{1}{2} C U^{2} = \iint \frac{ε_{0}}{2} (E x^{2} + E y^{2}) d x d y (5)

Lorsque le modèle de condensateur plan infini est adopté, le champ à l'intérieur et la capacité (par unité de longueur) sont :

\vec{E_{\infty}} = - \frac{U}{d} \vec{u_{x}} (6)

C_{\infty} = \frac{ε_{0} L}{d} (7)

2.b. Résolution par éléments finis

condensateurXY.py

import femm
import numpy as np
import matplotlib.pyplot as plt

On commence par ouvrir un document FEMM pour résoudre un problème d'électrostatique de type plan, avec le millimètre pour unité de longueur :

femm.openfemm()
femm.newdocument(1)
# 0 : magnetic, 1 : electrostatic, 2 ; heat flow, 3 : current flow
femm.ei_probdef('millimeters', 'planar', 1.0e-8, 1, 30);
# unit, type ('planar' ou 'axi'), precision, depth, minangle

Un matériau se définit par deux permittivités électriques (pour les deux axes) et une densité volumique de charge. On définit deux matériaux air et métal, de permittivité 1 :

femm.ei_addmaterial('air',1,1,0)
femm.ei_addmaterial('metal',1,1,0)

Deux conducteurs doivent être définis. Il y a deux types de conducteur : à potentiel imposé (type 1) et à charge imposée (type 2). On définit deux conducteurs à potentiel imposé avec une différence de potentiel U :

U = 1
femm.ei_addconductorprop('v0',U/2,0,1)
femm.ei_addconductorprop('v1',-U/2,0,1)

Voici les dimensions du condensateur (en mm) et le rayon du domaine de calcul (qui est circulaire) :

L = 8
e = 1
d = 2
R1 = 100

Les deux conducteurs sont définis géométriquement par deux rectangles :

femm.ei_drawrectangle(-d/2-e,-L/2,-d/2,L/2)
femm.ei_drawrectangle(d/2,-L/2,d/2+e,L/2)

Il en résulte trois domaines. Un matériau doit être attribué à chacun. Pour attribuer un matériau, on doit tout d'abord définir un label pour le domaine, puis sélectionner ce label et attribuer le matériau au label sélectionné :

femm.ei_addblocklabel(0,0)
femm.ei_selectlabel(0,0)
femm.ei_setblockprop('air',0,1,0)
femm.ei_clearselected()

femm.ei_addblocklabel(-d/2-e/2,0)
femm.ei_selectlabel(-d/2-e/2,0)
femm.ei_setblockprop('metal',0,1,0)
femm.ei_clearselected()

femm.ei_addblocklabel(d/2+e/2,0)
femm.ei_selectlabel(d/2+e/2,0)
femm.ei_setblockprop('metal',0,1,0)
femm.ei_clearselected()

Les 4 côtés de chaque conducteur doivent être associés au conducteur correspondant défini plus haut :

femm.ei_selectsegment(-d/2,0)
femm.ei_selectsegment(-d/2-e,0)
femm.ei_selectsegment(-d/2-e/2,L/2)
femm.ei_selectsegment(-d/2-e/2,-L/2)
automesh = 1
femm.ei_setsegmentprop('<None>',0,automesh,0,0,'v0')
femm.ei_clearselected()

femm.ei_selectsegment(d/2,0)
femm.ei_selectsegment(d/2+e,0)
femm.ei_selectsegment(d/2+e/2,L/2)
femm.ei_selectsegment(d/2+e/2,-L/2)
femm.ei_setsegmentprop('<None>',0,automesh,0,0,'v1')
femm.ei_clearselected()

Le maillage triangulaire est généré à partir des conducteurs. Le placement des nœuds sur les deux rectangles est fait en mode automatique.

La frontière du domaine de calcul est définie par la fonction ei_makeABC, qui mermet de simuler un domaine infini au moyen de n couches (Improvised Asymptotic Boundary Condition). On choisit n=5 et une condition de type Dirichlet sur dernière couche :

femm.ei_makeABC(5,R1,0,0,0)

Pour finir, le document doit être enregistré dans un ficher avant de lancer le calcul : l'application FEMM s'ouvre avec le fichier et effectue le calcul.

femm.ei_saveas('condensateurXY.fee')
femm.ei_analyze()
femm.ei_loadsolution()

Par défaut, le potentiel apparaît sous la forme d'une image en couleur. Voici comment obtenir un tracé de lignes équipotentielles :

femm.eo_hidedensityplot()
numcontours = 30
Vmin = -0.5
Vmax = 0.5
femm.eo_showcontourplot(numcontours,Vmin,Vmax)

Voici les lignes équipotentielles au voisinage des conducteurs, avec le tracé du maillage :

On peut remarquer que l'algorithme de maillage a généré, à partir des deux rectangles, un maillage plus dense au voisinage des angles. La possibilité d'obtenir un maillage plus ou moins dense selon de la région est un avantage du maillage par triangulation, impossible à obtenir avec le maillage rectangulaire de la méthode des différences finies. Sur la totalité du domaine, le maillage comporte 40517 triangles et 80506 nœuds. Pour comparaison, le calcul par différences finies présenté dans Condensateur plan : différences finies est fait avec un maillage rectangulaire de 4194304 nœuds, ce qui conduit à un système linéaire beaucoup plus grand. Dans le cas du maillage rectangulaire, le maillage doit être aussi fin à grande distance des conducteurs qu'à leur proximité, ce qui explique ce très grand nombre de nœuds.

Pour calculer l'énergie électrique, on sélectionne le bloc correspondant au vide (puisque le champ est nul dans les conducteurs) puis on fait appel à la fonction eo_blockintegral avec l'argument 0 (Stored energy) :

femm.eo_selectblock(0,0)
W = femm.eo_blockintegral(0) # énergie par mm de longueur
femm.eo_clearblock()

Il s'agit de l'énergie par unité de longueur (dans la direction Z) c'est-à-dire par millimètre. Voici le calcul de la capacité à partir de cette énergie et la comparaison avec celle du condensateur infini :

C = 2*W[0]*1e3/U**2 # capacité par mètre de longueur
eps0= 8.85e-12
Cinf = eps0*L/d # capacité par mètre de longueur
print("C/Cinf = %f"%(C/Cinf))

C/Cinf = 1.458939

On peut effectuer des tracés du champ électrique sur certaines droites. Voici tout d'abord la composante E_x sur la droite (Ox) :

N = 1000
x = np.linspace(-20,20,N)
Ex = np.zeros(N)
for i in range(N):
    E = femm.eo_gete(x[i],0)
    Ex[i] = E[0]
plt.figure()
plt.plot(x,Ex)
plt.title("y=0")
plt.grid()
plt.xlabel("x")
plt.ylabel("Ex")
plt.savefig("../../../../figures/sciphys/elecmag/condensateur3/Eaxe-L=8-e=1-d=2.png")

Le champ entre les deux plaques peut être comparé à celui donné par le modèle de condensateur infini :

print("E inf = %f"%(U/(d*1e-3)))

E inf = 500.000000

Voici la composante normale du champ électrique sur les deux faces du conducteur de potentiel U/2 :

N = 1000
y = np.linspace(-L/2,L/2,N)
Ex1 = np.zeros(N)
Ex2 = np.zeros(N)
eps = 1e-3 # décalage par rapport au bord du conducteur
for i in range(N):
    E = femm.eo_gete(-d/2+eps,y[i])
    Ex1[i] = E[0]
    E = femm.eo_gete(-d/2-e-eps,y[i])
    Ex2[i] = E[0]
Q = eps0*(Ex1-Ex2).sum()*(y[1]-y[0])*1e-3
plt.figure()
plt.plot(y,Ex1,label="face interne")
plt.plot(y,Ex2,label="face externe")
plt.grid()
plt.xlabel("y")
plt.ylabel("Ex")
plt.legend(loc="upper right")
plt.savefig("../../../../figures/sciphys/elecmag/condensateur3/Eplaque-L=8-e=1-d=2.png")

Il y a une forte augmentation du champ à l'approche des bords, donc une augmentation de la densité de charge au voisinage des bords.

Pour le calcul de la capacité, nous devons aussi tenir compte de la composante normale du champ sur les petits bords de la plaque, dont voici le tracé :

N = 100
x = np.linspace(-d/2-e,-d/2,N)
Ey1 = np.zeros(N)
Ey2 = np.zeros(N)
for i in range(N):
    E = femm.eo_gete(x[i],L/2+eps)
    Ey1[i] = E[1]
    E = femm.eo_gete(x[i],-L/2-eps)
    Ey2[i] = E[1]
Q += eps0*(Ey1-Ey2).sum()*(x[1]-x[0])*1e-3
plt.figure()
plt.plot(x,Ey1,label="bord y = L/2")
plt.plot(x,Ey2,label="bord y = -L/2")
plt.grid()
plt.legend(loc="upper right")
plt.xlabel("x")
plt.ylabel("Ey")
plt.savefig("../../../../figures/sciphys/elecmag/condensateur3/Eplaque2-L=8-e=1-d=2.png")

La quantité de charge par mètre de longueur est calculée par intégration de la densité de charge avec la méthode des rectangles. Voici le calcul de la capacité et la comparaison avec celle du condensateur plan infini :

C = Q/U
print("C/Cinf = %f"%(C/Cinf))

C/Cinf = 1.439109

plt.show()
femm.closefemm()

2.c. Influence de la largeur

À distance entre les plaques fixée, on fait varier leur largeur L. Voici le script effectuant le calcul :

condensateurXY-capacite.py

import femm
import numpy as np
import matplotlib.pyplot as plt

femm.openfemm()

def capacite(L,e,d,R1=100):
    femm.newdocument(1)
    femm.ei_probdef('millimeters', 'planar', 1.0e-8, 0, 30);
    femm.ei_addmaterial('air',1,1,0)
    femm.ei_addmaterial('metal',1,1,0)
    U = 1
    femm.ei_addconductorprop('v0',U/2,0,1)
    femm.ei_addconductorprop('v1',-U/2,0,1)
    femm.ei_drawrectangle(-d/2-e,-L/2,-d/2,L/2)
    femm.ei_drawrectangle(d/2,-L/2,d/2+e,L/2)
    femm.ei_addblocklabel(0,0)
    femm.ei_selectlabel(0,0)
    femm.ei_setblockprop('air',0,1,0)
    femm.ei_clearselected()
    femm.ei_addblocklabel(-d/2-e/2,0)
    femm.ei_selectlabel(-d/2-e/2,0)
    femm.ei_setblockprop('metal',0,1,0)
    femm.ei_clearselected()
    femm.ei_addblocklabel(d/2+e/2,0)
    femm.ei_selectlabel(d/2+e/2,0)
    femm.ei_setblockprop('metal',0,1,0)
    femm.ei_clearselected()
    femm.ei_selectsegment(-d/2,0)
    femm.ei_selectsegment(-d/2-e,0)
    femm.ei_selectsegment(-d/2-e/2,L/2)
    femm.ei_selectsegment(-d/2-e/2,-L/2)
    femm.ei_setsegmentprop('<None>',0,1,0,0,'v0')
    femm.ei_clearselected()
    femm.ei_selectsegment(d/2,0)
    femm.ei_selectsegment(d/2+e,0)
    femm.ei_selectsegment(d/2+e/2,L/2)
    femm.ei_selectsegment(d/2+e/2,-L/2)
    femm.ei_setsegmentprop('<None>',0,1,0,0,'v1')
    femm.ei_clearselected()
    femm.ei_makeABC(5,R1,0,0,0)
    femm.ei_saveas('condensateurXY.fee')
    femm.ei_analyze()
    femm.ei_loadsolution()
    femm.eo_selectblock(0,0)
    W = femm.eo_blockintegral(0) # stored energie
    femm.eo_clearblock()
    C = 2*W[0]*1e3/U**2 # capacité par mètre de longueur
    eps0= 8.85e-12
    Cinf = eps0*L/d # capacité par mètre de longueur
    print(C/Cinf)
    c1 = C/Cinf
    N = 1000
    y = np.linspace(-L/2,L/2,N)
    Ex1 = np.zeros(N)
    Ex2 = np.zeros(N)
    eps = 1e-3
    for i in range(N):
        E = femm.eo_gete(-d/2+eps,y[i])
        Ex1[i] = E[0]
        E = femm.eo_gete(-d/2-e-eps,y[i])
        Ex2[i] = E[0]
    Q = eps0*(Ex1-Ex2).sum()*(y[1]-y[0])*1e-3
    N = 100
    x = np.linspace(-d/2-e,-d/2,N)
    Ey1 = np.zeros(N)
    Ey2 = np.zeros(N)
    for i in range(N):
        E = femm.eo_gete(x[i],L/2+eps)
        Ey1[i] = E[1]
        E = femm.eo_gete(x[i],-L/2-eps)
        Ey2[i] = E[1]
    Q += eps0*(Ey1-Ey2).sum()*(x[1]-x[0])*1e-3
    C = Q/U
    c2 = C/Cinf
    return c1,c2


L_list = [4,6,8,10,12,14,16,18,22,24,26,30,36,40,45,50] # largeurs des plaques
e = 1 # épaisseur des plaques
d = 2 # distance entre les plaques
C1_list = []
C2_list = []
filename = "capaciteXY-e=1-d=2.txt"
for L in L_list:
    c1,c2 = capacite(L,e,d)
    C1_list.append(c1)
    C2_list.append(c2)
C1 = np.array(C1_list)
C2 = np.array(C2_list)
L = np.array(L_list)
np.savetxt(filename,np.array([L,C1,C2]).T)

plt.figure()
plt.plot(L,C1,"ro",label="C par energie")
plt.plot(L,C2,"bo",label="C par charge")
plt.grid()
plt.xlabel("L")
plt.ylabel("C/Cinf")
plt.show()
plt.xlim(0,20)
plt.ylim(0,2)
plt.legend(loc="upper right")
plt.show()
femm.closefemm()

import numpy as np
from matplotlib.pyplot import *

L,C1,C2 = np.loadtxt("capaciteXY-e=1-d=2.txt",unpack=True)
figure()
plot(L,C2,"b.",label="C par charge")
plot(L,C2,"b-")
plot(L,C1,"r.",label="C par energie")
plot(L,C1,"r-")
legend(loc="upper right")
grid()
xlabel("L",fontsize=16)
ylabel(r"$C/C_{\infty}$",fontsize=16)
xlim(0,40)
ylim(0,2)

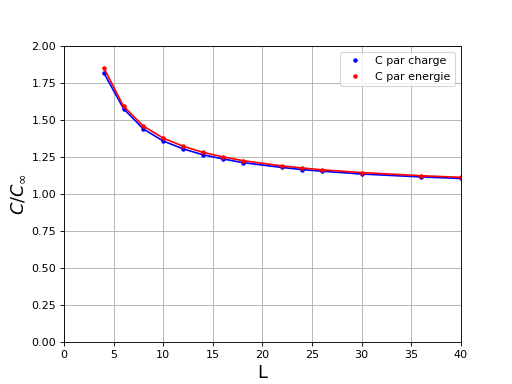fig1.pdf

La capacité évaluée au moyen de la densité de charge est légèrement inférieure à celle évaluée par l'énergie. C'est similaire à ce qui est obtenu par le calcul avec la méthode des différences finies (Condensateur plan : différences finies). Cependant, l'écart entre les deux méthodes est ici beaucoup plus faible, peut-être parce que les effets de bord du domaine de calcul sont plus faibles (le domaine est ici circulaire alors qu'il est carré pour la méthode des différences finies.

3. Condensateur axi-symétrique

3.a. Définition

Le condensateur est constitué de deux disques de rayon R, d'axe Oz, espacés d'une distance d et d'épaisseur e.

Figure pleine page

Le potentiel électrostatique en coordonnées cylindriques V(z,r) obéit à l'équation de Laplace :

\frac{1}{r} \frac{\partial}{\partial r} (r \frac{\partial V}{\partial r}) + \frac{\partial^{2} V}{\partial z^{2}} = 0 (8)

La charge portée par la plaque au potentiel U/2 est obtenue par l'intégrale suivante :

Q = 2 π \int_{0}^{R} (σ (r, - d / 2) + σ (r, - d / 2 - e)) r d r + 2 π R \int_{- d / 2 - e}^{- d / 2} σ (R, z) d z (9)

où la seconde intégrale se fait sur le bord du disque.

3.b. Résolution par éléments finis

En géométrie axisymétrique, on définit le système avec r en abscisse (positif) et z en ordonnée. Voici le script :

condensateurRZ.py

import femm
import numpy as np
import matplotlib.pyplot as plt   
                
femm.openfemm()
femm.newdocument(1)
# 0 : magnetic, 1 : electrostatic, 2 ; heat flow, 3 : current flow
femm.ei_probdef('millimeters', 'axi', 1.0e-8, 1, 30);
# unit, type ('planar' ou 'axi'), precision, depth, minangle
                
femm.ei_addmaterial('air',1,1,0)
femm.ei_addmaterial('metal',1,1,0)            
U = 1
femm.ei_addconductorprop('v0',U/2,0,1)
femm.ei_addconductorprop('v1',-U/2,0,1)

R = 8
e = 1
d = 2
R1 = 100

femm.ei_drawrectangle(0,d/2,R,d/2+e)
femm.ei_drawrectangle(0,-d/2-e,R,-d/2)
femm.ei_addblocklabel(1,0)
femm.ei_selectlabel(1,0)
femm.ei_setblockprop('air',0,1,0)
femm.ei_clearselected()

femm.ei_addblocklabel(R/2,-d/2-e/2)
femm.ei_selectlabel(R/2,-d/2-e/2)
femm.ei_setblockprop('metal',0,1,0)
femm.ei_clearselected()

femm.ei_addblocklabel(R/2,d/2+e/2)
femm.ei_selectlabel(R/2,d/2+e/2)
femm.ei_setblockprop('metal',0,1,0)
femm.ei_clearselected()

femm.ei_selectsegment(R/2,-d/2)
femm.ei_selectsegment(R/2,-d/2-e)
femm.ei_selectsegment(R,-d/2-e/2)
automesh = 1
femm.ei_setsegmentprop('<None>',0,automesh,0,0,'v0')
femm.ei_clearselected()

femm.ei_selectsegment(R/2,d/2)
femm.ei_selectsegment(R/2,d/2+e)
femm.ei_selectsegment(R,d/2+e/2)
femm.ei_setsegmentprop('<None>',0,automesh,0,0,'v1')
femm.ei_clearselected()
                   
femm.ei_makeABC(5,R1,0,0,0)

femm.ei_saveas('condensateurRZ.fee')
femm.ei_analyze()
femm.ei_loadsolution()            
                    
femm.eo_hidedensityplot()
numcontours = 30
Vmin = -0.5
Vmax = 0.5
femm.eo_showcontourplot(numcontours,Vmin,Vmax)

femm.eo_selectblock(0,0)
W = femm.eo_blockintegral(0) # énergie 
femm.eo_clearblock()       
                    
C = 2*W[0]/U**2 # capacité 
eps0= 8.85e-12
Cinf = eps0*np.pi*R**2/d*1e-3 
print("C/Cinf = %f"%(C/Cinf))

C/Cinf = 1.518176

Voici le tracé du champ électriquse sur l'axe :

N = 1000
z = np.linspace(-20,20,N)
Ez = np.zeros(N)
for i in range(N):
    E = femm.eo_gete(0,z[i])
    Ez[i] = E[1]
plt.figure()
plt.plot(z,Ez)
plt.grid()
plt.xlabel("z")
plt.ylabel("Ez")
plt.savefig("../../../../figures/sciphys/elecmag/condensateur3/Eaxe-R=8-e=1-d=2.png")

Voici la composante normale du champ (E_z) sur les deux faces d'une plaque, avec le calcul de la quantité de charge portée par ces deux faces :

N = 1000
r = np.linspace(0,R,N)
Ez1 = np.zeros(N)
Ez2 = np.zeros(N)
eps = 1e-2
for i in range(N):
    E = femm.eo_gete(r[i],d/2-eps)
    Ez1[i] = E[1]
    E = femm.eo_gete(r[i],d/2+e+eps)
    Ez2[i] = E[1]

Q = eps0*((Ez1-Ez2)*r).sum()*2*np.pi*(r[1]-r[0])*1e-6
plt.figure()
plt.plot(r,Ez1,label="face interne")
plt.plot(r,Ez2,label="face externe")
plt.grid()
plt.xlabel("r")
plt.ylabel("Ez")
plt.legend(loc="upper left")
plt.savefig("../../../../figures/sciphys/elecmag/condensateur3/Efaces-R=8-e=1-d=2.png")

Voici la composante normale du champ (E_r) sur le bord de la plaque et le calcul de la quantité de charge sur ce bord :

N = 300
z = np.linspace(-d/2-e,-d/2,N)
Er = np.zeros(N)
for i in range(N):
    E = femm.eo_gete(R+eps,z[i])
    Er[i] = E[0]
Q += eps0*Er.sum()*(z[1]-z[0])*2*np.pi*R*1e-6 
plt.figure()
plt.plot(z,Er,label="bord r=R")
plt.grid()
plt.xlabel("z")
plt.ylabel("Er")
plt.legend(loc="upper right")
plt.savefig("../../../../figures/sciphys/elecmag/condensateur3/Ebord-R=8-e=1-d=2.png")

Voici la capacité calculée avec la quantité de charge divisée par la capacité obtenue avec le condensateur infini :

C = Q/U
print("C/Cinf = %f"%(C/Cinf))

C/Cinf = 1.146540

plt.figure()
plt.show()
femm.closefemm()

3.c. Influence du rayon

À distance entre les plaques fixée, on fait varier de rayon R des plaques. Voici le script effectuant le calcul :

condensateurRZ-capacite.py

import femm
import numpy as np
import matplotlib.pyplot as plt

femm.openfemm()

def capacite(R,e,d,R1=100):
    femm.newdocument(1)
    femm.ei_probdef('millimeters', 'axi', 1.0e-8, 1, 30)
    femm.ei_addmaterial('air',1,1,0)
    femm.ei_addmaterial('metal',1,1,0)            
    U = 1
    femm.ei_addconductorprop('v0',U/2,0,1)
    femm.ei_addconductorprop('v1',-U/2,0,1)
    femm.ei_drawrectangle(0,d/2,R,d/2+e)
    femm.ei_drawrectangle(0,-d/2-e,R,-d/2)
    femm.ei_addblocklabel(1,0)
    femm.ei_selectlabel(1,0)
    femm.ei_setblockprop('air',0,1,0)
    femm.ei_clearselected()
    femm.ei_addblocklabel(R/2,-d/2-e/2)
    femm.ei_selectlabel(R/2,-d/2-e/2)
    femm.ei_setblockprop('metal',0,1,0)
    femm.ei_clearselected()
    femm.ei_addblocklabel(R/2,d/2+e/2)
    femm.ei_selectlabel(R/2,d/2+e/2)
    femm.ei_setblockprop('metal',0,1,0)
    femm.ei_clearselected()
    femm.ei_selectsegment(R/2,-d/2)
    femm.ei_selectsegment(R/2,-d/2-e)
    femm.ei_selectsegment(R,-d/2-e/2)
    automesh = 1
    femm.ei_setsegmentprop('<None>',0,automesh,0,0,'v0')
    femm.ei_clearselected()
    femm.ei_selectsegment(R/2,d/2)
    femm.ei_selectsegment(R/2,d/2+e)
    femm.ei_selectsegment(R,d/2+e/2)
    femm.ei_setsegmentprop('<None>',0,automesh,0,0,'v1')
    femm.ei_clearselected()                 
    femm.ei_makeABC(5,R1,0,0,0)
    femm.ei_saveas('condensateurRZ.fee')
    femm.ei_analyze()
    femm.ei_loadsolution()
    femm.eo_selectblock(0,0)
    W = femm.eo_blockintegral(0) # énergie 
    femm.eo_clearblock()       
    C = 2*W[0]/U**2 # capacité 
    eps0= 8.85e-12
    Cinf = eps0*np.pi*R**2/d*1e-3
    c1 = C/Cinf
    print(c1)
    N = 1000
    r = np.linspace(0,R,N)
    Ez1 = np.zeros(N)
    Ez2 = np.zeros(N)
    eps = 1e-2
    for i in range(N):
        E = femm.eo_gete(r[i],d/2-eps)
        Ez1[i] = E[1]
        E = femm.eo_gete(r[i],d/2+e+eps)
        Ez2[i] = E[1]
    Q = eps0*((Ez1-Ez2)*r).sum()*2*np.pi*(r[1]-r[0])*1e-6
    N = 100
    z = np.linspace(-d/2-e,-d/2,N)
    Er = np.zeros(N)
    for i in range(N):
        E = femm.eo_gete(R+eps,z[i])
        Er[i] = E[0]
    Q += eps0*Er.sum()*(z[1]-z[0])*2*np.pi*R*1e-6
    C = Q/U
    c2 = C/Cinf
    return c1,c2

R_list = [4,6,8,10,12,14,16,18,22,24,26,30,36,40] # rayons des plaques
e = 1 # épaisseur des plaques
d = 2 # distance entre les plaques
C1_list = []
C2_list = []
filename = "capaciteRZ-e=1-d=2.txt"
for R in R_list:
    c1,c2 = capacite(R,e,d)
    C1_list.append(c1)
    C2_list.append(c2)
C1 = np.array(C1_list)
C2 = np.array(C2_list)
R = np.array(R_list)
np.savetxt(filename,np.array([R,C1,C2]).T)

plt.figure()
plt.plot(R,C1,"ro",label="C par energie")
plt.plot(R,C2,"bo",label="C par charge")
plt.grid()
plt.xlabel("R")
plt.ylabel("C/Cinf")
plt.xlim(0,20)
plt.ylim(0,2)
plt.legend(loc="upper right")
plt.show()
femm.closefemm()

import numpy as np
from matplotlib.pyplot import *

R,C1,C2 = np.loadtxt("capaciteRZ-e=1-d=2.txt",unpack=True)
figure()
plot(R,C1,"r.",label="C par énergie")
plot(R,C1,"r-")
plot(R,C2,"b.",label="C par charge")
plot(R,C2,"b-")
legend(loc="upper right")
grid()
xlabel("R",fontsize=16)
ylabel(r"$C/C_{\infty}$",fontsize=16)
xlim(0,40)
ylim(0,2)

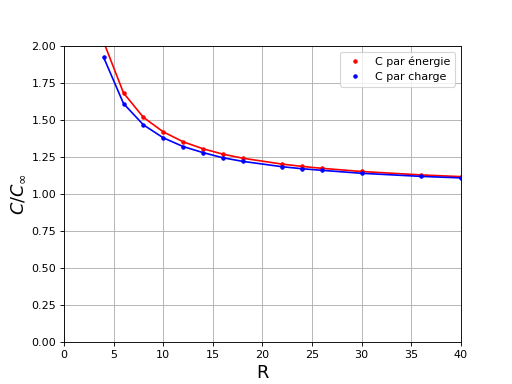fig2.pdf

Condensateur plan : éléments finis