Condensateur plan : différences finies

2.a. Définition

Le condensateur est constitué de deux plaques de largeur L infinies dans la direction z :

Figure pleine page

La distance entre les deux faces internes est notée d et l'épaisseur des plaques est notée e. Le domaine de calcul est un carré de largeur unité. On note V(x,y) le potentiel électrique de ce problème bidimensionnel. L'équation de Laplace à deux dimensions est :

$$\frac{{\partial }^{2}V}{\partial x^2}+\frac{{\partial }^{2}V}{\partial y^2}=0\text{(1)}$$

Nous optons pour un potentiel nul sur la frontière du domaine de calcul. Les deux plaques sont respectivement au potentiel U/2 et -U/2.

Le champ électrique est calculé par dérivation du potentiel ($\overrightarrow{E}=-\overrightarrow{grad}V$) puis la densité de charge sur la surface d'un plaque est calculée au moyen du théorème de Coulomb :

$$\sigma ={\epsilon }_0\overrightarrow{E}\cdot \overrightarrow{n}\text{(2)}$$

où $\overrightarrow{n}$ est le vecteur normal sortant du conducteur. La quantité de charge portée par une des plaques (par unité de longueur) est calculée par intégration sur sa surface de la densité de charge, qui est en fait une intégrale sur le contour C du conducteur dans le plan XY :

$$Q={\int }_C\sigma d\ell \text{(3)}$$

avec $d\ell =dx$ ou $d\ell =dy$ suivant l'orientation du côté du contour. La charge par unité de longueur portée par la plaque de potentiel U/2 s'écrit :

$$Q={\int }_{-L/2}^{L/2}(\sigma (-d/2,y)+\sigma (-d/2-e,y))dy+{\int }_{-d/2-e}^{-d/2}(\sigma (x,-L/2)+\sigma (x,L/2))dx\text{(4)}$$

On obtient ainsi la capacité par unité de longueur : $C=\frac{Q}{U}$.

Une autre manière de calculer la capacité consiste à calculer l'énergie électrique dans tout le domaine :

$$\frac{1}{2}C{U}^2=\iint \frac{{\epsilon }_0}{2}(E{x}^2+E{y}^2)dxdy\text{(5)}$$

Lorsque le modèle de condensateur plan infini est adopté, le champ à l'intérieur et la capacité (par unité de longueur) sont :

$$\overrightarrow{E_{\infty }}=-\frac{U}{d}\overrightarrow{u_x}\text{(6)}$$ $$C_{\infty }=\frac{{\epsilon }_{0}L}{d}\text{(7)}$$

Les calculs numériques seront faits avec un domaine de largeur 1 et une constante diélectrique égale à 1.

2.b. Résolution par différences finies

Les conducteurs sont définis sur un maillage comportant 2^p mailles dans chaque direction (x et y), que l'on nommera maillage P. Le calcul est fait sur un maillage plus fin, comportant 2ⁿ mailles dans chaque direction, avec n>p, que l'on nommera maillage N. Le passage du maillage N au maillage P se fait par n-p division par 2. Les n-p-2 maillages intermédiaires sont utilisés par l'algorithme multigrille. Les dimensions (distance, largeur et épaisseur) doivent être des nombres entiers car les frontières du conducteur doivent être définis par des nœuds du maillage P. La largeur du domaine carré est fixée par convention à 1 donc les pas d'espace des deux maillages sont :

$$\begin{array}{cc}\hfill & {\Delta }_{p}x=2^{-p}\hfill \\ \hfill & {\Delta }_{n}x=2^{-n}\hfill \end{array}$$

Les dimensions définies sur le maillage P devront donc être multipliées par ${\Delta }_{p}x$ pour obtenir les dimensions réelles.

Pour maintenir les effets de bord à un niveau acceptable, la largeur des plaques doit être inférieure à la moitié de la taille du domaine, c'est-à-dire inférieure à 2^p-1. Même si cette condition est respectée, les effets de bords ne sont peut-être pas négligeables. Pour les évaluer, il faut faire deux calculs avec les mêmes proportions des dimensions mais toutes deux fois plus petites, afin que le condensateur soit deux fois plus petit par rapport au domaine de calcul. Les dimensions du condensateur sur la maille P étant fixée, il suffira d'augmenter p et n d'une unité pour diviser par deux ces dimensions par rapport à la taille du domaine, mais le calcul sera évidemment plus long.

from matplotlib.pyplot import *
import numpy as np
import poisson.main
                    

La fonction suivante effectue le calcul et renvoie la capacité (divisée par $C_{\infty }$) et le champ électrique pour un condensateur plan infini. Les résultats sont enregistrés dans un fichier NPZ.

def condensateurXY(p,n,largeur,distance,epaisseur,filename,niter=50,ncycles=15):
    levels = n-p+1 
    laplace=poisson.main.Poisson(p,p,levels,1.0,1.0,x0=-0.5,y0=-0.5)
    laplace.laplacien()
    laplace.dirichlet_borders(0.0)
    xc = 2**(p-1) # centre du domaine
    yc = 2**(p-1)
    U = 1
    laplace.dirichlet_polygon(xc-distance//2,yc-largeur//2,[0,-epaisseur,0,epaisseur],[largeur,0,-largeur,0],U/2)
    laplace.dirichlet_polygon(xc+distance//2,yc-largeur//2,[0,epaisseur,0,-epaisseur],[largeur,0,-largeur,0],-U/2)
    # sommets du conducteur de potentiel U/2 sur le maillage fin, noeuds au dessus de la surface
    x1,y1 = (xc-distance//2)*2**(n-p),(yc-largeur//2)*2**(n-p)
    x2,y2 = x1,(yc+largeur//2)*2**(n-p)+1
    x3,y3 = (xc-distance//2-epaisseur)*2**(n-p)-1,y2
    x4,y4 = x3,y1
    result = laplace.multigrid_full_norm(ncycles,levels,niter,2,1)
    V = laplace.get_array()
    Ex=-laplace.get_derivX()
    Ey=-laplace.get_derivY()
    mask = laplace.get_mask()
    extent = laplace.get_extent()
    x=laplace.get_x()
    dx = x[1]-x[0]
    y = laplace.get_y()
    dy = y[1]-y[0]
    # calcul de la capacité à partir du champ sur le conducteur
    Ex_faceInt = Ex[y1:y2,x1+1]
    Ex_faceExt = Ex[y1:y2,x3-1]
    Q = (Ex_faceInt.sum()-Ex_faceExt.sum())*dy
    Ey_bordHaut = Ey[y2+1,x3:x1]
    Ey_bordBas = Ey[y1-1,x3:x1]
    Q += (Ey_bordHaut-Ey_bordBas).sum()*dx
    C = (Q/largeur*distance) # capacité par rapport à C infini
    # calcul de la capacité à partir de l'énergie
    C2 = (Ex*Ex+Ey*Ey).sum()*dx*dy
    C2 = C2/largeur*distance
    # calcul du champ E infini
    Einf = U/(distance/2**p)    
    if filename: np.savez(filename,V,Ex,Ey,mask,extent,x,y,np.array([C,C2,Einf,y1,y2,x1,x3]))
    return C,C2,Einf
                    

La fonction suivante récupère les résultats enregistrés dans un fichier NPZ sous forme de variables globales :

def readXY(filename):
    global V,Ex,Ey,mask,extent,x,y,C,C2,Einf,y1,y2,x1,x3
    npzfiles = np.load(filename)
    V = npzfiles['arr_0']
    Ex = npzfiles['arr_1']
    Ey = npzfiles['arr_2']
    mask = npzfiles['arr_3']
    extent = npzfiles['arr_4']
    x = npzfiles['arr_5']
    y = npzfiles['arr_6']
    A = npzfiles['arr_7']
    C,C2,Einf,y1,y2,x1,x3 = A[0],A[1],A[2],A[3],A[4],A[5],A[6]
    y1 = int(y1)
    y2 = int(y2)
    x1 = int(x1)
    x3 = int(x3)
                    

Voici un exemple, avec un maillage N de 2040x2048 et un maillage P de 128x128.

n=11
p=7
distance = 2 # distance entre les plaques
largeur = 6 # largeur des plaques
epaisseur = 1 #épaisseur des plaques
#condensateurXY(p,n,largeur,distance,epaisseur,"condensateurXY-d=2-L=6-e=1.npz")
                    

Voici le tracé de lignes équipotentielles sur la totalité du domaine de calcul :

 
readXY("condensateurXY-d=2-L=6-e=1.npz")
figure(figsize=(8,8))
contour(V,20,extent=extent)
imshow(~mask,extent=extent,alpha=0.5, cmap=cm.gray)
xlabel("x",fontsize=16)
ylabel("y",fontsize=16)
                    

fig1.pdf

puis sur une région restreinte :

figure(figsize=(8,8))
contour(V,10,extent=extent)
imshow(~mask,extent=extent,alpha=0.5, cmap=cm.gray)
xlabel("x",fontsize=16)
ylabel("y",fontsize=16)
size = largeur/2**p
xlim(-size,size)
ylim(-size,size)

                    

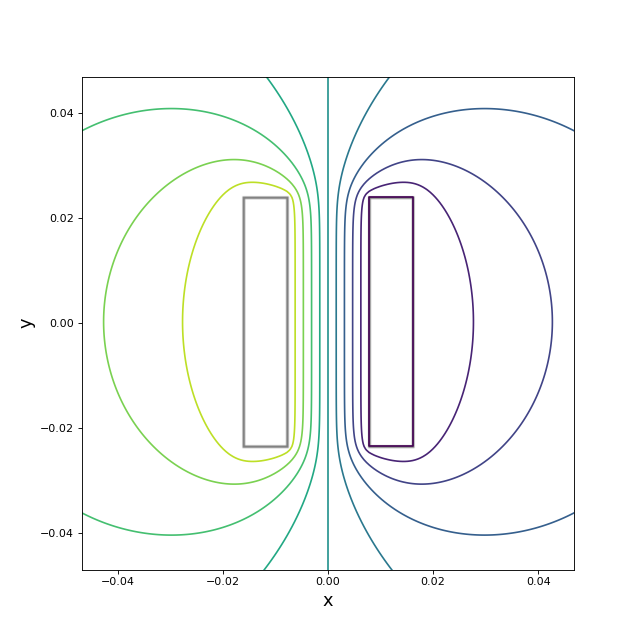fig2.pdf

Voici le champ électrique au centre des plaques (sur l'axe x) avec, pour comparaison, le champ du condensateur infini :

figure(figsize=(12,6))
plot(x,Ex[2**(n-1),:],'.')
xlabel('x',fontsize=16) 
ylabel('Ex',fontsize=16)
grid()
plot([-0.5,0.5],[Einf,Einf],"r--")
                    

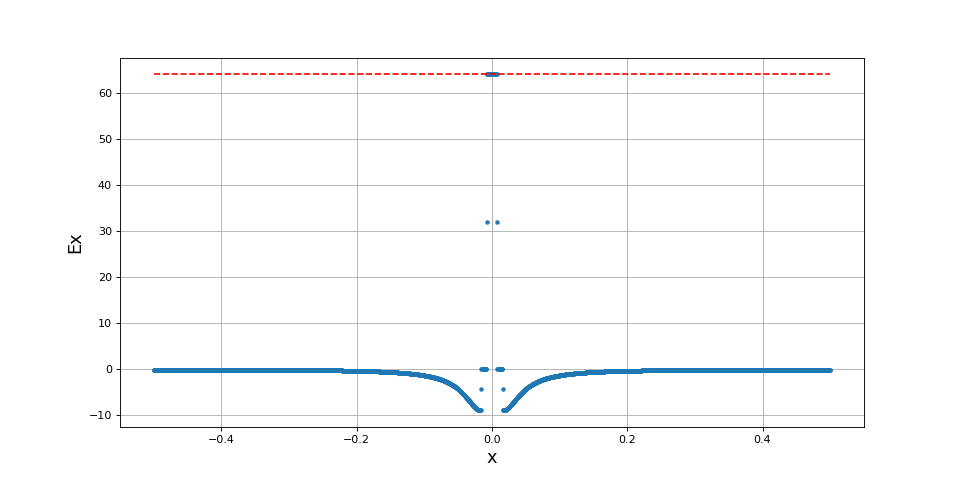fig3.pdf

Comme prévu, le champ électrique est nul dans les conducteurs. Sur la surface d'un conducteur, il y a discontinuité de E_x et sa valeur sur la surface est égale à la moyenne des valeurs des deux côtés. Pour le calcul de la densité surfacique de charge, on doit considérer le champ du côté du vide (et non pas sur la surface). Voici le tracé de ce champ pour le conducteur de potentiel -U/2, sur les faces interne et externe :

 
figure(figsize=(12,6))
Ex_faceInt = Ex[y1:y2,x1+1]
Ex_faceExt = Ex[y1:y2,x3-1]
plot(y[y1:y2],Ex_faceInt,label="face interne")
plot(y[y1:y2],Ex_faceExt,label="face externe")
legend(loc="upper right")
xlabel("y",fontsize=16)
ylabel("Ex",fontsize=16)
ylim(-100,100)
grid()                  
                      

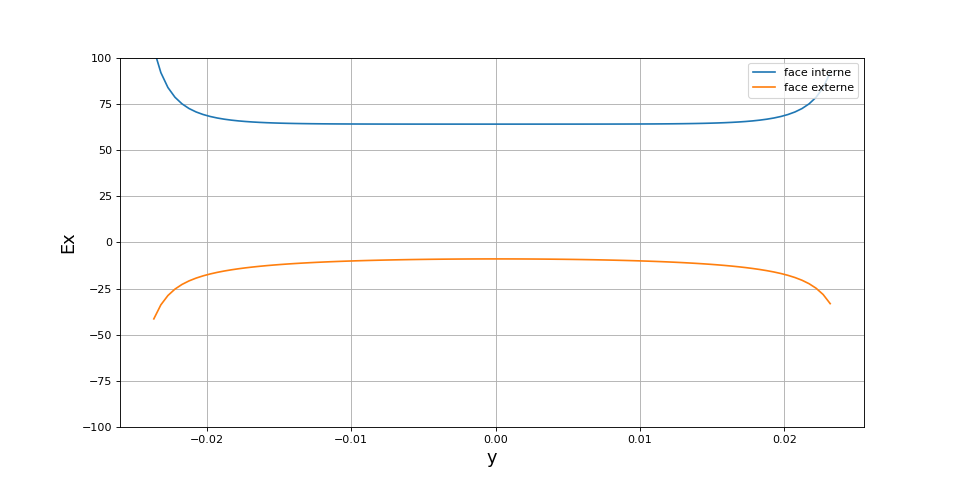fig4.pdf

Voici la composante normale du champ électrique sur les deux bords des plaques (en $y=\pm L/2$) :

figure(figsize=(12,6))
Ey_bordHaut = Ey[y2+1,x3:x1]
Ey_bordBas = Ey[y1-1,x3:x1]
plot(x[x3:x1],Ey_bordHaut,label="bord y = L/2")
plot(x[x3:x1],Ey_bordBas,label="bord y = -L/2")
xlabel("x",fontsize=16)
ylabel("Ey",fontsize=16)
legend(loc="upper right")
ylim(-100,100)
grid()                   

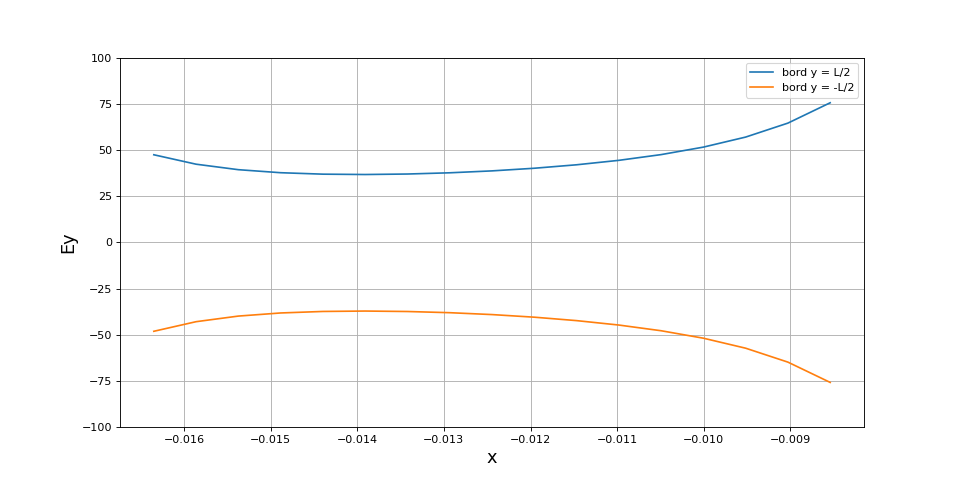fig5.pdf

La composante normale du champ sur les grandes faces augmente beaucoup à l'approche des bords, aussi bien à l'intérieur qu'à l'extérieur du condensateur, et la composante normale sur les bords de la plaque est aussi très grande. Sachant que le champ au centre est très proche du champ du condensateur infini, on peut s'attendre à une capacité nettement plus grande. Voici la valeur de la capacité divisée par celle obtenue avec le modèle du condensateur infini, autrement dit celle obtenue en négligeant les effets de bords du condensateur :

print(C)
--> np.float64(1.5141936774289444)

Pour ce condensateur, dont le rapport largeur sur distance est seulement de 3, la capacité est 1,5 fois plus grande que celle obtenue avec le modèle du condensateur plan infini.

Voici la capacité calculée au moyen de l'énergie :

print(C2)
--> np.float64(1.576146093079861)

2.c. Influence de la largeur

À distance entre les plaques fixée, on fait varier leur largeur (qui doit être paire) :

n=11
p=7
distance = 2 # distance entre les plaques
epaisseur = 1 #épaisseur des plaques
filename = "capacite-d=2-e=1-n=11-p=7.txt"
calcul = False
if calcul:
    C_list = []
    C2_list = []
    L_list = [4,6,8,10,12,14,16,18,22,24,26,30,36,40] # largeurs des plaques
    for L in L_list:
       C,C2,Einf = condensateurXY(p,n,L,distance,epaisseur,None)
       C_list.append(C)
       C2_list.append(C2)
    C = np.array(C_list)
    C2 = np.array(C2_list)
    L = np.array(L_list)
    np.savetxt(filename,np.array([L,C,C2]).T)
L,C,C2 = np.loadtxt(filename,unpack=True)
figure()
plot(L,C,"b.",label="C par Charge")
plot(L,C,"b-")
plot(L,C2,"r.",label="C par energie")
plot(L,C2,"r-")
legend(loc="upper right")
grid()
xlabel("L",fontsize=16)
ylabel(r"$C/C_{\infty}$",fontsize=16)
xlim(0,40)
ylim(0,2)
                

fig6.pdf

Le même calcul est effectué avec p et n augmenté de 1, ce qui permet de réduire la taille du condensateur par rapport à la taille du domaine :

n=12
p=8
filename = "capacite-d=2-e=1-n=12-p=8.txt"
calcul = False
if calcul:
    C_list = []
    C2_list = []
    for L in L_list:
        C,C2,Einf = condensateurXY(p,n,L,distance,epaisseur,None)
        C_list.append(C)
        C2_list.append(C2)
    C = np.array(C_list)
    C2 = np.array(C2_list)
    L = np.array(L_list)
    np.savetxt(filename,np.array([L,C,C2]).T)
L,C,C2 = np.loadtxt(filename,unpack=True)
figure()
plot(L,C,"b.",label="C par charge")
plot(L,C,"b-")
plot(L,C2,"r.",label="C par energie")
plot(L,C2,"r-")
legend(loc="upper right")
grid()
xlabel("L",fontsize=16)
ylabel(r"$C/C_{\infty}$",fontsize=16)
xlim(0,40)
ylim(0,2)
                

fig7.pdf

Les courbes sont les mêmes que précédemment, ce qui montre que l'effet des bords du domaine est négligeable.

La convergence vers la capacité du condensateur infini est très lente. Par ailleurs, la capacité calculée au moyen de l'énergie est un plus grande que celle calculée au moyen du champ électrique sur le conducteur, surtout à faible rapport longueur/distance.

3.a. Définition

Le condensateur est constitué de deux disques de rayon R, d'axe Oz, espacés d'une distance d et d'épaisseur e.

Figure pleine page

Le domaine de calcul est un rectangle de rapport 2.

Le potentiel électrostatique en coordonnées cylindriques V(z,r) obéit à l'équation de Laplace :

$$\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial V}{\partial r}\right)+\frac{{\partial }^{2}V}{\partial z^2}=0\text{(8)}$$

La charge portée par la plaque au potentiel U/2 est obtenue par l'intégrale suivante :

$$Q=2\pi {\int }_0^R(\sigma (r,-d/2)+\sigma (r,-d/2-e))rdr+2\pi R{\int }_{-d/2-e}^{-d/2}\sigma (R,z)dz\text{(9)}$$

où la seconde intégrale se fait sur le bord du disque.

3.b. Résolution par différences finies

def condensateurZR(p,n,rayon,distance,epaisseur,filename,niter=50,ncycles=20):
    levels = n-p+1
    laplace = poisson.main.PoissonAxial(p+1,p,levels,1.0,0.5,x0=-0.5,y0=0.0)
    laplace.laplacien()
    laplace.dirichlet_borders(0.0)
    zc = 2**p
    U = 1
    laplace.dirichlet_polygon(zc-distance//2,0,[0,-epaisseur,0,epaisseur],[rayon,0,-rayon,0],U/2)
    laplace.dirichlet_polygon(zc+distance//2,0,[0,epaisseur,0,-epaisseur],[rayon,0,-rayon,0],-U/2)
    # sommets du conducteur de potentiel U/2 sur le maillage fin
    z1,r1 = (zc-distance//2)*2**(n-p),0
    z2,r2 = z1,(rayon)*2**(n-p)+1
    z3,r3 = (zc-distance//2-epaisseur)*2**(n-p)-1,r2
    z4,r4 = z3,r1
    result = laplace.multigrid_full_norm(ncycles,levels,niter,2,1)
    V = laplace.get_array(symetry=True)
    Ez=-laplace.get_derivZ()
    Er=-laplace.get_derivR()
    mask = laplace.get_mask(symetry=True)
    extent = laplace.get_extent(symetry=True)
    z = laplace.get_z()
    dz = z[1]-z[0]
    r = laplace.get_r()
    dr = r[1]-r[0]
    #calcul de la capacité à partir du champ sur le conducteur
    Ez_faceInt = Ez[r1:r2,z1+1]
    Ez_faceExt = Ez[r1:r2,z3-1]
    Q = ((Ez_faceInt-Ez_faceExt)*r[r1:r2]).sum()*2*np.pi*dr
    Er_bord = Er[r2+1,z3:z1]
    Q += Er_bord.sum()*dz*2*np.pi*r[r2]
    e = distance/2**(p+1)
    R = rayon/2**(p+1)
    S = np.pi*R*R
    C = Q/S*e 
    Einf = U/(distance/2**(p+1))    
    if filename: np.savez(filename,V,Ez,Er,mask,extent,z,r,np.array([C,Einf,r1,r2,z1,z3]))
    return C,Einf
                

def readZR(filename):
    global V,Ez,Er,mask,extent,z,r,C,Einf,r1,r2,z1,z3
    npzfiles = np.load(filename)
    V = npzfiles['arr_0']
    Ez = npzfiles['arr_1']
    Er = npzfiles['arr_2']
    mask = npzfiles['arr_3']
    extent = npzfiles['arr_4']
    z = npzfiles['arr_5']
    r = npzfiles['arr_6']
    A = npzfiles['arr_7']
    C,Einf,r1,r2,z1,z3 = A[0],A[1],A[2],A[3],A[4],A[5]
    r1 = int(r1)
    r2 = int(r2)
    z1 = int(z1)
    z3 = int(z3)
                    

n = 10
p = 6
distance = 2 # distance entre les plaques
rayon = 3 # rayon des plaques
epaisseur = 1 #épaisseur des plaques
#C,Einf = condensateurZR(p,n,rayon,distance,epaisseur,"condensateurZR-d=2-r=3-e=1-n=10-p=6.npz")
readZR("condensateurZR-d=2-r=3-e=1-n=10-p=6.npz")
figure(figsize=(8,8))
contour(V,40,extent=extent)
imshow(~mask,extent=extent,alpha=0.5, cmap=cm.gray)
xlabel("z",fontsize=16)
ylabel("r",fontsize=16)
                    

fig8.pdf

figure(figsize=(8,8))
contour(V,10,extent=extent)
imshow(~mask,extent=extent,alpha=0.5, cmap=cm.gray)
xlabel("x",fontsize=16)
ylabel("y",fontsize=16)
size = 2*rayon/2**p
xlim(-size,size)
ylim(-size,size)
                    

fig9.pdf

Voici le champ électrique au centre des plaques (sur l'axe de symétrie) avec, pour comparaison, le champ du condensateur infini :

figure(figsize=(12,6))
plot(z,Ez[0,:],'.')
xlabel('z',fontsize=16) 
ylabel('Ez',fontsize=16)
grid()
plot([-0.5,0.5],[Einf,Einf],"r--")
                    

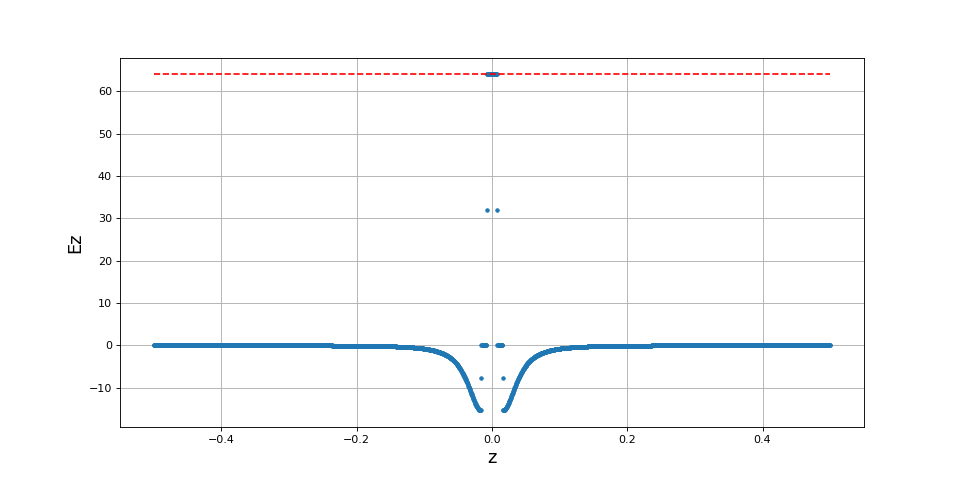fig10.pdf

Voici le tracé de la composante normale du champ sur les deux faces :

figure(figsize=(12,6))
Ez_faceInt = Ez[r1:r2,z1+1]
Ez_faceExt = Ez[r1:r2,z3-1]
plot(r[r1:r2],Ez_faceInt,label="face interne")
plot(r[r1:r2],Ez_faceExt,label="face externe")
legend(loc="upper right")
xlabel("r",fontsize=16)
ylabel("Ez",fontsize=16)
ylim(-100,100)
grid()                  
                      

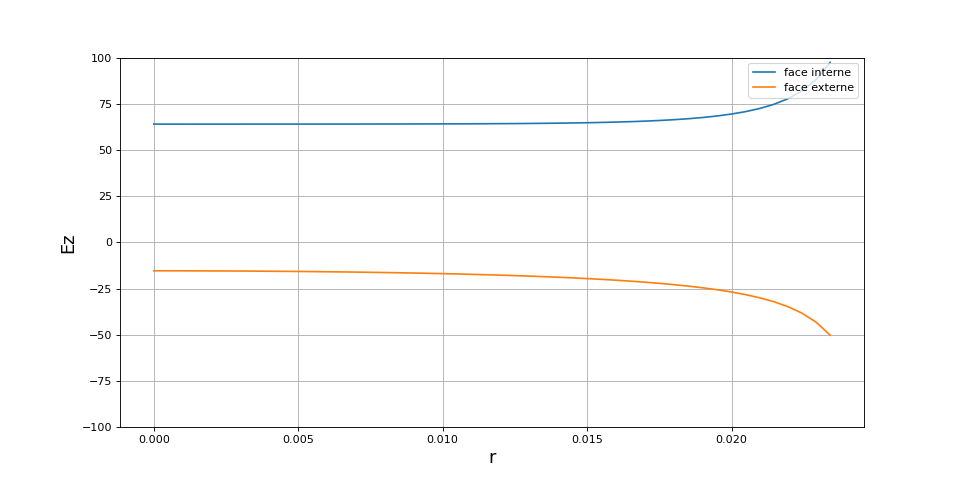fig11.pdf

et la composante normale sur le bord du disque (en r=R) :

figure(figsize=(12,6))
Er_bord = Er[r2+1,z3:z1]
plot(z[z3:z1],Er_bord,label="bord r = R")
xlabel("z",fontsize=16)
ylabel("Er",fontsize=16)
legend(loc="upper right")
ylim(-100,100)
grid()                   

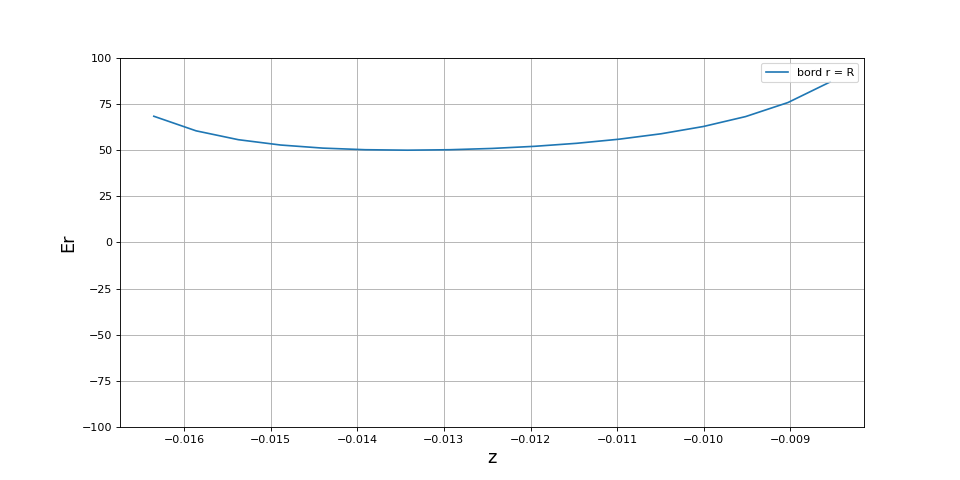fig12.pdf

Voici la capacité divisée par celle obtenue avec le modèle de condensateur infini :

print(C)
--> np.float64(2.1594513422069816)

3.c. Influence du rayon

À distance entre les plaques fixée, on fait varier leur rayon :

n=10
p=6
distance = 2 # distance entre les plaques
epaisseur = 1 #épaisseur des plaques
filename = "capaciteZR-d=2-e=1-n=10-p=6.txt"
calcul = False
if calcul:
    C_list = []
    R_list = [2,4,6,8,10,12,14,16,18,20,25,30,35,40,45,50] # rayons
    for R in R_list:
       C,Einf = condensateurZR(p,n,R,distance,epaisseur,None)
       C_list.append(C)
    C = np.array(C_list)
    R = np.array(R_list)
    np.savetxt(filename,np.array([R,C]).T)
R,C = np.loadtxt(filename,unpack=True)
figure()
plot(R,C,"b.")
grid()
xlabel("R",fontsize=16)
ylabel(r"$C/C_{\infty}$",fontsize=16)
xlim(0,50)
ylim(0,2)
                

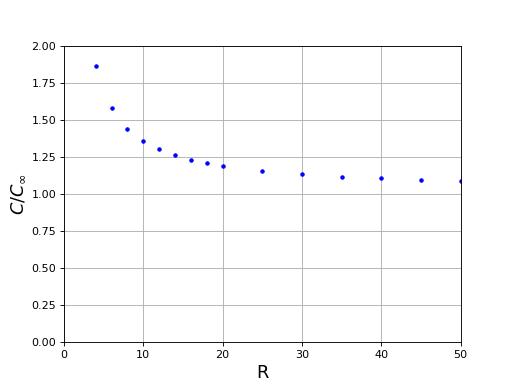fig13.pdf

n=11
p=7
distance = 2 # distance entre les plaques
epaisseur = 1 #épaisseur des plaques
filename = "capaciteZR-d=2-e=1-n=11-p=7.txt"
calcul = False
if calcul:
    C_list = []
    for R in R_list:
       C,Einf = condensateurZR(p,n,R,distance,epaisseur,None)
       C_list.append(C)
    C = np.array(C_list)
    R = np.array(R_list)
    np.savetxt(filename,np.array([R,C]).T)
R,C = np.loadtxt(filename,unpack=True)
figure()
plot(R,C,"b.")
grid()
xlabel("R",fontsize=16)
ylabel(r"$C/C_{\infty}$",fontsize=16)
xlim(0,50)
ylim(0,2)
                

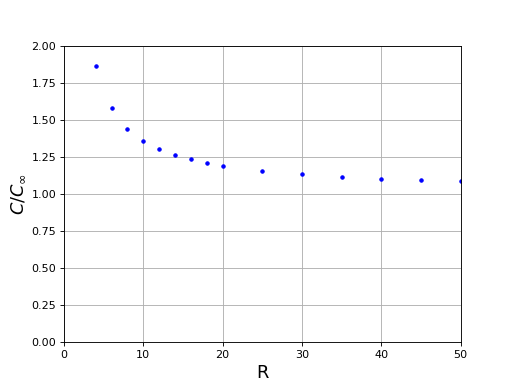fig14.pdf

La convergence vers la capacité du condensateur infini est très lente.