Racines d'un polynôme

2.a. Évaluation du polynôme et de ses dérivées

Il s'agit de calculer P(x) pour une valeur de x donnée (complexe en général) le plus efficacement possible et en minimisant les erreurs d'arrondis. L'évaluation repose sur la factorisation suivante [1]:

$$\begin{array}{cc}\hfill P\left(x\right)& =a_0+x(a_1+a_{2}x+\dots a_n{x}^{n-1})\hfill \\ \hfill & =a_0+x(a_1+x(a_2+a_{3}x+\dots a{n}_n{x}^{n-2}))\hfill \\ \hfill & =\dots \hfill \\ \hfill & =a_0+x(a_1+x(a_2+x(a_3+x\left(\dots \right))))\hfill \end{array}$$

qui conduit à l'algorithme récursif suivant :

$$\begin{array}{cc}\hfill & p\leftarrow a_n\hfill \\ \hfill & p\leftarrow a_{n-1}+px\hfill \\ \hfill & p\leftarrow a_{n-2}+px\hfill \\ \hfill & \dots \hfill \\ \hfill & p\leftarrow a_0+px\hfill \end{array}$$

import numpy as np
			

La fonction suivante effectue l'évaluation d'un polynôme dont les coefficients sont donnés dans une liste ou un tableau numpy.ndarray contenant des nombres complexes :

def evalPol(a,x):
	k=len(a)-1
	p = a[k] #a_n
	k -= 1
	while k>=0:
		p = a[k]+p*x
		k -= 1
	return p
	
			

Voici un exemple avec le polynome $P\left(x\right)=1+x+x^2$ :

a=[1+1j*0,1+1j*0,1+1j*0]
p = evalPol(a,1j)
			

print(p)
--> 1j

Considérons la dérivée du polynôme, définie par :

$$P\text{'}\left(x\right)=a_1+2a_{2}x+3a_3{x}^2+\dots n{a}_n{x}^{n-1}\text{(2)}$$

L'évalution de cette dérivée se fait de manière similaire à l'évaluation du polynôme, en multipliant chaque coefficient a_n par n :

def evalDerivPol(a,x):
	k=len(a)-1
	p = k*a[k] #(n-1)na_n
	k -= 1
	while k>=1:
		p = k*a[k]+p*x
		k -= 1
	return p
	
			

a=[1+1j*0,1+1j*0,1+1j*0]
p = evalDerivPol(a,1j)
			

print(p)
--> (1+2j)

Considérons la dérivée seconde du polynôme :

$$P\text{'}\text{'}\left(x\right)=2a_2+2\left(3\right)a_{3}x+\dots (n-1)n{a}_n{x}^{n-2}\text{(3)}$$

def evalDeriv2Pol(a,x):
	k=len(a)-1
	p = (k-1)*k*a[k] #na_n
	k -= 1
	while k>=2:
		p = (k-1)*k*a[k]+p*x
		k -= 1
	return p
	
			

a=[1+1j*0,1+1j*0,1+1j*0]
p = evalDeriv2Pol(a,1j)
			

print(p)
--> (2+0j)

a=[0+0j,0+0j,0+0j,1+0j]
p = evalDeriv2Pol(a,1)
			

print(p)
--> (6+0j)

2.b. Méthode de Laguerre

La méthode de Laguerre [1] permet d'obtenir la valeur approchée de la racine d'un polynôme la plus proche d'une valeur initiale donnée. Elle repose sur l'utilisation des dérivées première et seconde du polynôme. Notons $x_0,x_1,\dots x_{n-1}$ les n racines du polynôme puis sa factorisation :

$$P\left(x\right)=(x-x_0)(x-x_1)\dots (x-x_{n-1})\text{(4)}$$

La dérivée du polynôme (définie plus haut) peut se calculer à partir de cette expression (comme si x et les racines étaient réelles). On obtient aisément :

$$\frac{P\text{'}\left(x\right)}{P\left(x\right)}=\frac{1}{x-x_0}+\frac{1}{x-x_1}+\dots +\frac{1}{x-x_{n-1}}\text{(5)}$$

La dérivation de ce rapport conduit à :

$$(\frac{P\text{'}\left(x\right)}{P\left(x\right)}{)}^2-\frac{P\text{'}\text{'}\left(x\right)}{P\left(x\right)}=\frac{1}{{(x-x_0)}^2}+\frac{1}{{(x-x_1)}^2}+\dots +\frac{1}{{(x-x_{n-1})}^2}\text{(6)}$$

Soit x une valeur (complexe) supposée proche de la racine x₀, constituant une première estimation de cette racine. Si elle en est suffisamment proche, on peut considérer que la différence entre x est toutes les autres racines est pratiquement la même :

$$\begin{array}{ccc}\hfill & x-x_0=d\hfill & \hfill \text{(7)}\\ \hfill & x-x_k=e,k=1,2,\dots n-1\hfill & \hfill \text{(8)}\end{array}$$

D'après la relation $\mathrm{(5)}$, on a alors :

$$G\left(x\right)=\frac{P\text{'}\left(x\right)}{P\left(x\right)}=\frac{1}{d}+\frac{n-1}{e}\text{(9)}$$

et d'après la relation $\mathrm{(6)}$ :

$$H\left(x\right)=(\frac{P\text{'}\left(x\right)}{P\left(x\right)}{)}^2-\frac{P\text{'}\text{'}\left(x\right)}{P\left(x\right)}=\frac{1}{d^2}+\frac{n-1}{e^2}\text{(10)}$$

L'élimination de e de ces deux dernières équations conduit à une équation de degré 2 pour d, dont les solutions sont :

$$d=\frac{n}{G\left(x\right)\pm \sqrt{(n-1)(nH\left(x\right)-G{\left(x\right)}^2)}}\text{(11)}$$

La solution dont le module est le plus petit est retenue. La nouvelle estimation est x-d. On répète itérativement ces opérations jusqu'à obtenir une valeur de d dont le module est inférieur à une certaine tolérance. Les deux fonctions suivantes implémentent cet algorithme :

def iteration(a,x):
	n = len(a)-1
	p = evalPol(a,x)
	if p==0: return 0
	pp = evalDerivPol(a,x)
	ppp = evalDeriv2Pol(a,x)
	G = pp/p
	H = G*G-ppp/p
	sq = np.sqrt((n-1)*(n*H-G*G))
	z1 = G+sq
	z2 = G-sq
	if np.absolute(z2) > np.absolute(z1):
		z1 = z2
	d = n/z1
	return d
	
def laguerre(a,x,tol,maxiter=100):
	d = iteration(a,x)
	if d==0:
		return x
	x = x-d
	iter = 1
	while np.absolute(d)>tol:
		d = iteration(a,x)
		if d==0:
			return x
		x = x-d
		iter += 1
		if iter > maxiter:
			raise Exception("Non convergence")
	return x
	
	
				

Afin de tester cette fonction, nous écrivons une fonction qui renvoie les coefficients d'un polynôme de degré 3 dont les trois racines sont données :

def polynome(x0,x1,x2):
	return np.array([-x0*x1*x2,x0*x2+x0*x1+x1*x2,-(x0+x1+x2),1],dtype=np.complex128)
				

Voici un test. La valeur initiale de x est nulle.

x0 = 1
x1 = 2+3*1j
x2 = 2-3*1j
a = polynome(x0,x1,x2)
try:
	x = laguerre(a,0,1e-4)
except:
	print("Non convergence")
	x = 0
				

print(x)
--> np.complex128(1.0000000000000036+0j)

On obtient la racine la plus proche de la valeur initiale (nulle).

2.c. Factorisation

Une fois la racine x₀ obtenue (la plus proche de 0 si la valeur d'essai initiale est nulle), on factorise le polynome :

$$P\left(x\right)=(x-x_0)(b_0+b_{1}x+b_2{x}^2+\dots b_{n-1}{x}^{n-1})=(x-x_0)Q\left(x\right)\text{(12)}$$

puis on cherche la racine la plus proche de zéro de Q(x). On procède ainsi itérativement jusqu'à l'obtention des n racines.

Le développement de la forme factorisée permet d'obtenir :

$$\begin{array}{cc}\hfill & a_n=b_{n-1}\hfill \\ \hfill & a_{n-1}=b_{n-2}-x_0{b}_{n-1}\hfill \\ \hfill & a_{n-2}=b_{n-3}-x_0{b}_{n-2}\hfill \\ \hfill & \dots \hfill \\ \hfill & a_2=b_1-x_0{b}_2\hfill \\ \hfill & a_1=b_0-x_0{b}_1\hfill \\ \hfill & a_0=-x_0{b}_0\hfill \end{array}$$

On peut donc calculer les coefficients du polynôme Q de la manière suivante :

$$\begin{array}{cc}\hfill & b_{n-1}=a_n\hfill \\ \hfill & b_{n-2}=a_{n-1}+x_0{b}_{n-1}\hfill \\ \hfill & b_{n-3}=a_{n-2}+x_0{b}_{n-2}\hfill \\ \hfill & \dots \hfill \\ \hfill & b_1=a_2+x_0{b}_2\hfill \\ \hfill & b_0=a_1+x_0{b}_1\hfill \end{array}$$

La fonction suivante effectue la factorisation :

def factorisation(a,x0):
	n = len(a)-1
	b = np.zeros(n,dtype=np.complex128)
	k = n-1
	b[k] = a[k+1]
	k -= 1
	while k>=0:
		b[k] = a[k+1]+x0*b[k+1]
		k -= 1
	return b
				 

La fonction suivante détermine les n racines d'un polynôme :

def racines(a,tol=1e-4):
	n = len(a)-1
	r = []
	for k in range(n-1):
		x = laguerre(a,0,tol)
		r.append(x)
		a = factorisation(a,x)
	r.append(-a[0]/a[1]) # racine d'une polynome de degré 1
	return r
				 

Voici un test :

x0 = 1
x1 = 2+3*1j
x2 = 2-3*1j
a = polynome(x0,x1,x2)
r = racines(a)
				 

print(r[0])
--> np.complex128(1.0000000000000036+0j)

print(r[1])
--> np.complex128(1.9999999999999982+2.999999999999999j)

print(r[2])
--> np.complex128(1.9999999999999982-2.999999999999999j)

En raison des erreurs d'arrondis qui apparaissent lors de la factorisation, [1] recommande de considérer ces premières évaluations des racines et d'appliquer la méthode de Laguerre pour chacune d'elle sur le polynôme de départ afin d'affiner la précision :

def racines2(a,tol=1e-4):
	r = racines(a,tol)
	rac = []
	for x in r:
		x = laguerre(a,x,tol)
		rac.append(x)
	return rac
				  

Voici un test :

x0 = 1
x1 = 2+3*1j
x2 = 2-3*1j
a = polynome(x0,x1,x2)
r = racines2(a)
				 

print(r[0])
--> np.complex128(1+0j)

print(r[1])
--> np.complex128(1.9999999999999998+3j)

print(r[2])
--> np.complex128(1.9999999999999998-3j)

voici un autre exemple :

x0 = -3
x1 = 1+1j
x2 = 1-1j
a = polynome(x0,x1,x2)
r = racines2(a,tol=1e-6)
				 

print(r[0])
--> np.complex128(1+1j)

print(r[1])
--> np.complex128(1-1j)

print(r[2])
--> np.complex128(-3+0j)

Voici un exemple avec des racines multiples :

x0 = 1
x1 = 1
x2 = 2
a = polynome(x0,x1,x2)
r = racines2(a,tol=1e-6)
				 

print(r)
--> [np.complex128(0.9999999755927836+0j), np.complex128(1.0000000294952005+0j), np.complex128(2+0j)]

Voici un exemple avec un polynôme à coefficients complexes :

x0 = -3
x1 = 1+1j
x2 = 1+2j
a = polynome(x0,x1,x2)
r = racines2(a,tol=1e-6)
				 

print(a)
--> array([-3.+9.j, -7.-6.j,  1.-3.j,  1.+0.j])

print(r[0])
--> np.complex128(0.9999999999999998+1.0000000000000002j)

print(r[1])
--> np.complex128(1.0000000000000002+1.9999999999999998j)

print(r[2])
--> np.complex128(-3+0j)

3.a. Réponse indicielle d'un système linéaire

On considère un système linéaire dont la fonction de transfert s'écrit :

$$H\left(p\right)=\frac{b_0+b_{1}p+b_2{p}^2+\dots b_m{p}^m}{a_0+a_{1}p+a_2{p}^2+\dots a_n{p}^n}\text{(13)}$$

La réponse fréquence du système s'obtient en posant $p=j\omega$.

Si e(t) et s(t) sont respectivement l'entrée et la sortie du système, l'équation différentielle s'écrit :

$$a_{0}s+a_1\frac{ds}{dt}+a_2\frac{d^{2}s}{d{t}^2}+\dots a_n\frac{d^{n}s}{d{t}^2}=b_{0}e+b_1\frac{de}{dt}+b_2\frac{d^{2}e}{d{t}^2}+\dots a_m\frac{d^{m}e}{d{t}^m}\text{(14)}$$

La réponse indicielle est la fonction s(t) lorsque e(t) est un échelon, défini par :

$$\begin{array}{cc}\hfill & e\left(t\right)=0pourt<0\hfill \\ \hfill & e\left(t\right)=Epourt\ge 0\hfill \end{array}$$

L'équation différentielle vérifiée par la sortie pour $t\ge 0$ est donc :

$$a_{0}s+a_1\frac{ds}{dt}+a_2\frac{d^{2}s}{d{t}^2}+\dots a_n\frac{d^{n}s}{d{t}^2}=b_{0}E\text{(15)}$$

La condition initiale en t=0 pour s(t) correspond au régime permanent pour e=0, c'est-à-dire s(0)=0. L'équation différentielle nécessite n conditions initiales. Les conditions initiales sur les dérivées de s(t) d'ordre 1 à n-1 dépendent de propriétés du système qui n'apparaissent pas dans sa fonction de transfert. On considère ici que ces dérivées sont toutes nulles à l'instant t=0, mais la méthode pourra s'appliquer sans difficulté à des conditions initiales différentes.

Si l'on note $p_1,p_2\dots p_n$ les pôles de la fonction de transfert, c'est-à-dire les racines de son dénominateur, la réponse indicielle s'écrit, dans le cas où il n'y a aucun pôle multiple [2] :

$$s\left(t\right)=\frac{b_{0}E}{a_0}+K_1{e}^{p_{1}t}+K_2{e}^{p_{2}t}+\dots K_n{e}^{p_{n}t}\text{(16)}$$

Le système est stable si s(t) tend vers $\frac{b_{0}E}{a_0}$ lorsque $t\to \infty$, c'est-à-dire lorsque les pôles ont tous une partie réelle strictement négative.

Les conditions initiales permettent d'écrire le système linéaire pour les constantes $K_1,K_2,\dots K_n$ :

$$\begin{array}{cc}\hfill & K_1+K_2+\dots K_n=-\frac{b_{0}E}{a_0}\hfill \\ \hfill & p_1{K}_1+p_2{K}_2+\dots p_n{K}_n=0\hfill \\ \hfill & p_1^2{K}_1+p_2^2{K}_2+\dots p_n^2{K}_n=0\hfill \\ \hfill & \dots \hfill \\ \hfill & p_1^{n-1}{K}_1+p_2^{n-1}{K}_2+\dots p_n^{n-1}{K}_n=0\hfill \end{array}$$

Lorsque le système est stable, on s'intéresse à la forme de la réponse indicielle, en particulier à la présence d'un dépassement ou d'oscillations amorties. La valeur de $\frac{b_{0}E}{a_0}$ est sans importance et on la prendra donc égale à 1.

from numpy.linalg import solve

def reponseIndicielle(a,t,tol=1e-3):
	r = racines2(a,tol)
	n = len(r)
	A = np.zeros((n,n),dtype=np.complex128)
	for j in range(n):
		for i in range(n):
			A[i][j] = r[j]**i
	B = np.zeros(n)
	B[0] = -1
	K = solve(A,B)
	s = 1
	for i in range(n):
		s += K[i]*np.exp(r[i]*t)
	return np.real(s)
					 

Pour tester cette fonction, considérons l'exemple classique du système d'ordre 2 stable suivant :

$$H\left(p\right)=\frac{1}{1+2mTp+T^2{p}^2}\text{(17)}$$

Le discriminant du dénominateur est $\Delta =4T^2(m^2-1)$. Si m>1, la réponse est de type amortie sans dépassement. Si m<1, la réponse est pseudo-périodique amortie. La cas m=1 correspond au régime critique et nécessite un traitement spécial puisque dans ce cas il y un pôle double.

from matplotlib.pyplot import *
T = 1
t = np.linspace(0,20*T,1000)
figure()
for m in [0.5,0.8,0.99,2]:
	a=np.array([1,2*m*T,T**2],dtype=np.complex128)
	s = reponseIndicielle(a,t)
	plot(t,s,label="m=%0.2f"%m)
grid()
legend(loc="lower right")
xlabel("t/T")
ylabel("s")

					  

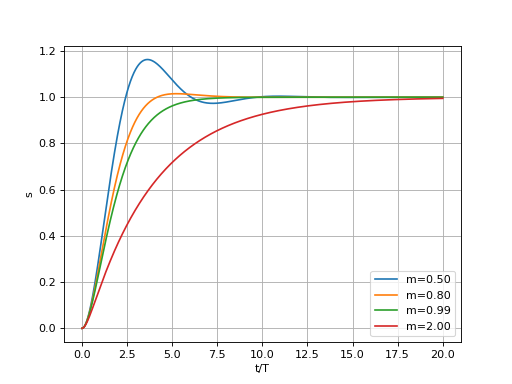fig1.pdf

Lorsque m=1 il y a une racine double :

m=1
a=np.array([1,2*m*T,T**2],dtype=np.complex128)
r = racines(a,1e-6)
					  

print(r)
--> [np.complex128(-1+0j), np.complex128(-1+0j)]

Dans cet exemple, il y a effectivement deux racines égales. Lorsque deux racines en théorie égales ne le sont pas à cause des erreurs d'arrondis, l'expression $\mathrm{(16)}$ reste valable. Pour traiter le cas où des racines doubles seraient effectivement obtenues par la méthode de Laguerre, nous devons tout d'abord repérer les racines multiples dans la liste des racines. La fonction suivante permet d'obtenir les racines distinctes et leur multiplicité :

def racinesMultiples(r):
	n = len(r)
	rac = []
	mul =[]
	for i in range(n):
		if r[i] in rac:
			j = rac.index(r[i])
			mul[j] += 1
		else:
			rac.append(r[i])
			mul.append(1)
	return rac,mul
			
						

rac,mul = racinesMultiples(r)
						

print(rac)
--> [np.complex128(-1+0j)]

print(mul)
--> [2]

Soit q le nombre de pôles distincts et $p_1,p_2,\dots p_q$ ces pôles. Pour un pôle $p_k$ de multiplicité $m_k$, les m solutions linéairement indépendantes qu'il faut considérer sont [2]:

$$e^{p_{k}t},t{e}^{p_{k}t},\dots t^{m-1}{e}^{p_{k}t}\text{(18)}$$

Supposons par exemple que le pôle $p_1$ soit double et tous les autres simples. La réponse impulsionnelle s'écrit :

$$s\left(t\right)=\frac{b_{0}E}{a_0}+K_1{e}^{p_{1}t}+K_{2}t{e}^{p_{2}t}+K_3{e}^{p_{3}t}\dots K_n{e}^{p_{n}t}\text{(19)}$$

avec $p_1=p_2$. On suppose que les n pôles sont regroupés par pôles égaux (les pôles égaux sont d'indices successifs).

La dérivée s'écrit :

$$\frac{ds\left(t\right)}{dt}=K_1{p}_1{e}^{p_{1}t}+K_2{e}^{p_{2}t}+K_{2}t{p}_2{e}^{p_{2}t}+K_3{e}^{p_{3}t}\dots K_n{e}^{p_{n}t}\text{(20)}$$

et la dérivée seconde :

$$\frac{d^{2}s\left(t\right)}{d{t}^2}=K_1{p}_1^2{e}^{p_{1}t}+2K_2{p}_2{e}^{p_{2}t}+K_{2}t{p}_2^2{e}^{p_{2}t}+K_3{e}^{p_{3}t}\dots K_n{e}^{p_{n}t}\text{(21)}$$

Le système linéaire vérifié par les constantes est :

$$\begin{array}{cc}\hfill & K_1+K_3+\dots K_n=-\frac{b_{0}E}{a_0}\hfill \\ \hfill & p_1{K}_1+K_2+p_2{K}_3\dots p_n{K}_n=0\hfill \\ \hfill & p_1^2{K}_1+2p_2^2{K}_2+p_3^2{K}_1+\dots p_n^2{K}_n=0\hfill \\ \hfill & p_1^3{K}_1+3p_2^2{K}_2+p_3^3{K}_3+\dots p_n^3{K}_n=0\hfill \\ \hfill & \dots \hfill \\ \hfill & p_1^{n-1}{K}_1+(n-1)p_2^{n-2}{K}_2+p_3^{n-1}{K}_3+\dots p_n^{n-1}{K}_n=0\hfill \end{array}$$

Pour que l'algorithme soit général, il faudrait traiter le cas général d'un pôle de multiplicité m, ce qui complique notablement la détermination du système linéaire pour les constantes.

Une autre approche, beaucoup plus simple à mettre en œuvre, consiste à supposer que si des pôles sont égaux, il suffit de les rendre très légèrement différents pour se ramener au cas de pôles tous distincts. Nous admettons que la solution s(t) évolue continûment lorsqu'on fait varier continûment la valeur d'un pôle (à confirmer). La fonction suivante calcule la réponse impulsionnelle avec cette méthode. Le paramètre eps, multiplié par le module de la racine, définit l'incrément ajouté à chaque racine multiple pour la différentier de la précédente.

def reponseIndicielleBis(a,t,tol=1e-3,eps=1e-8):
	r = racines2(a,tol)
	rac,mul = racinesMultiples(r)
	r = []
	for i in range(len(rac)):
		rho = np.absolute(rac[i])
		for k in range(mul[i]):
			r.append(rac[i]+k*eps*rho)
	n = len(r)
	A = np.zeros((n,n),dtype=np.complex128)
	for j in range(n):
		for i in range(n):
			A[i][j] = r[j]**i
	B = np.zeros(n)
	B[0] = -1
	K = solve(A,B)
	s = 1
	for i in range(n):
		s += K[i]*np.exp(r[i]*t)
	return np.real(s)
					

T = 1
t = np.linspace(0,20*T,1000)
figure()
for m in [0.5,0.8,1,2]:
	a=np.array([1,2*m*T,T**2],dtype=np.complex128)
	s = reponseIndicielleBis(a,t,eps=1e-3)
	plot(t,s,label="m=%0.2f"%m)
grid()
legend(loc="lower right")
xlabel("t/T")
ylabel("s")

					  

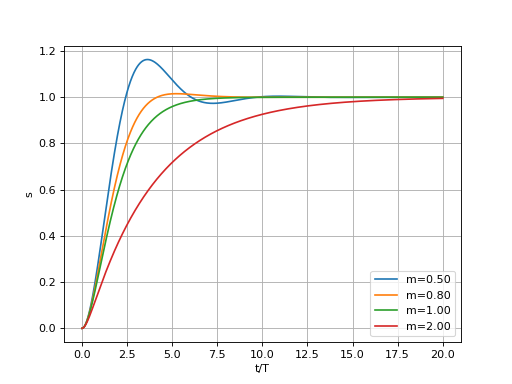fig2.pdf

Voici un exemple avec un pôle de multiplicité 3 :

x0 = -1+1j
x1 = -1+1j
x2 = -1+1j
a = polynome(x0,x1,x2)
r = racines2(a)
					  

print(r)
--> [np.complex128(-1+1j), np.complex128(-1+1j), np.complex128(-1+1j)]

Les pôles déterminés numériquement sont bien égaux. Voici la réponse impulsionnelle :

figure()
t = np.linspace(0,10,1000)
s = reponseIndicielleBis(a,t,eps=1e-3)
plot(t,s)
grid()
xlabel("t")
ylabel("s")
					  

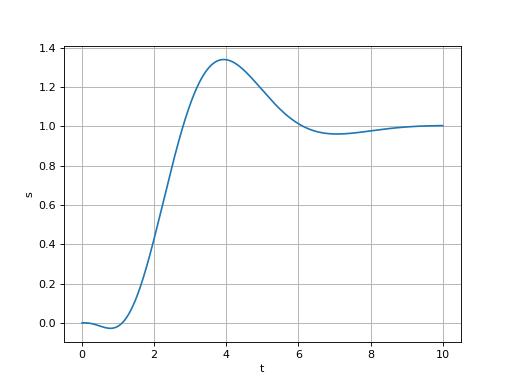fig3.pdf

Cette méthode semple bien fonctionner mais il faut éviter de choisir une valeur de eps trop petite :

figure()
t = np.linspace(0,10,1000)
s = reponseIndicielleBis(a,t,eps=1e-8)
plot(t,s)
grid()
xlabel("t")
ylabel("s")
					  

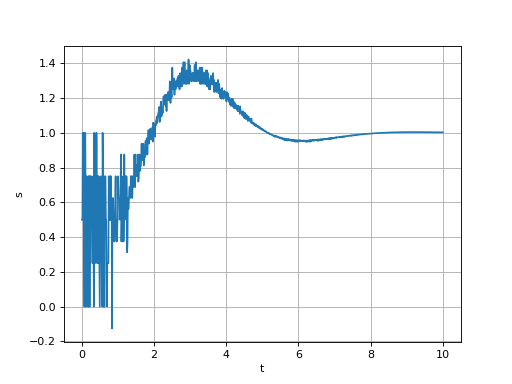fig4.pdf

La simulation Fonction de transfert utilise l'algorithme présenté ici pour tracer la réponse indicielle d'une fonction de transfert jusqu'à l'ordre 4.