Magnétostatique
1. Courant électrique
1.a. Flux de charge et densité de courant à une dimension
Dans un milieu conducteur, les particules chargées se déplacent sous l'effet d'un champ électromoteur. Lorsque le conducteur est immobile, le champ électromoteur est un champ électrique. Ce déplacement des charges constitue le courant électrique. Les métaux sont des conducteurs électroniques : les charges mobiles sont exclusivement les électrons libres, qui ne sont pas liés aux noyaux atomiques. Dans un électrolyte (solution contenant des ions), le courant électrique vient du déplacement des ions; on parle alors de conducteur ionique. Dans ce cas, il y déplacement des cations et des anions en sens opposé, avec des vitesses généralement différentes. Le résultat est un courant de charges positives dans le sens de déplacement des cations.
Pour décrire quantitativement le courant électrique, on introduit la notion de flux de charge.
Considérons pour cela un modèle simplifié, où les charges se déplacent dans une seule direction, donnée par un axe Ox. On suppose de plus qu'il n'y a que deux types de porteurs de charge, un type positif et un type négatif. Les conducteurs électroniques sont un cas particulier où la vitesse des porteurs positifs est nulle. On se place à l'échelle mésoscopique, et on considère une surface d'aire S traversée perpendiculairement par les particules. La surface est orientée, c'est-à-dire qu'un sens arbitraire est attribué à son vecteur normal. Sur la figure ci-dessous, la normale est orientée dans le sens de déplacement des charges positives, mais l'inverse est possible.
Figure pleine pageOn note q+ la charge des porteurs positifs et V+ leur vitesse moyenne. On se place à une échelle de temps à laquelle les fluctuations de vitesse causées par l'agitation thermique sont moyennées. On ne voit donc que la vitesse moyenne, causée par la présence d'un champ électrique. Soit n+ la densité de ces porteurs, c'est-à-dire leur nombre par unité de volume. On rappelle qu'il faut se placer à l'échelle mésoscopique pour définir cette densité. La densité volumique de charge est :
Le milieu conducteur est souvent neutre à l'échelle mésoscopique, c'est-à-dire que la densité est nulle ρ=0 (à l'exception de certains points du circuit, comme les conducteurs des condensateurs). Considérons un intervalle de temps Δt et comptons les charges positives qui traversent la surface pendant cette durée. Le volume cylindrique représenté sur la figure contient les particules positives qui franchissent la surface pendant cette durée. Leur nombre est donc :
Par définition, le flux de charge est la quantité de charge qui traverse la surface dans le sens de sa normale par unité de temps. Le flux de charge est aussi appelé intensité du courant électrique.
Le flux de charge est égal au flux de particules multiplié par la charge des particules. Pour les particules positives, le flux de charge est :
Pour les charges négatives, le flux est :
où V- désigne la norme de la vitesse (positive). On voit donc que le flux de charge des porteurs négatifs est de même signe que celui des porteurs positifs. Pour le cas représenté sur la figure, ce flux est positif. On peut aussi introduire la composante algébrique des vitesses sur l'axe Ox. On obtient alors le flux total de charge à travers la surface orientée, ou intensité du courant :
Il est important de voir que les deux contributions vont toujours dans le même sens, car les porteurs de charges opposées se déplacent en sens inverse.
Par définition, la densité de courant volumique j est l'intensité de courant par unité de surface.
On a donc dans ce modèle simplifié une densité de courant :
La notion de courant électrique a été introduite par Ampère (mathématicien et physicien français 1775-1836). C'est pourquoi son nom a été donné à l'unité de l'intensité du courant électrique. Il s'agit d'une des 7 unités fondamentales du système international d'unités. La densité de courant est donc en A/m2.
Pour une approche statistique du flux de particules à travers une surface mésoscopique, voir cette simulation, qui permet de faire varier la densité des particules et un intervalle de temps de moyennage temporel.
1.b. Vecteur densité de courant
Dans le cas général, le déplacement des charges en un point du conducteur (à l'échelle mésoscopique) a une direction et un sens quelconques. On définit alors un vecteur densité de courant volumique, noté , dont la direction et le sens correspond localement à la direction et au sens de déplacement des charges positives (opposé à celui des charges négatives).
À l'échelle macroscopique, la densité de courant volumique constitue un champ vectoriel. Par exemple en coordonnées cartésiennes :
Les lignes de courant sont les courbes où le vecteur densité de courant est en tout point tangent. Ces lignes sont orientées dans le sens du courant, c'est-à-dire dans le sens de déplacement des charges positives, opposé au sens de déplacement des charges négatives. La figure suivante représente un exemple de lignes de courant. Une surface élémentaire dS orientée est aussi représentée. Il s'agit en fait d'une surface d'échelle mésoscopique, très petite d'un point de vue macroscopique.
Figure pleine pagePour écrire le flux de charge à travers la surface orientée dS, on remarque qu'elle n'est pas en général perpendiculaire à la ligne de courant. Le flux est en fait proportionnel au cosinus de l'angle entre le vecteur normal et le vecteur densité de courant (on l'admet). Le flux de charge à travers la surface élémentaire s'écrit donc :
où dS désigne l'aire de la surface. On voit ainsi que le flux est nul lorsque la normale est perpendiculaire à la ligne de courant.
Pour une surface finie S quelconque, le flux s'obtient en sommant les flux élémentaires, c'est-à-dire en calculant une intégrale de surface.
Le flux de charge, ou intensité du courant électrique, à travers une surface S orientée, est égal au flux de la densité de courant à travers cette surface :
Il faut bien noter que l'orientation de la surface, c'est-à-dire le choix du sens de sa normale, est indépendante du sens du courant électrique. En revanche, le sens du vecteur densité de courant a une signification physique directe, puisqu'il correspond au sens du déplacement des charges positives. Si la surface est orientée dans le sens contraire au courant, alors l'intensité est négative.
En reprenant le modèle constitué de deux porteurs de charges, la densité de courant s'exprime en fonction des vitesses moyennes par :
1.c. Loi d'Ohm dans un conducteur immobile
Lorsque le conducteur est immobile, le champ électromoteur est le champ électrique. Dans un conducteur ohmique (métal, électrolyte, semi-conducteur), la densité de courant est proportionnelle au champ électrique.
La loi d'Ohm locale exprime la proportionnalité entre la densité de courant et le champ électrique :
γ est la conductivité électrique du matériau. Elle est positive, car les charges positives se déplacent dans le sens du champ électrique.
Le tableau suivant donne quelques conductivités à 25 degrés celcius.
| Materiau | γ (S/m) |
| Argent | 6.8e+07 |
| Cuivre | 5.8e+07 |
| Or | 4.2e+07 |
| Aluminium | 3.8e+07 |
| Fer | 1e+07 |
| Platine | 9.4e+06 |
| Graphite | 100000 |
| Germanium | 1 |
| Silicium | 0.0004 |
| Verre | 1e-13 |
La loi d'Ohm est une loi phénoménologique, déduites d'expériences effectuées à l'échelle macroscopique. Son explication à l'échelle microscopique est un sujet complexe. Pour la conduction dans les métaux, elle relève de la mécanique quantique. Pour la conduction dans les électrolytes, elle fait intervenir la théorie cinétique. On peut néanmoins en donner une explication simplifiée, avec le modèle mécanique suivant.
Un porteur de charge est soumis à une force électrique et à une force de frottement de la part du milieu, que l'on peut supposer proportionnelle à la vitesse. L'équation du mouvement de la particule s'écrit donc :
Il faut remarquer que la vitesse moyenne de la particule figure dans cette expression, alors que la loi de Newton s'applique en principe à la vitesse instantanée. En régime stationnaire, l'accélération est nulle et donc :
Ce modèle permet donc d'obtenir une vitesse proportionnelle au champ électrique. Le coefficient μ+ est la mobilité de l'ion. Dans un électrolyte, les différents ions ont des mobilités différentes. La mobilité d'un ion dépend en général de la présence d'autres ions dans son voisinage. Cependant, dans une solution très diluée, il est possible d'attribuer à chaque ion une mobilité propre, indépendante des autres ions. On obtient l'expression suivante de la conductivité :
La mobilité et la charge sont de même signe donc la conductivité est bien positive.
Le tableau suivant donne quelques valeurs de mobilité (en valeur absolue) pour des ions en solution aqueuse (10-4 cm2/s/V) :
1.d. Courant uniforme dans un conducteur cylindrique
Comme exemple simple de courant électrique, on considère le courant dans un conducteur cylindrique. On suppose que la densité de courant est uniforme sur toute la section du conducteur. C'est effectivement le cas lorsque le courant est constant (courant continu).
Figure pleine pageOn fixe arbitrairement un sens à l'axe du conducteur, ce qui permet d'orienter la section droite d'aire S. Comme la densité de courant est uniforme, on a :
La circulation du champ électrique sur le segment AB de longueur L donne :
On obtient alors la différence de potentiel en fonction de l'intensité :
La résistance d'un conducteur cylindrique parcouru par un courant uniforme est donc :
1.e. Courant stationnaire dans un circuit
Lorsque le rayon du cylindre est très faible à l'échelle macroscopique, on simplifie la modélisation en introduisant la notion de courant filiforme. Il s'agit d'un courant circulant dans une courbe. Puisque la densité de courant ne peut être définie dans ce cas (elle serait infinie), on donne simplement l'intensité du courant dans le sens choisi pour orienter le fil. En général, le fil est une courbe dans l'espace. En régime quasi stationnaire, l'intensité du courant est la même en tout point du fil. Pour qu'un courant circule, il faut former un circuit fermé comportant une force électromotrice (inductive ou chimique).
Figure pleine pageL'orientation du fil, utilisée pour définir l'intensité, est choisie arbitrairement. Elle est indépendante du sens réel du courant, qui par ailleurs peut être variable.
2. Champ magnétostatique
2.a. Force magnétique
Ampère a étudié (vers 1820) les forces entre conducteurs parcourus par des courants électriques. Il en a déduit une formule permettant de calculer la force entre deux éléments de courant (deux parties élémentaires de deux fils). Un exemple d'expérience réalisée par Ampère est l'étude de la force exercée entre deux tiges rectilignes parcourues par des courants. Si les deux courants sont de même sens, les tiges s'attirent.
On adopte aujourd'hui une approche différente, en utilisant la notion de champ magnétique. On considère qu'un circuit parcouru par un courant électrique génère dans l'espace environnant un champ magnétique . L'action de ce champ sur un élément de courant est donnée par la force de Laplace :
Plus fondamentalement, la force magnétique exercée sur une particule de charge q en mouvement dans un référentiel est :
On remarque que le champ magnétique dépend du référentiel utilisé (le champ électrique aussi). La force magnétique est perpendiculaire au déplacement des charges et au champ magnétique. On sait que le sens d'un produit vectoriel dépend d'une convention, la convention du trièdre direct. Or le sens de la force ne peut dépendre d'une telle convention, car elle a une signification physique évidente : c'est le sens de déplacement d'une particule initialement au repos. On en déduit la propriété importante suivante.
Le sens du champ magnétique dépend de la convention du trièdre direct.
Une grandeur physique ayant cette propriété est une grandeur axiale. Une grandeur indépendante de la convention du trièdre direct est une grandeur polaire. Le tableau suivant montre quelques exemples de grandeurs polaires et axiales.
D'une manière générale, le produit vectoriel de deux vecteurs polaires est un vecteur axial.
2.b. Théorème d'Ampère
Le calcul du champ magnétique à partir des courants électriques repose sur le théorème d'Ampère (en régime quasi stationnaire). Ce théorème n'a pas été établi par Ampère mais par Maxwell (physicien écossais, 1831-1879), qui est à l'origine des lois de l'électromagnétisme utilisées aujourd'hui. Néanmoins, Maxwell s'est appuyé sur les travaux d'Ampère, c'est pourquoi son nom a été attribué au théorème.
Il s'agit à l'origine d'un théorème car il peut être démontré à partir des lois de forces entre circuits (lois établies par Ampère) mais dans ce cours il apparaît plutôt comme un principe fondamental.
Le théorème d'Ampère s'applique à un champ magnétique généré par des courants électriques stationnaires (ou quasi stationnaires), que l'on nomme champ magnétostatique. Un champ magnétostatique dépend en général des variables d'espace mais pas du temps.
Le théorème s'énonce pour une courbe fermée orientée, sur laquelle on exprime la circulation du champ magnétostatique :
La figure suivante montre trois exemples de courbes fermées orientées. Deux de ces courbes encerclent un fil parcouru par un courant.
Figure pleine pageContrairement au champ électrostatique, le champ magnétostatique a une circulation non nulle en général sur une courbe fermée. La circulation est nulle pour la courbe C1 mais pas pour les courbes C2 et C3. La circulation est non nulle lorsque le circuit fermé enlace du courant électrique.
Théorème d'Ampère : la circulation du champ magnétostatique sur une courbe fermée est égale à l'intensité du courant enlacé par la courbe multipliée par la perméabilité magnétique du vide :
Le signe de la circulation dépend de l'orientation de la courbe. Il faut donc aussi définir dans quel sens le courant enlacé est défini. Cela se fait en suivant une règle qui découle de la convention du trièdre direct, comme le montre la figure suivante.
Figure pleine pagePour les trois courbes fermées de l'exemple précédent, on a donc :
Lorsqu'on change la convention du trièdre direct (ce que l'on ne fait jamais en pratique), le signe du courant enlacé change, ce qui est bien en accord avec le fait que le sens du champ magnétostatique change.
La constante μ0 est la perméabilité magnétique du vide (le milieu entourant les conducteurs est le vide). Il s'agit d'une constante fondamentale dont la valeur est fixée par convention à :
La raison de cette convention sera donnée plus loin.
Lorsque plusieurs fils sont enlacés par la courbe fermée, il faut bien sûr considérer la somme des intensités des courants enlacés. Une autre manière de formuler le théorème d'Ampère, plus générale, consiste à utiliser une surface S délimitée par la courbe fermée. Il s'agit d'une surface ouverte dont le bord est la courbe C. Par exemple, la surface délimitée par un cercle peut être un disque, un hémisphère, ou toute autre surface dont le bord est ce cercle. La normale de cette surface doit être orientée en utilisant la convention du trièdre direct, comme indiqué sur la figure ci-dessus (de la même manière que le courant enlacé). On arrive ainsi à l'expression suivante du théorème d'Ampère, qui fait appel à l'intensité du courant enlacé écrite sous forme de flux de la densité de courant :
Il est important de bien utiliser une surface ouverte, car le flux de la densité de courant à travers une surface fermée est toujours nul (nous démontrerons cela plus loin). Cette formulation du théorème d'Ampère suppose que le flux de la densité de courant ne dépend que de la courbe C et pas de la surface S délimitée par cette courbe. C'est effectivement le cas lorsqu'on se place en régime quasi stationnaire.
2.c. Principe de superposition
Soit un champ B1 créé par un circuit parcouru par un courant I1. Soit un champ B2 créé par un circuit (éventuellement le même) de courant I2. Le théorème d'Ampère appliqué pour chaque champ à une courbe fermée conduit à
Comme cela doit être vrai pour toute courbe fermée, on en déduit que le champ créé par la superposition des deux courants est égal à la somme des deux champs. Une conséquence de cette propriété est que le champ dépend linéairement de l'intensité du courant. Quel que soit la configuration des fils, doubler l'intensité du courant a pour effet de doubler le champ magnétostatique.
2.d. Conservation du flux magnétique
Une autre propriéré fondamentale du champ magnétique est la suivante.
Le flux du champ magnétique à travers une surface fermée est nul :
Alors que le théorème d'Ampère n'est valable qu'en régime stationnaire (ou approximativement en régime quasi stationnaire) la conservation du flux est toujours vérifiée.
Une conséquence de cette loi est la possibilité de définir le flux magnétique pour une courbe fermée. Considérons une courbe fermée orientée C (qui peut coïncider avec un fil conducteur) et deux surfaces S1 et S2 délimitées par cette courbe. Les normales de ces surfaces sont orientées en suivant la convention donnée ci-dessus. Pour fixer les idées, on peut imaginer que C est un cercle, que la première surface est un disque et la seconde un hémisphère.
Figure pleine pageOn considère la surface fermée constituée de la réunion de S1 et de S2. Pour écrire le flux du champ magnétique sortant sur cette surface, il faut inverser le sens de la normale de S1. On obtient ainsi :
En revenant à la normale orientée en fonction de la courbe fermée, on a donc :
Le flux est indépendant de la surface choisie. Il est donc possible de définir le flux à travers une courbe fermée de manière unique. Pour le calculer, on utilise une surface quelconque délimitée par la courbe (la plus simple).
La principale application de ce flux est le calcul de la force électromotrice d'induction par la loi de Faraday (physicien et chimiste britannique 1791-1867) :
Rappelons que cette force électromotrice apparaît si le champ magnétique est variable ou si le circuit se déplace dans un champ magnétique statique (ou les deux en même temps).
Une autre conséquence est la conservation du flux le long d'un tupe de champ, de manière similaire au cas du champ électrostatique dans le vide.
2.e. Plans de symétrie et d'antisymétrie
Les propriétés de symétrie du champ magnétique sont différentes de celles du champ électrique, car c'est un vecteur axial.
Supposons qu'il existe dans le problème étudié un plan de symétrie du courant, c'est-à-dire un plan de symétrie du champ vectoriel de la densité de courant. La densité de courant est un vecteur polaire (son sens est celui du mouvement des charges positives). La figure suivante rappelle ce que signifie la symétrie. Il faut distinguer le cas d'une composante parallèle au plan et celui d'une composante perpendiculaire au plan.
Figure pleine pageLa figure montre aussi comment se transforme par symétrie le produit vectoriel de deux vecteurs polaires, qui est un vecteur axial. On voit que le vecteur axial est antisymétrique par rapport au plan de symétrie. Il doit en être de même du champ magnétostatique, qui est un vecteur axial.
Un plan de symétrie du courant électrique est un plan d'antisymétrie du champ magnétique.
On en déduit le théorème suivant : pour un point M appartenant à un plan de symétrie du courant, le champ magnétostatique en ce point est perpendiculaire au plan.
Les propriétés d'un plan d'antisymétrie se déduisent par changement de signe.
Un plan d'antisymétrie du courant électrique est un plan de symétrie du champ magnétostatique.
On en déduit le théorème suivant : pour un point M appartenant à un plan d'antisymétrie du courant, le champ magnétostatique en ce point est contenu dans le plan.
2.f. Invariances
Pour les invariances par translation et par rotation autour d'un axe, les règles sont les mêmes que pour le champ électrostatique.
Si une distribution de courants est invariante par rotation, alors le champ magnétostatique est invariant pour la même rotation. Si l'axe de rotation est utilisé comme axe de coordonnées cylindriques, cela signifie que les composantes sur la base locale sont indépendantes de la variable θ :
En d'autre terme, une rotation d'un point de l'espace donne la même rotation pour le vecteur. Cela ne signifie pas que ces champs n'ont pas de composante orthoradiale.
L'invariance par translation dans la direction x signifie :
Là encore, les champs peuvent avoir une composante selon x.
3. Applications
3.a. Fil rectiligne infini
Champ magnétique
Le champ magnétique au voisinage d'un fil rectiligne parcouru par un courant électrique peut être obtenu en utilisant le modèle du fil rectiligne infini.
Tout plan contenant le fil est un plan de symétrie du courant; c'est donc un plan d'antisymétrie du champ magnétique. Tout plan perpendiculaire au fil est un plan d'antisymétrie du courant; c'est donc un plan de symétrie du champ magnétique.
Figure pleine pagePour un point M appartenant au plan d'antisymétrie du champ magnétique, celui-ci est perpendiculaire à ce plan. Si l'on utilise les coordonnées cylindriques avec un axe Oz confondu avec le fil, on obtient :
L'invariance par translation et par rotation autour du fil conduisent à
Le champ magnétique est donc orthoradial et ne dépend que de la distance au fil. L'expression du champ s'obtient avec le théorème d'Ampère, en utilisant le cercle de rayon r passant par le point M, inscrit dans un plan perpendiculaire au fil :
Si le sens de la courbe est changé, le signe du courant enlacé est changé aussi, ce qui donne finalement le même résultat :
Le champ décroît proportionnellement à l'inverse de la distance, comme le champ électrostatique créé par un fil rectiligne chargé infini.
Pour comparaison, le champ magnétique terrestre en France est d'environ 45 μT.
Force entre deux fils
Ampère a étudié expérimentalement la force entre deux fils rectilignes et observé que la force est attractive lorsque les courants sont de même sens. Cette vidéo présente cette expérience et quelques autres. On considère deux fils rectilignes assez proches pour que la force soit détectable. Si les portions rectilignes sont assez grandes par rapport à la distance entre les deux fils, le modèle du fil infini permet de calculer le champ magnétique créé par l'un des fils, et d'en déduire son action sur l'autre fil en utilisant la force de Laplace. On suppose que les fils qui amènent le courant à ces deux portions rectilignes ont une action négligeable.
Figure pleine pageEn supposant que le champ magnétique créé par le fil 1 aux points du fil 2 est identique à celui créé par un fil infini, la force exercée sur le fil 2, dirigée vers le fil 1, s'écrit :
La force est attractive si les deux courants ont le même sens, répulsive dans le cas contraire.
Cette relation servait à définir l'unité de l'intensité du courant électrique dans le système international d'unités (avant les nouvelles définition de 2019). C'est pour cette raison que la perméabilité magnétique a été fixée à 4π 10-7 H/m.
3.b. Solénoïde
Solénoïde de taille finie
Un solénoïde est un enroulement d'un fil sur un tube de section circulaire. Il a été réalisé la première fois par Ampère, qui a observé qu'un solénoïde parcouru par un courant électrique constant se comporte comme un aimant, ce qui l'a conduit à supposer que les aimants comportent des courants microscopiques.
On considère un solénoïde de longueur et de rayon R comportant N spires.
Figure pleine pageTout plan contenant l'axe est un plan d'antisymétrie du courant, donc c'est un plan de symétrie du champ magnétique. En tout point de ce plan le champ est donc contenu dans le plan. Comme il y invariance par rotation autour de l'axe Oz, on peut écrire en coordonnées cylindriques :
Sur l'axe du solénoïde, le champ est colinéaire à l'axe. Le sens du champ sur l'axe et lié au sens du courant dans les spires. Si le courant est positif dans le sens trigonométrique autour de l'axe Oz, alors le champ est dans le sens de z croissant.
Le calcul du champ magnétique d'un ensemble de spires coaxiales peut être fait numériquement. La figure suivante montre les lignes de champ, qu'il faut orienter en fonction du sens du courant dans les spires.
Figure pleine pageLes lignes de champ sont pratiquement parallèles à l'intérieur du solénoïde, à l'exception d'une petite zone proche des bords. L'application de la conservation du flux magnétique le long d'un tube de champ montre que le champ est pratiquement uniforme à l'intérieur. Dès qu'on sort du solénoïde, les lignes de champ divergent fortement, ce qui indique une forte décroissance du champ. Sur le côté du solénoïde (par exemple en z=0) il y a un champ magnétique mais il est très faible comparé au champ à l'intérieur. Plus le rapport a/b est grand, plus le champ à l'extérieur est faible.
Les lignes de champ d'un solénoïde sont semblables à celles d'un aimant permanent droit. Le solénoïde se comporte d'ailleurs comme une aiguille aimantée : si on lui permet de tourner, il s'oriente sous l'effet d'un champ magnétique extérieur. Cette vidéo montre l'expérience.
Solénoïde infini
Lorsque la longueur du solénoïde est très grande devant son rayon, on peut utiliser le modèle du solénoïde de longueur infinie pour calculer le champ. On doit pour cela supposer que le champ à l'extérieur est nul, conformément à ce que montre un calcul exact pour un solénoïde fini de grande longueur.
Figure pleine pageEn plus des symétries déjà mentionnées pour le solénoïde fini, tout plan perpendiculaire à l'axe est un plan de symétrie du courant, donc un plan d'antisymétrie du champ magnétique. Le champ est donc colinéaire à l'axe et comme il y a invariance par translation on a :
Pour déterminer le champ, il faut appliquer le théorème d'Ampère sur la courbe fermée orientée ABCD représentée sur la figure :
Il s'agit d'un rectangle inscrit dans un plan contenant l'axe. Le côté AB est à une distance r de l'axe. Le côté CD est à l'extérieur du solénoïde, là où le champ est nul. Sur les côtés BC et DA la circulation est nulle car le champ est perpendiculaire à la tangente. Il reste donc la circulation sur AB. Compte tenu du choix d'orientation du circuit, le courant enlacé est égal à I multiplié par le nombre de fils enlacés. Si l'on suppose que ces spires sont enroulées de manière uniforme, le nombre de fils est égal à la longueur L multipliée par le nombre de spires par unité de longueur n=N/a. Finalement, le théorème d'Ampère s'écrit :
Le champ mégnatostatique est donc uniforme à l'intérieur du solénoïde infini :
Pour augmenter le champ sans changer l'intensité du courant et la longueur du solénoïde, il faut faire plusieurs couches d'enroulement de fil. Le champ résultant est le champ ci-dessus multiplié par le nombre de couches.
4. Dipôle magnétique
4.a. Définition
Le moment magnétique est un vecteur perpendiculaire à la boucle, orienté en fonction du courant en utilisant la convention déjà utilisée pour orienter une surface à partir de son contour. La norme du moment magnétique est égale à l'aire de la surface plane (un disque) multipliée par l'intensité du courant :
Le moment dipolaire est un vecteur axial car son sens dépend de la convention du trièdre direct.
Un exemple de dipôle à l'échelle macroscopique est un solénoïde (ou plus généralement une bobine), observé à grande distance par rapport à sa longueur. Son moment magnétique s'obtient en multipliant le moment d'une de ses spires par le nombre de spires.
La principale application du dipôle à l'échelle macroscopique est l'aimant permament droit, qui se comporte comme un dipôle à grande distance devant sa taille. Le moment magnétique d'un aimant droit est orienté du pôle sud vers le pôle nord.
En raison de la similitude entre les propriétés d'un aimant et celles d'un solénoïde, Ampère pensait que le magnétisme d'un aimant pouvait s'expliquer par des courants électriques microscopiques à l'intérieur de l'aimant. On sait aujourd'hui qu'il est dû aux moments magnétiques des électrons.
4.b. Moments magnétiques électroniques
Moment magnétique orbital
L'électron en mouvement autour du noyau est équivalent à un courant électrique, positif dans le sens inverse de son mouvement. Bien que le mouvement de l'électron relève de la mécanique quantique, un modèle classique permet d'expliquer le moment magnétique orbital. Ce modèle consiste à attribuer à l'électron une trajectoire circulaire de rayon a. Si T est la période de révolution, l'intensité du courant électrique est égale à la charge de l'électron divisée par cette période. Le moment magnétique orbital est donc :
Le signe moins vient du fait que la normale est choisie en fonction du sens du mouvement de l'électron. En introduisant la vitesse de l'électron, on obtient :
où est le moment cinétique orbital de l'électron et me sa masse.
Il se trouve que cette relation entre le moment magnétique et le moment cinétique est encore valable en mécanique quantique. Cependant, le moment cinétique obtenu en mécanique quantique est quantifié, et peut être nul.
Ce moment magnétique orbital est effectivement responsable d'un magnétisme observé à l'échelle macroscopique, le paramagnétisme
Moment magnétique de spin
L'électron possède aussi un moment magnétique intrinsèque, indépendamment de son moment orbital. L'expérience de Stern et Gerlach, réalisée en 1921, a mis en évidence ce moment magnétique (qui est quantifié). Par ailleurs, l'électron possède aussi un moment cinétique de spin S associé à ce moment magnétique, mais la relation entre les deux n'est pas exactement la même que pour le mouvement orbital :
où g est le facteur de Landé, dont la valeur est très proche de 2.
L'existence de ces moments magnétique et cinétique intrinsèques suggère l'image d'une rotation de l'électron sur lui-même, d'où le nom de spin donné à cette propriété de l'électron. Le proton possède aussi un moment magnétique de spin, mais sa valeur est beaucoup plus faible car sa masse est beaucoup plus grande. Néanmoins, il intervient dans le phénomène de résonance magnétique nucléaire, utilisé par exemple en imagerie par résonance magnétique.
Le spin de l'électron est à l'origine du ferromagnétisme, une propriété de certains métaux (Fe, Co, Ni) et oxydes métalliques. Dans un matériau ferromagnétique, les moments magnétiques de spin de certains électrons ont la faculté de s'orienter collectivement dans la même direction, même en l'absence de champ magnétique extérieur, ce qui donne à un échantillon macroscopique un moment magnétique non nul. Un aimant permanent est un morceau de matériau ferromagnétique, dont le moment magnétique a été orienté par application d'un champ magnétique très intense. Une fois le champ retiré, il garde une aimantation permanente.
Figure pleine pagePour obtenir des ordres de grandeur, il faut savoir que le moment cinétique de spin de l'électron mesuré sur un axe z ne peut prendre que deux valeurs :
où est la constante de Planck. Le magnéton de Bohr est défini par :
Dans un atome isolé, la dernière couche électronique est responsable du moment magnétique total de l'atome, qui résulte de la combinaison des moments magnétiques orbitaux et des moments de spin. Une paire d'électrons de spins opposés ne contribuent pas à ce moment magnétique. Pour les électrons célibataires, il faut prendre aussi en compte le moment cinétique orbital, qui peut éventuellement s'opposer au moment de spin.
Pour un matériau ferromagnétique, on définit l'aimantation M comme le moment magnétique par unité de volume. Il suffit de multiplier l'aimantation par le volume de l'aimant pour obtenir son moment magnétique. Le maximum d'aimantation est obtenu lorsque les moments magnétiques de tous les atomes sont orientés dans le même sens. Il est donc égal au nombre d'atomes N/V par unité de volume multiplié par le moment magnétique de chaque atome, qui est lui même égal au magnéton de Bohr multiplié par nB, le nombre effectif de magnéton de bohr de chaque atome.
Voici quelques valeurs de nB :
4.c. Champ magnétostatique
On s'intéresse au champ magnétostatique créé par un dipôle de moment magnétique constant. On se place dans le cadre de l'approximation dipolaire : r>>a. Le dipôle est équivalent à une boucle de courant circulaire. On utilise des coordonnées sphériques, l'axe Oz étant l'axe de la spire. Le moment magnétique est donc colinéaire à Oz.
Figure pleine pageTout plan contenant l'axe de la spire est un plan d'antisymétrie du courant, donc un plan de symétrie du champ. Le champ magnétique en un point de ce plan est donc contenu dans ce plan. Compte tenu de l'invariance par rotation, il en résulte en coordonnées sphériques :
Il y a aussi une symétrie du courant par rapport au plan contenant la spire (plan passant par le dipôle et perpendiculaire à son moment). Le champ magnétique est donc antisymétrique par rapport à ce plan. La figure suivante montre les lignes de champ d'une spire dans un plan contenant l'axe Oz.
Figure pleine pageLe résultat du calcul dans le cadre de l'approximation dipolaire est :
Le champ a la même expression que pour le dipôle électrostatique, avec bien sûr une constante multiplicative différente. Les lignes de champ d'un dipôle magnétique sont donc identiques aux lignes de champ d'un dipôle électrostatique. Cela est vrai lorsqu'on se place dans l'approximation dipolaire, à une distance très grande par rapport à la taille du dipôle. Pour les dipôles atomiques, cette condition est toujours vérifiée. En revanche, à l'échelle de la spire, les lignes de champ sont tout à fait différentes de celles d'un doublet de charges.
La figure suivante montre les lignes de champ dans le cadre de l'approximation dipolaire.
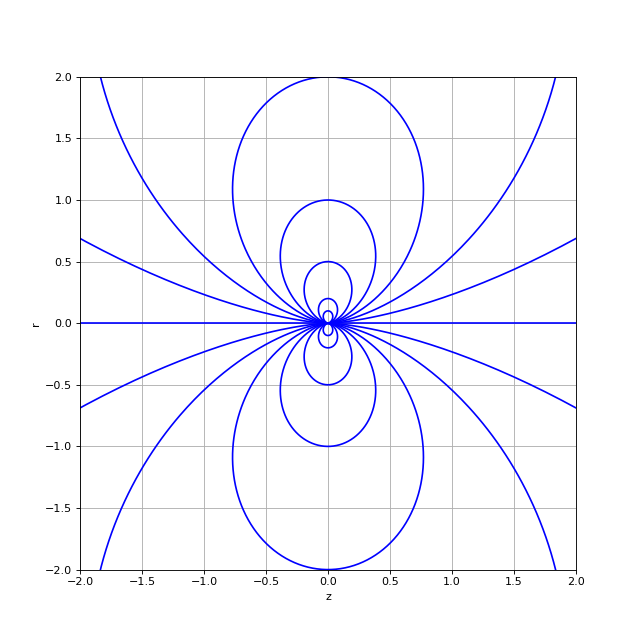 lignesDipole.pdf
lignesDipole.pdf
4.d. Action d'un champ sur un dipôle
Moment dans un champ uniforme
L'action d'un champ magnétostatique sur un dipôle magnétique est similaire à l'action d'un champ électrostatique sur un dipôle électrostatique.
Dans un champ uniforme, la résultante des forces est nulle. Il s'agit donc d'un couple, dont le moment est :
Un exemple d'application est l'orientation d'une aiguille de boussole dans le champ magnétique terrestre. L'aiguille de boussole est un petit aimant permanent, dont le pôle nord magnétique pointe vers le nord magnétique de la Terre (qui est en fait un pôle sud). Le champ magnétique de la Terre est lui-même assimilable à celui d'un dipôle (grossièrement), mais en un lieu donné il est pratiquement uniforme.
Considérons une aiguille de boussole placée sur un pivot vertical et soumise à un champ uniforme horizontal (le champ terrestre a aussi une composante verticale).
Figure pleine pageSi J est le moment d'inertie de la boussole autour de son axe et m son moment magnétique, l'équation différentielle du mouvement de rotation est :
Il s'agit de l'équation du pendule. Pour des petites oscillations (en pratique quelques degrés), la fréquence des oscillations est proportionnelle au champ magnétostatique. On peut donc se servir d'une aiguille de boussole pour mesurer un champ magnétique. C'est comme cela que Biot (physicien français 1774-1862) a montré que le champ créé par un fil parcouru par un courant décroît comme l'inverse de la distance. La vidéo ci-dessous montre l'oscillation d'une boussole dans le champ terrestre, ralentie 4 fois.
Une aiguille de boussole montée sur un pivot vertical peut servir à étudier le champ magnétique créé par un aimant permament ou une bobine. La boussole indique la direction et le sens du champ, et la mesure de la période d'oscillation permet de voir comment le champ évolue avec la distance.
La figure ci-dessous montre un dispositif (bobines de Helmholtz) comportant deux bobines de rayon R=6 cm espacées d'une distance d=12 cm. Le champ magnétique entre les bobines est à peu près uniforme. Un champ pratiquement uniforme est obtenu lorsque d=R.
Figure pleine pageUn dispositif électronique à photodiode permet de mesurer la période d'oscillation du barreau aimanté posé sur un pivot vertical, pour différentes valeurs de l'intensité du courant.
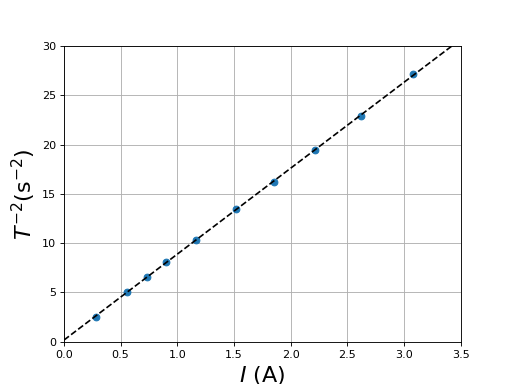 periodeOscillation.pdf
periodeOscillation.pdf
L'inverse de la période d'oscillation au carrée est proportionnel à l'intensité du courant, et donc au champ magnétique. Cette méthode de mesure permet de comparer des champs magnétiques avec une très grande précision. Pour faire une mesure absolue du champ magnétique, on utilise une sonde à effet Hall. Voici le champ mesuré au centre des bobines :
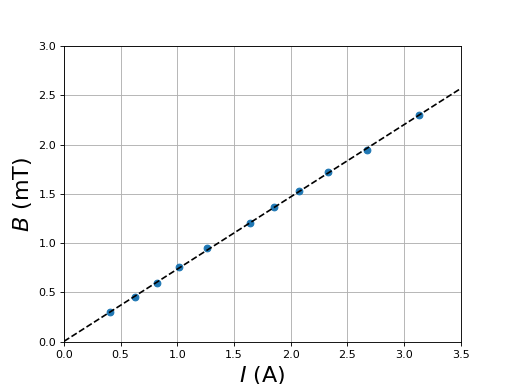 champBbobines.pdf
champBbobines.pdf
On peut simplement obtenir le moment magnétique d'un barreau aimanté de la manière suivante. On l'approche lentement d'une aiguille de boussole initialement à l'équilibre dans le champ terrestre, pôle sud dirigé vers le pôle sud de l'aiguille.
Figure pleine pageLorsque l'aiguille change d'orientation, c'est que le champ magnétique créé par l'aimant au niveau de la boussole est opposé à celui de la Terre. Connaissant le champ magnétique terrestre (47 μT en Bretagne), on en déduit le moment magnétique de l'aimant en utilisant :
Énergie potentielle
L'énergie potentielle d'interaction d'un dipôle avec le champ extérieur est :
En utilisant cette énergie, on montre qu'un dipôle s'oriente dans la direction et dans le sens du champ, car c'est l'orientation qui minimise l'énergie potentielle.
Considérons un ensemble de dipôles libres de tourner mais fixés sur les mailles d'un réseau. La figure suivante montre deux configurations d'équilibre possibles :
Figure pleine pageOn cherche l'énergie de chaque configuration, en considérant seulement l'interaction de chaque dipôle avec ses quatre voisins les plus proches. Dans la configuration 1, tous les dipôles sont alignés. Pour les deux dipôles D1 et D2, l'un est parallèle au champ créé par l'autre. Il y donc une contribution négative -Ea pour cette paire. Pour la paire D2 et D3, l'un est anti-parallèle au champ créé par l'autre, donc la contribution est positive +Eb. Dans la configuration 2, la contribution de la paire D2 et D3 est négative -Eb. On en déduit que la configuration 2 est d'énergie plus basse que la configuration 1. Elle est donc plus stable. Dans un système thermodynamique soumis à l'agitation thermique, la configuration 2 sera favorisée.
Cela montre que l'interaction dipolaire ne peut expliquer le ferromagnétisme. Dans un matériau ferromagnétique, les moments magnétiques des atomes du réseau sont tous parallèles et de même sens, ce qui ne correspond pas à la configuration la plus stable du point de vue de l'interaction dipolaire.
La vidéo ci-dessous montre une expérience réalisée avec des aiguilles de boussole placées dans un champ nul. Le réseau est placé entre deux bobines de Helmholtz, dont le courant a été ajusté de manière à compenser le champ magnétique terrestre. Initialement, les boussoles sont mises en mouvement.
Dans cette expérience, la dissipation permet au système d'atteindre un état d'équilibre mécanique. En refaisant plusieurs fois l'expérience, on constate que les dipôles ne sont jamais tous alignés dans le même sens, même s'il arrive que deux rangées sur trois le soient.
La simulation Réseau de dipôles permet de voir le comportement du réseau de dipôles ponctuels, en particulier en l'absence de frottement. Même avec un frottement, on n'observe pas d'alignement des dipôles en l'absence de champ extérieur.
En conclusion, l'interaction dipolaire (définie par l'énergie potentielle ), ne permet pas d'expliquer l'alignement des spins dans un matériau ferromagnétique.
Le ferromagnétisme s'explique par un principe de physique quantique, le principe d'exclusion de Pauli, qui dit que des électrons (ou plus généralement des particules de la classe des fermions) ne peuvent être dans le même état quantique. Cela signifie que si deux électrons ont leur spin de même sens, il ne peuvent s'approcher l'un de l'autre, ou du moins ont une très faible probabilité de le faire. En revanche, deux électrons de spins opposés peuvent s'approcher et sont alors soumis à la répulsion électrostatique, ce qui a pour effet d'augmenter l'énergie de deux électrons de spins opposés. Ainsi la configuration de plus basse énergie est celle où tous les spins sont dans le même sens. Dans les matériaux ferromagnétiques, les électrons sont trop éloignés les uns des autres pour que l'interaction dipolaire entre en jeu, et l'alignement est donc un phénomène quantique.
Force dans un champ non uniforme
Dans un champ non uniforme, il y a toujours le moment donné par . Il y a en plus une résultante, que l'on obtient avec l'énergie potentielle :
Voir interaction entre deux dipôles pour obtenir le sens de la force en fonction de l'orientation du dipôle, placé dans le champ créé par un autre dipôle.
Lorsque le dipôle est déjà aligné avec le champ, et de même sens, l'énergie potentielle s'écrit simplement :
Les composantes de la force se calculent de la manière suivante :
On voit ainsi que la force est dirigée dans la direction et le sens du gradient de la norme du champ magnétique. Le dipôle est donc attiré vers les régions de champ plus intense. On peut aussi remarquer que le dipôle a tendance à se déplacer de manière à minimiser son énergie potentielle.
L'action d'un champ non uniforme sur un dipôle magnétique atomique est utilisée dans l'expérience de Stern et Gerlach. Cette expérience historique, faite en 1922, a permis de vérifier la quantification des moments magnétiques atomiques et a joué un rôle important dans la découverte du spin de l'électron.
5. Équations locales
5.a. Forme locale de la conservation du flux
Le théorème d'Ostrogradsky permet d'exprimer la conservation du flux sous la forme d'une intégrale de volume :
où l'intégrale de volume est calculée sur le volume délimitée par la surface fermée. Cette intégrale étant nulle quelque soit le volume, on en déduit l'équation locale :
Cette équation est vérifiée par le champ magnétique en général, pas seulement en magnétostatique. Elle exprime de manière locale la conservation du flux. En coordonnées cartésiennes, elle s'écrit :
5.b. Forme locale du théorème d'Ampère
La forme locale du théorème d'Ampère s'obtient en procédant comme pour la forme locale de la conservation de la circulation en électrostatique.
Considérons la courbe fermée rectangulaire représentée sur la figure ci-dessous. Le rectangle est inscrit dans un plan parallèle à Oxy, à une hauteur z. Le courant enlacé est le flux de la composante Jz.
Figure pleine pageLe vecteur tangent unitaire a été représenté pour les quatre côtés du rectangle. Exprimons la circulation sur les côtés DA et BC :
En procédant de même pour les deux autres côtés, on obtient :
En divisant par dxdy et en passant à la limite on obtient :
Deux autres équations sont obtenues en effectuant des permutations circulaires sur (x,y,z). Ces trois équations s'expriment sous forme vectorielle en utilisant l'opérateur rotationnel :
Il s'agit de la forme locale du théorème d'Ampère, valable en magnétostatique et plus généralement dans le cadre de l'approximation des régimes quasi-stationnaires.
On peut écrire à nouveau le théorème d'Ampère sous la forme :
Il s'agit du théorème de Stokes (mathématicien et physicien britannique 1819-1903), valable pour un champ vectoriel en général et pour tout surface S délimitée par une courbe fermée C.
En pratique, on utilisera ce théorème pour passer de la forme intégrale à la forme locale, et inversement.