Électrostatique

1.a. Loi de Coulomb

Coulomb (ingénieur et physicien français 1736-1806) a étudié expérimentalement les forces entre des petites sphères chargées électriquement, au moyen d'une balance de torsion. Il en a déduit que cette force décroît comme l'inverse du carré de la distance entre les sphères (comme la loi de gravitation de Newton), et qu'elle est proportionnelle à la quantité de charge portée par chacune des sphères.

Cette loi a depuis été confirmée à l'échelle microscopique, et même à l'échelle de l'atome. Dans sa formulation moderne, on l'énonce pour des charges ponctuelles. En pratique, une charge est ponctuelle si sa taille est négligeable par rapport aux dimensions du système étudié. Par exemple, les électrons sont si petits qu'on peut les considérer comme ponctuels, même à l'échelle de l'atome.

Il existe deux types de charges électriques de signes opposés. Lorsque les charges sont de même signe, la force est répulsive. Lorsque les charges sont de signes opposés, la force est attractive. Par convention, on a attribué une valeur négative à l'un des types. Par exemple, les électrons ont une charge négative alors que les protons ont une charge positive.

Dans le système d'unités international, la quantité de charge s'exprime en Coulomb (C). La constante ε₀ est la permittivité électrique du vide (ou constante diélectrique). Il s'agit d'une constante fondamentale, dont la valeur approchée est :

$${\epsilon }_0=8,85\cdot 10^{-12}F\cdot m^{-1}\text{(3)}$$

Une autre constante fondamentale est la quantité de charge portée par un électron :

$$e=-1,60\cdot 10^{-19}C\text{(4)}$$

D'après la loi de Coulomb, la force électrostatique agit instantanément à distance, ce qui ne pose pas de problème tant que les charges sont fixes, et qu'elle vérifie le principe des actions réciproques (qui n'est pas toujours valable pour les actions électromagnétiques à distance).

Il est fréquent que des charges soient soumises à une force électrostatique sans que l'on sache vraiment où sont les charges qui en sont la cause. On introduit alors la notion de champ électrostatique, qui est un champ vectoriel, c'est-à-dire une application qui à tout point de l'espace associe un vecteur.

Lorsqu'une charge ponctuelle q se trouve au point M, elle subit donc la force :

$$\overrightarrow{F}=q\overrightarrow{E}\left(M\right)\text{(6)}$$

Le champ électrostatique est une force par unité de charge; il s'exprime en V/m.

Par beau temps, il y a un champ électrostatique à la surface de la Terre, de l'ordre de 100 V⋅m^-1. Par temps orageux, il peut atteindre plusieurs milliers de V/m.

1.b. Principe de superposition

Lorsque plusieurs charges statiques sont présentes, on constate expérimentalement que les forces exercées sur une charge donnée s'ajoutent comme des vecteurs. La force électrostatique vérifie donc le principe de superposition. En terme de champ électrostatique, cela signifie qu'on peut calculer le champ créé par un ensemble de N charges (P_i,q_i) par la somme suivante :

$$\begin{array}{ccc}\hfill \overrightarrow{E}\left(M\right)& =\frac{1}{4\pi {\epsilon }_0}\sum _{i=0}^N\frac{q_i}{{\left(P_{i}M\right)}^2}{\overrightarrow{u}}_i\hfill & \hfill \text{(7)}\\ \hfill & =\frac{1}{4\pi {\epsilon }_0}\sum _{i=0}^N\frac{q_i\overrightarrow{P_{i}M}}{{\left(P_{i}M\right)}^3}\hfill & \hfill \text{(8)}\end{array}$$

1.c. Lignes de champ

Ce sont des courbes orientées, c'est-à-dire auquelles on attribue un sens, qui est celui du champ électrique.

Pour tracer les lignes de champ de différentes distributions de charges ponctuelles : charges ponctuelles.

Pour une charge ponctuelle seule, les lignes de champ sont des droites radiales. Voici par exemple des lignes pour une charge positive, représentées dans un plan contenant la charge.

Figure pleine page

Ce champ présente une invariance par rotation autour du point où se trouve la charge. Les lignes doivent donc avoir une répartition angulaire uniforme (l'angle entre deux lignes voisines est constant).

Voyons les lignes de champ pour deux charges de signes opposés :

Figure pleine page

Les propriétés générales des lignes de champ électrostatique sont visibles sur ces deux exemples. Les lignes partent des charges positives et vont, soit vers une charge négative, soit à l'infini. À proximité d'une charge ponctuelle, les lignes de champ sont radiales, pratiquement identiques à celles d'une charge seule. Une ligne de champ électrostatique n'est jamais fermée sur elle-même.

1.d. Plan de symétrie

Dans le cas d'une charge ponctuelle seule, tout plan contenant la charge est un plan de symétrie. Dans l'exemple précédent, tout plan contenant les deux charges est un plan de symétrie. Voici un autre exemple, avec deux charges de même signe :

Figure pleine page

Dans cet exemple, tout plan contenant les deux charges est plan de symétrie, mais le plan médian (d'équation x=0) est aussi un plan de symétrie.

Par ailleurs, le champ est nul au point (0,0) et on voit 4 lignes se rejoindre en ce point.

La symétrie des charges par rapport à un plan implique des propriétés de symétrie pour le champ électrostatique. Une distribution symétrique par rapport à un plan peut se décomposer en paires de charges symétriques, comme celle de l'exemple précédent. Il suffit donc de considérer ce cas particulier; le principe de superposition permettra de généraliser. Notons P et P' les deux points symétriques par rapport au plan Π_s, portant la même charge q.

Figure pleine page

Considérons alors une décomposition du vecteur $\overrightarrow{PM}$ en une composante perpendiculaire au plan et une composante parallèle au plan :

$$\overrightarrow{PM}={\overrightarrow{PM}}_{\perp }+{\overrightarrow{PM}}_{\parallel }\text{(9)}$$

La même décomposition est faite pour les vecteurs $\overrightarrow{P\text{'}M\text{'}}$, $\overrightarrow{PM\text{'}}$ et $\overrightarrow{P\text{'}M}$

On arrive ainsi au résultat suivant, valable pour tout point M :

En utilisant le principe de superposition, ce résultat est généralisé à une distribution symétrique par rapport au plan. La composante perpendiculaire au plan change de signe lorsqu'on passe d'un point M à son symétrique M', alors que la composante parallèle est inchangée. Un champ vectoriel vérifiant cette propriété est dit symétrique par rapport au plan.

Un cas particulier intéressant est celui d'un point M situé sur le plan de symétrie. Dans ce cas, la composante perpendiculaire en ce point est égale à son opposée, ce qui implique qu'elle est nulle (à condition qu'il n'y ait pas de charge en ce point). En un point du plan de symétrie, le champ électrostatique est donc contenu dans ce plan. On vérifie cette propriété sur les trois exemples précédents.

1.e. Plan d'antisymétrie

Pour démontrer les propriétés du champ électrostatique en présence d'un plan d'antisymétrie, on procède comme précédemment, en considérant le cas du doublet antisymétrique.

Figure pleine page

On arrive au résultat suivant :

Un champ vectoriel vérifiant cette propriété est dit antisymétrique par rapport au plan.

Lorsque le point M appartient au plan d'antisymétrie, le champ électrostatique en ce point est perpendiculaire à ce plan.

Dans le cas du doublet de charges opposées, le plan médian x=0 est un plan d'antisymétrie :

Figure pleine page

1.f. Invariance par rotation

Certaines distributions de charges sont invariantes par rotation autour d'un axe : une rotation d'un angle quelconque autour de cette axe ne modifie pas la distribution. Par exemple, un doublet de charges est invariant par rotation autour de la droite contenant les deux charges. D'une manière générale, si toutes les charges d'une distribution sont sur une droite, il y a invariance par rotation autour de cette droite.

Soit M un point quelconque de l'espace et le point M' obtenu en faisant une rotation d'un angle θ autour de l'axe. Si O est un point de l'axe, on peut écrire la rotation sous la forme suivante :

$$\overrightarrow{OM\text{'}}=R_{\theta }\left(\overrightarrow{OM}\right)\text{(14)}$$

où R_θ désigne la rotation appliquée aux vecteurs. L'invariance par rotation de la distribution des charges implique celle du champ électrique, c'est-à-dire :

$$\overrightarrow{E}\left(M\text{'}\right)=R_{\theta }\left(\overrightarrow{E}\left(M\right)\right)\text{(15)}$$ Figure pleine page

Une manière simple d'exprimer l'invariance par rotation du champ électrostatique est d'utiliser les coordonnées cylindriques autour de cet axe, et la base locale associée. Sachant que les vecteurs de la base locale sont eux-mêmes invariants par rotation, l'invariance par rotation du champ électrostatique est équivalente à l'invariance des composantes sur la base locale par rapport à θ :

$$\begin{array}{ccc}\hfill & E_r(r,z)\hfill & \hfill \text{(16)}\\ \hfill & E_{\theta }(r,z)\hfill & \hfill \text{(17)}\\ \hfill & E_z(r,z)\hfill & \hfill \text{(18)}\end{array}$$

2.a. Circulation du champ électrostatique

Soit une courbe orientée allant d'un point A à un point B.

Figure pleine page

En tout point M de cette courbe, on considère le vecteur tangent unitaire $\overrightarrow{t}$ orienté dans le sens de la courbe. Si on divise la courbe en N petits intervalles égaux de longueur curviligne Δl, on peut considérer la somme suivante :

$$\sum _{i=1}^N\overrightarrow{E}\left(M\right)\cdot \overrightarrow{t}\left(M\right)\Delta l\text{(19)}$$

où le produit scalaire du champ électrostatique et du vecteur tangent unitaire est évalué au milieu de chaque segment. En faisant tendre Δl vers zéro (et donc N vers l'infini), on obtient une intégrale appelée circulation du champ électrostatique sur la courbe orientée, que l'on écrit :

On peut aussi introduire le vecteur déplacement élémentaire sur la courbe: $d\overrightarrow{r}=\overrightarrow{t}dl$ et écrire la circulation sous la forme :

$$C_{AB}={\int }_A^B\overrightarrow{E}\left(M\right)\cdot d\overrightarrow{r}\text{(21)}$$

Supposons que $\overrightarrow{E}$ soit le champ électrostatique créé par une charge ponctuelle située au point O. L'utilisation des coordonnées sphériques par rapport à ce point permet d'écrire ce champ :

$$\overrightarrow{E}=\frac{q}{4\pi {\epsilon }_0}\frac{\overrightarrow{u_r}}{r^2}\text{(22)}$$

Un déplacement élémentaire le long de la courbe s'écrit :

$$d\overrightarrow{r}=dr{\overrightarrow{u}}_r+rd\theta {\overrightarrow{u}}_{\theta }+rsin\theta d\phi {\overrightarrow{u}}_{\phi }\text{(23)}$$

En conséquence, la circulation sur la courbe s'écrit :

$$C_{AB}=\frac{q}{4\pi {\epsilon }_0}{\int }_A^B\frac{dr}{r^2}=\frac{q}{4\pi {\epsilon }_0}(\frac{1}{r_A}-\frac{1}{r_A})\text{(24)}$$

Il s'agit d'une intégrale d'une fonction de r entre r_A et r_B. Cette intégrale ne dépend que de la distance des points A et B à la charge.

On en conclut que la circulation du champ électrostatique créé par une charge ponctuelle ne dépend que des points initial et final (A et B) et pas de la courbe entre ces deux points. Un champ vérifiant cette propriété est appelé champ conservatif. Avec le principe de superposition, cette propriété est généralisée au champ créé par un ensemble de charges ponctuelles.

On remarque par ailleurs que la circulation change de signe lorsqu'on change le sens de parcours :

$${\int }_A^B\overrightarrow{E}\left(M\right)\cdot \overrightarrow{t}\left(M\right)dl=-{\int }_B^A\overrightarrow{E}\left(M\right)\cdot \overrightarrow{t\text{'}}\left(M\right)dl\text{(25)}$$

Cela est dû au changement de sens du vecteur tangent unitaire (la longueur dl est positive).

Si la courbe est la trajectoire suivie par une charge ponctuelle, le travail de la force électrique est :

$$W_{AB}=q{C}_{AB}\text{(26)}$$

Ce travail est indépendant du chemin suivi entre les deux points : la force est conservative.

2.b. Potentiel

La conservation de la circulation permet de définir un champ scalaire appelé potentiel électrostatique. À tout point M de l'espace, on peut associer un potentiel V(M). Pour cela, il faut tout d'abord fixer une convention pour la valeur du potentiel en un certain point. Dans le cas d'une charge ponctuelle, il est commode de choisir ce point de référence à une distance infinie de la charge, et de fixer le potentiel en ce point à zéro. On définit alors le potentiel au point M comme la circulation entre ce point et un point à l'infini, que l'on peut écrire :

$$V\left(M\right)={\int }_M^{\infty }\overrightarrow{E}\cdot \overrightarrow{t}dl\text{(27)}$$

Cette intégrale ne dépend que de la position du point M (c'est ce qui permet de définir une valeur unique en chaque point). Pour la calculer, il suffit de considérer un chemin rectiligne, le long de la droite passant par la charge. On obtient, si P₁ est le point où se trouve la charge :

Dans le système d'unités SI, le potentiel s'exprime en volt (V) et le champ électrique en volt par mètre (V/m).

Le potentiel obéit au principe de superposition. Pour un ensemble de charges, on a donc

$$V\left(M\right)=\frac{1}{4\pi {\epsilon }_0}\sum _{i=1}^N\frac{q_i}{P_{i}M}\text{(29)}$$

La relation entre le champ électrostatique et le potentiel a été écrite sous forme d'une intégrale $\mathrm{(27)}$. On en déduit que la circulation du champ électrostatique entre deux points est l'opposée de la différence de potentiel entre ces deux points :

Le potentiel électrostatique a une signification énergétique : l'énergie potentielle d'une charge ponctuelle q est en effet :

$$E_p\left(M\right)=qV\left(M\right)\text{(31)}$$

Cela se démontre en remarquant que la travail de la force électrostatique entre deux points est égal à l'opposé de la variation d'énergie potentielle entre ces deux points.

Si la particule chargée a une masse m, et n'est soumise qu'à la force électrostatique, son énergie mécanique, qui est conservée, s'écrit :

$$E=\frac{1}{2}m{v}^2+qV\left(M\right)\text{(32)}$$

Considérons comme exemple deux charges ponctuelles q₁ et q situées initialement à une distance a l'une de l'autre. La charge q₁ est fixe dans le référentiel. Soit ${\overrightarrow{v}}_0$ la vitesse de la seconde dans ce référentiel à l'instant initial. La charge q est en mouvement mais le champ qu'elle ressent est bien un champ électrostatique car il est créé par une charge immobile dans le référentiel.

Figure pleine page

L'énergie mécanique de la charge q est :

$$E=\frac{1}{2}m{v}_0^2+\frac{1}{4\pi {\epsilon }_0}\frac{q{q}_1}{a}\text{(33)}$$

La conservation de l'énergie mécanique permet de déterminer la norme de la vitesse de la particule lorsqu'elle parvient à une distance r de la charge fixe, sans connaître la trajectoire. On a en effet :

$$\frac{1}{2}m{v}_0^2+\frac{1}{4\pi {\epsilon }_0}\frac{q{q}_1}{a}=\frac{1}{2}m{v}^2+\frac{1}{4\pi {\epsilon }_0}\frac{q{q}_1}{r}\text{(34)}$$

On peut en particulier déterminer la vitesse v₀ minimale qui permet à la charge de s'éloigner à l'infini, en considérant la limite $r\to \infty$ et v=0.

2.c. Opérateur gradient

Considérons un segment infinitésimal de longueur dl. On introduit un point fixe O et on pose :

$$\overrightarrow{t}dl=d\overrightarrow{OM}\text{(35)}$$

qui est la variation infinitésimale (ou élémentaire) du vecteur position. La variation infinitésimale du potentiel entre ces deux points est l'opposée de la circulation du champ électrostatique :

$$dV=-\overrightarrow{E}\cdot d\overrightarrow{OM}\text{(36)}$$

Si l'on utilise les coordonnées cartésiennes (x,y,z), le potentiel est en fait une fonction des trois variables V(x,y,z). dV peut alors être considéré comme la différentielle (différence infinitésimale) de cette fonction. On admet que les différentielles sont reliées par la relation suivante :

$$dV=\frac{\partial V}{\partial x}dx+\frac{\partial V}{\partial y}dy+\frac{\partial V}{\partial z}dz\text{(37)}$$

$\frac{\partial V}{\partial x}$ est la dérivée partielle de V par rapport à x. Une dérivée partielle se calcule comme une dérivée simple, en considérant les autres variables comme des constantes.

Par ailleurs, le vecteur $d\overrightarrow{OM}$ est le déplacement infinitésimal, dont les composantes sont (dx,dy,dz). On a donc :

$$-\overrightarrow{E}\cdot d\overrightarrow{OM}=-E_{x}dx-E_{y}dy-E_{z}dz\text{(38)}$$

On comparant les deux expressions précédentes, qui doivent être égales pour tout déplacement infinitésimal, on en déduit :

$$\begin{array}{c}\hfill E_x=-\frac{\partial V}{\partial x}\hfill \\ \hfill E_y=-\frac{\partial V}{\partial y}\hfill \\ \hfill E_z=-\frac{\partial V}{\partial z}\hfill \end{array}\text{(39)}$$

Pour écrire cette relation sous forme vectorielle, on introduit l'opérateur gradient, qui agit sur un champ scalaire pour donner un champ vectoriel. L'expression du gradient d'un champ scalaire f en coordonnées cartésiennes est :

$$\overrightarrow{grad}f=\frac{\partial f}{\partial x}{\overrightarrow{u}}_x+\frac{\partial f}{\partial y}{\overrightarrow{u}}_y+\frac{\partial f}{\partial y}{\overrightarrow{u}}_y\text{(40)}$$

La relation entre le champ électrostatique et le potentiel peut donc s'écrire :

En plus de sa concision, cette écriture a l'avantage de pouvoir s'employer en coordonnées cylindriques ou sphériques, alors que la relation $\mathrm{(39)}$ n'est valable qu'en coordonnées cartésiennes. Pour les expressions du gradient en coordonnées cylindriques et sphériques, voir le formulaire donné en annexe.

D'une manière générale, la circulation du gradient d'un champ scalaire le long d'une courbe orientée s'écrit :

$${\int }_A^B\overrightarrow{grad}f\cdot \overrightarrow{t}dl={\int }_A^{B}df=f\left(B\right)-f\left(A\right)\text{(42)}$$

En conséquence, la circulation d'un gradient le long d'une courbe fermée (A=B) est nulle. En particulier, la circulation du champ électrostatique le long d'une courbe fermée est nulle.

2.d. Surfaces équipotentielles

En coordonnées cartésiennes, une surface équipotentielle est définie par l'équation :

$$V(x,y,z)=V_i\text{(43)}$$

où V_i est une constante. Il existe une infinité de surfaces équipotentielles, obtenues en faisant varier la valeur de V_i.

Considérons un point M sur une surface équipotentielle et faisons un déplacement élémentaire de ce point tangent à la surface en ce point. La variation infinitésimale du potentiel pour ce déplacement est :

$$dV=\overrightarrow{E}\left(M\right)\cdot d\overrightarrow{OM}\text{(44)}$$

Comme le déplacement se fait sur la surface (localement celle-ci est assimilable à son plan tangent), la variation de potentiel est nulle. On en déduit que le vecteur $\overrightarrow{E}\left(M\right)$ est perpendiculaire à la surface au point M.

Sur une figure, on représente un plan contenant des lignes de champ et non coupé par des lignes de champ. C'est le cas d'un plan contenant toutes les charges, car il s'agit alors d'un plan de symétrie. L'intersection des surfaces avec ce plan sont des lignes équipotentielles. On choisit de représenter des lignes dont les valeurs du potentiel sont équidistantes, par exemple une ligne tous les volts. Voici un exemple de tracé pour le doublet de charges opposées :

Figure pleine page

Au voisinage des deux charges, les lignes équipotentielles n'ont pas été traçées car elles seraient trop rapprochées pour être discernées.

On remarque que le plan x=0 est une surface équipotentielle de potentiel nul, ce qui se démontre aisément avec la relation $\mathrm{(29)}$.

La circulation du champ électrique le long d'une ligne de champ est égale à l'opposée de la variation de potentiel. Les potentiels sont donc décroissants dans le sens des lignes de champ. Lorsqu'on suit une ligne de champ, la norme du champ est inversement proportionnelle à l'espacement entre les lignes équipotentielles. La représentation des lignes et de champ et des lignes équipotentielles permet donc d'avoir en tout point la direction et le sens du champ, et aussi une information sur son intensité. Sur la figure ci-dessus, l'intensité du champ augmente lorsqu'on s'approche d'une charge (et tend vers l'infini). Sur l'axe x=0 (correspondant au plan de symétrie), l'écartement progressif des lignes équipotentielles lorsque |y| augmente donne une information sur l'évolution du champ avec y.

3.a. Flux du champ électrique

Figure pleine page

Soit une surface notée S. En tout point de la surface, on peut définir un vecteur normal (perpendiculaire) à la surface. Ce vecteur est unitaire, c'est-à-dire de norme 1. Il y a deux sens possibles pour ce vecteur normal. L'orientation de la surface consiste à choisir un sens au vecteur normal.

Considérons une subdivision de la surface en petites parcelles d'aire Δs. On suppose pour simplifier qu'elles ont toutes la même aire. Soit M le centre d'une parcelle. On considère le produit scalaire suivant :

$$\overrightarrow{E}\left(M\right)\cdot \overrightarrow{n}\left(M\right)\Delta s\text{(45)}$$

Le champ électrique, aussi bien que le vecteur normal, dépendent en général du point M. On considère alors la somme sur les N parcelles, de manière à couvrir toute la surface:

$$\sum _{i=1}^N\overrightarrow{E}\left(M\right)\cdot \overrightarrow{n}\left(M\right)\Delta S\text{(46)}$$

Lorsqu'on fait tendre ΔS vers zéro, c'est-à-dire N vers l'infini, la limite obtenue est une intégrale de surface appelée flux du champ électrique à travers la surface, et notée :

Dans cette écriture, dS est une aire infinitésimale. On associe à cette surface infinitésimale un vecteur

$$\overrightarrow{dS}=\overrightarrow{n}dS\text{(48)}$$

Le flux est la somme (au sens intégral) du produit scalaire de ce vecteur et du champ électrique. En calcul numérique, cette intégrale est calculée de manière approchée sous la forme d'une somme discrète, avec N parcelles.

3.b. Flux à travers une surface fermée

On considère le cas d'une surface S fermée. La figure suivante montre deux exemples de surface fermée : une sphère et un cylindre de révolution. D'une manière générale, une surface fermée permet de définir un domaine intérieur, dont il n'est pas possible de sortir sans franchir la surface.

Figure pleine page

Pour une surface fermée, l'orientation de la normale se fait implicitement dans le sens sortant (sauf mention contraire). Le flux du champ électrique à travers cette surface fermée est le flux sortant du champ électrique.

3.c. Théorème de Gauss

Considérons l'exemple d'une surface sphérique, que l'on place dans le champ électrique créé par une charge ponctuelle q₁. Dans la représentation bidimensionnelle ci-dessous, la sphère est représentée par son cercle équatorial, contenu dans le plan de la figure, qui contient aussi des lignes de champ. On commence par centrer la sphère (de rayon r) sur la charge.

Figure pleine page

Le champ électrique est en tout point de la sphère colinéaire au vecteur normal, et le produit scalaire est indépendant du point considéré. Le flux sortant du champ électrique à travers cette sphère est donc :

$${\Phi }_S=\frac{1}{4\pi {\epsilon }_0}\frac{q_1}{r^2}\iint dS=\frac{q_1}{{\epsilon }_0}\text{(49)}$$

Considérons à présent une sphère non centrée sur la charge, mais la contenant encore :

Figure pleine page

Dans ce cas le calcul du flux est beaucoup plus difficile car le produit scalaire n'est pas uniforme sur la surface. D'une part les deux vecteurs ne sont plus colinéaires, d'autre part la distance à la charge n'est pas constante et donc la norme du champ électrique ne l'est pas. Le flux est pourtant identique à celui de la sphère centrée (on l'admet) :

$${\Phi }_S=\frac{q_1}{{\epsilon }_0}\text{(50)}$$

Cette propriété vient du fait que le champ électrique est une force centrale variant comme l'inverse du carré de la distance. Voyons maintenant le cas d'une sphère ne contenant pas la charge :

Figure pleine page

Dans ce cas, on remarque que le produit scalaire est négatif dans une partie de la sphère (la zone proche de la charge), positif ailleurs. Le résultat est un flux nul (on l'admet) :

$${\Phi }_S=0\text{(51)}$$

Pour généraliser ces résultats à un ensemble de charges ponctuelles, il suffit de remarquer que le flux obéit au principe de superposition : le flux du champ électrostatique créé par un ensemble de charges est la somme des flux des champs électrostatiques créés par chaque charge. Lorsqu'une charge se trouve à l'intérieur de la surface, elle contribue au flux total. Lorsqu'elle se trouve à l'extérieur, elle ne contribue pas au flux total. On obtient ainsi :

Ce résultat constitue le théorème de Gauss (mathématicien et physicien Allemand, 1777-1855).

Le théorème de Gauss est équivalent à la loi de Coulomb de l'électrostatique, mais sa portée dépasse le cadre de l'électrostatique, car il s'applique de manière générale au champ électrique, même lorsque les charges se déplacent. Appliqué au champ électrique en général, il s'agit en fait d'une loi fondamentale et non d'un théorème.

D'autre part, le théorème de Gauss peut servir à la résolution de certains problèmes d'électrostatique.

Si une des charges de la distribution se trouve sur la surface fermée, le champ électrostatique n'est pas défini au point où se trouve cette charge, ce qui fait que le flux à travers cette surface n'est pas a priori défini.

3.d. Exemple : monopôle

Le monopôle le plus simple est constitué d'une seule charge ponctuelle. Soit une charge q placée au point O, que l'on suppose seule dans l'espace. Il s'agit bien sûr d'une hypothèse théorique mais, si aucune autre charge n'est présente au voisinage immédiat de cette charge, on peut supposer que le champ électrostatique dans un voisinage de la charge est à peu près le même que si cette charge était seule dans l'espace. Compte tenu de cette hypothèse, tout plan contenant la charge est un plan de symétrie de la distribution, donc un plan de symétrie du champ électrostatique. Soit M un point quelconque de l'espace (différent de O). La droite OM appartient à deux plans de symétrie perpendiculaires. Le champ en M étant contenu dans chacun de ces plans, il est aussi contenu dans cette droite. L'utilisation des coordonnées sphériques et de la base locale associée permet d'exprimer simplement cette propriété :

$$\overrightarrow{E}=E_r(r,\theta ,\phi ){\overrightarrow{u}}_r\text{(53)}$$

Par ailleurs, la distribution est invariante par rotation autour de tout axe passant par O, ce qui implique que $E_r$ est en fait indépendant de θ et ϕ. Considérons alors le flux sortant du champ électrostatique à travers la sphère de centre O et de rayon r :

$${\Phi }_S=E_r\left(r\right)\iint {\overrightarrow{u}}_r\cdot \overrightarrow{n}dS=E_r\left(r\right)\iint dS=E_r\left(r\right)4\pi r^2\text{(54)}$$

D'après le théorème de Gauss, ce flux est égal à $\frac{q}{{\epsilon }_0}$. On en déduit que :

$$E_r\left(r\right)=\frac{1}{4\pi {\epsilon }_0}\frac{q}{r^2}\text{(55)}$$

L'utilisation des propriétés de symétrie et du théorème de Gauss permet ainsi de retrouver la loi de Coulomb (nous avons admis la réciproque). Nous voyons aussi la raison du facteur 4π dans la loi de Coulomb : il permet de simplifier l'expression du théorème de Gauss, qui est considéré comme plus important (car plus général) que la loi de Coulomb.

Considérons à présent le champ créé par deux charges de même signe, l'une deux fois plus grande que l'autre. La figure suivante montre les lignes de champ sur une échelle assez grande par rapport à la distance entre les deux charges :

Figure pleine page

Lorsqu'on se place très loin, c'est-à-dire à une distance r très grande devant la distance a des deux charges, toutes les lignes de champ semblent venir du même point, le point O où se trouvent pratiquement confondues les deux charges. Appliquons alors le théorème de Gauss à une sphère de centre O et de rayon r :

$${\Phi }_s=\frac{3q}{{\epsilon }_0}\text{(56)}$$

Ce résultat suggère que le champ électrostatique à grande distance est pratiquement identique à celui d'une charge ponctuelle portant la quantité de charge 3q. C'est effectivement ce que l'on peut montrer en effectuant un développement limité pour r grand devant a.

Une distribution de charges dont la quantité de charge totale est non nulle est appelée monopôle. À grande distance de la distribution, le champ électrique est identique à celui d'une charge ponctuelle.

3.e. Tubes de champ

Un tube de champ est une surface engendrée par des lignes de champ. Par exemple, pour le champ créé par une charge ponctuelle, un tube de champ est un cône centré sur la charge. La figure suivante représente une vue en perspective d'une partie d'un tube de champ, avec les lignes de champ qui le délimitent. La portion de tube est fermée par deux disques, de manière à obtenir une surface fermée.

Pour faire tourner le tube dans l'espace, suivre ce lien.

Considérons la surface latérale, générée par les lignes de champ. En tout point de cette surface le champ est tangent donc le flux à travers cette surface est nul. Le flux du champ électrostatique à travers la surface fermée est donc la somme du flux à travers le disque S1 et le disque S2. Comme il n'y a pas de charge à l'intérieur de la surface, le théorème de Gauss donne :

$${\Phi }_{S1}+{\Phi }_{S2}=0\text{(57)}$$

Dans cette expression, les deux flux sont calculés avec une normale sortante par rapport à l'intérieur de la surface. Supposons que la charge soit positive, et que la normale pour S1 soit orientée dans le sens du champ, comme celle de S2.

Figure pleine page

Le flux sur S1 change de signe et on obtient donc :

$${\iint }_{S1}\overrightarrow{E}\cdot \overrightarrow{n{\text{'}}_1}dS={\iint }_{S2}\overrightarrow{E}\cdot \overrightarrow{n_2}dS\text{(58)}$$

Le flux est le même pour ces deux surfaces. On voit aussi que le choix de la surface coupée par les lignes n'a pas d'importance, pourvu qu'elle soit délimitée par le tube de champ choisi. On peut donc en conclure que le flux se conserve le long d'un tube de champ. La surface S2 étant plus grande que S1, le champ électrique est plus intense sur S1. Cette propriété permet de voir comment varie l'intensité du champ électrique (la norme du vecteur) en observant les lignes de champ. Un écartement des lignes correspond à une diminution de l'intensité du champ. Lorsque les lignes sont parallèles, le champ ne varie pas le long du tube.

4.a. Définition

Voici par exemple un doublet de charges opposées :

Figure pleine page

et voici trois charges dont la somme est nulle, deux charges q>0 et une charge 2q<0, qui pourraient représenter les charges partielles dans la molécule d'eau :

Figure pleine page

Nous allons nous intéresser au cas du doublet afin de déterminer la structure du champ créé par un dipôle à grande distance. La charge -q se trouve au point A, la charge q au point B. Le moment dipolaire est défini par :

Pour un ensemble de charges dont la somme est nulle, le moment dipolaire est :

$$\overrightarrow{p}=\sum _{i=1}^N{q}_i\overrightarrow{O{P}_i}\text{(60)}$$

Pour préciser la définition du dipôle, on doit ajouter que le moment dipolaire ne doit pas être nul. Dans le cas contraire, il ne s'agit pas d'un dipôle.

On admet la propriété suivante :

4.b. Dipôles moléculaires

De nombreuses molécules ont un moment dipolaire, car les électrons de valence ont une probabilité de présence plus forte sur certains atomes. On les désigne comme molécules polaires mais molécules dipolaires serait le terme exact. Par exemple dans la molécule HCl, la probabilité de présence des deux électrons formant la liaison est plus forte à proximité de l'atome de chlore. On dit que l'atome de chlore est plus électronégatif que l'atome d'hydrogène. Vu de loin, tout se passe comme si l'atome d'hydrogène portait une charge 0,17e et celui de chlore une charge -0,17e.

On utilise en chimie une unité plus adapté à ces moments dipolaires très petits : le debye :

$$1D=3,33\cdot 10^{-30}C\cdot m\text{(61)}$$

La molécule d'eau est aussi dipolaire, car l'oxygène est plus électronégatif que l'hydrogène. Son moment dipolaire est 1,85 D. L'atome d'oxygène porte une charge partielle -2δe alors que chacun des atomes d'hydrogène porte une charge partielle +δe. Connaissant la géométrie de la molécule (distances et angle), on peut calculer son moment dipolaire en utilisant la formule $\mathrm{(60)}$. On peut aussi le voir comme la somme de deux moments dipolaires :

$$\overrightarrow{p}=\delta e\overrightarrow{O{H}_1}+\delta e\overrightarrow{O{H}_2}$$

4.c. Potentiel et champ électrostatiques

Nous allons calculer le potentiel électrostatique créé par un doublet de charges opposées, comme défini sur la figure suivante :

Figure pleine page

On utilise pour cela les coordonnées sphériques $M(r,\theta ,\phi )$, les deux charges étant placées sur l'axe OZ, à une distance a l'une de l'autre.

Tout plan contenant les deux charges est un plan de symétrie de la distribution, donc un plan de symétrie du champ électrostatique. Il s'en suit que le champ n'a pas de composante selon le vecteur ${\overrightarrow{u}}_{\phi }$.

Le potentiel électrostatique en un point M est :

$$V\left(M\right)=\frac{q}{4\pi {\epsilon }_0}(\frac{1}{BM}-\frac{1}{AM})\text{(62)}$$

On obtient ainsi le potentiel dans l'approximation dipolaire :

$$V(r,\theta )=\frac{1}{4\pi {\epsilon }_0}\frac{pcos\theta }{r^2}\text{(64)}$$

où p=qa est la norme du moment dipolaire.

En utilisant l'expression du gradient en coordonnées sphériques, on obtient le champ électrostatique :

$$\begin{array}{ccc}\hfill & E_r=-\frac{\partial V}{\partial r}=\frac{1}{4\pi {\epsilon }_0}\frac{2pcos\theta }{r^3}\hfill & \hfill \text{(65)}\\ \hfill & E_{\theta }=-\frac{1}{r}\frac{\partial V}{\partial \theta }=\frac{1}{4\pi {\epsilon }_0}\frac{psin\theta }{r^3}\hfill & \hfill \text{(66)}\end{array}$$

On remarque que le champ électrostatique décroît comme l'inverse du cube de la distance, c'est-à-dire beaucoup plus vite que le champ d'un monopôle, qui décroît comme l'inverse du carré de la distance.

La figure suivante représente des lignes du champ électrostatique créé par le dipôle :

Figure pleine page

4.d. Action d'un champ sur un dipôle

On considère une molécule dipolaire soumise à un champ électrostatique. Ce champ est qualifié de champ extérieur car sa cause est extérieure au dipôle. On suppose que la molécule reste rigide. En conséquence, les charges qui constituent le dipôle restent liées entre elles de manière à former un système de points rigides, mais pouvant tourner sur lui même ou se déplacer dans l'espace.

On raisonne sur un doublet de charges opposées et on admettra la généralisation à un dipôle quelconque. Considérons tout d'abord le cas d'un champ extérieur uniforme. La résultante des forces est alors nulle. Il y a en revanche un moment de force par rapport au centre du dipôle :

$${\overrightarrow{\Gamma }}_O=q(\overrightarrow{OB}\wedge {\overrightarrow{E}}_{ext}-\overrightarrow{OA}\wedge {\overrightarrow{E}}_{ext})\text{(67)}$$

En introduisant le vecteur moment dipolaire, on obtient :

Ce moment s'annule lorsque le dipôle est aligné avec le champ extérieur. Il y a donc deux positions d'équilibre, l'une parallèle au champ extérieur, l'autre antiparallèle.

Supposons que le champ électrostatique extérieur soit dirigé suivant l'axe X et notons α l'angle que fait le dipôle avec cet axe. Le potentiel électrostatique du champ extérieur est :

$$V_{ext}\left(x\right)=-x{E}_{ext}\text{(69)}$$

L'énergie potentielle du dipôle dans ce champ se calcule comme la somme de l'énergie potentielle de chaque charge du doublet :

$$E_p=q{V}_{ext}\left(B\right)-q{V}_{ext}\left(A\right)=-q(x_B-x_A)E_{ext}=-q\overrightarrow{AB}\cdot {\overrightarrow{E}}_{ext}\text{(70)}$$

L'énergie potentielle s'écrit donc :

L'expression de l'énergie potentielle en fonction de l'angle α montre que l'angle α=0 constitue une position d'équilibre stable, l'angle α=π une position d'équilibre instable.

Si le champ extérieur n'est pas uniforme, la résultante des forces n'est plus nulle et elle dépend de l'orientation du dipôle par rapport au champ extérieur.

Nous admettrons que les expressions établies ci-dessus pour le moment des forces et pour l'énergie potentielle sont toujours valables dans un champ non uniforme. Cette dernière permet d'obtenir la résultante des forces avec l'opérateur gradient :

$$\overrightarrow{F}=-\overrightarrow{grad}\left(E_p\right)\text{(72)}$$

Si (x,y,z) sont les coordonnées du dipôle dans un repère cartésien, les composantes de la résultante ont la forme suivante :

$$F_x=\frac{\partial }{\partial x}\left(\overrightarrow{p}\cdot {\overrightarrow{E}}_{ext}\right)\text{(73)}$$

Dans cette expression, le champ extérieur est celui où se trouve le dipôle; il dépend donc de (x,y,z).

Supposons que le dipôle soit dans une orientation d'équilibre stable, c'est-à-dire parallèle au champ (de même direction et de même sens). La résultante des forces s'écrit :

$$\overrightarrow{F}=\left|\right|\overrightarrow{p}\left|\right|\overrightarrow{grad}\left(\right|\left|{\overrightarrow{E}}_{ext}\right|\left|\right)\text{(74)}$$

Cette force est dirigée dans la direction et le sens du gradient de la norme du champ, c'est-à-dire en direction de la région de l'espace où le champ est le plus intense.

4.e. Application : interactions ions/molécules et molécules/molécules

L'interaction entre un ion et une molécule dipolaire peut se modéliser par une interaction entre une charge ponctuelle et un dipôle. En moyenne (sur un grand nombre d'ions et de molécules) le moment dipolaire d'une molécule est parallèle (de même direction et de même sens) que le champ électrique créé par l'ion au point où se trouve la molécule. En raison de l'agitation thermique, les orientations peuvent être très différentes, mais l'orientation parallèle correspond à la moyenne.

Figure pleine page

Le dipôle étant aligné avec le champ de l'ion, soit Ox l'axe joignant l'ion et la molécule. La force ressentie par la molécule s'écrit :

$$\overrightarrow{F}=p\frac{\partial \left|\right|E_{ext}\left|\right|}{\partial x}{\overrightarrow{u}}_x\text{(75)}$$

La norme du champ est croissante lorsqu'on s'approche de l'ion. Il s'en suit que le gradient est dirigé vers l'ion et que la force ressentie par la molécule est attractive (en moyenne), dirigée vers l'ion.

Les interactions de van der Waals sont des interactions entre molécules, causées par les dipôles permanents ou les dipôles induits. On distingue :

• L'interaction entre deux dipôles permanents, c.a.d. deux molécules polaires (Keesom).
• L'interaction entre un dipôle permanent et un dipôle induit (Debye).
• L'interaction entre un dipôle instantané et un dipôle induit (London).

Dans les trois cas, l'énergie d'interaction entre les deux dipôles est plus basse si les deux moments dipolaires sont de même direction et de même sens (parallèles). Comme il sera vu dans le chapitre de physique statistique, cela implique que les états parallèles sont plus probables et qu'en moyenne on peut considérer que les dipôles sont effectivement parallèles. Il s'en suit que la force est en moyenne attractive.

D'une manière générale, le gradient de la norme du champ est dirigé vers le point de convergence apparent des lignes de champ, et si le dipôle est parallèle au champ, la force qu'il ressent est dirigée vers ce point de convergence.

Cette simulation montre la force entre deux dipôles.

5.a. Distributions volumiques

Les distributions continues sont utilisées lorsque le nombre de charges ponctuelles est trop grand pour qu'on puisse les traiter individuellement. Par exemple, lorsqu'un un corps macroscopique solide est chargé, c'est en raison d'un excès d'électrons ou d'un défaut d'électrons et le nombre d'électrons en plus ou en moins peut être très grand. Les nuages électroniques dans les atomes ou dans les molécules peuvent être modélisés par des distributions continues.

Notons d la distance moyenne entre les charges ponctuelles. Si on considère une sphère de rayon R inclue dans le corps chargé, on peut définir une densité volumique de charge pour cette sphère par :

$$\rho \left(R\right)=\frac{N\left|e\right|}{\frac{4}{3}\pi R^3}\text{(76)}$$

où N est le nombre algébrique de charges positives et e la charge élémentaire.

Les charges sont généralement réparties de manière aléatoire dans le volume. Si R est de l'ordre de la distance d, la densité fluctue beaucoup lorsque R varie. En revanche, lorsque R devient grand devant d, la densité est pratiquement constante. La figure suivante montre le résultat d'une simulation. La distance moyenne entre les charges est d'environ 0,03.

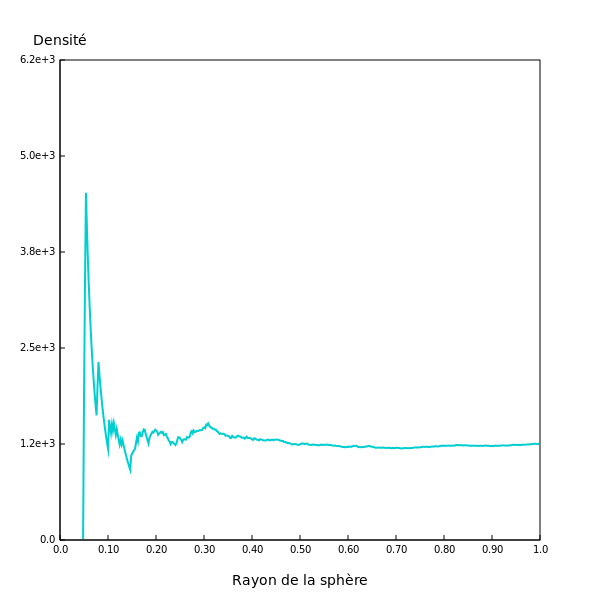
On définit alors trois échelles de longueur :

• L'échelle microscopique, où la densité présente des fluctuations importantes.
• L'échelle mésoscopique, où la densité ne dépend plus du rayon de la sphère.
• L'échelle macroscopique, beaucoup plus grande que la précédente. À cette échelle, un volume mésoscopique peut être assimilé à un point.

Ces échelles ne font pas référence à des longueurs numériques précises, car celles-ci dépendent du problème considéré. À l'échelle mésoscopique, on peut définir une densité volumique de charge, que l'on notera ρ (quantité de charge par unité de volume). À l'échelle macroscopique, on observe généralement des variations de la densité d'un point à l'autre, souvent continues mais pouvant aussi présenter des discontinuités. D'un point de vue macroscopique, la densité de charge est un champ scalaire :

$$\rho (x,y,z)\text{(77)}$$

Ce type de distribution des charges est appelé distribution continue, par opposition aux distributions discrètes formées de charges ponctuelles.

Soit un point M de l'espace et un volume infinitésimal dV centré sur ce point (on peut imaginer un cube). La quantité de charge portée par ce volume est :

$$dq=\rho \left(M\right)dV\text{(78)}$$

La quantité de charge portée par un volume V macroscopique est l'intégrale de volume

$$Q={\iiint }_V\rho \left(M\right)dV\text{(79)}$$

Le théorème de Gauss s'applique bien sûr à ce type de distribution. Pour une surface fermée S la charge intérieure est l'intégrale de volume de la densité sur le volume V intérieur à la surface :

$${\iint }_S\overrightarrow{E}\left(M\right)\cdot \overrightarrow{n}\left(M\right)dS=\frac{1}{{\epsilon }_0}{\iiint }_V\rho \left(M\right)dV\text{(80)}$$

5.b. Sphère chargée en volume

Considérons comme exemple une sphère macroscopique de rayon R, chargée uniformément en volume, avec une densité ρ₀. La densité de charge à l'extérieur de la sphère est nulle. Pour traiter ce problème, on suppose que la sphère est très éloignée d'autres charges et donc qu'elle se trouve dans un milieu infini vide de charge.

Si O est le centre de la sphère, cette distribution présente une symétrie sphérique (ou symétrie centrale) : la densité ρ(r) ne dépend que de la distance r au centre.

On remarque que tout plan passant par le centre est un plan de symétrie de la distribution des charges. Soit un point M de l'espace. Il y a au moins deux plans de symétrie non confondus contenant la droite OM. Pour chacun de ces plans, le champ électrostatique en M est contenu dans le plan. On en déduit que le champ en M est porté par la droite OM. Cette propriété s'écrit simplement en coordonnées sphériques :

$$\overrightarrow{E}=E_r{\overrightarrow{u}}_r\text{(81)}$$

La symétrie sphérique de la distribution implique celle du champ électrostatique, ce qui implique que E_r ne dépend que de r.

L'expression de E_r(r) est obtenue à l'aide du théorème de Gauss, appliqué à une sphère S de rayon r. En effet, le champ électrostatique est colinéaire au vecteur normal en tout point de cette sphère et sa norme est la même en tout point, puisque r est constant sur la sphère. Le flux sortant du champ électrostatique sur la sphère s'écrit donc :

$${\Phi }_S=E_r\left(r\right)4\pi r^2\text{(82)}$$

Lorsque r>R (en dehors de la sphère), la quantité de charge dans la sphère S est :

$$Q=\frac{4}{3}\pi R^3{\rho }_0\text{(83)}$$

C'est bien sûr la quantité de charge de la sphère chargée. Le théorème de Gauss conduit donc à :

$$E_r\left(r\right)=\frac{1}{4\pi {\epsilon }_0}\frac{Q}{r^2}\text{(84)}$$

On voit que ce champ est identique à celui créé par une charge ponctuelle qui serait placée au centre de la sphère.

Cet exemple permet, par analogie, de calculer le champ de gravitation créé par un corps sphérique. Le champ de gravitation a en effet la même forme que le champ électrostatique : c'est un champ central en 1/r². Pour passer de l'un à l'autre, il suffit de changer la constante multiplicative de la manière suivante :

$$\frac{q}{4\pi {\epsilon }_0}\to -Gm\text{(85)}$$

On montre ainsi que le champ de gravitation créé par une masse sphérique (la répartition des masses doit avoir la symétrie sphérique) est identique (hors de la sphère) à celui créé par une masse ponctuelle qui serait placée au centre.

Remarque : le champ créé par une sphère chargée est une fonction continue des variables d'espace et il a partout une valeur finie (il est nul au centre de la sphère). Pour une charge ponctuelle, obtenue lorsque R tend vers zéro, le champ devient infini en r=0.

5.c. Distributions surfaciques

En pratique, les corps chargés sont très souvent des conducteurs métalliques, dont les charges libres sont des électrons. Dans un conducteur, il n'y a pas d'excès ou de défaut d'électrons dans le volume, mais seulement au voisinage de la surface, sur une profondeur d'échelle mésoscopique. À l'échelle macroscopique, cette profondeur peut généralement être négligée, ce qui conduit à introduire la notion de charge de surface.

Localement, la surface du conducteur est assimilée à son plan tangent. On s'intéresse donc à une surface plane. La figure suivante représente une petite portion du conducteur, avec l'épaisseur e chargée, juste sous la surface.

Figure pleine page

D'un point de vue macroscopique, on considère que la charge est répartie sur une épaisseur nulle. Voyons comment se fait le passage à la limite. Si on note dS l'aire de la surface infinitésimale du conducteur, la quantité de charge portée sous cette surface est :

$$dq=\rho edS\text{(86)}$$

où ρ est la densité de charge dans la couche chargée. Lorsque e tend vers zéro, il faut faire tendre la densité volumique ρ vers l'infini pour que la quantité de charge reste constante. On définit la densité surfacique de charge par la limite suivante :

$$\underset{e\to 0}{lim}\rho e=\sigma \text{(87)}$$

Finalement, la quantité de charge portée par la surface infinitésimale s'écrit :

$$dq=\sigma dS\text{(88)}$$

Une distribution surfacique de charge est définie par sa densité surfacique, qui est un champ scalaire puisqu'elle peut varier d'un point à l'autre de la surface du conducteur.

5.d. Plan chargé infini

Un exemple de distribution surfacique est le plan infini chargé uniformément, c'est-à-dire dont la densité de charge surfacique σ est la même en tout point. Bien sûr, les distributions infinies n'existent pas dans la nature. Elles sont néanmoins intéressantes car elles permettent de modéliser certaines situations. Le plan infini a l'avantage de posséder un haut degré de symétrie, ce qui rend la détermination du champ électrostatique très facile.

Figure pleine page

Soit (0xyz) un repère cartésien, le plan chargé étant confondu avec le plan (Oxy). Soit M un point quelconque de l'espace, hors du plan chargé. Tout plan contenant ce point et perpendiculaire à (Oxy) est un plan de symétrie de la distribution donc le champ électrostatique en ce point est contenu dans ce plan. Considérons deux de ces plans perpendiculaires entre eux, Π_s et Π'_s. Le champ électrostatique au point M (qui appartient à ces deux plans) est contenu dans ces deux plans, ce qui implique qu'il est dirigé suivant z :

$$\overrightarrow{E}=E_z(x,y,z){\overrightarrow{u}}_z\text{(89)}$$

L'utilisation des plans de symétrie a donc permis de déterminer la direction du champ. Un autre plan de symétrie est le plan chargé lui-même. Le champ électrostatique est symétrique par rapport à ce plan. Comme le champ est perpendiculaire au plan, cette symétrie s'écrit :

$$E_z(-z,x,y)=-E_z(z,x,y)\text{(90)}$$

Une autre propriété du plan infini est l'invariance par translation dans la direction x et dans la direction y. En effet, si on déplace le plan chargé dans l'une de ces deux directions, cela ne change pas la distribution des charges. Le champ électrostatique doit posséder la même invariance, ce qui signifie qu'il ne dépend pas des variables x et y. On a donc finalement :

$$\overrightarrow{E}=E_z\left(z\right){\overrightarrow{u}}_z\text{(91)}$$

Voilà tout ce que permettent de dire les symétries et les invariances. Il reste à déterminer la fonction E_z(z). Le théorème de Gauss permet de le faire. Pour cela, il faut choisir une surface fermée S particulière. Soit M(z) un point de l'espace hors du plan chargé et M'(-z) son symétrique par rapport au plan. La surface à utiliser est un cylindrique droit délimité par deux plans parallèles à Oxy et contenant respectivement les point M' et M. La génératrice du cylindre est perpendiculaire au plan Oxy. La figure ci-dessous représente un cylindre de révolution, mais un cylindre à base carrée convient aussi.

Figure pleine page

Soit Σ la base contenant M, de normale sortante $\overrightarrow{n}\left(z\right)={\overrightarrow{u}}_z$. Soit Σ' la base contenant M', de normale sortante $\overrightarrow{n}(-z)=-{\overrightarrow{u}}_z$. On note A l'aire de ces deux surfaces (leur forme exacte n'a pas d'importance). Le flux du champ électrostatique à travers la première se calcule très simplement car le champ est colinéaire à la normale et sa norme ne dépend pas du point de la surface puisque le champ ne dépend que de z :

$${\iint }_{\Sigma }\overrightarrow{E}\left(z\right)\cdot \overrightarrow{n}\left(z\right)dS=E_z\left(z\right)A\text{(92)}$$

Pour l'autre base, on obtient :

$${\iint }_{\Sigma \text{'}}\overrightarrow{E}(-z)\cdot \overrightarrow{n}(-z)dS=-E_z(-z)A=E_z\left(z\right)A\text{(93)}$$

où l'on a utilisé la symétrie du champ par rapport au plan Oxy. Ces deux flux sont donc égaux. Le flux à travers la surface latérale est nul puisque le champ est en tout point perpendiculaire à la normale. Le théorème de Gauss s'écrit donc :

$$2E_z\left(z\right)A=\frac{q_{int}}{{\epsilon }_0}\text{(94)}$$

La charge située à l'intérieur de la surface est représentée sur la figure : il s'agit d'un disque d'aire A chargé avec une densité σ. On obtient finalement pour z>0 :

$$E_z\left(z\right)=\frac{\sigma }{2{\epsilon }_0}\text{(95)}$$

Pour z<0 on a :

$$E_z\left(z\right)=-\frac{\sigma }{2{\epsilon }_0}\text{(96)}$$

On remarque que le champ est uniforme de chaque côté du plan chargé. Lorsqu'on s'éloigne du plan, l'intensité du champ ne décroît pas. Cela peut sembler étrange mais c'est une conséquence du caractère infini du plan. Dans la réalité, les surfaces planes chargées sont finies, et donnent bien un champ tendant vers zéro à l'infini.

On voit par ailleurs que le champ présente une discontinuité sur le plan chargé. Le plan chargé étant un plan de symétrie de la distribution, le champ sur ce plan doit être contenu dans ce plan, ce qui implique que E_z(0)=0. La présence d'une discontinuité de la composante normale du champ électrique sur les surfaces chargées est une propriété générale.

Déterminons un potentiel électrostatique. En raison de l'invariance par translation, le potentiel est une fonction de z seulement. Le champ électrostatique s'écrit donc :

$$\overrightarrow{E}=-\frac{dV}{dz}{\overrightarrow{u}}_z\text{(97)}$$

On obtient l'équation différentielle suivante :

$$\begin{array}{ccc}\hfill & \frac{dV}{dz}=-\frac{\sigma }{2{\epsilon }_0}pourz>0\hfill & \hfill \text{(98)}\\ \hfill & \frac{dV}{dz}=\frac{\sigma }{2{\epsilon }_0}pourz<0\hfill & \hfill \text{(99)}\end{array}$$

dont la solution générale est :

$$\begin{array}{ccc}\hfill & V\left(z\right)=-\frac{\sigma }{2{\epsilon }_0}z+Apourz>0\hfill & \hfill \text{(100)}\\ \hfill & V\left(z\right)=\frac{\sigma }{2{\epsilon }_0}z+Bpourz<0\hfill & \hfill \text{(101)}\end{array}$$

On constate que le potentiel ne peut pas tendre vers 0 lorsque $\left|z\right|\to \infty$. D'une manière générale, il n'est pas possible d'annuler le potentiel à l'infini pour les distributions qui ne sont pas localisées dans un volume fini. Le potentiel n'est pas unique. Dans le cas présent, il y a deux constantes A et B que l'on peut choisir librement. Quelque soient les constantes choisies, l'opposé du gradient du potentiel est le champ électrostatique écrit plus haut. Il est cependant d'usage de choisir les constantes afin que le potentiel soit une fonction continue. On prendra donc A=B=0.

Il faut remarquer que V(z) n'est pas dérivable en z=0, ce qui fait qu'on ne peut utiliser le gradient pour obtenir le champ électrostatique sur le plan chargé (nous avons vu qu'il est nul).

5.e. Condensateur plan

Un condensateur plan est constitué de deux plaques conductrices parallèles, auquelles on applique une différence de potentiel avec un générateur. Si la différence de potentiel est constante, un champ électrostatique est généré dans l'espace. Soit e la distance entre les deux plaques (l'entrefer). Si cette distance est très petite par rapport à la largeur des plaques, le champ électrostatique est négligeable en dehors du condensateur et on peut assimiler les deux conducteurs à deux plaques infinies. Ce modèle constitue le condensateur plan infini.

On peut montrer que les charges se répartissent sur les faces internes des conducteurs. Une des plaques porte une charge uniforme σ, l'autre plaque porte une charge uniforme opposée -σ. Les faces externes ne portent pas de charge pour un condensateur infini. Nous admettrons cette propriété.

Figure pleine page

Le champ électrique peut donc se calculer en considérant la superposition du champ d'un plan infini de densité surfacique de charge σ, avec le champ d'un plan infini de charge opposée. La figure montre les champs à superposer. Le résultat est un champ nul à l'extérieur, uniforme à l'intérieur du condensateur, de norme :

$$E=\frac{\sigma }{{\epsilon }_0}\text{(102)}$$

Le vecteur est dirigé des charges positives vers les charges négatives (sur la figure σ>0). Le champ est uniforme à l'intérieur du condensateur plan infini, nul en dehors. Les surfaces équipotentielles sont des plans parallèles aux plaques. Chaque plaque conductrice est elle-même équipotentielle dans tout son volume. Pour voir la relation avec la différence de potentiel entre les deux plaques, il faut écrire la circulation du champ électrostatique entre les deux plaques, par exemple entre deux points A et B en vis-à-vis. Sachant que cette circulation ne dépend pas de la courbe reliant les deux points, on prend un segment. La circulation est égale à l'opposée de la différence de potentiel :

$${\int }_A^B\overrightarrow{E}\cdot \overrightarrow{t}dl=V_A-V_B\text{(103)}$$

Le champ étant uniforme et colinéaire à la tangente, on obtient :

$$E=\frac{V_A-V_B}{e}=\frac{U}{e}\text{(104)}$$

où l'on a introduit la tension U entre les deux plaques. Pour la figure ci-dessus, on a V_A>V_B. Soit S l'aire des plaques (qui en réalité sont finies). Les charges portées par les plaques sont Q=Sσ et -Q. En utilisant les résultats précédents, on en déduit :

$$Q=\frac{{\epsilon }_{0}S}{e}U\text{(105)}$$

La quantité de charge des plaques est proportionnelle à la tension. Le coefficient de proportionnalité est la capacité du condensateur :

$$C=\frac{{\epsilon }_{0}S}{e}\text{(106)}$$

L'unité de la capacité dans le système d'unités international est le Farad (F). La capacité est proportionnelle à l'aire et inversement proportionnelle à l'entrefer. En pratique, les condensateurs à grande capacité sont réalisés en enroulant deux feuilles métalliques séparées par une feuille isolante.

Le calcul approché du potentiel créé dans l'espace par deux plaques auquelles on applique une différence de potentiel peut être effectué par une méthode numérique. Voici le résultat d'un calcul pour deux disques de rayon 6 mm espacés de 2 mm. Les lignes équipotentielles sont représentées dans un plan contenant l'axe des deux disques.

Figure pleine page

Les lignes équipotentielles sont parallèles et régulièrement espacées dans le condensateur, sauf au voisinage des bords. Il s'en suit que la relation E=U/e est tout à fait valable. On constate la présence d'un champ électrique au voisinage des faces externes des deux plaques, environ 10 fois plus faible qu'à l'intérieur (car les équipotentielles sont 10 fois plus espacées). Il y donc une faible densité de charge sur les faces externes. Celle-ci diminue lorsqu'on augmente de rayon des disques (sans changer l'espacement). On remarque aussi que la structure du champ électrostatique en dehors du condensateur est celle d'un dipôle.

6.a. Forme locale du théorème de Gauss

Une forme locale du théorème de Gauss s'obtient en considérant un volume infinitésimal. Plaçons-nous en coordonnées cartésiennes et considérons le volume infinitésimal (parallélépipède rectangle) défini sur la figure suivante :

Figure pleine page

Chaque face est rectangulaire et a une normale colinéaire avec un des vecteurs de la base. Par exemple, les faces en vis-à-vis notées y et y+dy ont pour normale sortante respectivement $-{\overrightarrow{u}}_y$ et ${\overrightarrow{u}}_y$. Le flux sortant du champ électrique à travers ces deux faces s'écrit :

$$-E_y(x,y,z)dxdz+E_y(x,y+dy,z)dxdz\text{(107)}$$

Dans ce type de calcul, on considère que le champ ne varie pas sur la face (cela peut se justifier par un calcul plus rigoureux).

On procède de même pour les autres paires de faces en vis-à-vis. La quantité de charge intérieure au volume est :

$$\rho (x,y,z)dxdydy\text{(108)}$$

En écrivant le théorème de Gauss et en divisant par le volume dxdydz, on obtient :

$$\frac{E_x(x+dx,y,z)-E_x\left(x\right)}{dx}+\frac{E_y(x,y+dy,z)-E_y(x,y,z)}{dy}+\frac{E_z(x,y,z+dz)-E_z(x,y,z)}{dz}=\frac{\rho (x,y,z)}{{\epsilon }_0}\text{(109)}$$

Les longueurs dx, dy et dz tendent vers zéro. On voit ainsi apparaître des dérivées partielles des composantes du champ électrique :

Cette équation est la forme locale du théorème de Gauss. Il s'agit d'une équation différentielle à dérivées partielles vérifiée par le champ électrique (pas seulement électrostatique) en tout point de l'espace.

À première vue, on perd en généralité en écrivant la forme locale puisqu'elle s'applique à une distribution volumique seulement. En fait, les mathématiciens ont résolu ce problème en introduisant les distributions, qui permettent de définir la densité ρ même en présence de charges ponctuelles ou surfaciques.

On introduit l'opérateur divergence défini en coordonnées cartésiennes par :

La divergence est un opérateur linéaire qui transforme un champ vectoriel en champ scalaire. Il permet d'exprimer la forme locale du théorème de Gauss sous une forme indépendante du système de coordonnées :

Cette équation constitue une loi fondamentale de l'électromagnétisme, vérifiée par le champ électrique en toute circonstance. Dans le domaine de l'électrostatique, elle est équivalente à la loi de Coulomb.

Pour l'expression de la divergence en coordonnées cylindriques et sphériques, voir le formulaire en annexe.

Revenons à la forme intégrale du théorème de Gauss, en exprimant la charge intérieure comme l'intégrale de volume de la densité, et en remplaçant cette dernière par la divergence du champ électrique multipliée par ε₀ :

Ce résultat se généralise à un champ vectoriel quelconque (dérivable en tout point) et constitue le théorème d'Ostrogradsky (physicien et mathématicien ukrainien 1801-1862):

On utilisera ce théorème pour passer de la forme intégrale à la forme locale et inversement, ce qui nous évitera de refaire le calcul infinitésimal présenté plus haut.

6.b. Forme locale de la conservation de la circulation

Nous avons vu que la circulation du champ électrostatique entre deux points est indépendante de la courbe, égale à l'opposée de la différence de potentiel. Considérons alors une courbe fermée C orientée. La circulation sur cette courbe est nulle (on part d'un point pour revenir au même point) :

$${\oint }_C\overrightarrow{E}\cdot \overrightarrow{t}dl=0\text{(114)}$$

Cette propriété constitue la conservation de la circulation. Elle n'est vraie qu'en électrostatique, en l'absence de champ magnétique variable. Pour obtenir une forme locale, considérons la courbe fermée rectangulaire représentée sur la figure ci-dessous. Le rectangle est inscrit dans un plan parallèle à Oxy, à une hauteur z.

Figure pleine page

Le vecteur tangent unitaire a été représenté pour les quatre côtés du rectangle. Exprimons la circulation sur les côtés DA et BC :

$$\begin{array}{ccc}\hfill & {\int }_D^A\overrightarrow{E}\cdot tdt=-E_y(x,y,z)dy\hfill & \hfill \text{(115)}\\ \hfill & {\int }_B^C\overrightarrow{E}\cdot tdl=E_y(x+dx,y,z)dy\hfill & \hfill \text{(116)}\end{array}$$

En procédant de même pour les côté AB et CD et en divisant par dxdy, on obtient la circulation sur tout le rectangle, qui est nulle. Le passage à la limite donne ainsi :

$$\frac{\partial E_y}{\partial x}-\frac{\partial E_x}{\partial y}=0\text{(117)}$$

En effectuant deux permutations circulaires sur les axes (x,y,z), on obtient deux autres équations similaires. Ce résultat peut s'exprimer plus simplement en introduisant l'opérateur rotationnel, qui est défini en faisant le produit vectoriel d'un opérateur de dérivation avec le champ :

Dans cette écriture, les composantes du rotationnel sur la base sont calculées sous forme d'un produit vectoriel. Pour l'expression en coordonnées cylindriques ou sphériques, voir le formulaire en annexe.

Le rotationnel est un opérateur vectoriel linéaire, qui transforme un champ vectoriel en un champ vectoriel. D'après ce qui précède, les trois composantes du rotationnel du champ électrostatique sont nulles, donc :

Cette équation constitue la forme locale de la conservation de la circulation. Elle n'est pas aussi générale que l'équation $\mathrm{(112)}$ puisqu'elle n'est pas valable en présence d'un champ magnétique variable (phénomène d'induction).

6.c. Équation de Poisson de l'électrostatique

Nous avons finalement deux équations locales pour les lois de l'électrostatique :

La deuxième est en fait équivalente à l'existence d'un potentiel V tel que :

$$\overrightarrow{E}=-\overrightarrow{grad}V\text{(122)}$$

En reportant cette équation dans la forme locale du théorème de Gauss, on obtient :

$$div\left(\overrightarrow{grad}V\right)=-\frac{\rho }{{\epsilon }_0}\text{(123)}$$

La divergence du gradient peut être explicitée en coordonnées cartésiennes :

C'est une équation différentielle à dérivées partielles appelée équation de Poisson de l'électrostatique (Poisson, mathématicien français, 1781-1840).

Là encore, on simplifie l'écriture en introduisant un opérateur de dérivation appelé laplacien, et défini en coordonnées cartésiennes par :

Voir le formulaire en annexe pour les expressions du laplacien en coordonnées cylindriques et sphériques.

Le laplacien est aussi noté ΔV, qui ne doit pas être confondu avec une différence (notation utilisée en thermodynamique).

6.d. Équation de Laplace de l'électrostatique

Pour réaliser un champ électrostatique, on utilise généralement des conducteurs auquel on applique des différences de potentiel. Par exemple, les champs électrostatiques utilisés pour accélérer les particules chargées (électrons, ions) sont produits de cette manière. La figure suivante montre un exemple, avec deux conducteurs cylindriques.

Figure pleine page

Chaque conducteur est équipotentiel. Ici, les potentiels sont V₀ et V₁. La différence de potentiel appliquée est U=V₁-V₀. En dehors des conducteurs, le milieu peut être le vide, ou un gaz équivalent électriquement au vide. L'équation locale vérifiée par le potentiel est donc :

C'est l'équation de Laplace de l'électrostatique (Laplace, mathématicien et physicien français 1749-1827).

La solution recherchée est par hypothèse une fonction continue des variables d'espaces. La continuité du potentiel n'est pas nécessaire d'un point de vue physique mais elle s'impose pour la résolution de l'équation de Laplace.

Pour que la solution continue soit unique, il faut définir aussi des conditions limites. Sur la surface des conducteurs le potentiel est fixé. Si un conducteur possède un potentiel V₁ alors le potentiel dans le vide au voisinage de ce conducteur est V₁ (par continuité du potentiel). Physiquement, c'est la différence de potentiel entre deux conducteurs qui importe. On peut donc arbitrairement attribuer un potentiel nul à l'un des conducteurs. Pour que la solution soit unique, il faut néanmoins une condition limite supplémentaire, sur une surface fermée qui englobe les conducteurs (représentée en pointillé sur la figure). Idéalement, cette surface devrait être infiniment grande, ce qui revient à fixer le potentiel à l'infini, en général à une valeur nulle. En pratique, surtout lorsqu'on effectue une résolution numérique, on doit se contenter d'une surface finie, de taille assez grande par rapport à la taille du dispositif étudié.

6.e. Complément (hors programme) : discrétisation de l'équation de Laplace

Ce type de problème est le plus souvent résolu de manière numérique. Pour cela, il faut faire une discrétisation de l'équation de Laplace. Voyons comment se fait la discrétisation pour un problème à deux dimensions, où le potentiel V(x,y) ne dépend que de x et y :

$$\frac{{\partial }^{2}V}{\partial x^2}+\frac{{\partial }^{2}V}{\partial y^2}=0\text{(127)}$$

Il faut tout d'abord définir un maillage du plan. Un maillage comporte plusieurs dizaines de milliers de nœuds. La figure suivante représente une partie du maillage. Les mailles sont des rectangles de dimensions (Δx,Δy). Les nœuds sont repérés par deux indices (i,j). L'objectif du calcul numérique est d'obtenir une valeur approchée des potentiels aux nœuds, que l'on note V_i,j.

Figure pleine page

Pour discrétiser une dérivée seconde, considérons les développements de Taylor suivants, pour une fonction f à une variable :

$$\begin{array}{ccc}\hfill & f(x+h)=f\left(x\right)+hf\text{'}\left(x\right)+\frac{h^2}{2}f\text{'}\text{'}\left(x\right)+\frac{h^3}{3}f\text{'}\text{'}\text{'}\left(x\right)+O\left(h^4\right)\hfill & \hfill \text{(128)}\\ \hfill & f(x-h)=f\left(x\right)-hf\text{'}\left(x\right)+\frac{h^2}{2}f\text{'}\text{'}\left(x\right)-\frac{h^3}{3}f\text{'}\text{'}\text{'}\left(x\right)+O\left(h^4\right)\hfill & \hfill \text{(129)}\end{array}$$

En sommant ces deux équations, on obtient :

$$f\text{'}\text{'}\left(x\right)=\frac{f(x+h)+f(x-h)-2f\left(x\right)}{h^2}+O\left(h^2\right)\text{(130)}$$

Cette relation permet de discrétiser les dérivées secondes, par exemple :

$$\frac{{\partial }^{2}V}{\partial x^2}\to \frac{V_{i+1,j}-2V_{i,j}+V_{i-1,j}}{\Delta x^2}\text{(131)}$$

En procédant de même pour l'autre dérivée, on obtient l'équation suivante pour chaque nœud du maillage :

$$\Delta y^2(V_{i+1,j}+V_{i-1,j})+\Delta x^2(V_{i,j+1}+V_{i,j-1})-2(\Delta x^2+\Delta y^2)V_{i,j}=0\text{(132)}$$

Pour les conditions limites, il suffit d'attribuer une valeur fixe au potentiel des points situés sur les conducteurs, ou sur le bord du domaine :

$$V_{i,j}^{bord}=V^{bord}\text{(133)}$$

Si le maillage comporte N nœuds, on obtient ainsi un système de N équations linéaires à résoudre (la linéarité vient de celle de l'équation de Laplace). En principe, ce système pourrait être résolu par la méthode d'élimination de Gauss. En pratique, cela ne fonctionne pas bien car le nombre d'inconnues (plusieurs milliers ou millions) est trop grand, ce qui conduit à des erreurs importantes. Ce type de système est résolu par des méthodes itératives, comme la méthode de Gauss-Seidel.

Pour en savoir plus sur la méthode de Gauss-Seidel : Équation de Poisson : résolution numérique.

Exemples de résolution numérique : Condensateur plan à deux dimensions, Lentille électrostatique à deux conducteurs.

La méthode de discrétisation précédente est appelée méthode des différences finies, car elle consiste à remplacer les dérivées par des différences. Une autre manière de procéder consiste à utiliser le théorème de Gauss. Considérons pour cela une surface S fermée parallélépipédique, dont la projection sur le plan XY est le rectangle (A,B,C,D). L'extension verticale de cette surface est notée Δz.

Comme il n'y a pas de charges, le théorème de Gauss nous dit que flux sortant du champ électrique sur cette surface est nul. Voyons par exemple comment le flux sur la face (AB) peut se discrétiser. L'aire de cette face est ΔxΔz. La composante du champ électrique qui intervient dans ce flux est E_y :

$$E_y=-\frac{\partial V}{\partial y}\text{(134)}$$

Il faut donc discrétiser une dérivée première :

$$E_y\to -\frac{V_{i,j}-V_{i,j-1}}{\Delta y}\text{(135)}$$

On obtient finalement pour la discrétisation du flux sur la face (AB) :

$${\iint }_{AB}\overrightarrow{E}\cdot \overrightarrow{n}dS\to -\frac{V_{i,j}-V_{i,j-1}}{\Delta y}\Delta x\Delta z\text{(136)}$$

La discrétisation du théorème de Gauss conduit donc au même résultat que la discrétisation du laplacien. Cette méthode est appelée méthode des volumes finis. Comparée à la méthode des différences finies, elle a l'avantage de permettre une discrétisation aisée de certaines conditions limites, ou des problèmes à géométrie complexe, par exemple les problèmes en coordonnées cylindriques.

7.a. Coordonnées cylindriques

Opérateur gradient :

$$\overrightarrow{grad}f=\frac{\partial f}{\partial r}{\overrightarrow{u}}_r+\frac{1}{r}\frac{\partial f}{\partial \theta }{\overrightarrow{u}}_{\theta }+\frac{\partial f}{\partial z}{\overrightarrow{u}}_z\text{(137)}$$

Opérateur divergence :

$$div\overrightarrow{a}=\frac{1}{r}\frac{\partial \left(r{a}_r\right)}{\partial r}+\frac{1}{r}\frac{\partial a_{\theta }}{\partial \theta }+\frac{\partial a_z}{\partial z}\text{(138)}$$

Opérateur rotationnel :

$$\overrightarrow{rot}\overrightarrow{a}=(\frac{1}{r}\frac{\partial a_z}{\partial \theta }-\frac{\partial a_{\theta }}{\partial z}){\overrightarrow{u}}_r+(\frac{\partial a_r}{\partial z}-\frac{\partial a_z}{\partial r}){\overrightarrow{u}}_{\theta }+\frac{1}{r}(\frac{\partial \left(r{a}_{\theta }\right)}{\partial r}-\frac{\partial a_r}{\partial \theta }){\overrightarrow{u}}_z\text{(139)}$$

Opérateur laplacien :

$${\nabla }^{2}f=\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial f}{\partial r}\right)+\frac{1}{r^2}\frac{{\partial }^{2}f}{\partial {\theta }^2}+\frac{{\partial }^{2}f}{\partial z^2}\text{(140)}$$

7.b. Coordonnées sphériques

Opérateur gradient :

$$\overrightarrow{grad}f=\frac{\partial f}{\partial r}{\overrightarrow{u}}_r+\frac{1}{r}\frac{\partial f}{\partial \theta }{\overrightarrow{u}}_{\theta }+\frac{1}{rsin\theta }\frac{\partial f}{\partial \phi }{\overrightarrow{u}}_{\phi }\text{(141)}$$

Opérateur divergence :

$$div\overrightarrow{a}=\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2{a}_r\right)+\frac{1}{rsin\theta }\frac{\partial }{\partial \theta }\left(sin\theta a_{\theta }\right)+\frac{1}{rsin\theta }\frac{\partial a_{\phi }}{\partial \phi }\text{(142)}$$

Opérateur rotationnel :

$$\overrightarrow{rot}\overrightarrow{a}=\frac{1}{rsin\theta }(\frac{\partial }{\partial \theta }\left(sin\theta a_{\phi }\right)-\frac{\partial a_{\theta }}{\partial \phi }){\overrightarrow{u}}_r+(\frac{1}{rsin\theta }\frac{\partial a_r}{\partial \phi }-\frac{1}{r}\frac{\partial r{a}_{\phi }}{\partial r}){\overrightarrow{u}}_{\theta }+\frac{1}{r}(\frac{\partial r{a}_{\theta }}{\partial r}-\frac{\partial a_r}{\partial \theta }){\overrightarrow{u}}_{\phi }\text{(143)}$$

Opérateur laplacien :

$${\nabla }^{2}f=\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial f}{\partial r}\right)+\frac{1}{r^{2}sin\theta }\frac{\partial }{\partial \theta }\left(sin\theta \frac{\partial f}{\partial \theta }\right)+\frac{1}{r^2{sin}^2\theta }\frac{{\partial }^{2}f}{\partial {\phi }^2}\text{(144)}$$