Moteur asynchrone

1. Introduction

Ce document montre la réalisation d'un moteur asynchrone expérimental.

Le moteur asynchrone, nommé aussi moteur à induction, comporte un stator bobiné produisant un champ magnétique tournant au niveau de l'entrefer avec le rotor. Le rotor est constitué d'une cage comportant des barreaux parallèles à l'axe (cage d'écureuil). Le rotor tourne moins vite que le champ tournant (d'où le nom de moteur asynchrone), ce qui a pour conséquence l'apparition d'une force électromotrice d'induction dans les barreaux. Ceux-ci étant connectés aux extrémités du rotor, la force électromotrice génère un courant dans ces barreaux. Le couple est engendré par l'interaction de ces courants avec le champ tournant.

Le moteur asynchrone est très répandu dans l'industrie. Les dernières générations de TGV sont équipées de moteurs asynchrones. La simplicité de son rotor et l'absence d'aimants permanents le rendent relativement peu coûteux et très fiable. Dans le domaine des petits véhicules électriques, le moteur synchrone (rotor à aimants permanents ou rotor bobiné) est cependant prépondérant.

Le moteur asynchrone réalisé comporte un rotor en cage d'écureuil est un stator constitué de deux paires de bobines (alimentation diphasée). Le champ tournant généré est bipolaire. L'électronique de commande est un onduleur diphasé réalisé au moyen de deux ponts de transistors MOSFET (convertisseur DC-AC à découpage, nommé inverter en anglais). Les moteurs industriels de dernière génération et les moteurs équipant les véhicules (asynchrones ou synchrones) sont commandés par ce type de convertisseur, qui permet de faire varier à la fois la fréquence du champ tournant et son amplitude.

2. Théorie du moteur asynchrone

La figure suivante montre le schéma de principe d'un rotor de type cage d'écureuil :

Figure pleine page

Les barreaux conducteurs sont reliés aux extrémités par deux anneaux conducteurs. Ces barreaux sont encastrés dans un noyau cylindrique en fer doux (réalisé par assemblage de tôles perpendiculaires à l'axe (Oz)).

La figure suivante représente une coupe transversale du moteur.

Figure pleine page

Le stator est représenté schématiquement par sa partie en fer. Les encoches contenant le bobinage et le noyau en fer du rotor ne sont pas représentés. On se limite au cas d'un moteur à deux pôles (car le dispositif expérimental décrit plus loin en comporte deux).

Idéalement, un stator à pôles lisses génère un champ magnétique dans l'entrefer radial, qui s'écrit en fonction de l'angle θ et du temps sous la forme :

B_{r} (θ, t) = B_{0} cos (ω_{s} t - θ) (1)

où $ω_{s}$ est la vitesse angulaire du champ tournant (l'indice s faisant référence à stator). Des simulations par éléments finis (Champ magnétique généré par un stator) montrent que l'obtention d'un champ de cette forme n'est pas aisé mais qu'on peut y parvenir approximativement avec un stator à encoches et un bobinage convenablement réparti. Très souvent, le champ radial n'est pas parfaitement sinusoïdal et comporte des harmoniques non négligeables.

On verra plus loin que l'expression $(1)$ doit être modifiée pour tenir compte de l'influence de la distance à l'axe.

Le champ comporte deux pôles. Le pôle Nord (N) correspond à $B_{r} = - B_{0}$ , le pôle sud à $B_{r} = B_{0}$ . Le pôle nord (N) se trouve en $θ = π$ à t=0 et le pôle sud se trouve en $θ = 0$ à cet instant. Ces deux pôles tournent à la vitesse angulaire $ω_{s}$ . Voici les positions des deux pôles aux instants $t = 0, T_{s} / 4, T_{s} / 2, 3 T_{2} / 4$ :

Figure pleine page

Soit $ω$ la vitesse de rotation du moteur. En fonctionnement moteur, le rotor tourne toujours moins vite que le champ : $ω < ω_{s}$ .

Soit N le nombre de barreaux du rotor. Si la vitesse angulaire est constante, la position angulaire du barreau d'indice k est :

θ_{k} (t) = ω t + 2 π \frac{k}{N} (2)

Pour déterminer le couple développé dans le rotor, il faut tout d'abord déterminer le courant électrique induit dans les barreaux. Rappelons la loi de Faraday, qui permet de calculer aisément le courant induit lorsque celui-ci se fait le long d'une courbe fermée C. Si $Φ_{C} (t)$ désigne le flux magnétique à travers une surface quelconque délimitée par la courbe C, la force électromotrice (f.é.m.) sur ce circuit est :

e (t) = - \frac{d Φ_{C}}{d t} (3)

Dans le cas de la cage d'écureuil, le courant électrique ne suit pas un chemin qui peut se définir par une courbe fermée; il n'est donc pas possible d'utiliser la loi de Faraday.

La f.é.m. peut aussi être calculée par l'intégrale suivante :

e (t) = \oint_{C} (\vec{v} \land \vec{B}) \cdot d \vec{ℓ} - \oint_{C} \frac{\partial \vec{A}}{\partial t} \cdot d \vec{ℓ} (4)

où $\vec{v}$ est la vitesse du conducteur au point considéré et $\vec{A}$ un potentiel vecteur, c'est-à-dire un vecteur tel que $\vec{B} = \vec{r o t} \vec{A}$ . Pour un champ magnétique $\vec{B}$ donné, le potentiel vecteur n'est pas unique mais sa circulation sur une courbe fermée l'est. Le premier terme de $(4)$ est la f.é.m. causée par le déplacement du conducteur, le second est celle causée par la variation au cours du temps du champ magnétique.

Définissons la force électromotrice dans le barreau d'indice k comme l'intégrale suivante (voir figure ci-dessus) :

e_{k} (t) = \int_{A}^{B} (\vec{v} \land \vec{B}) \cdot d \vec{ℓ} - \int_{A}^{B} \frac{\partial \vec{A}}{\partial t} \cdot d \vec{ℓ} (5)

Faisons de plus l'hypothèse que le champ électromagnétique est invariant par translation dans la direction z (les effets de bord aux extrémités du stator sont négligés). La f.é.m. pour le barreau d'indice k s'écrit alors :

e_{k} (t) = ℓ (\vec{v} \land \vec{B} - \frac{\partial \vec{A}}{\partial t}) \cdot {\vec{u}}_{z} (6)

où $ℓ$ est la longueur du barreau. Remarquons que cette f.é.m. à elle seule ne permet pas a priori de déterminer le courant induit dans le barreau, ni même son sens. Pour déterminer le courant induit, il faut considérer l'ensemble des N barreaux, selon le schéma équivalent suivant :

Figure pleine page

Ce schéma suppose que la résistance électrique et l'auto-inductance des deux anneaux qui font la liaison aux extrémités de la cage sont négligeables, ce qui n'est pas réaliste. On peut cependant considérer que la résistance des anneaux est incluse dans celle des barreaux.

Le potentiel vecteur n'est pas unique mais cette indétermination disparaît lorsqu'on considère le circuit complet. Autrement dit, c'est la comparaison entre les f.é.m. dans les différents barreaux qui permet de déterminer le sens du courant induit dans chaque barreau.

L'évaluation du premier terme de $(6)$ ne pose pas de difficultés car il fait intervenir seulement le champ magnétique dans l'entrefer, défini par $(1)$ . Le second terme est plus difficile à évaluer car la détermination d'un potentiel vecteur doit se faire par résolution de l'équation :

\vec{B} = \vec{r o t} \vec{A} (7)

Pour cela, il faut savoir comment le champ $\vec{B}$ varie dans l'espace. Or l'expression $(1)$ du champ dans l'entrefer correspond en fait au champ moyen dans l'entrefer (la variation avec r n'apparaît pas). On remarque d'ailleurs que la divergence de cette expression n'est pas nulle alors qu'on devrait avoir $d i v \vec{B} = 0$ . Si l'on suppose que le champ est radial et ne dépend que de r (la distance à l'axe), la divergence en coordonnées cylindriques s'écrit :

d i v \vec{B} = \frac{1}{r} \frac{\partial (r B_{r})}{\partial r} (8)

Cette divergence étant nulle, $r B_{r}$ doit être indépendant de r. On adopte donc l'expression suivante du champ dans l'entrefer :

B_{r} (r, θ, t) = B_{0} \frac{r_{0}}{r} cos (ω_{s} t - θ) (9)

où r₀ est le rayon du rotor (distance à l'axe des barreaux) et B₀ l'amplitude du champ ressenti par les barreaux. Cette expression du champ n'est valable que localement, au voisinage des barreaux du rotor. À l'intérieur du rotor (pour r<r₀), le champ magnétique est proche d'un champ uniforme dirigé selon l'axe nord-sud.

Le potentiel vecteur est dans la direction des courants qui génèrent le champ magnétique. Celui-ci étant invariant par translation selon z, ces courants sont dans la direction z. On a donc $\vec{A} = A_{z} (r, θ, t) \vec{u_{z}}$ . L'équation $\vec{r o t} \vec{A} = \vec{B}$ s'écrit en coordonnées cylindriques :

\frac{1}{r} \frac{\partial A_{z}}{\partial θ} = B_{0} \frac{r_{0}}{r} cos (θ - ω_{s} t) (10)

ce qui conduit à :

\frac{\partial A_{z}}{\partial θ} = B_{0} r_{0} cos (θ - ω_{s} t) (11)

Le potentiel vecteur est donc indépendant de r. On obtient :

A_{z} (θ, t) = B_{0} r_{0} sin (ω_{s} t - θ) (12)

Nous pouvons à présent expliciter la f.é.m. dans le barreau d'indice k :

\begin{matrix} e_{k} (t) & = - ℓ r_{0} ω B_{0} cos (ω_{s} t - θ_{k} (t)) + ℓ B_{0} r_{0} ω_{s} cos (ω_{s} t - θ_{k} (t)) \\ = ℓ B_{0} r_{0} (ω_{s} - ω) cos (ω_{s} t - θ_{k} (t)) \\ = ℓ r_{0} (ω_{s} - ω) B_{r} (θ_{k} (t), t) \end{matrix}

et finalement :

e_{k} (t) = ℓ r_{0} (ω_{s} - ω) B_{0} cos ((ω_{s} - ω) t - 2 π \frac{k}{N}) (13)

L'amplitude est proportionnelle à la différence des vitesses angulaires $ω_{s} - ω$ , nommée vitesse (angulaire) de glissement. En fonctionnement moteur, la vitesse de glissement est positive. En conséquence, la f.é.m. est positive dans les barreaux qui font face au pôle S du stator ( $B_{r} > 0$ ) et négative dans les barreaux qui font face au pôle N du stator ( $B_{r} < 0$ ). La figure suivante montre le signe de la f.é.m. dans les barreaux aux instants multiples de T_s :

Figure pleine page

Si les courants dans les barreaux sont dans le même sens que la f.é.m., la force de Laplace dans chaque barreau est bien dans le sens de rotation du rotor.

Pour déterminer les courants induits dans les barreaux, considérons le réseau électrique équivalent représenté plus haut. La tension entre les deux extrémités du barreau d'indice k s'écrit :

u_{k} (t) = e_{k} (t) - L \frac{d i_{k} (t)}{d t} - R i_{k} (t) (14)

La f.é.m. dans les deux anneaux qui ferment la cage aux extrémités peut être négligée car le champ électromoteur est perpendiculaire au conducteur. Cependant, la résistance électrique et le coefficient d'auto-inductance de ces anneaux ne sont pas négligeables. En première approche, on considère néanmoins qu'ils le sont (cohérent avec l'hypothèse d'une cage très longue), ce qui conduit au schéma électrique équivalent représenté plus haut. On a donc :

u_{0} (t) = u_{1} (t) = \dots u_{N - 1} (t) (15)

On obtient ainsi N-1 équations pour les N inconnues i_k(t), auxquels il faut ajouter la loi des nœuds :

i_{0} (t) + i_{1} (t) + \dots i_{N - 1} (t) = 0 (16)

Les f.é.m. dans les barreaux sont sinusoïdales, de pulsation $Ω = ω_{s} - ω$ (la vitesse de glissement). On recherche les intensités des courants en régime permanent, qui sont aussi sinusoïdales et de pulsation $Ω$ . L'amplitude complexe de la f.é.m. est :

\underset{̲}{E_{k}} = ℓ r_{0} B_{0} Ω exp (- j 2 π \frac{k}{N}) (17)

Les équations vérifiées par les amplitudes complexes des intensités des courants sont :

\begin{matrix} \underset{̲}{E_{k}} - j L Ω \underset{̲}{I_{k}} - R \underset{̲}{I_{k}} = \underset{̲}{E_{k + 1}} - j L Ω \underset{̲}{I_{k + 1}} - R \underset{̲}{I_{k + 1}} p o u r k = 0, 1, \dots N - 2 & (18) \\ \underset{̲}{I_{0}} + \underset{̲}{I_{1}} + \dots \underset{̲}{I_{N - 1}} = 0 & (19) \end{matrix}

La vitesse de glissement peut être très faible (lorsque le moteur tourne à vide), donc le terme résistif $R \underset{̲}{I_{k}}$ n'est pas en général négligeable.

Posons $\underset{̲}{Z} = R + j L ω$ . Voici l'écriture matricielle du système d'équations permettant de déterminer les courants induits (dans le cas N=6) :

(\begin{matrix} \underset{̲}{Z} & - \underset{̲}{Z} & 0 & 0 & 0 & 0 \\ 0 & \underset{̲}{Z} & - \underset{̲}{Z} & 0 & 0 & 0 \\ 0 & 0 & \underset{̲}{Z} & - \underset{̲}{Z} & 0 & 0 \\ 0 & 0 & 0 & \underset{̲}{Z} & - \underset{̲}{Z} & 0 \\ 0 & 0 & 0 & 0 & \underset{̲}{Z} & - \underset{̲}{Z} \\ 1 & 1 & 1 & 1 & 1 & 1 \end{matrix}) (\begin{matrix} \underset{̲}{I_{0}} \\ \underset{̲}{I_{1}} \\ \underset{̲}{I_{2}} \\ \underset{̲}{I_{3}} \\ \underset{̲}{I_{4}} \\ \underset{̲}{I_{5}} \end{matrix}) = (\begin{matrix} \underset{̲}{E_{0}} - \underset{̲}{E_{1}} \\ \underset{̲}{E_{1}} - \underset{̲}{E_{2}} \\ \underset{̲}{E_{2}} - \underset{̲}{E_{3}} \\ \underset{̲}{E_{3}} - \underset{̲}{E_{4}} \\ \underset{̲}{E_{4}} - \underset{̲}{E_{5}} \\ 0 \end{matrix}) (20)

La force de Laplace sur un barreau est orthoradiale. Le moment de cette force par rapport à l'axe de rotation est :

Γ_{k} (t) = ℓ r_{0} i_{k} (t) B_{r} (θ_{k} (t), t) (21)

Si l'on note $φ_{k}$ l'agument de $\underset{̲}{I_{k}}$ et $I_{k}$ son module, on a :

Γ_{k} (t) = ℓ r_{0} I_{k} cos (Ω t + φ_{k}) B_{0} cos (Ω t - 2 π \frac{k}{N}) (22)

Le moment total sur le rotor (moment du couple moteur) est :

Γ (t) = \sum_{k = 0}^{N - 1} Γ_{k} (t) (23)

Recherchons une expression de ce couple moteur. Il faut tout d'abord résoudre le système $(20)$ par élimination. On démontre par récurrence que :

\underset{̲}{I_{k}} = \underset{̲}{I_{0}} + \frac{\underset{̲}{E_{k}} - \underset{̲}{E_{0}}}{\underset{̲}{Z}} (24)

La dernière équation du système s'écrit donc :

N \underset{̲}{I_{0}} + \frac{1}{\underset{̲}{Z}} \sum_{k = 0}^{N - 1} (\underset{̲}{E_{k}} - \underset{̲}{E_{0}}) = 0 (25)

d'où l'on déduit :

\underset{̲}{I_{0}} = \frac{1}{N \underset{̲}{Z}} (N \underset{̲}{E_{0}} - \sum_{k = 0}^{N - 1} \underset{̲}{E_{k}}) (26)

puis par récurrence :

\underset{̲}{I_{k}} = \frac{1}{N \underset{̲}{Z}} (N \underset{̲}{E_{k}} - \sum_{k = 0}^{N - 1} \underset{̲}{E_{k}}) (27)

La somme des amplitudes complexes des f.é.m. s'écrit :

\sum_{k = 0}^{N - 1} \underset{̲}{E_{k}} = ℓ r_{0} B_{0} Ω \sum_{k = 0}^{N - 1} exp (- j 2 π \frac{k}{N}) = 0 (28)

On a donc :

\underset{̲}{I_{k}} = \frac{\underset{̲}{E_{k}}}{\underset{̲}{Z}} (29)

Finalement, nous constatons que chaque barreau peut être traité comme un circuit fermé. Posons $\underset{̲}{Z} = Z exp (j Φ)$ . L'amplitude complexe de l'intensité du courant s'écrit :

\underset{̲}{I_{k}} = \frac{ℓ r_{0} B_{0} Ω}{Z} exp (- j (2 π \frac{k}{N} + Φ)) (30)

On a donc :

φ_{k} = - 2 π \frac{k}{N} - Φ (31)

Le moment de la force de Laplace sur le barreau d'indice k s'écrit :

\begin{matrix} Γ_{k} (t) & = {(ℓ r_{0} B_{0})}^{2} \frac{Ω}{Z} cos (Ω t - 2 π \frac{k}{N} - Φ) cos (Ω t - 2 π \frac{k}{N}) & (32) \\ = {(ℓ r_{0} B_{0})}^{2} \frac{Ω}{2 Z} (cos (Φ) + cos (2 Ω t - 2 π \frac{k}{N} - Φ)) & (33) \end{matrix}

La somme de ces moments pour k allant de 0 à N-1 est le moment du couple moteur (ou couple moteur). La somme de $cos (2 Ω t - 2 π \frac{k}{N} - Φ)$ est nulle :

\sum_{k = 0}^{N - 1} cos (2 Ω t - 2 π \frac{k}{N} - Φ) = R e [exp (j (2 Ω t - Φ)) \sum_{k = 0}^{N - 1} exp (- j 2 π \frac{k}{N})] = R e [exp (j (2 Ω t - Φ)) \frac{1 - exp (- j 2 π)}{1 - exp (- j \frac{2 π}{N})}] = 0 (34)

Γ = N {(ℓ r_{0} B_{0})}^{2} \frac{Ω}{2 Z} cos (Φ) (35)

Ce moment est donc indépendant du temps (quel que soit le nombre de barreaux). En explicitant l'impédance, on obtient :

Γ (Ω) = \frac{N {(ℓ r_{0} B_{0})}^{2} R Ω}{2 (R^{2} + L^{2} Ω^{2})} (36)

Si $\frac{R}{L} < ω_{s}$ , le moment du couple moteur présente un maximum pour $Ω = \frac{R}{L}$ . Le couple maximal dans ce cas est :

Γ_{m a x} = \frac{N {(ℓ r_{0} B_{0})}^{2}}{4 L} (37)

Si $\frac{R}{L} > ω_{s}$ , le couple est une fonction croissante de $Ω$ et le couple maximal est obtenu pour $Ω = ω_{s}$ (rotor fixe). Son expression est :

Γ'_{m a x} = \frac{N {(ℓ r_{0} B_{0})}^{2} R ω_{s}}{2 (R^{2} + L^{2} ω_{s}^{2})} (38)

Le moment du couple moteur est proportionnel au nombre de barreaux et au carré de l'amplitude du champ magnétique. Cette dernière dépendance montre que la bonne conception du stator et la faible épaisseur de l'entrefer sont très importantes pour l'obtention d'un couple élevé.

Remarque : la modélisation classique du moteur à cage d'écureuil consiste à considérer un cadre formé de deux barreaux diamétralement opposés et à considérer sa rotation dans un champ magnétique tournant uniforme. Ce modèle est développé en annexe. Il conduit aux mêmes mêmes résultats que le modèle présenté ci-dessus.

On introduit la vitesse relative de glissement (nommée glissement), définie par :

s = \frac{ω_{s} - ω}{ω_{s}} = \frac{Ω}{ω_{s}} (39)

Le moment du couple moteur s'exprime en fonction du glissement :

Γ (s) = \frac{N {(ℓ r_{0} B_{0})}^{2} R ω_{s} s}{2 (R^{2} + L^{2} ω_{s}^{2} s^{2})} (40)

Si $\frac{R}{L} < ω_{s}$ le moment du couple admet un maximum pour :

s_{m a x} = \frac{R}{L ω_{s}} (41)

et le moment maximal est :

Γ_{m a x} = \frac{N {(ℓ r_{0} B_{0})}^{2}}{L} (42)

Si $\frac{R}{L} > ω_{s}$ le moment est une fonction croissante de s et il est donc maximal pour s=1.

Voici un exemple de calcul numérique des courants, des moments de force sur chaque barreau et du moment total, pour un rotor contenant 16 barreaux (comme sur les figures ci-dessus). Les ordres de grandeur des paramètres sont ceux du moteur expérimental décrit plus loin.

import numpy as np
from scipy.linalg import solve
from matplotlib.pyplot import *

l = 0.1
r0 = 0.03
B0 = 100e-3
N = 16
R=1e-5
L=1e-5
ws = 10 # vitesse angulaire du champ tournant
def courants(s):
    # s : vitesse de glissement relative
    Omega = s*ws
    E = l*r0*B0*Omega*np.exp(-1j*2*np.pi*np.arange(N)/N)
    Z = R+1j*L*Omega
    return E/Z
    
def moment_barreau(I,s,k,t):
    Ik = I[k]
    Omega = s*ws
    return l*r0*np.absolute(Ik)*np.cos(Omega*t+np.angle(Ik))*B0*np.cos(Omega*t-2*np.pi*k/N)
    
s = 0.05
Omega = s*ws
t = np.linspace(0,2*np.pi/Omega,1000)
I = courants(s)

figure(figsize=(16,6))
for k in range(N):
    Gk = moment_barreau(I,s,k,t)
    plot(t,Gk,label="k = %d"%k)
grid()
xlabel("t (s)")
ylabel(r"$\Gamma_k\ (\rm N\cdot m)$")
legend(loc='upper right')

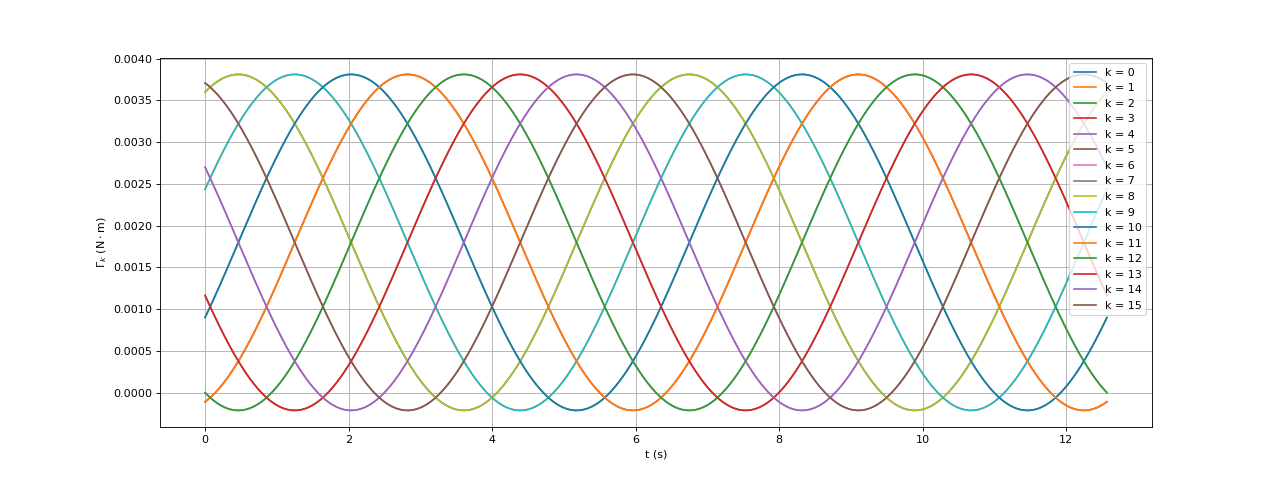fig1.pdf

Le moment de la force de Laplace sur un barreau n'est pas toujours positif mais sa valeur moyenne est bien positive. Voici le moment du couple moteur en fonction du temps :

def moment(I,s,t):
    G = 0
    for k in range(N):
        G += moment_barreau(I,s,k,t)
    return G
    
def Gamma(ws,N,R,L,s):
    Omega = s*ws
    return N*(l*r0*B0)**2*Omega*R/(2*(R**2+(L*Omega)**2))
    
G = moment(I,s,t)
figure(figsize=(16,6))
plot(t,G)
xlabel("t (s)")
ylabel(r"$\Gamma\ (\rm N\cdot m)$")
grid()

print(Gamma(ws,N,R,L,s))
--> 0.0288

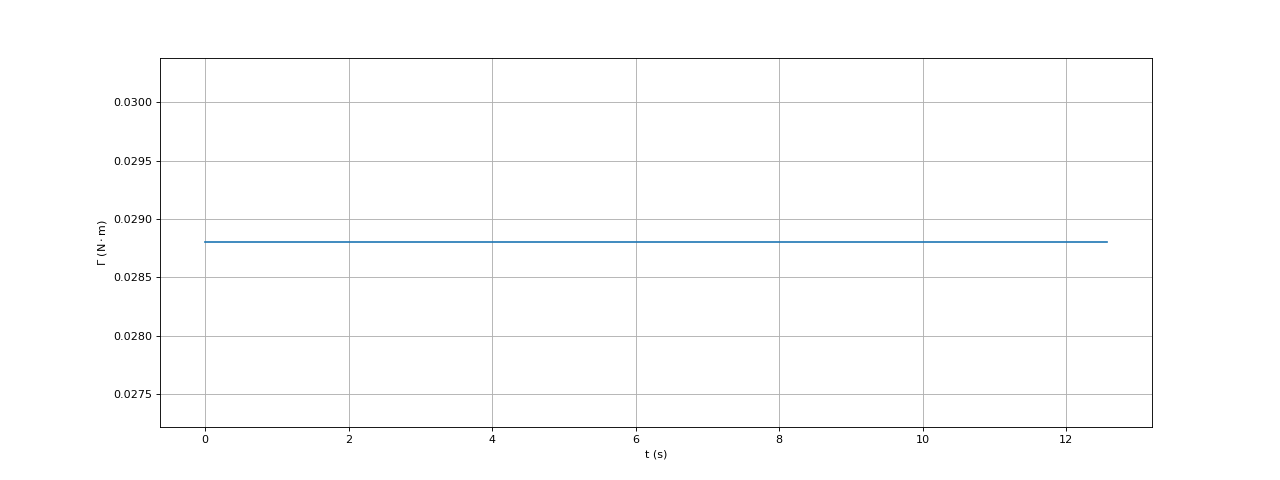fig2.pdf

Le moment du couple moteur est bien constant (comme le montre le calcul précédent). Voici le tracé de ce moment en fonction de la vitesse relative de glissement :

R=1e-5
L=1e-5
s = np.linspace(0,1,1000)
G = Gamma(ws,N,R,L,s)
figure()
plot(s,G)
grid()
xlabel("s")
ylabel(r"$\Gamma\ (\rm N\cdot m)$")

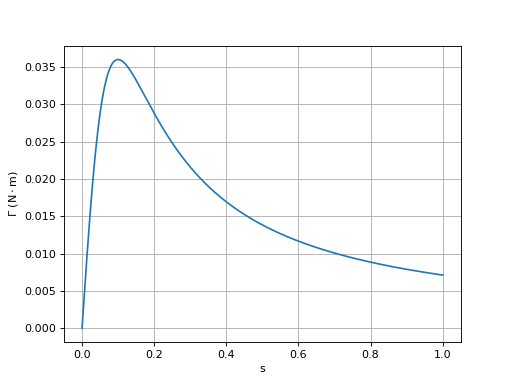fig3.pdf

Pour ces valeurs de R et L, le couple présente un maximum. Il faut remarquer que lorsque le rotor est immobile, la vitesse de glissement relative est 1. Le couple moteur au démarrage est donc nettement plus bas que le couple maximal, ce qui peut poser problème si la charge mécanique est présente dès le démarrage.

La forme de la courbe dépend de l'importance relative de la résistance des barreaux et de leur impédance inductive pour la fréquence de rotation du champ. Voici un autre exemple, avec une résistance 10 fois plus grande :

R=1e-4
L=1e-5
G = Gamma(ws,N,R,L,s)
figure()
plot(s,G)
grid()
xlabel("s")
ylabel(r"$\Gamma\ (\rm N\cdot m)$")

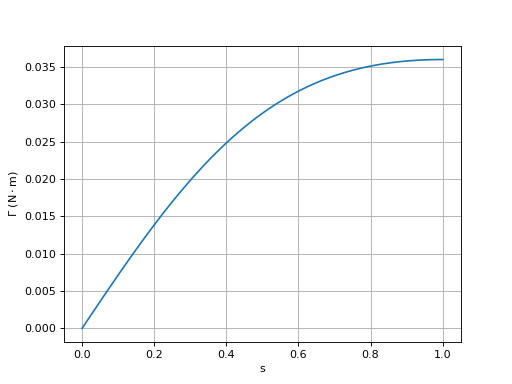fig4.pdf

Lorsque la résistance est relativement grande (par rapport à l'impédance inductive), le couple est une fonction croissante de la vitesse de glissement. En conséquence, la vitesse de glissement peut être proche de 1 lorsque le couple demandé est grand, ce qui signifie que la vitesse de rotation peut être beaucoup plus faible que la vitesse du champ tournant. Le couple de démarrage (lorsque s=1) est plus grand avec cette résistance 10 fois plus grande : en effet, si on prolonge la courbe pour s>1, on voit que le point de glissement 1 se trouve un peu avant le maximum du couple. Au contraire, si la résistance est très faible, la vitesse de rotation du moteur peut être proche de celle du champ tournant mais le couple de démarrage est nettement plus bas que le couple maximal. Dans le cas d'un rotor de type cage d'écureuil, les valeurs de L et R sont déterminées par construction. Lorsque le rotor est constitué d'un bobinage, il est possible d'ajouter une résistance dans le circuit du rotor afin d'augmenter R, ce qui permet d'avoir un couple de démarrage plus grand. Une résistance additionnelle est placée en dehors du moteur et reliée au rotor bobiné par des balais. Lorsque le moteur est lancé, la résistance peut être abaissée afin d'augmenter la vitesse du moteur.

Il faut remarquer que l'évaluation de R pour une cage d'écureuil donnée ne pose pas de problème (l'effet de peau peut être négligé car la fréquence est basse). En revanche, l'évaluation de L est beaucoup plus difficile. Par ailleurs, la prise en compte de l'effet des deux anneaux qui ferment la cage aux extrémités aurait probablement un effet on négligeable (sans modifier la forme de la courbe ni les ordres de grandeur).

Voici plusieurs courbes de couple moteur pour différentes valeurs de R :


figure(figsize=(12,6))
G = Gamma(ws,N,10e-6,L,s)
plot(s,G,label="R=10 u")
G = Gamma(ws,N,50e-6,L,s)
plot(s,G,label="R=50 u")
G = Gamma(ws,N,100e-6,L,s)
plot(s,G,label="R=100 u")
G = Gamma(ws,N,200e-6,L,s)
plot(s,G,label="R=200 u")
G = Gamma(ws,N,400e-6,L,s)
plot(s,G,label="R=400 u")
grid()
xlabel("s",fontsize=16)
ylabel(r"$\Gamma\ (\rm N\cdot m)$",fontsize=16)
legend(loc='lower right')

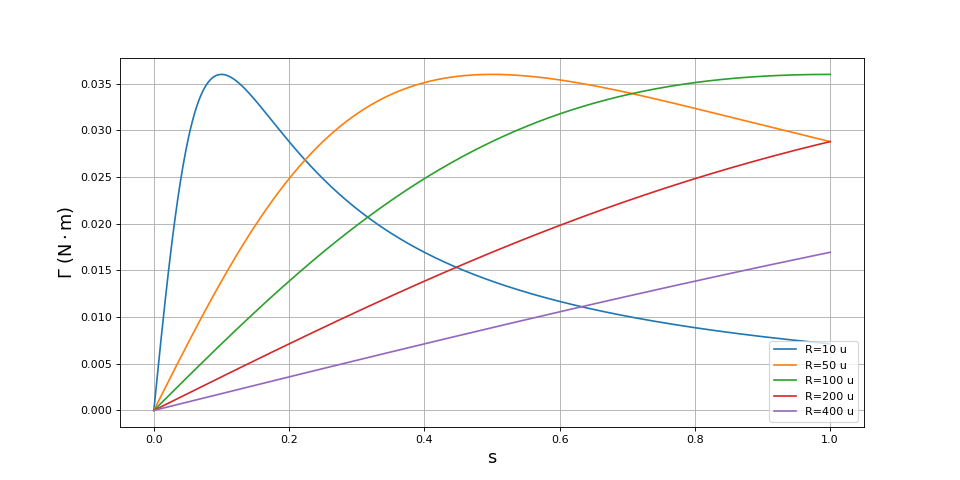fig5.pdf

Ces courbes montrent que le couple de démarrage (s=1) est maximal pour une résistance d'environ 100 μΩ. Pour une résistance plus grande, le couple de démarrage diminue. La résistance de 100 μΩ fournit un couple au démarrage maximal mais si le couple en régime permanent est proche du maximum alors la vitesse de rotation du moteur est faible (par rapport à la vitesse de rotation du champ). Si la résistance est 10 μΩ, le couple au démarrage est plus faible mais la vitesse en régime permanent (qui se situe dans la partie croissante) est beaucoup plus grande.

La vitesse de glissement du moteur en régime permanent dépend de la charge appliquée au rotor. Supposons que celle-ci consiste en un couple constant, noté $Γ_{c}$ , ce qui est par exemple le cas si le moteur doit soulever une charge dans le champ de pesanteur et si le couple de frottement est négligeable. Si cette charge est appliquée dès le démarrage, il faut que le couple moteur au démarrage soit supérieur à $Γ_{c}$ . La théorie développée ci-dessus suppose que le moteur tourne à vitesse constante mais admettons que le moment du couple moteur obtenu $(40)$ soit valable aussi en régime transistoire. Le moment du couple moteur au démarrage est $Γ (s = 1)$ . En régime permanent, la vitesse angulaire du rotor est constante donc on doit avoir :

Γ (s) + Γ_{c} = 0 (43)

Le moment $Γ_{c}$ est négatif puisqu'il résulte de forces qui s'opposent à la rotation du rotor. Reprenons l'exemple précédent avec une résistance de 10 μΩ. Voici un exemple vraisemblable de détermination du point de fonctionnement :

figure(figsize=(12,6))
G = Gamma(ws,N,10e-6,L,s)
plot(s,G,label="R=10 u")
Gc = -5e-3
plot([0,1],[-Gc,-Gc],'k-')
grid()
xlabel("s",fontsize=16)
ylabel(r"$\Gamma\ (\rm N\cdot m)$",fontsize=16)
legend(loc='lower right')

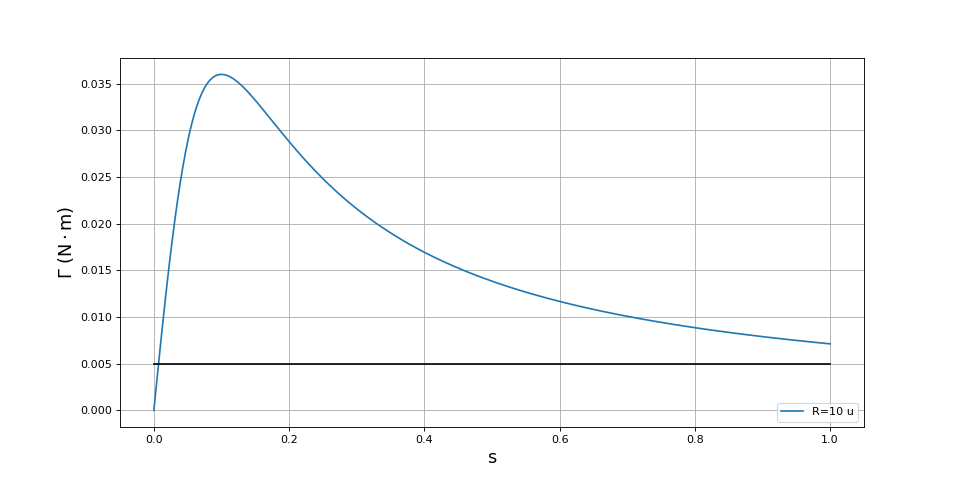fig6.pdf

Le point de fonctionnement est à l'intersection de ces deux courbes. Il est dans la partie croissante du couple en fonction du glissement et le glissement est faible, ce qui signifie que le rotor tourne à une vitesse proche de la vitesse du champ tournant. Le fonctionnement est stable : si la vitesse du rotor augmente, le glissement diminue et le couple total qui lui est appliqué devient négatif.

Considérons le cas d'une résistance de 100 μΩ avec une valeur de $Γ_{c}$ six fois plus grande :

figure(figsize=(12,6))
G = Gamma(ws,N,100e-6,L,s)
plot(s,G,'g-',label="R=10 u")
Gc = -30e-3
plot([0,1],[-Gc,-Gc],'k-')
grid()
xlabel("s",fontsize=16)
ylabel(r"$\Gamma\ (\rm N\cdot m)$",fontsize=16)
legend(loc='lower right')

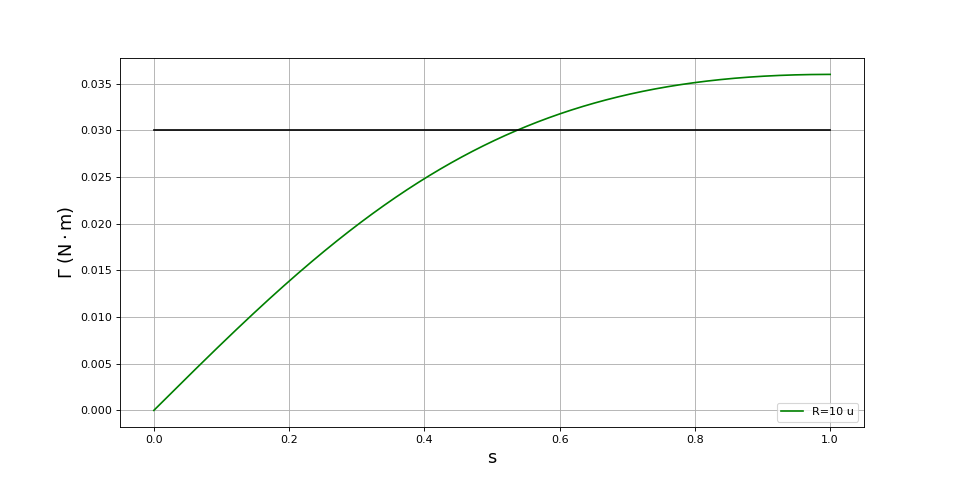fig7.pdf

Dans ce cas, la vitesse de rotation du moteur est environ la moitié de celle du champ tournant. Un rotor avec une résistance plus faible a l'avantage de permettre un couple au démarrage plus fort mais il a l'inconvénient de conduire à une vitesse de rotation plus faible. L'inconvénient de ce point de fonctionnement est surtout que la vitesse du rotor est très sensible à $Γ_{c}$ . Au contraire, si la résistance est faible, le glissement en régime permanent reste très faible donc la vitesse de rotation reste très proche de celle du champ tournant : la vitesse du moteur est donc quasi constante (à $B_{0}$ et $ω_{s}$ constants). Dans le premier cas, maintenir la vitesse constante nécessitera un asservissement afin de modifier soit la valeur de $B_{0}$ soit la valeur de $ω_{s}$ .

Par ailleurs, le rendement de la conversion électromécanique dans le rotor est meilleur lorsque la vitesse de glissement est faible (cette propriété est démontrée en annexe). En régime permanent, on doit donc faire fonctionner le moteur avec une résistance de rotor faible, afin que le point de fonctionnement soit à faible glissement.

Remarque : dans le cas où le couple moteur présente un maximum (résistance faible), il est possible que le point de fonctionnement soit dans la partie décroissante lorsque le couple $- Γ_{c}$ est une fonction croissante de la vitesse angulaire (voir l'expérience plus loin). Cependant, si $Γ_{c}$ est constante, un point de fonctionnement dans cette partie est instable : une augmentation de la vitesse du rotor se traduit par une augmentation du couple total.

Il est aussi intéressant de voir l'influence de la fréquence du champ tournant sur la courbe du couple moteur :

figure(figsize=(12,6))
R = 10e-6
G = Gamma(5,N,R,L,s)
plot(s,G,label=r"$\omega_s=5\,\rm rad\cdot s^{-1}$")
G = Gamma(10,N,R,L,s)
plot(s,G,label=r"$\omega_s=10\,\rm rad\cdot s^{-1}$")
G = Gamma(20,N,R,L,s)
plot(s,G,label=r"$\omega_s=20\,\rm rad\cdot s^{-1}$")
G = Gamma(30,N,R,L,s)
plot(s,G,label=r"$\omega_s=40\,\rm rad\cdot s^{-1}$")
grid()
xlabel("s",fontsize=16)
ylabel(r"$\Gamma\ (\rm N\cdot m)$",fontsize=16)
legend(loc='upper right')

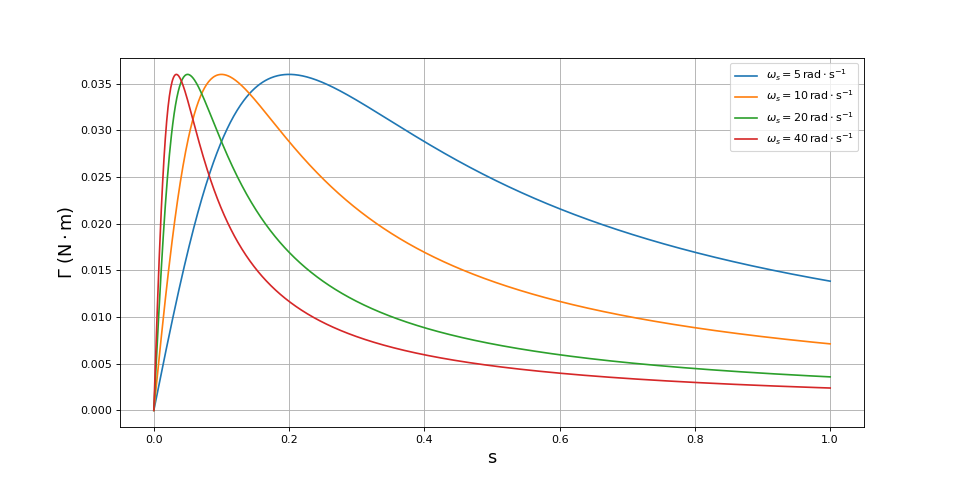fig8.pdf

L'augmentation de la fréquence de rotation du champ a pour effet de réduire le couple moteur au démarrage et conduit à une vitesse de glissement plus faible. Pour obtenir une rotation rapide, on a donc intérêt à démarrer le moteur à une faible fréquence et à l'augmenter progressivement dès que le point de fonctionnement atteint la partie croissante.

Un autre point à considérer est l'intensité du courant dans le rotor. L'amplitude de crête de l'oscillation du courant dans un barreau est :

I_{0} = \frac{ℓ r_{0} B_{0} Ω}{\sqrt{R^{2} + L^{2} Ω^{2}}} (44)

def courant(ws,N,R,L,s):
    Omega = ws*s
    return l*r0*B0*Omega/np.sqrt(R**2+(L*Omega)**2)
figure(figsize=(12,6))
R = 10e-6
I = courant(5,N,R,L,s)
plot(s,I,label=r"$\omega_s=5\,\rm rad\cdot s^{-1}$")
I = courant(10,N,R,L,s)
plot(s,I,label=r"$\omega_s=10\,\rm rad\cdot s^{-1}$")
I = courant(20,N,R,L,s)
plot(s,I,label=r"$\omega_s=20\,\rm rad\cdot s^{-1}$")
I = courant(30,N,R,L,s)
plot(s,I,label=r"$\omega_s=40\,\rm rad\cdot s^{-1}$")
grid()
xlabel("s",fontsize=16)
ylabel(r"$I\ (\rm A)$",fontsize=16)
legend(loc='lower right')

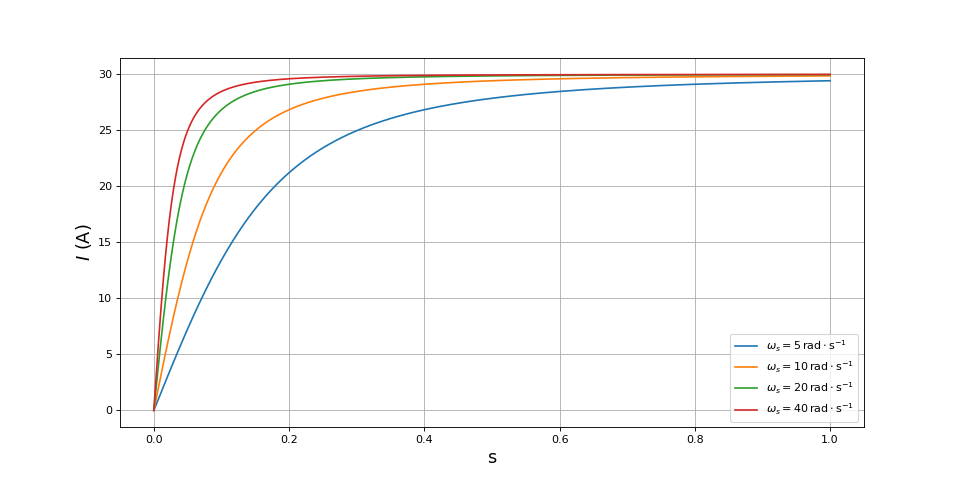fig9.pdf

Le courant est très fort au moment du démarrage. En régime permanent, le glissement est faible et le courant est nettement moins grand.

La puissance mécanique développée par le rotor (produit $Γ ω$ ) provient bien sûr de la source d'énergie. Une étude complète du moteur doit aussi s'intéresser à l'effet de la rotation du rotor sur le stator. Le courant induit dans le rotor produit un champ magnétique qui engendre une f.é.m. dans le stator (force contre-électromotrice). Une théorie détaillée permettant de calculer l'effet du rotor sur le stator sort du cadre de ce document car elle devrait faire intervenir les bobinages du stator ainsi que les parties en fer. Il est généralement admis que le champ dans l'entrefer (celui qui intervient dans le cacul du couple moteur) n'est que très peu affecté par le champ créé par le rotor (nous supposons que ce point a été vérifié par des simulations). Il est certain qu'il y a un effet mais nous supposons qu'il est négligeable et qu'en conséquence l'expression du champ magnétique dans l'entrefer $(9)$ reste valable lorsque le rotor tourne.

Il est possible de donner un schéma électrique équivalent du moteur. Le rotor est assimilé à un circuit à une seule maille. Notons i(t) l'intensité du courant dans ce rotor. Il faut remarquer que i(t) n'est certainement pas la somme des courants dans les barreaux car cette dernière est nulle à tout instant. La force électromotrice d'induction dans le rotor est notée e(t) (là aussi, il ne s'agit pas de la somme des e_k). On introduit L_r le coefficient d'auto-inductance du rotor et R_r sa résistance. Le circuit du stator est constitué de la source d'énergie, que l'on supposera assimillable à une source de tension V_s(t), d'une résistance R_s (traduisant l'ensemble des pertes dans le stator) et d'une auto-inductance L_s. La force contre-électromotrice est notée e_s(t).

Figure pleine page

La force contre-électromotrice ainsi définie est la f.é.m. qui apparaît dans le stator à cause des courants induits dans le rotor, que celui-ci soit fixe ou en mouvement. En conséquence, cette force contre-électromotrice n'est pas nulle lorsque le rotor est fixe. Nous remarquons cette propriété car dans un moteur synchrone (ou dans un moteur à courant continu) la force contre-électromotrice n'apparaît que si le rotor tourne et augmente avec la vitesse de rotation. Dans le cas du moteur asynchrone, la force contre-électromotrice est au contraire maximale lorsque le rotor ne tourne pas et son amplitude se réduit lorsque la vitesse de rotation augmente (voir l'expression donnée plus loin).

Un point important à remarquer est l'impossibilité d'utiliser un modèle faisant intervenir une inductance mutuelle constante entre le stator et le rotor. En effet, comme le montre le modèle développé en annexe, le coefficient d'inductance mutuelle varie au cours du temps à cause de la rotation du rotor.

La puissance instantanée fournie par la source s'écrit :

P_{s} (t) = V_{s} (t) i_{s} (t) = R_{s} i_{s}^{2} + L_{s} i_{s} \frac{d i_{s}}{d t} + e_{s} i_{s} (45)

Le premier terme est la puissance dissipée dans le stator (fil de cuivre et noyau), le deuxième est la puissance fournie au champ magnétique créé par le stator seul (nulle en moyenne) et le troisième est la puissance transmise au rotor. En valeur moyenne, ce bilan de puissance s'écrit :

< P_{s} > = < R i_{s}^{2} > + < e_{s} i_{s} > (46)

Le bilan de puissance dans le rotor doit faire intervenir la puissance mécanique $P_{m} = Γ ω$ (qui est constante en régime permanent). La puissance moyenne reçue du stator est égale à la puissance dissipée plus la puissance mécanique (la puissance échangée avec le champ est nulle en moyenne) :

< e_{s} i_{s} > = < R_{r} i^{2} > + Γ ω (47)

La loi des mailles dans le rotor implique que :

e i = L_{r} i \frac{d i}{d t} + R_{r} i^{2} (48)

qui s'écrit en moyenne :

< e i > = < R_{r} i^{2} >

En conséquence, on a :

< e_{s} i_{s} > = < e i > + Γ ω (49)

e_s(t) est la force électromotrice induite dans le stator par les courants dans le rotor. Le rotor produit un champ magnétique tournant à la pulsation $ω_{s} - ω$ dans le référentiel tournant avec lui. Dans le référentiel du stator, ce champ tourne à la vitesse $ω_{s}$ . Il s'en suit que la pulsation de e_s(t) est $ω_{s}$ , c'est-à-dire la pulsation de la source (cette propriété est démontrée en annexe). Il en va de même pour le courant i_s(t) : la maille modélisant le stator oscille donc à la pulsation $ω_{s}$ alors que celle modélisant le rotor oscille à la pulsation $ω_{s} - ω$ .

Une expression de la force contre-électromotrice est obtenue avec le modèle développé en annexe (dans le cas idéal d'un couplage sans pertes entre le stator et le rotor). L'amplitude complexe de la force contre-électromotrice obtenue est :

\underset{̲}{E_{s}} = μ_{0} n \frac{N {(ℓ r_{0})}^{2} Ω ω_{s} B_{0}}{\sqrt{R^{2} + L^{2} Ω^{2}}} exp (j Ψ_{c}) (50)

avec :

Ψ_{c} = a r c c o s (\frac{R}{\sqrt{R^{2} + L^{2} Ω^{2}}}) (51)

R et L sont toujours la résistance et l'auto-inductance d'un barreau. n est la densité linéïque de spires des deux bobines du stator.

La courbe de l'amplitude d'oscillation de la force contre-électromotrice en fonction du glissement est similaire à celle du courant dans le rotor : cette amplitude est nulle pour s=0 puis croît jusqu'à s=1. Elle est donc maximale lorsque le rotor ne tourne pas (au démarrage). Lorsque le moteur est dans son régime de fonctionnement optimal (glissement très faible), l'amplitude de la f.é.m. est très faible mais $Ψ_{c} \approx 0$ .

Notons pour finir que le moteur asynchrone peut fonctionner en générateur. Si, le moteur étant en régime permanent avec un glissement faible, on abaisse subitement la vitesse de rotation du champ, le glissement devient négatif. Une machine asynchrone peut fonctionner en génératrice (par exemple dans une éolienne) : il suffit d'ajuster la fréquence de rotation du champ pour qu'elle soit toujours légèrement inférieure à la fréquence de rotation du rotor. Le couple moteur est une fonction impaire de s donc la courbe de couple moteur pour un glissement négatif est exactement l'opposée de celle tracée plus haut. Le couple est dans ce cas négatif et il y a un transfert d'énergie positif du rotor vers le stator. Dans le cas d'un moteur de véhicule, ce fonctionnement en générateur survient en cas de freinage (dès qu'on relâche l'accélérateur). Il faut alors que l'électronique de commande (l'onduleur) permette de récupérer cette énergie, soit pour recharger l'accumulateur, soit pour charger un condensateur.

3. Réalisation d'un moteur asynchrone expérimental

3.a. Description du moteur

Le stator est réalisé avec deux paires de bobines. L'axe de la première paire (bobines B1 et B2) est (Ox), l'axe de la seconde (bobines B2 et B3) est (Oy). Dans chaque bobine est placé un noyau formé de lames de fer doux. Les deux bobines d'une paire produisent un champ dans le même sens. Une simulation par éléments finis du champ créé par ce dispositif est donnée en annexe.

Figure pleine page

La cage d'écureuil est réalisée au moyen de barres de laiton de 2 mm de diamètre. Les barreaux sont reliés aux anneaux par soudure à l'étain. Le corps du rotor est fabriqué par impression 3D. Il est constitué de deux anneaux qui maintiennent les barreaux, reliés chacun par trois rayons au moyeu où se trouve un roulement à bille pour assurer la liaison pivot avec un tube fixé verticalement. La cage contient 18 barreaux de longueur $ℓ = 75 m m$ . Son rayon est r₀=32 mm.

Voici une vue de dessus :

et une vue latérale prise après avoir enlevé une bobine :

Pour une des bobines de chaque paire, on place un capteur à effet Hall, plaqué contre le noyau et en son centre. Pour la paire (B1,B2), le capteur mesure le champ B_x, pour la paire (B2,B3) il mesure le champ B_y. La structure du champ ressenti par les barreaux est très différente du champ radial défini dans le modèle présenté plus haut. En effet, le champ au voisinage des barreaux qui ne font pas face aux pôles (dans les coins) est très faible par rapport au champ sur l'axe des bobines. Ce stator est donc très loin d'être optimal (en terme de forme) et le rotor ne comporte pas de noyau. En conséquence, il ne faut pas s'attendre à un couple élevé pour ce moteur expérimental, dans le sens où un moteur optimal de même force magnétomotrice doit produire un couple beaucoup plus élevé. La simulation montré en annexe montre en effet qu'il est nécessaire, pour augmenter le couple d'un facteur 200, d'ajouter un noyau dans la cage du rotor (au plus près des barreaux) et de changer la forme des têtes des noyaux des bobines afin que l'entrefer soit très petit sur toute la circonférence du rotor.

Les caractéristiques des bobines (250 spires) avec leur moyau inséré sont les suivantes (mesurées avec un LRC-mètre) : à 100 Hz, L=9,3 mH et R=1,3 Ω, à 10 kHz, L=8,4 mH et R=61 Ω.

3.b. Onduleur

L'alimentation du moteur est diphasée. La paire (B1,B2) est traversée par un courant sinusoïdal de pulsation $ω_{s}$ , la paire (B2,B3) par un courant de même pulsation et de même amplitude mais déphasé de $π / 2$ par rapport au premier. De plus, les bobines d'une paire ont leur courant tournant dans le même sens, donc produisent des champs de même sens. Le champ produit au niveau des barreaux de la cage comporte donc deux pôles, comme le champ utilisé dans le modèle développé plus haut. La vitesse de rotation du champ est $ω_{s}$ . Les moteurs industriels sont en général triphasés : il comportent trois bobinages alimentés avec un déphasage de $2 π / 3$ . Si un moteur triphasé comporte trois paires de bobines disposées à $2 π / 3$ l'une de l'autre, le champ produit est aussi à deux pôles.

La source d'énergie pour alimenter le stator est une alimentation de laboratoire de tension maximale 32 V et de courant maximal 16 A. Elle est réglée en régulation de tension.

La tension sinusoïdale appliquée aux bobines est obtenue par modulation de largeur d'impulsion (MLI), au moyen de deux ponts de transistors MOSFET. Nous utilisons deux ponts intégrés ST L6203, un pour chaque paire de bobines. Chaque pont peut délivrer jusqu'à 4 A efficace sous une tension de 42 V. En cas d'échauffement excessif du circuit intégré, le pont est coupé autmatiquement et redémarre dès que la température est à nouveau acceptable. Voici le shéma de la platine de commande comportant ces deux ponts :

Figure pleine page

Le circuit comporte deux ponts L6203, notés A et B. Chaque demi-pont d'un pont L6203 peut être commandé séparément (entrées IN1 et IN2). Dans le cas présent, les deux demi-ponts doivent être commandés en opposition. Afin de faire la commande depuis une seule sortie de l'Arduino, nous ajoutons une porte NON. La commande du pont A se fait donc avec l'entrée INA et ENA (Enable, qui active les deux demi-ponts ou les désactive). De même, le pont B est commandé avec INB et ENB. La sortie du pont A est branchée sur la paire de bobines (B1,B2). La sortie du pont B est branchée sur la paire de bobines (B3,B4). Les sorties SENSE_A et SENSE_B peuvent être branchées sur un oscilloscope afin de visualiser le courant qui circule dans les ponts. La résistance de 0,2 Ω est une résistance de puissance non bobinée. Il ne s'agit pas exactement du courant circulant dans la bobine car la tension de SENSE_A change de signe à chaque front de la porteuse (donc à 10 kHz), mais l'enveloppe du signal donne une visualisation du courant dans la bobine.

Voici le schéma du dispositif complet. Les capteurs à effet Hall sont alimentés en 5 V par l'Arduino. Les sorties analogiques de ces capteurs sont reliées à un oscilloscope pour visualisation des champs magnétiques produits par les bobines.

Figure pleine page

Les deux bobines d'une paire doivent être connectées de telle manière que les deux champs magnétiques soient dans le même sens : lorsque B2 génère un pôle nord vers le rotor, B1 doit générer un pôle sud vers le rotor. Les deux bobines d'une paire sont branchées en série. La manière dont une paire est branchée par rapport à l'autre détermine le sens de rotation.

À chaque paire de bobines est appliquée une tension carrée alternant de -V_s à +V_s, où V_s est la tension en sortie de l'alimentation. Cette tension alternative constitue la porteuse. Sa fréquence est 10 kHz. Son rapport cyclique est modulé lentement, à une pulsation $ω_{s}$ , la fréquence correspondante étant inférieure à 100 Hz. Le rapport entre la fréquence de la porteuse et celle de la modulation est donc supérieur à 100. Soit L_b l'auto-inductance d'une paire de bobines et R_b sa résistance (celle-ci dépend de la fréquence). L'intensité du courant dans la paire de bobines, pour une tension appliquée sinusoïdale d'amplitude $\underset{̲}{U_{b}}$ et de pulsation $ω$ , s'écrit :

\underset{̲}{I_{b}} = \frac{\underset{̲}{U_{b}}}{R_{b} + j L_{b} ω} (52)

Pour une fréquence de 10 kHz, nous avons R_b=120 Ω et L_b=17 mH. Pour la porteuse, on a donc $I_{b} = \frac{U_{b}}{1080}$ . Pour un signal modulant de 100 Hz, nous avons R_b=2,6 Ω et L_b=18,6 mH, soit $I_{b} = \frac{U_{b}}{12}$ . En conséquence, la forme d'onde de l'intensité du courant dans la paire de bobines est principalement celle de la modulation sinusoïdale de fréquence 100 Hz (la porteuse est environ 100 fois plus faible que la modulation). Pour un tension d'alimentation de 30 V, l'amplitude de l'intensité est de 2,5 A à 100 Hz. Pour une fréquence de modulation de 50 Hz, on a $L_{b} ω_{s} = 2, 9 Ω$ , valeur un peu plus grande que la résistance à cette fréquence. En conséquence, dans le domaine de fréquence de modulation choisi, l'amplitude d'oscillation du courant diminue notablement lorsque la fréquence augmente, sans qu'on soit pour autant dans un domainre purement inductif. Les bobines des stators des moteurs asynchrones industriels ont une résistance faible devant l'impédance inductive et dans ce cas l'amplitude de l'intensité est inversement proportionnelle à la fréquence (à amplitude de tension fixée).

Nous faisons le contrôle du courant dans les bobines au moyen des deux sondes à effet Hall. Pour un noyau de fer doux, on peut en effet supposer que le champ magnétique produit par une bobine au voisinage du noyau est proportionnel à l'intensité du courant. Même si cette proportionnalité n'est pas tout à fait vérifiée, ce qui nous importe en fin de compte est bien le contrôle du champ magnétique.

La période de rotation du moteur est déterminée au moyen d'une fourche optique H21A1 et d'une languette en carton fixée sur la partie basse du rotor.

3.c. Programme Arduino

Le programme Arduino accomplit trois tâches :

Configuration du Timer 1 pour la génération des deux signaux de commande (INA sur D11 et INB sur D12) avec modulation du rapport cyclique (modulation MLI).
Lecture échantillonnée de l'entrée analogique A0 reliée à un des deux capteurs à effet Hall. Calcul de la valeur efficace de l'oscillation du champ magnétique. La connaissance de cette valeur donne la possibilité d'ajuster l'amplitude de la modulation MLI afin d'obtenir une amplitude de champ magnétique souhaitée.
Communication avec le PC pour recevoir des commandes et fournir des informations.

La génération d'un signal MLI au moyen d'un Timer est expliqué en détail dans Génération d'un signal par modulation de largeur d'impulsion. Nous rappellons ici son principe. La figure suivante représente l'état du compteur de Timer 1 (TCNT1) en fonction du temps et l'état de la sortie OC1A (sortie D11) en fonction du temps.

Figure pleine page

Le compteur est incrémenté à une fréquence d'horloge (sous-multiple de la fréquence de l'horloge principale de l'Arduino) jusqu'à la valeur donnée par ICR1 puis est décrémenté jusqu'à 0. La durée de ce cycle est la période T de la porteuse de la modulation MLI. La valeur de OCR1A constitue un seuil qui permet de piloter la sortie OC1A. Le rapport cyclique est défini par le rapport OCR1A/ICR1. Une bonne précision de la modulation nécessite une valeur de ICR1 relativement élevée (au moins 100). La sortie OC1B est utilisée (avec le registre OCR1B) pour générer un signal MLI avec une modulation en quadrature par rapport au premier.

La modulation du rapport cyclique est effectuée de la manière suivante. Lorsque TCNT1 atteint sa valeur maximale (ICR1), une interruption est déclenchée. Dans le gestionnaire d'interruption (Timer 1 overflow interrupt), le rapport cyclique est mis à jour : la valeur de OCR1A est modifiée à partir d'une table calculée au préalable. L'indice de l'élément à prendre dans la table est déterminé par calcul de la phase du signal modulant. Afin d'avoir la vitesse de traitement la plus rapide possible, la phase n'est pas calculée avec des flottants (il n'y a pas d'implémentation en dur des flottants dans le microprocesseur du microcontrôleur de l'Arduino MEGA) mais avec un entier 32 bits (nommé accumulateur de phase). Cet entier représente la phase mais avec une position de la virgule fixe (alors que dans un flottant la position de la virgule est flottante).

La configuration du convertisseur analogique-numérique pour des conversions à fréquence déterminée est expliquée dans Conversion analogique-numérique multivoies avec échantillonnage. le Timer 3 est utilisé pour générer des interruptions périodiques. Dans le gestionnaire d'interruption, la conversion de l'entrée A0 (reliée à une sonde à effet Hall) est effectuée.

L'échange d'informations avec le PC se fait avec le protocole décrit dans Échange des données avec un Arduino.

onduleur2phases-capteurHall.ino

#include "Arduino.h"
#define NECHANT 128
#define SHIFT_ACCUM 25
#define GET_DATA 10
#define SET_DATA 11
#define DATA_0_SIZE 4 // fréquence, flottant 32 bits
#define DATA_1_SIZE 4 // amplitude, flottant 32 bits
uint8_t data_0[DATA_0_SIZE];
uint8_t data_1[DATA_1_SIZE];
bool data_0_ready = true;
bool data_0_request = false;
bool data_1_ready = true;
bool data_1_request = false;
float frequence = 10; // data_0
float amp = 0.0;
uint32_t period_pwm = 100; // en microsecondes (10 kHz)

uint32_t icr;
uint32_t table_onde_A[NECHANT];
uint32_t table_onde_B[NECHANT];
uint32_t indexA,indexB;
uint32_t accum1,accum2,increm;
uint16_t diviseur[6] = {0,1,8,64,256,1024};


// numérisation sonde Hall analogique
#define SAMPLE_PERIOD 1000
#define BUF_SIZE 500
volatile uint16_t buffer[2][BUF_SIZE];
volatile uint16_t indice_buf, nbuf;
volatile float B0_std;
volatile float B0_sum = 0;
volatile float B0_sum2 = 0;
#define NMOY 2000
volatile uint16_t imoy = 0;
#define DATA_2_SIZE 4 // B0_std, flottant 32 bits
uint8_t data_2[DATA_2_SIZE];
bool data_2_ready = true;
bool data_2_request = false;
#define DATA_3_SIZE 2000 // BUF_SIZE*4, buffer
uint8_t data_3[DATA_3_SIZE];
bool data_3_ready = true;
bool data_3_request = false;
#define DATA_4_SIZE 4 // Bstd cible, flottant 32 bits
uint8_t data_4[DATA_4_SIZE];
bool data_4_ready = true;
bool data_4_request = false;
float BstdCible;

//période de rotation
float period;
#define DATA_5_SIZE 4 // period, flottant 32 bits
uint8_t data_5[DATA_5_SIZE];
bool data_5_ready = true;
bool data_5_request = false;
unsigned long temps;

La fonction init_pwm_timer1 configure le Timer 1 pour la génération des signaux MLI sur OC1A (D11) et OC1B (D12). Le compteur est incrémenté à une fréquence sous-multiple de la fréquence de l'horloge (16 MHz). Le diviseur d'horloge est choisi en fonction de la période demandée afin d'avoir une valeur de ICR la plus grande possible.

void init_pwm_timer1(uint32_t period) {
    char clockBits;
    cli();
    TCCR1A = 0;
    TCCR1A |= (1 << COM1A1); //Clear OCnA/OCnB/OCnC on compare match, set OCnA/OCnB/OCnC at BOTTOM (non-inverting mode)
    TCCR1A |= (1 << COM1B1);
    TCCR1A |= (1 << COM1C1);
    TCCR1B = 1 << WGM13; // phase and frequency correct pwm mode, top = ICR1
    int d = 1;
    icr = (F_CPU/1000000*period/2);
    while ((icr>0xFFFF)&&(d<6)) { // choix du diviseur d'horloge
        d++;
        icr = (F_CPU/1000000*period/2/diviseur[d]);
   } 
   clockBits = d;
   ICR1 = icr; // valeur maximale du compteur
   TIMSK1 = 1 << TOIE1; // overflow interrupt enable
   sei(); // activation des interruptions
   TCNT1 = 0; // mise à zéro du compteur
   TCCR1B |= clockBits; // déclenchement du compteur
}

Une interruption est déclenchée à chaque fois que le compteur atteint la valeur maximale. Voici la fonction exécutée lors de cette interruption :

ISR(TIMER1_OVF_vect) { // Timer 1 Overflow interrupt
  accum1 += increm;
  accum2 += increm;
  indexA = accum1 >> SHIFT_ACCUM;
  OCR1A = table_onde_A[indexA];
  indexB = accum2 >> SHIFT_ACCUM;
  OCR1B = table_onde_B[indexB];
}

Les deux accumulateurs de phase sont incrémentés (la valeur de l'incrément dépend évidemment de la fréquence de modulation). Le décalage de SHIFT_ACCUM bits permet d'obtenir la valeur de l'indice dans la table qui contient les valeurs de OCR1A (ou OCR1B). Nous utilisons deux tables différentes au cas où les deux signaux seraient différents mais dans le cas présent on pourrait utiliser la même table pour les deux signaux. Cette fonction est appelée à une fréquence pouvant aller jusqu'à 100 kHz (fréquence de la porteuse). Il est donc important que son temps d'exécution soit très court. Elle comporte deux additions d'entier 32 bits, deux décalages de bits sur ces entiers et deux accès à la mémoire. Des calculs en virgule flottante sont à proscrire car sur l'Arduino MEGA ceux-ci ne sont pas implémentés par le microprocesseur mais sont mis en place par le compilateur. Le temps d'une simple addition en virgule flottante est donc beaucoup plus long que celui d'une addition d'entiers.

La fonction timer3_init configure le Timer 3 pour la génération des interruptions périodiques servant à la conversion analogique-numérique :

void timer3_init(uint32_t period) {// timer pour l'ADC
  TCCR3A = 0;
    TCCR3B = 0;
    TCCR3B |= (1 << WGM12); // mode CTC avec OCR1A pour le maximum
    uint32_t top = (F_CPU/1000000*period);
    int clock = 1;
    while ((top>0xFFFF)&&(clock<5)) {
          clock++;
          top = (F_CPU/1000000*period/diviseur[clock]);
      }
    OCR3A = top; // période
    TIMSK3 = (1 << OCIE1A); // interruption lorsque TCNT3=OCR3A
    TCCR3B |= clock;
}

La fonction adc_init initialise le convertisseur A/N :

void adc_init(uint8_t prescaler) {
  ADCSRA = 0;
  ADCSRA |= (1 << ADEN); // enable ADC
  ADCSRA |= prescaler ;
  ADCSRB = 0;)
}

La fonction ISR(TIMER3_COMPA_vect) est appelée lors de l'interruption déclenchée par le Timer 3 (la période est définie par SAMPLE_PERIOD). La valeur numérisée (10 bits) est stockée dans un tampon d'entiers 16 bits. Il s'agit en fait d'un double tampon (tableau buffer). Lorsqu'un des tampons est en cours de remplissage, l'autre est disponible pour une transmission au PC (sur demande de celui-ci). On procède par ailleurs au calcul de la somme des valeurs (converties en flottant) et de la somme des carrés, ce qui permet après NMOY conversions de faire le calcul de la valeur efficace de l'oscillation du champ magnétique. Celle-ci est calculée en mT et stockée dans la variable globale B0_std. Le passage de data_2_ready à true permet d'informer le programme principal que la valeur efficace est prête pour transmission au PC. Le passage de data_3_ready à true indique que le remplissage du tampon est terminé : on change alors de tampon et le tampon qui vient d'être rempli est disponible pour une transmission au PC.

ISR(TIMER3_COMPA_vect) { // gestionnaire d'interruption de l'ADC
    uint8_t v;
    uint16_t data;
    float B,Bm;
    
    ADMUX  = 0b01000000 | 0; // REFS0 et multiplex
    ADCSRA |= 0b01000000; // start ADC
    while (ADCSRA & 0b01000000);
    data = ADCL | (ADCH << 8);
    buffer[nbuf][indice_buf] = data;
    B = data;
    B0_sum += B;
    B0_sum2 += B*B;
     imoy += 1;
     if (imoy==NMOY) {
        Bm = B0_sum/NMOY;
        B0_std = sqrt(B0_sum2/NMOY-Bm*Bm)*0.1565;
        B0_sum = B0_sum2 = 0;
        data_2_ready = true;
        imoy = 0;
     }
     indice_buf += 1;
     if (indice_buf==BUF_SIZE) {
      indice_buf=0;
      if (nbuf==1) nbuf=0;
      else nbuf = 1;
      data_3_ready = true;
     }
}

Les fonctions suivantes remplissent les deux tables de valeurs pour OCR1A et OCR1B. Ces deux tables sont identiques (on aurait pu en utiliser qu'une seule). L'amplitude et l'offset sont deux nombres compris entre 0 et 1. Dans le cas présent, l'offset sera toujours nul car la valeur moyenne du courant dans une bobine doit être nulle.

void set_sinus_table_A(float amp, float offset) {
  int i;
  float dt = 2*3.1415926/NECHANT;
  for(i=0; i<NECHANT; i++) {
    table_onde_A[i] = icr*0.5*(1.0+offset+amp*sin(i*dt));
  }  
}

void set_sinus_table_B(float amp, float offset) {
  int i;
  float dt = 2*3.1415926/NECHANT;
  for(i=0; i<NECHANT; i++) {
    table_onde_B[i] = icr*0.5*(1.0+offset+amp*sin(i*dt));
  }  
}

La fonction set_frequence modifie l'incrément des accumulateurs de phase, en fonction de la valeur de fréquence donnée par la variable globale frequence (qui peut changer) et de celle de la période de la porteuse définie dans la variable globale period_pwm (qui est fixée à la compilation).

void set_frequence() {
  increm = (uint32_t) (((float)(0xFFFFFFFF))*((float)(frequence)*1e-6*(float)(period_pwm))); // incrément de l'accumulateur de phase
}

Le changement de fréquence de signal modulant sinusoïdal (qui donne la tension aux bornes de la paire de bobines) est donc très rapide; il peut être considéré comme instantané à l'échelle de la période de modulation.

La fonction compteur_tour est la routine de service d'une interruption matérielle déclenchée par un front descendant sur D3, reliée à l'émetteur du phototransistor de la fourche optique. La période de rotation, qui est la durée entre deux fronts descendants, est déterminée au moyen de la fonction millis.

void compteur_tour() {
  unsigned long t = millis();
  if (t-temps > 200) {
      period = 1e-3*(t-temps);
      data_5_ready = true;
      temps = t;
  } 
}

La fonction setup effectue toutes les configurations. La valeur par défaut de l'amplitude de modulation est nulle. Les deux accumulateurs de phase sont initialisés, le second avec une valeur non nulle permettant d'obtenir un décalage de $π / 2$ par rapport au premier. Le remplissage des deux tables doit se faire après la configuration du Timer 1 car il utilise la valeur de icr (la valeur maximale du compteur).

void setup() {
  Serial.begin(115200);
  Serial.setTimeout(0);
  char c = 0;
  Serial.write(c);
  c = 255;
  Serial.write(c);
  c = 0;
  Serial.write(c);
   pinMode(4,OUTPUT);
   digitalWrite(4,HIGH); // +5 V pour capteur
    pinMode(2,OUTPUT);
    digitalWrite(2,HIGH); // +5 V pour capteur
    pinMode(8,OUTPUT); 
    digitalWrite(8,HIGH); // commande ENABLE A
    pinMode(6,OUTPUT);
    digitalWrite(6,HIGH); // commande ENABLE B
    pinMode(11,OUTPUT); // PWM A, vers INA
    pinMode(12,OUTPUT); // PWM B, vers INB
    pinMode(3,INPUT); // sortie fourche optique
    for (int i=0; i<BUF_SIZE; i++) buffer[0][i] = buffer[1][i] = 0;
    cli();
    init_pwm_timer1(period_pwm);
    set_sinus_table_A(amp,0.0);
    set_sinus_table_B(amp,0.0);
    accum1 = 0;
    accum2 = ((uint32_t)(NECHANT * 0.25)) << SHIFT_ACCUM;
    set_frequence();
    indice_buf = 0;
    nbuf = 0;
    timer3_init(SAMPLE_PERIOD);
    adc_init(7);
    temps = millis();
    attachInterrupt(digitalPinToInterrupt(3), compteur_tour, FALLING);
    sei();
}

La fonction set_data gère la réception de données provenant de la liaison série (donc du PC). La donnée numéro 0 est la fréquence de modulation, la donnée numéro 1 est l'amplitude de modulation, la donnée numéro 4 est la valeur cible du champ magnétique efficace. Si une fréquence est reçue, la variable globale frequence reçoit sa valeur et la fréquence de la modulation est modifiée. Si une amplitude est reçue, la variable globale amp reçoit la valeur et le contenu des tables est regénéré. Si une valeur de champ magnétique efficace cible est reçue, une nouvelle amplitude de modulation est calculée, prenant en compte la valeur efficace précédemment calculée à partir des mesures et la valeur cible. Ce calcul part du principe que le champ magnétique généré par une bobine est proportionnel au rapport cyclique du signal MLI. Bien entendu, l'amplitude maximale est 1.

La fonction get_data gère l'envoi de données vers le PC. Ces données sont la fréquence (numéro 0), l'amplitude (numéro 1), la valeur efficace du champ magnétique (numéro 2), et le contenu du tampon (numéro 4) contenant les données bruts (entiers 10 bits) de champ magnétique échantillonné. La conversion en valeur de champ en mT sera faite dans le script Python. La transmission des données à proprement parler n'est pas effectuée dans cette fonction mais dans la suivante.

void get_data() {
  char n;
  while (Serial.available()<1) {};
  n = Serial.read();
  if (n==0) {
    data_0_request = true;
    memcpy(data_0,&frequence,DATA_0_SIZE);
  }
  if (n==1) {
    data_1_request = true;
    memcpy(data_1,&amp,DATA_1_SIZE);
  }
  if (n==2) {
    data_2_request = true;
    memcpy(data_2,&B0_std,DATA_2_SIZE);
  }
  if (n==3) {
    data_3_request = true;
    if (nbuf==1) memcpy(data_3,&buffer[0],DATA_3_SIZE);
    else memcpy(data_3,&buffer[1],DATA_3_SIZE);
  }
  if (n==5) {
    data_5_request = true;
    memcpy(data_5,&period,DATA_5_SIZE);
  }
}

La fonction send_data effectue l'envoi des données vers le PC, lorsque la donnée correspondante est disponible (mais les données numéro 0 et 1 sont toujours disponibles) :

void send_data() {
  if ((data_0_ready)&&(data_0_request)) {
      //data_0_ready = false;
      data_0_request = false;
      Serial.write(data_0,DATA_0_SIZE);
  }
  if ((data_1_ready)&&(data_1_request)) {
      //data_1_ready = false;
      data_1_request = false;
      Serial.write(data_1,DATA_1_SIZE);
  }
  if ((data_2_ready)&&(data_2_request)) {
      data_2_ready = false;
      data_2_request = false;
      Serial.write(data_2,DATA_2_SIZE);
  }
  if ((data_3_ready)&&(data_3_request)) {
      data_3_ready = false;
      data_3_request = false;
      Serial.write(data_3,DATA_3_SIZE);
  }
  if ((data_5_ready)&&(data_5_request)) {
      //data_5_ready = false;
      data_5_request = false;
      Serial.write(data_5,DATA_5_SIZE);
  }
}

La fonction read_serial reçoit un charactère de commande provenant du PC. Ce caractère indique si ce qui suit est une transmission de données en provenance du PC (SET_DATA) ou si celui-ci fait une demande de données (GET_DATA).

void read_serial() {
   char com;
   if (Serial.available()>0) {
        com = Serial.read();
        if (com==GET_DATA) get_data();
        else if (com==SET_DATA) set_data();
   }
}

La fonction loop appelle la fonction précédente et la fonction qui envoie des données au PC.

void loop() {
  read_serial();
  send_data();

}

3.d. Programme Python

La classe Python qui permet de gérer les communications est dans le fichier Arduino.py. L'utilisation de cette classe est décrite dans Échanges de données avec un Arduino.

Voici le script Python de pilotage :

pilotageOnduleur2phases.py

import numpy as np
from Arduino import Arduino
import matplotlib.pyplot as plt

ard = Arduino('COM4',[4,4,4,2000,4,4])
amp = 0.0
ard.write_float(1,amp)
freq = 10.0
ard.write_float(0,freq)
plot_B = false
while True:
    r = input("Commande ?")
    if r=='n': break
    if r=='b':
        B0_std = ard.read_float(2)
        print("B0_std = %f mT"%B0_std)
        if plot_B:
            B0 = 1.0*ard.read_int16_array(3,signed=False)
            B0 = B0-B0.mean()
            B0 *= 0.1565
            plt.figure()
            plt.plot(B0)
            plt.show()
    elif r=='a':
        a = ard.read_float(1)
        print("a = %f"%a
    elif r=='p':
        p = ard.read_float(5)
        print("T = %f s"%p)
    elif ',' in r:
        v = r.split(',')
        f = float(v[0])
        a = float(v[1])
        ard.write_float(0,f)
        ard.write_float(1,a)
    elif r=='h':
        print("n : terminer")
        print("b : valeur de B efficace")
        print("a : valeur de l'amplitude")
        print("fréquence (Hz), amplitude (0 à 1)")
        print("p : période de rotation")
        print("B efficace cible (mT)")
    else:
        Bstd = float(r)
        ard.write_float(4,Bstd)

Après initialisation de la liaison avec l'Arduino, l'amplitude de la modulation est configurée à 0, la fréquence à 10 Hz puis le programme entre dans une boucle pour recevoir des commandes de la part de l'utilisateur. Il y a 4 types de commande :

Le caractère 'n', qui permet de sortir de la boucle.
Le caractère 'b', qui permet de récupérer la dernière valeur de champ magnétique efficace et de l'afficher, éventuellement de récupérer le signal stocké dans le tampon et d'en faire un tracé.
Le caractère 'a', qui permet de récupérer l'amplitude de modulation et de l'afficher.
Le caractère 'p', qui permet de récupérer la période de rotation.
Deux valeurs séparées par une virgule, permettant de changer la fréquence (en Hz) et l'amplitude (de 0 à 1).
Une seule valeur, spécifiant la valeur de champ magnétique efficace cible.

Lorsque une valeur cible pour le champ efficace est entrée, il convient de vérifier le résultat avec la commande 'b'. La nouvelle amplitude est accessible par la commande 'a'. Cette interface de commande peut sembler rudimentaire mais elle s'avère à l'usage beaucoup plus efficace qu'une interface graphique avec boutons et autres widgets (celle-ci est aussi beaucoup plus longue à programmer).

4. Étude expérimentale

4.a. Test de l'onduleur

Ce test est effectué avec une amplitude de modulation de 0,8 et une fréquence variant de 10 à 80 Hz. Les signaux délivrés par les deux capteurs à effet Hall sont visualisés à l'oscilloscope et leur valeur efficace est extraite. Nous avons utilisé l'oscilloscope USB l'Analog Discovery 2 avec l'interface Python développée dans Interface Python pour Analog Discovery. Celle-ci permet de faire une acquisition avec un très frand nombre d'échantillons (alors que le logiciel Waveforms ne permet pas d'acquérir plus de 8192 échantillons).

Voici les deux champs magnétiques (un pour chaque paire de bobines) pour une fréquence de modulation de 10 Hz, avec une analyse spectrale pour vérifier que la fréquence est bien de 10 Hz :

from numpy.fft import fft,ifft
from scipy.signal import blackman

def analyseSpectrale(t,x):
    te = t[1]-t[0]
    N=len(x)
    p = int(np.log(10*N)/np.log(2))
    N1 = 2**(p)
    x1=np.concatenate((x*blackman(N),np.zeros(N1-N)))
    spectre = np.absolute(fft(x1))*2.0/N/0.42
    N1 = len(x1)
    T1 = N1*te
    freq=np.arange(N1)*1/T1
    return freq,spectre
    
f = 10
[t,B0,B1] = np.load("champB-%dHz-A=0,8.npy"%f)
figure(figsize=(16,6))
plot(t,B0,label="$B_A$")
plot(t,B1,label="$B_B$")
xlim(1,2)
ylim(-30,30)
grid()
xlabel("t (s)",fontsize=16)
ylabel("B (mT)",fontsize=16)

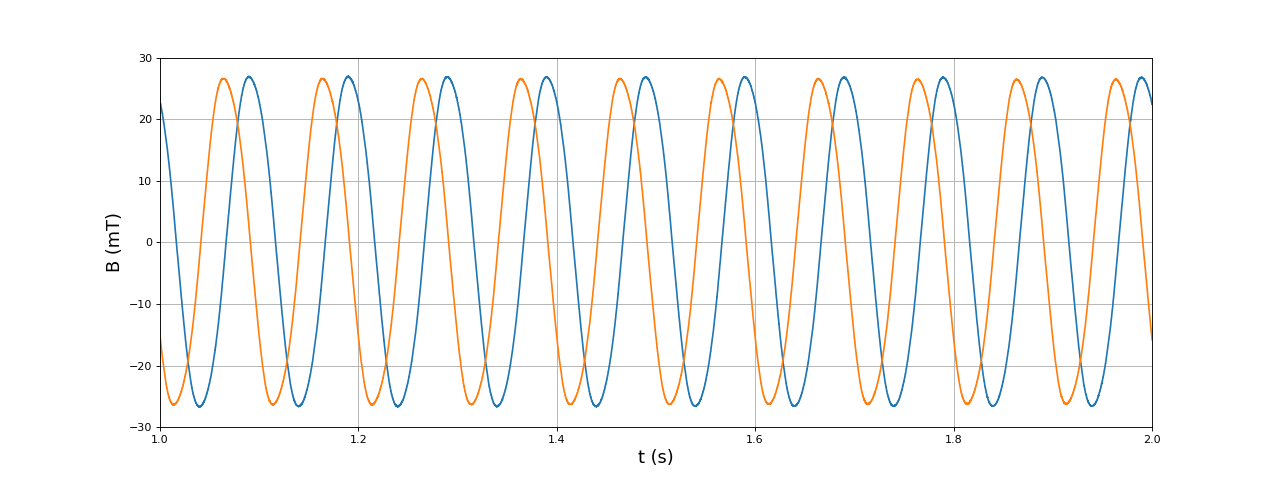fig10.pdf

freq,spectre = analyseSpectrale(t,B0)   
figure(figsize=(12,6))
plot(freq,spectre)
xlabel('f (Hz)',fontsize=16)
ylabel('B (mT)', fontsize=16)
xlim(0,100)
grid()

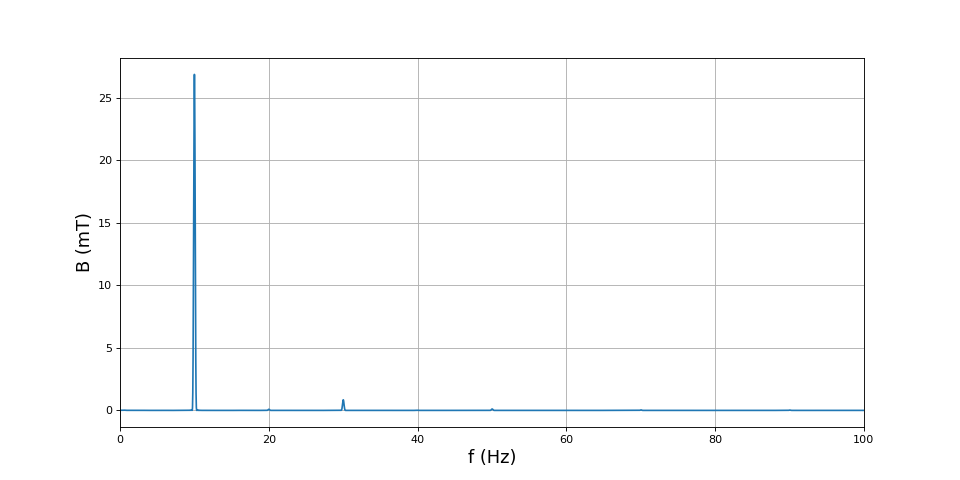fig11.pdf

Les deux champs magnétiques ont bien une fréquence de 10 Hz et oscillent en quadrature. Bien évidemment, ces mesures ne permettent pas de vérifier le sens de branchement des deux bobines dans une paire : pour obtenir un champ de stator à deux pôles, les deux bobines d'une paire doivent produire deux champs dans le même sens. On constate une légère distorsion de la forme d'onde par rapport à la sinusoïde (présence d'un harmonique de rang 3). Nous ne savons pas quelle est l'origine de cette distorsion (peut-être vient-elle du noyau en fer). Elle est sans conséquence sur le fonctionnement du moteur.

Voici l'analyse de la variation du champ pour une fréquence de 80 Hz :

 
f = 80
[t,B0,B1] = np.load("champB-%dHz-A=0,8.npy"%f)
figure(figsize=(16,6))
plot(t,B0,label="$B_A$")
plot(t,B1,label="$B_B$")
xlim(1,2)
ylim(-30,30)
grid()
xlabel("t (s)",fontsize=16)
ylabel("B (mT)",fontsize=16)

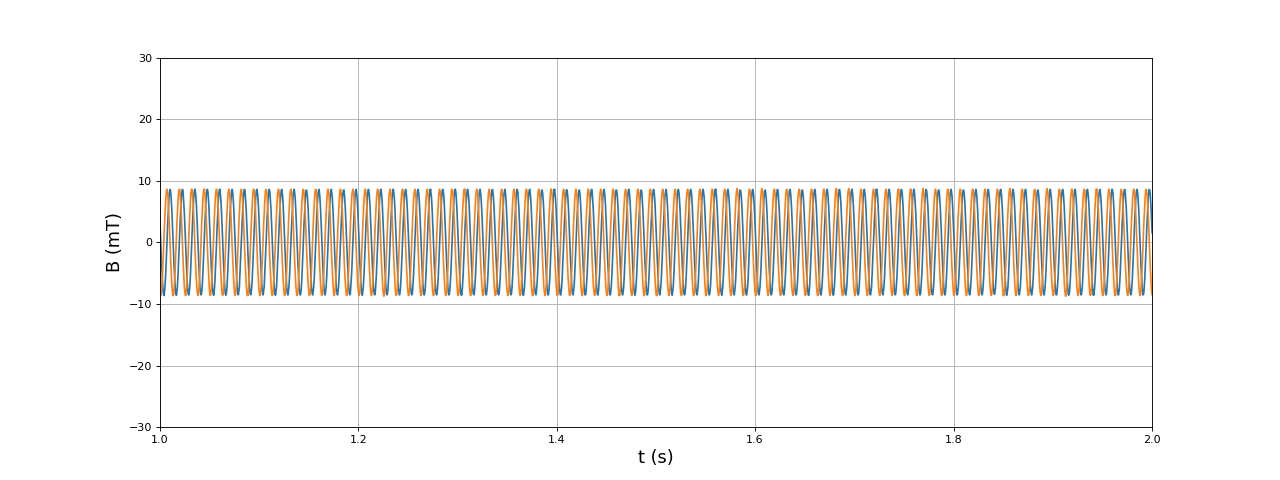fig12.pdf

freq,spectre = analyseSpectrale(t,B0)   
figure(figsize=(12,6))
plot(freq,spectre)
xlabel('f (Hz)',fontsize=16)
ylabel('B (mT)', fontsize=16)
xlim(0,100)
grid()

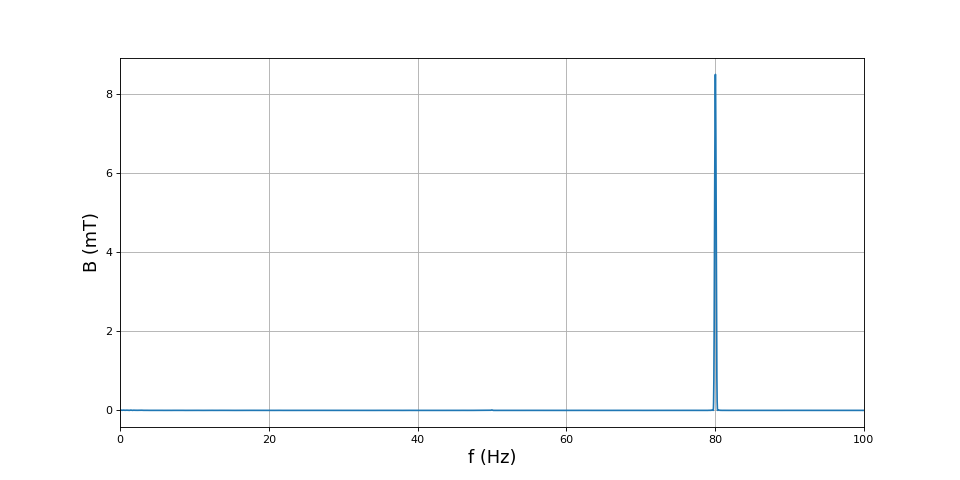fig13.pdf

Voici le tracé de la valeur efficace du champ magnétique en fonction de la fréquence :

B0_std = []
freq = [10,20,30,40,50,60,70,80]
for f in freq:
    [t,B0,B1] = np.load("champB-%dHz-A=0,8.npy"%f)
    B0_std.append(B0.std())
figure()
plot(freq,B0_std,"o-")
grid()
xlabel("f (Hz)",fontsize=16)
ylabel("B eff (mT)",fontsize=16) 
ylim(0,20)

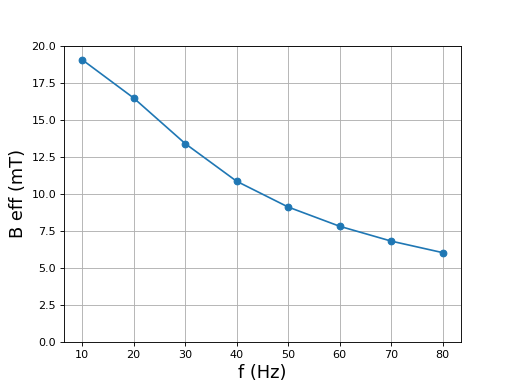fig14.pdf

La décroissance de la valeur afficace lorsque la fréquence augmente confirme la prévision faite plus haut : l'impédance inductive de la bobine est prépondérante pour des fréquences de 10 à 100 Hz. C'est pour cette raison que nous avons prévu la possibilité de modifier l'amplitude de la modulation en fonction d'une valeur cible du champ magnétique efficace. Remarquons que ce comportement du stator est plutôt souhaitable : plus la résistance est faible par rapport à l'impédance inductive, moins il y a de pertes dans la bobine (il s'agit des pertes par effet Joule dans les fils et des pertes dans le noyau). Dans les moteurs industriels, la résistance du stator est négligeable à la fréquence de travail donc l'amplitude de la tension appliquée à la bobine doit être proportionnelle à la fréquence pour que la valeur efficace du champ magnétique reste constante.

Afin de mesurer la composante radiale du champ dans la direction de 45 degrés par rapport à l'axe des bobines, nous avons fixé la sonde à effet Hall sur un tube en PVC de diamètre 80 mm. Voici la composante radiale du champ à 0 degré et à 45 degrés, pour une fréquence de 20 Hz et une amplitude de 0,5 :

[t,u1] = np.loadtxt("f=20Hz-A=0,5-Br-0deg.txt",unpack=True,skiprows=1)
[t,u2] = np.loadtxt("f=20Hz-A=0,5-Br-45deg.txt",unpack=True,skiprows=1)
B1 = (u1-u1.mean())/31.25*1e3
B2 = (u2-u2.mean())/31.25*1e3
figure(figsize=(12,6))
plot(t,B1,label=r"$\theta=0$")
plot(t,B2,label=r"$\theta=45\,{\rm deg}$")
xlabel('t (s)',fontsize=16)
ylabel(r"$B_r\ (\rm mT)$",fontsize=16)
grid()
B1eff = B1.std()
B2eff = B2.std()

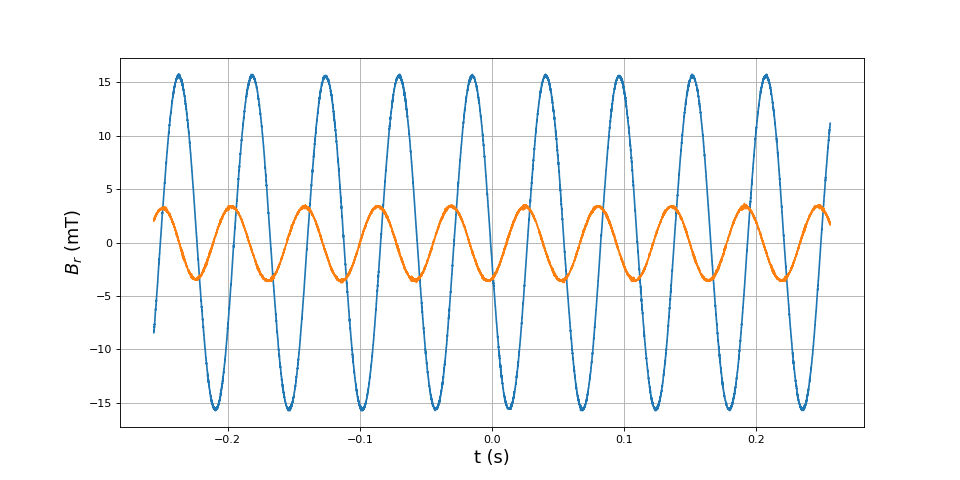fig15.pdf

print(B2eff/B1eff)
--> 0.2248059777209858

Le champ radial dans la direction de 45 degrés a donc une amplitude environ 5 fois plus faible que dans l'axe des bobines.

4.b. Test du moteur

Le mouvement du rotor est enregistré par une caméra dont l'axe optique coïncide avec l'axe de rotation, située à environ 50 cm au dessus du moteur. La caméra Basler utilisée est déclenchée image par image de manière matérielle au moyen d'un Arduino nano (script décrit dans Déclenchement d'une caméra Balser). La fréquence d'image est 50 images par secondes.

Au début de la vidéo, aucun courant ne traverse les bobines. Après environ 1 s, on déclenche l'onduleur en choisissant la fréquence et l'amplitude. L'enregistrement vidéo est déclenché en même temps que l'enregistrement des signaux provenant des capteurs Hall. Ce dispositif permet d'étudier le démarrage du moteur. Nous n'avons pas cependant fait d'étude systématique du démarrage car il s'avère très sensible au frottement dans les roulements et il est donc non reproductible.

La caméra est pilotée avec le logiciel Pylon Viever. Le fichier video généré par ce logiciel est malheureusement faiblement comprimé, ce qui limite considérablement le nombre d'images enregistrable (environ 1000 à pleine résolution). Pour obtenir un fichier vidéo diffusable sur le web, il faut le comprimer avec FFMPEG.

Voici comment se fait la conversion d'un fichier vidéo vers le format WEBM (un format pour le web avec un taux de compression très élevé) :

ffmpeg -i f=20Hz-A=0,9-50fps.avi -b:v 500k f=20Hz-A=0,9-50fps.webm

Un taux de 500 kbits par seconde est choisi. La qualité d'image finale dépend de ce taux mais plus il est élevé plus le fichier est volumineux. Dans le cas présent, le fichier AVI initial a 2054 Mo et le fichier WEBM final a 1,6 Mo.

Le script Python suivant (utilisant OpenCV) permet de faire une analyse du fichier vidéo afin de déterminer la vitesse de rotation du rotor. Les images défilent si on appuie sur la barre d'espace. Lorsque le repère rouge collé sur le haut du rotor est situé juste avant la vis située en bas de l'image, on appuie sur 't' pour enregistrer l'instant correspondant. Ces instants sont enregistrés dans un fichier texte. Le temps et le numéro d'image sont affichés et on enregistre le fichier vidéo au format MPEG4 (XVid), ce qui permet d'obtenir un taux de compression déjà beaucoup plus élevé que le fichier initial (mais inférieur au fichier WEBM).

analyseRotation.py

import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt

nom = "f=20Hz-A=0,9-50fps"
fechant = 50
techant = 1/fechant
video = cv.VideoCapture("%s.avi"%nom)
n= 0
success,frame = video.read()
cv.namedWindow("frame")
(height,width,c)=frame.shape
t = 0
color = (255,0,0)
fourcc = cv.VideoWriter_fourcc(*'XVID')
out = cv.VideoWriter("%s-final.mp4"%nom, fourcc, 30.0, (width,height))
tours = []
while success:
    cv.putText(frame,"frame = %d"%n,(900,100),cv.FONT_HERSHEY_SIMPLEX,1,color)
    cv.putText(frame,"t = %0.2f s"%t,(900,150),cv.FONT_HERSHEY_SIMPLEX,1,color)
    
    cv.imshow('frame',frame)
    out.write(frame)
    key = cv.waitKey()
    if key == ord('q'):
        break
    elif key==ord('t'):
        print(t)
        tours.append(t)
    success,frame = video.read()
    n += 1
    t += techant

np.savetxt("%s-tours.txt"%nom,tours)
out.release()

Voici l'enregistrement vidéo (50 images par seconde) pour une fréquence de modulation de 20 Hz et une amplitude de 0,9 :

Voici les durées d'un tour complet du rotor :

tours = np.loadtxt("f=20Hz-A=0,9-tours.txt")
T = []
for k in range(1,len(tours)-1):
    T.append(tours[k]-tours[k-1])
figure()
plot(T,"o-")
ylim(0,2)
grid()
xlabel("tour",fontsize=16)
ylabel("T (s)",fontsize=16)

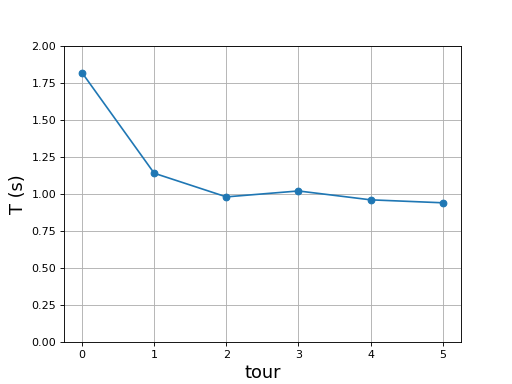fig16.pdf

La fréquence de rotation atteinte en régime permanent est d'environ 1 Hz, ce qui correspond à une vitesse de glissement relative s=0,95.

4.c. Étude expérimentale

Il s'agit de mesurer la vitesse du rotor en régime permanent pour différentes valeurs de fréquence de rotation ( $ω_{s}$ ) du champ et différentes valeurs de valeur efficace du champ magnétique ( $B_{0} / \sqrt{2}$ ). Lorsque la fréquence est modifiée, il faut changer aussi l'amplitude de la modulation afin que la valeur efficace du champ magnétique reste constante. Autrement dit, on veut faire varier la pulsation $ω_{s}$ sans modifier B₀. Le programme Arduino de pilotage et le script Python associé permettent de choisir une valeur cible de champ magnétique efficace. L'amplitude de modulation est ajustée afin de parvenir au plus proche de cette valeur cible. En pratique, nous avons constaté que la précision de ce réglage est de l'ordre de $5 %$ .

La première série de mesures est faite avec une valeur efficace de 11,3 mT et les fréquences 50, 40, 30, 25 et 20 Hz. Pour faire ces mesures, on commence par la fréquence 40 Hz avec une amplitude de 1, ce qui permet de garder l'amplitude du champ magnétique constante lorsqu'on abaisse la fréquence.

fs = np.array([50,40,30,25,20])
A = [1,0.86,0.7,0.64,0.58]
T = np.array([0.51,0.7,1.0,1.6,2.7])
f = 1/T
s = (fs-f)/fs
figure()
xlim(0,100)
plot(fs,f,'-o')
xlabel(r'$f_s\ (\rm Hz)$',fontsize=16)
ylabel(r'$f\ (\rm Hz)$',fontsize=16)
grid()

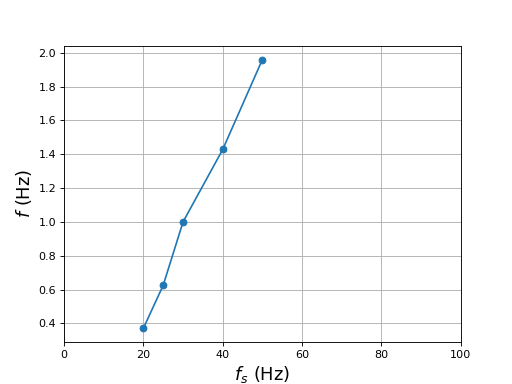fig17.pdf

figure()
plot(fs,s,'-o')
xlabel(r'$f_s\ (\rm Hz)$',fontsize=16)
ylabel(r'$s$',fontsize=16)
ylim(0.8,1)
grid()

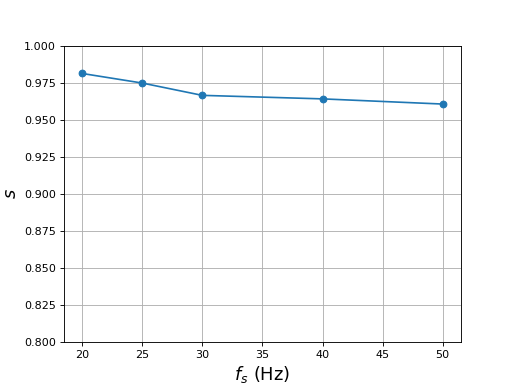fig18.pdf

La fréquence de rotation du rotor est beaucoup plus faible que la fréquence de rotation du champ. Le glissement est donc grand mais il diminue un peu quand la fréquence du champ augmente.

La deuxième série de mesures est faite avec une valeur efficace de 9,6 mT et les fréquences 60, 50, 40, 35, 30 (à 20 Hz le rotor s'arrête).

fs = np.array([60,50,40,35,30])
A = [1,0.86,0.71,0.65,0.60]
T = np.array([0.59,0.78,1.16,1.5,2.6])
f = 1/T
s = (fs-f)/fs
figure()
xlim(0,100)
plot(fs,f,'-o')
xlabel(r'$f_s\ (\rm Hz)$',fontsize=16)
ylabel(r'$f\ (\rm Hz)$',fontsize=16)
grid()

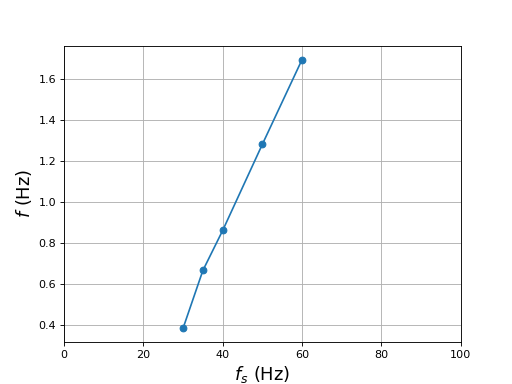fig19.pdf

figure()
plot(fs,s,'-o')
xlabel(r'$f_s\ (\rm Hz)$',fontsize=16)
ylabel(r'$s$',fontsize=16)
ylim(0.8,1)
grid()

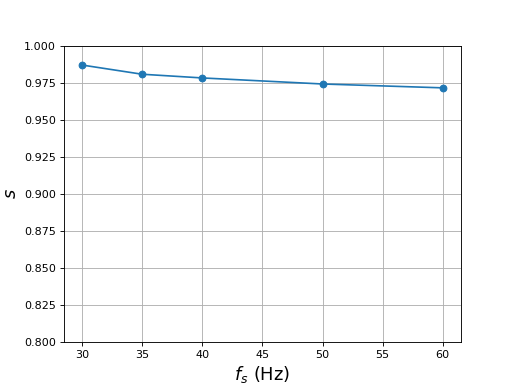fig20.pdf

Comment expliquer ces résultats ? Il faut tracer la courbe théorique de couple en fonction de la vitesse de glissement pour différentes valeurs de fréquence de champ tournant. La résistance d'un barreau de laiton est R=1,5 mΩ mais nous ne connaissons pas L.

Supposons que $L > \frac{R}{ω_{s}}$ pour toutes les fréquences utilisées. Dans ce cas, le couple présente un maximum.

def Gamma(ws,B0,N,R,L,s):
    r0 = 0.033
    l = 0.075
    Omega = s*ws
    return N*(l*r0*B0)**2*Omega*R/(2*(R**2+(L*Omega)**2))
R= 1.5e-3
L=0.5e-4
B0 = 11e-3*np.sqrt(2)
N=18
s = np.linspace(0,1,1000)
figure(figsize=(16,6))
ws1 = 2*np.pi*40
G1 = Gamma(ws1,B0,N,R,L,s)
plot(s,G1,"r-",label="40 Hz")
ws2 = 2*np.pi*30
G2 = Gamma(ws2,B0,N,R,L,s)
plot(s,G2,"b-",label="30 Hz")
ws3 = 2*np.pi*20
G3 = Gamma(ws3,B0,N,R,L,s)
plot(s,G3,"g-",label="20 Hz")
legend(loc='upper left')
grid()
xlabel("s",fontsize=16)
ylabel(r"$\Gamma\ (\rm N\cdot m)$",fontsize=16)

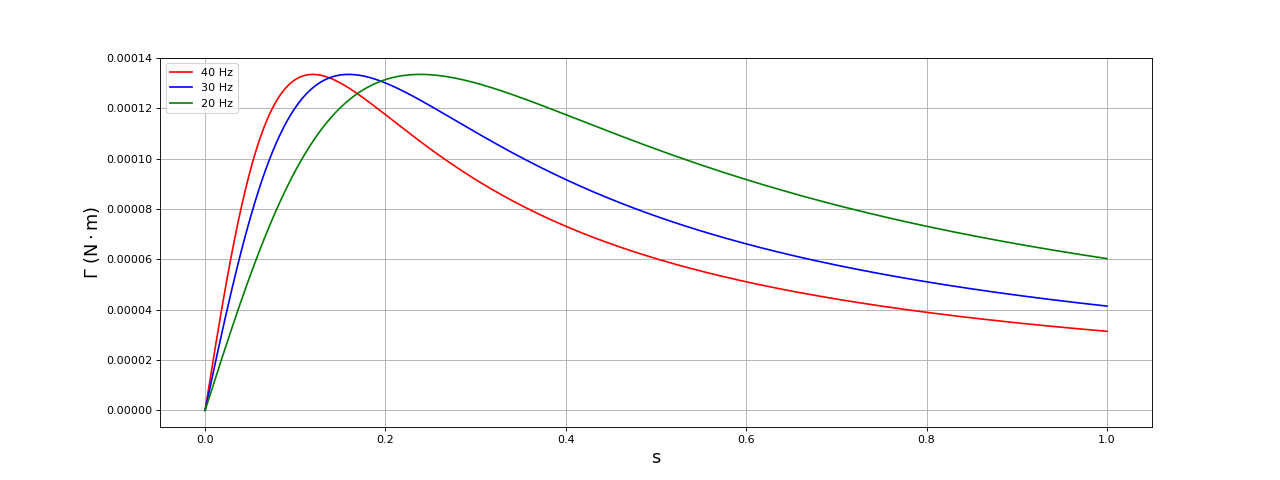fig21.pdf

Pour un couple donné, la vitesse de glissement est d'autant plus petite que la fréquence est élevée. Pour trouver le point de fonctionnement, il faut faire une hypothèse sur la force de frottement de la liaison pivot (qui est ici la seule cause du couple). Supposons que le moment du couple de frottement soit proportionnel à $ω$ (la vitesse angulaire du rotor). Le moment du couple de frottement est alors :

Γ_{f} = - β - α ω = - β - α ω_{s} (1 - s) (53)

Nous ajoutons une composante constante $β$ dans le couple de frottement car nous constatons que le moteur de démarrage pas si le couple moteur est très faible.

Le point de fonctionnement est défini par un moment total nul :

Γ + Γ_{f} = 0 (54)

Bien sûr, nous n'avons aucune idée a priori des valeurs de $α$ et $β$ . Nous les ajustons de manière à obtenir un point de fonctionnement dans la partie décroissante de la courbe de couple moteur en fonction du glissement, avec une valeur de s proche de 1.

alpha = 0.5e-5
beta = 2e-5
G1f = beta+alpha*ws1*(1-s)
G2f = beta+alpha*ws2*(1-s)
G3f = beta+alpha*ws3*(1-s)
plot(s,G1f,"r--")
plot(s,G2f,"b--")
plot(s,G3f,"g--")
ylim(0,2e-4)

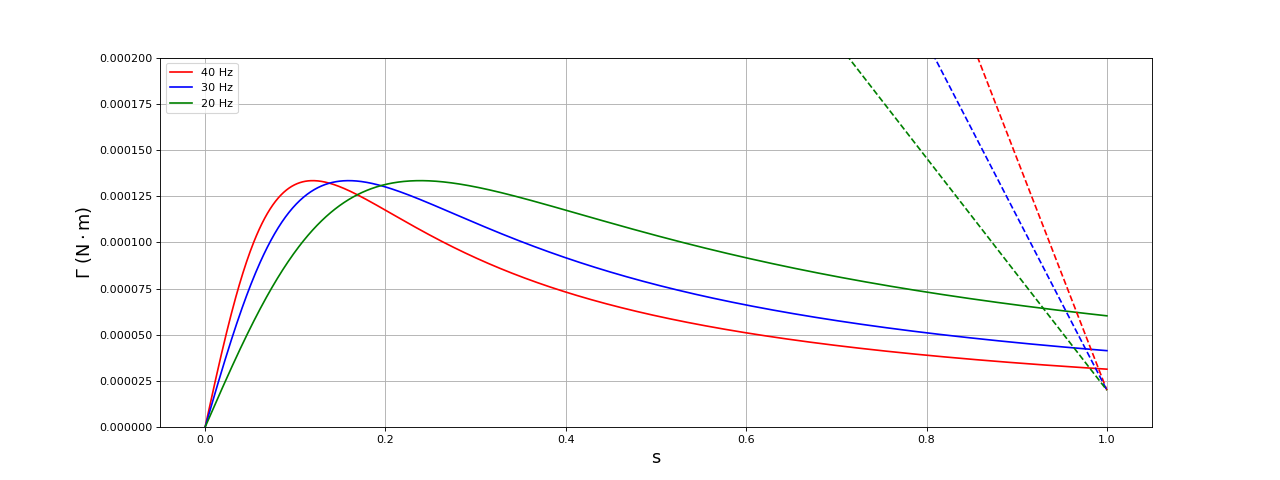fig22.pdf

Le point de fonctionnement pour chaque fréquence est l'intersection de la courbe en trait plein et de la courbe en pointillé (qui représente l'opposé du couple de frottement). Le glissement augmente lorsque la fréquence augmente. C'est l'inverse de ce que nous observons dans l'expérience. Remarquons que ce point de fonctionnement est bien stable : si la vitesse de rotation du rotor diminue alors le glissement augmente et le couple moteur devient supérieur au couple de frottement.

Supposons que $L < \frac{R}{ω_{s}}$ pour toutes les fréquences utilisées. Dans ce cas, le couple est une fonction toujours croissante du glissement.

R= 1.5e-3
L=0.5e-5
B0 = 11e-3*np.sqrt(2)
N=18
s = np.linspace(0,1,1000)
figure(figsize=(16,6))
ws1 = 2*np.pi*40
G1 = Gamma(ws1,B0,N,R,L,s)
plot(s,G1,"r-",label="40 Hz")
ws2 = 2*np.pi*30
G2 = Gamma(ws2,B0,N,R,L,s)
plot(s,G2,"b-",label="30 Hz")
ws3 = 2*np.pi*20
G3 = Gamma(ws3,B0,N,R,L,s)
plot(s,G3,"g-",label="20 Hz")
legend(loc='upper left')
grid()
xlabel("s",fontsize=16)
ylabel(r"$\Gamma\ (\rm N\cdot m)$",fontsize=16)
alpha = 1e-4
beta = 4e-4
G1f = beta+alpha*ws1*(1-s)
G2f = beta+alpha*ws2*(1-s)
G3f = beta+alpha*ws3*(1-s)
plot(s,G1f,"r--")
plot(s,G2f,"b--")
plot(s,G3f,"g--")
ylim(0,2e-3)

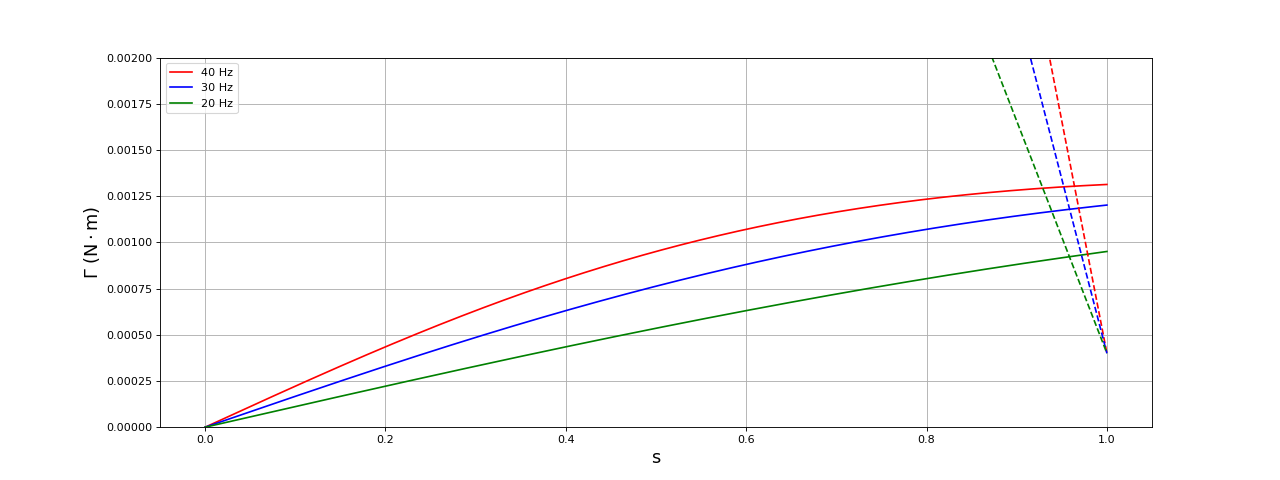fig23.pdf

Le glissement est toujours une fonction croissante de la fréquence, à l'inverse de ce qui est observé.

Pour que le glissement soit décroissant lorsque la fréquence augmente, nous devons modifier les paramètres du frottement :

R= 1.5e-3
L=0.5e-5
B0 = 11e-3*np.sqrt(2)
N=18
s = np.linspace(0,1,1000)
figure(figsize=(16,6))
ws1 = 2*np.pi*40
G1 = Gamma(ws1,B0,N,R,L,s)
plot(s,G1,"r-",label="40 Hz")
ws2 = 2*np.pi*30
G2 = Gamma(ws2,B0,N,R,L,s)
plot(s,G2,"b-",label="30 Hz")
ws3 = 2*np.pi*20
G3 = Gamma(ws3,B0,N,R,L,s)
plot(s,G3,"g-",label="20 Hz")
legend(loc='upper left')
grid()
xlabel("s",fontsize=16)
ylabel(r"$\Gamma\ (\rm N\cdot m)$",fontsize=16)
alpha = 0.7e-5
beta = 5e-4
G1f = beta+alpha*ws1*(1-s)
G2f = beta+alpha*ws2*(1-s)
G3f = beta+alpha*ws3*(1-s)
plot(s,G1f,"r--")
plot(s,G2f,"b--")
plot(s,G3f,"g--")
ylim(0,2e-3)

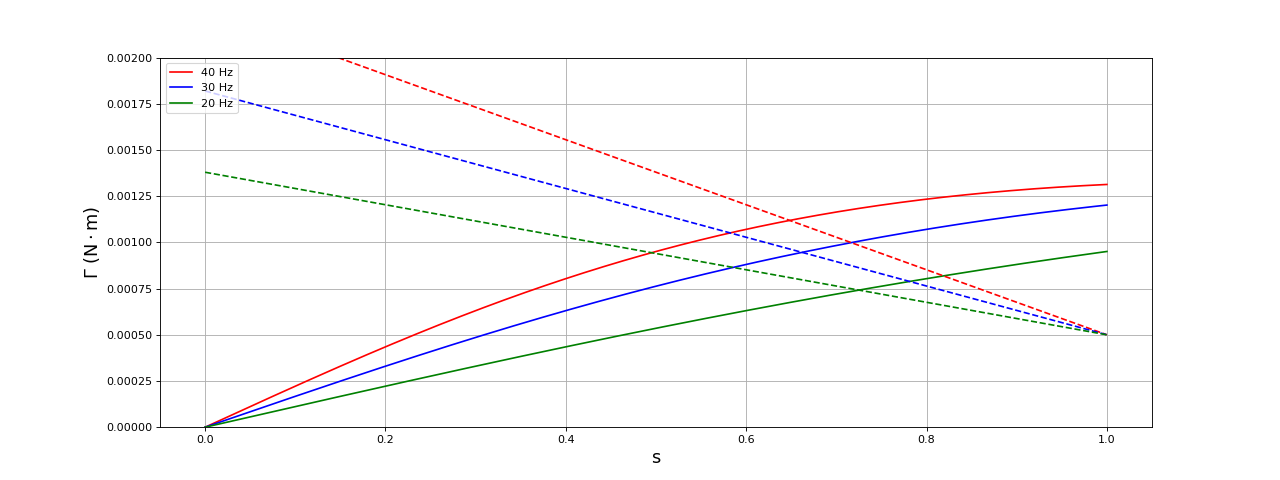fig24.pdf

Dans ce cas, on a bien une diminution du glissement lorsque la fréquence augmente, conformément à ce qui est observé. Cependant, le glissement est beaucoup plus faible que les valeurs expérimentales. Il est vraisemblable que la modélisation du frottement par une fonction affine ne soit pas réaliste.

Ces premiers résultats montrent que notre rotor est probablement un rotor à forte résistance, dont le couple est maximal lorsque s=1. Les barreaux sont en effet relativement minces par rapport à leur espacement, ce qui fait que le rapport R/L est vraisemblablement plus grand que la plus grande fréquence utilisée. Le fait d'avoir un rotor à forte résistance est un avantage pour le démarrage : le couple lorsque le rotor ne tourne pas est plus élevé que lorsque la résistance est faible. L'inconvénient est que le glissement en régime permanent est grand, ce qui implique un moindre rendement énergétique du moteur (voir annexe 1).

Dans la série de mesures suivantes, la fréquence est fixée et nous faisons varier l'amplitude, ce qui a pour effet de faire varier la valeur efficace d'oscillation du champ magnétique :

fs = 30
A = [1,0.9,0.8,0.7,0.6]
Beff = np.array([16,14.3,12.6,11.1,9.7])
T = np.array([0.43,0.52,0.68,0.96,2.1])
f = 1/T
s = (fs-f)/fs
figure()
xlim(0,30)
plot(Beff*np.sqrt(2),s,'-o',label='30 Hz')
fs = 40
A = [1,0.9,0.8,0.7,0.6]
Beff = np.array([13,11.8,10.5,9.3,8])
T = np.array([0.44,0.52,0.73,1.1,2.6])
f = 1/T
s = (fs-f)/fs
plot(Beff*np.sqrt(2),s,'-o',label='40 Hz')
xlabel(r'$B_0\ (\rm mT)$',fontsize=16)
ylabel(r'$s$',fontsize=16)
grid()
ylim(0.8,1)
legend(loc='upper right')

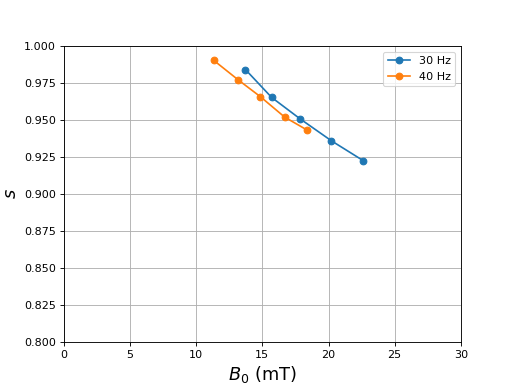fig25.pdf

Le glissement diminue lorsque l'amplitude du champ magnétique augmente. Voyons ce que donne le modèle lorsqu'on fait varier l'amplitude du champ magnétique :

R= 1.5e-3
L=0.5e-5
N=18
s = np.linspace(0,1,1000)
figure(figsize=(16,6))
ws1 = 2*np.pi*40
B0 = 10e-3
G1 = Gamma(ws1,B0,N,R,L,s)
plot(s,G1,"r-",label="10 mT")
B0 = 15e-3
G2 = Gamma(ws1,B0,N,R,L,s)
plot(s,G2,"b-",label="15 mT")
B0 = 20e-3
G3 = Gamma(ws1,B0,N,R,L,s)
plot(s,G3,"g-",label="20 mT")
legend(loc='upper left')
grid()
xlabel("s",fontsize=16)
ylabel(r"$\Gamma\ (\rm N\cdot m)$",fontsize=16)
alpha = 0.7e-5
beta = 5e-4
G1f = beta+alpha*ws1*(1-s)
G2f = beta+alpha*ws2*(1-s)
G3f = beta+alpha*ws3*(1-s)
plot(s,G1f,"r--")
plot(s,G2f,"b--")
plot(s,G3f,"g--")
ylim(0,2e-3)

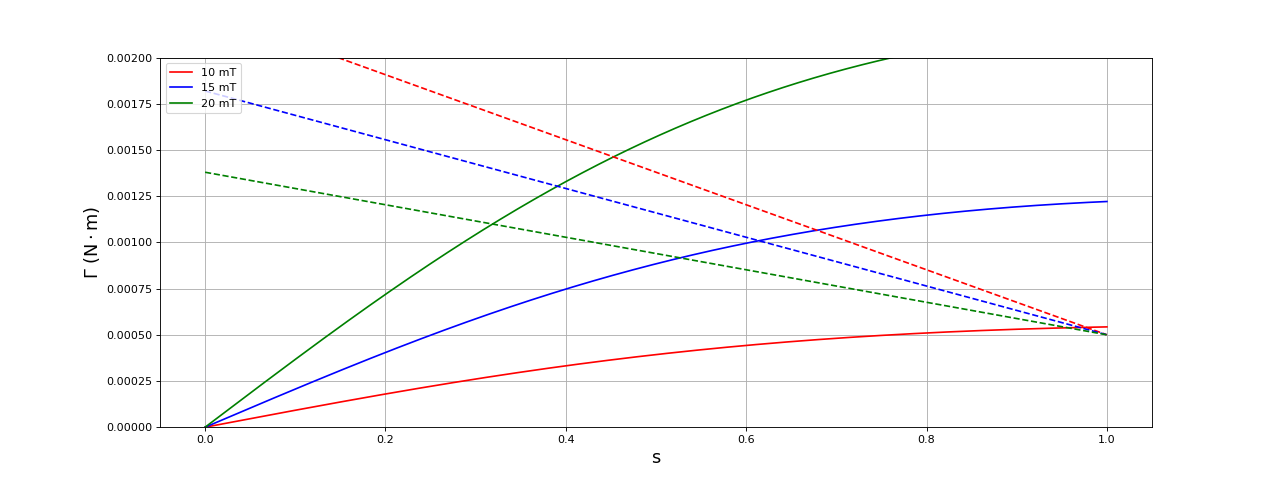fig26.pdf

Lorsque le champ augmente, le glissement diminue, conformément à ce qui est observé.

5. Annexe 1 : modèle de moteur asynchrone

Dans ce modèle, le stator produit un champ tournant uniforme, défini par :

\begin{matrix} B_{x} (t) = B_{0} cos (ω_{s} t) & (55) \\ B_{y} (t) = B_{0} sin (ω_{s} t) & (56) \end{matrix}

Un tel champ peut être en principe généré par deux paires de bobines, l'une d'axe (Ox) l'autre d'axe (Oy), alimentées en quadrature. Sa divergence est bien nulle. Ce champ est très différent de celui défini plus haut comme champ dans l'entrefer car il n'est pas radial. On en effet en coordonnées cylindriques :

\begin{matrix} B_{r} (θ, t) = \vec{B} \cdot {\vec{u}}_{r} = B_{x} (t) sin (θ) + B_{y} (t) cos (θ) = B_{0} cos (ω_{s} t - θ) & (57) \\ B_{θ} (θ, t) = \vec{B} \cdot {\vec{u}}_{θ} = - B_{x} (t) sin (θ) + B_{y} (t) cos (θ) = B_{0} sin (ω_{s} t - θ) & (58) \end{matrix}

Ce champ uniforme est peu réaliste pour un champ généré par le stator au niveau des barreaux du rotor (dans la zone d'enrefer), même si le champ à l'intérieur du rotor est peut-être proche d'un champ uniforme. Nous allons voir cependant que ce champ uniforme conduit au même résultat que le champ radial.

Le rotor est (dans un premier temps) un cadre rectangulaire constitué de deux barreaux diamètralement opposés.

Figure pleine page

Le cadre définit une courbe fermée pour le circuit du courant. Avec l'orientation définie sur la figure, le flux magnétique à travers ce cadre est :

Φ_{C} (t) = 2 ℓ r_{0} \vec{n} \cdot \vec{B} = 2 ℓ r_{0} B_{0} sin ((ω_{s} - ω) t) (59)

La f.é.m. dans le cadre est donc :

e (t) = - \frac{d Φ_{C} (t)}{d t} = - 2 ℓ r_{0} B_{0} (ω_{s} - ω) cos ((ω_{s} - ω) t) = - 2 ℓ r_{0} B_{0} Ω cos (Ω t) (60)

où $Ω = ω_{s} - ω$ est la vitesse angulaire de glissement.

Introduisons la résistance électrique du cadre R_c et son coefficient d'auto-inductance L_c. L'intensité du courant électrique dans le cadre est :

i (t) = - \frac{2 ℓ r_{0} B_{0} Ω}{\sqrt{R_{c}^{2} + L_{c}^{2} Ω^{2}}} cos (Ω t - Ψ_{c})

avec :

Ψ_{c} = a r c c o s (\frac{R_{c}}{\sqrt{R_{c}^{2} + L_{c}^{2} Ω^{2}}}) (61)

Le moment des forces de Laplace sur le cadre est :

\vec{Γ} = 2 ℓ r_{0} i (t) \vec{n} \land \vec{B} = - 2 ℓ r_{0} i (t) B_{0} cos ((ω_{s} - ω) t) {\vec{u}}_{z} (62)

Le moment du couple moteur s'écrit donc :

Γ (t) = \frac{4 {(ℓ r_{0} B_{0})}^{2} Ω}{\sqrt{R_{c}^{2} + L_{c}^{2} Ω^{2}}} cos (Ω t - Ψ_{c}) cos (Ω t) = \frac{2 {(ℓ r_{0} B_{0})}^{2} Ω}{\sqrt{R_{c}^{2} + L_{c}^{2} Ω^{2}}} (cos (2 Ω t - Ψ_{c}) + cos (Φ_{c})) (63)

On peut considérer que le rotor complet est constitué de N/2 cadres comme celui-ci. Le cadre d'indice k fait un angle $φ_{k} = 2 π \frac{k}{N}$ par rapport à celui d'indice 0. En conséquence, il faut ajouter $φ_{k}$ à l'angle $ω t$ pour obtenir le moment du couple sur le cadre d'indice k :

Γ_{k} (t) = \frac{2 {(ℓ r_{0} B_{0})}^{2} Ω}{\sqrt{R_{c}^{2} + L_{c}^{2} Ω^{2}}} (cos (2 Ω t - Ψ_{c} - 2 φ_{k}) + cos (Φ_{c})) (64)

Le moment total est :

Γ (t) = \sum_{k = 0}^{N / 2 - 1} Γ_{k} (t) (65)

La somme de $cos (2 Ω t - Φ_{c} - 2 φ_{k})$ est nulle. En conséquence, le moment total est constant :

Γ = \frac{N {(ℓ r_{0} B_{0})}^{2} Ω}{\sqrt{R_{c}^{2} + L_{c}^{2} Ω^{2}}} cos (Φ_{c}) = \frac{N {(ℓ r_{0} B_{0})}^{2} R_{c} Ω}{(R_{c}^{2} + L_{c}^{2} Ω^{2})} (66)

Introduisons $R = R_{c} / 2$ et $L = L_{c} / 2$ (résistance et auto-inductance d'un barreau). On obtient :

Γ = \frac{N {(ℓ r_{0} B_{0})}^{2} R Ω}{2 (R^{2} + L^{2} Ω^{2})} (67)

C'est la même expression que $(36)$ . Finalement, ce modèle où le rotor est considéré comme un ensemble de N/2 cadres indépendants dans un champ uniforme tournant donne la même expression du couple moteur que le modèle développé dans la partie 2. Cette similitude est a priori étonnante puisque la structure du champ magnétique n'est pas la même dans les deux modèles.

Si l'on reprend l'expression de la f.é.m. dans le barreau d'indice k, il est possible de définir un flux magnétique associé :

Φ_{k} = - \int e_{k} (t) d t = - ℓ r_{0} B_{0} sin (Ω t - 2 π \frac{k}{N}) (68)

Compte tenu du fait que tous les barreaux étaient orientés dans le sens de ${\vec{u}}_{z}$ , et qu'un cadre est constitué du barreau k et du barreau k+N/2, on peut en déduire le flux pour les deux barreaux constituant un cadre :

Φ_{c, k} = - Φ_{k} + Φ_{k + N / 2} = 2 ℓ r_{0} B_{0} sin (Ω t - 2 π \frac{k}{N}) (69)

qui est bien l'expression du flux magnétique à travers un cadre pour le champ uniforme. Ainsi, les deux modèles sont bien équivalents.

Le calcul des forces de Laplace fait intervenir la composante radiale du champ magnétique. Or celle-ci est la même dans les deux modèles donc le couple moteur a la même expression.

Le modèle du cadre dans un champ uniforme permet aussi de calculer la force contre-électromotrice dans le stator, à condition de faire des hypothèses sur ses bobines. On peut considérer que la composante B_x du champ magnétique est générée par un solénoïde long d'axe (Ox) (notons le S_x). On a alors $B_{x} (t) = μ_{0} n i_{x} (t)$ où n est la densité linéique de spires du solénoïde et i_x(t) le courant dans ce solénoïde. De même, la composante B_y est créée par un solénoïde d'axe (Oy) (notons le S_y) et on a $B_{y} (t) = μ_{0} n i_{y} (t)$ . Les flux magnétiques créés par ces deux solénoïdes à travers un cadre (constitué de deux barreaux diamétralement opposés) faisant un angle θ avec l'axe (Ox) s'écrivent :

\begin{matrix} Φ_{x} = - B_{x} 2 ℓ r_{0} sin (θ) = - 2 μ_{0} n ℓ r_{0} sin (θ) i_{x} & (70) \\ Φ_{y} = B_{y} 2 ℓ r_{0} cos (θ) = 2 μ_{0} n ℓ r_{0} cos (θ) i_{y} & (71) \end{matrix}

Les coefficients d'inductance mutuelles avec le rotor pour ces deux bobines sont donc :

\begin{matrix} M_{x} (θ) = - 2 μ_{0} n ℓ r_{0} sin (θ) & (72) \\ M_{y} (θ) = 2 μ_{0} n ℓ r_{0} cos (θ) & (73) \end{matrix}

Connaissant ces inductances mutuelles, on peut calculer l'effet du rotor sur le stator. Considérons le cadre d'indice k, faisant avec l'axe (0x) l'angle $θ_{k} = ω t + 2 π \frac{k}{N}$ ( $k = 0, 1, \dots N / 2 - 1$ ). Comme démontré plus haut, l'intensité du courant induit dans ce cadre s'écrit :

i_{k} (t) = - \frac{2 ℓ r_{0} B_{0} Ω}{\sqrt{R_{c}^{2} + L_{c}^{2} Ω^{2}}} cos (Ω t - Ψ_{c} - 2 π \frac{k}{N}) (74)

Le flux magnétique généré par ce courant à travers le solénoïde S_x est :

Φ'_{k, x} = M_{x} (θ_{k}) i_{k} (t) = - μ_{0} n sin (ω t + 2 π \frac{k}{N}) \frac{4 {(ℓ r_{0})}^{2} B_{0} Ω}{\sqrt{R_{c}^{2} + L_{c}^{2} Ω^{2}}} cos (Ω t - Ψ_{c} - 2 π \frac{k}{N}) (75)

qui s'écrit aussi :

Φ'_{k, x} = - μ_{0} n \frac{2 {(ℓ r_{0})}^{2} B_{0} Ω}{\sqrt{R_{c}^{2} + L_{c}^{2} Ω^{2}}} (sin (ω_{s} t - Ψ_{c}) + sin (2 ω t - ω_{s} t + Ψ_{c} + 4 π \frac{k}{N})) (76)

Le flux créé par tout le rotor à travers le solénoïde S_x est égal à la somme du précédent pour k variant de 0 à N/2-1. La somme du second terme est nulle. On obtient donc :

Φ'_{x} = - μ_{0} n \frac{N {(ℓ r_{0})}^{2} B_{0} Ω}{\sqrt{R_{c}^{2} + L_{c}^{2} Ω^{2}}} sin (ω_{s} t - Ψ_{c}) (77)

Il faut remarquer que la pulsation d'oscillation de flux est $ω_{s}$ , c'est-à-dire la pulsation de la source qui alimente le stator.

Le flux généré par le rotor dans le solénoïde S_y se calcule de manière similaire :

Φ'_{k, y} = M_{y} (θ_{k}) i_{k} (t) = μ_{0} n cos (ω t + 2 π \frac{k}{N}) \frac{4 {(ℓ r_{0})}^{2} B_{0} Ω}{\sqrt{R_{c}^{2} + L_{c}^{2} Ω^{2}}} cos (Ω t - Ψ_{c} - 2 π \frac{k}{N}) (78)

et :

Φ'_{y} = μ_{0} n \frac{N {(ℓ r_{0})}^{2} B_{0} Ω}{\sqrt{R_{c}^{2} + L_{c}^{2} Ω^{2}}} cos (ω_{s} t - Φ_{c}) (79)

Les f.é.m. induites par les variations de ces flux dans les solénoïdes sont les forces contre-électromotrices :

\begin{matrix} e'_{x} = - \frac{d Φ'_{x}}{d t} = μ_{0} n \frac{N {(ℓ r_{0})}^{2} B_{0} Ω ω_{s}}{\sqrt{R_{c}^{2} + L_{c}^{2} Ω^{2}}} cos (ω_{s} t - Ψ_{c}) & (80) \\ e'_{y} = - \frac{d Φ'_{y}}{d t} = μ_{0} n \frac{N {(ℓ r_{0})}^{2} B_{0} Ω ω_{s}}{\sqrt{R_{c}^{2} + L_{c}^{2} Ω^{2}}} sin (ω_{s} t - Ψ_{c}) & (81) \end{matrix}

De plus, les intensités des courants dans les deux solénoïdes sont :

\begin{matrix} i_{x} (t) = \frac{1}{n μ_{0}} B_{x} (t) = \frac{B_{0}}{μ_{0} n} cos (ω_{s} t) & (82) \\ i_{y} (t) = \frac{1}{n μ_{0}} B_{y} (t) = \frac{B_{0}}{μ_{0} n} sin (ω_{s} t) & (83) \end{matrix}

On voit donc que, dans les deux bobines du stator, la force contre-électromotrice est retardée de $Ψ_{c}$ par rapport au courant. Dans un modèle de stator à une maille, on écrira donc la relation suivante entre le courant dans le stator et la force contre-électromotrice :

e_{s} (t) = 2 \times {(μ_{0} n)}^{2} \frac{N {(ℓ r_{0})}^{2} Ω ω_{s}}{\sqrt{R_{c}^{2} + L_{c}^{2} Ω^{2}}} i_{s} (t - Ψ_{c}) (84)

avec :

Ψ_{c} = a r c c o s (\frac{R_{c}}{\sqrt{R_{c}^{2} + L_{c}^{2} Ω^{2}}}) (85)

Le facteur deux vient du fait qu'il y a deux bobines dans le modèle : il faut donc multiplier la f.é.m. par deux pour obtenir celle du modèle à une maille. Remarquons que la force contre-électromotrice est la f.é.m. qui se développe dans le stator à cause de la présence du rotor, que celui-ci soit en rotation ou pas. L'amplitude d'oscillation de la force contre-électromotrice est maximale lorsque la vitesse du rotor et nulle et elle diminue lorsque le glissement diminue. Lorsque le glissement est très faible, on a :

e_{s} (t) \approx 2 {(μ_{0} n)}^{2} \frac{N {(ℓ r_{0})}^{2} ω_{s}^{2}}{R_{c}} i_{s} (t) (86)

La puissance moyenne transmise du stator au rotor (puissance active) est :

< e_{s} i_{s} > = {(μ_{0} n)}^{2} \frac{N {(ℓ r_{0})}^{2} Ω ω_{s}}{\sqrt{R_{c}^{2} + L_{c}^{2} Ω^{2}}} \frac{B_{0}^{2}}{{(μ_{0} n)}^{2}} cos (Ψ_{c}) = \frac{N {(ℓ r_{0} B_{0})}^{2} R_{c} Ω ω_{s}}{(R_{c}^{2} + L_{c}^{2} Ω^{2})} (87)

La puissance mécanique est :

Γ ω = \frac{N {(ℓ r_{0} B_{0})}^{2} R_{c} Ω ω}{(R_{c}^{2} + L_{c}^{2} Ω^{2})} (88)

La différence des deux puissances est :

< e_{s} i_{s} > - Γ ω = \frac{N {(ℓ r_{0} B_{0})}^{2} R_{c} Ω^{2}}{(R_{c}^{2} + L_{c}^{2} Ω^{2})} (89)

Or la puissance moyenne dissipée dans un cadre est :

< R_{c} i_{k}^{2} > = \frac{2 {(ℓ r_{0} B_{0})}^{2} R_{c} Ω^{2}}{R_{c}^{2} + L_{c}^{2} Ω^{2}} (90)

On a donc :

< e_{s} i_{s} > = N < R_{c} i_{k}^{2} > + Γ ω (91)

Cette égalité représente le bilan de puissance : la puissance transmise du stator au rotor est la somme de la puissance dissipée dans le rotor et de la puissance mécanique.

Le rendement de la conversion électro-mécanique (qui ne tient pas compte des pertes dans le stator) est :

η = \frac{Γ ω}{< e_{s} i_{s} >} = \frac{ω}{ω_{s}} = 1 - s (92)

Du point de vue du rendement énergétique, on a donc intérêt à faire fonctionner le moteur à un glissement faible. Pour cette raison, il est préférable que R/L soit beaucoup plus petit que la pulsation de rotation du champ, afin que la courbe de couple présente un maximum à faible glissement. Le démarrage du moteur peut cependant poser problème dans ce cas car le couple lorsque le rotor ne tourne pas est faible.

6. Annexe 2: simulation du stator expérimental

Cette annexe présente une simulation du champ magnétique généré par le stator expérimental constitué de 4 bobines (deux paires perpendiculaires) contenant chacune un noyau en fer doux. La simulation est faite avec le logiciel libre Finite Element Method Magnetic. Nous utilisons l'interface pour Python (pyfemm), qui permet de piloter le logiciel depuis un script Python. Ce script permet de définir une géométrie complexe dépendant d'un ou de plusieurs paramètres et d'obtenir des tracés de champ sur des courbes particulières. Les commandes de l'interface Python sont des répliques des opérations que l'on effectue lorsqu'on utilise directement l'interface utilisateur. Il faut donc bien se familiariser avec cette interface avant d'aborder l'écriture des scripts Python.

Le logiciel FEMM permet d'effectuer la résolution numérique d'un problème de magnétostatique (ou d'électrostatique ou de diffusion thermique) par la méthode des éléments finis. Il résout les problèmes bidimensionnels, en géométrie plane ou axisymétrique.

Pour notre problème comportant quatre bobines, on calcule le champ magnétique pour un problème bidimensionnel similaire, dans le plan (Oxy). Chaque bobine est modélisée par deux plaques (infinies dans la direction z) parcourues par deux courants opposés. Les noyaux sont en fer (loi de comportement linéaire). Chaque bobine comporte 250 spires parcourues par un courant de 1 A. Le nombre de spires et l'intensité du courant ont une influence sur l'intensité du champ (celle-ci est proportionnelle à NI) mais pas sur les variations spatiales du champ.

Remarquons que la résolution numérique du problème tridimensionnel (tenant compte de la géométrie réelle des bobines) ne pourrait se faire qu'avec un logiciel d'éléments finis tridimensionnel. Le temps de calcul serait beaucoup plus long pour obtenir la même précision.

Voici le script Python. Les dimensions des bobines correspondent à celles de l'expérience.

statorBipolaire-4bobines.py

import femm
import numpy as np
import matplotlib.pyplot as plt

femm.openfemm()
femm.newdocument(0)
# 0 : magnetic, 1 : electrostatic, 2 ; heat flow, 3 : current flow
femm.mi_probdef(0, 'millimeters', 'planar', 1.0e-8, 0, 30);
# freq, unit, type ('planar' ou 'axis'), precision, depth, minangle

d = 37 # distance entre le centre et les noyaux
a = 22.5 # demi-largeur des noyaux
b = 15 # épaisseur des bobines
c = 15 # longueur de dépassement du noyau
l = 80 # longueur des bobines et des noyaux
Rc = 30 # rayon du noyau central (rotor) = 0 si pas de noyau
Rc = 0
e = 3 #épaisseur du noyau central

# courants dans les bobines
t = 1/8
i1 = np.cos(2*np.pi*t)
i2 = np.sin(2*np.pi*t)
Ns = 250 # nombre de spires dans chaque bobine

# bobine B1
femm.mi_drawrectangle(-d,-a,-d-l,a) # noyau
femm.mi_drawrectangle(-d-c,a,-d-c-l,a+b)
femm.mi_drawrectangle(-d-c,-a,-d-c-l,-a-b)

# bobine B2
femm.mi_drawrectangle(d,-a,d+l,a) # noyau
femm.mi_drawrectangle(d+c,a,d+c+l,a+b)
femm.mi_drawrectangle(d+c,-a,d+c+l,-a-b)

#bobine B3
femm.mi_drawrectangle(-a,d,a,d+l) # noyau
femm.mi_drawrectangle(-a-b,d+c,-a,d+c+l)
femm.mi_drawrectangle(a,d+c,a+b,d+c+l)

#bobine B4
femm.mi_drawrectangle(-a,-d,a,-d-l) # noyau
femm.mi_drawrectangle(-a-b,-d-c,-a,-d-c-l)
femm.mi_drawrectangle(a,-d-c,a+b,-d-c-l)

if Rc!=0: # noyau central (rotor)
    femm.mi_drawarc(Rc,0,-Rc,0,180,1)
    femm.mi_drawarc(-Rc,0,Rc,0,180,1)
    femm.mi_drawarc(Rc-e,0,-Rc+e,0,180,1)
    femm.mi_drawarc(-Rc+e,0,Rc-e,0,180,1)
    
femm.mi_makeABC()

femm.mi_addblocklabel(0,(Rc+d)/2) # air
femm.mi_addblocklabel(-d-l/2,0) #noyau B1
femm.mi_addblocklabel(-d-l/2-c,a+b/2) # B1 Jz
femm.mi_addblocklabel(-d-l/2-c,-a-b/2) # B1 -Jz
femm.mi_addblocklabel(d+l/2,0) #noyau B2
femm.mi_addblocklabel(d+l/2+c,a+b/2) # B2 Jz
femm.mi_addblocklabel(d+l/2+c,-a-b/2) # B2 -Jz
femm.mi_addblocklabel(0,d+l/2) #noyau B3
femm.mi_addblocklabel(-a-b/2,d+c+l/2) # B3 Jz
femm.mi_addblocklabel(a+b/2,d+c+l/2) # B3 -Jz
femm.mi_addblocklabel(0,-d-l/2) #noyau B4
femm.mi_addblocklabel(-a-b/2,-d-c-l/2) # B4 Jz
femm.mi_addblocklabel(a+b/2,-d-c-l/2) # B4 -Jz

femm.mi_addmaterial('Air', 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0)
femm.mi_addmaterial('Coil', 1, 1, 0, 0, 58*0.65, 0, 0, 1, 0, 0, 0)
femm.mi_addmaterial('LinearIron', 2100, 2100, 0, 0, 0, 0, 0, 1, 0, 0, 0)

femm.mi_addcircprop('paire_1_plus', i1, 1)
# name, current, 1=series, 0=parallel
femm.mi_addcircprop('paire_1_moins', -i1, 1)
femm.mi_addcircprop('paire_2_plus', i2, 1);
femm.mi_addcircprop('paire_2_moins', -i2, 1)

femm.mi_selectlabel(d+l/2,0)
femm.mi_setblockprop('LinearIron', 0, 1, '<None>', 0, 0, 0)
femm.mi_clearselected()
femm.mi_selectlabel(-d-l/2,0)
femm.mi_setblockprop('LinearIron', 0, 1, '<None>', 0, 0, 0)
femm.mi_clearselected()
femm.mi_selectlabel(0,d+l/2)
femm.mi_setblockprop('LinearIron', 0, 1, '<None>', 0, 0, 0)
femm.mi_clearselected()
femm.mi_selectlabel(0,-d-l/2)
femm.mi_setblockprop('LinearIron', 0, 1, '<None>', 0, 0, 0)
femm.mi_clearselected()

femm.mi_selectlabel(d+l/2+c,a+b/2)
femm.mi_setblockprop('Coil', 0, 1, 'paire_1_plus', 0, 0, 250)
femm.mi_clearselected()
femm.mi_selectlabel(-d-l/2-c,a+b/2)
femm.mi_setblockprop('Coil', 0, 1, 'paire_1_plus', 0, 0, 250)
femm.mi_clearselected()

femm.mi_selectlabel(d+l/2+c,-a-b/2)
femm.mi_setblockprop('Coil', 0, 1, 'paire_1_moins', 0, 0, Ns)
femm.mi_clearselected()
femm.mi_selectlabel(-d-l/2-c,-a-b/2)
femm.mi_setblockprop('Coil', 0, 1, 'paire_1_moins', 0, 0, Ns)
femm.mi_clearselected()

femm.mi_selectlabel(-a-b/2,d+c+l/2)
femm.mi_setblockprop('Coil', 0, 1, 'paire_2_plus', 0, 0, Ns)
femm.mi_clearselected()
femm.mi_selectlabel(-a-b/2,-d-c-l/2)
femm.mi_setblockprop('Coil', 0, 1, 'paire_2_plus', 0, 0, Ns)
femm.mi_clearselected()

femm.mi_selectlabel(a+b/2,d+c+l/2)
femm.mi_setblockprop('Coil', 0, 1, 'paire_2_moins', 0, 0, Ns)
femm.mi_clearselected()
femm.mi_selectlabel(a+b/2,-d-c-l/2)
femm.mi_setblockprop('Coil', 0, 1, 'paire_2_moins', 0, 0, Ns)
femm.mi_clearselected()

femm.mi_selectlabel(0,(Rc+d)/2)
femm.mi_setblockprop('Air', 0, 1, '<None>', 0, 0, 0)
femm.mi_clearselected()

if Rc!=0:
    femm.mi_addblocklabel(Rc-e/2,0) # fer
    femm.mi_selectlabel(Rc-e/2,0)
    femm.mi_setblockprop('LinearIron', 0, 1, '<None>', 0, 0, 0)
    femm.mi_clearselected()
    if e<Rc:
        femm.mi_addblocklabel(0,0) # air
        femm.mi_selectlabel(0,0)
        femm.mi_setblockprop('Air', 0, 1, '<None>', 0, 0, 0)
        femm.mi_clearselected()

femm.mi_zoomnatural()
femm.mi_saveas('4bobines-v2.fem')
femm.mi_analyze()
femm.mi_loadsolution()


# composantes radiale et orthoradiale de B sur un cercle de rayon ar
ar = 33
theta = np.linspace(0,2*np.pi,360)
cos = np.cos(theta)
sin = np.sin(theta)
Br = np.zeros(len(theta))
Btheta = np.zeros(len(theta))
for k in range(len(theta)):
    B = femm.mo_getb(ar*cos[k],ar*sin[k])
    Br[k] = cos[k]*B[0]+sin[k]*B[1]
    Btheta[k] = -sin[k]*B[0]+cos[k]*B[1]
np.savetxt("4bobines-B-ar=%d-t=%0.3f.txt"%(ar,t),np.array([theta,Br,Btheta]).T)
plt.figure(figsize=(16,6))
plt.title(r"$t = %0.3f$"%t,fontsize=16)
plt.plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plt.plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
plt.grid()
plt.xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
plt.ylabel(r"$B\ (mT)$",fontsize=16)
plt.legend(loc='upper right')
plt.show()

femm.closefemm()

Voici les lignes du champ $\vec{B}$ lorsqu'un courant parcourt la paire de bobines (B1,B2) et aucun courant ne parcourt la paire (B2,B3), c'est-à-dire à l'instant t=0 :

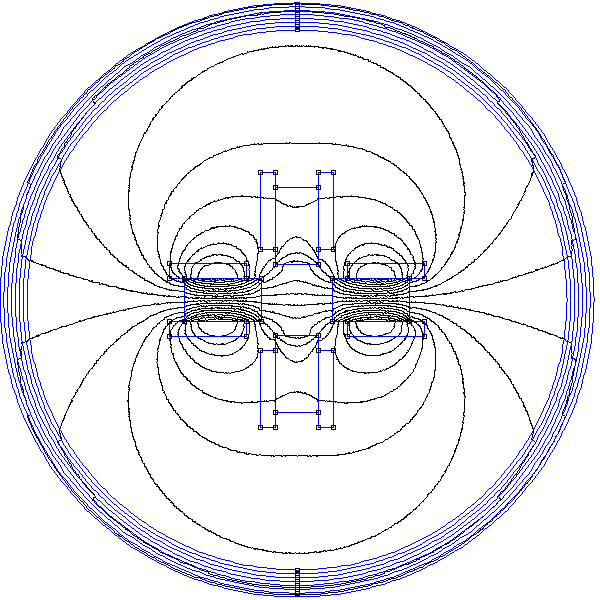
L'amplitude du courant dans les bobines est de 1 A. Voici les composantes radiale et orthoradiale du champ magnétique $\vec{B}$ à une distance de 33 mm du centre (4 mm de la face des noyaux des bobines), ce qui correspond à la position des barreaux du rotor :

[theta,Br,Btheta] = np.loadtxt("4bobines-B-ar=33-t=0.000.txt",unpack=True)
figure(figsize=(16,6))
title(r"$t = 0$",fontsize=16)
plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
grid()
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$B\ (mT)$",fontsize=16)
legend(loc='upper right')

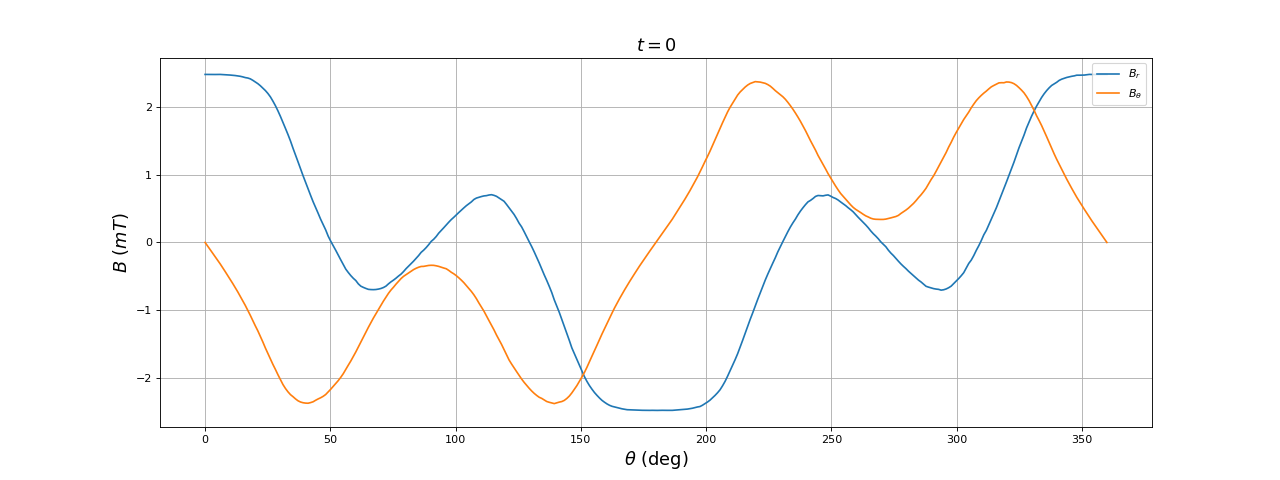fig27.pdf

Voici les lignes lorsque les deux paires de bobines sont parcourues par le même courant (instant t=T/8) :

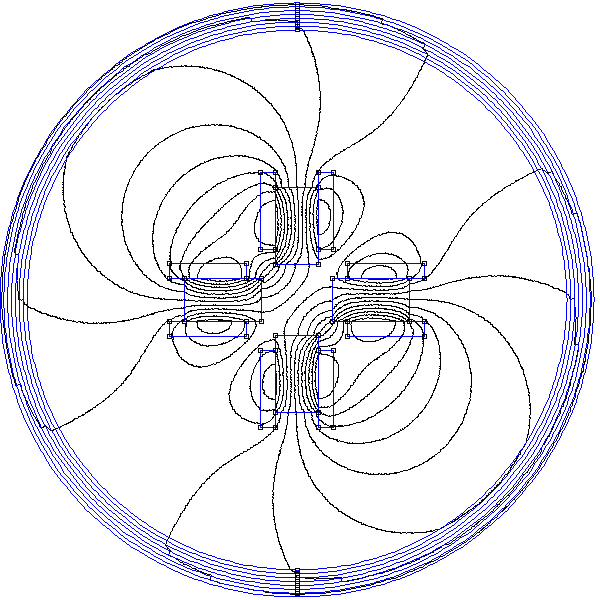
Voici les composantes radiale et orthoradiale du champ magnétique $\vec{B}$ à une distance de 33 mm du centre :

[theta,Br,Btheta] = np.loadtxt("4bobines-B-ar=33-t=0.125.txt",unpack=True)
figure(figsize=(16,6))
title(r"$t = 0.125$",fontsize=16)
plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
grid()
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$B\ (mT)$",fontsize=16)
legend(loc='upper right')

fig28.pdf

Ces résultat montrent la principale faiblesse de ce stator : le champ dans la direction de 45 degrés lorsque t=1/8 est très faible. La mesure du champ dans cette direction donne en effet une amplitude d'oscillation 5 fois plus faible que sur l'axe des bobines.

Voici les résultats lorsqu'un noyau creux en fer est placé dans le rotor, de diamètre externe 30 mm et d'épaisseur 3 mm (ce noyau pourrait être placé dans la cage du rotor) :

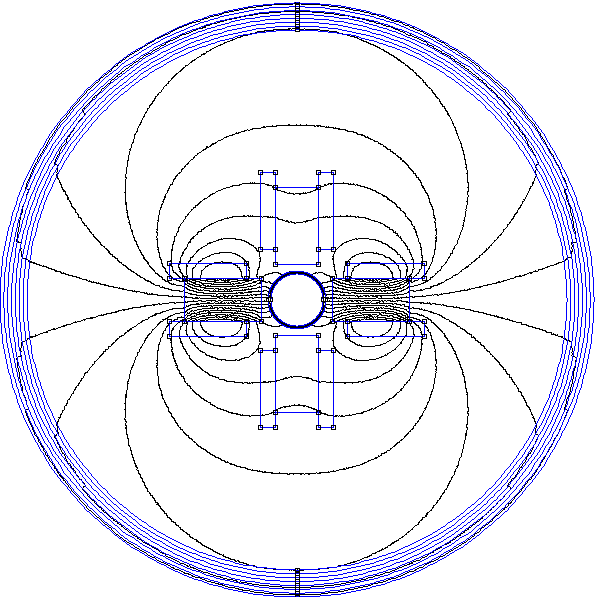
[theta,Br,Btheta] = np.loadtxt("4bobines-noyau-B-ar=33-t=0.000.txt",unpack=True)
figure(figsize=(16,6))
title(r"$t = 0$",fontsize=16)
plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
grid()
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$B\ (mT)$",fontsize=16)
legend(loc='upper right')

fig29.pdf

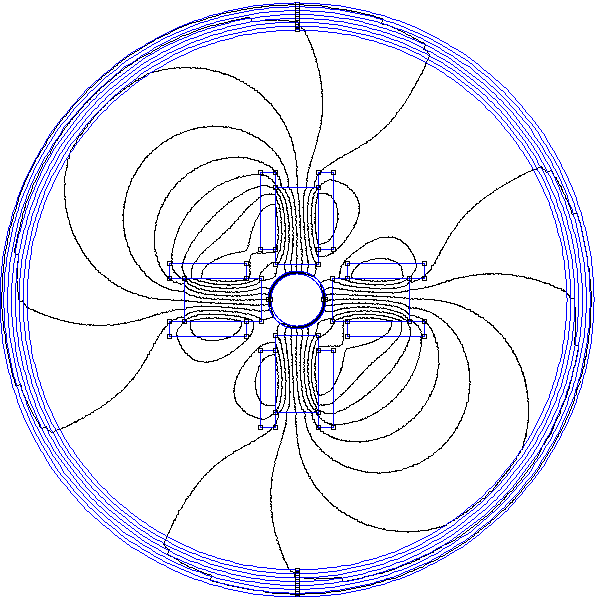
[theta,Br,Btheta] = np.loadtxt("4bobines-noyau-B-ar=33-t=0.125.txt",unpack=True)
figure(figsize=(16,6))
title(r"$t = 0.125$",fontsize=16)
plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
grid()
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$B\ (mT)$",fontsize=16)
legend(loc='upper right')

fig30.pdf

L'intensité du champ dans la direction 45 degrés lorsque t=1/8, bien que non maximale, est nettement plus grande qu'en l'absence de noyau (par rapport au champ sur l'axe). Par ailleurs, l'effet du noyau est une augmentation d'un facteur deux du champ magnétique.

Une autre différence très importante entre le champ sans et avec noyau est la composante orthoradiale du champ magnétique, beaucoup plus grande en l'absence de noyau.

On peut conclure de cette simulation que ce stator à deux paires de bobines (stator bipolaire diphasé) ne peut produire un véritable champ tournant dans l'entrefer. Pourtant, sans noyau central ou avec un noyau plein, le champ à l'intérieur du rotor est bien un champ tournant. Si l'on se réfère au modèle présenté en annexe 2, qui considère le flux sur un cadre constitué de deux barreaux diamétralement opposés, le fait que le champ ne soit pas véritablement tournant au niveau de l'entrefer devrait être sans conséquence majeure sur les courants induits dans le rotor (et cela doit être vrai aussi pour le noyau creux). On peut en revanche s'interroger sur le couple moteur, car celui fait évidemment intervenir le champ magnétique dans l'entrefer. La composante orthoradiale de la force de Laplace sur un barreau (qui contribue au couple) est proportionnelle à la composante radiale du champ magnétique. La faiblesse de celle-ci à t=T/8 rend cette force très faible à cet instant pour les barreaux qui sont dans la direction de 45 degrés (et 180+45 degrés). Cela étant, nous ne savons pas si le couple total est affecté par la faiblesse du champ radial à 45 degrés.

La faible intensité du champ magnétique est probablement la principale raison de la faible efficacité du moteur expérimental étudié. Pour augmenter cette intensité, il faut que les extrémités des noyaux des bobines aient une forme cylindrique qui épouse au plus près le rotor, et l'entrefer doit être plus étroit. Le script permettant de simuler ce type de stator est présenté dans Champ magnétique généré par un stator. Il s'agit d'un stator à bobinage sur dents à 4 bobines. Nous définissons 4 bobines ayant un nombre de spire de 250, comme les bobines que nous utilisons pour l'expérience.

Voici le résultat à t=0 :

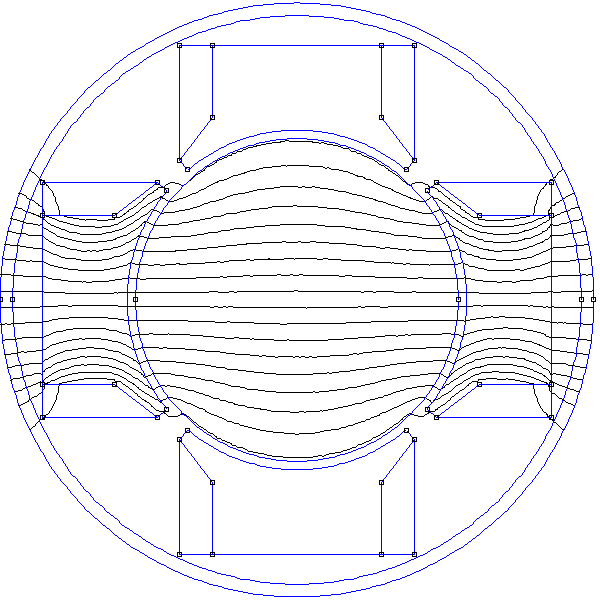
[theta,Br,Btheta] = np.loadtxt("4bobines-dents-ar=39-t=0.000.txt",unpack=True)
figure(figsize=(16,6))
title(r"$t = 0$",fontsize=16)
plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
grid()
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$B\ (mT)$",fontsize=16) 
legend(loc='upper right')

fig31.pdf

Voici le résultat à t=1/8 :

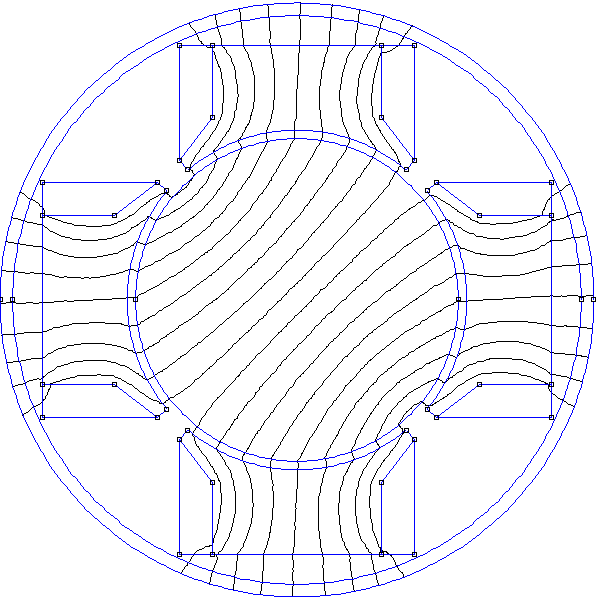
[theta,Br,Btheta] = np.loadtxt("4bobines-dents-ar=39-t=0.125.txt",unpack=True)
figure(figsize=(16,6))
title(r"$t = 0$",fontsize=16)
plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
grid()
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$B\ (mT)$",fontsize=16) 
legend(loc='upper right')

fig32.pdf

Par rapport à la configuration du moteur expérimental, constituée de deux bobines à noyaux droits et sans noyau de rotor, le champ magnétique sur l'axe des bobines est environ 15 fois plus fort. Le couple moteur étant proportionnel au carré du champ, il serait 220 fois plus grand. Si l'on compare à la configuration identique à celle étudiée expérimentalement mais où un noyau est ajouté au rotor (voir ci-dessus), ce rapport est 25. On en conclut que pour obtenir un moteur de fort couple il faut à la fois ajouter un noyau dans le rotor, adapter la forme des têtes des noyaux des bobines et réduire l'entrefer.

Moteur asynchrone diphasé

1. Introduction

2. Théorie du moteur asynchrone

3. Réalisation d'un moteur asynchrone expérimental

3.a. Description du moteur

3.b. Onduleur

3.c. Programme Arduino

3.d. Programme Python

4. Étude expérimentale

4.a. Test de l'onduleur

4.b. Test du moteur

4.c. Étude expérimentale

5. Annexe 1 : modèle de moteur asynchrone

6. Annexe 2: simulation du stator expérimental