Champ magnétique généré par un stator

1. Introduction

Cette page présente le calcul par éléments finis du champ généré par un stator de moteur à courant alternatif (moteur synchrone ou asynchrone), en présence d'un rotor en fer parfaitement lisse.

Les calculs sont faits avec le logiciel libre Finite Element Method Magnetic. Nous utilisons l'interface pour Python (pyfemm), qui permet de piloter le logiciel depuis un script Python. Ce script permet de définir une géométrie complexe dépendant d'un ou de plusieurs paramètres et d'obtenir des tracés de champ sur des courbes particulières. Les commandes de l'interface Python sont des répliques des opérations que l'on effectue lorsqu'on utilise directement l'interface utilisateur. Il faut donc bien se familiariser avec cette interface avant d'aborder l'écriture des scripts Python.

Le logiciel FEMM permet d'effectuer la résolution numérique d'un problème de magnétostatique (ou d'électrostatique ou de diffusion thermique) par la méthode des éléments finis. Il résout les problèmes bidimensionnels, en géométrie plane ou axisymétrique. Contrairement au logiciel FreeFEM, dont l'utilisation pour un problème de magnétostatique est exposée dans Équation de Poisson : méthode des éléments finis, le logiciel FEMM peut être utilisé sans aucune connaissance sur la méthode des éléments finis ni même des équations de la magnétostatique. Le système magnétique est en effet défini directement par ses caractéristiques physiques.

Le stator est modélisé par un système bidimensionnel. Si (Oz) désigne l'axe du stator (l'axe de rotation du moteur), les courants dans les fils du bobinage sont supposés être dans la direction de cet axe et indépendants de z. Le champ magnétique est donc indépendant de z et le calcul donne le champ magnétique dans le plan (Oxy) (qui est contenu dans ce plan, alors que le potentiel vecteur est orthogonal à ce plan). Ce modèle donne des résultats très proches de la réalité si le rotor a une longueur grande devant son rayon ou si les parties du bobinage qui sont aux extrémités du stator ont une contribution négligeable.

Dans ce document, on désigne par bobine une partie du bobinage qui produit un champ magnétique d'une direction déterminée. Une bobine est constituée de deux demi-bobines parcourues par deux courants opposés. Dans le modèle bidimensionnel considéré, une demi-bobine est un conducteur rectiligne de direction l'axe (Oz).

On distingue deux types de stator :

Stator à encoches : l'intérieur du stator est un cyclindre muni d'encoches régulièrement espacées sur la circonférence. Une bobine peut être réalisée avec deux encoches non consécutives et peut même occuper plus que deux encoches.
Stator à bobinage sur dents (ou bobinage dentaire) : chaque bobine est enroulée sur une dent.

Les gros moteurs industriels ont un stator à encoches alors que le stator dentaire semble prépondérant sur les petits moteurs (robotique, modélisme). Le stator à bobinage dentaire offre moins de possibilités de bobinage car une bobine est nécessairement localisée sur une dent (ce qui n'empêche pas d'avoir deux dents consécutives avec deux bobines identiques).

La photo ci-dessous montre un stator à encoches avec son bobinage :

On remarque sur cette photo que la partie du bobinage qui se trouve à l'extrémité du stator en dehors du noyau a vraisemblablement peu d'effet sur le champ magnétique dans l'entrefer. La partie en fer de ce type de stator est réalisée par empilement de plaques de fer magnétique (fer doux) découpées selon la forme voulue. Ces plaques ont un revêtement isolant afin de limiter la taille des boucles de courant induit (qui occasionnent des pertes d'énergie dans le fer). Cette vidéo montre comment les stators et rotors des machines industrielles sont fabriqués.

La photo ci-dessous montre un exemple de bobinage sur dents comportant 12 bobines (configuration très courante dans les moteurs de modélisme) :

Dans ce type de bobinage, il est évident que la partie qui se trouve aux deux extrémités du stator a une influence non négligeable sur le champ dans l'entrefer. Le modèle bidimensionnel est d'ailleurs loin de la réalité dans ce cas.

Les stators à bobinage sur dents sont parfois qualifiés de stators à pôles saillants, en raison de la forme du champ produit par ce type de stator, qui présente des variations plus abruptes du champ magnétique d'un pôle à l'autre. Cependant, cette différence vient plus du bobinage que de la forme de la partie en fer du stator. Les dents sont parfois nommées pôles. Il s'agit d'une appelation à éviter car elle pourrait faire croire que le champ magnétique a autant de pôles que de dents, ce qui est évidemment faux. Il semble d'ailleurs que l'expression stators à pôles saillants soit souvent employée pour signifier que les dents sont des parties en fer saillantes.

Si l'on regarde seulement la partie en fer, il ne semble pas y avoir de différence fondamentale entre les deux types de stator, mais seulement une plus grande quantité de fer dans le stator à encoches alors que la stator dentaire qui est montré ci-dessus comporte beaucoup d'air. Il semble que la caractéristique la plus importante du stator à encoches soit de permettre un enchevêtrement des bobines, c'est-à-dire que deux bobines peuvent se répartir sur des secteurs angulaires qui se chevauchent. Par exemple sur la photographie ci-dessus, on voit qu'un groupe de fils passe dans une encoche puis dans une autre encoches située deux encoches plus loin. Dans un stator à bobinage dentaire, chaque bobine est au contraire localisée sur une dent. C'est donc plutôt la structure du bobinage qui différencie vraiment ces deux types de stator (les calculs montrés plus loin le confirment).

Dans le cas du stator à bobinage dentaire, on peut aussi parler d'encoches dans la partie en fer mais celle-ci sont plus larges que dans le stator à encoches et recoivent toujours deux demi-bobines de deux bobines adjacentes. Pour éviter toute confusion, nous réservons le terme encoche aux stators à encoches. Pour le stator à bobinage dentaire, il est préférable de parler de dents séparées par un espace plus ou moins grand.

Idéalement, un stator doit produire un champ radial dans l'entrefer ayant une forme sinusoïdale en fonction de l'angle :

B_{r} (θ, t) = B_{0} cos (ω t - \frac{p}{2} θ) (1)

où $ω$ est la pulsation des courants dans les bobines et p le nombre de pôles, c'est-à-dire le nombre de pôles sud et de pôles nord (ce nombre est nécessairement pair). Il y a donc dans l'entrefer une onde de champ magnétique qui se déplace à la vitesse angulaire $\frac{2}{p} ω$ . Dans le cas p=2 (stator bipolaire) la longueur d'onde est 2π. Dans le cas p=4 (stator quadrupolaire) la longueur d'onde est π. Dans le cas du moteur synchrone, le rotor tourne à la pulsation $\frac{2}{p} ω$ . Dans le cas du moteur asynchrone en régime permanent, la vitesse est proche de $\frac{2}{p} ω$ .

Il est difficile d'obtenir une forme sinusoïdale pure et on cherche au moins à avoir une forme quasi sinusoïdale, c'est-à-dire une forme dont le fondamental (de période angulaire $4 π / p$ ) est prépondérant sur les harmoniques.

Nous considérons dans ce document que la qualification de stator à pôles lisses s'applique à un stator qui produit un champ (avec un rotor lisse) dont les harmoniques ont des amplitudes faibles par rapport au fondamental. Un stator à pôles saillants produit au contraire un champ qui présente des harmoniques de grande amplitude. Comme le montrent les simulations ci-dessous, le caractère plus ou moins lisse des pôles dans le cas d'un stator à encoches vient de la structure du bobinage.

2. Stator bipolaire diphasé à encoches

Un stator bipolaire génère un champ comportant deux pôles, c'est-à-dire un pôle nord et un pôle sud. Un stator diphasé comporte deux paires de bobines, alimentés par deux courants en quadrature :

\begin{matrix} i_{1} (t) = I_{0} cos (ω t) & (2) \\ i_{2} (t) = I_{0} cos (ω t + \frac{π}{2}) & (3) \end{matrix}

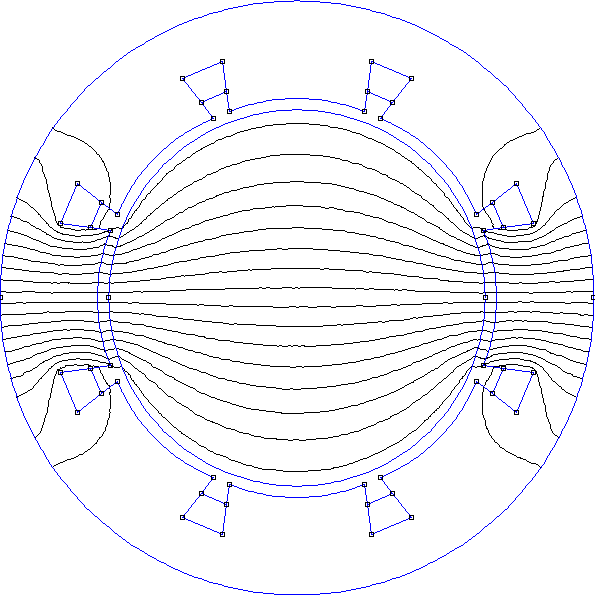
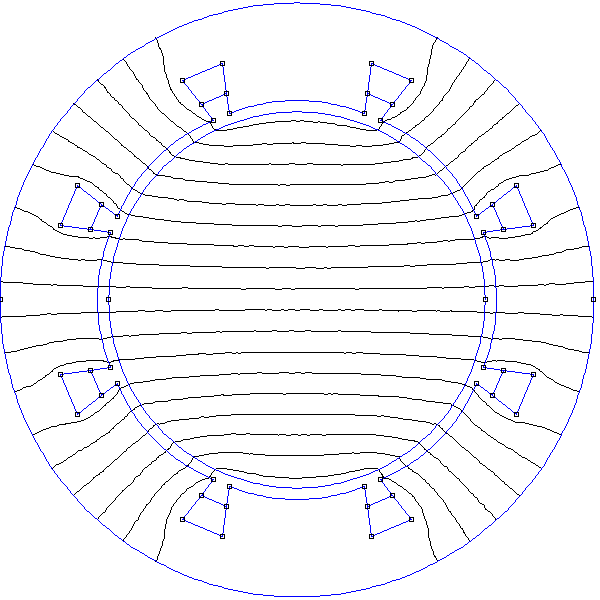
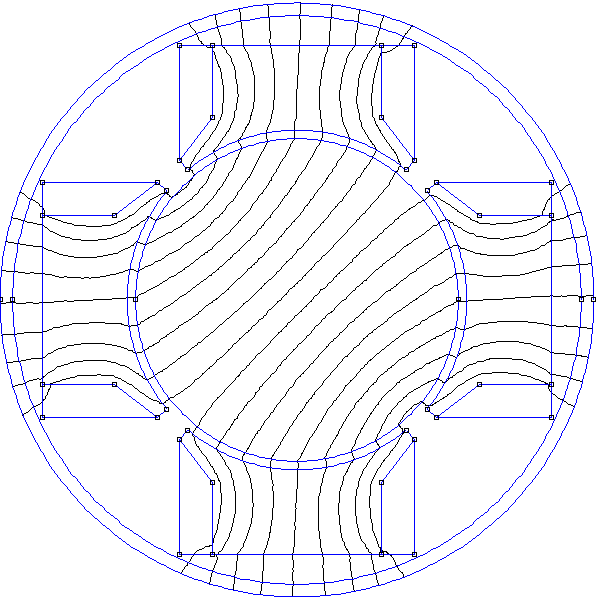
Ces deux paires permettent de générer un champ tournant. Considérons tout d'abord un stator à encoches avec 4 bobines et 8 encoches. Ces encoches sont réparties sur la surface interne du stator, ce qui fait un angle de 45 degrés entre deux encoches consécutives. La figure suivante représente les encoches et les courants dans les fils qu'ils contiennent :

Figure pleine page

Les bobines B_1,1 et B_1,2 constituent la phase 1, les bobines B_2,1 et B_2,2 la phase 2.

Dans cette géométrie, les 4 bobines sont bien séparées. Elle pourrait donc tout aussi bien être réalisée avec un stator à dents comportant 4 dents.

La géométrie du stator de notre modèle est définie par :

Le rayon interne de la partie en fer du stator et son rayon externe.
Le diamètre angulaire des encoches au niveau de la surface interne du stator.
Le diamètre angulaire du fond des encoches (souvent plus grande que la précédente).
L'épaisseur de cuivre à partir du fond de l'encoche.

Pour une paire de bobines, les courants dans deux encoches diamètralement opposées doivent être opposés afin que ces deux bobines produisent un champ dans le même sens.

On place un noyau central en fer (cyclindre de révolution) qui représente de manière sommaire un rotor à pôles lisses. Un rotor bobiné réel comporte bien évidemment des encoches mais nous nous limitons au cas idéal d'un rotor parfaitement lisse.

Voici le script Python :

statorEncoches-2phases.py

import femm
import numpy as np
import matplotlib.pyplot as plt

femm.openfemm()
femm.newdocument(0)
# 0 : magnetic, 1 : electrostatic, 2 ; heat flow, 3 : current flow
femm.mi_probdef(0, 'millimeters', 'planar', 1.0e-8, 0, 30);
# freq, unit, type ('planar' ou 'axis'), precision, depth, minangle

R1 = 40 # rayon interne du stator
R2 = 60 # rayon externe
Rc = 38 # rayon du noyau (rotor) = 0 si pas de noyau
a1 = 10 # largeur angulaire du fond des encoches (en degrés)
a2 = 5 # largeur angulaire du haut des encoches (en degrés)
e = 10 # profondeur des encoches
d = 6 # épaisseur du cuivre (depuis le fond de l'encoche)
u = d/e
Ne = 8 # nombre d'encoches
# définition des courants dans les régions cuivre
circ = ['1+','2-','2+','1+','1-','2+','2-','1-']
increm = 1 # incrément d'indice entre deux encoches voisines
t = 0
i1 = np.cos(2*np.pi*t)
i2 = np.sin(2*np.pi*t)
Ns = 250 # nombre de spires dans chaque bobine
angle = 360/Ne

theta = -angle/2
x = R1*np.cos((theta+a2/2)*np.pi/180)
y = R1*np.sin((theta+a2/2)*np.pi/180)
cuivre = []
for k in range(Ne):
    theta = angle/2+angle*k
    x1 = R1*np.cos((theta-a2/2)*np.pi/180)
    y1 = R1*np.sin((theta-a2/2)*np.pi/180)
    femm.mi_drawarc(x,y,x1,y1,angle,1)
    x,y = x1,y1
    x2,y2 = x,y
    x1 = (R1+e)*np.cos((theta-a1/2)*np.pi/180)
    y1 = (R1+e)*np.sin((theta-a1/2)*np.pi/180)
    femm.mi_drawline(x,y,x1,y1)
    x,y = x1,y1
    x1 = (R1+e)*np.cos((theta+a1/2)*np.pi/180)
    y1 = (R1+e)*np.sin((theta+a1/2)*np.pi/180)
    femm.mi_drawline(x,y,x1,y1)
    x,y = x1,y1
    x1 = R1*np.cos((theta+a2/2)*np.pi/180)
    y1 = R1*np.sin((theta+a2/2)*np.pi/180)
    femm.mi_drawline(x,y,x1,y1)
    x,y = x1,y1
    x,y = R1*np.cos((theta-a2/2)*np.pi/180),R1*np.sin((theta-a2/2)*np.pi/180)
    x1,y1 = (R1+e)*np.cos((theta-a1/2)*np.pi/180),(R1+e)*np.sin((theta-a1/2)*np.pi/180)
    x2 = (u*x+(1-u)*x1)
    y2 = (u*y+(1-u)*y1)
    x,y = R1*np.cos((theta+a2/2)*np.pi/180),R1*np.sin((theta+a2/2)*np.pi/180)
    x1,y1 = (R1+e)*np.cos((theta+a1/2)*np.pi/180),(R1+e)*np.sin((theta+a1/2)*np.pi/180)
    x3 = (u*x+(1-u)*x1)
    y3 = (u*y+(1-u)*y1)
    femm.mi_drawline(x2,y2,x3,y3)
    cuivre.append([(R1+0.9*e)*np.cos((theta)*np.pi/180),(R1+0.9*e)*np.sin((theta)*np.pi/180)])
    
femm.mi_drawarc(R2,0,-R2,0,180,1)
femm.mi_drawarc(-R2,0,R2,0,180,1)
if Rc!=0:
    femm.mi_drawarc(Rc,0,-Rc,0,180,1)
    femm.mi_drawarc(-Rc,0,Rc,0,180,1)


femm.mi_addmaterial('Air', 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0)
femm.mi_addmaterial('Coil', 1, 1, 0, 0, 58*0.65, 0, 0, 1, 0, 0, 0)
femm.mi_addmaterial('LinearIron', 2100, 2100, 0, 0, 0, 0, 0, 1, 0, 0, 0)

femm.mi_addcircprop('1+', i1, 1)
# name, current, 1=series, 0=parallel
femm.mi_addcircprop('1-', -i1, 1)
femm.mi_addcircprop('2+', i2, 1);
femm.mi_addcircprop('2-', -i2, 1)

femm.mi_addblocklabel(0,(R1+Rc)/2) # air
femm.mi_addblocklabel(0,(R1+R2)/2) # fer
femm.mi_selectlabel(0,(R1+R2)/2)
femm.mi_setblockprop('LinearIron', 0, 1, '<None>', 0, 0, 0)
femm.mi_clearselected()
femm.mi_selectlabel(0,(R1+Rc)/2)
femm.mi_setblockprop('Air', 0, 1, '<None>', 0, 0, 0)
femm.mi_clearselected()

if Rc!=0:
    femm.mi_addblocklabel(0,0)
    femm.mi_selectlabel(0,0)
    femm.mi_setblockprop('LinearIron', 0, 1, '<None>', 0, 0, 0)
    femm.mi_clearselected()

i = 0
for p in cuivre:
    femm.mi_addblocklabel(p[0],p[1])
    femm.mi_selectlabel(p[0],p[1])
    femm.mi_setblockprop('Coil', 0, 1, circ[int(i)], 0, 0, Ns)
    femm.mi_clearselected()
    i += increm


femm.mi_zoomnatural()
femm.mi_saveas('stator2phases.fem')
femm.mi_analyze()
femm.mi_loadsolution()


# composantes radiale et orthoradiale de B sur un cercle de rayon ar
ar = 39
theta = np.linspace(0,2*np.pi,360)
cos = np.cos(theta)
sin = np.sin(theta)
Br = np.zeros(len(theta))
Btheta = np.zeros(len(theta))
for k in range(len(theta)):
    B = femm.mo_getb(ar*cos[k],ar*sin[k])
    Br[k] = cos[k]*B[0]+sin[k]*B[1]
    Btheta[k] = -sin[k]*B[0]+cos[k]*B[1]
np.savetxt("4bobines-noyau-B-ar=%d-t=%0.3f.txt"%(ar,t),np.array([theta,Br,Btheta]).T)
plt.figure(figsize=(16,6))
plt.title(r"$t = %0.3f$"%t,fontsize=16)
plt.plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plt.plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
plt.grid()
plt.xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
plt.ylabel(r"$B\ (mT)$",fontsize=16)
plt.legend(loc='upper right')
plt.show()

femm.closefemm()

Le rayon interne du stator est 40 mm et celui du noyau central est 38 mm, ce qui fait un entrefer de 2 mm d'épaisseur. On trace les composantes radiale et orthoradiale du champ magnétique (champ $\vec{B}$ ) sur un cercle situé au milieu de l'entrefer (cercle de rayon 39 mm).

Voici les résultats à l'instant t=0 :

import numpy as np
from matplotlib.pyplot import *
from numpy.fft import fft

[theta,Br,Btheta] = np.loadtxt("4bobines-noyau-B-ar=39-t=0.000.txt",unpack=True)
figure(figsize=(16,6))
title(r"$t = 0$",fontsize=16)
plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
grid()
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$B\ (mT)$",fontsize=16)
legend(loc='upper right')

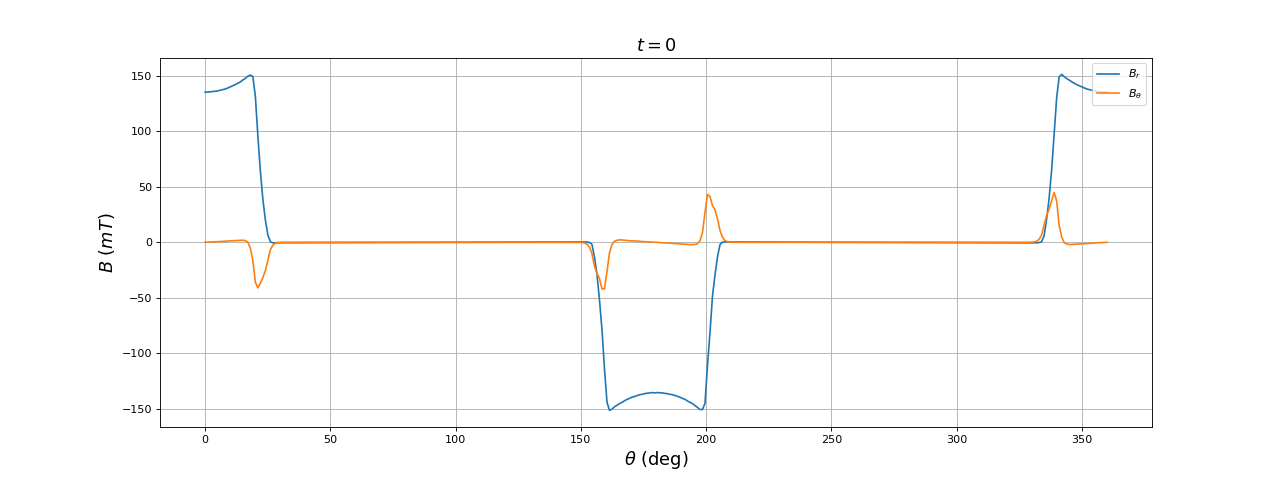fig1.pdf

Voici les résultats à t=T/8 :

[theta,Br,Btheta] = np.loadtxt("4bobines-noyau-B-ar=39-t=0.125.txt",unpack=True)
figure(figsize=(16,6))
title(r"$t = T/4$",fontsize=16)
plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
grid()
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$B\ (mT)$",fontsize=16)
legend(loc='upper right')

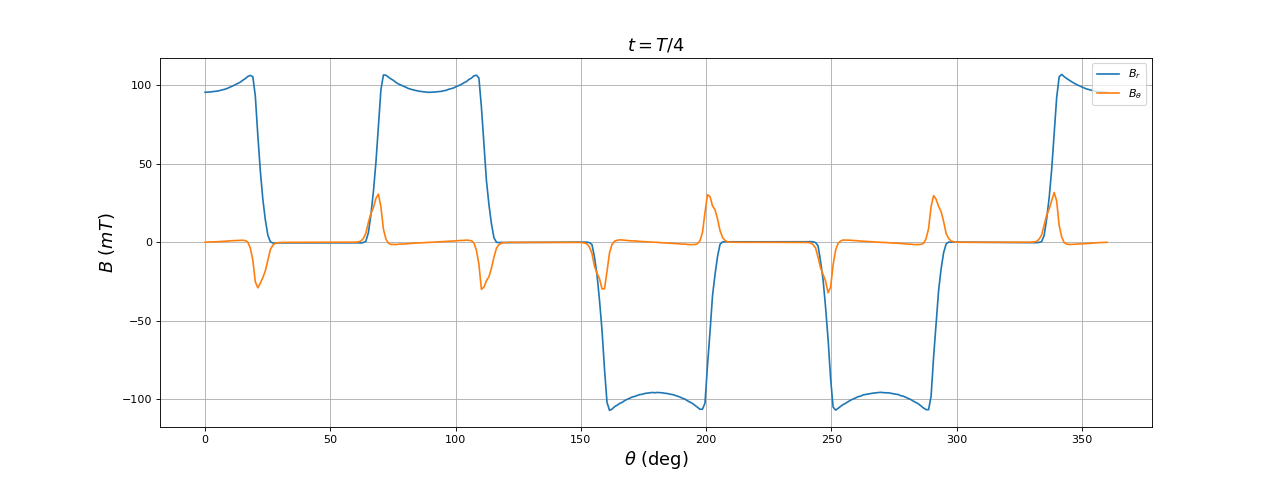fig2.pdf

Voici les modules des coefficients de Fourier du champ radial :

harm = np.absolute(fft(Br))
figure()
stem(harm)
xlim(0,10)
grid()
xlabel(r"$n$",fontsize=16)
ylabel(r"$B_r\ (mT)$",fontsize=16)

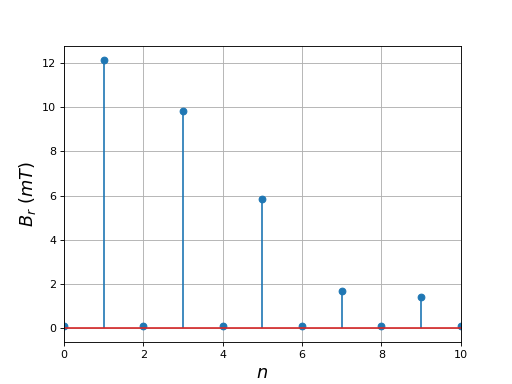fig3.pdf

La composante orthoradiale du champ magnétique est non nulle au dessus des encoches. On constate que, pour t=T/8 la direction moyenne du champ dans la zone centrale est de 45 degrés comme prévu mais que la composante radiale dans l'entrefer est nulle dans cette direction. Dans l'entrefer, le champ est toujours maximal dans l'axe des deux paires de bobines.

La forme du champ radial est loin d'une forme sinusoïdale : les harmoniques de rang 3 et 5 sont très intenses.

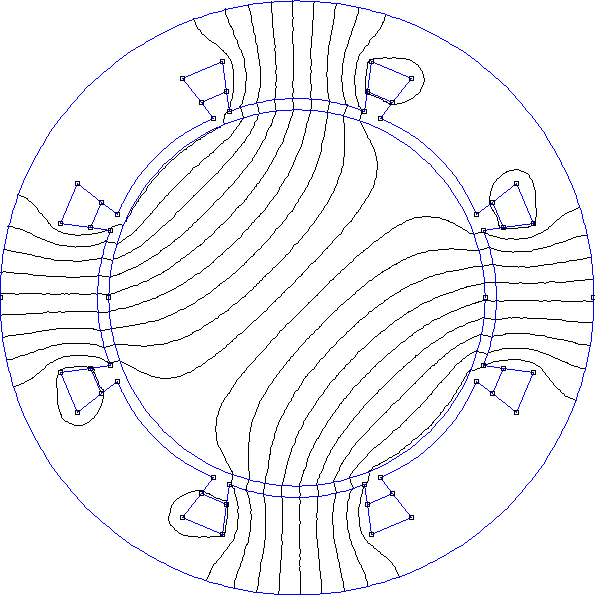
On devine que cette forme du champ vient du fait que les bobines sont trop localisées. Voyons s'il est possible d'améliorer la forme du champ sans augmenter le nombre d'encoches et sans mettre deux phases dans une encoche, avec la configuration suivante :

Figure pleine page

Dans cette nouvelle configuration, chaque bobine occupe un angle deux fois plus grand que précédemment. Une bobine est réalisée en faisant passer des fils dans deux encoches non consécutives (il y a deux encoches entre les deux encoches d'une bobine). C'est une configuration qui est réalisable sans difficulté avec un stator à encoches mais qui est impossible avec un stator à dents, dans la mesure où une bobine est nécessairement réalisée sur une dent.

Pour l'obtenir, il suffit de poser :

circ = ['2-','1+','1+','2+','2+','1-','1-','2-']

Voici le résultat à t=0 :

[theta,Br,Btheta] = np.loadtxt("2phases-8encoches-ar=39-t=0.000.txt",unpack=True)
figure(figsize=(16,6))
title(r"$t = 0$",fontsize=16)
plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
grid()
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$B\ (mT)$",fontsize=16)
legend(loc='upper right')

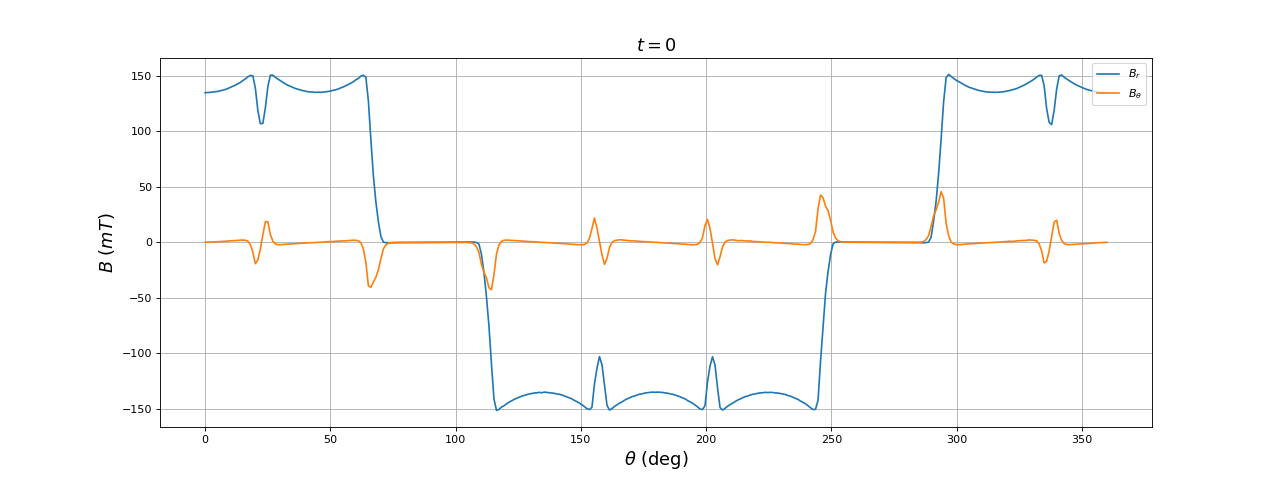fig4.pdf

Voici les modules des coefficients de Fourier du champ radial :

harm = np.absolute(fft(Br))
figure()
stem(harm)
xlim(0,10)
grid()
xlabel(r"$n$",fontsize=16)
ylabel(r"$B_r\ (mT)$",fontsize=16)

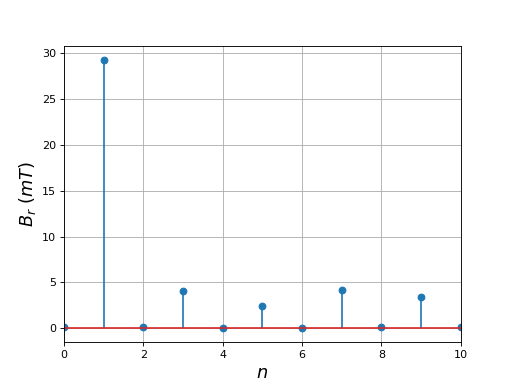fig5.pdf

La forme est bien améliorée, dans le sens où les amplitudes des harmoniques du champ sont réduites (on se rapproche d'une sinusoïde), mais les pôles sont toujours saillants.

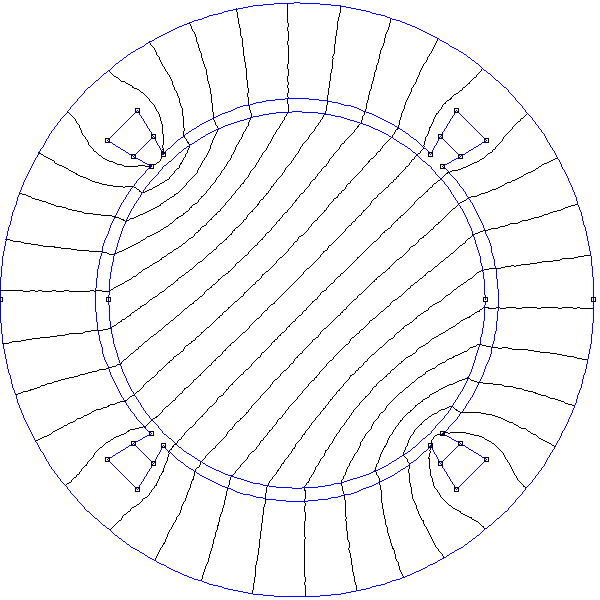
Dans cette configuration, chaque demi-bobine se trouve à côté d'une demi-bobine parcourue par le même courant. En conséquence, il est possible de simplifier en réunissant ces deux demi-bobines en une seule encoche. On obtient ainsi la configuration suivante à 4 encoches :

Figure pleine page

Dans cette version simplifiée, il n'y a plus qu'une bobine par phase mais cette configuration n'est réalisable que sur un stator à encoches. Il faut noter que la réalisation de ce bobinage aurait pour conséquence une partie importante de cuivre sur l'extrémité du stator, une demi-circonférence pour former chaque bobine. Cette partie du bobinage n'intervient presque pas dans la forme du champ car elle se trouve en dehors du noyau en fer, mais elle augmente les pertes par effet Joule.

Voici les resultats à t=0 :

[theta,Br,Btheta] = np.loadtxt("4encoches-2phases-ar=39-t=0.000.txt",unpack=True)
figure(figsize=(16,6))
title(r"$t = 0$",fontsize=16)
plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
grid()
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$B\ (mT)$",fontsize=16)
legend(loc='upper right')

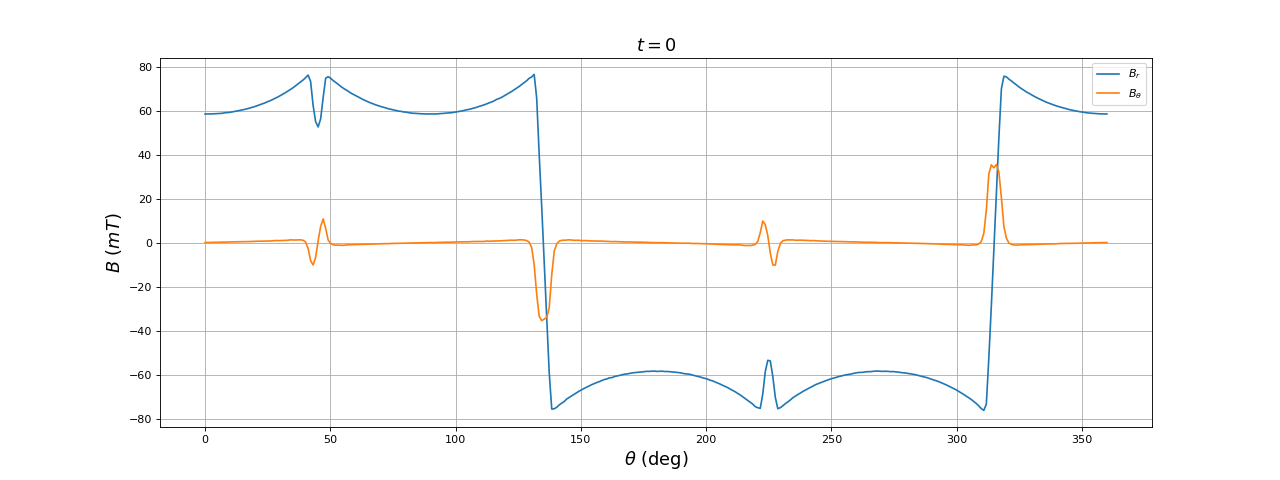fig6.pdf

Les axes sont tournés de 45 degrés par rapport à la figure ci-dessus, ce qui fait que le champ à t=0 est incliné de 45 degrés.

Voici les modules des coefficients de Fourier du champ radial :

harm = np.absolute(fft(Br))
figure()
stem(harm)
xlim(0,10)
grid()
xlabel(r"$n$",fontsize=16)
ylabel(r"$B_r\ (mT)$",fontsize=16)

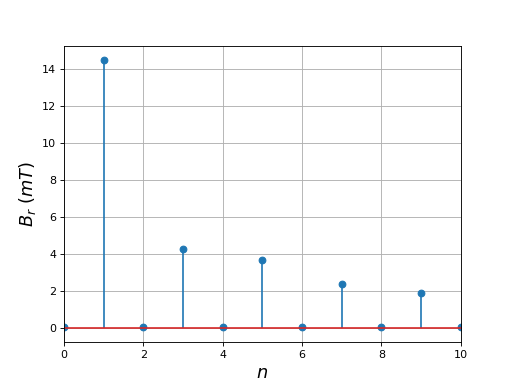fig7.pdf

Ce bobinage est moins bon que le bobinage équivalent à 8 encoches dans le sens où les harmoniques (en particulier de rang 3 et 5) ont une plus grande amplitude. On peut clairement qualifier ce stator de stator à pôles saillants.

La forme du champ peut être améliorée à partir du stator à 8 encoches, en faisant passer les deux phases dans chaque encoche de telle manière que chaque demi-bobine soit répartie sur deux encoches successives. Cette amélioration est montrée plus loin dans le cas du stator triphasé.

3. Stator bipolaire diphasé à bobinage sur dents

Ce stator est constitué de deux paires de bobines. Voici le script :

statorDents-2phases.py

     
import femm
import numpy as np
import matplotlib.pyplot as plt

femm.openfemm()
femm.newdocument(0)
# 0 : magnetic, 1 : electrostatic, 2 ; heat flow, 3 : current flow
femm.mi_probdef(0, 'millimeters', 'planar', 1.0e-8, 0, 30);
# freq, unit, type ('planar' ou 'axis'), precision, depth, minangle

R1 = 40 # rayon interne du stator
R2 = 60 # rayon externe des noyaux des bobines
R3 = 67 # rayon interne de la partie périphérique du stator
R4 = 70 # rayon externe du stator
Rc = 38 # rayon du noyau (rotor) = 0 si pas de noyau
L = 40 # largeur des noyaux des bobines
e = 3 # épaisseur des parties cylindriques
a = 80 # largeur angulaire des parties cylindriques
Nb = 4 # nombre de bobines
circ = ['1-','1+','2-','2+','1+','1-','2+','2-']
Ns = 250 # nombre de spires dans chaque bobine
t = 1/8
i1 = np.cos(2*np.pi*t)
i2 = np.sin(2*np.pi*t)
angle = 360/Nb

cuivre = []
fer = []

def rotation(x,y,theta):
    cos = np.cos(theta)
    sin = np.sin(theta)
    return x*cos-y*sin,x*sin+y*cos


def bobine(theta):
    aa = a*np.pi/180
    x1,y1 = rotation(R1*np.cos(aa/2),-R1*np.sin(aa/2),theta)
    x8,y8 = rotation(R1*np.cos(aa/2),R1*np.sin(aa/2),theta)
    x2,y2 = rotation((R1+e)*np.cos(aa/2),-(R1+e)*np.sin(aa/2),theta)
    x7,y7 = rotation((R1+e)*np.cos(aa/2),(R1+e)*np.sin(aa/2),theta)
    x3,y3 = rotation(R1+e,-L/2,theta)
    x6,y6 = rotation(R1+e,L/2,theta)
    x4,y4 = rotation(R2,-L/2,theta)
    x5,y5 = rotation(R2,L/2,theta)
    femm.mi_drawline(x1,y1,x2,y2)
    femm.mi_drawline(x2,y2,x3,y3)
    femm.mi_drawline(x3,y3,x4,y4)
    femm.mi_drawline(x4,y4,x5,y5)
    femm.mi_drawline(x5,y5,x6,y6)
    femm.mi_drawline(x6,y6,x7,y7)
    femm.mi_drawline(x7,y7,x8,y8)
    x9,y9 = rotation(R2,-(R1+e)*np.sin(aa/2),theta)
    x10,y10 = rotation(R2,(R1+e)*np.sin(aa/2),theta)
    femm.mi_drawline(x2,y2,x9,y9)
    femm.mi_drawline(x9,y9,x4,y4)
    femm.mi_drawline(x7,y7,x10,y10)
    femm.mi_drawline(x10,y10,x5,y5)
    femm.mi_addarc(x1,y1,x8,y8,a,1)
    xf,yf = rotation(R1+e,0,theta)
    fer.append([xf,yf])
    xc,yc = (x3+x9)/2,(y3+y9)/2
    cuivre.append([xc,yc])
    xc,yc = (x7+x5)/2,(y7+y5)/2
    cuivre.append([xc,yc])
    

femm.mi_drawarc(R3,0,-R3,0,180,1)
femm.mi_drawarc(-R3,0,R3,0,180,1)
femm.mi_drawarc(R4,0,-R4,0,180,1)
femm.mi_drawarc(-R4,0,R4,0,180,1)


for k in range(Nb):
    theta = angle*k
    bobine(theta*np.pi/180)

if Rc!=0:
    femm.mi_drawarc(Rc,0,-Rc,0,180,1)
    femm.mi_drawarc(-Rc,0,Rc,0,180,1)


femm.mi_addmaterial('Air', 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0)
femm.mi_addmaterial('Coil', 1, 1, 0, 0, 58*0.65, 0, 0, 1, 0, 0, 0)
femm.mi_addmaterial('LinearIron', 2100, 2100, 0, 0, 0, 0, 0, 1, 0, 0, 0)

femm.mi_addcircprop('1+', i1, 1)
# name, current, 1=series, 0=parallel
femm.mi_addcircprop('1-', -i1, 1)
femm.mi_addcircprop('2+', i2, 1);
femm.mi_addcircprop('2-', -i2, 1)


femm.mi_addblocklabel(0,(R1+Rc)/2) # air
femm.mi_selectlabel(0,(R1+Rc)/2)
femm.mi_setblockprop('Air', 0, 1, '<None>', 0, 0, 0)
femm.mi_clearselected()

femm.mi_addblocklabel(0,(R4+R3)/2) # fer
femm.mi_selectlabel(0,(R4+R3)/2)
femm.mi_setblockprop('LinearIron', 0, 1, '<None>', 0, 0, 0)
femm.mi_clearselected()

if Rc!=0:
    femm.mi_addblocklabel(0,0)
    femm.mi_selectlabel(0,0)
    femm.mi_setblockprop('LinearIron', 0, 1, '<None>', 0, 0, 0)
    femm.mi_clearselected()

i=0
for p in cuivre:
    femm.mi_addblocklabel(p[0],p[1])
    femm.mi_selectlabel(p[0],p[1])
    femm.mi_setblockprop('Coil', 0, 1, circ[int(i)], 0, 0, Ns)
    femm.mi_clearselected()
    i += 1

for p in fer:
    femm.mi_addblocklabel(p[0],p[1])
    femm.mi_selectlabel(p[0],p[1])
    femm.mi_setblockprop('LinearIron', 0, 1, '<None>', 0, 0,0)
    femm.mi_clearselected()


femm.mi_zoomnatural()
femm.mi_saveas('stator2phases.fem')
femm.mi_analyze()
femm.mi_loadsolution()


# composantes radiale et orthoradiale de B sur un cercle de rayon ar
ar = 39
theta = np.linspace(0,2*np.pi,360)
cos = np.cos(theta)
sin = np.sin(theta)
Br = np.zeros(len(theta))
Btheta = np.zeros(len(theta))
for k in range(len(theta)):
    B = femm.mo_getb(ar*cos[k],ar*sin[k])
    Br[k] = cos[k]*B[0]+sin[k]*B[1]
    Btheta[k] = -sin[k]*B[0]+cos[k]*B[1]
np.savetxt("4bobines-dents-ar=%d-t=%0.3f.txt"%(ar,t),np.array([theta,Br,Btheta]).T)
plt.figure(figsize=(16,6))
plt.title(r"$t = %0.3f$"%t,fontsize=16)
plt.plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plt.plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
plt.grid()
plt.xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
plt.ylabel(r"$B\ (mT)$",fontsize=16)
plt.legend(loc='upper right')
plt.show()

femm.closefemm()

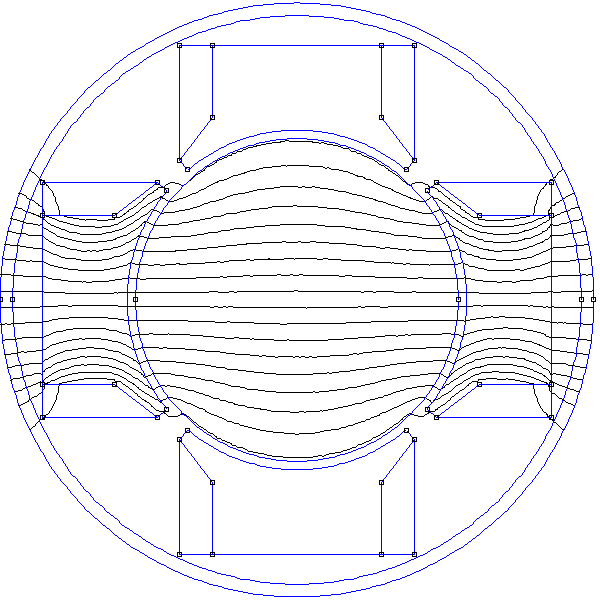
Voici le résultat à t=0 :

[theta,Br,Btheta] = np.loadtxt("4bobines-dents-ar=39-t=0.000.txt",unpack=True)
figure(figsize=(16,6))
title(r"$t = 0$",fontsize=16)
plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
grid()
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$B\ (mT)$",fontsize=16) 
legend(loc='upper right')

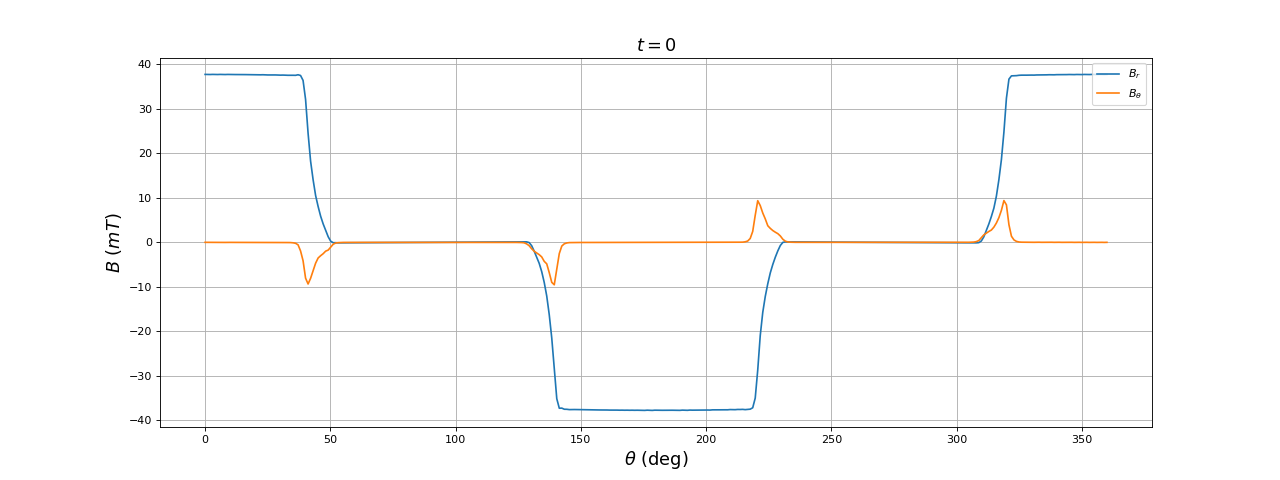fig8.pdf

harm = np.absolute(fft(Br))
figure()
stem(harm)
xlim(0,10)
grid()
xlabel(r"$n$",fontsize=16)
ylabel(r"$B_r\ (mT)$",fontsize=16)

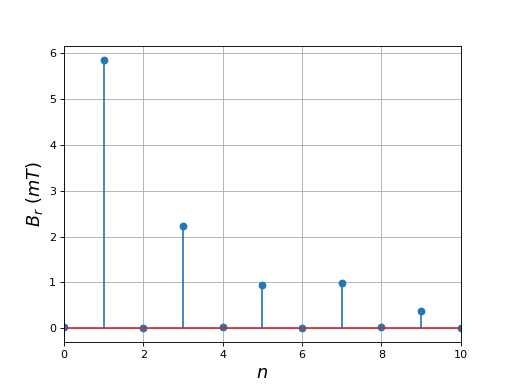fig9.pdf

Voici le résultat à t=1/8 :

[theta,Br,Btheta] = np.loadtxt("4bobines-dents-ar=39-t=0.125.txt",unpack=True)
figure(figsize=(16,6))
title(r"$t = 0$",fontsize=16)
plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
grid()
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$B\ (mT)$",fontsize=16) 
legend(loc='upper right')

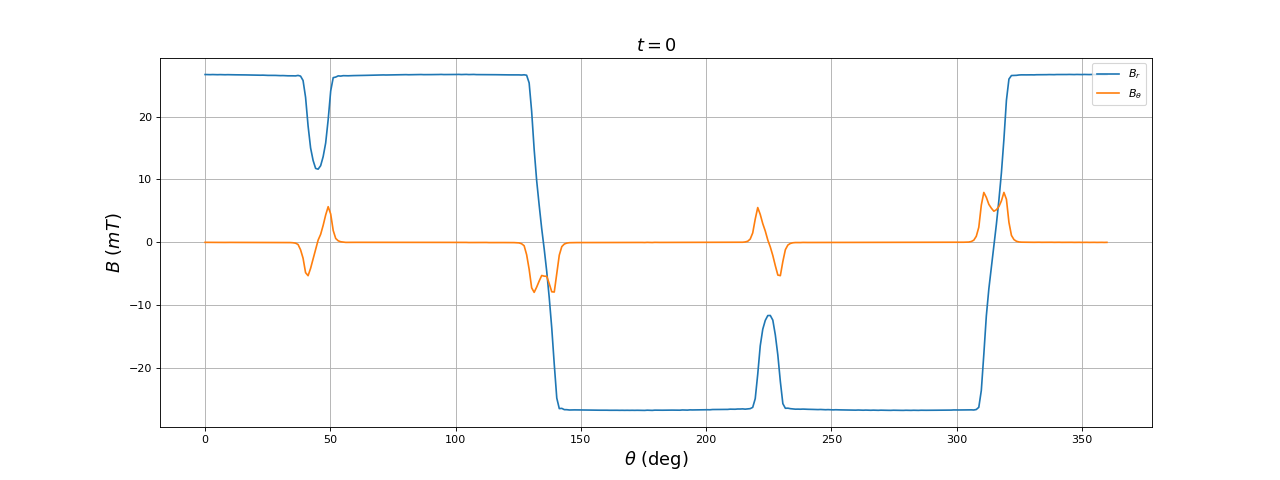fig10.pdf

harm = np.absolute(fft(Br))
figure()
stem(harm)
xlim(0,10)
grid()
xlabel(r"$n$",fontsize=16)
ylabel(r"$B_r\ (mT)$",fontsize=16)

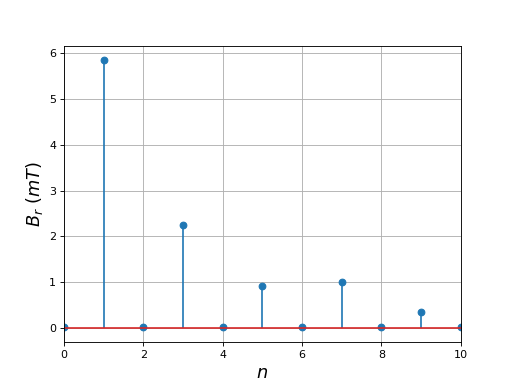fig11.pdf

Cette configuration est similaire à la première étudiée plus haut pour le stator à encoches. Le résultat est pourtant bien meilleur, sans doute parce que les bobines sont plus larges. Les pôles sont cependant très saillants. Au dessus de l'espace entre deux dents, il y a une diminution notable du champ radial. Réduisons la distance entre les dents en augmentant leur largeur angulaire :

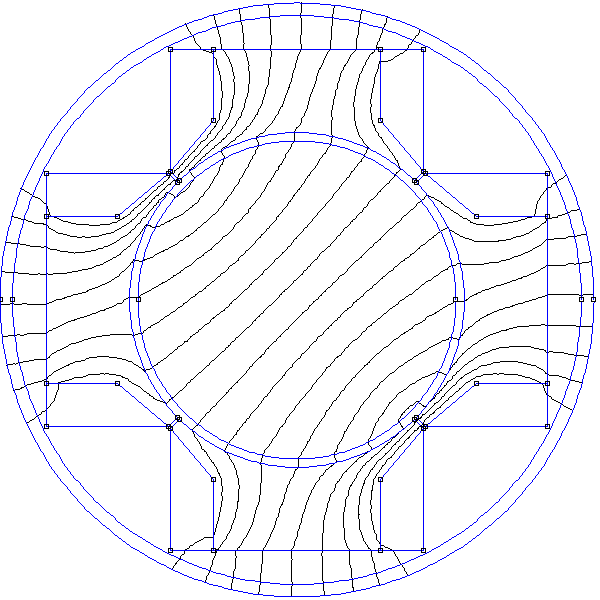
[theta,Br,Btheta] = np.loadtxt("4bobines-dents-B-ar=39-t=0.125.txt",unpack=True)
figure(figsize=(16,6))
title(r"$t = 0$",fontsize=16)
plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
grid()
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$B\ (mT)$",fontsize=16) 
legend(loc='upper right')

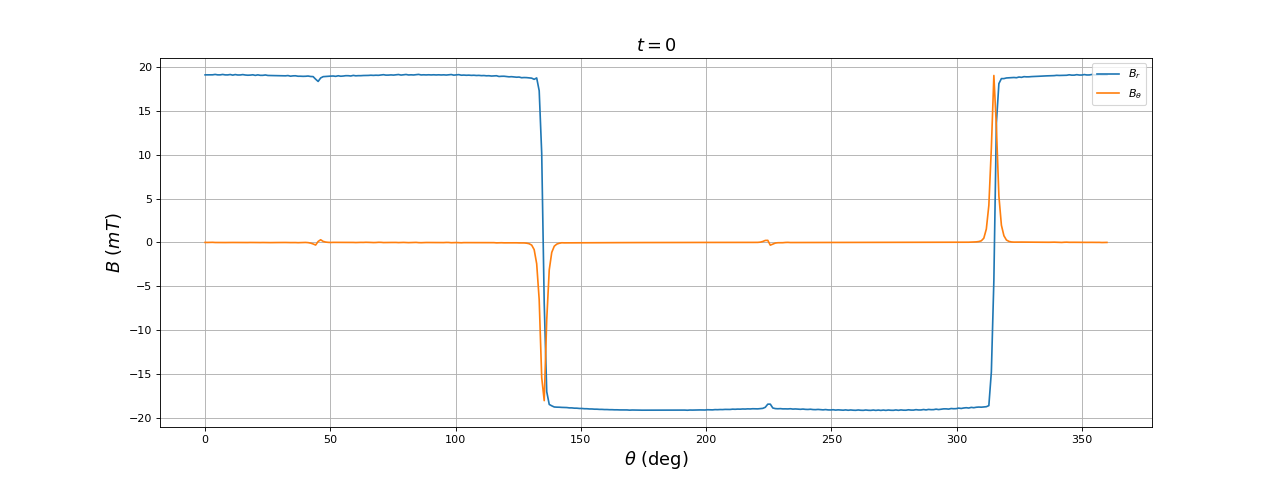fig12.pdf

Dans cette configuration, l'espace entre les dents est très faible donc la diminution du champ au dessus de cet espace est à peine visible. En contrepartie, l'intensité du champ est moindre que si les dents sont plus espacées (car le flux magnétique dans l'entrefer est mieux réparti).

Il semble que très peu de moteurs aient un stator diphasé. On trouve tout de même dans cette catégorie les petits moteurs des ventilateurs pour les circuits électroniques, qui ont un bobinage dentaire similaire à celui simulé ci-dessus. Les moteurs synchrones et asynchrones sont dans leur très grande majorité des moteurs triphasés, y compris les moteurs nommés à courant continu sans balais (Brushless Direct Current Motor, ou BLDC).

4. Stator bipolaire triphasé à encoches

Le champ est toujours bipolaire mais il est généré par trois paires de bobines dont les axes sont espacés de 120 degrés et alimentées par les courants suivants :

\begin{matrix} i_{1} (t) = I_{0} cos (ω t) & (4) \\ i_{2} (t) = I_{0} cos (ω t - \frac{2 π}{3}) & (5) \\ i_{3} (t) = I_{0} cos (ω t + \frac{2 π}{3}) & (6) \end{matrix}

Dans la version la plus simple à 6 bobines, il y a 12 encoches et chaque bobine occupe deux encoches voisines.

Figure pleine page

La modification du script précédent consiste à changer le nombre d'encoches, à ajouter un circuit pour la troisième phase et à définir les courants dans les encoches (liste circ) : comme pour le stator diphasé, deux bobines d'une paire doivent produire un champ de même sens, donc deux encoches diamétralement opposées doivent être parcourues par deux courants de sens opposés.

Voici le script Python :

stator-12encoches-3phases.py

import femm
import numpy as np
import matplotlib.pyplot as plt

femm.openfemm()
femm.newdocument(0)
# 0 : magnetic, 1 : electrostatic, 2 ; heat flow, 3 : current flow
femm.mi_probdef(0, 'millimeters', 'planar', 1.0e-8, 0, 30);
# freq, unit, type ('planar' ou 'axis'), precision, depth, minangle

R1 = 40 # rayon interne du stator
R2 = 60 # rayon externe
Rc = 38 # rayon du noyau (rotor) = 0 si pas de noyau
a1 = 8 # largeur angulaire du fond des encoches (en degrés)
a2 = 3 # largeur angulaire du haut des encoches (en degrés)
e = 10 # profondeur des encoches
d = 8 # épaisseur du cuivre (depuis le fond de l'encoche)
u = d/e
Ne = 12 # nombre d'encoches
circ = ['1+','3+','3-','2-','2+','1+','1-','3-','3+','2+','2-','1-']
increm = 1
Ns = 250 # nombre de spires dans chaque bobine
t = 1/4
i1 = np.cos(2*np.pi*t)
i2 = np.cos(2*np.pi*t-2*np.pi/3)
i3 = np.cos(2*np.pi*t+2*np.pi/3)
angle = 360/Ne


theta = -angle/2
x = R1*np.cos((theta+a2/2)*np.pi/180)
y = R1*np.sin((theta+a2/2)*np.pi/180)
cuivre = []
for k in range(Ne):
    theta = angle/2+angle*k
    x1 = R1*np.cos((theta-a2/2)*np.pi/180)
    y1 = R1*np.sin((theta-a2/2)*np.pi/180)
    femm.mi_drawarc(x,y,x1,y1,angle,1)
    x,y = x1,y1
    x2,y2 = x,y
    x1 = (R1+e)*np.cos((theta-a1/2)*np.pi/180)
    y1 = (R1+e)*np.sin((theta-a1/2)*np.pi/180)
    femm.mi_drawline(x,y,x1,y1)
    x,y = x1,y1
    x1 = (R1+e)*np.cos((theta+a1/2)*np.pi/180)
    y1 = (R1+e)*np.sin((theta+a1/2)*np.pi/180)
    femm.mi_drawline(x,y,x1,y1)
    x,y = x1,y1
    x1 = R1*np.cos((theta+a2/2)*np.pi/180)
    y1 = R1*np.sin((theta+a2/2)*np.pi/180)
    femm.mi_drawline(x,y,x1,y1)
    x,y = x1,y1
    x,y = R1*np.cos((theta-a2/2)*np.pi/180),R1*np.sin((theta-a2/2)*np.pi/180)
    x1,y1 = (R1+e)*np.cos((theta-a1/2)*np.pi/180),(R1+e)*np.sin((theta-a1/2)*np.pi/180)
    x2 = (u*x+(1-u)*x1)
    y2 = (u*y+(1-u)*y1)
    x,y = R1*np.cos((theta+a2/2)*np.pi/180),R1*np.sin((theta+a2/2)*np.pi/180)
    x1,y1 = (R1+e)*np.cos((theta+a1/2)*np.pi/180),(R1+e)*np.sin((theta+a1/2)*np.pi/180)
    x3 = (u*x+(1-u)*x1)
    y3 = (u*y+(1-u)*y1)
    femm.mi_drawline(x2,y2,x3,y3)
    cuivre.append([(R1+0.9*e)*np.cos((theta)*np.pi/180),(R1+0.9*e)*np.sin((theta)*np.pi/180)])

femm.mi_drawarc(R2,0,-R2,0,180,1)
femm.mi_drawarc(-R2,0,R2,0,180,1)
if Rc!=0:
    femm.mi_drawarc(Rc,0,-Rc,0,180,1)
    femm.mi_drawarc(-Rc,0,Rc,0,180,1)


femm.mi_addmaterial('Air', 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0)
femm.mi_addmaterial('Coil', 1, 1, 0, 0, 58*0.65, 0, 0, 1, 0, 0, 0)
femm.mi_addmaterial('LinearIron', 2100, 2100, 0, 0, 0, 0, 0, 1, 0, 0, 0)

femm.mi_addcircprop('1+', i1, 1)
# name, current, 1=series, 0=parallel
femm.mi_addcircprop('1-', -i1, 1)
femm.mi_addcircprop('2+', i2, 1);
femm.mi_addcircprop('2-', -i2, 1)
femm.mi_addcircprop('3+', i3, 1);
femm.mi_addcircprop('3-', -i3, 1)

femm.mi_addblocklabel(0,(R1+Rc)/2) # air
femm.mi_addblocklabel(0,(R1+R2)/2) # fer
femm.mi_selectlabel(0,(R1+R2)/2)
femm.mi_setblockprop('LinearIron', 0, 1, '<None>', 0, 0, 0)
femm.mi_clearselected()
femm.mi_selectlabel(0,(R1+Rc)/2)
femm.mi_setblockprop('Air', 0, 1, '<None>', 0, 0, 0)
femm.mi_clearselected()

if Rc!=0:
    femm.mi_addblocklabel(0,0)
    femm.mi_selectlabel(0,0)
    femm.mi_setblockprop('LinearIron', 0, 1, '<None>', 0, 0, 0)
    femm.mi_clearselected()

i = 0

for p in cuivre:
    femm.mi_addblocklabel(p[0],p[1])
    femm.mi_selectlabel(p[0],p[1])
    femm.mi_setblockprop('Coil', 0, 1, circ[int(i)], 0, 0, Ns)
    femm.mi_clearselected()
    i += 1


femm.mi_zoomnatural()
femm.mi_saveas('stator2phases.fem')
femm.mi_analyze()
femm.mi_loadsolution()


# composantes radiale et orthoradiale de B sur un cercle de rayon ar
ar = 39
theta = np.linspace(0,2*np.pi,360)
cos = np.cos(theta)
sin = np.sin(theta)
Br = np.zeros(len(theta))
Btheta = np.zeros(len(theta))
for k in range(len(theta)):
    B = femm.mo_getb(ar*cos[k],ar*sin[k])
    Br[k] = cos[k]*B[0]+sin[k]*B[1]
    Btheta[k] = -sin[k]*B[0]+cos[k]*B[1]
np.savetxt("6bobines-noyau-B-ar=%d-t=%0.3f.txt"%(ar,t),np.array([theta,Br,Btheta]).T)
plt.figure(figsize=(16,6))
plt.title(r"$t = %0.3f$"%t,fontsize=16)
plt.plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plt.plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
plt.grid()
plt.xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
plt.ylabel(r"$B\ (mT)$",fontsize=16)
plt.legend(loc='upper right')
plt.show()

femm.closefemm()

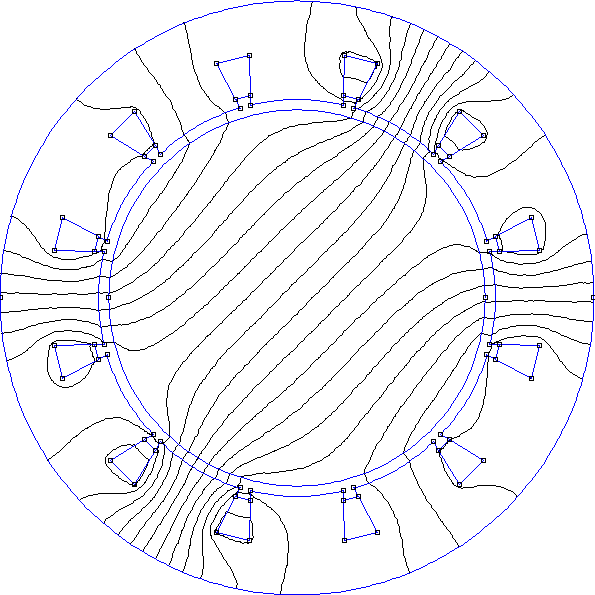
Voici les résultats à t=0 :

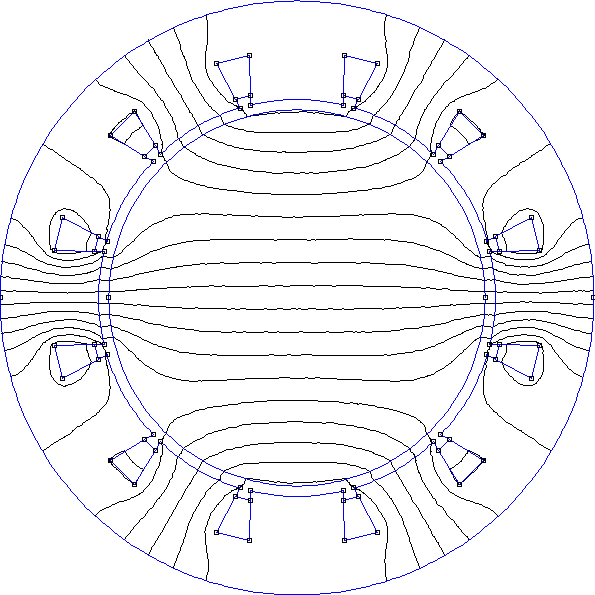
[theta,Br,Btheta] = np.loadtxt("6bobines-noyau-B-ar=39-t=0.000.txt",unpack=True)
figure(figsize=(16,6))
title(r"$t = 0$",fontsize=16)
plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
grid()
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$B\ (mT)$",fontsize=16)
legend(loc='upper right')

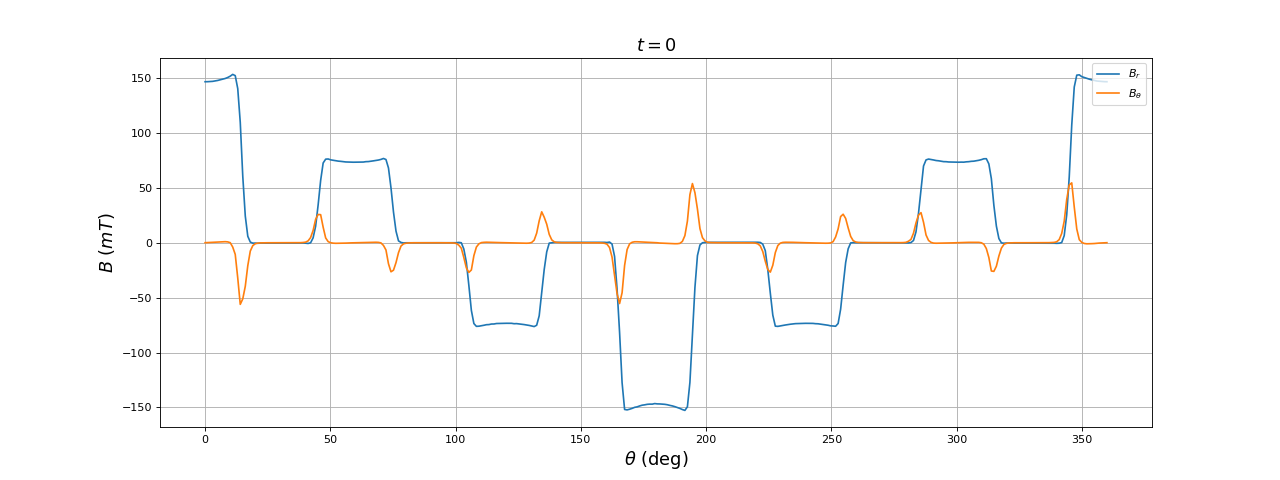fig13.pdf

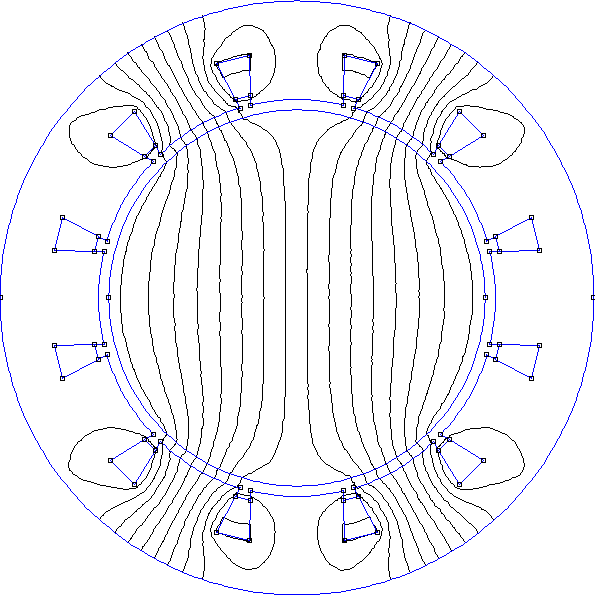
Voici les résultats à t=T/8 :

[theta,Br,Btheta] = np.loadtxt("6bobines-noyau-B-ar=39-t=0.125.txt",unpack=True)
figure(figsize=(16,6))
title(r"$t = T/8$",fontsize=16)
plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
grid()
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$B\ (mT)$",fontsize=16)
legend(loc='upper right')

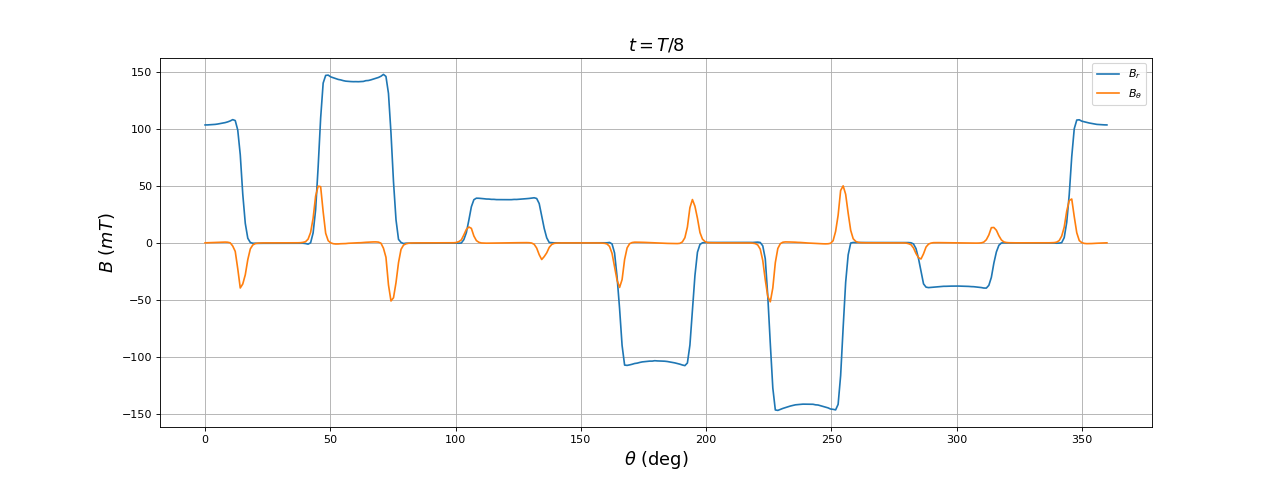fig14.pdf

Voici les résultats à t=T/4 :

[theta,Br,Btheta] = np.loadtxt("6bobines-noyau-B-ar=39-t=0.250.txt",unpack=True)
figure(figsize=(16,6))
title(r"$t = T/4$",fontsize=16)
plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
grid()
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$B\ (mT)$",fontsize=16)
legend(loc='upper right')

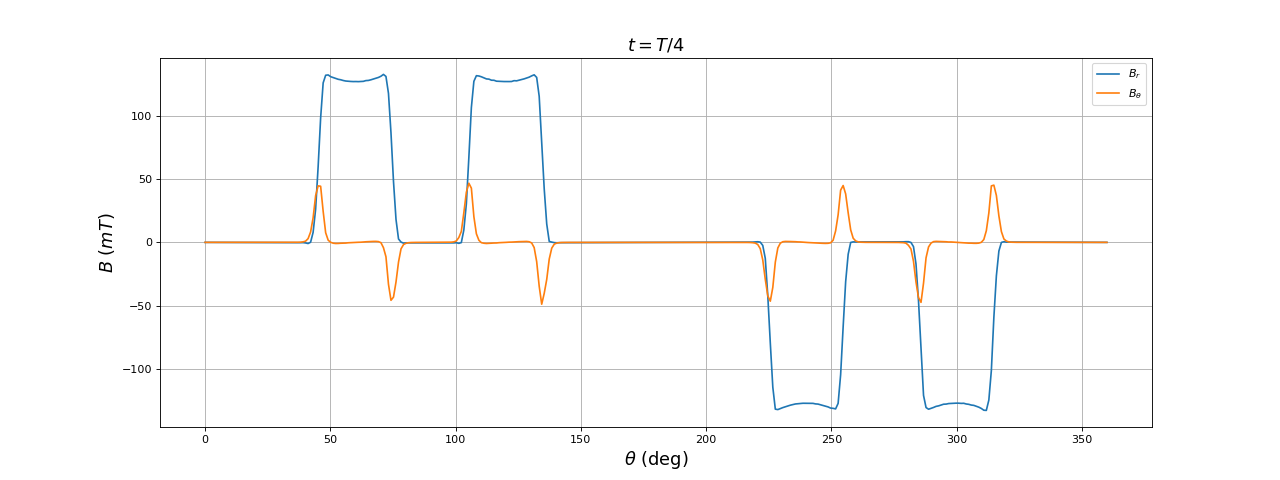fig15.pdf

Voici les modules des coefficients de Fourier du champ radial :

harm = np.absolute(fft(Br))
figure()
stem(harm)
xlim(0,10)
grid()
xlabel(r"$n$",fontsize=16)
ylabel(r"$B_r\ (mT)$",fontsize=16)

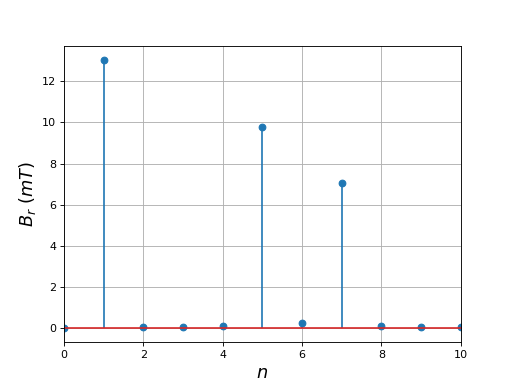fig16.pdf

La forme de la composante radiale du champ dans l'entrefer en fonction de l'angle est très loin d'être sinusoïdale : les harmoniques de rang 5 et 7 sont très intenses. On remarque aussi qu'à t=T/4 le champ n'est pas maximal à 90 degrés alors qu'il l'est pour un stator diphasé (puisque cette direction est un axe d'une des deux paires de bobines).

Pour améliorer la forme du champ dans l'entrefer, il faut que chaque bobine occupe un secteur angulaire plus grand (comme montré plus haut dans le cas du stator diphasé). Cela est possible sans augmenter le nombre d'encoches : il suffit d'écarter d'une encoche chaque demi-bobine. On obtient la configuration suivante :

Figure pleine page

Chaque bobine est constituée de deux conducteurs faisant un angle de 90 degrés mais on peut aussi voir deux bobines constituées de deux conducteurs diamétralement opposés. Pour obtenir cette configuration, il suffit de modifier les courants de la manière suivante :

circ = ['3+','1+','2-','3-','1+','2+','3-','1-','2+','3+','1-','2-']

Voici le résultat à t=0 :

[theta,Br,Btheta] = np.loadtxt("12encoches-2poles-3phases-A-ar=39-t=0.000.txt",unpack=True)
figure(figsize=(16,6))
title(r"$t = 0$",fontsize=16)
plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
grid()
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$B\ (mT)$",fontsize=16)
legend(loc='upper right')

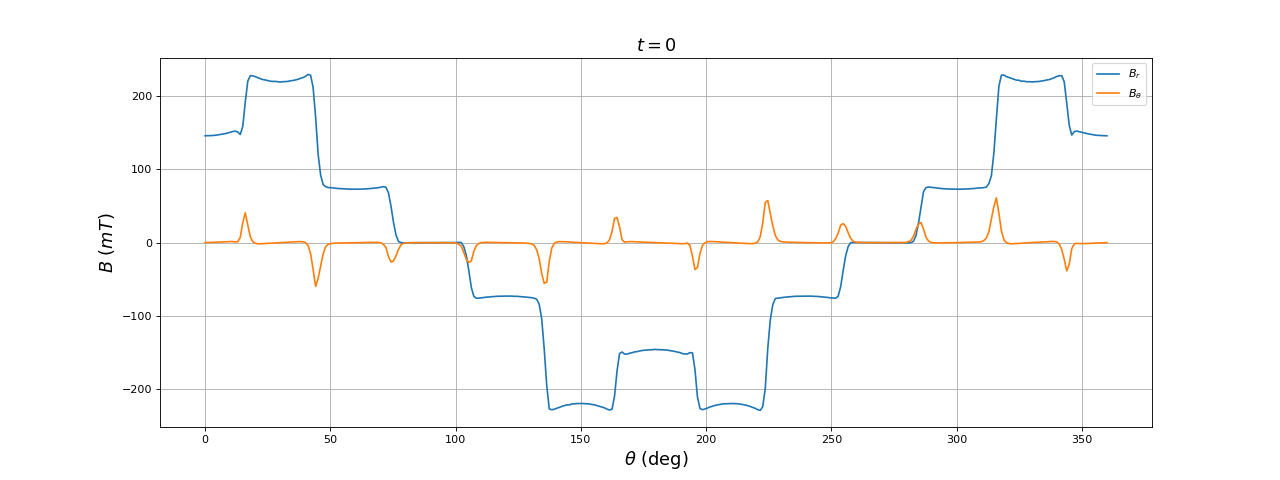fig17.pdf

Voici les modules des coefficients de Fourier du champ radial :

harm = np.absolute(fft(Br))
figure()
stem(harm)
xlim(0,10)
grid()
xlabel(r"$n$",fontsize=16)
ylabel(r"$B_r\ (mT)$",fontsize=16)

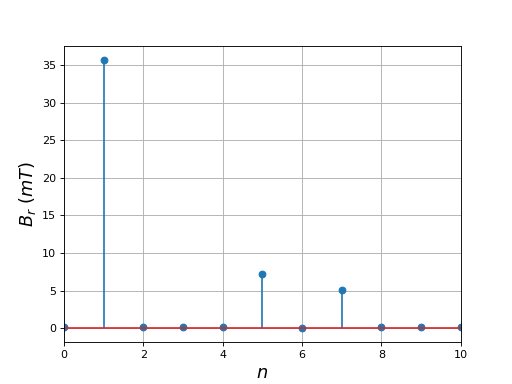fig18.pdf

Par rapport à la configuration précédente, les harmoniques de rang 5 et 7 sont effectvement réduites.

Pour améliorer encore la forme, il faut répartir chaque demi-bobine sur plusieurs encoches. Cela est possible sans augmenter le nombre total d'encoches si une encoche recoit les fils des trois phases. Si l'on examine la répartition des fils précédentes, on constate que deux demi-bobines consécutives d'une même phase sont parcourues par le même courant. En conséquence, il est possible de réunir ces deux demi-bobines en une série de 6 encoches consécutives, l'autre paire de demi-bobines occupant les 6 autres encoches. Ainsi, chaque phase est constituée de deux groupes d'encoches : 6 encoches consécutives avec un courant dans un sens et 6 encoches consécutives avec un courant dans l'autre sens. L'avantage de celle solution où les trois phases occupent chaque encoche est la possibilité d'augmenter ensuite le nombre d'encoches.

Figure pleine page

Dans cette configuration, chaque demi-bobine réunie avec la demi-bobine voisine de la même phase occupe un secteur de presque 180 degrés.

Le script doit être modifié car il faut à présent définir trois domaines de cuivre pour chaque encoche. Ces trois parties doivent avoir la même surface donc il est plus simple de définir des encoches de forme rectangulaire.

Voici le script :

stator-12encoches-3phases-2poles-reparti.py

 
import femm
import numpy as np
import matplotlib.pyplot as plt

femm.openfemm()
femm.newdocument(0)
# 0 : magnetic, 1 : electrostatic, 2 ; heat flow, 3 : current flow
femm.mi_probdef(0, 'millimeters', 'planar', 1.0e-8, 0, 30);
# freq, unit, type ('planar' ou 'axis'), precision, depth, minangle

R1 = 40 # rayon interne du stator
R2 = 60 # rayon externe
Rc = 38 # rayon du noyau (rotor) = 0 si pas de noyau
a = 6# largeur angulaire du haut des encoches (en degrés)
e = 12 # profondeur des encoches
ee = e/3 # profondeur de chaque phase
Ne = 12 # nombre d'encoches
circ_1 = ['1+','1+','1+','1+','1+','1+','1-','1-','1-','1-','1-','1-']
circ_2 = ['3+','3+','3-','3-','3-','3-','3-','3-','3+','3+','3+','3+']
circ_3 = ['2-','2-','2-','2-','2+','2+','2+','2+','2+','2+','2-','2-']
Ns = 125 # nombre de spires dans chaque bobine
t = 0.0
i1 = np.cos(2*np.pi*t)
i2 = np.cos(2*np.pi*t-2*np.pi/3)
i3 = np.cos(2*np.pi*t+2*np.pi/3)
angle = 360/Ne

cuivre_1 = []
cuivre_2 = []
cuivre_3 = []

def rotation(x,y,theta):
    cos = np.cos(theta)
    sin = np.sin(theta)
    return x*cos-y*sin,x*sin+y*cos

def encoche(theta):
    b = a*np.pi/180*R1
    x1,y1 = rotation(R1,-b/2,theta)
    x2,y2 = rotation(R1+ee,-b/2,theta)
    femm.mi_drawline(x1,y1,x2,y2)
    x3,y3 = rotation(R1+ee,b/2,theta)
    femm.mi_drawline(x2,y2,x3,y3)
    x4,y4 = rotation(R1,b/2,theta)
    femm.mi_drawline(x3,y3,x4,y4)
    cuivre_1.append([(x1+x3)/2,(y1+y3)/2])
    x1,y1 = rotation(R1+ee,-b/2,theta)
    x2,y2 = rotation(R1+2*ee,-b/2,theta)
    femm.mi_drawline(x1,y1,x2,y2)
    x3,y3 = rotation(R1+2*ee,b/2,theta)
    femm.mi_drawline(x2,y2,x3,y3)
    x4,y4 = rotation(R1+ee,b/2,theta)
    femm.mi_drawline(x3,y3,x4,y4)
    cuivre_2.append([(x1+x3)/2,(y1+y3)/2])
    x1,y1 = rotation(R1+2*ee,-b/2,theta)
    x2,y2 = rotation(R1+3*ee,-b/2,theta)
    femm.mi_drawline(x1,y1,x2,y2)
    x3,y3 = rotation(R1+3*ee,b/2,theta)
    femm.mi_drawline(x2,y2,x3,y3)
    x4,y4 = rotation(R1+2*ee,b/2,theta)
    femm.mi_drawline(x3,y3,x4,y4)
    cuivre_3.append([(x1+x3)/2,(y1+y3)/2])
    

R1p = R1+0.1
femm.mi_drawarc(R1p,0,-R1p,0,180,1)
femm.mi_drawarc(-R1p,0,R1p,0,180,1)
femm.mi_drawarc(R2,0,-R2,0,180,1)
femm.mi_drawarc(-R2,0,R2,0,180,1)

theta = -angle/2
for k in range(Ne):
    theta = angle/2+angle*k
    encoche(theta*np.pi/180)

print(cuivre_1)

if Rc!=0:
    femm.mi_drawarc(Rc,0,-Rc,0,180,1)
    femm.mi_drawarc(-Rc,0,Rc,0,180,1)


femm.mi_addmaterial('Air', 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0)
femm.mi_addmaterial('Coil', 1, 1, 0, 0, 58*0.65, 0, 0, 1, 0, 0, 0)
femm.mi_addmaterial('LinearIron', 2100, 2100, 0, 0, 0, 0, 0, 1, 0, 0, 0)

femm.mi_addcircprop('1+', i1, 1)
# name, current, 1=series, 0=parallel
femm.mi_addcircprop('1-', -i1, 1)
femm.mi_addcircprop('2+', i2, 1);
femm.mi_addcircprop('2-', -i2, 1)
femm.mi_addcircprop('3+', i3, 1);
femm.mi_addcircprop('3-', -i3, 1)

femm.mi_addblocklabel(0,(R1+Rc)/2) # air
femm.mi_addblocklabel(0,(R1+R2)/2) # fer
femm.mi_selectlabel(0,(R1+R2)/2)
femm.mi_setblockprop('LinearIron', 0, 1, '<None>', 0, 0, 0)
femm.mi_clearselected()
femm.mi_selectlabel(0,(R1+Rc)/2)
femm.mi_setblockprop('Air', 0, 1, '<None>', 0, 0, 0)
femm.mi_clearselected()

if Rc!=0:
    femm.mi_addblocklabel(0,0)
    femm.mi_selectlabel(0,0)
    femm.mi_setblockprop('LinearIron', 0, 1, '<None>', 0, 0, 0)
    femm.mi_clearselected()
    
i=0
for p in cuivre_1:
    femm.mi_addblocklabel(p[0],p[1])
    femm.mi_selectlabel(p[0],p[1])
    femm.mi_setblockprop('Coil', 0, 1, circ_1[int(i)], 0, 0, Ns)
    femm.mi_clearselected()
    i += 1

i=0
for p in cuivre_2:
    femm.mi_addblocklabel(p[0],p[1])
    femm.mi_selectlabel(p[0],p[1])
    femm.mi_setblockprop('Coil', 0, 1, circ_2[int(i)], 0, 0, Ns)
    femm.mi_clearselected()
    i += 1

i=0
for p in cuivre_3:
    femm.mi_addblocklabel(p[0],p[1])
    femm.mi_selectlabel(p[0],p[1])
    femm.mi_setblockprop('Coil', 0, 1, circ_3[int(i)], 0, 0, Ns)
    femm.mi_clearselected()
    i += 1


femm.mi_zoomnatural()
femm.mi_saveas('stator2phases.fem')
femm.mi_analyze()
femm.mi_loadsolution()


# composantes radiale et orthoradiale de B sur un cercle de rayon ar
ar = 39
theta = np.linspace(0,2*np.pi,360)
cos = np.cos(theta)
sin = np.sin(theta)
Br = np.zeros(len(theta))
Btheta = np.zeros(len(theta))
for k in range(len(theta)):
    B = femm.mo_getb(ar*cos[k],ar*sin[k])
    Br[k] = cos[k]*B[0]+sin[k]*B[1]
    Btheta[k] = -sin[k]*B[0]+cos[k]*B[1]
np.savetxt("12encoches-2poles-3phases-reparti-ar=%d-t=%0.3f.txt"%(ar,t),np.array([theta,Br,Btheta]).T)
plt.figure(figsize=(16,6))
plt.title(r"$t = %0.3f$"%t,fontsize=16)
plt.plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plt.plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
plt.grid()
plt.xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
plt.ylabel(r"$B\ (mT)$",fontsize=16)
plt.legend(loc='upper right')
plt.show()

femm.closefemm()

Voici les résultats à t=0 :

[theta,Br,Btheta] = np.loadtxt("12encoches-2poles-3phases-reparti-ar=39-t=0.000.txt",unpack=True)
figure(figsize=(16,6))
title(r"$t = 0$",fontsize=16)
plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
grid()
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$B\ (mT)$",fontsize=16)
legend(loc='upper right')

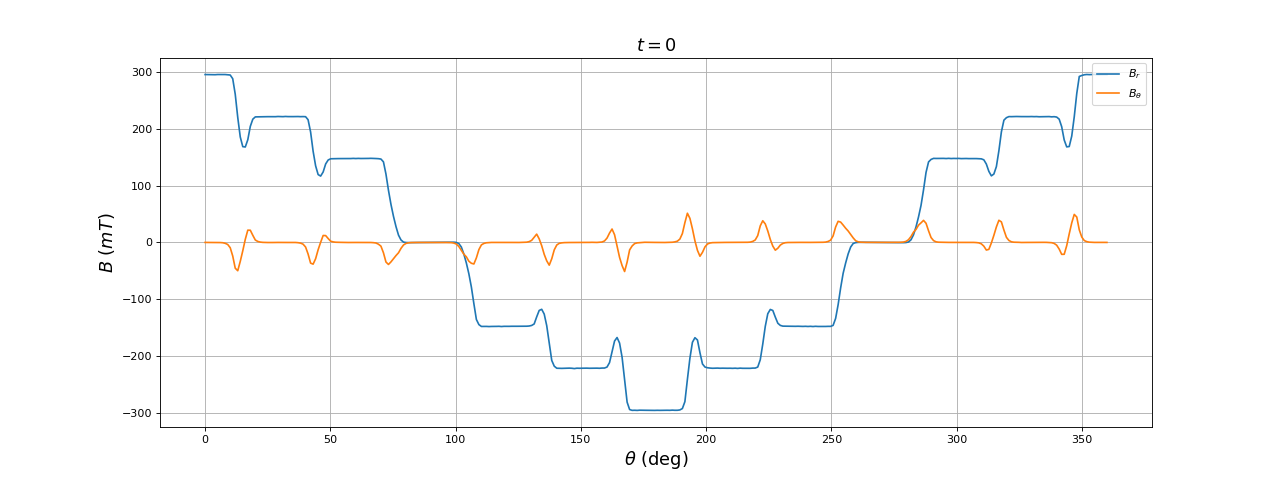fig19.pdf

On obtient une forme proche d'une sinusoïde. On peut la lisser en doublant le nombre d'encoches. Pour cela, il suffit de d'écrire :

Ne = 24
increm = 0.5

Avec ce nouvel incrément pour la boucle de remplissage du cuivre, deux encoches consécutives se voient attribuer le même courant.

[theta,Br,Btheta] = np.loadtxt("24encoches-2poles-3phases-reparti-ar=39-t=0.000.txt",unpack=True)
figure(figsize=(16,6))
title(r"$t = 0$",fontsize=16)
plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
grid()
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$B\ (mT)$",fontsize=16)
legend(loc='upper right')

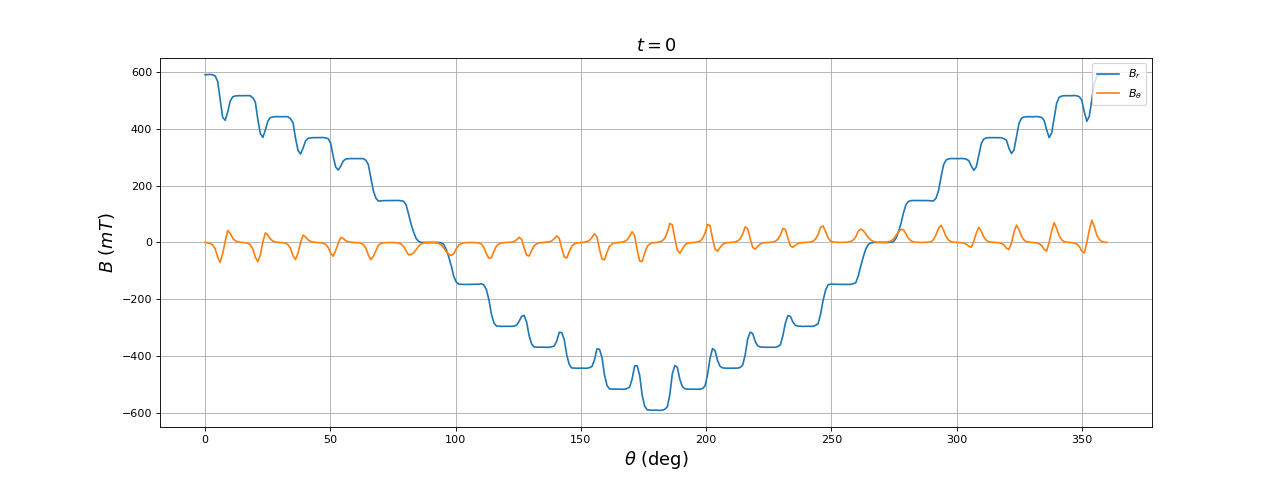fig20.pdf

Voici le champ à t=0.25 :

[theta,Br,Btheta] = np.loadtxt("24encoches-2poles-3phases-reparti-ar=39-t=0.250.txt",unpack=True)
figure(figsize=(16,6))
title(r"$t = 0$",fontsize=16)
plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
grid()
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$B\ (mT)$",fontsize=16)
legend(loc='upper right')

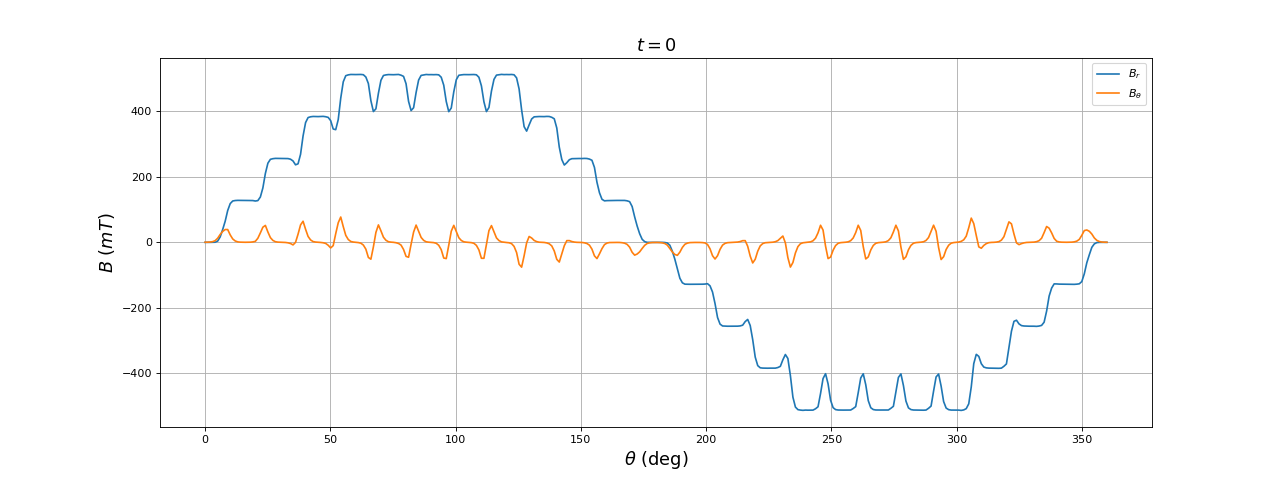fig21.pdf

Voici les modules des coefficients de Fourier de la composante radiale du champ magnétique :

harm = np.absolute(fft(Br))
figure()
stem(harm)
xlim(0,10)
grid()
xlabel(r"$n$",fontsize=16)
ylabel(r"$B_r\ (mT)$",fontsize=16)

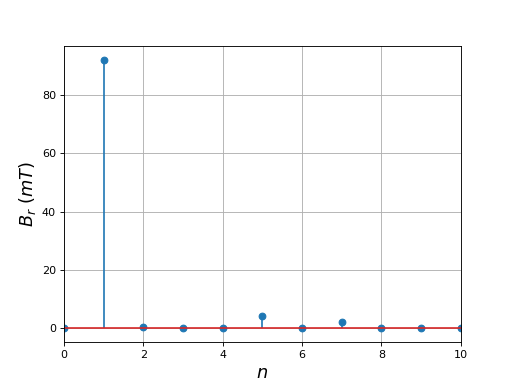fig22.pdf

On obtient ainsi une forme de la composante radiale du champ magnétique très proche d'une forme sinusoïdale : le premier harmonique non nul est de rang 5 et son amplitude est faible. Le résultat peut sans doute être amélioré en changeant la forme des encoches et la répartition des phases dans chaque encoche.

5. Stator bipolaire triphasée à bobinage sur dents

Chacune des 6 bobines du stator bipolaire triphasé est une simple bobine enroulée sur une dent dont l'extrémité du coté de l'entrefer est élargie pour épouser au mieux la forme cylindrique (l'entrefer doit être le plus étroit possible).

Voici le script Python :

statorDents-3phases.py

import femm
import numpy as np
import matplotlib.pyplot as plt

femm.openfemm()
femm.newdocument(0)
# 0 : magnetic, 1 : electrostatic, 2 ; heat flow, 3 : current flow
femm.mi_probdef(0, 'millimeters', 'planar', 1.0e-8, 0, 30);
# freq, unit, type ('planar' ou 'axis'), precision, depth, minangle

R1 = 40 # rayon interne du stator
R2 = 60 # rayon externe des noyaux des bobines
R3 = 65 # rayon interne de la partie périphérique du stator
R4 = 70 # rayon externe du stator
Rc = 38 # rayon du noyau (rotor) = 0 si pas de noyau
L = 20 # largeur des noyaux des bobines
e = 3 # épaisseur des parties cylindriques
a = 55 # largeur angulaire des parties cylindriques
Nb = 6 # nombre de bobines
circ = ['1-','1+','3+','3-','2-','2+','1+','1-','3-','3+','2+','2-']
Ns = 125 # nombre de spires dans chaque bobine
t = 0.0
i1 = np.cos(2*np.pi*t)
i2 = np.cos(2*np.pi*t-2*np.pi/3)
i3 = np.cos(2*np.pi*t+2*np.pi/3)
angle = 360/Nb

cuivre = []
fer = []

def rotation(x,y,theta):
    cos = np.cos(theta)
    sin = np.sin(theta)
    return x*cos-y*sin,x*sin+y*cos


def bobine(theta):
    aa = a*np.pi/180
    x1,y1 = rotation(R1*np.cos(aa/2),-R1*np.sin(aa/2),theta)
    x8,y8 = rotation(R1*np.cos(aa/2),R1*np.sin(aa/2),theta)
    x2,y2 = rotation((R1+e)*np.cos(aa/2),-(R1+e)*np.sin(aa/2),theta)
    x7,y7 = rotation((R1+e)*np.cos(aa/2),(R1+e)*np.sin(aa/2),theta)
    x3,y3 = rotation(R1+e,-L/2,theta)
    x6,y6 = rotation(R1+e,L/2,theta)
    x4,y4 = rotation(R2,-L/2,theta)
    x5,y5 = rotation(R2,L/2,theta)
    femm.mi_drawline(x1,y1,x2,y2)
    femm.mi_drawline(x2,y2,x3,y3)
    femm.mi_drawline(x3,y3,x4,y4)
    femm.mi_drawline(x4,y4,x5,y5)
    femm.mi_drawline(x5,y5,x6,y6)
    femm.mi_drawline(x6,y6,x7,y7)
    femm.mi_drawline(x7,y7,x8,y8)
    x9,y9 = rotation(R2,-(R1+e)*np.sin(aa/2),theta)
    x10,y10 = rotation(R2,(R1+e)*np.sin(aa/2),theta)
    femm.mi_drawline(x2,y2,x9,y9)
    femm.mi_drawline(x9,y9,x4,y4)
    femm.mi_drawline(x7,y7,x10,y10)
    femm.mi_drawline(x10,y10,x5,y5)
    femm.mi_addarc(x1,y1,x8,y8,a,1)
    xf,yf = rotation(R1+e,0,theta)
    fer.append([xf,yf])
    xc,yc = (x3+x9)/2,(y3+y9)/2
    cuivre.append([xc,yc])
    xc,yc = (x7+x5)/2,(y7+y5)/2
    cuivre.append([xc,yc])
    

femm.mi_drawarc(R3,0,-R3,0,180,1)
femm.mi_drawarc(-R3,0,R3,0,180,1)
femm.mi_drawarc(R4,0,-R4,0,180,1)
femm.mi_drawarc(-R4,0,R4,0,180,1)


for k in range(Nb):
    theta = angle*k
    bobine(theta*np.pi/180)

if Rc!=0:
    femm.mi_drawarc(Rc,0,-Rc,0,180,1)
    femm.mi_drawarc(-Rc,0,Rc,0,180,1)


femm.mi_addmaterial('Air', 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0)
femm.mi_addmaterial('Coil', 1, 1, 0, 0, 58*0.65, 0, 0, 1, 0, 0, 0)
femm.mi_addmaterial('LinearIron', 2100, 2100, 0, 0, 0, 0, 0, 1, 0, 0, 0)

femm.mi_addcircprop('1+', i1, 1)
# name, current, 1=series, 0=parallel
femm.mi_addcircprop('1-', -i1, 1)
femm.mi_addcircprop('2+', i2, 1);
femm.mi_addcircprop('2-', -i2, 1)
femm.mi_addcircprop('3+', i3, 1);
femm.mi_addcircprop('3-', -i3, 1)

femm.mi_addblocklabel(0,(R1+Rc)/2) # air
femm.mi_selectlabel(0,(R1+Rc)/2)
femm.mi_setblockprop('Air', 0, 1, '<None>', 0, 0, 0)
femm.mi_clearselected()

femm.mi_addblocklabel(0,(R4+R3)/2) # fer
femm.mi_selectlabel(0,(R4+R3)/2)
femm.mi_setblockprop('LinearIron', 0, 1, '<None>', 0, 0, 0)
femm.mi_clearselected()

if Rc!=0:
    femm.mi_addblocklabel(0,0)
    femm.mi_selectlabel(0,0)
    femm.mi_setblockprop('LinearIron', 0, 1, '<None>', 0, 0, 0)
    femm.mi_clearselected()

i=0
for p in cuivre:
    femm.mi_addblocklabel(p[0],p[1])
    femm.mi_selectlabel(p[0],p[1])
    femm.mi_setblockprop('Coil', 0, 1, circ[int(i)], 0, 0, Ns)
    femm.mi_clearselected()
    i += 1

for p in fer:
    femm.mi_addblocklabel(p[0],p[1])
    femm.mi_selectlabel(p[0],p[1])
    femm.mi_setblockprop('LinearIron', 0, 1, '<None>', 0, 0,0)
    femm.mi_clearselected()


femm.mi_zoomnatural()
femm.mi_saveas('stator2phases.fem')
femm.mi_analyze()
femm.mi_loadsolution()


# composantes radiale et orthoradiale de B sur un cercle de rayon ar
ar = 39
theta = np.linspace(0,2*np.pi,360)
cos = np.cos(theta)
sin = np.sin(theta)
Br = np.zeros(len(theta))
Btheta = np.zeros(len(theta))
for k in range(len(theta)):
    B = femm.mo_getb(ar*cos[k],ar*sin[k])
    Br[k] = cos[k]*B[0]+sin[k]*B[1]
    Btheta[k] = -sin[k]*B[0]+cos[k]*B[1]
np.savetxt("6bobines-dents-ar=%d-t=%0.3f.txt"%(ar,t),np.array([theta,Br,Btheta]).T)
plt.figure(figsize=(16,6))
plt.title(r"$t = %0.3f$"%t,fontsize=16)
plt.plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plt.plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
plt.grid()
plt.xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
plt.ylabel(r"$B\ (mT)$",fontsize=16)
plt.legend(loc='upper right')
plt.show()

femm.closefemm()

Voici le résultat pour t=0 :

[theta,Br,Btheta] = np.loadtxt("6bobines-dents-ar=39-t=0.000.txt",unpack=True)
figure(figsize=(16,6))
title(r"$t = 0$",fontsize=16)
plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
grid()
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$B\ (mT)$",fontsize=16)
legend(loc='upper right')

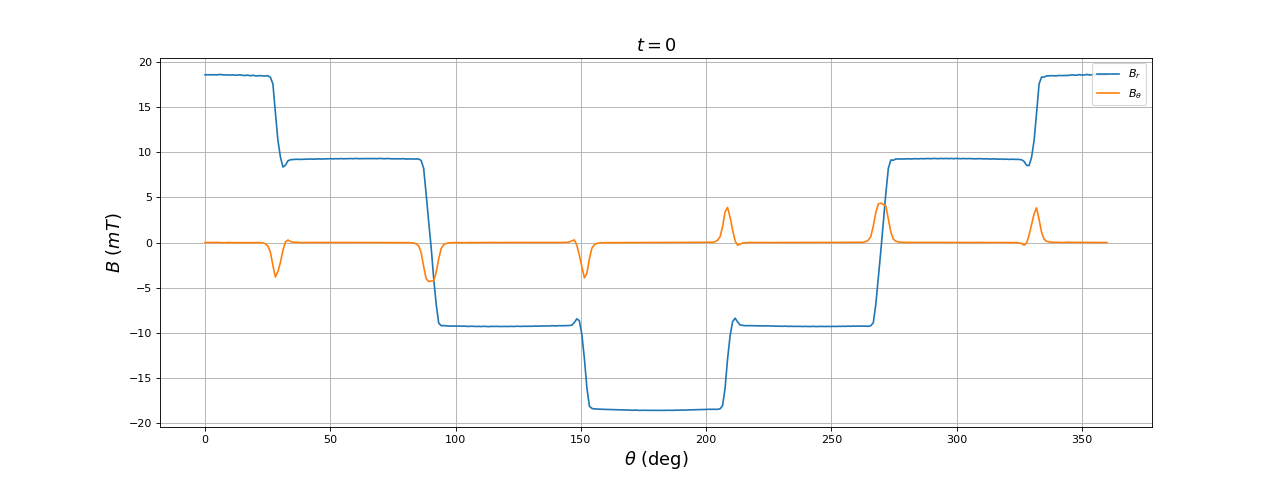fig23.pdf

Voici les modules des coefficients de Fourier du champ radial :

harm = np.absolute(fft(Br))
figure()
stem(harm)
xlim(0,10)
grid()
xlabel(r"$n$",fontsize=16)
ylabel(r"$B_r\ (mT)$",fontsize=16)

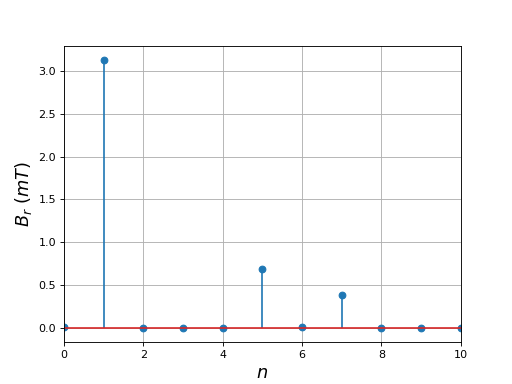fig24.pdf

Une autre configuration de stator bipolaire triphasé consiste à bobiner 12 dents, deux dents consécutives étant bobinées par la même phase et dans le même sens. Cette configuration se rencontre sur les moteurs qualifiés de moteurs à courant continu sans balais (qui sont en réalité des moteurs alternatifs synchrones). La photo suivante montre un exemple de stator à 12 dents (mais il existe d'autres configurations de bobinage pour les stators à 12 dents) :

Voici les paramètres qui permettent d'obtenir ce stator :

R1 = 40 # rayon interne du stator
R2 = 60 # rayon externe des noyaux des bobines
R3 = 65 # rayon interne de la partie périphérique du stator
R4 = 70 # rayon externe du stator
Rc = 38 # rayon du noyau (rotor) = 0 si pas de noyau
L = 10 # largeur des noyaux des bobines
e = 3 # épaisseur des parties cylindriques
a = 25 # largeur angulaire des parties cylindriques
Nb = 12 # nombre de bobines
circ = ['1-','1+','1-','1+','3+','3-','3+','3-','2-','2+','2-','2+','1+','1-','1+','1-','3-','3+','3-','3+','2+','2-','2+','2-']
increm = 1
Ns = 125 # nombre de spires dans chaque bobine

Voici le résultat pour t=0 :

[theta,Br,Btheta] = np.loadtxt("12bobines-dents-ar=39-t=0.000.txt",unpack=True)
figure(figsize=(16,6))
title(r"$t = 0$",fontsize=16)
plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
grid()
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$B\ (mT)$",fontsize=16)
legend(loc='upper right')

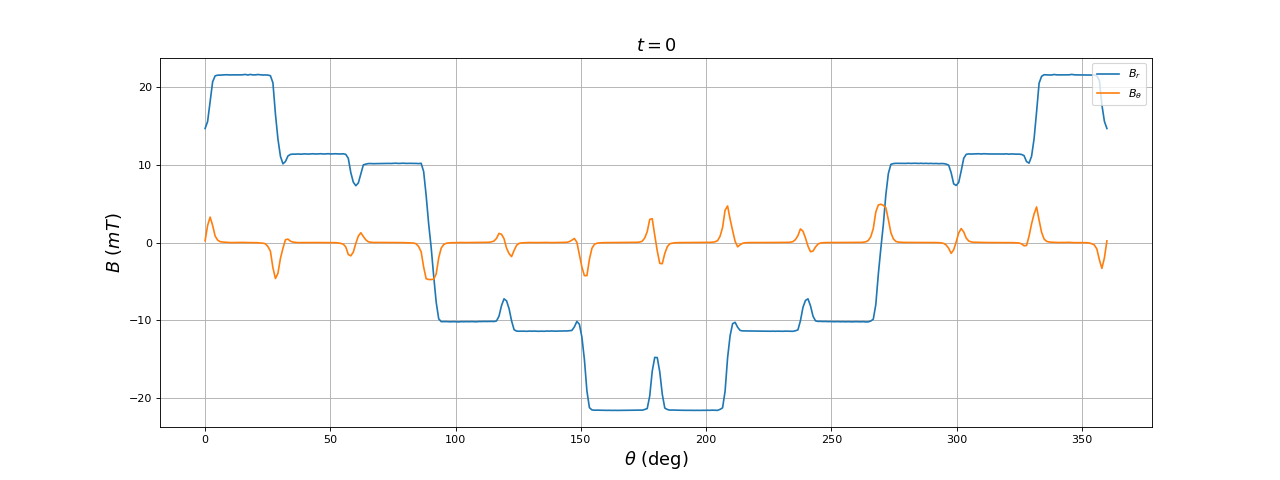fig25.pdf

Voici les modules des coefficients de Fourier du champ radial :

harm = np.absolute(fft(Br))
figure()
stem(harm)
xlim(0,10)
grid()
xlabel(r"$n$",fontsize=16)
ylabel(r"$B_r\ (mT)$",fontsize=16)

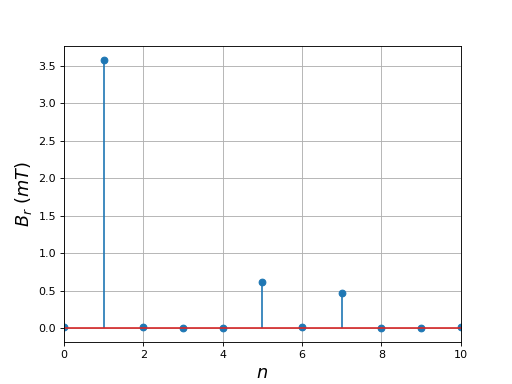fig26.pdf

La forme du champ est très voisine de celle obtenue avec seulement 6 dents. D'après ces résultats, l'intérêt du stator à 12 dents n'est pas dans la forme du champ.

La forme du champ radial est proche d'une forme sinusoïdale mais beaucoup moins que celle obtenue avec le stator à encoches : les harmoniques de rang 5 et 7 ont une amplitude relativement importante. Il semble difficile de faire mieux avec un stator dentaire triphasé car chaque bobine reste localisée sur une dent ou au maximum deux comme dans cet exemple (en réalité deux bobines voisines identiques). La forte pente du champ lors du passage d'une bobine à la suivante explique la qualification de stator à pôles saillants donnée à ce type de stator.

Dans le cas des moteurs à courant continu sans balais (Brushless DC motors), les courants qui circulent dans les trois phases ne sont pas sinusoïdaux mais présentent une forme trapézoïdale. La commande de ce type de moteur consiste à appliquer une tension à une phase (c.-à-d. au bobinage d'une phase), une tension opposée à une autre phase et aucune tension à la troisième (en quelque sorte une commande en tout ou rien). La valeur de cette tension est régulée par modulation de largeur de d'impulsion. Le fait que la tension appliquée à une phase est constante par morceaux explique le nom donné à ces moteurs. Pour étudier le champ magnétique produit par le stator dans ces conditions, on doit considérer les trois phases parcourues par les courants suivants :

\begin{matrix} i_{1} = I_{0} \\ i_{2} = - I_{0} \\ i_{3} = 0 \end{matrix}

Il y a évidemment 5 autres possibilités mais toutes donnent une forme de champ magnétique similaire avec différentes orientations des deux pôles. On définit donc la configuration de la manière suivante :

R1 = 40 # rayon interne du stator
R2 = 60 # rayon externe des noyaux des bobines
R3 = 65 # rayon interne de la partie périphérique du stator
R4 = 70 # rayon externe du stator
Rc = 38 # rayon du noyau (rotor) = 0 si pas de noyau
L = 10 # largeur des noyaux des bobines
e = 3 # épaisseur des parties cylindriques
a = 25 # largeur angulaire des parties cylindriques
Nb = 12 # nombre de bobines
circ = ['1-','1+','1-','1+','3+','3-','3+','3-','2-','2+','2-','2+','1+','1-','1+','1-','3-','3+','3-','3+','2+','2-','2+','2-']
increm = 1
Ns = 125 # nombre de spires dans chaque bobine
i1=1
i2=-1
i3=0
angle = 360/Nb

[theta,Br,Btheta] = np.loadtxt("12bobines-dents-BLDC-ar=39-t=0.000.txt",unpack=True)
figure(figsize=(16,6))
title(r"$i_1=1, i_2=-1, i_3=0$",fontsize=16)
plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
grid()
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$B\ (mT)$",fontsize=16)
legend(loc='upper right')

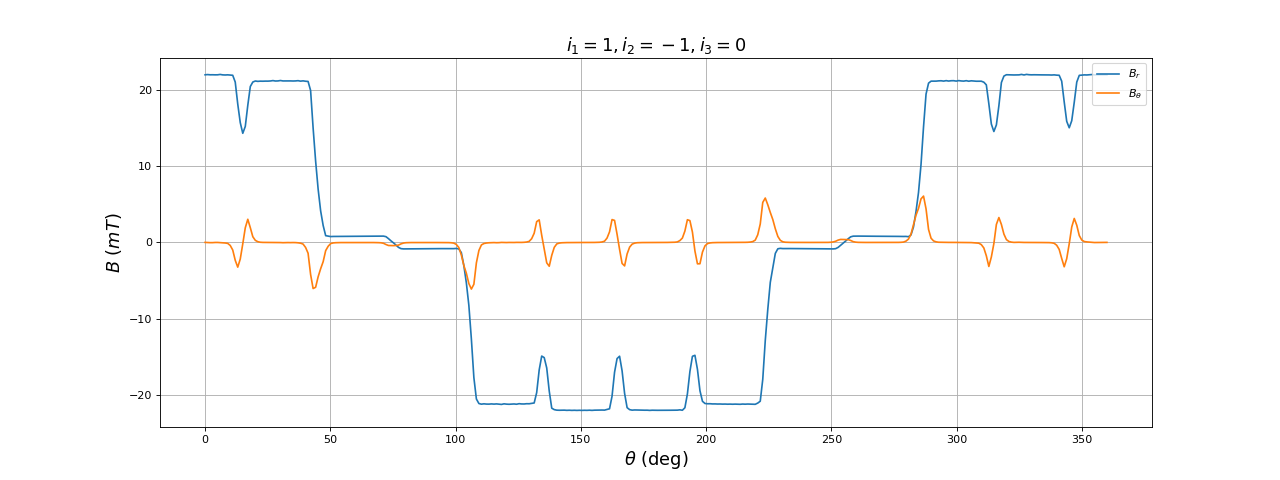fig27.pdf

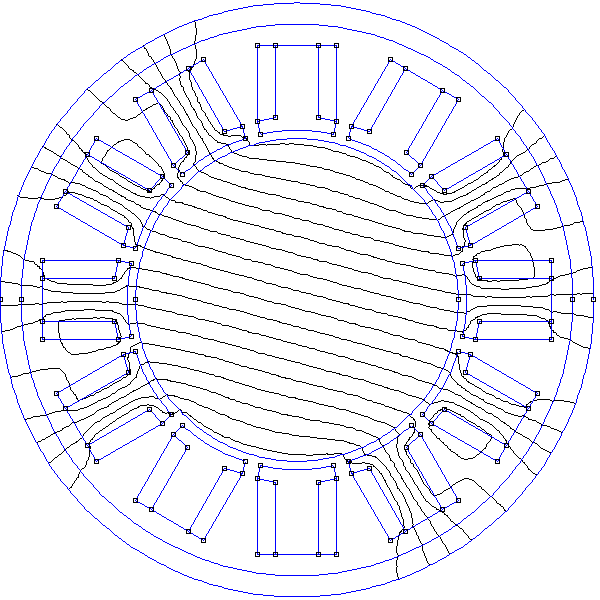
Il y a 6 combinaisons de courants dans les trois phases, ce qui conduit à 6 orientations des deux pôles espacées de 60 degrés. Voici par exemple le champ obtenu pour $i_{1} = I_{0}, i_{2} = 0, i_{3} = - I_{0}$ :

[theta,Br,Btheta] = np.loadtxt("12bobines-dents-BLDC-2-ar=39-t=0.000.txt",unpack=True)
figure(figsize=(16,6))
title(r"$i_1=1, i_2=0, i_3=-1$",fontsize=16)
plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
grid()
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$B\ (mT)$",fontsize=16)
legend(loc='upper right')

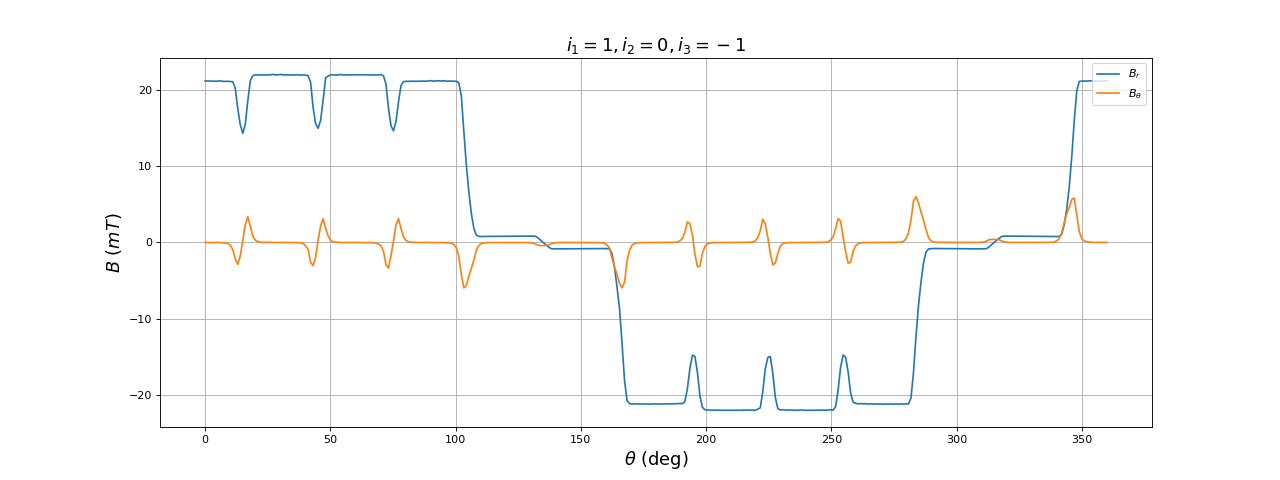fig28.pdf

Par rapport à la configuration précédente des courants, les pôles ont tourné de 60 degrés.

En réalité, le courant dans les phases varie continûment et on a bien une rotation continue du champ mais avec des paliers d'orientation. Ce type de commande de stator triphasé produit donc des pôles très saillants et, de plus, la vitesse de rotation du champ n'est pas constante. Malgré ces inconvénients, ce mode de commande est très répandu sur les petits moteurs, sans doute en raison de la relative simplicité de l'électronique de commande (qui doit aussi comporter une détection de la position du rotor).

6. Stator quadrupolaire triphasé à encoches

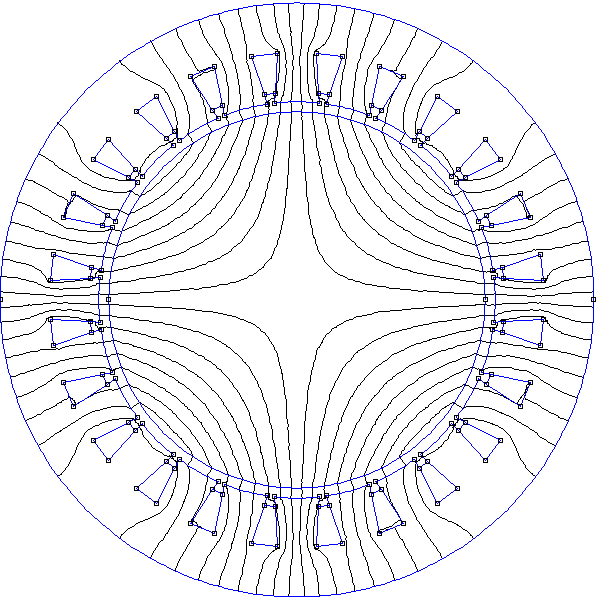
Le stator à encoche permet d'obtenir une forme de champ radial dans l'entrefer proche d'une forme sinusoïdale. Comme montré plus haut dans le cas d'un stator bipolaire, le meilleur résultat est obtenu lorsque chaque demi-bobine occupe un secteur angulaire le plus grand possible. Dans le cas du stator quadrupolaire, chaque demi-bobine doit occuper un angle de presque 90 degrés. La configuration suivante consiste à obtenir la largeur maximale avec 24 encoches et une seule phase par encoche :

Figure pleine page

Les quatre bobines de la première phase sont entourées sur la figure. Pour les deux autres phases, les bobines se déduisent par une rotation de 120 degrés et de -120 degrés. Chaque bobine est composée de seulement deux encoches mais celles-ci sont espacées de 75 degrés. Chaque demi-bobine se trouve à côté d'une demi-bobine parcourue par le même courant (dans le même sens); la largeur angulaire effective d'une bobine est donc 90 degrés. Comme vu plus haut dans le cas du stator bipolaire, cette configuration pourrait être simplifiée en réunissant en une seule encoche les deux demi-bobines adjacentes parcourues par le même courant (ce qui diviserait par deux le nombre d'encoches) ; le forme du champ serait cependant moins lisse.

On reprend le script précédent, avec les paramètres suivants (on réduit un peu la taille des encoches) :

R1 = 40 # rayon interne du stator
R2 = 60 # rayon externe
Rc = 38 # rayon du noyau (rotor) = 0 si pas de noyau
a1 = 6 # largeur angulaire du fond des encoches (en degrés)
a2 = 2# largeur angulaire du haut des encoches (en degrés)
e = 10 # profondeur des encoches
d = 8 # épaisseur du cuivre (depuis le fond de l'encoche)
u = d/e
Ne = 24 # nombre d'encoches
circ = ['2-','2-','1+','1+','3-','3-','2+','2+','1-','1-','3+','3+','2-','2-','1+','1+','3-','3-','2+','2+','1-','1-','3+','3+']
increm = 1
Ns = 250 # nombre de spires dans chaque bobine

Voici les résultats à t=0 :

[theta,Br,Btheta] = np.loadtxt("12bobines-noyau-B-ar=39-t=0.000.txt",unpack=True)
figure(figsize=(16,6))
title(r"$t = 0$",fontsize=16)
plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
grid()
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$B\ (mT)$",fontsize=16)
legend(loc='upper right')

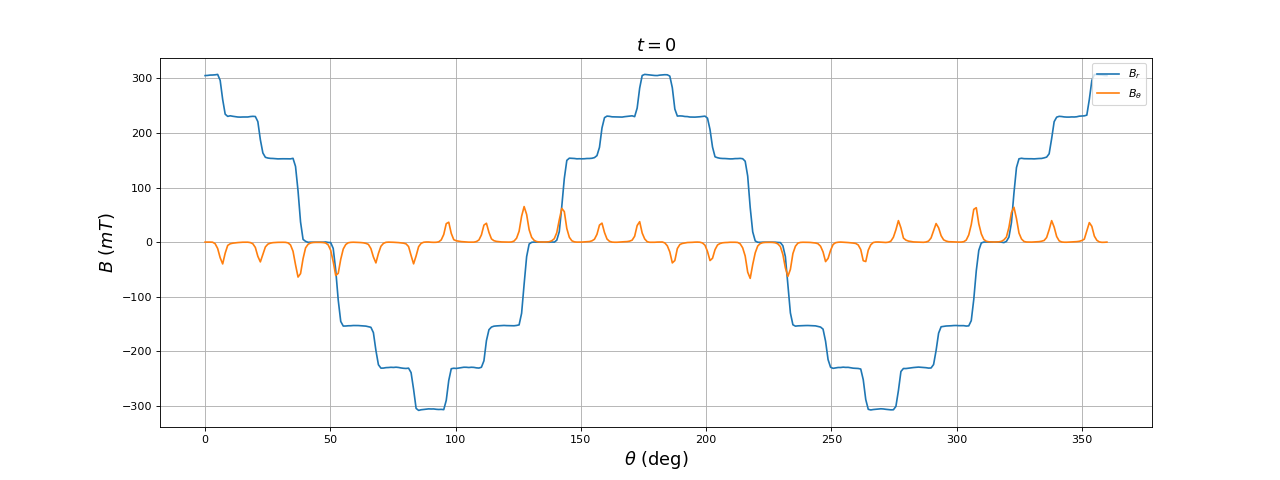fig29.pdf

harm = np.absolute(fft(Br[0:len(Br)//2]))
figure()
stem(harm)
xlim(0,10)
grid()
xlabel(r"$n$",fontsize=16)
ylabel(r"$B_r\ (mT)$",fontsize=16)

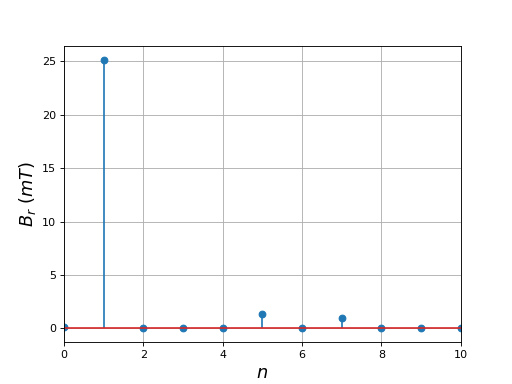fig30.pdf

À l'instant t=0 le champ est maximal sur l'axe (Ox) (deux pôles sud) et minimal sur l'axe (Oy) (deux pôles nord).

La forme du champ magnétique radial en fonction de l'angle s'approche d'un forme sinusoïdale, grossièrement mais mieux que dans le cas du stator bibolaire triphasé étudié précédemment. La composante orthoradiale du champ est faible mais pas négligeable au dessus des encoches (mais elle ne diminue pas si on réduit la taille de l'ouverture des encoches.

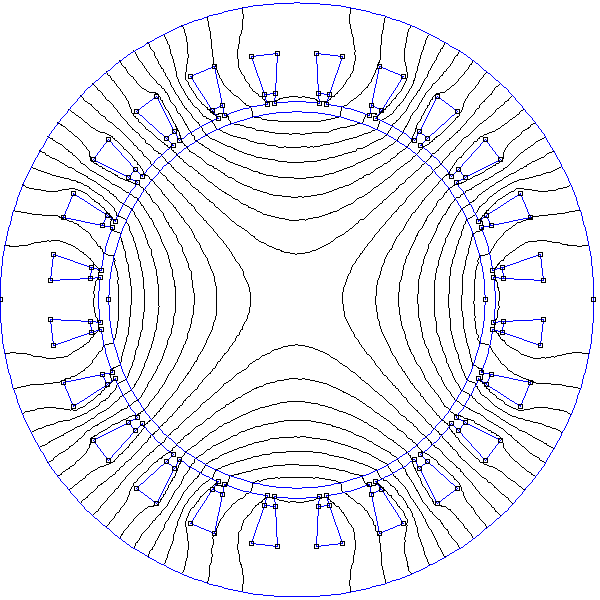
Voici les résultats à t=T/4 :

[theta,Br,Btheta] = np.loadtxt("12bobines-noyau-B-ar=39-t=0.250.txt",unpack=True)
figure(figsize=(16,6))
title(r"$t = T/4$",fontsize=16)
plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
grid()
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$B\ (mT)$",fontsize=16)
legend(loc='upper right')

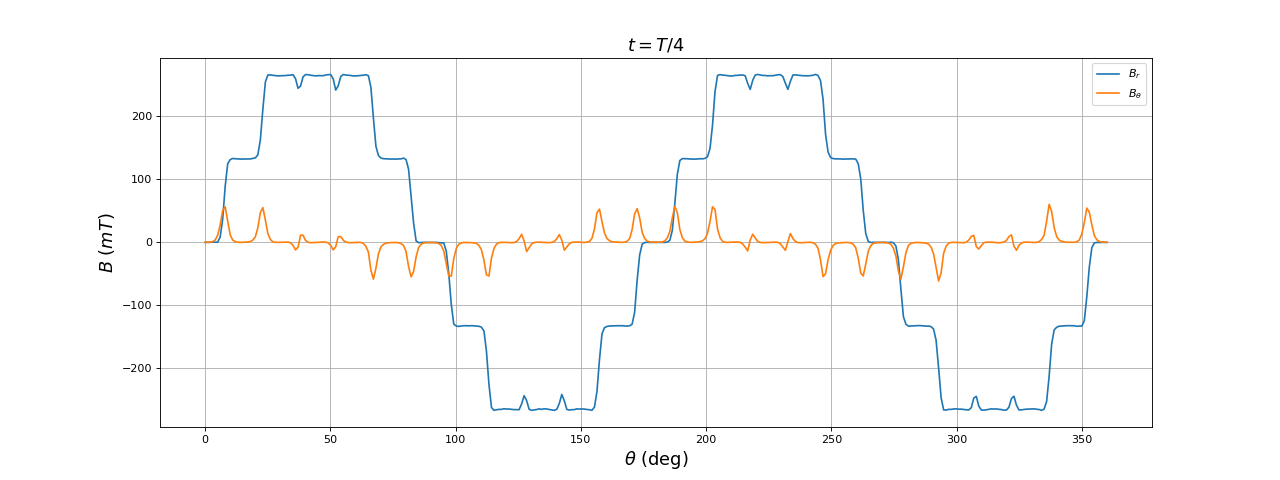fig31.pdf

En un quart de période du courant, le champ a tourné de 45 degrés. Cependant, la forme du champ au voisinage de cet angle est plus plate car cette direction ne correspond pas à l'axe d'un paire de bobines.

Voici les résultats à t=T/2 :

[theta,Br,Btheta] = np.loadtxt("12bobines-noyau-B-ar=39-t=0.500.txt",unpack=True)
figure(figsize=(16,6))
title(r"$t = T/2$",fontsize=16)
plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
grid()
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$B\ (mT)$",fontsize=16)
legend(loc='upper right')

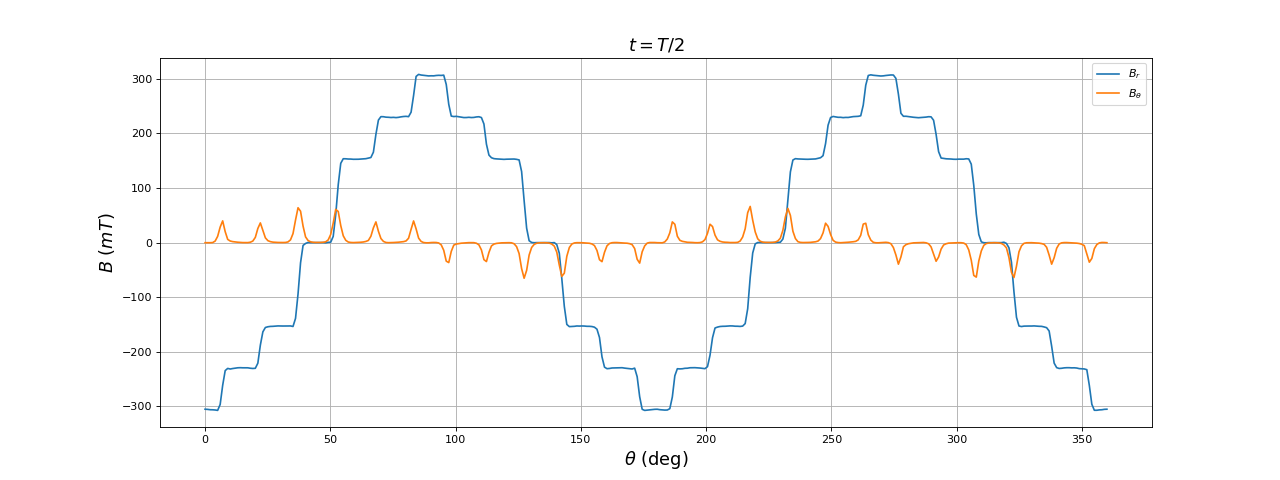fig32.pdf

En une demi-période du courant, le champ a tourné de 90 degrés. À l'instant t=T/2 le champ est maximal sur l'axe (Oy) (deux pôles sud) et minimal sur l'axe (Ox) (deux pôles nord).

Dans les gros moteurs, il est possible de lisser la forme du champ en augmentant le nombre d'encoches sans augmenter le nombre de pôles. Supposons par exemple que l'on souhaite doubler le nombre d'encoches. Chaque circuit (1+, 1-, 2+, etc.) doit être réparti sur deux encoches adjacentes. Il suffit pour cela de poser Ne=48, de réduire la taille des encoches et de modifier l'incrément de la boucle de définition des circuits dans les partie en cuivre :

R1 = 40 # rayon interne du stator
R2 = 60 # rayon externe
Rc = 38 # rayon du noyau (rotor) = 0 si pas de noyau
a1 = 4 # largeur angulaire du fond des encoches (en degrés)
a2 = 2# largeur angulaire du haut des encoches (en degrés)
e = 6 # profondeur des encoches
d = 5 # épaisseur du cuivre (depuis le fond de l'encoche)
u = d/e
Ne = 48 # nombre d'encoches
circ = ['2-','2-','1+','1+','3-','3-','2+','2+','1-','1-','3+','3+','2-','2-','1+','1+','3-','3-','2+','2+','1-','1-','3+','3+']
increm = 0.5
Ns = 125 # nombre de spires dans chaque bobine

Le nombre de spires dans chaque bobine, qui est aussi le nombre de fils dans chaque encoche, a été divisé par deux (car les encoches sont en principe deux fois plus petites). Ce paramètre n'a cependant aucune influence sur les lignes de champ et la forme du champ dans l'entrefer.

Voici les résultats à t=0 :

[theta,Br,Btheta] = np.loadtxt("12bobines-noyau-B-ar=39-t=0.000-Ne=48.txt",unpack=True)
figure(figsize=(16,6))
title(r"$t = 0$",fontsize=16)
plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
grid()
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$B\ (mT)$",fontsize=16)
legend(loc='upper right')

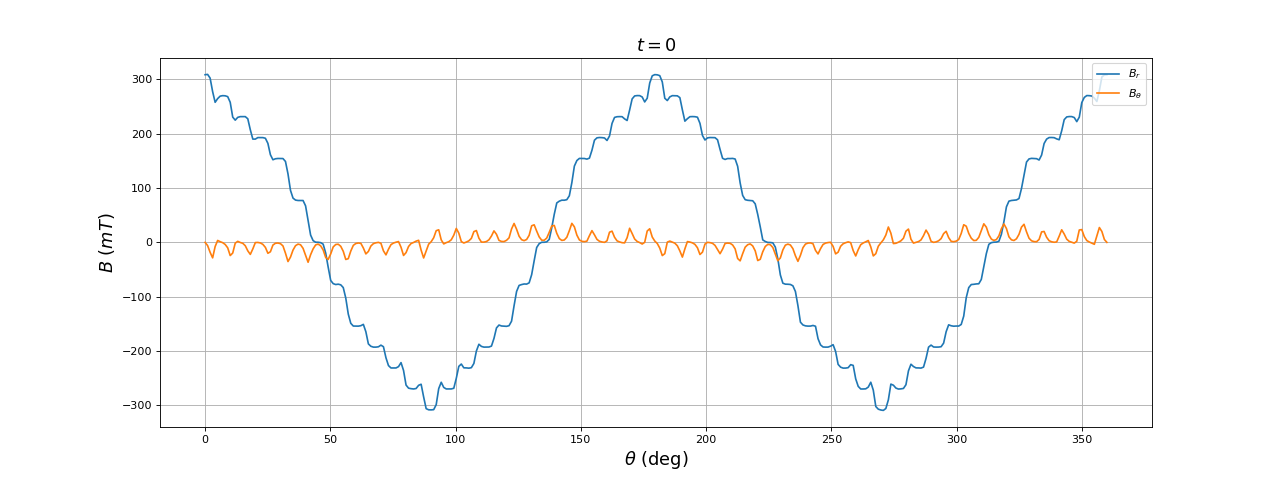fig33.pdf

et voici la courbe du champ pour t=T/4 :

[theta,Br,Btheta] = np.loadtxt("12bobines-noyau-B-ar=39-t=0.250-Ne=48.txt",unpack=True)
figure(figsize=(16,6))
title(r"$t = 0$",fontsize=16)
plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
grid()
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$B\ (mT)$",fontsize=16)
legend(loc='upper right')

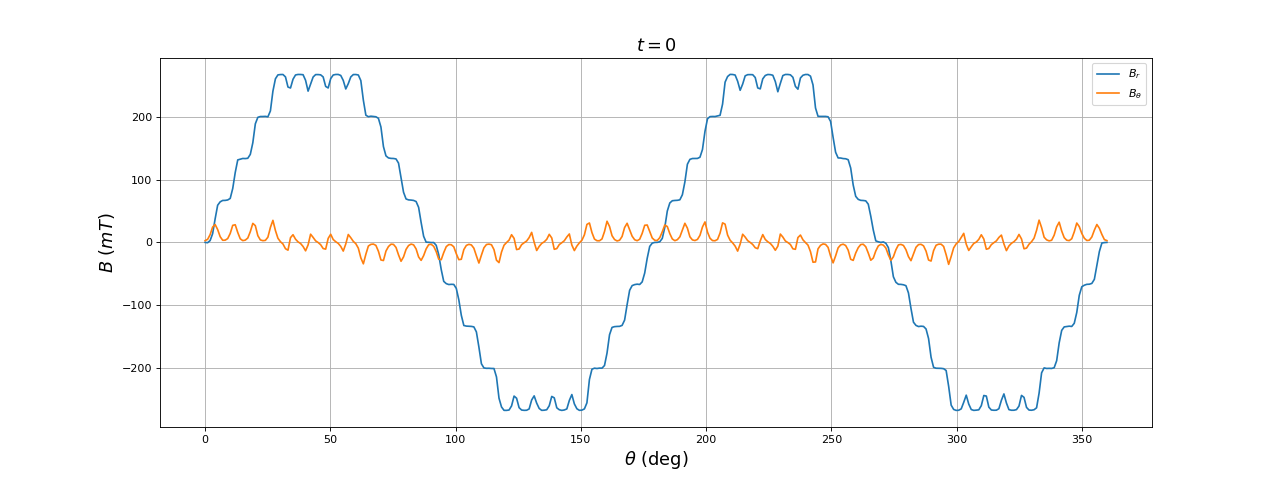fig34.pdf

Voici les modules des coefficients de Fourier du champ radial :

harm = np.absolute(fft(Br[0:len(Br)//2]))
figure()
stem(harm)
xlim(0,10)
grid()
xlabel(r"$n$",fontsize=16)
ylabel(r"$B_r\ (mT)$",fontsize=16)

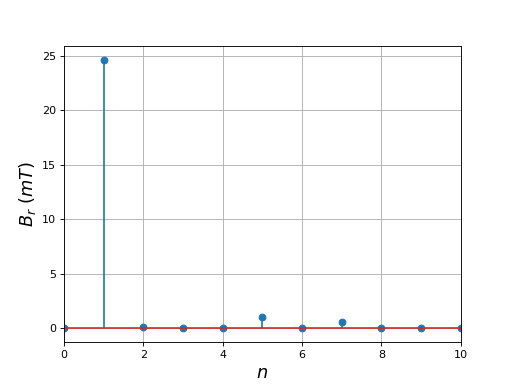fig35.pdf

Le doublement du nombre d'encoches apporte bien un lissage du champ, qui se rapproche encore d'une forme sinusoïdale.

En réalité, on cherche à maximiser le nombre de spires pour chaque bobine pour un stator de diamètre donné. Pour y parvenir, il faut que chaque encoche recoive des fils de plusieurs phases. Le meilleur résultat est obtenu si chaque encoche comporte trois parties, une pour chaque phase. Si l'on examine la figure donnée plus haut représentant les courants dans les bobines, on constate que chaque demi-spire d'une bobine est adjacente à une demi-spire de la bobine voisine de la même phase et parcourue par le même courant. En conséquence, il est possible de répartir ce courant non pas seulement sur deux encoches mais sur six encoches. Ce changement est indiqué sur la figure suivante :

Figure pleine page

On fait la même transformation pour les deux autres phases. De cette manière, les fils de chaque phase sont répartis uniformément sur la totalité de la surface du stator. La notion de bobine a toujours un sens mais chaque demi-bobine (constituée de 6 encoches et délimitée par deux rayons en pointillé sur la figure) est commune à deux bobines voisines de la même phase. Pour chaque phase, il y a donc 4 demi-bobines pour ce stator à 4 pôles.

Voici le script :

statorLisse-3phases4poles-reparti.py

import femm
import numpy as np
import matplotlib.pyplot as plt

femm.openfemm()
femm.newdocument(0)
# 0 : magnetic, 1 : electrostatic, 2 ; heat flow, 3 : current flow
femm.mi_probdef(0, 'millimeters', 'planar', 1.0e-8, 0, 30);
# freq, unit, type ('planar' ou 'axis'), precision, depth, minangle

R1 = 40 # rayon interne du stator
R2 = 60 # rayon externe
Rc = 38 # rayon du noyau (rotor) = 0 si pas de noyau
a = 5# largeur angulaire du haut des encoches (en degrés)
e = 9 # profondeur des encoches
ee = e/3 # profondeur de chaque phase
Ne = 24 # nombre d'encoches
circ_1 = ['1+','1+','1+','1+','1+','1+','1-','1-','1-','1-','1-','1-','1+','1+','1+','1+','1+','1+','1-','1-','1-','1-','1-','1-']
circ_2 = ['2-','2-','2-','2-','2+','2+','2+','2+','2+','2+','2-','2-','2-','2-','2-','2-','2+','2+','2+','2+','2+','2+','2-','2-']
circ_3 = ['3+','3+','3-','3-','3-','3-','3-','3-','3+','3+','3+','3+','3+','3+','3-','3-','3-','3-','3-','3-','3+','3+','3+','3+']
Ns = 125 # nombre de spires dans chaque bobine
t = 0.0
i1 = np.cos(2*np.pi*t)
i2 = np.cos(2*np.pi*t-2*np.pi/3)
i3 = np.cos(2*np.pi*t+2*np.pi/3)
angle = 360/Ne

cuivre_1 = []
cuivre_2 = []
cuivre_3 = []

def rotation(x,y,theta):
    cos = np.cos(theta)
    sin = np.sin(theta)
    return x*cos-y*sin,x*sin+y*cos
 
def encoche(theta):
    b = a*np.pi/180*R1
    x1,y1 = rotation(R1,-b/2,theta)
    x2,y2 = rotation(R1+ee,-b/2,theta)
    femm.mi_drawline(x1,y1,x2,y2)
    x3,y3 = rotation(R1+ee,b/2,theta)
    femm.mi_drawline(x2,y2,x3,y3)
    x4,y4 = rotation(R1,b/2,theta)
    femm.mi_drawline(x3,y3,x4,y4)
    cuivre_1.append([(x1+x3)/2,(y1+y3)/2])
    x1,y1 = rotation(R1+ee,-b/2,theta)
    x2,y2 = rotation(R1+2*ee,-b/2,theta)
    femm.mi_drawline(x1,y1,x2,y2)
    x3,y3 = rotation(R1+2*ee,b/2,theta)
    femm.mi_drawline(x2,y2,x3,y3)
    x4,y4 = rotation(R1+ee,b/2,theta)
    femm.mi_drawline(x3,y3,x4,y4)
    cuivre_2.append([(x1+x3)/2,(y1+y3)/2])
    x1,y1 = rotation(R1+2*ee,-b/2,theta)
    x2,y2 = rotation(R1+3*ee,-b/2,theta)
    femm.mi_drawline(x1,y1,x2,y2)
    x3,y3 = rotation(R1+3*ee,b/2,theta)
    femm.mi_drawline(x2,y2,x3,y3)
    x4,y4 = rotation(R1+2*ee,b/2,theta)
    femm.mi_drawline(x3,y3,x4,y4)
    cuivre_3.append([(x1+x3)/2,(y1+y3)/2])
    

R1p = R1+0.1
femm.mi_drawarc(R1p,0,-R1p,0,180,1)
femm.mi_drawarc(-R1p,0,R1p,0,180,1)
femm.mi_drawarc(R2,0,-R2,0,180,1)
femm.mi_drawarc(-R2,0,R2,0,180,1)

theta = -angle/2
for k in range(Ne):
    theta = angle/2+angle*k
    encoche(theta*np.pi/180)

print(cuivre_1)

if Rc!=0:
    femm.mi_drawarc(Rc,0,-Rc,0,180,1)
    femm.mi_drawarc(-Rc,0,Rc,0,180,1)


femm.mi_addmaterial('Air', 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0)
femm.mi_addmaterial('Coil', 1, 1, 0, 0, 58*0.65, 0, 0, 1, 0, 0, 0)
femm.mi_addmaterial('LinearIron', 2100, 2100, 0, 0, 0, 0, 0, 1, 0, 0, 0)

femm.mi_addcircprop('1+', i1, 1)
# name, current, 1=series, 0=parallel
femm.mi_addcircprop('1-', -i1, 1)
femm.mi_addcircprop('2+', i2, 1);
femm.mi_addcircprop('2-', -i2, 1)
femm.mi_addcircprop('3+', i3, 1);
femm.mi_addcircprop('3-', -i3, 1)

femm.mi_addblocklabel(0,(R1+Rc)/2) # air
femm.mi_addblocklabel(0,(R1+R2)/2) # fer
femm.mi_selectlabel(0,(R1+R2)/2)
femm.mi_setblockprop('LinearIron', 0, 1, '<None>', 0, 0, 0)
femm.mi_clearselected()
femm.mi_selectlabel(0,(R1+Rc)/2)
femm.mi_setblockprop('Air', 0, 1, '<None>', 0, 0, 0)
femm.mi_clearselected()

if Rc!=0:
    femm.mi_addblocklabel(0,0)
    femm.mi_selectlabel(0,0)
    femm.mi_setblockprop('LinearIron', 0, 1, '<None>', 0, 0, 0)
    femm.mi_clearselected()

i=0
for p in cuivre_1:
    femm.mi_addblocklabel(p[0],p[1])
    femm.mi_selectlabel(p[0],p[1])
    femm.mi_setblockprop('Coil', 0, 1, circ_1[int(i)], 0, 0, Ns)
    femm.mi_clearselected()
    i += 1

i=0
for p in cuivre_2:
    femm.mi_addblocklabel(p[0],p[1])
    femm.mi_selectlabel(p[0],p[1])
    femm.mi_setblockprop('Coil', 0, 1, circ_2[int(i)], 0, 0, Ns)
    femm.mi_clearselected()
    i += 1

i=0
for p in cuivre_3:
    femm.mi_addblocklabel(p[0],p[1])
    femm.mi_selectlabel(p[0],p[1])
    femm.mi_setblockprop('Coil', 0, 1, circ_3[int(i)], 0, 0, Ns)
    femm.mi_clearselected()
    i += 1


femm.mi_zoomnatural()
femm.mi_saveas('stator2phases.fem')
femm.mi_analyze()
femm.mi_loadsolution()


# composantes radiale et orthoradiale de B sur un cercle de rayon ar
ar = 39
theta = np.linspace(0,2*np.pi,360)
cos = np.cos(theta)
sin = np.sin(theta)
Br = np.zeros(len(theta))
Btheta = np.zeros(len(theta))
for k in range(len(theta)):
    B = femm.mo_getb(ar*cos[k],ar*sin[k])
    Br[k] = cos[k]*B[0]+sin[k]*B[1]
    Btheta[k] = -sin[k]*B[0]+cos[k]*B[1]
np.savetxt("12bobines-noyau-B-ar=%d-t=%0.3f-reparti.txt"%(ar,t),np.array([theta,Br,Btheta]).T)
plt.figure(figsize=(16,6))
plt.title(r"$t = %0.3f$"%t,fontsize=16)
plt.plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plt.plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
plt.grid()
plt.xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
plt.ylabel(r"$B\ (mT)$",fontsize=16)
plt.legend(loc='upper right')
plt.show()

femm.closefemm()

Voici le résultat pour 24 encoches à t=0 :

[theta,Br,Btheta] = np.loadtxt("12bobines-noyau-B-ar=39-t=0.000-reparti.txt",unpack=True)
figure(figsize=(16,6))
title(r"$t = 0$",fontsize=16)
plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
grid()
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$B\ (mT)$",fontsize=16)
legend(loc='upper right')

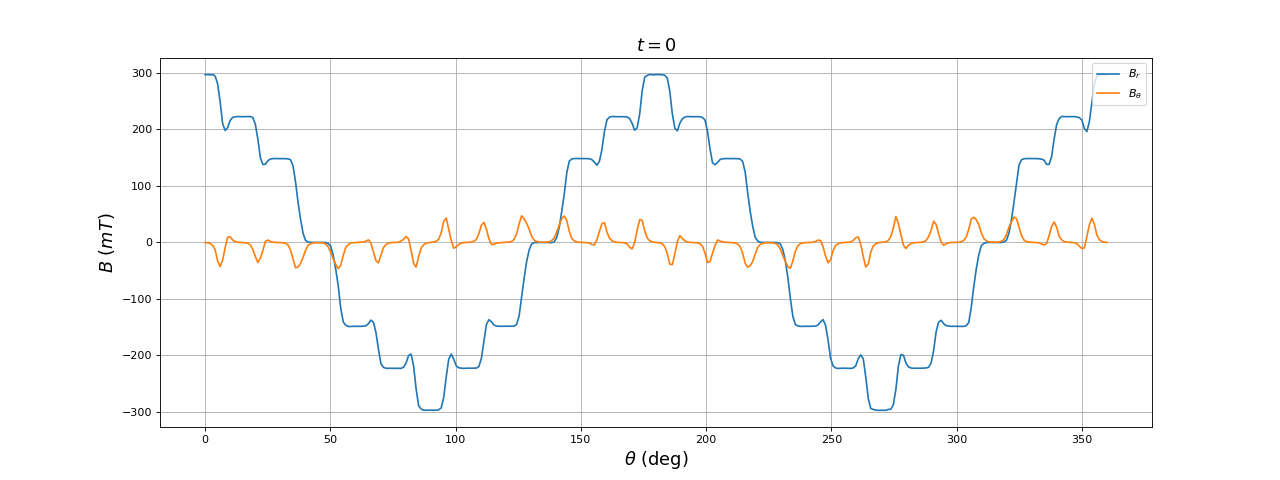fig36.pdf

Voici les modules des coefficients de Fourier du champ radial :

harm = np.absolute(fft(Br[0:len(Br)//2]))
figure()
stem(harm)
xlim(0,10)
grid()
xlabel(r"$n$",fontsize=16)
ylabel(r"$B_r\ (mT)$",fontsize=16)

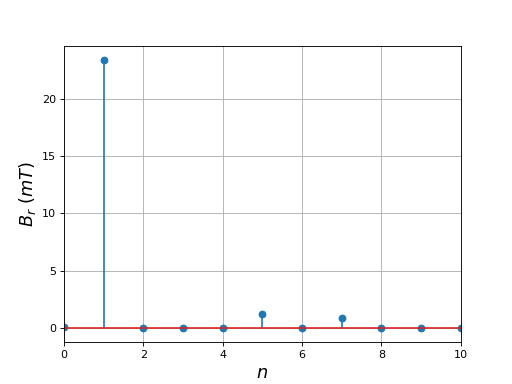fig37.pdf

Cette solution n'apporte pas d'amélioration de la forme du champ radial (les harmoniques de rang 5 et 7 ont la même amplitude). L'intérêt d'une répartition des bobinages de chaque phase sur la totalité du stator est de permettre d'obtenir une plus grande force magnétomotrice (produit de l'intensité du courant par le nombre de spires) donc un plus grand champ magnétique dans l'entrefer. Pour améliorer le lissage et s'approcher d'une forme sinusoïdale, il faut augmenter le nombre d'encoches.

Cette simulation montre que l'obtention d'une forme de champ radial sinusoïdale nécessite que chaque bobine soit la plus large possible, soit 90 degrés pour un stator quadrupolaire (180 degrés pour un stator bipolaire), ce qui implique évidemment un enchevêtrement des bobines des différentes phases. Le fait de répartir chaque bobine sur le maximum d'encoches ne semble pas avoir d'effet positif sur la forme du champ.

7. Stator quadrupolaire triphasé à bobinage sur dents

Chacune des 12 bobines du stator quadrupolaire triphasé est une simple bobine enroulée sur un noyau (une dent) dont l'extrémité du coté de l'entrefer est élargie pour épouser au mieux la forme cylindrique (l'entrefer doit être le plus étroit possible).

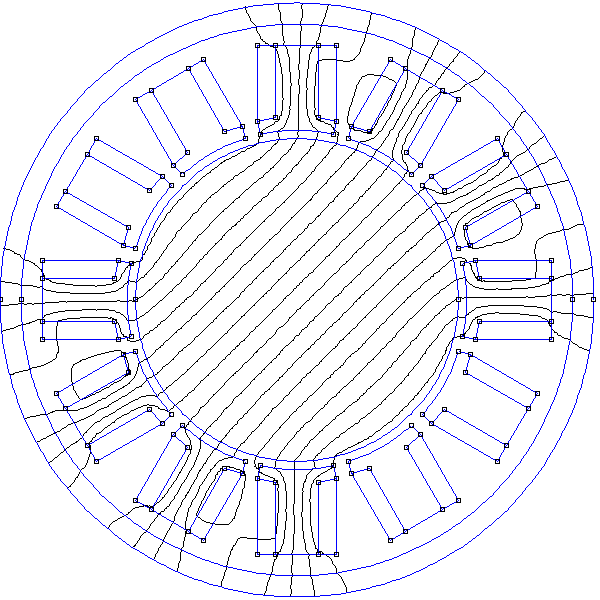
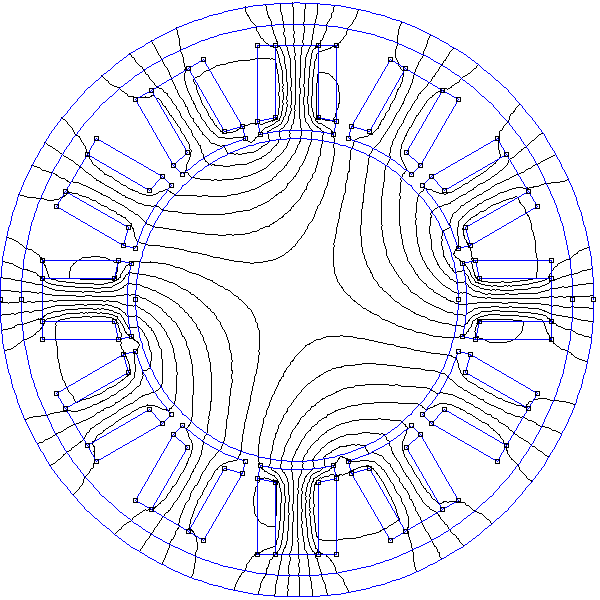
La figure suivante montre les courants dans les 12 bobines. À la différence du stator quadrupolaire triphasé à encoches, les 12 bobines ne sont pas enchevêtrées.

Figure pleine page

Voici le résultat à t=0 :

[theta,Br,Btheta] = np.loadtxt("12dents-4poles-ar=39-t=0.000.txt",unpack=True)
figure(figsize=(16,6))
title(r"$t = 0$",fontsize=16)
plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
grid()
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$B\ (mT)$",fontsize=16)
legend(loc='upper right')

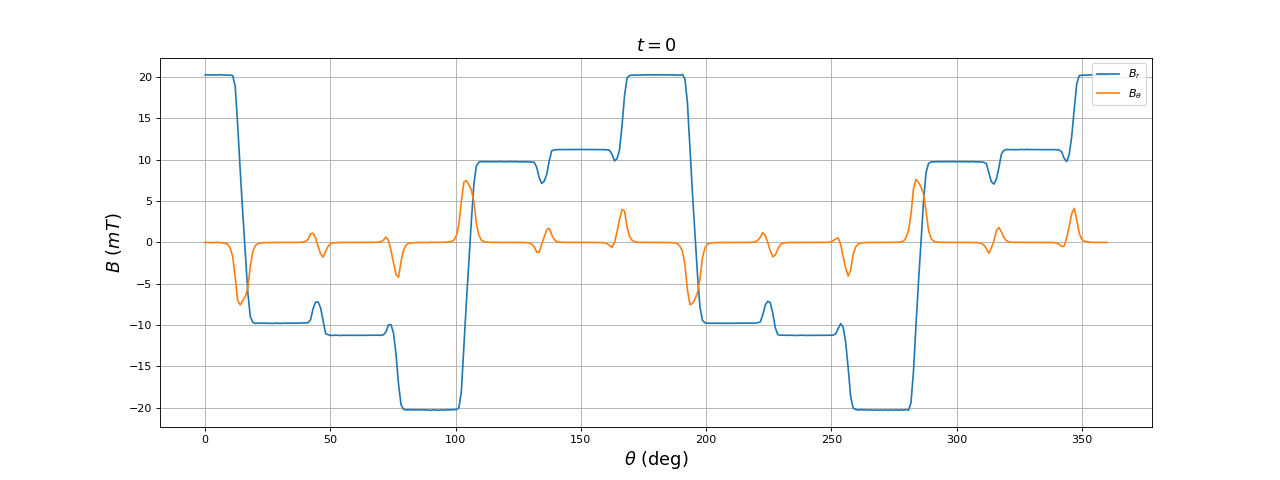fig38.pdf

Voici les modules des coefficients de Fourier du champ radial :

harm = np.absolute(fft(Br[0:len(Br)//2]))
figure()
stem(harm)
xlim(0,10)
grid()
xlabel(r"$n$",fontsize=16)
ylabel(r"$B_r\ (mT)$",fontsize=16)

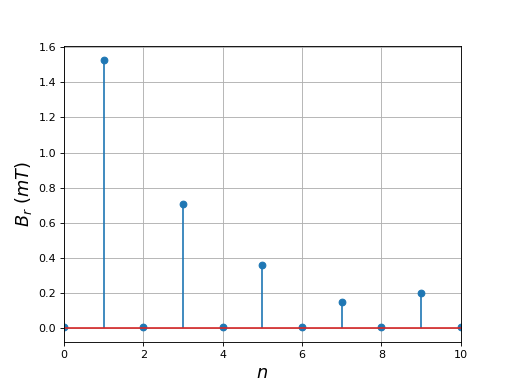fig39.pdf

La forme du champ est très éloignée d'une forme sinusoïdale : les harmoniques de rang 3 et 5 sont très intenses. Le passage d'un pôle au suivant se fait avec une pente très forte, ce qui justifie le nom de stator à pôles saillants donné à ce type de stator. On constate d'ailleurs que les pôles du stator quadrupolaire sont plus saillants que ceux du stator bipolaire. Les pôles saillants sont indésirables car ils ont pour conséquence des ondulations du couple sur le rotor.

8. Stator à encoches multipolaire triphasé

Nous pouvons établir la méthode générale de bobinage d'un stator à encoches à p pôles, dans le cas où une seule phase passe dans chaque encoche (il semble que cette configuration soit la plus répandue). Pour p=2, il faut 6 encoches. Pour p=4, il faut 12 encoches. Dans le cas général, le nombre d'encoches est 3p. Les deux cas traîtés précédemment (stator bipolaire et quadrupolaire) suggèrent la règle suivante pour la définition des courants dans les encoches lorsqu'on les parcourt dans l'ordre :

On choisit un ordre d'alternance des phases, par exemple 1,2,3.
On affecte les courants en faisant alterner les sens : 1+,2-,3+,1-,2+,3-,1+,2-,3+, etc.

Cette configuration conduit à une réalisation du bobinage relative aisée. Chaque nappe de fils d'une phase (par ex. 1+) est placée dans une encoche et on la fait revenir de l'autre côté du stator en la faisant passer 2 encoches plus loin dans l'autre sens (1-). La photo au début de cette page montre un exemple de bobinage de ce type.

Pour lisser la forme du champ (réduire les harmoniques de rang 5 et 7), on prévoit la possibilité d'augmenter le nombre d'encoches d'un facteur n_e. Ainsi, chaque nappe de fils avec un courant donné se répartit en fait sur n_e encoches successives.

La figure suivante montre comment se fait le bobinage des encoches. Chaque trait représente une nappe de plusieurs spires, autant que l'encoche peut en contenir pour le diamètre de fil choisi (qui dépend du courant maximal). Il y a trois fils, un pour chaque phase. Chaque fil suit le trajet indiqué puis revient au point de départ pour former la spire suivante. Ce bobinage comporte une part importante de fil en dehors du fer, aux extrémités du stator. Cette part contribue aux pertes par effet Joule sans contribuer au champ dans l'entrefer : c'est le prix à payer pour obtenir un champ lisse.

Figure pleine page

Voici le script :

statorEncochesMultipoles.py

import femm
import numpy as np
import matplotlib.pyplot as plt

femm.openfemm()
femm.newdocument(0)
# 0 : magnetic, 1 : electrostatic, 2 ; heat flow, 3 : current flow
femm.mi_probdef(0, 'millimeters', 'planar', 1.0e-8, 0, 30);
# freq, unit, type ('planar' ou 'axis'), precision, depth, minangle

R1 = 40 # rayon interne du stator
R2 = 60 # rayon externe
Rc = 38 # rayon du noyau (rotor) = 0 si pas de noyau
a1 = 3 # largeur angulaire du fond encoches (en degrés)
a2 = 2 # largeur angulaire du haut des encoches (en degrés)
e = 10 # profondeur des encoches
d = 8 # épaisseur du cuivre (depuis le fond de l'encoche)
u = d/e
poles = 8 # nombre de pôles
ne = 2 # nombre d'encoches successive pour un courant 
Ne = poles*3*ne # nombre d'encoches

increm = 1
Ns = 250 # nombre de spires dans chaque bobine
t = 0.0
i1 = np.cos(2*np.pi*t)
i2 = np.cos(2*np.pi*t-2*np.pi/3)
i3 = np.cos(2*np.pi*t+2*np.pi/3)
angle = 360/Ne

ordre = ['1+','2-','3+','1-','2+','3-']
circ = []
for n in range(Ne):
    circ.append(ordre[(n//ne)%6])


theta = -angle/2
x = R1*np.cos((theta+a2/2)*np.pi/180)
y = R1*np.sin((theta+a2/2)*np.pi/180)
cuivre = []
for k in range(Ne):
    theta = angle/2+angle*k
    x1 = R1*np.cos((theta-a2/2)*np.pi/180)
    y1 = R1*np.sin((theta-a2/2)*np.pi/180)
    femm.mi_drawarc(x,y,x1,y1,angle,1)
    x,y = x1,y1
    x2,y2 = x,y
    x1 = (R1+e)*np.cos((theta-a1/2)*np.pi/180)
    y1 = (R1+e)*np.sin((theta-a1/2)*np.pi/180)
    femm.mi_drawline(x,y,x1,y1)
    x,y = x1,y1
    x1 = (R1+e)*np.cos((theta+a1/2)*np.pi/180)
    y1 = (R1+e)*np.sin((theta+a1/2)*np.pi/180)
    femm.mi_drawline(x,y,x1,y1)
    x,y = x1,y1
    x1 = R1*np.cos((theta+a2/2)*np.pi/180)
    y1 = R1*np.sin((theta+a2/2)*np.pi/180)
    femm.mi_drawline(x,y,x1,y1)
    x,y = x1,y1
    x,y = R1*np.cos((theta-a2/2)*np.pi/180),R1*np.sin((theta-a2/2)*np.pi/180)
    x1,y1 = (R1+e)*np.cos((theta-a1/2)*np.pi/180),(R1+e)*np.sin((theta-a1/2)*np.pi/180)
    x2 = (u*x+(1-u)*x1)
    y2 = (u*y+(1-u)*y1)
    x,y = R1*np.cos((theta+a2/2)*np.pi/180),R1*np.sin((theta+a2/2)*np.pi/180)
    x1,y1 = (R1+e)*np.cos((theta+a1/2)*np.pi/180),(R1+e)*np.sin((theta+a1/2)*np.pi/180)
    x3 = (u*x+(1-u)*x1)
    y3 = (u*y+(1-u)*y1)
    femm.mi_drawline(x2,y2,x3,y3)
    cuivre.append([(R1+0.9*e)*np.cos((theta)*np.pi/180),(R1+0.9*e)*np.sin((theta)*np.pi/180)])

femm.mi_drawarc(R2,0,-R2,0,180,1)
femm.mi_drawarc(-R2,0,R2,0,180,1)
if Rc!=0:
    femm.mi_drawarc(Rc,0,-Rc,0,180,1)
    femm.mi_drawarc(-Rc,0,Rc,0,180,1)


femm.mi_addmaterial('Air', 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0)
femm.mi_addmaterial('Coil', 1, 1, 0, 0, 58*0.65, 0, 0, 1, 0, 0, 0)
femm.mi_addmaterial('LinearIron', 2100, 2100, 0, 0, 0, 0, 0, 1, 0, 0, 0)

femm.mi_addcircprop('1+', i1, 1)
# name, current, 1=series, 0=parallel
femm.mi_addcircprop('1-', -i1, 1)
femm.mi_addcircprop('2+', i2, 1);
femm.mi_addcircprop('2-', -i2, 1)
femm.mi_addcircprop('3+', i3, 1);
femm.mi_addcircprop('3-', -i3, 1)

femm.mi_addblocklabel(0,(R1+Rc)/2) # air
femm.mi_addblocklabel(0,(R1+R2)/2) # fer
femm.mi_selectlabel(0,(R1+R2)/2)
femm.mi_setblockprop('LinearIron', 0, 1, '<None>', 0, 0, 0)
femm.mi_clearselected()
femm.mi_selectlabel(0,(R1+Rc)/2)
femm.mi_setblockprop('Air', 0, 1, '<None>', 0, 0, 0)
femm.mi_clearselected()

if Rc!=0:
    femm.mi_addblocklabel(0,0)
    femm.mi_selectlabel(0,0)
    femm.mi_setblockprop('LinearIron', 0, 1, '<None>', 0, 0, 0)
    femm.mi_clearselected()

i = 0

for p in cuivre:
    femm.mi_addblocklabel(p[0],p[1])
    femm.mi_selectlabel(p[0],p[1])
    femm.mi_setblockprop('Coil', 0, 1, circ[int(i)], 0, 0, Ns)
    femm.mi_clearselected()
    i += 1


femm.mi_zoomnatural()
femm.mi_saveas('stator2phases.fem')
femm.mi_analyze()
femm.mi_loadsolution()


# composantes radiale et orthoradiale de B sur un cercle de rayon ar
ar = 39
theta = np.linspace(0,2*np.pi,360)
cos = np.cos(theta)
sin = np.sin(theta)
Br = np.zeros(len(theta))
Btheta = np.zeros(len(theta))
for k in range(len(theta)):
    B = femm.mo_getb(ar*cos[k],ar*sin[k])
    Br[k] = cos[k]*B[0]+sin[k]*B[1]
    Btheta[k] = -sin[k]*B[0]+cos[k]*B[1]
np.savetxt("multipoles-p=%d-ar=%d-t=%0.3f.txt"%(poles,ar,t),np.array([theta,Br,Btheta]).T)
plt.figure(figsize=(16,6))
plt.title(r"$t = %0.3f$"%t,fontsize=16)
plt.plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plt.plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
plt.grid()
plt.xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
plt.ylabel(r"$B\ (mT)$",fontsize=16)
plt.legend(loc='upper right')
plt.show()

femm.closefemm()

Voici le résultat pour p=4 et ne=2 à t=0 :

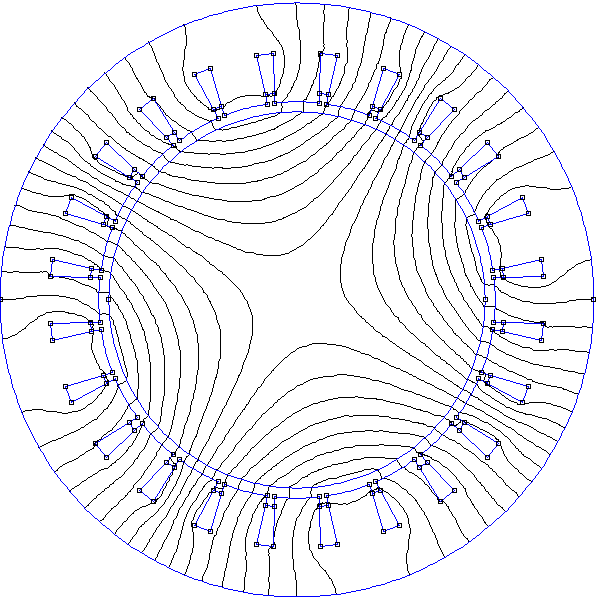
[theta,Br,Btheta] = np.loadtxt("multipoles-p=4-ar=39-t=0.000.txt",unpack=True)
figure(figsize=(16,6))
title(r"$t = 0$",fontsize=16)
plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
grid()
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$B\ (mT)$",fontsize=16)
legend(loc='upper right')

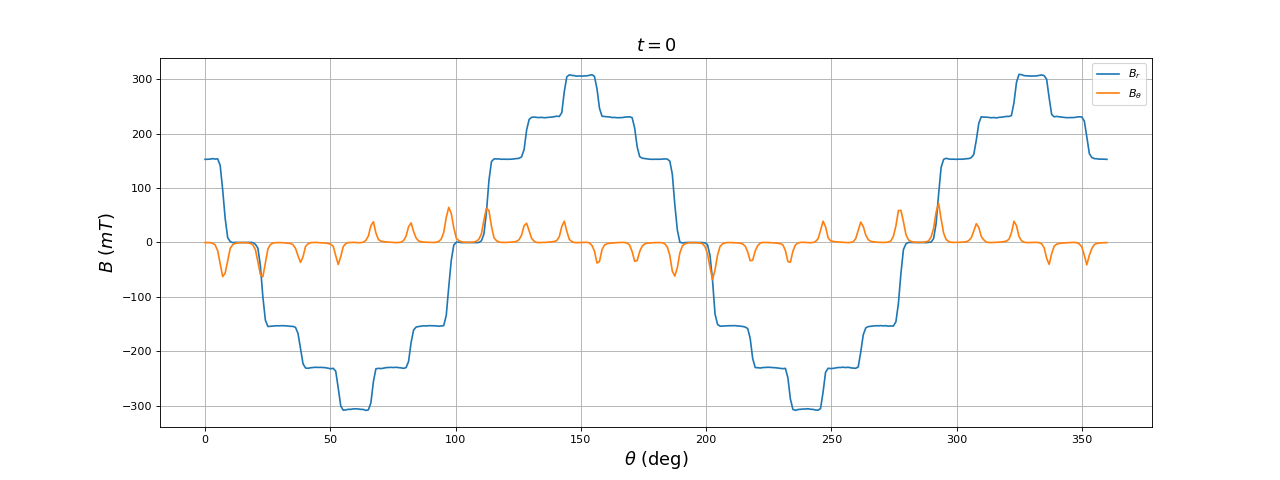fig40.pdf

harm = np.absolute(fft(Br[0:len(Br)//2]))
figure()
stem(harm)
xlim(0,10)
grid()
xlabel(r"$n$",fontsize=16)
ylabel(r"$B_r\ (mT)$",fontsize=16)

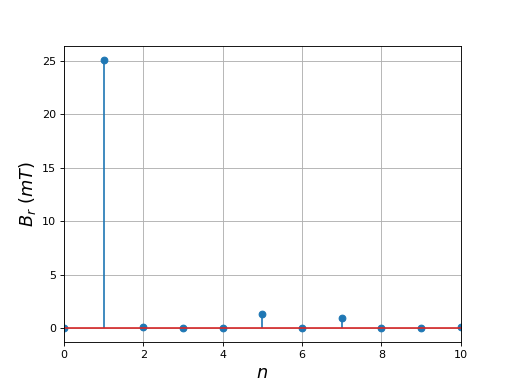fig41.pdf

Voici le résultat pour p=8 et ne=2 à t=0 :

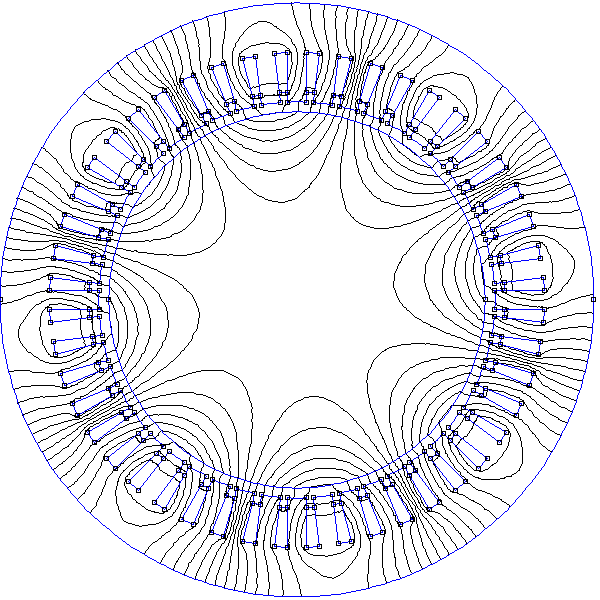
[theta,Br,Btheta] = np.loadtxt("multipoles-p=8-ar=39-t=0.000.txt",unpack=True)
figure(figsize=(16,6))
title(r"$t = 0$",fontsize=16)
plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
grid()
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$B\ (mT)$",fontsize=16)
legend(loc='upper right')

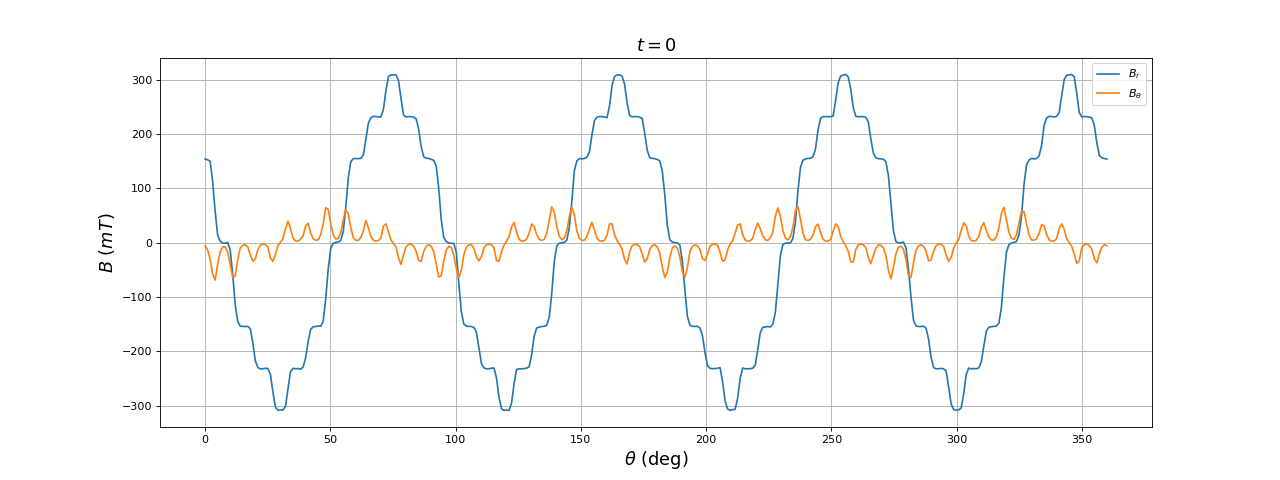fig42.pdf

harm = np.absolute(fft(Br[0:len(Br)//4]))
figure()
stem(harm)
xlim(0,10)
grid()
xlabel(r"$n$",fontsize=16)
ylabel(r"$B_r\ (mT)$",fontsize=16)

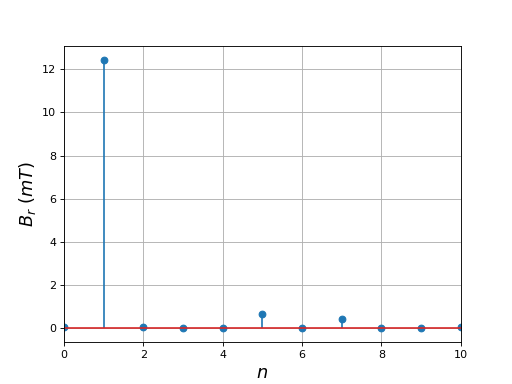fig43.pdf

Ce stator peut être qualifié de stator à pôles lisses car les harmoniques de rang 5 et 7 sont relativement faibles. Le lissage peut être amélioré en augmentant encore n_e. En remarquera que si l'on augmente le nombre d'encoches sans changer leur taille ni en conséquence le nombre de fils qui y passent, on multiplie d'autant la force magnétomotrice donc l'intensité du champ.

Voici le résultat pour p=8 et ne=3 à t=0 :

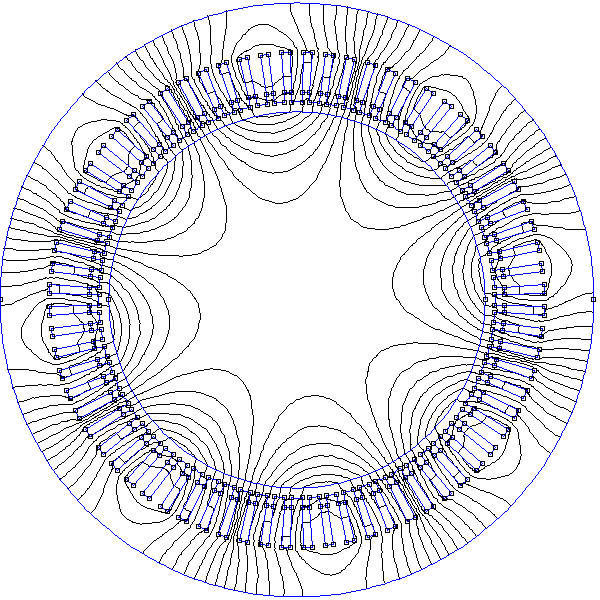
[theta,Br,Btheta] = np.loadtxt("multipoles-p=8-ne=3-ar=39-t=0.000.txt",unpack=True)
figure(figsize=(16,6))
title(r"$t = 0$",fontsize=16)
plot(theta*180/np.pi,Br*1e3,label=r"$B_r$")
plot(theta*180/np.pi,Btheta*1e3,label=r"$B_{\theta}$")
grid()
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$B\ (mT)$",fontsize=16)
legend(loc='upper right')

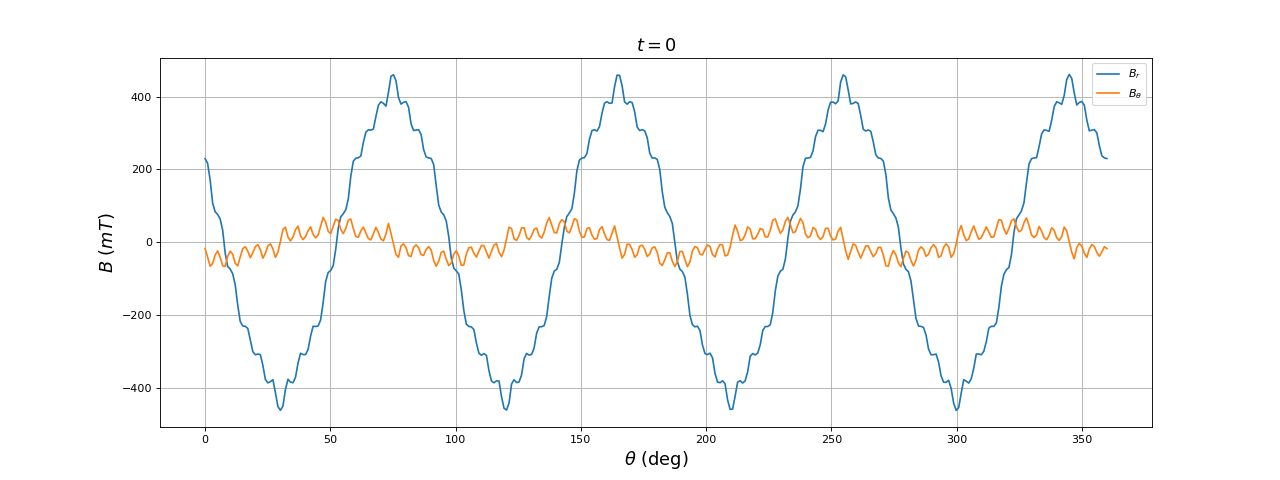fig44.pdf

harm = np.absolute(fft(Br[0:len(Br)//4]))
figure()
stem(harm)
xlim(0,10)
grid()
xlabel(r"$n$",fontsize=16)
ylabel(r"$B_r\ (mT)$",fontsize=16)

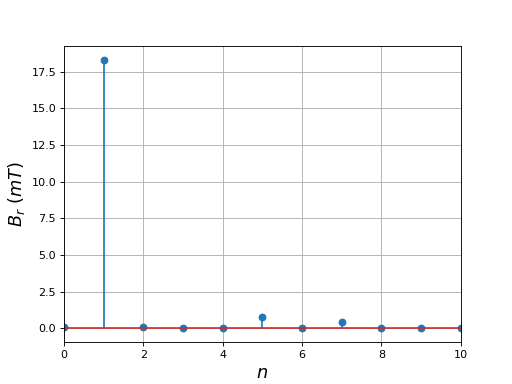fig45.pdf