Filtrage numérique sur un microcontrôleur

3.a. Forme directe de type I

Cette réalisation consiste à calculer directement la somme :

$$y_n=\sum _{k=0}^{N-1}{b}_k{x}_{n-k}-\sum _{k=1}^{M-1}{a}_k{y}_{n-k}\text{(2)}$$

Il faut deux tampons circulaires pour les variables d'état, l'un pour les valeurs antérieures de l'entrée x, l'autre pour les valeurs antérieures de la sortie y.

Voici la déclaration des variables :

uint8_t nb; // nombre de coefficients b
float b[nb]; // coefficients b
uint8_t na; // nombre de coefficients a
float a[na]; // coefficients a
#define TAILLE_TAMPON 0x1000 // supérieure à max(na,nb)
#define MASQUE_TAMPON 0b0001111 // TAILLE_TAMPON-1
int16_t x[TAILLE_TAMPON]; // tampon pour les x_k
int16_t y[TAILLE_TAMPON]; // tampon pour les y_k
uint16_t J; // indice pour les tampons
              

Voici le calcul de la somme. On suppose que le convertisseur A/N fournit la conversion dans l'entier 16 bits entree. La valeur de la sortie est copiée dans sortie, qui peut être envoyée vers un convertisseur N/A, ou subir un autre traitement.

float accum;
int k;
uint16_t i;
int16_t entree; // x_n
int16_t sortie; // y_n
x[J] = entree;
accum = 0;
i = J;
for (k=0; k<nb; k++) {
    accum += x[i]*b[k];
    i = (i-1)&MASQUE_TAMPON;
}
i = J-1;
for (k=1; k<na; k++) {
    accum -= y[i]*a[k];
    i = (i-1)&MASQUE_TAMPON;
}
sortie = accum;
y[J] = sortie;
J = (J+1)&MASQUE_TAMPON;
              

3.b. Forme directe de type II

Cette réalisation est définie par :

$$\begin{array}{ccc}\hfill & w_n=x_n-a_1{w}_{n-1}-a_2{w}_{n-2}-\cdots \hfill & \hfill \text{(3)}\\ \hfill & y_n=b_0{w}_n+b_1{w}_{n-1}+b_2{w}_{n-2}+\cdots \hfill & \hfill \text{(4)}\end{array}$$

Voir Conception et mise en œuvre des filtres numériques pour sa justification. Les variables d'état sont w_n-1, w_n-2, etc. Il y a en a Max(M,N). Le nombre de variables d'état est environ deux fois moindre que pour la forme directe de type I, mais cela ne constitue un critère important que lorsque la mémoire disponible est très faible. Sur les microcontroleurs, il y en général assez de mémoire pour la forme de type I. Cette réalisation est équivalente à la forme de type I pour des signaux sinusoidaux en régime permanent, mais sa réponse transitoire peut être assez différente, en particulier pour les filtres récursifs. Voici l'implémentation :

uint8_t nb; // nombre de coefficients b
float b[nb]; // coefficients b
uint8_t na; // nombre de coefficients a
float a[na]; // coefficients a
#define TAILLE_TAMPON 0x1000 // supérieure à max(na,nb)
#define MASQUE_TAMPON 0b0001111 // TAILLE_TAMPON-1
int16_t w[TAILLE_TAMPON]; // tampon pour les w_k
uint16_t J; // indice pour les tampons
                   

float accum;
uint_8 k;
uint16_t i;
int16_t entree; // x_n
int16_t sortie; // y_n
accum = entree*a[0];
i = J-1;
for (k=1; k<na; k++) {
    accum -= w[i]*a[k];
    i = (i-1)&MASQUE_TAMPON;
}
w[J] = accum;
accum = 0;
i=J;
for (k=0; k<nb; k++) {
    accum += w[i]*b[k];
    i = (i-1)&MASQUE_TAMPON;
}
sortie = accum;
J = (J+1)&MASQUE_TAMPON;
              

3.c. Forme directe transposée de type II

Cette forme est définie par la relation de récurrence suivante :

$$\begin{array}{ccc}\hfill & y_n=b_0{x}_n+v_1\hfill & \hfill \text{(5)}\\ \hfill & v_1=b_1{x}_n-a_1{y}_n+v_2\hfill & \hfill \text{(6)}\\ \hfill & v_2=b_2{x}_n-a_2{y}_n+v_3\hfill & \hfill \text{(7)}\\ \hfill & v_3=b_3{x}_n-a_3{y}_n\hfill & \hfill \text{(8)}\end{array}$$

La première affectation utilise la valeur de v₁ calculée à l'itération précédente. La deuxième affectation utilise la valeur de v₂ calculée à l'itération précédente, etc.

Le variables d'état v₁,v₂,v₃,etc sont stockées dans un tampon simple (non circulaire), puisque le premier élément v₁ peut être toujours mémorisé à l'indice 1, le second à l'indice 2, etc (l'indice 0 n'est pas utilisé).

Il est commode d'écrire une seule boucle en annulant les coefficients a_k ou b_k qui ne servent pas.

uint8_t max_na_nb;
float b[max_na_nb]; // coefficients b
float a[max_na_nb]; // coefficients a
int16_t v[max_na_nb]; // tampon pour les v_k
                   

uint_8 k;
uint16_t i;
int16_t entree; // x_n
int16_t sortie; // y_n
sortie = b[0]*entree+v[1];
i = 1;
for (k=1; k<max_na_nb; k++) {
  v[i] = b[k]*entree-a[k]*sortie+v[i+1];
  i++;  
}
                   

Cette réalisation est très efficace, surtout si le nombre de coefficients est fixé. Par exemple, pour un filtre bi-quadratique, on écrira :

sortie = b[0]*entree+v[1];
v[1] = b[1]*entree-a[1]*sortie+v[2];
v[2] = b[2]*entree-a[2]*sortie;
                    

4.a. Calcul avec des entiers signés

Le signal d'entrée est constitué d'entiers codés sur Q bits. Par exemple, les convertisseurs A/N de l'ATmega328 et de l'ATmega2560 numérisent en 10 bits, mais la résolution peut être réduite pour accélérer la numérisation. De manière générale, Q est compris entre 8 et 12 bits. Ces entiers sont signés, car le signal d'entrée peut prendre des valeurs négatives. On stockera donc le signal dans des variables de type int16_t.

Les nombres négatifs sont codés avec la méthode du complément à 2, qui fonctionne de la manière suivante, dans le cas 8 bits. Les nombres compris entre 00000000 et 01111111 (127) sont positifs. Pour changer le signe d'un nombre positif, par exemple 00001001 (9), il faut appliquer le complément binaire, ce qui donne 11110110, puis ajouter 1, ce qui donne finalement 11110111 (-9). On remarque que ce nombre serait interprété comme 247 (soit 256-9) dans le cadre d'un entier 8 bits non signé. Le dernier bit des nombres positifs est 0, alors qu'il est 1 pour les nombres négatifs. Le dernier bit est donc le bit de signe, mais il ne suffit pas d'annuler ce bit pour obtenir la valeur absolue d'un nombre négatif, puisqu'il faut enlever 1 puis prendre le complément à 2.

Lorsqu'on somme deux entiers, il peut se produire un débordement, par exemple (en 8 bits) :

$$100+50\to -106\text{(9)}$$

Comme 150 est supérieur à 127 il y débordement et on obtient un résultat (-106=256-150) incorrect. Considérons à présent l'opération suivante :

$$100+50-30\text{(10)}$$

le résultat est 120, qui est bien dans la gamme de valeurs permises en 8 bits signé [-128,127]. Lorsque le processeur évalue cette expression, il calcule tout d'abord 100+50 et obtient -106. En retranchant 30, il obtient -136, c'est-à-dire 256-136=120, qui est le résultat correct. On voit l'intérêt de cette représentation des nombres négatifs : lorsque le résultat d'une somme d'entiers 8 bits est dans l'intervalle [-128,127], la somme peut être calculée sans précaution particulière. Les débordements qui se produisent dans la somme partielle conduisent à un résultat correct de la somme complète.

Considérons le produit de deux entiers signés x et b, l'un comportant Q bits (en comptant le signe), l'autre comportant P bits. On a les inégalités :

$$\begin{array}{ccc}\hfill & \left|x\right|<2^{Q-1}\hfill & \hfill \text{(11)}\\ \hfill & \left|b\right|<2^{P-1}\hfill & \hfill \text{(12)}\\ \hfill & \left|xb\right|<2^{Q+P-2}\hfill & \hfill \text{(13)}\end{array}$$

On en déduit que le produit nécessite P+Q-1 bits (en comptant celui du signe).

Par exemple, le calcul suivant est convenable si P+Q-1<=16 :

int16_t b; // P bits
int16_t x; // Q bits
int16_t u=b*x; // P+Q-1 bits
                

Si P+Q-1>16, il se produit un débordement. Contrairement au cas de l'addition, le débordement dans le cas de la multiplication doit être évité car le résultat n'a aucun sens. Par exemple pour des entiers 8 bits, 100 multiplié par 2 conduit à -56.

4.b. Calcul en virgule fixe

Les coefficients a_k et b_k sont des réels positifs ou négatifs, dont la valeur absolue est souvent inférieure à 1. On cherche à représenter ces coefficients sous forme d'entiers signés à P bits. Pour cela, il faut les multiplier par une puissance de 2 de telle sorte que le plus grand coefficient (en valeur absolue) tienne sur P bits :

$$E\left(max\left(\right|a_k|,|b_k\left|\right)2^s\right)<2^{P-1}\text{(14)}$$

où E() désigne la partie entière. L'entier s est le plus grand entier vérifiant cette condition. L'entier P devra être choisi en fonction du type d'entiers utilisés, pour éviter les débordement des multiplications.

Le calcul de la somme est appelée accumulation et la variable qui contient la somme est l'accumulateur. Lorsque l'accumulation est terminée, on doit diviser le résultat par 2^s. Il s'agit d'un décalage de s bits vers la droite :

accum = accum >> s;
                    

Dans l'opération de multiplication des coefficients, un coefficient égal à 1 devient 2^s. Cela signifie qu'on utilise s bits pour la partie fractionnaire du coefficient, et P-s bits pour la partie entière (avec le signe). Autrement dit, on fait les calculs avec une virgule fixe, placée juste après le bit s-1. Dans le cas où s>P (si les coefficients ont une valeur absolue inférieure à 1), il y a seulement une partie fractionnaire à P-1 bits, plus un bit de signe. La notation standard pour désigner un nombre à virgule fixe de ce type est Qm.n. Dans le cas présent m=P-s et n=s. Par exemple, si s=16 et P=19 (Q3.16), un nombre binaire se noterait avec la virgule 010.1000101100101111. L'inconvénient des calculs en virgule fixe est la possibilité d'un débordement dans les opérations d'addition et de multiplication. Ils ont l'avantage d'être plus rapides que les calculs en virgule flottante.

Certains processeurs disposent d'instructions permettant de calculer directement en virgule fixe, pour des nombres dont la valeur absolue est inférieure à 1. Par exemple, le format q15 correspond à Q1.15 et nécessite donc 16 bits. Le principal intérêt de ces instructions est de permettre la multiplication sans débordement, avec bien sûr une perte des bits les moins significatifs et donc des erreurs d'arrondi.

4.c. Réalisation directe de type I

Voyons plus en détail l'implémentation de la forme directe de type I, qui consiste à calculer la somme :

$$y_n=\sum _{k=0}^{N-1}{b}_k{x}_{n-k}-\sum _{k=1}^{M-1}{a}_k{y}_{n-k}\text{(15)}$$

Il faut deux tampons circulaires pour les variables d'état, l'un pour les valeurs antérieures de l'entrée x, l'autre pour les valeurs antérieures de la sortie y. Cette forme de réalisation est bien adaptée aux calculs en virgule fixe, car les variables d'état ont une valeur maximale connue d'avance. En effet, si les x_k sont des entiers codés sur Q bits (avec le signe), et si le filtre a un gain maximal de 1, alors les valeurs de y_k sont aussi sur Q bits.

Si P et Q sont choisis pour qu'il n'y ait pas de débordements lors des multiplications, alors la somme peut être calculée même si des débordements se produisent dans les sommes partielles. En effet, le résultat de la somme est nécessairement dans la gamme de valeur prévue (Q bits). Si le gain maximal du filtre est supérieur à 1, il est aisé de diviser tous les coefficients b_k par le gain pour se ramener à un gain égal à 1, puis de multiplier par le gain une fois la somme calculée.

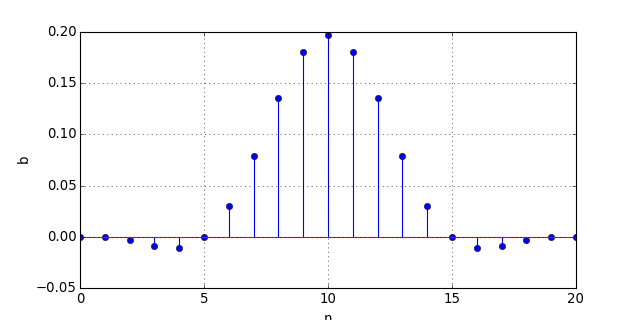
Considérons tout d'abord une implémentation avec des entiers 16 bits. Si Q=10 (convertisseur A/N 10 bits), la condition P+Q-1<=16 nous permet de choisir P=7 bits pour les coefficients. Voyons les conséquences d'une limitation aussi forte du nombre de bits des coefficients sur un exemple de filtre RIF (ne comportant que des coefficients b_k).

import numpy
import scipy.signal
from matplotlib.pyplot import *
b = scipy.signal.firwin(numtaps=21,cutoff=[0.1],window='hann',nyq=0.5)
figure(figsize=(8,4))
stem(b)
xlabel("n")
ylabel("b")
grid()
                   

figA.pdf

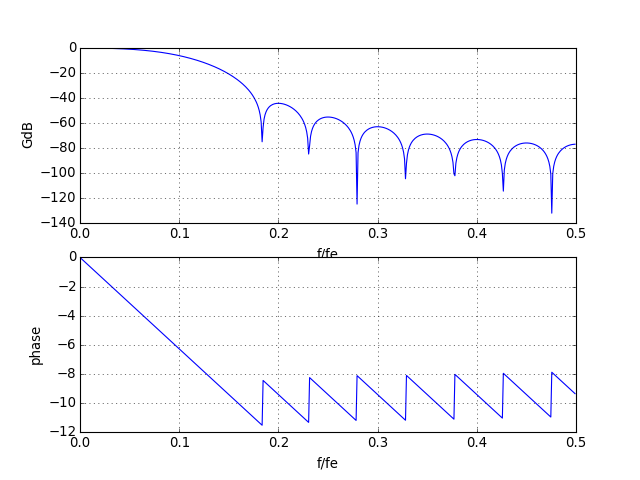
La valeur absolue maximale des coefficients est 0,2. Voici la réponse fréquentielle :

w,h=scipy.signal.freqz(b)
figure()
subplot(211)
plot(w/(2*numpy.pi),20*numpy.log10(numpy.absolute(h)))
xlabel("f/fe")
ylabel("GdB")
grid()
subplot(212)      
plot(w/(2*numpy.pi),numpy.unwrap(numpy.angle(h)))
xlabel("f/fe")
ylabel("phase")
grid()
                   

figB.pdf

La plus grande valeur de s vérifiant la condition $\mathrm{(14)}$ se calcule de la manière suivante :

$$s=E(P-1-\frac{ln\left(max\right)}{ln\left(2\right)})\text{(16)}$$

P=7
max = numpy.max(numpy.absolute(b))
s = numpy.floor(P-1-numpy.log(max)/numpy.log(2))
                    

print(s)
--> 8.0

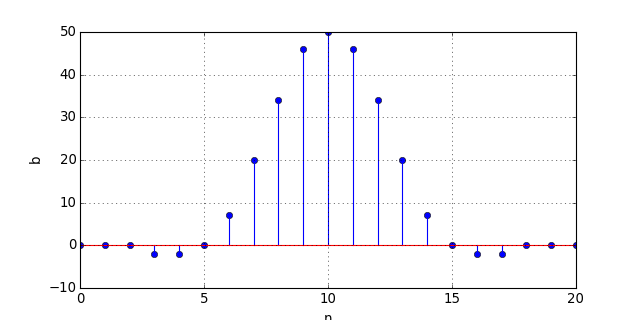
Dans ce cas, on a P=7 bits utilisés pour la partie fractionnaire des coefficients. Calculons les coefficients entiers :

b_int16 = numpy.array(b*2**s,dtype=numpy.int16)
figure(figsize=(8,4))
stem(b_int16)
xlabel("n")
ylabel("b")
grid()

                     

figC.pdf

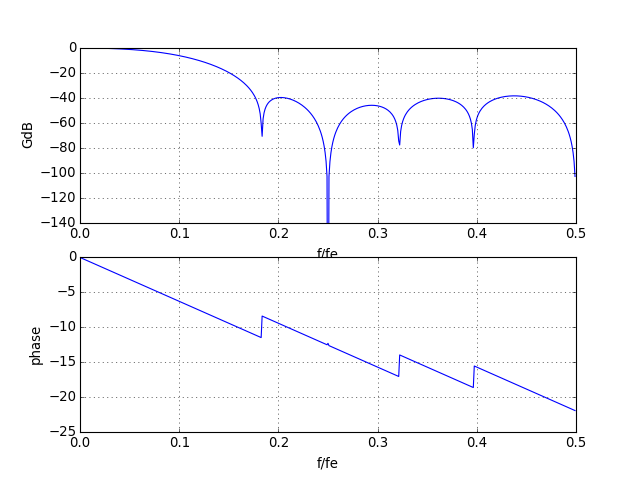
Pour tracer la réponse fréquentielle, on convertit ces entiers en flottants avant de les diviser par 2^s :

w,h=scipy.signal.freqz(numpy.array(b_int16,dtype=numpy.float32)/2**s)
figure()
subplot(211)
plot(w/(2*numpy.pi),20*numpy.log10(numpy.absolute(h)))
xlabel("f/fe")
ylabel("GdB")
axis([0,0.5,-140,0])
grid()
subplot(212)      
plot(w/(2*numpy.pi),numpy.unwrap(numpy.angle(h)))
xlabel("f/fe")
ylabel("phase")
grid()
                     

figD.pdf

Le filtre est moins efficace que le filtre de départ mais le résultat est acceptable. D'autre part, un filtre RIF est toujours stable. Dans le cas d'un filtre récursif, il faudrait aussi vérifier la stabilité après le choix du nombre de bits. On peut donc réaliser un filtre passe-bas avec P=7. Voici les coefficients entiers :

print(b_int16)
--> array([ 0,  0,  0, -2, -2,  0,  7, 20, 34, 46, 50, 46, 34, 20,  7,  0, -2,
       -2,  0,  0,  0], dtype=int16)

On remarque que les trois premiers et les trois derniers coefficients sont nuls, à cause de la limitation à 7 bits. Cela signifie qu'il ne sert à rien d'augmenter le nombre de coefficients du filtre. Dans le cas présent, il faut même enlever ces 6 coefficients nuls. Pour obtenir un filtre plus sélectif que celui-ci, il faut augmenter le nombre de bits P. On peut le faire en réduisant le nombre de bits pour le signal de Q=10 à Q=9 ce qui permet d'avoir P=8. Si cela ne suffit pas, ou si l'on souhaite garder la résolution maximale pour le signal, il faut opérer avec des entiers 32 bits. Sur un microcontrôleur 8 bits, les calculs seront moins rapides qu'en 16 bits. Le choix doit bien sûr être fait en fonction de la fréquence d'échantillonnage et du nombre de coefficients. L'idéal est d'utiliser un microcontrôleur 32 bits, comme celui de l'Arduino Due. Dans ce cas, la condition à respecter est P+Q-1<=32. Avec Q=12 (cas de l'Arduino Due), il reste P=21, ce qui est largement suffisant pour tout type de filtre.

Voyons à présent une implémentation du filtrage en 16 bits. Voici tout d'abord la déclaration des différentes variables et tableaux :

uint8_t nb; // nombre de coefficients b
int16_t b[nb]; // coefficients b
uint8_t na; // nombre de coefficients a
int16_t a[na]; // coefficients a
uint8_t s;
#define TAILLE_TAMPON 0b10000 // supérieure à max(na,nb)
#define MASQUE_TAMPON 0b0001111 // TAILLE_TAMPON-1
int16_t x[TAILLE_TAMPON]; // tampon pour les x_k
int16_t y[TAILLE_TAMPON]; // tampon pour les y_k
uint16_t J; // indice pour les tampons
              

Voici le calcul de la somme. On suppose que le convertisseur A/N fournit la conversion dans l'entier 16 bits entree. La valeur de la sortie est copiée dans sortie, qui peut être envoyée vers un convertisseur N/A, ou subir un autre traitement.

int16_t accum;
uint16_t k,i;
int16_t entree; // x_n
int16_t sortie; // y_n
x[J] = entree;
accum = 0;
i = J;
for (k=0; k<nb; k++) {
    accum += x[i]*b[k];
    i = (i-1)&MASQUE_TAMPON;
}
i = J-1;
for (k=1; k<na; k++) {
    accum -= y[i]*a[k];
    i = (i-1)&MASQUE_TAMPON;
}
sortie = accum >> s;
y[J] = sortie;
J = (J+1)&MASQUE_TAMPON;
              

4.d. Réalisation directe de type II

On rappelle les relations de récurrence pour cette réalisation :

$$\begin{array}{ccc}\hfill & w_n=x_n-a_1{w}_{n-1}-a_2{w}_{n-2}-\cdots \hfill & \hfill \text{(17)}\\ \hfill & y_n=b_0{w}_n+b_1{w}_{n-1}+b_2{w}_{n-2}+\cdots \hfill & \hfill \text{(18)}\end{array}$$

Nous avons vu plus haut son implémentation avec des flottants, qui fonctionne sans problèmes. Dans certains filtres récursifs, le type II fonctionne mieux que le type I.

L'implémentation avec des entiers est plus difficile car les nombres w_n dépassent en général la gamme de valeurs des échantillons du signal. Il faut donc prendre des précautions pour éviter un débordement de l'accumulateur. Nous optons pour une solution simple consistant à prévoir des bits de sécurité (guard bits) pour éviter le débordement. Pour un accumulateur 16 bits, nous utilisons Q=10 bits pour le signal, ce qui laisse 16+1-10=5 bits pour les coefficients. Il n'y a donc aucune marge pour des bits de sécurité et il faut utiliser un accumulateur 32 bits. Sur un microcontrôleur 8 bits, l'exécution du filtrage sera un peu moins rapide, mais c'est le prix à payer pour utiliser cette forme de filtrage. Dans ce cas, on peut par exemple prévoir 6 bits de sécurité, ce qui laisse 32+1-10-6=17 bits pour les coefficients, largement suffisant pour éviter les erreurs d'arrondi. On peut même sans problème traiter un signal avec Q=12 bits.

Les coefficients du filtre, l'accumulateur et le tampon pour stocker les w_n doivent être de type int32_t. Voici la déclaration des variables globales :

uint8_t nb; // nombre de coefficients b
int32_t b[nb]; // coefficients b
uint8_t na; // nombre de coefficients a
int32_t a[na]; // coefficients a
uint8_t s;
#define TAILLE_TAMPON 0b10000 // supérieure à max(na,nb)
#define MASQUE_TAMPON 0b0001111 // TAILLE_TAMPON-1
int32_t w[TAILLE_TAMPON]; // tampon pour les w_k
uint16_t J; // indice pour le tampon
                    

Voici l'implémentation du filtrage en 32 bits :

int32_t accum;
uint16_t k,i;
int16_t entree; // x_n
int16_t sortie; // y_n
accum = entree;
i = J-1;
for (k=1; k<na; k++) {
    accum += w[i]*a[k];
    i = (i-1)&MASQUE_TAMPON;
}
w[J] = accum >> s;
i = J;
accum = 0;
for (k=0; k<nb; k++) {
    accum += w[i]*b[k];
    i = (i-1)&MASQUE_TAMPON;
}
J = (J+1)&MASQUE_TAMPON;
sortie = accum >> s;
                    

Voyons un exemple de calcul des coefficients, pour un filtre récursif bi-quadratique :

b,a = scipy.signal.iirfilter(N=2,Wn=[0.1*2],btype="lowpass",ftype="butter")
w,h=scipy.signal.freqz(b)
figure()
subplot(211)
plot(w/(2*numpy.pi),20*numpy.log10(numpy.absolute(h)))
xlabel("f/fe")
ylabel("GdB")
grid()
subplot(212)      
plot(w/(2*numpy.pi),numpy.unwrap(numpy.angle(h)))
xlabel("f/fe")
ylabel("phase")
grid()
                    

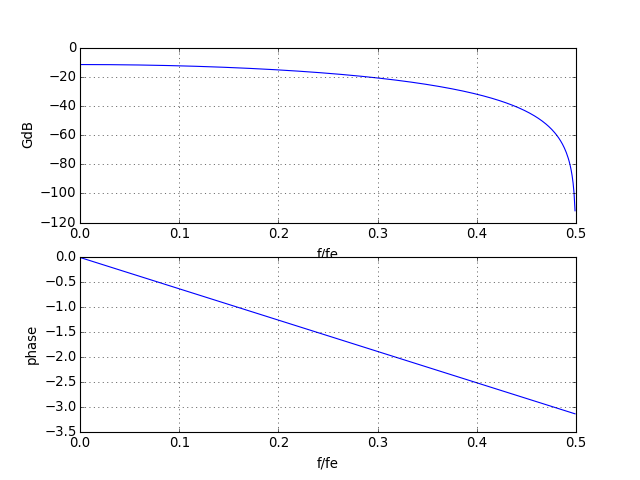figE.pdf

On fixe le nombre de bits de sécurité G et en calcule le décalage s :

Q = 10
G = 6
P = 32+1-Q-G
max_a = numpy.max(numpy.absolute(a))
max_b = numpy.max(numpy.absolute(b))
m = numpy.max(max_a,max_b)
s = numpy.floor(P-1-numpy.log(m)/numpy.log(2))
                    

print(P)
--> 17

print(s)
--> 15.0

Voici les coefficients entiers

a_int32 = numpy.array(a*2**s,dtype=numpy.int32)
b_int32 = numpy.array(b*2**s,dtype=numpy.int32)
                    

print(a_int32)
--> array([ 32768, -37453,  13526])

print(b_int32)
--> array([2210, 4420, 2210])

4.e. Réalisation directe transposée de type II

On rappelle la relation de récurrence de cette réalisation :

$$\begin{array}{ccc}\hfill & y_n=b_0{x}_n+v_1\hfill & \hfill \text{(19)}\\ \hfill & v_1=b_1{x}_n-a_1{y}_n+v_2\hfill & \hfill \text{(20)}\\ \hfill & v_2=b_2{x}_n-a_2{y}_n+v_3\hfill & \hfill \text{(21)}\\ \hfill & v_3=b_3{x}_n-a_3{y}_n\hfill & \hfill \text{(22)}\end{array}$$

Les variables d'état v₁,v₂,v₃, etc sont stockées dans un tableau simple, dont la taille est supérieur au nombre maximal de coefficients a_k ou b_k. Pour une entrée sur Q bits, ces variables d'état peuvent contenir des nombres qui occupent plus que Q bits, bien que le débordement soit moins important que dans la réalisation directe de type II. Il est donc préférable de travailler en 32 bits, bien qu'une implémentation en 16 bits fonctionne aussi pour Q=8. Les variables d'état sont alors du type int32_t. Il faudra penser à annuler les coefficients inutilisés.

uint8_t max_na_nb;
int32_t b[max_na_nb]; // coefficients b
int32_t a[max_na_nb]; // coefficients a
uint_t s;
int32_t v[max_na_nb]; // tampon pour les v_k
                  

int16_t i,k;
int16_t entree; // x_n
int16_t sortie; // y_n
sortie = (b[0]*entree+v[1]) >> s;
i = 1;
for (k=0; k<max_na_nb; k++) {
    v[i] = entree*b[k]-sortie*a[k]+v[i+1];
    i++;
}