Conception et mise en œuvre des filtres numériques
1. Introduction
Ce document explique comment concevoir des filtres numériques avec le module scipy.signal et tracer leur réponse fréquentielle. On verra différentes manières de réaliser le filtrage numérique, que l'on appliquera sur des signaux stockés en mémoire. Le filtrage sera réalisé soit avec des fonctions écrites en python, soit en utilisant les fonctions scipy.signal.convolve et scipy.signal.lfilter.
2. Généralités
2.a. Relation de récurrence
On considère un signal numérique xn, obtenu avec une période d'échantillonnage Te.
Le filtrage numérique linéaire consiste à obtenir un nouveau signal numérique yn en utilisant une relation de récurrence de la forme suivante :
Les coefficients an et bn sont réels. D'une manière générale, un échantillon de la sortie est obtenu en faisant une combinaison linéaire des N échantillons précédents de l'entrée et des M-1 échantillons précédents de la sortie.
Considérons par exemple le filtre à 5 coefficients suivant :
Il peut être représenté sous la forme d'un schéma bloc :
Figure pleine page2.b. Réponse fréquentielle
Lors de l'étude d'un filtre numérique, on est amené à rechercher comment le filtre répond à une entrée sinusoïdale, c'est-à-dire à un signal sinusoïdal échantillonné à la période Te. Un tel signal a la forme suivante :
où l'on a introduit la variable complexe :
Le décalage d'une unité dans le temps s'écrit :
Sur le schéma bloc, ce décalage est donc représenté par l'opérateur z-1.
Reprenons l'exemple précédent et écrivons la récurrence sous la forme :
Le terme de droite, combinaison linéaire des entrées, s'écrit pour une entrée sinusoïdale :
Si l'on admet que la sortie est sinusoïdale (en régime stationnaire), on peut l'écrire sous la forme :
H(z) est par définition la fonction de transfert en z du filtre. En reportant l'expression de yn dans la relation de récurrence, on obtient l'expression de la fonction de transfert en fonction des coefficients du filtre :
Pour obtenir la réponse fréquentielle du filtre, c'est-à-dire le gain et le déphasage en fonction de la fréquence, il suffit de remplacer z par l'expression .
On voit que cette réponse fréquentielle est une fonction du rapport de la fréquence par la fréquence d'échantillonnage.
2.c. Réponse impulsionnelle et stabilité
Une impulsion est un signal numérique défini par :
La réponse impulsionnelle est la sortie yn obtenue pour cette entrée.
La réponse impulsionnelle est dite finie si le nombre d'échantillons non nuls est fini. Un filtre est stable si la réponse impulsionnelle tend vers zéro lorsque n tend vers l'infini. Un filtre à réponse impulsionnele finie (RIF) est donc toujours stable.
Pour étudier la stabilité d'un filtre, il faut déterminer les pôles de sa fonction de transfert en Z, c'est-à-dire les racines de son dénominateur. Un filtre à réponse impulsionnelle infinie (RII) est stable si et seulement si tous les pôles de sa fonction de transfert ont un module strictement inférieur à 1. Lorsqu'un filtre RII est stable, sa réponse impulsionnelle décroît de manière exponentielle avec n, si bien qu'elle peut être en pratique considérée comme finie.
Un filtre RII instable a une réponse impulsionnelle qui présente soit un comportement oscillatoire, soit une divergence vers l'infini.
3. Conception d'un filtre
3.a. Filtre à réponse impulsionnelle finie
Lorsque les coefficients an sont tous nuls, la sortie s'exprime comme une combinaison linéaire des échantillons de l'entrée :
L'opération ainsi réalisée est un produit de convolution, c'est pourquoi on parle dans ce cas de filtrage par convolution. Ce type de filtrage est aussi employé en traitement d'image.
La réponse impulsionnelle est :
Autrement dit, les coefficients bn constituent la réponse impulsionnelle du filtre. Cette réponse impulsionnelle est dite finie car le nombre d'échantillons non nuls en sortie est fini, égal au nombre de coefficients bn non nuls.
Le type le plus répandu de filtre à réponse impulsionnelle finie (filtre RIF) est le filtre RIF à phase linéaire, dont les coefficients sont obtenus par série de Fourier. Voir le document Filtres à réponse impulsionnelle finie pour une explication détaillée de cette méthode. On se contente ici de montrer comment calculer un tel filtre avec la fonction scipy.signal.firwin.
import numpy
import scipy.signal
from matplotlib.pyplot import *
Pour définir un filtre passe-bas, on procède de la manière suivante :
P=20
b1 = scipy.signal.firwin(numtaps=2*P+1,cutoff=[0.1],window='hann',nyq=0.5)
numptaps est le nombre de coefficients du filtre. On définit un nombre impair, pour faciliter la suite de l'étude. cutoff est une liste de fréquences de coupure (une seule pour un passe-bas). Ces fréquences sont relatives à la fréquence d'échantillonnage. La fréquence de Nyquist est donc 0.5, ce qui est précisé par l'argument nyq (la valeur par défaut est 1). Enfin l'argument window permet de choisir une fenêtre multiplicative pour les coefficients. Par exemple, une fenêtre de Hanning permet de réduire les ondulations dans la bande passante, qui seraient trop importantes avec une fenêtre rectangulaire.
Il est intéressant de tracer la réponse impulsionnelle :
figure(figsize=(10,5))
stem(b1)
xlabel("n")
ylabel("b")
grid()
Figure pleine pageIl s'agit d'une fonction sinus cardinal dont le maximum est à l'indice P. Lors du calcul de yn, ce maximum est centré sur xn-P. On peut donc s'attendre à un décalage PTe entre l'entrée et la sortie.
La réponse fréquentielle peut être obtenue avec la fonction freqz :
w,h=scipy.signal.freqz(b1)
figure()
subplot(211)
plot(w/(2*numpy.pi),20*numpy.log10(numpy.absolute(h)))
xlabel("f/fe")
ylabel("GdB")
grid()
subplot(212)
plot(w/(2*numpy.pi),numpy.unwrap(numpy.angle(h)))
xlabel("f/fe")
ylabel("phase")
grid()
Figure pleine pageLes filtres RIF peuvent être très sélectifs lorsque le nombre de coefficients est élevé. Par ailleurs la phase est parfaitement linéaire par rapport à la fréquence dans la bande passante. Les signaux dont le spectre est dans la bande passante sont donc transmis sans distorsion, avec un décalage constant, égal ici à PTe.
Pour définir un filtre passe-bande ou passe-bas, il faut donner la valeur False à l'argument pass_zero. Voici par exemple un filtre RIF passe-bande :
P=20
b2 = scipy.signal.firwin(numtaps=2*P+1,cutoff=[0.1,0.3],pass_zero=False,window='hann',nyq=0.5)
w,h=scipy.signal.freqz(b2)
figure()
subplot(211)
plot(w/(2*numpy.pi),20*numpy.log10(numpy.absolute(h)))
xlabel("f/fe")
ylabel("GdB")
grid()
subplot(212)
plot(w/(2*numpy.pi),numpy.unwrap(numpy.angle(h)))
xlabel("f/fe")
ylabel("phase")
grid()
Figure pleine page3.b. Filtre à réponse impulsionnelle infinie
Lorsque les coefficients an sont non nuls, on parle de filtre récursif :
La réponse impulsionnelle d'un tel filtre est infinie, c'est-à-dire qu'elle comporte un nombre infini d'échantillons non nuls (du moins en théorie). Il peut arriver que le filtre soit instable, c'est-à-dire que sa réponse impulsionnelle ne tende pas vers zéro.
Une méthode de calcul de ce type de filtre consiste à partir de la fonction de transfert d'un filtre analogique et à effectuer une transformation bilinéaire pour obtenir la fonction de transfert en z, d'où l'on déduit les coefficients an et bn. Cette méthode est expliquée en détail dans le document Filtre à réponse impulsionnelle infinie.
La fonction scipy.signal.iitfilter permet d'obtenir un filtre RII à partir de fonctions de transfert analogiques standard (Butterworth, Chebychev, etc). Voici par exemple comment obtenir un filtre passe-bas d'ordre 2 avec une fréquence de coupure fc/fe=0.1 :
b3,a3 = scipy.signal.iirfilter(N=2,Wn=[0.1*2],btype="lowpass",ftype="butter")
print(a3) --> array([ 1. , -1.1429805, 0.4128016])
print(b3) --> array([ 0.06745527, 0.13491055, 0.06745527])
La fréquence de coupure relative a été multipliée par deux, car la fréquence de Nyquist est par convention égale à 1.
Ce filtre comporte 3 coefficients bn et 3 coefficients an (en comptant a0=1). Voici sa réponse fréquentielle :
w,h=scipy.signal.freqz(b3,a3)
figure()
subplot(211)
plot(w/(2*numpy.pi),20*numpy.log10(numpy.absolute(h)))
xlabel("f/fe")
ylabel("GdB")
grid()
subplot(212)
plot(w/(2*numpy.pi),numpy.unwrap(numpy.angle(h)))
xlabel("f/fe")
ylabel("phase")
grid()
Figure pleine pageLes filtres RII ont l'avantage de comporter peu de coefficients, d'introduire un faible déphasage (à peu près linéaire dans la bande passante), et d'être très proches des filtres analogiques. En revanche, ils ne permettent pas d'obtenir la très forte sélectivité des filtres RIF, car les filtres RII d'ordre élevé sont instables. À nombre de coefficients identique, ils sont toutefois plus efficaces que les filtres RIF. Les filtres RII sont très utilisés en traitement du son.
L'inconvénient des filtres RII est la possibilité d'obtenir un filtre instable lorsque l'ordre est élevé (à partir de l'ordre 6 environ). Pour savoir si un filtre est stable, il faut calculer ses pôles :
(zeros,poles,gain) = scipy.signal.tf2zpk(b3,a3)
et vérifier que leur module est strictement inférieur à 1 :
print(numpy.absolute(poles)) --> array([ 0.64249638, 0.64249638])
4. Réalisation du filtrage
4.a. Introduction
Le filtrage consiste à appliquer la relation de récurrence pour calculer chaque échantillon du signal de sortie.
L'implémentation du filtrage en temps réel, sur un processeur de signal (DSP) ou sur microcontrôleur, pose des problèmes spécifiques liés aux ressources disponibles sur ce type d'unité (quantité de mémoire, vitesse de calcul, calculs en virgule flottante, etc).
On s'intéresse ici au filtrage réalisé en Python, sur un signal entièrement disponible en mémoire, sous forme d'un tableau d'échantillons. On montrera l'effet de différents filtres sur un signal obtenu par numérisation à la fréquence d'échantillonnage fe=10 kHz d'un signal périodique comportant 3 harmoniques. 5000 échantillons ont été acquis. La fréquence du fondamental est f=400,3000 Hz. Le signal a été stocké dans un fichier texte. On commence donc par récupérer les échantillons, avec les instants correspondant :
[t,x] = numpy.loadtxt("signal-400.3.txt")
figure(figsize=(8,5))
plot(t,x)
axis([0,0.02,-2,2])
xlabel("t (s)")
ylabel("x (V)")
grid()
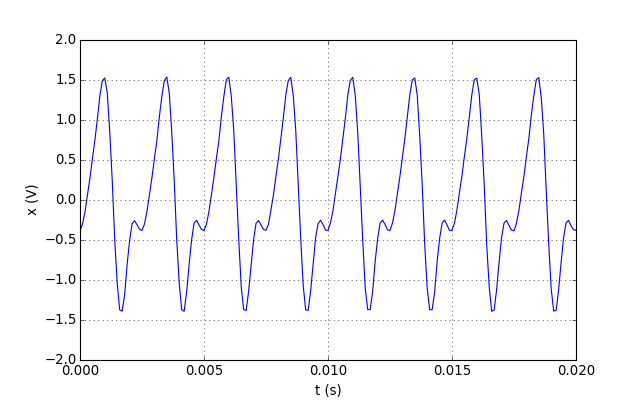 figF.pdf
figF.pdf
4.b. Réalisation d'un filtrage RIF par convolution
L'opération à réaliser sur le signal est un produit de convolution :
Le nombre de coefficients N=2P+1 a été défini par numtaps dans la fonction firwin. On remarque que les 2P premières valeurs de yn ne peuvent pas être calculées avec cette somme. Il y deux manières de procéder pour ces 2P premiers échantillons : soit on les calcule en utilisant une partie des coefficients, soit on ne les filtre pas et on annule la sortie. Nous allons adopter la seconde solution, plus facile à implémenter. Voici une fonction réalisant le filtrage :
def filtrage_convolution(x,b):
N = len(b)
ne = len(x)
y = numpy.zeros(ne)
for n in range(N-1,ne):
accum = 0.0
for k in range(N):
accum += b[k]*x[n-k]
y[n] = accum
return y
On utilise le filtre RIF passe-bas défini plus haut, puis on trace le signal de départ avec le signal filtré :
y = filtrage_convolution(x,b1)
figure(figsize=(8,6))
subplot(211)
plot(t,x)
axis([0,0.02,-2,2])
xlabel("t (s)")
ylabel("x(V)")
grid()
subplot(212)
plot(t,y)
axis([0,0.02,-2,2])
xlabel("t (s)")
ylabel("y(V)")
grid()
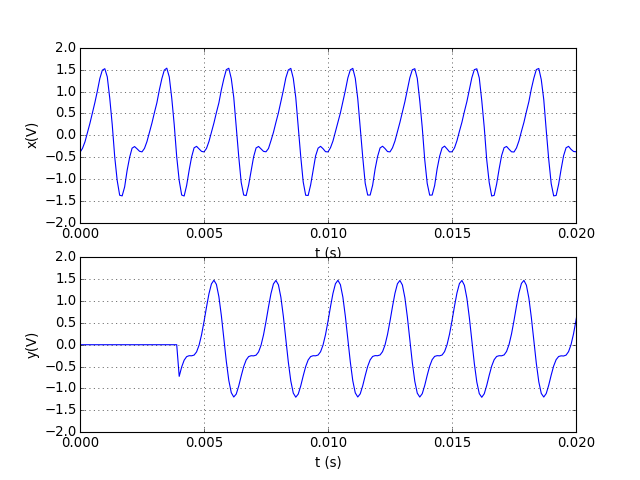 figG1.pdf
figG1.pdf
Le filtre passe-bas a une fréquence de coupure de 1 kHz. L'harmonique de rang 3 (fréquence 1200 Hz) est donc légèrement réduite, mais l'essentiel du signal se trouve dans la bande passante. On constate qu'il y a un décalage entre la sortie et l'entrée. C'est une conséquence de la variation linéaire du déphasage avec la fréquence dans la bande passante. Pour ce type de filtre RIF, le décalage est τ=PTe, ici égal à 20 ms.
La fonction utilisée ci-dessus est lente car la boucle est écrite en python. Le temps de calcul est proportionnel au nombre d'échantillons multiplié par le nombre de coefficients du filtre. Pour traiter rapidement des grandes listes d'échantillons, il est préférable d'utiliser la fonction scipy.signal.convolve, de la manière suivante :
y = scipy.signal.convolve(x,b1,mode='same')
Le mode same permet d'obtenir une sortie de même taille que l'entrée.
figure(figsize=(8,6))
subplot(211)
plot(t,x)
axis([0,0.02,-2,2])
xlabel("t (s)")
ylabel("x(V)")
grid()
subplot(212)
plot(t,y)
axis([0,0.02,-2,2])
xlabel("t (s)")
ylabel("y(V)")
grid()
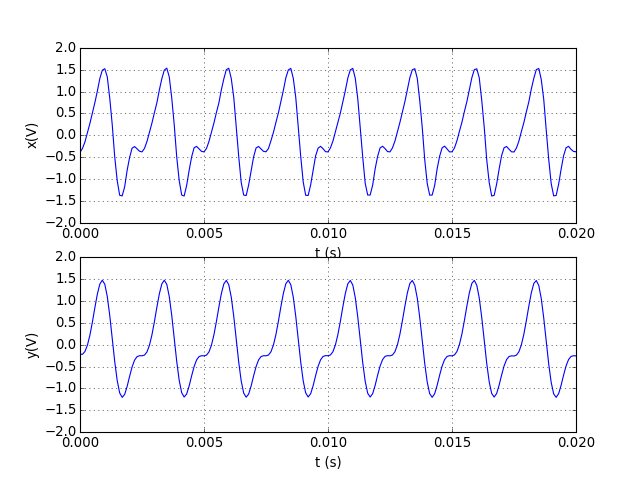 figG2.pdf
figG2.pdf
Le signal de sortie n'est pas décalé par rapport au signal d'entrée. Cela est du au fait que la convolution appliquée est en fait centrée. Si N=2P+1 est le nombre de coefficients, la relation utilisée est :
Pour les P premiers et les P derniers points, une partie de la somme est calculée.
Ce mode de calcul de la convolution, appelé convolution centrée, convient bien au filtrage des images, où l'on veut que chaque pixel filtré coïncide avec le pixel d'origine, mais il ne correspond pas à la réalité du filtrage numérique en temps-réel, où les échantillons du futur ne sont évidemment pas disponibles lorsqu'on calcule yn.
Si l'on souhaite utiliser la fonction convolve et reproduire le décalage, on peut utiliser le mode valid, qui permet de limiter le calcul de la convolution aux points valides, c'est-à-dire à tous les points sauf les P premiers et les P derniers. Il faut aussi construire une nouvelle échelle de temps pour tracer la sortie, en remarquant que le premier point calculé est en fait celui d'indice 2P.
y = scipy.signal.convolve(x,b1,mode='valid')
Te = t[1]-t[0]
ty = (numpy.arange(y.size)+2*P)*Te
figure(figsize=(8,4))
plot(t,x,'b')
plot(ty,y,'r')
axis([0,0.02,-2,2])
xlabel("t (s)")
ylabel("y(V)")
grid()
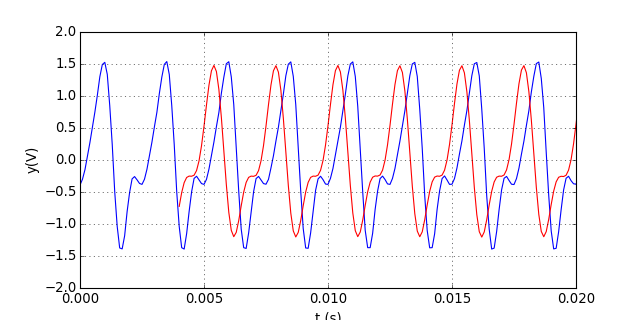 figG3.pdf
figG3.pdf
On obtient ainsi la sortie avec le décalage qu'elle aurait dans un filtre temps-réel. Le retard de la sortie est ici de 2 ms.
4.c. Réalisations d'un filtrage récursif
Forme directe de type I
Dans le but d'appliquer un filtre récursif (à réponse impulsionnelle infinie), on s'intéresse à présent à l'application de la relation générale :
Une première manière de procéder est d'appliquer directement cette relation de récurrence pour calculer les valeurs yn. Ce mode de calcul est appelé réalisation directe de type I. Le démarrage du filtre nécessite la donnée de condition initiales (on introduit des indices négatifs, de manière à démarrer à n=0) :
Le plus souvent, on peut prendre des valeurs initiales nulles.
Pour calculer yn, il faut avoir en mémoire les N-1 valeurs précédentes de l'entrée et les M-1 valeurs précédentes de la sortie. Cela ne pose pas de problème dans une implémentation en python, mais peut compliquer notablement une implémentation sur processeur, en particulier si la mémoire disponible est très faible.
Voici le schéma bloc de cette réalisation pour un filtre comportant 3 coefficients bn et 2 coefficients an :
Figure pleine pageForme directe de type II
La réalisation directe de type II repose sur la factorisation suivante de la fonction de transfert en z :
Cette réalisation nécessite l'introduction d'un signal intermédiaire wn. On obtient ainsi deux relations de récurrence :
Seule la première de ces relations est récursive. Les valeurs initiales de wn doivent être définies, et sont le plus souvent choisies nulles.
On voit que cette méthode ne nécessite aucune mémorisation des échantillons de l'entrée et de la sortie. Le signal wn contient un nombre d'échantillons égal à max(M,N). Les deux réalisations directes (types I et II) sont équivalentes en régime permanent, mais leur comportement au démarrage peut être assez différent. L'expérience montre que la réalisation de type II a un comportement transitoire meilleur que la première sur certains filtres récursifs, par exemple les filtres intégrateurs. La différence entre ces deux réalisations se manifeste surtout lorsqu'on implémente le filtrage avec des nombres entiers (sur les DSP ne calculant pas en virgule flottante).
La figure suivante montre le schéma bloc d'une réalisation directe de type II, pour un filtre récursif comportant 3 coefficients bn et 2 coefficients an (sans compter a0=1) :
Figure pleine pagePour faire le calcul, on doit mémoriser wn-2 et wn-1. On dit que cette réalisation nécessite deux variables d'état. D'une manière générale, le nombre de variables d'état est égal au nombre de bloc z-1. Pour la réalisation directe de type I de ce filtre, il y a quatre variables d'état.
Voici une fonction qui réalise ce filtrage :
def filtrage(b,a,x):
N = len(b)
M = len(a)
y = x.copy()
Nw = max(N,M)
w = numpy.zeros(Nw)
p = 0
for n in range(x.size):
accum = x[n]
for k in range(1,M):
accum -= a[k]*w[p-k]
w[p] = accum
accum = 0.0
for k in range(N):
accum += b[k]*w[p-k]
y[n] = accum
p = (p+1)%Nw
return y
Cette fonction écrite en python permet de comprendre l'implémentation du filtrage récursif, mais son exécution est relativement lente. Pour un filtrage rapide, il est préférable d'utiliser la fonction scipy.signal.lfilter décrite plus loin.
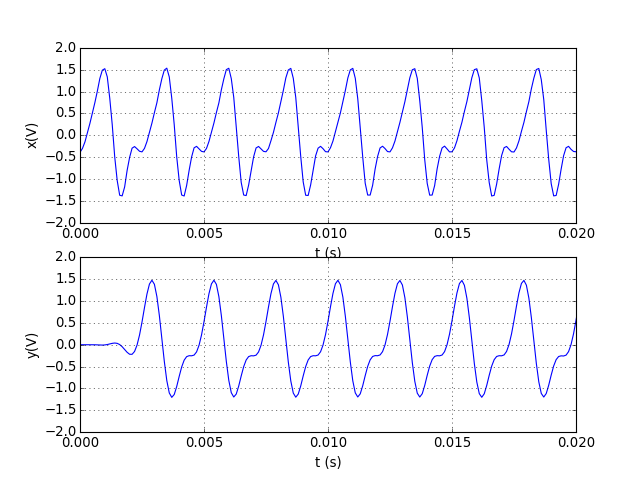
On teste tout d'abord cette fonction avec le filtre RIF considéré plus haut :
y = filtrage(b1,[],x)
figure(figsize=(8,6))
subplot(211)
plot(t,x)
axis([0,0.02,-2,2])
xlabel("t (s)")
ylabel("x(V)")
grid()
subplot(212)
plot(t,y)
axis([0,0.02,-2,2])
xlabel("t (s)")
ylabel("y(V)")
grid()
 figI.pdf
figI.pdf
La sortie est décalée par rapport à l'entrée, conformément au déphasage linéaire obtenu lors de l'étude de la réponse fréquentielle. On voit que le filtrage commence plut tôt que pour la méthode de convolution directe.
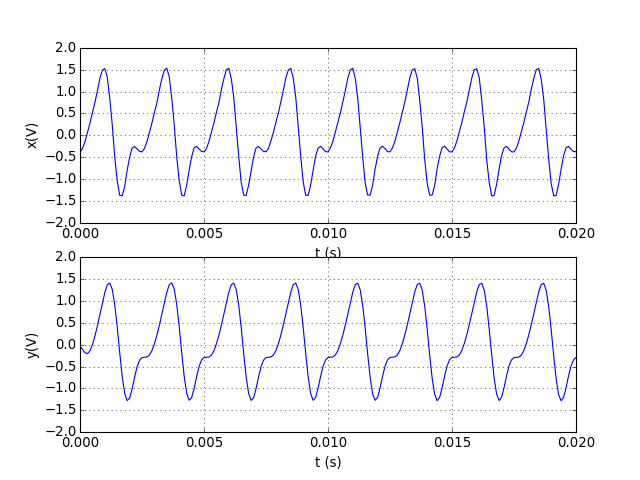
Appliquons à présent le filtre RII passe-bas du second ordre calculé plus haut :
y = filtrage(b3,a3,x)
figure(figsize=(8,6))
subplot(211)
plot(t,x)
axis([0,0.02,-2,2])
xlabel("t (s)")
ylabel("x(V)")
grid()
subplot(212)
plot(t,y)
axis([0,0.02,-2,2])
xlabel("t (s)")
ylabel("y(V)")
grid()
 figJ.pdf
figJ.pdf
Forme directe transposée de type II
Voici le schéma bloc de la forme directe transposée de type II pour le filtre récursif à cinq coefficients :
Figure pleine pageCette forme nécessite deux variables d'état v1 et v2. Voici les relations de récurrence, à appliquer dans cet ordre :
La première affectation utilise la valeur de v1 calculée à l'itération précédente. La deuxième affectation utilise la valeur de v2 calculée à l'itération précédente.
La fonction scipy.signal.lfilter réalise la forme directe transposée de type II. Elle s'utilise de la manière suivante :
zi = scipy.signal.lfiltic(b3,a3,y=[0,0],x=[0,0]) # condition initiale
[y,zf] = scipy.signal.lfilter(b3,a3,x,zi=zi)
Le vecteur d'état zi contient les variables d'état du filtre. La fonction lfiltic permet de déterminer le vecteur d'état à partir d'une condition initiale. La fonction lfilter renvoit le signal de sortie et le vecteur d'état. Cela permer d'appliquer la fonction de filtrage sur des blocs de signal consécutifs.
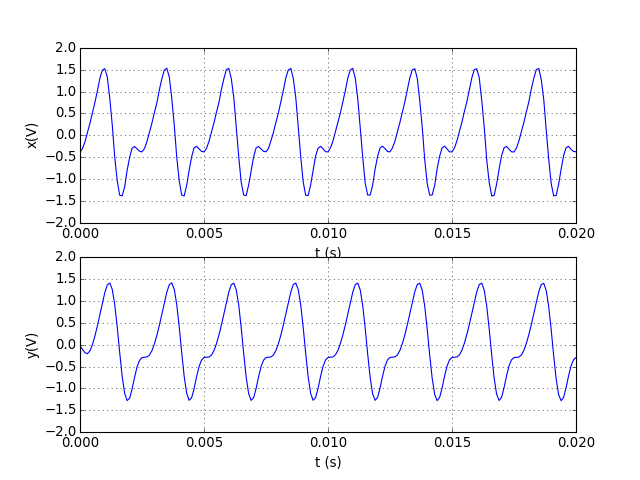
Voici le résultat du filtrage :
figure(figsize=(8,6))
subplot(211)
plot(t,x)
axis([0,0.02,-2,2])
xlabel("t (s)")
ylabel("x(V)")
grid()
subplot(212)
plot(t,y)
axis([0,0.02,-2,2])
xlabel("t (s)")
ylabel("y(V)")
grid()
 figK.pdf
figK.pdf
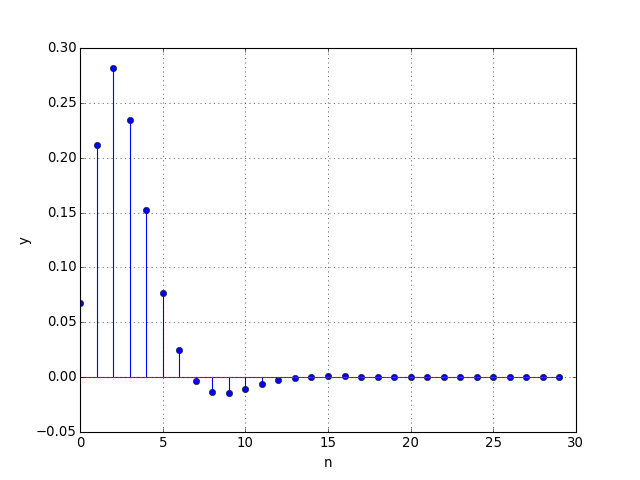
On peut aussi calculer la réponse impulsionnelle du filtre :
x = numpy.zeros(30)
x[0] = 1.0
zi = scipy.signal.lfiltic(b3,a3,y=[0,0],x=[0,0])
[y,zf] = scipy.signal.lfilter(b3,a3,x,zi=zi)
figure()
stem(y)
xlabel("n")
ylabel("y")
grid()
 figL.pdf
figL.pdf
Pour ce filtre passe-bas récursif, la réponse impulsionnelle est en théorie infinie. Cependant, la décroissance exponentielle de la réponse impulsionnelle fait qu'on peut en pratique considérer que la réponse impulsionnelle est finie.