Réseau de fentes : mesures de longeurs d'onde.

1. Introduction

L'objectif est d'utiliser un réseau de fentes pour faire des mesures de longueurs d'onde.

Matériel

• Goniomètre
• Réseau 300 traits/mm.
• Lampe Hg.
• Miroir plan.
• Bloc de verre à faces parallèles.

2. Rappels théoriques

Le réseau est constitué de traits équidistants. Si n est le nombre de traits par millimètres, la période du réseau est a=1/n (en millimètres). Il est éclairé par la lumière sortant d'un collimateur. Les interférences sont observées à l'infini au moyen d'une lunette.

Figure pleine page

On note i l'angle des rayons incidents par rapport à la normale au réseau. L'angle de diffraction par rapport à la normale pour l'interférence constructive d'ordre p est noté α_p. L'angle de cette interférence constructive par rapport à l'ordre 0 est noté β_p. L'angle β_p est aussi l'angle de déviation.

Figure pleine page

[1] Faire un schéma avec le tracé des rayons permettant de calculer la différence de marche pour deux fentes espacées de a.

[2] Déterminer l'expression de la différence de marche δ en fonction de i, a et l'angle α des rayons diffractés.

[3] En déduire la relation entre i, α_p, a, l'ordre d'interférence p et la longueur d'onde λ.

[4] Exprimer l'angle de déviation β_p en fonction de α_p et de i.

[5] Soit Δ_p l'angle entre la raie d'ordre p et la raie d'ordre -p. Dans le cas de l'incidence normale (i=0), montrer que :

$$sin\left(\frac{{\Delta }_p}{2}\right)=p\frac{\lambda }{a}\text{(1)}$$

[6] En déduire une méthode de mesure de λ (méthode 1).

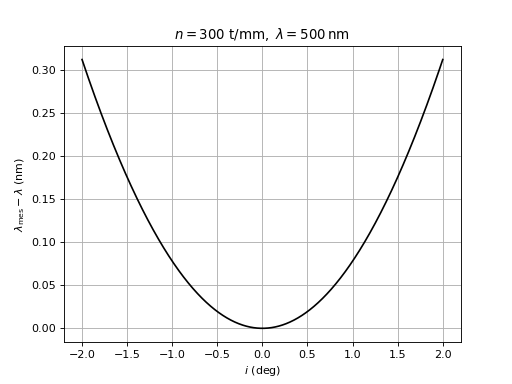
[7] La courbe suivante montre l'écart entre la longueur d'onde mesurée par la méthode 1 et la longueur d'onde réelle en fonction de l'angle d'incidence (courbe simulée pour un réseau de 300 traits par mm, voir annexe). Commenter cette courbe. Pour un angle d'incidence de 1 degré, calculer la valeur de Δ₁/2. Quel est l'intérêt de mesurer Δ_p et non pas simplement β_p ?

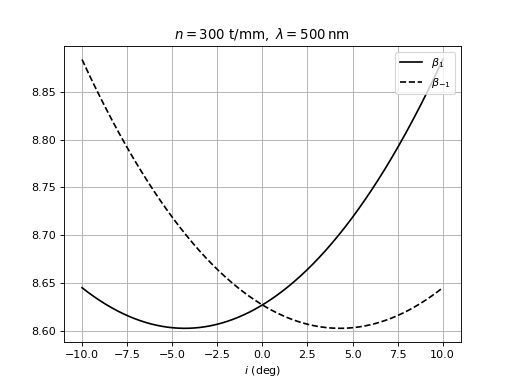
La courbe suivante montre les angles de déviation β₁ et β_-1 en fonction de l'angle d'incidence. Elle met en évidence l'existence d'un angle d'incidence qui réalise un minimum de la déviation.

[8] Montrer que pour l'angle d'incidence qui minimise la déviation β_p, on a α_p=-i. En déduire que pour ce minimum on a :

$$2sin\left(\frac{{\beta }_p}{2}\right)=p\frac{\lambda }{a}\text{(2)}$$

La méthode de mesure de λ par le minimum de déviation (méthode 2) consiste à faire tourner le réseau jusqu'à obtenir le minimum de déviation pour la raie étudiée et à mesurer la déviation correspondante β_p. La relation $\mathrm{(2)}$ permet de calculer λ.

3. Mesures de longueurs d'onde

4. Annexe : simulation

import numpy as np
from matplotlib.pyplot import *

L = 500 # longueur d'onde (nm)
n = 300 # nombre de traits par mm
a = 1/n
i = np.linspace(-2,2,1000) # angle d'incidence en degrés
alpha_1 = np.arcsin(L*1e-6/a+np.sin(i*np.pi/180))*180/np.pi
alpha_m1 = np.arcsin(-L*1e-6/a+np.sin(i*np.pi/180))*180/np.pi
Lmesuree = a*1e6*np.sin((alpha_1-alpha_m1)/2*np.pi/180)
figure()
plot(i,Lmesuree-L,'k-')
xlabel(r"$i\ (\rm deg)$")
ylabel(r"$\lambda_{\rm mes}-\lambda\ (\rm nm)$")
title(r"$n=%d\ {\rm t/mm},\ \lambda=%d\,\rm nm$"%(n,L))
grid()
            

ecartLongueurOnde.pdf

i = np.linspace(-10,10,1000) # angle d'incidence en degrés
alpha_1 = np.arcsin(L*1e-6/a+np.sin(i*np.pi/180))*180/np.pi
alpha_m1 = np.arcsin(-L*1e-6/a+np.sin(i*np.pi/180))*180/np.pi          
beta_1 = alpha_1 - i
beta_m1 = alpha_m1-i
figure()
plot(i,beta_1,'k-',label=r"$\beta_1$")
plot(i,-beta_m1,'k--',label=r"$\beta_{-1}$")
xlabel(r"$i\ (\rm deg)$")
legend(loc='upper right')
title(r"$n=%d\ {\rm t/mm},\ \lambda=%d\,\rm nm$"%(n,L))
grid()
            

deviation.pdf

i = np.linspace(-20,20,1000) # angle d'incidence en degrés
alpha_2 = np.arcsin(2*L*1e-6/a+np.sin(i*np.pi/180))*180/np.pi
alpha_m2 = np.arcsin(-2*L*1e-6/a+np.sin(i*np.pi/180))*180/np.pi
beta_2 = alpha_2 - i
beta_m2 = alpha_m2-i
figure()
plot(i,beta_2,'k-',label=r"$\beta_2$")
plot(i,-beta_m2,'k--',label=r"$\beta_{-2}$")
xlabel(r"$i\ (\rm deg)$")
legend(loc='upper right')
title(r"$n=%d\ {\rm t/mm},\ \lambda=%d\,\rm nm$"%(n,L))
grid()
            

deviation2.pdf

5. Annexe : calcul d'incertitudes

On rappelle le principe du calcul des incertitudes par une simulation de Monte-Carlo.

Soit X une grandeur dont une mesure donne une valeur X₀ avec une incertitude ΔX. On simule un ensemble de N mesures en supposant que les valeurs sont réparties selon une loi de probabilité normale d'espérance X₀ et d'écart-type ΔX :

from numpy.random import normal
import numpy as np

X_rand = normal(X0,DeltaX,N)
             

Soit Y une grandeur calculée à partir de la grandeur mesurée au moyen d'une fonction :

Y_rand = calculY(X_rand)
             

La valeur de Y est la moyenne arithmérique des valeurs aléatoires :

Y0 = Y_rand.mean()
             

L'incertitude de Y est l'écart-type empirique :

DeltaY = Y_rand.std()
             

Dans le cas où un ajustement affine sur des données expérimentales conduit à des coefficients a et b, il faut déterminer les incertitudes Δa et Δb. Il faut pour cela faire N fois l'ajustement affine avec à chaque fois un jeu de données aléatoires obtenues à partir des valeurs expérimentales et de la loi normale (d'espérance la valeur expérimentale et d'écart-type l'incertitude). On obtient ainsi deux tableaux a_rand et b_rand contenant les coefficients de ces N ajustements affines. Les incertitudes Δa et Δb s'en déduisent par le calcul des écart-types.