Production d'entropie dans la diffusion thermique

1.a. Production d'entropie locale

On considère la conduction thermique dans un solide, en se limitant au cas d'un système à une dimension rectiligne. On suppose que le seul processus irréversible ayant lieu est la conduction (ou diffusion) thermique. L'équation de diffusion thermique est dans ce cas :

$$\frac{\partial T}{\partial t}=D\frac{{\partial }^{2}T}{\partial x^2}$$

Le coefficient de diffusion thermique est

$$D=\frac{\lambda }{\rho c}$$

Le bilan d'entropie local repose sur l'hypothèse d'équilibre thermodynamique local. Si u(x,t) et s(x,t) désignent respectivement l'énergie interne et l'entropie volumiques, la relation suivante valable à l'équilibre est appliquée localement :

$$du=Tds-Pdv$$

Dans le cas d'un solide, on néglige la variation de volume. On obtient donc :

$$\frac{\partial u}{\partial t}=T\frac{\partial s}{\partial t}$$

En utilisant l'équation locale de conservation de l'énergie, on obtient :

$$T\frac{\partial s}{\partial t}=-\frac{\partial j}{\partial x}$$

Effectuons à présent un bilan d'entropie pour le volume compris entre x et x+dx (section d'aire A), entre les instants t et t+dt.

$$\frac{\partial s}{\partial t}Adxdt=\frac{j\left(x\right)}{T\left(x\right)}Adt-\frac{j(x+dx)}{T(x+dx)}Adt+{\sigma }_{s}Adxdt$$

Les deux premiers termes de droite sont les entropies échangées respectivement à la frontière x et x+dx. Le troisième terme est la production d'entropie.

On obtient ainsi la forme locale du second principe :

$$\frac{\partial s}{\partial t}=-\frac{\partial }{\partial x}\left(\frac{j}{T}\right)+{\sigma }_s$$

avec un taux volumique de production d'entropie positif, ou nul à l'équilibre :

$${\sigma }_s\ge 0$$

En associant ce résultat à l'équation obtenue plus haut, on obtient :

$${\sigma }_s=j\frac{\partial }{\partial x}\left(\frac{1}{T}\right)$$

Le taux de production d'entropie s'exprime ainsi comme le produit d'un flux par la force thermodynamique correspondante.

Avec la loi de Fourier, le taux volumique de production d'entropie s'écrit :

$${\sigma }_s=\frac{\lambda }{T^2}(\frac{\partial T}{\partial x}{)}^2$$

1.b. Bilan d'entropie intégré sur le temps

Le transfert thermique (par unité de surface) sur un plan d'abscisse x entre l'instant 0 et l'instant t s'écrit :

$$Q\left(t\right)={\int }_0^t-\lambda \frac{\partial T}{\partial x}dt$$

L'entropie échangée (par unité de surface) sur cette surface est

$$S^e\left(t\right)={\int }_0^t-\frac{\lambda }{T}\frac{\partial T}{\partial x}dt$$

La densité d'entropie produite à cette abscisse (par unité de volume) est

$$S^p\left(t\right)={\int }_0^t\frac{\lambda }{T^2}(\frac{\partial T}{\partial x}{)}^{2}dt$$

Pour les calculs numériques, on divisera par ρ c pour utiliser directement le coefficient de diffusion D.

3.a. Échange thermique entre deux corps

Le premier corps est initialement chaud, de température T=2 et s'étend sur l'intervalle [0,0.99]. Le deuxième est initialement froid, de température T=1; il est beaucoup plus petit puisqu'il s'étend sur l'intervalle [0.99,1]. L'ensemble est isolé donc les conditions limites en x=0 et x=1 sont de type Neumann, avec un flux nul.

getf('diffusionThermique1D.sci');
N=2000;
T=ones(N,1); 
X=linspace(0,1,N).';
for j=1:int(N*0.99),
    T(j)=2;
end;
coef=[[1,1]];
xa=0; xb=0.99;
t=0; Q=zeros(N,1); Se=zeros(N,1); Sp=zeros(N,1);
[T1,t,Q1,Se1,Sp1]=diffusion(N,'neumann',0,'neumann',0,coef,T,t,Q,Se,Sp,1e-9,1e-7);
[T2,t,Q2,Se2,Sp2]=diffusion(N,'neumann',0,'neumann',0,coef,T1,t,Q1,Se1,Sp1,1e-8,1e-6);
[T3,t,Q3,Se3,Sp3]=diffusion(N,'neumann',0,'neumann',0,coef,T2,t,Q2,Se2,Sp2,1e-7,1e-5);
[T4,t,Q4,Se4,Sp4]=diffusion(N,'neumann',0,'neumann',0,coef,T3,t,Q3,Se3,Sp3,1e-6,1e-4);
[T5,t,Q5,Se5,Sp5]=diffusion(N,'neumann',0,'neumann',0,coef,T4,t,Q4,Se4,Sp4,1e-5,1e-3);
[T6,t,Q6,Se6,Sp6]=diffusion(N,'neumann',0,'neumann',0,coef,T5,t,Q5,Se5,Sp5,1e-4,1e-2);
[T7,t,Q7,Se7,Sp7]=diffusion(N,'neumann',0,'neumann',0,coef,T5,t,Q6,Se6,Sp6,1e-3,1e-1);
             

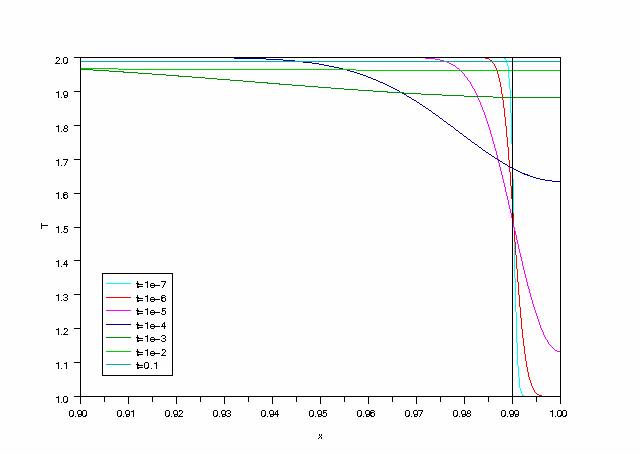
Profils de température au voisinage de la frontière x=0.99

plotA=scf();

rct=[0.9,1,1,2];
plot2d(X,T1,style=4,rect=rct)
plot2d(X,T2,style=5,rect=rct)
plot2d(X,T3,style=6,rect=rct)
plot2d(X,T4,style=9,rect=rct)
plot2d(X,T5,style=13,rect=rct)
plot2d(X,T6,style=15,rect=rct)
plot2d(X,T7,style=17,rect=rct)
xsegs([0.99,0.99],[1,2])
plotA.children.x_label.text='x';
plotA.children.y_label.text='T';
legends(['t=1e-7','t=1e-6','t=1e-5','t=1e-4','t=1e-3','t=1e-2','t=0.1'],[4,5,6,9,13,15,17])
             

plotA.pdf

On constate que la température finale est très proche de la température initiale du grand corps (T=2). Celui-ci se comporte vis à vis du petit comme un thermostat.

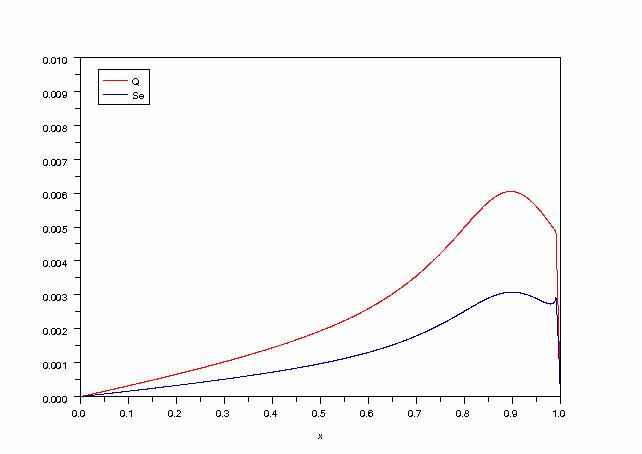
Échange thermique et entropie échangée au début (t=1e-7) et à la fin de la transformation (t=0.1) :

plotB=scf();

rct=[0,0,1,0.01]
plot2d(X,Q7,style=5,rect=rct)            
plot2d(X,Se7,style=9,rect=rct)
plotB.children.x_label.text='x';
legends(['Q','Se'],[5,9])
             

plotB.pdf

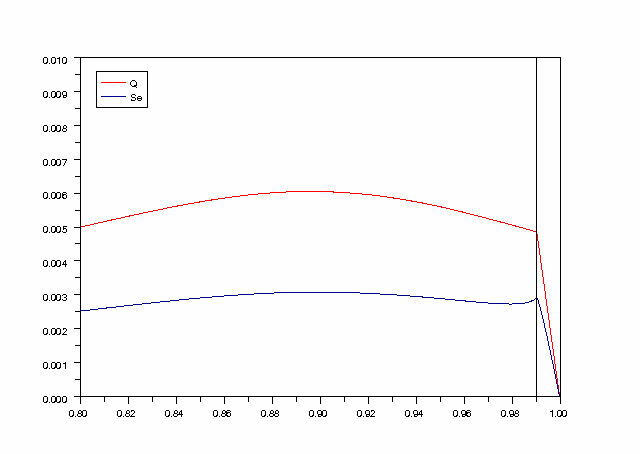
On remarque que les transferts thermiques, et les transferts d'entropie associés, ont lieu dans la totalité du système. L'examen des profils de température peut laisser croire que le gradient de température est beaucoup plus important près de la frontière; en fait ceci n'est vrai que pendant un temps très court. Intégré entre l'instant initial et l'instant final, le transfert thermique passe par un maximum puis décroît lentement lorsqu'on s'éloigne de la frontière.

Détail au voisinage de la frontière :

plotC=scf();

plot2d(X,Q7,style=5,rect=[0.8,0,1,0.01])
plot2d(X,Se7,style=9,rect=[0.8,0,1,0.01])
xsegs([0.99,0.99],[0,0.01])
plotB.children.x_label.text='x';
legends(['Q','Se'],[5,9])
             

plotC.pdf

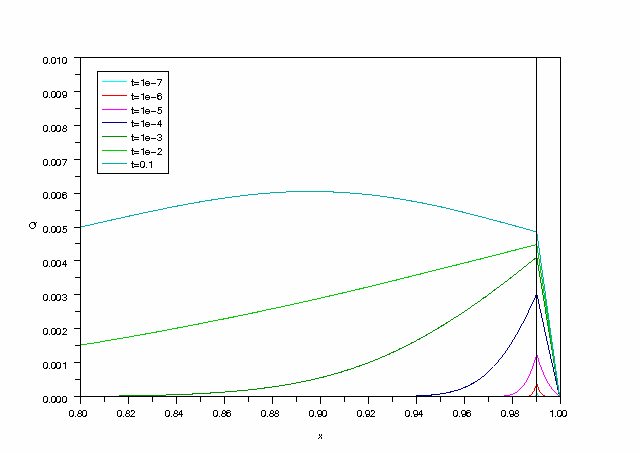
Voyons le déroulement dans le temps du transfert thermique au voisinage de la frontière :

plotC1=scf();

rct=[0.8,0,1,0.01]
plot2d(X,Q1,style=4,rect=rct)
plot2d(X,Q2,style=5,rect=rct)
plot2d(X,Q3,style=6,rect=rct)
plot2d(X,Q4,style=9,rect=rct)
plot2d(X,Q5,style=13,rect=rct)
plot2d(X,Q6,style=15,rect=rct)
plot2d(X,Q7,style=17,rect=rct)
xsegs([0.99,0.99],[0,0.01])
plotC1.children.x_label.text='x';
plotC1.children.y_label.text='Q';
legends(['t=1e-7','t=1e-6','t=1e-5','t=1e-4','t=1e-3','t=1e-2','t=0.1'],[4,5,6,9,13,15,17])
             

plotC1.pdf

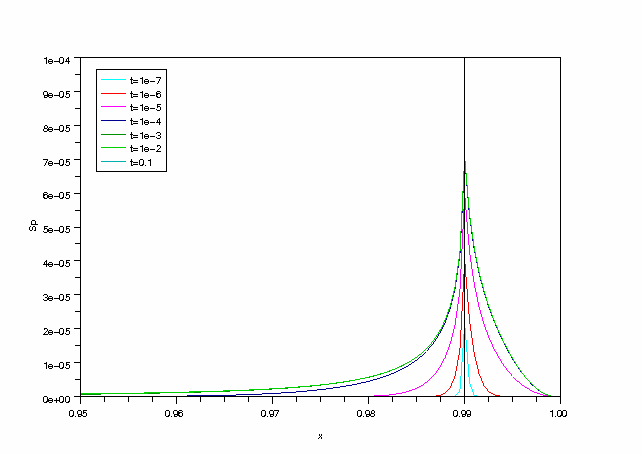
Entropie produite :

plotD=scf();

rct=[0.95,0,1,1e-4];
plot2d(X,Sp1,style=4,rect=rct)
plot2d(X,Sp2,style=5,rect=rct)
plot2d(X,Sp3,style=6,rect=rct)
plot2d(X,Sp4,style=9,rect=rct)
plot2d(X,Sp5,style=13,rect=rct)
plot2d(X,Sp6,style=15,rect=rct)
plot2d(X,Sp7,style=15,rect=rct)
xsegs([0.99,0.99],[0,1e-4])
plotD.children.x_label.text='x';
plotD.children.y_label.text='Sp';
legends(['t=1e-7','t=1e-6','t=1e-5','t=1e-4','t=1e-3','t=1e-2','t=0.1'],[4,5,6,9,13,15,17])
             

plotD.pdf

L'entropie est produite principalement dans le petit corps et dans le thermostat au voisinage de la frontière. On constate aussi qu'une part importante de la production d'entropie se fait au début de la transformation : à partir de t=1e-4, la production d'entropie est très faible par rapport à la production totale.

Dans le cas d'un échange thermique avec un thermostat, il est d'usage d'écrire l'entropie échangée sous la forme :

$$S^e=\frac{Q}{T_0}$$

où T₀ est la température du thermostat.

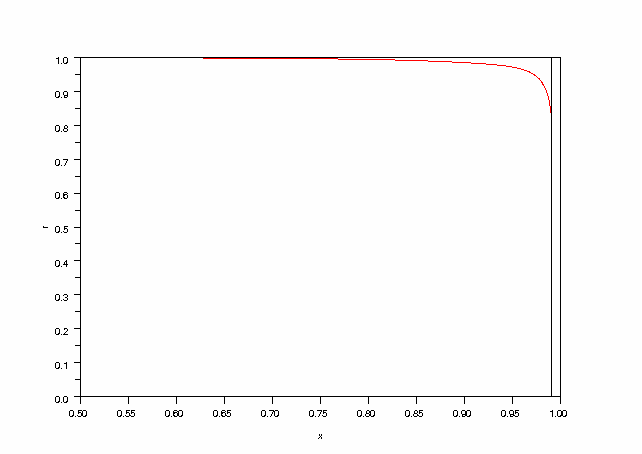
Pour vérifier cette égalité, on trace le rapport suivant

$$r=\frac{Q}{T_0{S}^e}$$

où T₀ est la température en x=0 à la fin de la transformation.

r=zeros(N,1);
for j=int(N*0.5):int(N*0.99),
    r(j)=Q7(j)/(T7(1)*Se7(j));
end        
             

plotE=scf();

plot2d(X,r,style=5,rect=[0.5,0,1,1])
xsegs([0.99,0.99],[0,1])
plotE.children.x_label.text='x';
plotE.children.y_label.text='r';
            

plotE.pdf

On constate que la relation n'est valable que si on l'applique sur une surface située assez loin de la frontière, à un endroit où la production d'entropie est négligeable. Appliquée à la frontière du corps (x=0.99), l'erreur commise est de l'ordre de 15 pour cent. On peut aussi évaluer la température moyenne de la frontière, que l'on définit par :

$$T_m=\frac{Q}{S_e}$$

où le transfert thermique et l'entropie échangée sont évalués à la frontière :

j=int(0.99*N); Tm=Q7(j)/Se7(j)

1.6571401 

valeur nettement inférieure à la température du thermostat.