Interféromètre de Michelson

1.a. Lame séparatrice

Albert Abraham Michelson (physicien américain 1852-1932) a inventé son interféromètre en 1881, dans le but de mettre en évidence le mouvement de la Terre par rapport à un hypothétique milieu supposé au repos absolu (l'éther), dans lequel la lumière aurait une vitesse fixe. Il a mené de nombreuses expériences avec Edward Morley, qui ont démontré l'inexistence de ce milieu, ce qui a ouvert la voie au principe de relativité restreinte (la lumière a une vitesse indépendante du référentiel).

Les dispositifs interférométriques modernes sont souvent des variantes de l'interféromètre de Michelson. Par exemple, la détection des ondes gravitationnelles (projet VIRGO) se fait avec un interféromètre géant.

Dans l'interféromètre de Michelson, la division de l'onde est réalisée par une lame de verre à faces parallèles (planes et polies). L'une des faces est recouverte d'un dépôt métallique très mince, dont l'épaisseur est inférieure à la distance de pénétration de la lumière dans le métal. En choisissant bien l'épaisseur de cette couche, on obtient une surface qui réfléchit la moitié de l'intensité incidente et transmet l'autre moitié.

Figure pleine page

La face arrière de la lame reçoit un traitement antireflet pour minimiser les réflexions. L'utilisation les lois de Descartes de la réfraction permet de montrer que le rayon transmis est parallèle au rayon incident.

Lorsqu'un rayon incident est séparé en deux rayons, on parle de division d'amplitude. Par comparaison, le dispositif de Young, qui réalise une division du front d'onde, produit deux ondes à partir de deux rayons différents.

1.b. Dispositif optique

L'interféromètre et constitué principalement d'une lame séparatrice et de deux miroirs plans. Ceux-ci sont des pièces en verre poli recouvertes d'une couche métallique (argent ou aluminium) dont l'épaisseur est très supérieure à la profondeur de pénétration de la lumière, ce qui permet d'obtenir une réflexion pratiquement totale (95 pour 100). Ces miroirs ont un diamètre de l'ordre de 2 à 4 centimètres, et doivent avoir un défaut de planéité sur toute leur surface qui n'excède pas λ/10 (de même pour la lame séparatrice).

Figure pleine page

La lame compensatrice est une lame de verre identique à la lame séparatrice mais sans couche semi-réfléchissante. Sa fonction sera expliquée plus loin.

La lumière transmise par la lame rencontre un miroir, que l'on notera M₁, qui est fixé sur un chariot mobile en translation. Le système de translation est une mécanique de précision, qui assure un mouvement en translation à la fraction de longueur d'onde près. Le chariot est ramené en arrière par un contrepoids et une vis micrométrique vient le pousser. Cette vis permet de mesurer le déplacement du chariot à 10 μm près, mais la finesse du réglage est de l'ordre de la longueur d'onde.

La lumière réfléchie par le miroir M₁ est réfléchie en retour par la couche semi-réfléchissante de la séparatrice, et sort du dispositif dans une direction environ perpendiculaire à la direction incidente. Il y a la moitié de l'intensité qui repart vers la source de lumière.

Le second miroir M₂ est disposé perpendiculairement au premier. Il reçoit la lumière réfléchie par la séparatrice. Après réflexion, cette lumière ressort du dispositif après avoir traversé la séparatrice.

Dans le réglage de base, l'image de M₂ par le plan de la couche semi-réfléchissante (plan séparateur) est parallèle à M₁. On note M'₂ cette image et e la distance entre M₁ et le miroir virtuel M'₂. Sur le papier, cette configuration est obtenue lorsque les deux miroirs sont perpendiculaires, et lorsque le plan séparateur est à 45 degrés des miroirs. En pratique, cette condition n'est pas strictement vérifiée, car il suffit que l'image de M₂ par la séparatrice soit parallèle à M₁. Ce réglage est appelé réglage en lame d'air, car les deux plans M₁ et M'₂ forment une lame d'air à faces parallèles.

Sur la figure, on a représenté en rouge le rayon passant par M₁, en bleu le rayon passant par M₂. En sortie du dispositif, ces deux rayons ont une différence de phase qui est fonction de l'espacement e. Il faudra prévoir un dispositif complémentaire en sortie pour obtenir le recoupement des rayons. Ces deux rayons ont pratiquement la même intensité. On obtient donc en sortie l'interférence de deux ondes cohérentes de même intensité.

Le parallélisme de M₁ et M'₂ doit être réalisé au dixième de micromètre près. Pour cela, deux vis d'inclinaison sont disposées à l'arrière des deux miroirs. Les vis du miroir M₁ (le miroir du chariot), permettent un réglage relativement grossier de l'inclinaison relative des miroirs. Les vis du miroir M₂ ont un pas plus fin et permettent un réglage très fin de l'inclinaison relative. La lame séparatrice est fixée sur le support. On joue donc uniquement sur les inclinaisons des miroirs pour obtenir le réglage en lame d'air.

1.c. Lame compensatrice

La figure suivante montre le chemin de la lumière dans la lame séparatrice :

Figure pleine page

On constate que le rayon réfléchi par M₁ traverse 3 fois la lame alors que le rayon réfléchi par M₂ ne la traverse qu'une fois. La lame introduit donc une différence de marche entre les deux rayons.

On souhaite obtenir en sortie une différence de marche entre les deux rayons qui soit indépendante de la lame séparatrice. Le rôle de la lame compensatrice est de compenser la différence de marche introduite par la lame séparatrice. Elle a la même épaisseur que la lame séparatrice. Le schéma suivant en montre le fonctionnement :

Figure pleine page

Après la séparation, le rayon réfléchi par M₁ traverse une fois le verre sur une longueur a et deux fois sur une longueur b. Il en est de même pour le rayon réfléchi par M₂. En sortie, la différence de marche ne dépend plus de la traversée des lames.

1.d. Schémas simplifiés

La première simplification consiste à remplacer la combinaison séparatrice-compensatrice par un plan séparateur S_p. Pour la lumière réfléchie vers M₂, ce plan constitue un miroir plan, et n'a pas d'effet sur la lumière transmise vers M₁. La simulation Interféromètre de Michelson utilise cette simplification.

La seconde simplification consiste à enlever le plan séparateur et à remplacer le miroir M₂ par son image M'₂. Avec ce schéma, la séparation du rayon incident se fait sur le miroir M'₂, et la lumière ressort de l'interféromètre dans la direction de la source. Ce schéma simplifié est parfaitement équivalent au schéma de départ, mais simplifie beaucoup les raisonnements et les calculs.

Figure pleine page

2.a. Source ponctuelle

Dans le réglage en lame d'air, les miroirs M₁ et M'₂ sont parallèles. On considère tout d'abord les interférences produites avec une source ponctuelle quasi monochromatique.

Soit S le point source. On considère son image S₁ par le miroir M₁, et son image S₂ par le miroir M'₂. Ces deux images sont situées sur la droite Sz contenant la source et perpendiculaire aux miroirs, et sont à une distance 2e l'une de l'autre. Elles constituent deux sources secondaires synchrones. On considère un plan d'observation perpendiculaire à l'axe Sz. Pour tracer les deux rayons parvenant en un point M de ce plan, il faut faire la construction en partant de ce point.

Figure pleine page

Les deux rayons partant de la source ne sont pas confondus : il s'agit donc d'une division du front d'onde. Comme nous l'avons montré dans le chapitre Ondes lumineuses et interférences, les franges obtenues sur ce plan sont des anneaux centrés sur le point C, qui se trouve sur la droite passant par S et perpendiculaire aux miroirs. Si l'on introduit l'angle θ défini sur la figure, la différence de marche est (l'indice de l'air est n=1) :

$$\delta =2necos\theta \text{(1)}$$

Ces interférences sont non localisées, car une translation du plan d'observation dans la direction Z ne change pas leur visibilité.

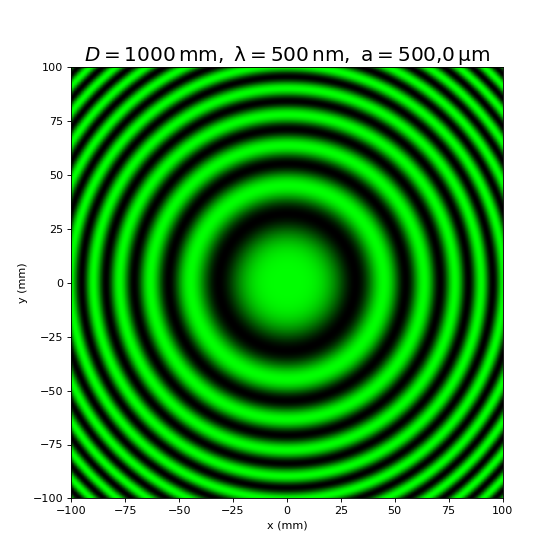
Lorsque les deux plans M₁ et M'₂ sont confondus (e=0), on parle de contact optique des deux miroirs. La différence de marche est alors nulle pour tous les points du plan d'observation donc l'éclairement sur ce plan est uniforme. Pour régler l'interféromètre, il faut être en mesure de parvenir au contact optique en partant d'un espacement quelconque, alors qu'on ne sait pas en général le signe de e. On remarque que la différence de marche diminue lorsqu'on s'éloigne du centre des anneaux. Si l'on veut réduire la distance entre les miroirs, c'est-à-dire réduire la différence de marche au centre, il faut donc que le rayon d'un anneau d'ordre donné diminue. Pour réduire la distance entre les miroirs, il faut tourner la vis de translation du chariot dans le sens qui donne des anneaux entrant, c'est-à-dire dont le rayon diminue. La simulation Interféromètre de Michelson montre l'évolution des anneaux lorsqu'on fait varier e.

Si la source est déplacée perpendiculairement à l'axe d'une distance x_s, les anneaux sont déplacés de la même distance. Lorsqu'on remplace la source ponctuelle par une source étendue (de type lampe à décharge), il faut considérer les interférences produites par les différents points de la source, qui sont incohérents. Soit d la distance la plus petite entre deux anneaux consécutifs sur le plan d'observation. Si la taille de la source est petite devant d, les interférences produites par les différents points de la source coïncident pratiquement. Au contraire, si la source a une taille de l'ordre de d ou plus grande, les interférences ne coïncident pas : il se produit alors un brouillage des franges qui deviennent complètement invisibles si la source est très étendue. Si l'on éloigne le plan d'observation, la distance d augmente donc on peut utiliser une source plus grande. Nous allons à présent considérer le cas d'un plan d'observation situé à l'infini, qui permet d'utiliser une source de taille quelconque.

2.b. Source étendue

Une manière pratique de placer le plan d'observation à l'infini est de le placer dans le plan focal image d'une lentille convergente (que l'on supposera parfaitement stigmatique). Dans ce cas, les deux rayons qui parviennent en un point du plan d'observation, et qui proviennent du même point S de la source étendue, sont nécessairement confondus au départ de la source. Lorsqu'on observe à l'infini, il y a donc division d'amplitude. Pour tracer ces deux rayons, le plus simple et de tracer un rayon à partir d'un point quelconque de la source. Ce rayon arrive sur les miroirs avec un angle d'inclinaison θ.

Figure pleine page

Pour calculer la différence de marche entre ces deux rayons au point M, on remarque que la séparation (virtuelle) se fait au point I. C'est à partir de ce point que les deux rayons ont un chemin différent. Pour prendre en compte l'effet de la lentille sur le chemin optique, on utilise le théorème de Malus : si l'on reporte depuis le point M des chemins optiques égaux, on obtient une surface perpendiculaire aux rayons. Considérons alors le point K projeté orthogonal de I sur le rayon réfléchi par M₁. Les points I et K sont sur un plan perpendiculaire aux deux rayons réfléchis. On en déduit, en utilisant le théorème de Malus, que les chemins optiques depuis le point M jusqu'à ces deux points sont égaux :

$$[MI]=\left[MK\right]\text{(2)}$$

La différence de marche cherchée est :

$$\delta \left(M\right)=[IJ]+\left[JK\right]+\left[KM\right]-\left[IM\right]=\left[IJ\right]+\left[JK\right]=n(IJ+JK)\text{(3)}$$

où n est l'indice de l'air.

Le triangle rectange (IJK) a un angle 2θ en son sommet J, donc :

$$IJcos\left(2\theta \right)=JK\text{(4)}$$

D'autre part :

$$IJcos\theta =e\text{(5)}$$

On en déduit :

Les franges d'interférence sont donc des anneaux de centre F', le foyer image de la lentille. On obtient bien sûr les mêmes franges qu'avec la source ponctuelle, mais le centre des anneaux est déterminé par la position de la lentille, et non par le point S d'où les rayons proviennent.

Chaque frange correspond à une égale inclinaison θ des rayons, c'est pourquoi on parle de franges d'égale inclinaison.

En pratique, l'angle θ reste petit et on peut utiliser l'approximation suivante

$$r=f\text{'}\theta \text{(7)}$$

Voyons à présent pourquoi ces interférences sont parfaitement visibles avec une source étendue. La différence de marche ne dépend que de la position du point considéré sur le plan d'observation (elle ne dépend que de r). Elle est indépendante de la position du point S de la source d'où les rayons partent. Il faut comparer cela à la situation étudiée au paragraphe précédent, où le plan d'observation était à distance finie, et où la position de la source avait une importance. En conséquence, toutes les paires de rayons qui parviennent au point M, et qui viennent de différents points de la source étendue, ont en ce point exactement la même différence de marche. Les figures d'interférence produites par les différents points de la source (qui sont incohérents), sont donc exactement coïncidantes sur le plan d'observation.

Lorsque le plan d'observation n'est pas à l'infini, nous avons vu que l'extension permise à la source est très limitée, d'autant plus que le plan est proche. Pour cette raison, on peut conclure que :

En pratique, on utilise couramment une lampe à décharge. Pour que le maximum d'anneaux soit visible, il faut que l'angle θ balaye une plage [-θ_m,θ_m] la plus large possible (quelques degrés). Pour cela, il faut utiliser un condenseur (lentille convergente de gros diamètre et de courte focale) et former (à peu près) l'image de la lampe sur le miroir M₁. La lentille de projection doit avoir une grande focale (de l'ordre du mètre) pour que les anneaux soient grands. La figure suivante montre le montage complet.

Figure pleine page

Pour l'influence de la position du plan d'observation et de la taille de la source, voir la simulation Interféromètre de Michelson.

L'image suivante est une phographie des franges obtenues sur un écran blanc. La source de lumière est une lampe spectrale Na.

L'image suivante montre les anneaux obtenus avec une lampe Hg-Cd. Ils sont colorés en raison de la présence de nombreuses raies dans le spectre de ces gaz.

L'observation de l'évolution des anneaux lorsqu'on tourne très lentement la vis de translation du chariot permet de déterminer le sens de variation de e (épaisseur de la lame d'air). Soit p_c l'ordre d'interférence au centre (supposé entier). L'ordre d'interférence du premier anneau est p_c-1. Si e diminue, l'ordre au centre diminue donc le rayon du premier anneau diminue. On voit donc le rayon des anneaux diminuer : on dit que les anneaux entrent, et inversement qu'ils sortent lorsque e augmente. La vidéo ci-dessous montre, pour un éclairage avec une lampe à vapeur de mercure, l'évolution des anneaux lorsque e diminue (entraînement motorisé). La vitesse apparente de déplacement du chariot est de 85 nm⋅s¹. La cadence de prise de vue est de 198 images par secondes et le scintillement est dû aux cycles de la lampe à décharge, de fréquence 100 Hz.

2.c. Analyse spectrale d'une source

L'interféromètre de Michelson réglé en lame d'air peut servir à faire l'analyse spectrale d'une source.

3.a. Source ponctuelle

La configuration en coin d'air s'obtient à partir du contact optique, en inclinant légèrement le miroir M₁. Les deux images de la source ponctuelle sont alors diposées à peu près transversalement par rapport à l'axe passant par la source et perpendiculaire aux miroirs. La construction de deux rayons parvenant au point M se fait en partant de ce point.

Figure pleine page

Les deux rayons partant de la source ne sont pas confondus : il s'agit d'une division du front d'onde. Nous avons vu dans le chapitre Ondes lumineuses et interférences que les interférences observées sur un plan parallèle à la droite joignant les deux sources sont rectilignes. Ces franges sont perpendiculaires à la droite S₁S₂, c'est-à-dire parallèles à la droite Δ d'intersection des plans M₁ et M'₂, qui est selon y sur la figure.

L'interfrange est d'autant plus petit que l'angle entre les deux miroirs est grand. Voir la simulation Interféromètre de Michelson.

Un déplacement de la source ponctuelle dans la direction x conduit à une translation des franges dans la même direction. Pour une source étendue, les différents points de la source produisent des interférences qui ne coïncident pas. En conséquence, les interférences se produisant sur le plan représenté ci-dessus ne sont pas visibles avec une source étendue. Nous allons voir néanmoins qu'il est possible d'observer ces franges avec une source étendue, à condition de modifier le dispositif d'observation.

3.b. Source étendue

Avec une source étendue, il faut utiliser une lentille convergente pour faire l'image des miroirs (qui sont presque confondus) sur le plan d'observation. Soit P un point quelconque sur les miroirs et M son point conjugué par la lentille. Les deux rayons qui interfèrent au point M se coupent nécessairement au point P (à cause du stigmatisme). Ces deux rayons sont confondus lorsqu'ils quittent la source : il y a division d'amplitude.

Figure pleine page

On admet le résultat suivant pour la différence de marche, valable si les rayons incidents ont un angle d'incidence faible par rapport au miroir (quelques degrés) :

où n est l'indice de l'air et e l'épaisseur du coin d'air au point P. Les franges observées sont donc des lignes d'égale épaisseur du coin d'air, c'est-à-dire des lignes sur lesquelles la distance entre les deux faces du coin est constante. Ces franges sont appelées franges d'égale épaisseur. Pour un coin d'air, les franges d'égale épaisseur sont des franges rectilignes parallèles à la droite Δ d'intersection des deux plans M₁ et M'₂. Sur le plan d'observation, la frange d'ordre zéro est l'image de cette droite. La différence de marche s'exprime en fonction de l'angle α entre les deux miroirs et de la distance x à cette droite :

$$\delta =2n\alpha x\text{(17)}$$

Les interférences observées sur le plan des miroirs sont bien visibles avec une source étendue. En effet, la différence de marche au point P ne dépend pas de l'angle d'incidence du rayon venant de la source (du moins tant qu'il reste inférieur à quelques degrés). Les différents points de la source produisent donc des interférences qui coïncident.

Nous avons vu plus faut qu'une observation sur un autre plan ne peut se faire avec une source étendue.

Ces interférences localisées sur les miroirs s'observent très facilement en regardant directement à l'œil nu. Pour les observer sur un écran, il faut faire l'image avec une lentille de courte focale (par exemple 20 cm), de manière à obtenir une image des miroirs avec un facteur de grandissement de 2 ou 3. Pour l'éclairage, il faut placer la lampe environ au foyer du condenseur, de manière à éclairer les miroirs à peu près en incidence normale.

Figure pleine page

Pour l'influence de la position du plan d'observation et de la taille de la source, voir la simulation Interféromètre de Michelson.

L'image suivante est une photographie de l'écran sur lequel l'image des miroirs avec la lentille est formée. La source de lumière est une lampe spectrale Na.

La vidéo ci-dessous montre, pour une lampe spectrale Hg, l'évolution de l'image des miroirs lorsqu'on incline très lentement le miroir M₁ en partant du contact optique.

3.c. Lumière blanche

Au voisinage de l'ordre zéro, les franges du coin d'air sont visibles avec une lumière blanche, comme le sont les franges d'Young. Voir aussi la simulation Interférences avec deux sources ponctuelles. La figure suivante montre la photographie de l'image formée par la lentille sur un écran blanc.

La lumière blanche est utile pour repérer la frange d'ordre zéro, qui est blanche avec des bords marrons, entourée de deux franges noires.

Les franges d'égale épaisseur s'observent aussi sur les films de savon éclairés par la lumière du jour. Un film de savon est en fait un film mince d'eau qui doit sa stabilité aux molécules de surfactant qui se placent sur ses deux surfaces. Lorsqu'on regarde un film de savon, on voit les interférences d'égale épaisseur localisées sur le film (la source de lumière est généralement le ciel ou le Soleil). La photographie ci-dessous montre un film de savon dans un cadre métallique :

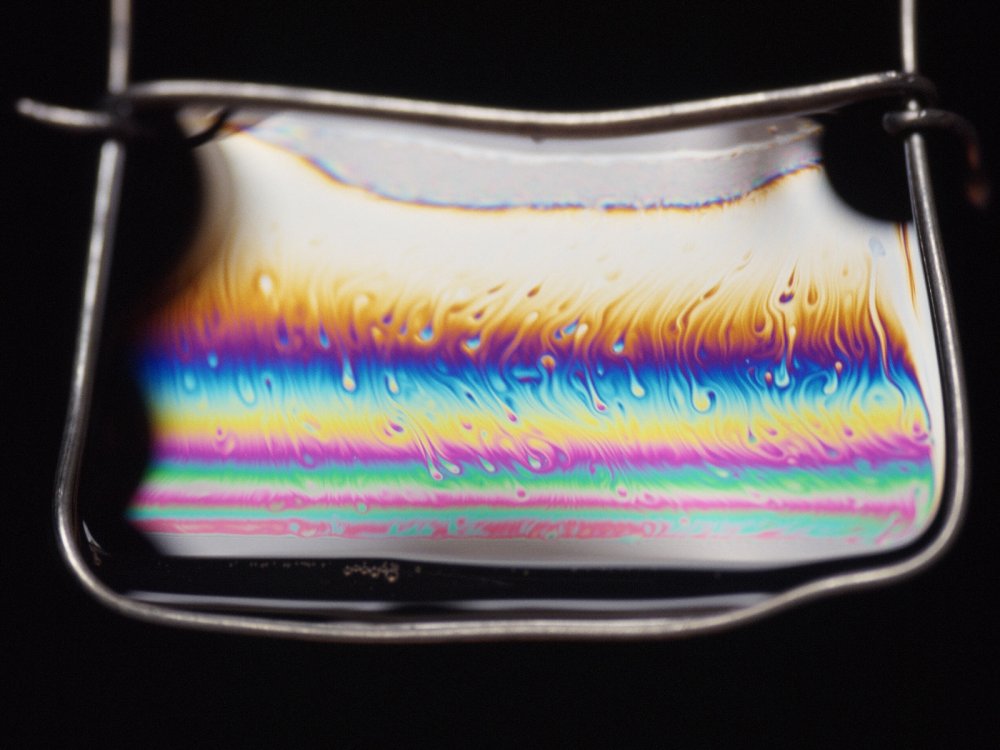
Le film est plus mince sur sa partie haute (la gravité est vers le bas). On voit donc une frange d'ordre zéro blanche et très large.

Les franges d'égale épaisseur ne sont pas toujours rectilignes, comme le montre la photographie suivante, prise lorsque le film n'est pas encore stabilisé (il est le siège de mouvements turbulents) :

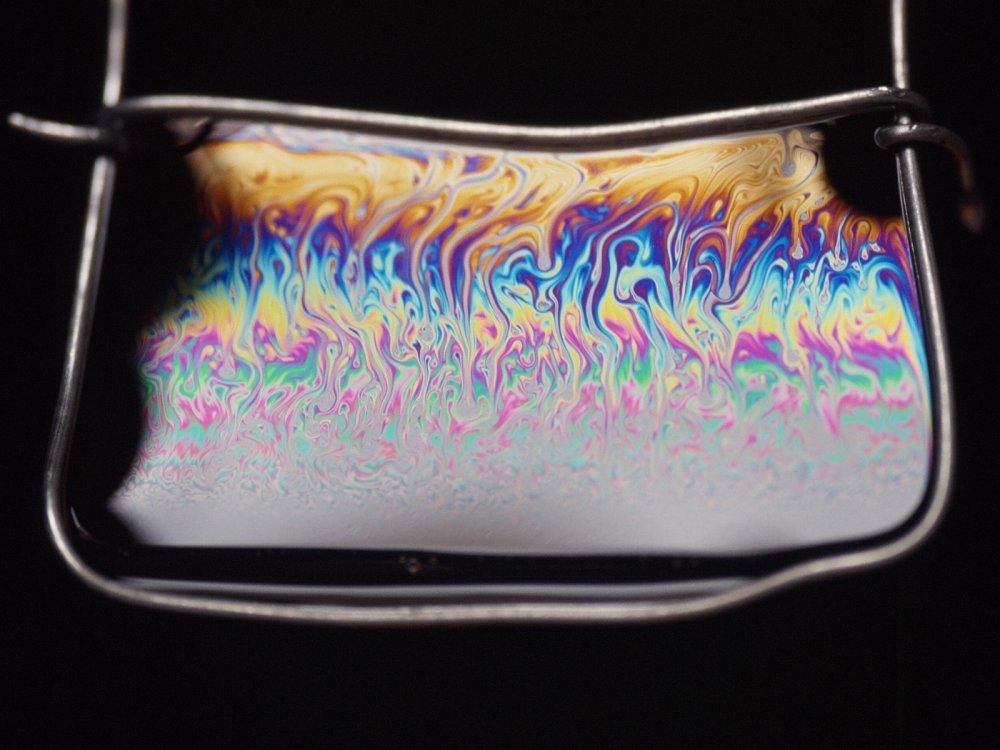
Pour l'explication des couleurs observées, voir aussi la simulation Franges d'égale épaisseur en lumière blanche. Les couleurs vues sur le film permettent de déterminer son épaisseur. Lorsqu'elle dépasse 2 micromètres, il n'y a plus d'interférences visibles.

Dans certains interféromètres de Michelson, la frange d'ordre zéro est noire. Cela est dû à la présence d'un déphasage de π lors de la réflexion sur la face semi-réfléchissante de la lame séparatrice.

3.d. Contrôle des surfaces optiques

Une autre application des franges d'égale épaisseur est le contrôle des surfaces optiques. Par exemple, on peut se servir de l'interféromètre pour contrôler la planéité d'un miroir plan. Le miroir à contrôler est par exemple le miroir M'₂. Si le miroir est bien plan (à l'échelle optique), les franges d'égale épaisseur sont bien rectilignes et d'interfrange constant. Un défaut de planéité se traduit soit par des franges déformées, soit par un interfrange non constant.

Les miroirs sphériques sont aussi contrôlés de cette manière. Les franges d'égale épaisseur sont alors des anneaux, qui peuvent être déformés si le miroir n'est pas tout à fait sphérique.