Expérience des fentes d'Young
1. Introduction
Ce document montre une étude théorique et expérimentale de la diffraction de la lumière par une double fente. La source de lumière est une lampe spectrale émettant une lumière quasi monochromatique, devant laquelle une fente de largeur réglable est placée, ce qui permet d'étudier l'influence de la cohérence spatiale de l'éclairage de la double fente.
Voir aussi : Diffraction de la lumière et Simulation de l'expérience des fentes d'Young.
2. Étude théorique
2.a. Schéma de l'expérience
La lumière est émise par une lampe contenant un gaz à basse pression. Si la lumière émise par le gaz comporte plusieurs raies, un filtre en verre coloré permet de sélectionner une raie particulière. On obtient ainsi une lumière quasi monochromatique. Un écran percé d'une fente F est placé à quelques millimètres de cette lampe. Cette fente, dont la largeur est réglable, a une longueur . Un deuxième écran, situé à une distance zs du premier, comporte deux fentes F1,F2 identiques, de largeur a et de longueur . Ces deux fentes sont parallèles à la fente F. La distance entre les centres des deux fentes est notée d. Le plan d'observation est placé à une distance z de cet écran. Le plan Σ contenant les deux fentes est menu d'un repère (Oxy) dont l'axe (Oy) est parallèle aux fentes.
Figure pleine pageUn point P de l'ouverture (c'est-à-dire un point de F1 ou F2) a pour coordonnées . La fonction de transmission de l'ouverture est définie par :
La distance d est de l'ordre de grandeur du mm alors que les distances zs et z sont au moins de 100 mm.
2.b. Source ponctuelle quasi monochromatique
La théorie scalaire de la diffraction, reposant sur le principe de Huygens-Fresnel, est exposée dans Diffraction de la lumière.
Rappelons que cette théorie repose sur l'hypothèse que l'onde peut être décrite par un champ scalaire (qui représente une des composantes du champ électromagnétique) et que l'amplitude complexe de cette onde en un point du plan Σ est nulle sur la partie coïncidant avec la partie opaque et égale sur l'ouverture à ce qu'elle serait en l'absence de l'écran. Autrement dit, cette théorie néglige tout effet matériel de l'écran sur l'onde (à part bien sûr l'obstruction). Il est généralement admis que cette théorie donne des résultats en accord avec l'expérience si la largeur des ouvertures est grande devant la longueur d'onde. Dans cette expérience, les fentes ont une largeur de l'ordre de 1/10 millimètre, ce qui est beaucoup plus grand que la longueur d'onde.
Pour une lampe à décharge, deux points distincts de la zone d'émission de la lumière émettent de manière complètement incohérente. Compte tenu de la taille de la zone d'émission, l'éclairage de la fente F est complètement incohérent, ce qui signifie qu'en deux points S et S' de l'ouverture, la fonction de corrélation de l'amplitude complexe prend des valeurs nulles :
En vertu du principe de Huygens-Fresnel, nous faisons l'hypothèse que chaque points S de la fente F peut être assimilé à une source ponctuelle quasi monochromatrique, de longueur d'onde moyenne λ. Deux points distincts de la fente F constituent donc deux sources incohérentes. En d'autres termes, la source de lumière effective est une source spatialement incohérente de forme rectangulaire, de largeur et de longueur .
On s'intéresse tout d'abord à l'intensité lumineuse dans le plan Π pour une source ponctuelle monochromatique située au point S.
Le calcul de l'intensité est aisé dans le cadre de l'approximation de Fraunhofer (Diffraction de la lumière), qui est vérifiée lorsque :
où désigne les coordonnées d'un point de l'ouverture (fentes F1 et F2).
Dans l'expérience décrite ci-dessus, est au plus de l'ordre du millimètre mais atteint 10 mm. Cependant, la condition et l'emploi d'une source étendue dans la direction (Oy) (fente F) fait que la figure de diffraction qui sera observée correspond à une diffraction dans la direction x uniquement. La condition de Fraunhofer s'écrit donc :
Dans le cas présent, et la condition s'écrit : . En principe, l'approximation de Fraunhofer est très loin d'être vérifiée pour cette expérience, puisque z est inférieur à 1 m. Bien sûr, cela ne signifie pas qu'utiliser l'approximation de Fraunhofer donne des résultats dont l'écart à l'expérience soit notable. Si l'on veut se placer réellement dans les conditions de Fraunhofer, une solution pratique est de placer virtuellement le plan d'observation à l'infini, en le plaçant au plan focal image d'une lentille convergente L2. Dans ce cas, il est intéressant de placer la fente F dans le plan focal objet d'une lentille convergente L1 :
Figure pleine pageDans la mesure où les deux lentilles convergentes sont parfaitement stigmatiques, ce montage réalise parfaitement l'approximation de Fraunhofer. Cependant, les lentilles utilisées sont le plus souvent des lentilles simples et leur astigmatisme est probablement non négligeable. En fin de compte, il n'est pas évident a priori que ce montage fournisse des résultats expérimentaux plus proche de la théorie de Fraunhofer que le montage sans lentilles. Une étude rigoureuse du système avec les lentilles est possible mais sort du cadre de ce document. Quoi qu'il en soit, nous allons faire le calcul dans le cadre de l'approximation de Fraunhofer et nous allons réaliser les deux montages expérimentaux.
Le calcul de cette intensité, détaillé dans Diffraction de la lumière, conduit à l'expression suivante lorsque la source ponctuelle est sur l'axe (Oz) :
où fx et fy sont les fréquences spatiales associées à la position du point M :
Dans le cas du montage avec les deux lentilles (montage dit de Fraunhofer), on a :
L'angle est défini sur la figure ci-dessus, en projection sur le plan (Oxy); l'angle se définit dans le plan (Oyz) de manière similaire.
Le facteur constant est sans importance dans la mesure où on s'intéresse uniquement aux variations de l'intensité sur le plan Π. On utilisera donc l'expression suivante, où Im désigne l'intensité maximale :
La fonction suivante permet de calculer cette intensité pour fy=0 (avec Im=1) :
import numpy as np
from matplotlib.pyplot import *
def diffraction(a,d,fx):
return (np.sinc(fx*a))**2*0.5*(1+np.cos(2*np.pi*fx*d))
Voici un exemple de profil d'intensité :
d = 0.5 # en mm
a = 0.1
fx = np.linspace(-20,20,1000)
I = diffraction(a,d,fx)
figure(figsize=(10,6))
plot(fx,I)
grid()
xlabel(r"$f_x\ (\rm mm^{-1}$",fontsize=16)
ylabel(r"$I/I_m$",fontsize=16)
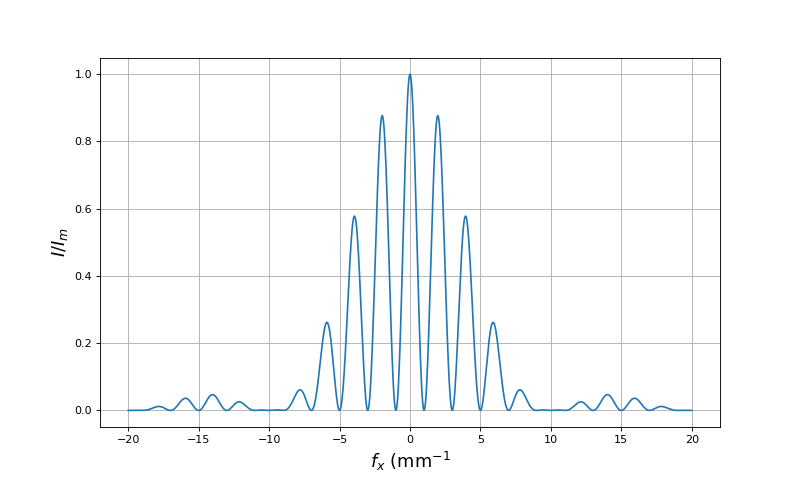 fig1.pdf
fig1.pdf
Le terme , qui correspond à la diffraction par une fente de largeur a, varie beaucoup plus lentement que l'autre terme; il constitue donc une enveloppe. Le terme correspond à l'interférence de deux sources ponctuelles cohérentes qui seraient placées en et (aux centres des fentes).
Si la source ponctuelle est à une position quelconque, celle-ci est définie par les deux fréquences spatiales :
ou bien dans le montage de Fraunhofer :
Comme il est démontré dans Diffraction de la lumière, la fonction d'intensité vérifie la propriété suivante :
La figure de diffraction pour une position quelconque de la source est donc identique à celle pour la source centrée sur l'axe mais elle est centrée en (fx,fy)=(-sx,-sy).
2.c. Source étendue
Comme justifié plus haut, on peut considérer que la source de lumière est sur la surface de la fente F. Il s'agit d'une source non cohérente spatialement, c'est-à-dire que deux points distincts de cette source sont incohérents. En conséquence l'intensité de la lumière sur le plan Π est la somme des intensités produites par les différentes sources ponctuelles. Cette somme peut s'écrire sous la forme d'une intégrale double (bien que son calcul numérique sera bien une somme) :
où K est une constante (ayant les dimensions d'une surface) dont la valeur est sans importance puisqu'on s'intéresse seulement aux variations d'intensité dans le plan Π. Voici l'expression complète de l'intégrale :
Les deux variables sont séparables :
Considérons le terme en facteur qui dépend de fy :
avec .
Afin d'évaluer cette intégrale faisons le tracé de la fonction à intégrer :
ly = 5 # en mm
zs = 300
lamb = 500e-6
b_s = ly/(zs*lamb)
b = 10
sy = np.linspace(-b_s,b_s,10000)
def f(fy,sy):
return (np.sinc(b*(fy+sy)))**2
F = f(0,sy)
figure(figsize=(12,6))
plot(sy,F)
grid()
xlabel(r"$s_y\ (\rm mm^{-1})$",fontsize=16)
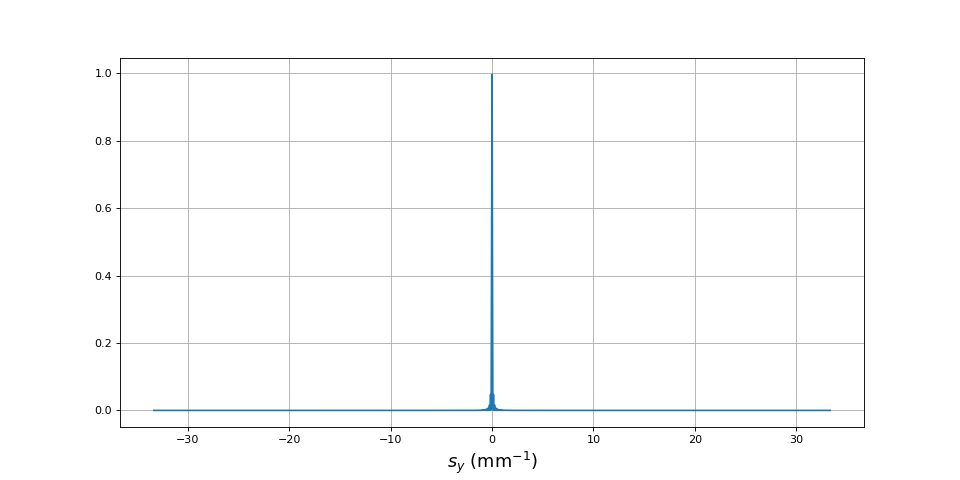 fig2.pdf
fig2.pdf
Voici un détail de la tache de diffraction :
xlim(-1,1)
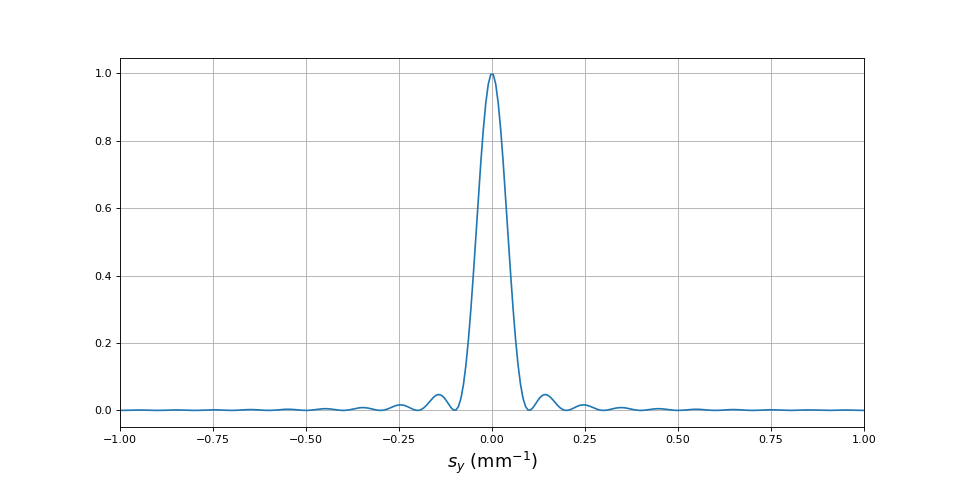 fig3.pdf
fig3.pdf
Le tracé de la fonction pour une valeur quelconque de fy se déduit d'une simple translation : la nouvelle tache de diffraction est centrée en sy=-fy. Si on se limite à des valeurs de fy inférieures à s, l'intégrale est quasi indépendante de fy. Cette condition s'écrit :
Sur une plage de valeurs de y de plusieurs millimètres, on a donc une intensité qui ne dépend pratiquement pas de y. Pour cette raison, on observe dans le plan Π des franges rectilignes parallèles aux fentes. Dans cette zone, on peut donc considérer que l'intensité prend la forme suivante :
avec .
Traçons la fonction à intégrer pour différentes valeurs de fx :
lx = 0.1
a_s = lx/(2*lamb*zs)
sx = np.linspace(-a_s,a_s,10000)
def g(sx,fx):
return diffraction(a,d,fx+sx)
G1 = g(sx,0)
G2 = g(sx,1)
G3 = g(sx,2)
figure(figsize=(12,6))
plot(sx,G1)
plot(sx,G2)
plot(sx,G3)
xlabel(r"$s_x\ (\rm mm^{-1})$",fontsize=16)
grid()
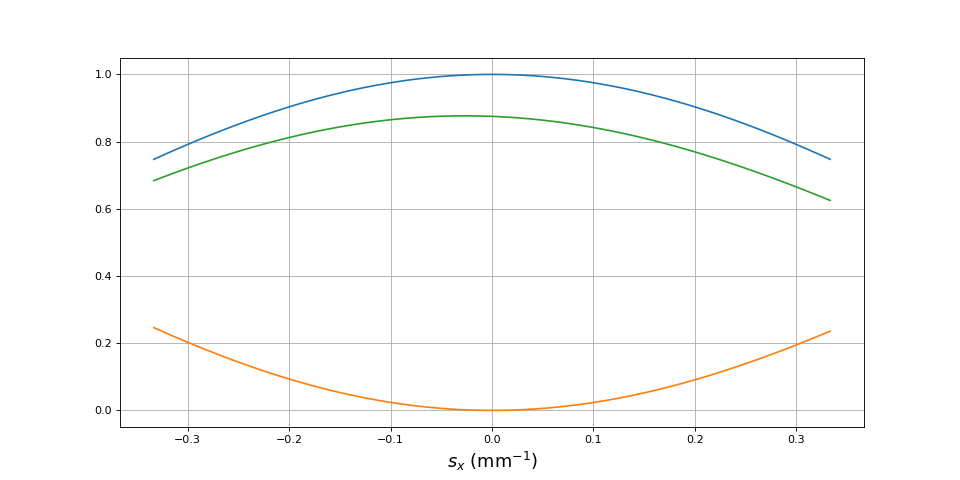 fig4.pdf
fig4.pdf
Calculons l'intensité en évaluant l'intégrale par la méthode des rectangles :
def intensite(a,d,fx_max,lx,N):
a_s = lx/(2*lamb*zs)
sx = np.linspace(-a_s,a_s,10000)
def g(sx,fx):
return diffraction(a,d,fx+sx)
def intensite(fx):
G = g(sx,fx)
return G.sum()*(sx[1]-sx[0])
fx = np.linspace(-20,20,N)
I = np.zeros(N)
for k in range(N):
I[k] = intensite(fx[k])
return (fx,I)
(fx,I) = intensite(a,d,20,0.1,1000)
figure(figsize=(12,6))
plot(fx,I)
grid()
xlabel(r"$f_x\ (\rm mm^{-1})$",fontsize=16)
ylabel("I",fontsize=16)
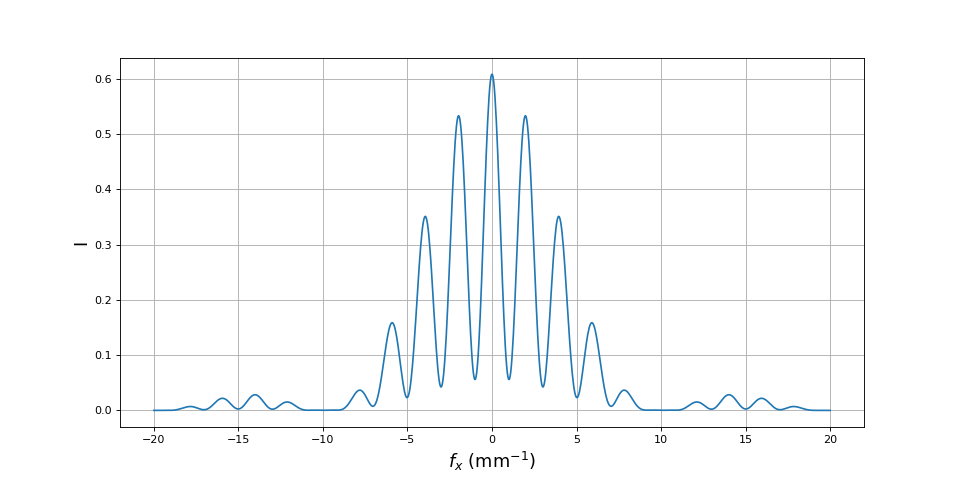 fig5.pdf
fig5.pdf
Voici la courbe d'intensité pour une fente F deux fois plus large :
(fx,I) = intensite(a,d,20,0.2,1000)
figure(figsize=(12,6))
plot(fx,I)
grid()
xlabel(r"$f_x\ (\rm mm^{-1})$",fontsize=16)
ylabel("I",fontsize=16)
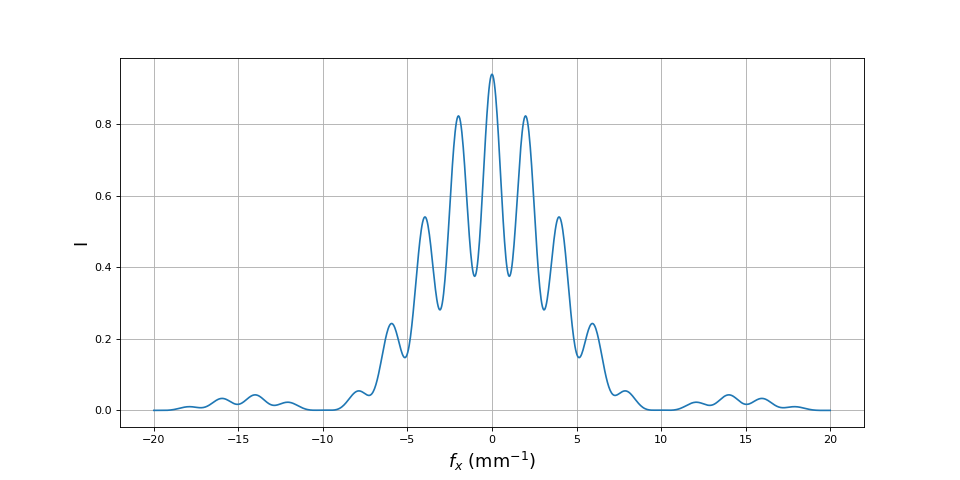 fig6.pdf
fig6.pdf
L'élargissement de la fente F se traduit par une diminution de la cohérence spatiale de l'onde qui éclaire les deux fentes et par conséquent par une baisse du contraste des franges d'interférences.
D'après le calcul fait dans Diffraction de la lumière, la fonction de corrélation normalisée pour deux points de l'ouverture est :
On peut s'attendre à avoir un contraste minimal lorsque pour deux points de l'ouverture espacés de la corrélation est nulle :
soit pour une largeur de fente :
Voyons la courbe d'intensité pour cette valeur :
lx = lamb*zs/d
(fx,I) = intensite(a,d,20,lx,1000)
figure(figsize=(12,6))
plot(fx,I)
grid()
xlabel(r"$f_x\ (\rm mm^{-1})$",fontsize=16)
ylabel("I",fontsize=16)
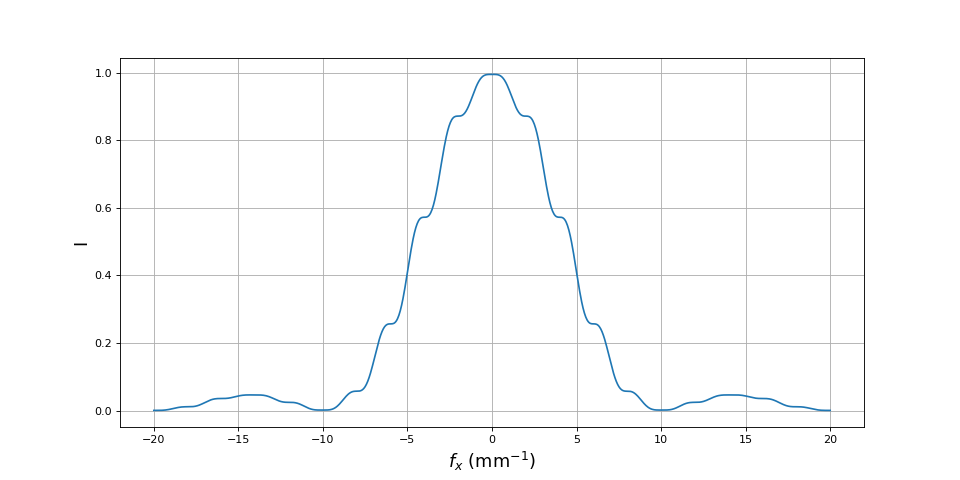 fig7.pdf
fig7.pdf
De part est d'autre du maximum d'intensité, celle-ci décroît de manière monotone. Il n'y a plus à proprement parler de franges d'interférences mais il y a tout de même des points d'inflexion, contrairement à ce que prévoit la théorie pour des fentes infiniment fines.
Lorsque a tend vers zéro, l'intégrale à calculer s'écrit :
Le calcul de cet intégrale se fait sans difficulté. On obtient :
ou encore :
D'où l'on déduit le facteur de visibilité des franges (ou contraste):
qui est le module de la fonction de corrélation pour .
Si les fentes sont assez fines (par rapport la distance d) pour que la fonction de corrélation soit à peu près constante sur chaque fente, chaque fente est éclairée de manière cohérence et on a [1]:
On peut se demander dans quelle mesure cette expression reste valable pour des largeurs de fente relativement grandes. Comparons la courbe obtenue par cette relation avec celle obtenue pas intégration numérique :
def intensite2(a,d,fx_max,lx,N):
fx = np.linspace(-fx_max,fx_max,N)
return fx,(np.sinc(fx*a))**2*0.5*(1+np.sinc(lx*d/(lamb*zs))*np.cos(2*np.pi*fx*d))
a = 0.1
d = 0.5
lx = 0.2
(fx,I1) = intensite(a,d,20,lx,1000)
(fx,I2) = intensite2(a,d,20,lx,1000)
figure(figsize=(12,6))
plot(fx,I1/I1.max(),label='I')
plot(fx,I2/I2.max(),label='$I_2$')
grid()
legend(loc='upper right')
xlabel(r"$f_x\ (\rm mm^{-1})$",fontsize=16)
ylabel("I",fontsize=16)
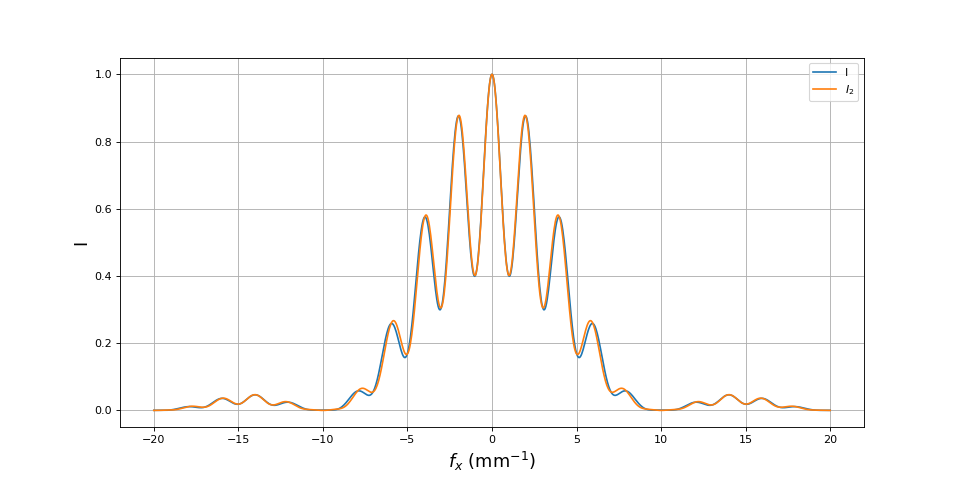 fig8.pdf
fig8.pdf
Pour ces valeurs, la formule approchée convient. Voici la comparaison pour les mêmes fentes mais une fente F plus large :
a = 0.1
d = 0.5
lx = lamb*zs/d
(fx,I1) = intensite(a,d,20,lx,1000)
(fx,I2) = intensite2(a,d,20,lx,1000)
figure(figsize=(12,6))
plot(fx,I1/I1.max(),label='I')
plot(fx,I2/I2.max(),label='$I_2$')
grid()
legend(loc='upper right')
xlabel(r"$f_x\ (\rm mm^{-1})$",fontsize=16)
ylabel("I",fontsize=16)
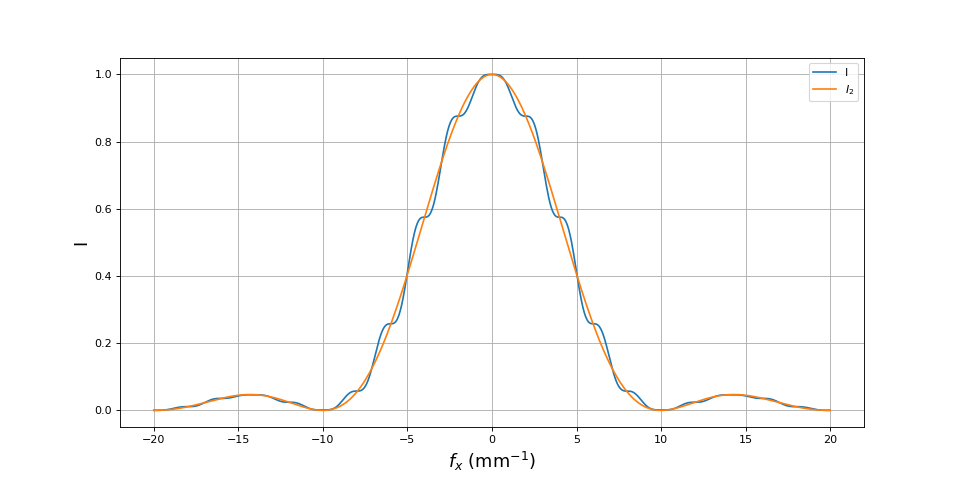 fig9.pdf
fig9.pdf
Pour cette valeur de , qui annule la fonction de corrélation entre les centres des deux fentes, les deux courbes sont très différentes. Nous avons bien sûr vérifié que le nombre de points pour l'intégration numérique est suffisant. Pour cette valeur de , on peut dire qu'il n'y a plus de franges d'interférences mais il y a tout de même des points d'inflexion qui n'existent pas dans la courbe I2(x). En réalité, il y a bien des interférences car, étant donné que les fentes ont une largeur non négigeable (par rapport à d), il existe bien des pairs de points (dont la distance est inférieure à d) qui donnent des interférences. L'annulation complète du contraste des interférences ne se produit que si les fentes sont infiniment fines. La forme de la courbe est confirmée expérimentalement plus loin.
Voici la comparaison pour une fente encore plus large :
a = 0.1
d = 0.5
lx = lamb*zs/d*1.5
(fx,I1) = intensite(a,d,20,lx,1000)
(fx,I2) = intensite2(a,d,20,lx,1000)
figure(figsize=(12,6))
plot(fx,I1/I1.max(),label='I')
plot(fx,I2/I2.max(),label='$I_2$')
grid()
legend(loc='upper right')
xlabel(r"$f_x\ (\rm mm^{-1})$",fontsize=16)
ylabel("I",fontsize=16)
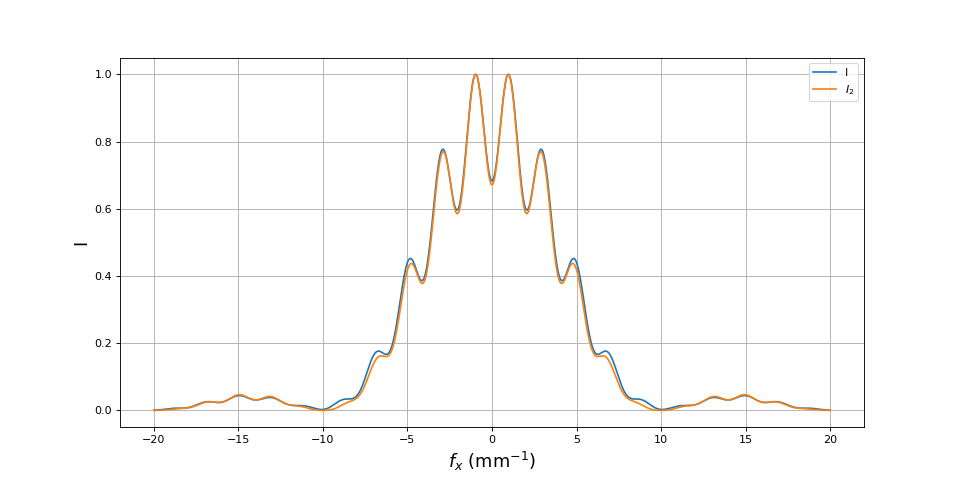 fig10.pdf
fig10.pdf
Voyons ce qu'il en est si les fentes F1 et F2 sont plus larges :
a = 0.2
d = 0.5
lx = 0.1
(fx,I1) = intensite(a,d,20,lx,1000)
(fx,I2) = intensite2(a,d,20,lx,1000)
figure(figsize=(12,6))
plot(fx,I1/I1.max(),label='I')
plot(fx,I2/I2.max(),label='$I_2$')
grid()
legend(loc='upper right')
xlabel(r"$f_x\ (\rm mm^{-1})$",fontsize=16)
ylabel("I",fontsize=16)
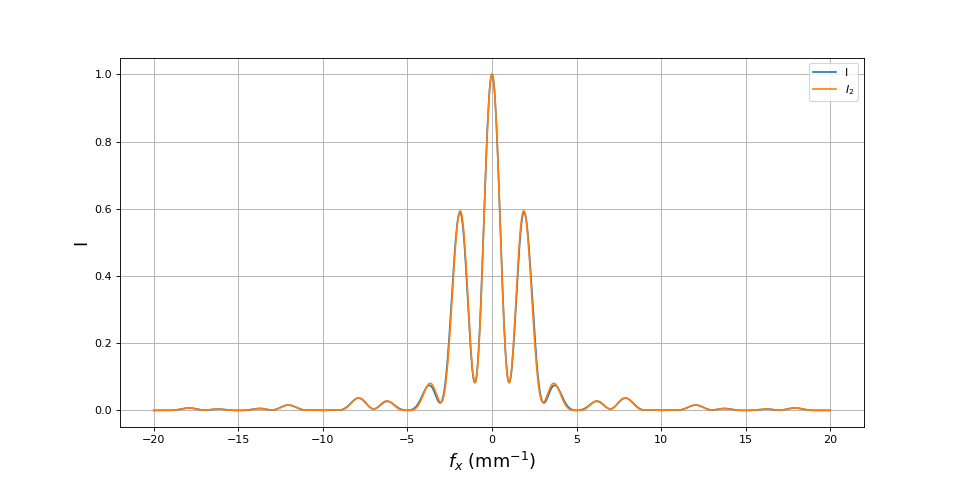 fig11.pdf
fig11.pdf
a = 0.2
d = 0.5
lx = 0.2
(fx,I1) = intensite(a,d,20,lx,1000)
(fx,I2) = intensite2(a,d,20,lx,1000)
figure(figsize=(12,6))
plot(fx,I1/I1.max())
plot(fx,I2/I2.max())
grid()
legend(loc='upper right')
xlabel(r"$f_x\ (\rm mm^{-1})$",fontsize=16)
ylabel("I",fontsize=16)
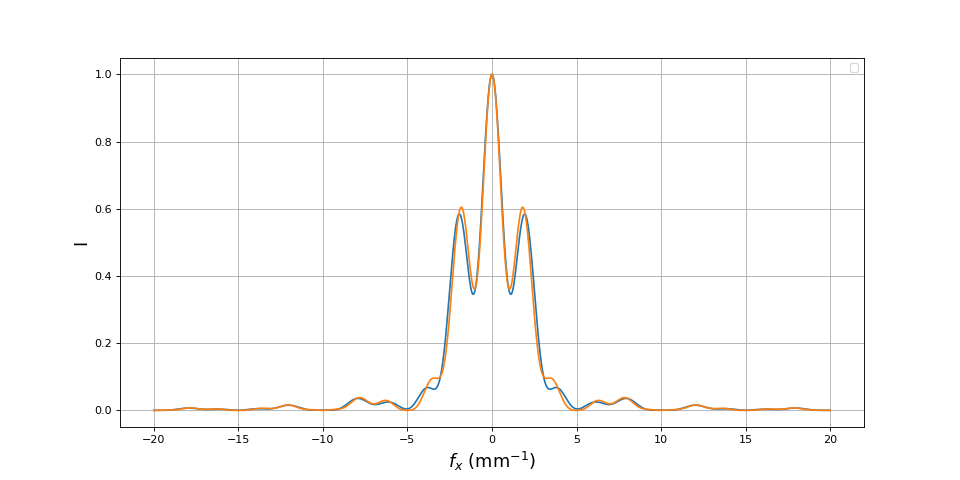 fig12.pdf
fig12.pdf
a = 0.2
d = 0.5
lx = lamb*zs/d
(fx,I1) = intensite(a,d,20,lx,1000)
(fx,I2) = intensite2(a,d,20,lx,1000)
figure(figsize=(12,6))
plot(fx,I1/I1.max())
plot(fx,I2/I2.max())
grid()
legend(loc='upper right')
xlabel(r"$f_x\ (\rm mm^{-1})$",fontsize=16)
ylabel("I",fontsize=16)
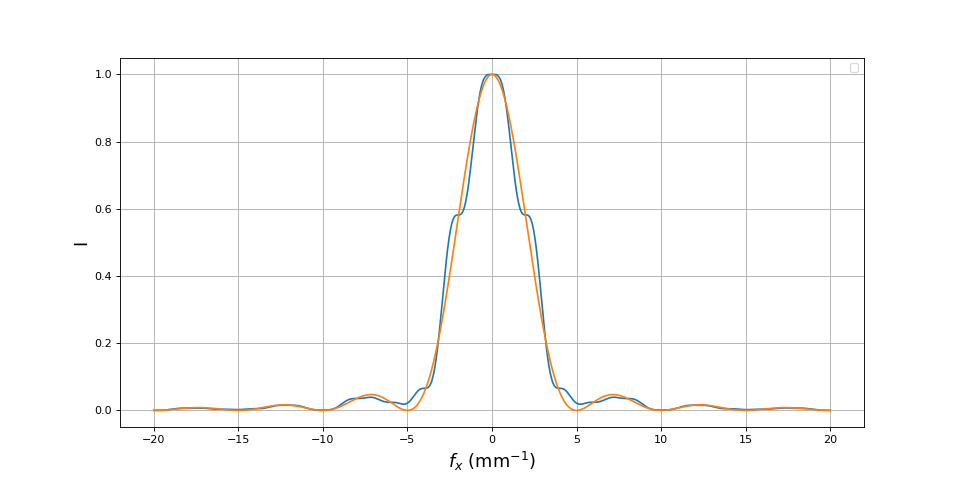 fig13.pdf
fig13.pdf
Ces comparaisons montrent que l'expression donnent une courbe très proche de celle obtenue par un calcul plus précis, excepté au voisinage d'une annulation du contraste.
3. Expérience
3.a. Montage simple
L'expérience est réalisée avec une lampe à vapeur de sodium, qui émet une lumière quasi monochromatique de longueur d'onde λ=589 nm. Les caractéristiques des deux bifentes utilisées sont :
- Bi-fente 1 : a=70 μm et d=430 μm.
- Bi-fente 2 : a=70 μm et d=230 μm.
Les distances sont mesurées avec une régle graduée. L'imprécision des distances vient de l'évaluation difficile de la position exacte des plans où se trouvent les fentes et du plan où se trouve le capteur. La distance entre la fente F et la bi-fente est . La distance entre la bi-fente et le plan d'observation est .
L'intensité en fonction de x est relevée avec une barette CCD contenant 3647 pixels dont chacun a une largeur de 8 micromètres. Le convertisseur analogique-numérique a une précision de 16 bits.
Voici les profils d'intensité pour la bi-fente 1 et différentes valeurs de . La valeur 1 de l'intensité correspond au maximum du convertisseur A/N.
def tracer(n,lx):
[x,I] = np.loadtxt('young-Na-%d-Ds370-D300-b%d.txt'%(n,lx),unpack=True,skiprows=1)
plot(x,I,label=r"$\ell_x=%0.2f\,\rm mm$"%(lx/100))
figure(figsize=(12,16))
subplot(611)
tracer(1,10)
ylim(0,0.5)
grid()
legend(loc='upper right')
ylabel(r"$I$",fontsize=16)
subplot(612)
tracer(1,20)
ylim(0,0.5)
grid()
legend(loc='upper right')
ylabel(r"$I$",fontsize=16)
subplot(613)
tracer(1,30)
ylim(0,0.5)
grid()
legend(loc='upper right')
ylabel(r"$I$",fontsize=16)
subplot(614)
tracer(1,40)
ylim(0,0.5)
grid()
legend(loc='upper right')
ylabel(r"$I$",fontsize=16)
subplot(615)
tracer(1,50)
ylim(0,0.5)
grid()
legend(loc='upper right')
ylabel(r"$I$",fontsize=16)
subplot(616)
tracer(1,60)
ylim(0,0.5)
grid()
legend(loc='upper right')
ylabel(r"$I$",fontsize=16)
xlabel(r"$x\,\rm mm$",fontsize=16)
ylabel(r"$I$",fontsize=16)
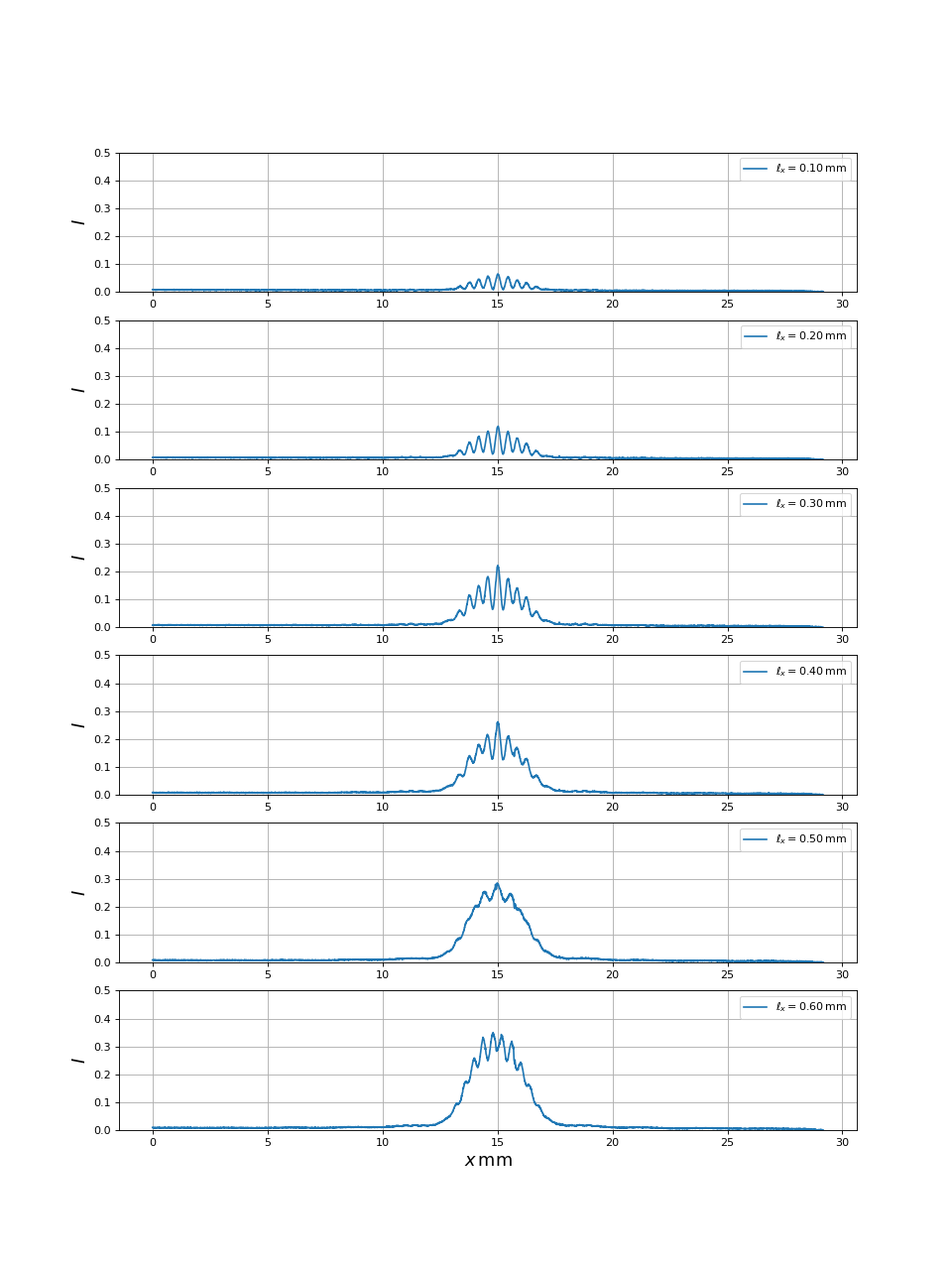 fig14.pdf
fig14.pdf
Pour cette configuration, la première annulation du contraste devrait en théorie se produire pour la largeur suivante de :
a = 70e-3
d = 430e-3
lamb = 589e-6
zs = 370
lx = lamb*zs/d
print(lx) --> 0.5068139534883721
Voici la courbe d'intensité pour une largeur très proche de celle-ci :
figure(figsize=(12,6))
tracer(1,50)
ylim(0,0.5)
grid()
legend(loc='upper right')
ylabel(r"$I$",fontsize=16)
xlabel(r"$x\,\rm mm$",fontsize=16)
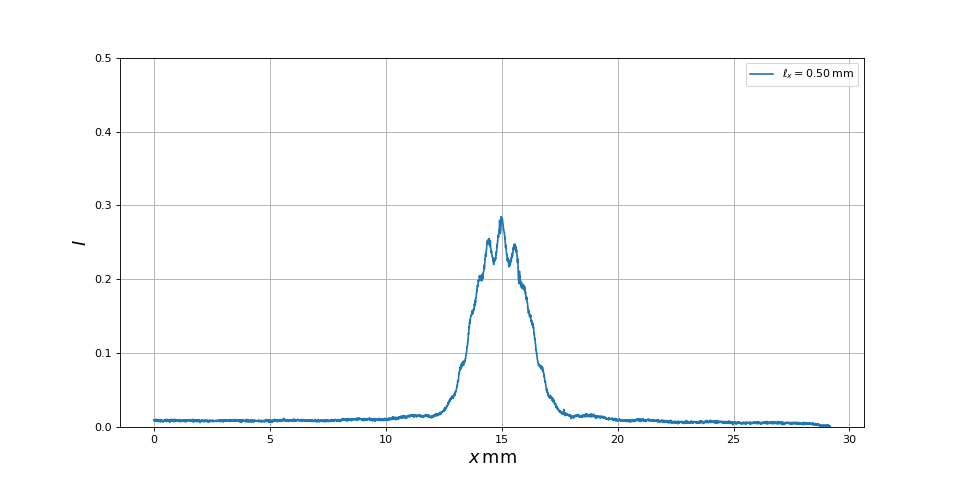 fig15.pdf
fig15.pdf
Voici la valeur théorique de l'interfrange :
z = 300
i = lamb/d*z
print(i) --> 0.41093023255813954
Compararons à la valeur expérimentale :
figure(figsize=(12,6))
lx = 10
[x,I] = np.loadtxt('young-Na-%d-Ds370-D300-b%d.txt'%(1,lx),unpack=True,skiprows=1)
x0=15.02
plot(x,I,label=r"$\ell_x=%0.2f\,\rm mm$"%(lx/100))
y1 = 0.3
plot([x0,x0],[0,y1],'k--')
for k in [1,2,3]:
plot([x0+k*i,x0+k*i],[0,y1],'k--')
plot([x0-k*i,x0-k*i],[0,y1],'k--')
ylim(0,y1)
xlim(10,20)
grid()
legend(loc='upper right')
ylabel(r"$I$",fontsize=16)
xlabel(r"$x\,\rm mm$",fontsize=16)
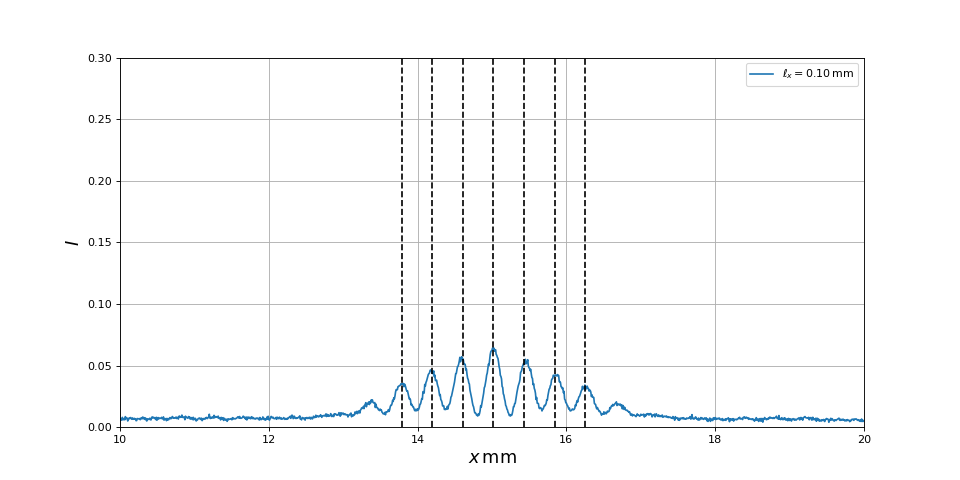 fig16.pdf
fig16.pdf
Voici les profils d'intensité pour la bi-fente 2 et différentes valeurs de :
figure(figsize=(12,16))
subplot(611)
tracer(2,20)
ylim(0,0.6)
grid()
legend(loc='upper right')
ylabel(r"$I$",fontsize=16)
subplot(612)
tracer(2,40)
ylim(0,0.6)
grid()
legend(loc='upper right')
ylabel(r"$I$",fontsize=16)
subplot(613)
tracer(2,60)
ylim(0,0.6)
grid()
legend(loc='upper right')
ylabel(r"$I$",fontsize=16)
subplot(614)
tracer(2,80)
ylim(0,0.6)
grid()
legend(loc='upper right')
ylabel(r"$I$",fontsize=16)
subplot(615)
tracer(2,90)
ylim(0,0.6)
grid()
legend(loc='upper right')
ylabel(r"$I$",fontsize=16)
subplot(616)
tracer(2,100)
ylim(0,0.6)
grid()
legend(loc='upper right')
ylabel(r"$I$",fontsize=16)
xlabel(r"$x\,\rm mm$",fontsize=16)
ylabel(r"$I$",fontsize=16)
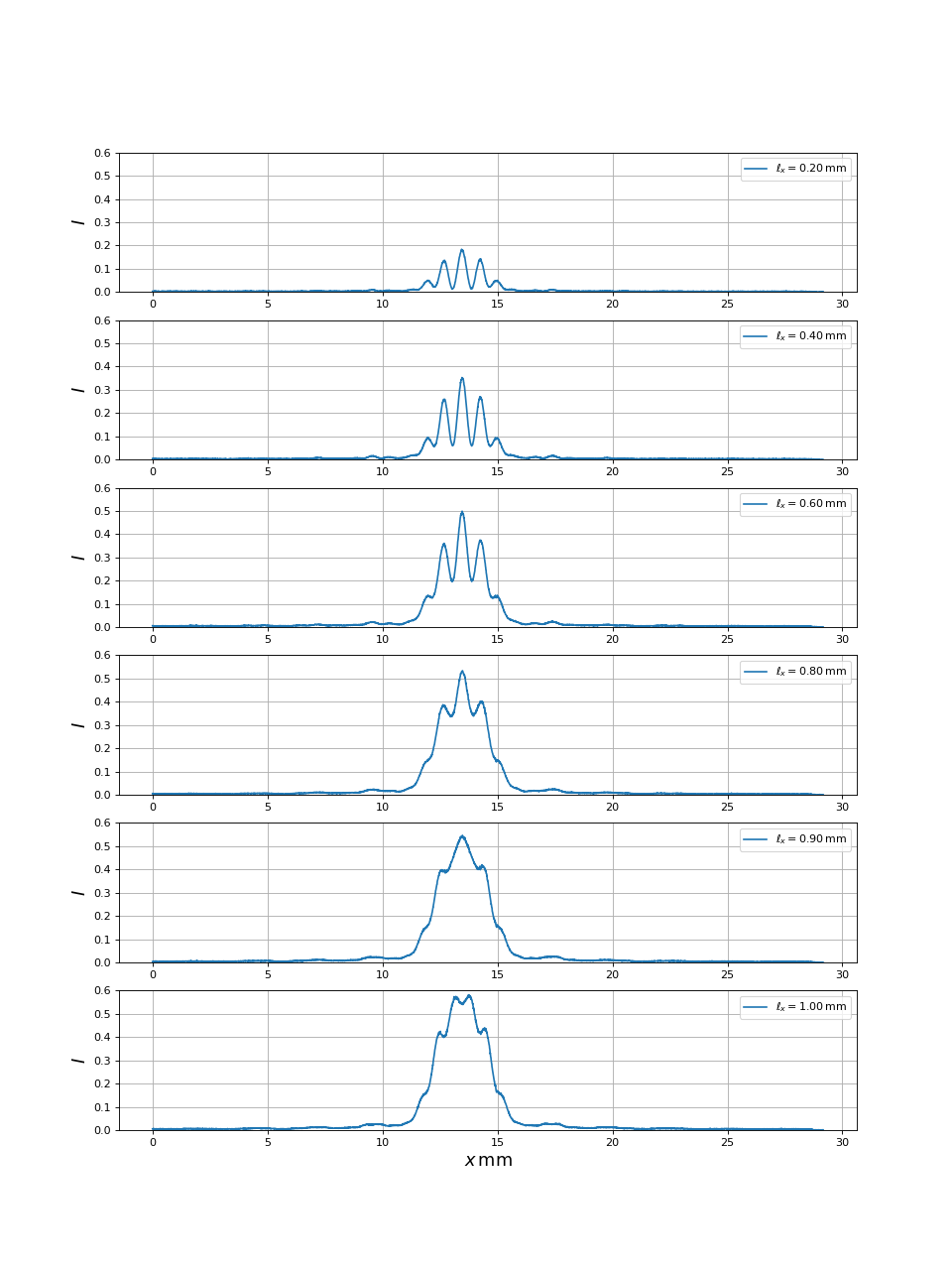 fig17.pdf
fig17.pdf
Pour cette configuration, la première annulation du contraste devrait en théorie se produit pour la larguer suivante de :
a = 70e-3
d = 230e-3
lamb = 589e-6
zs = 370
lx = lamb*zs/d
print(lx) --> 0.9475217391304348
Voici la valeur théorique de l'interfrange :
z = 300
i = lamb/d*z
print(i) --> 0.7682608695652173
Compararons à la valeur expérimentale :
figure(figsize=(12,6))
lx = 20
[x,I] = np.loadtxt('young-Na-%d-Ds370-D300-b%d.txt'%(2,lx),unpack=True,skiprows=1)
x0=13.46
plot(x,I,label=r"$\ell_x=%0.2f\,\rm mm$"%(lx/100))
y1 = 0.3
plot([x0,x0],[0,y1],'k--')
for k in [1,2]:
plot([x0+k*i,x0+k*i],[0,y1],'k--')
plot([x0-k*i,x0-k*i],[0,y1],'k--')
ylim(0,y1)
xlim(5,20)
grid()
legend(loc='upper right')
ylabel(r"$I$",fontsize=16)
xlabel(r"$x\,\rm mm$",fontsize=16)
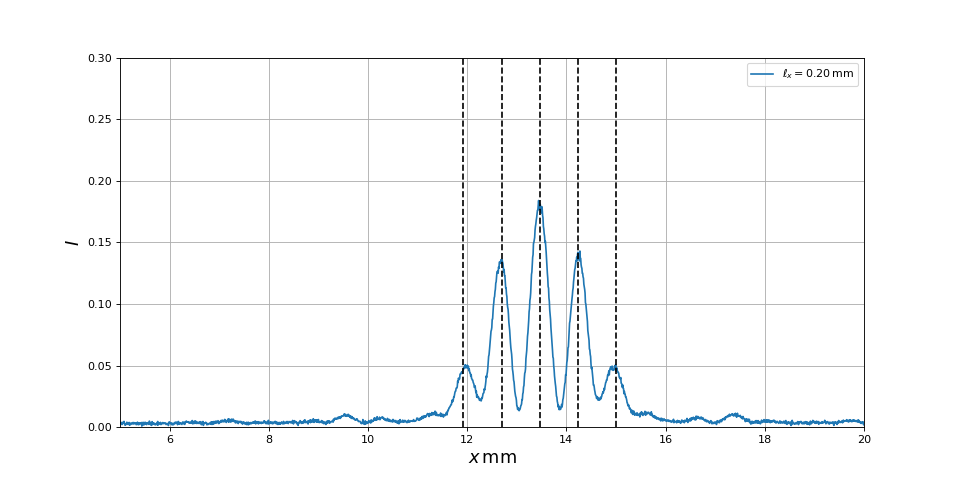 fig18.pdf
fig18.pdf
3.b. Montage de Fraunhofer
Ce montage, qui utilise deux lentilles convergentes, permet en principe d'être plus proche des conditions de l'approximation de Fraunhofer. Nous employons des lentilles de focales f'1=200 mm et f'2=400 mm. Le réglage consiste à placer la fente F sur le plan focal objet de L1 par la méthode d'auto-collimation (au moyen d'un miroir plan) puis à placer le capteur sur le plan focal image de L2 en formant l'image de la fente F sur ce capteur. La précision de ces réglages est de l'ordre de plus ou moins 2 mm.
Voici les profils d'intensité pour la bi-fente 2 et différentes valeurs de .
def tracer(n,lx):
[x,I] = np.loadtxt('young-Na-%d-f1=200-f2=400-b%d.txt'%(n,lx),unpack=True,skiprows=1)
plot(x,I,label=r"$\ell_x=%0.2f\,\rm mm$"%(lx/100))
figure(figsize=(12,16))
subplot(611)
tracer(2,10)
ylim(0,0.5)
grid()
legend(loc='upper right')
ylabel(r"$I$",fontsize=16)
subplot(612)
tracer(2,20)
ylim(0,0.5)
grid()
legend(loc='upper right')
ylabel(r"$I$",fontsize=16)
subplot(613)
tracer(2,30)
ylim(0,0.5)
grid()
legend(loc='upper right')
ylabel(r"$I$",fontsize=16)
subplot(614)
tracer(2,40)
ylim(0,0.5)
grid()
legend(loc='upper right')
ylabel(r"$I$",fontsize=16)
subplot(615)
tracer(2,50)
ylim(0,0.5)
grid()
legend(loc='upper right')
ylabel(r"$I$",fontsize=16)
subplot(616)
tracer(2,60)
ylim(0,0.5)
grid()
legend(loc='upper right')
ylabel(r"$I$",fontsize=16)
xlabel(r"$x\,\rm mm$",fontsize=16)
ylabel(r"$I$",fontsize=16)
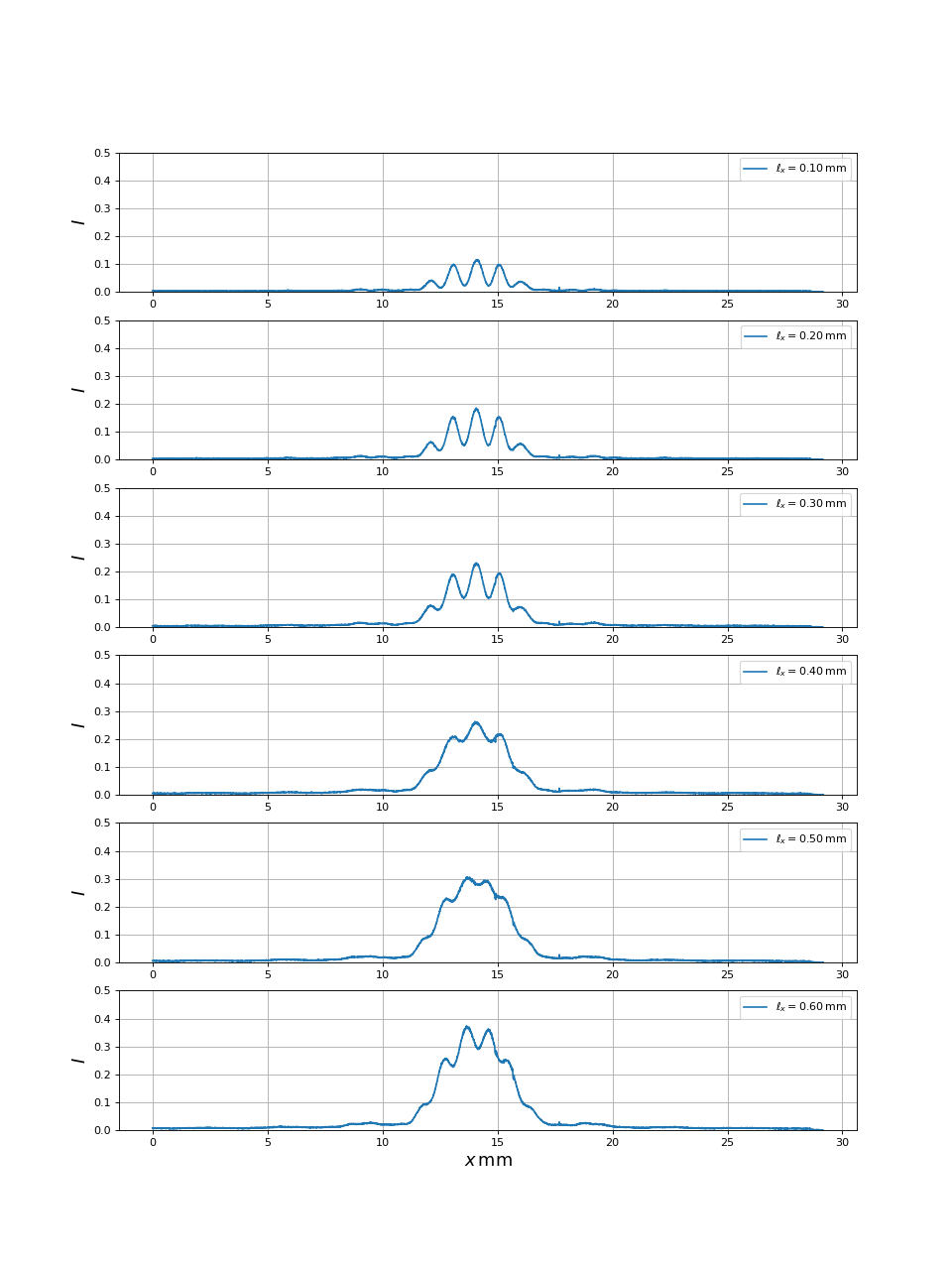 fig19.pdf
fig19.pdf
Pour cette configuration, la première annulation du contraste devrait en théorie se produire pour la largeur suivante de :
a = 70e-3
d = 230e-3
lamb = 589e-6
f1 = 200
f2 = 400
lx = lamb*f1/d
print(lx) --> 0.5121739130434783
Voici la valeur théorique de l'interfrange :
z = 300
i = lamb/d*f2
print(i) --> 1.0243478260869565
Compararons à la valeur expérimentale :
figure(figsize=(12,6))
lx = 20
[x,I] = np.loadtxt('young-Na-%d-f1=200-f2=400-b%d.txt'%(2,lx),unpack=True,skiprows=1)
x0=14.07
plot(x,I,label=r"$\ell_x=%0.2f\,\rm mm$"%(lx/100))
y1 = 0.3
plot([x0,x0],[0,y1],'k--')
for k in [1,2]:
plot([x0+k*i,x0+k*i],[0,y1],'k--')
plot([x0-k*i,x0-k*i],[0,y1],'k--')
ylim(0,y1)
xlim(5,20)
grid()
legend(loc='upper right')
ylabel(r"$I$",fontsize=16)
xlabel(r"$x\,\rm mm$",fontsize=16)
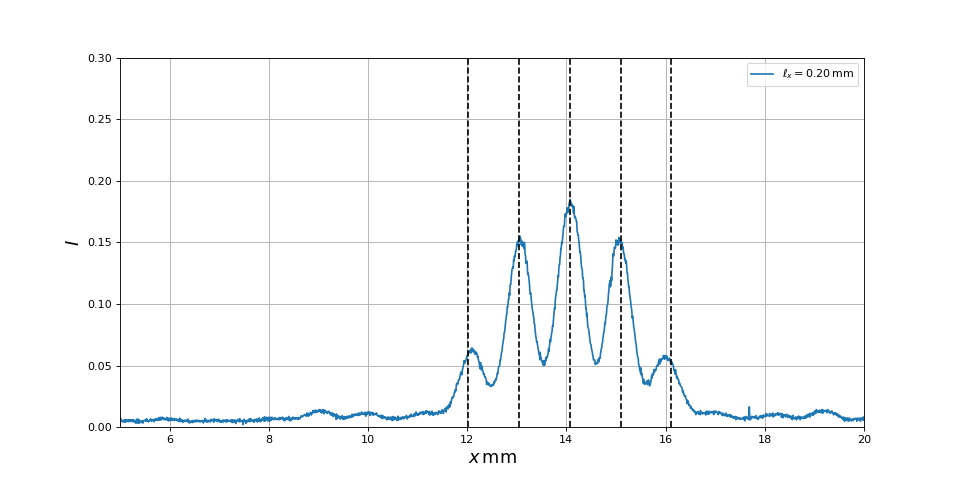 fig20.pdf
fig20.pdf
Contrairement à ce qu'on pouvait espérer, le montage à deux lentilles donne un accord moins bon avec le résultat théorique. Il est probable que le réglage de ce montage soit en réalité plus imprécis que la mesure des distances dans le montage sans lentilles. Par ailleurs, comme déjà remarqué, ce montage donne théoriquement des résultats plus proches de l'approximation de Fraunhofer mais à condition que les lentilles soient parfaitement stigmatiques, ce qu'elles ne sont évidemment pas (et ce point est difficile à quantifier). Il faut remarquer à ce propos que la distance focale utilisée pour les calculs est celle marquée sur les lentilles et que cette distance focale dépend en réalité de la longueur d'onde. Une étude plus précise nécessiterait donc une mesure préalable de la distance focale des lentilles à la longueur d'onde utilisée et une procédure de réglage du dispositif plus précise.