Boussole chaotique : résonances principales

1. Introduction

L'équation du mouvement d'une boussole dans un champ fixe et un champ tournant est :

$$\begin{array}{cc}\hfill & \frac{d\theta }{dt}=u\hfill \\ \hfill & \frac{du}{dt}=-{\omega }_1^{2}sin\theta -{\omega }_2^{2}sin(\theta -\phi )\hfill \\ \hfill & \frac{d\phi }{dt}=\Omega \hfill \end{array}$$

Voir Boussole chaotique : définition du problème pour plus de précisions.

On se place dans le cas où le champ fixe et le champ tournant ont la même intensité :

$${\omega }_1={\omega }_2$$

Le paramètre de stochasticité est dans ce cas :

$$s=\frac{2{\omega }_1}{\Omega }=4a_1$$

On étudie tout d'abord le mouvement lorsque ce paramètre est petit.

2. Résonances pour s=0.1

Les paramètres de l'équation sont a1=a2=s/4=0.025.

Les trajectoires pour lesquelles la boussole oscille autour du champ fixe constituent la résonance autour du champ fixe.

La résonance autour du champ tournant est constituée des trajectoires pour lesquelles la boussole suit le champ tournant, tout en oscillant autour. Pour représenter une telle trajectoire sur la section de Poincaré, on pose le changement de variable :

$${\theta }_1=\theta -\Omega t=\theta -2\pi t$$

Chargement des modules et définition de l'équation différentielle :

import dynode.main as dyn
import numpy
from matplotlib.pyplot import *
import math
import numpy.fft
solver=dyn.CVOde(dyn.OdeBoussole,dyn.OdeAdams,dyn.OdeFunctional)
a1=0.025
a2=a1
solver.set_cst([(2*math.pi*a1)**2,(2*math.pi*a2)**2])
reltol=1e-5
abstol=1e-6
        

La fonction suivante trace la section de Poincaré sans changement de variable, pour une condition initiale et un temps maximal donnés :

def poincare(y0,tmax):
    global solver,reltol,abstol
    solver.init(0.0,y0,reltol,[abstol])
    data=solver.solve(1,tmax)
    t = data[0]
    theta = data[1]
    dtheta = data[2]
    plot(theta,dtheta,marker='.',linestyle=" ",markersize=2)
        

La seconde fonction fait la même chose avec le changement de variable introduit plus haut :

def poincare_tournant(y0,tmax):
    global solver,reltol,abstol
    solver.init(0.0,y0,reltol,[abstol])
    data=solver.solve(1,tmax)
    t = data[0]
    theta = data[1]-2*math.pi*t
    dtheta = data[2]
    plot(theta,dtheta,marker='.',linestyle=" ",markersize=2)
        

On trace les sections de Poincaré de résonances autour du champ fixe, et autour du champ tournant, en lançant la boussole à une vitesse angulaire proche de celle du champ :

figure(figsize=(6,12))
xlabel('theta') 
ylabel('dtheta')
tmax=500
init1 = [[0.5,0],[1,0],[2,0],[3,0]]
for y0 in init1:
    poincare(y0,tmax) 
init2=[[0,6.0],[0,6.2],[0,6.3],[0,6.4]]
for y0 in init2:
    poincare_tournant(y0,tmax)
axis([-3,3,-1,8])
        

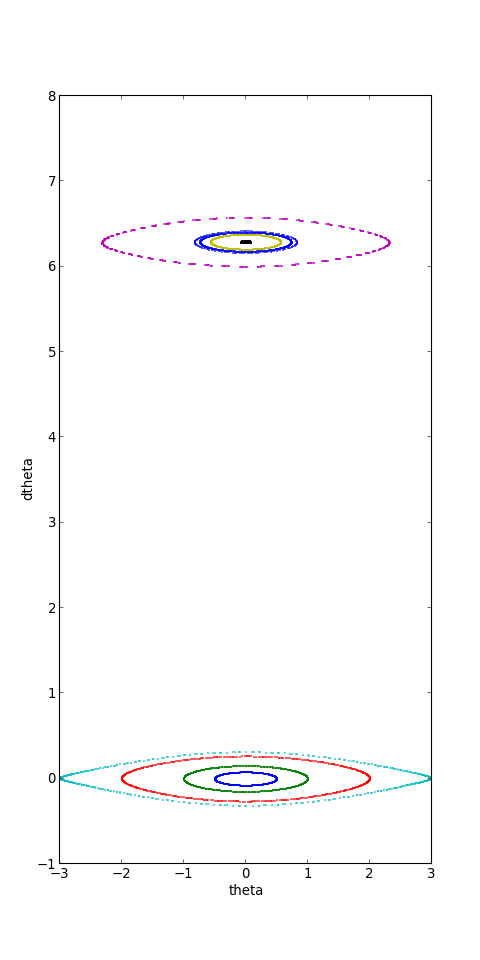plotA.pdf

Dans l'espace des phases, les trajectoires sont inscrites sur des tores (tores et non cylindres à cause de la périodicité de ϕ). Par exemple, pour la résonance du champ fixe, ces tores s'enroulent autour de la position d'équilibre de la boussole dans le champ fixe. Sur la section de Poincaré, l'intersection avec un tore est une courbe fermée. Si la simulation est prolongée, tout point de cette courbe est tôt ou tard coupée par la trajectoire. Cela signifie que la trajectoire recouvre la surface du tore de manière dense.

Lorsque le paramètre de stochasticité est très faible, les tores des deux résonances sont largement séparés.

Considérons une trajectoire particulière de la résonance autour du champ fixe, celle obtenue pour un angle initial de 2.0 radians.

solver.init(0,[2,0],reltol,[abstol])
tmax=5000
data=solver.solve(0.1,tmax)
t = data[0]
theta = data[1]
dtheta = data[2]
figure(figsize=(8,2))
plot(t,theta)
axis([0,2000,-4,4])
        

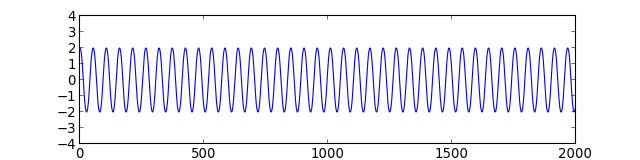plotC.pdf

On trace le spectre de l'évolution temporelle de l'angle :

def spectre(theta,tmax):
    tfd=numpy.fft.fft(theta)
    n=tfd.size
    f=numpy.zeros(n)
    dB=numpy.zeros(n)
    for k in range(n):
        f[k] = (k-1)*1.0/tmax
        dB[k] = 20*math.log10(abs(tfd[k]))
    figure()
    plot(f,dB)
    xlabel('f')
    ylabel('dB')
spectre(theta,tmax)
axis([0,0.2,-20,100])
        

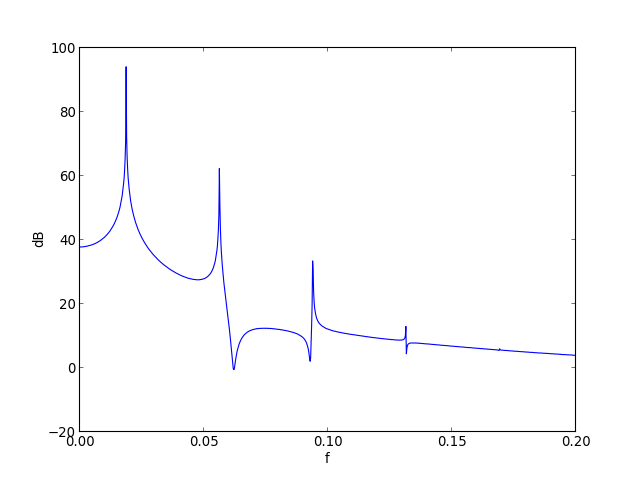plotD.pdf

On retrouve ici le mouvement d'un pendule pesant, avec une fréquence fondamentale de l'oscillation abaissée par rapport à la fréquence 0.025 qu'elle aurait aux petits angles.

Calculons une trajectoire pour un angle initial de 3.1 radians :

theta0=3.1
reltol=1e-7
abstol=1e-10
solver.init(0,[theta0,0],reltol,[abstol])
tmax=5000
data=solver.solve(0.1,tmax)
t = data[0]
theta = data[1]
dtheta = data[2]
spectre(theta,tmax)
axis([0,0.2,-20,100])
        

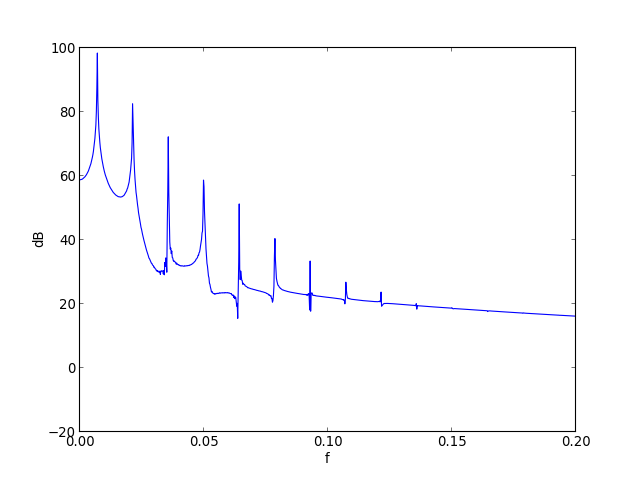plotE.pdf

Voyons la section de Poincaré correspondante :

figure(figsize=(8,4))
xlabel('theta') 
ylabel('dtheta')
poincare([theta0,0],tmax)

        

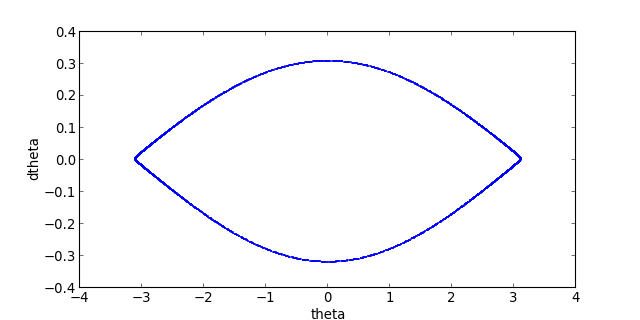plotF.pdf

Là encore, l'effet du champ tournant est très faible. On obtient une trajectoire située très proche de la séparatrice : la boussole passe très près de la position d'équilibre instable θ=π. Remarquer que l'obtention de cette trajectoire nécessite une tolérance relative plus faible (1e-7).

3. Résonances pour s=0.2

a1=0.05
a2=a1
solver.set_cst([(2*math.pi*a1)**2,(2*math.pi*a2)**2])
reltol=1e-5
abstol=1e-6
        

figure(figsize=(6,12))
xlabel('theta') 
ylabel('dtheta')
tmax=500
for y0 in init1:
    poincare(y0,tmax) 
for y0 in init2:
    poincare_tournant(y0,tmax)
axis([-3,3,-1,8])
        

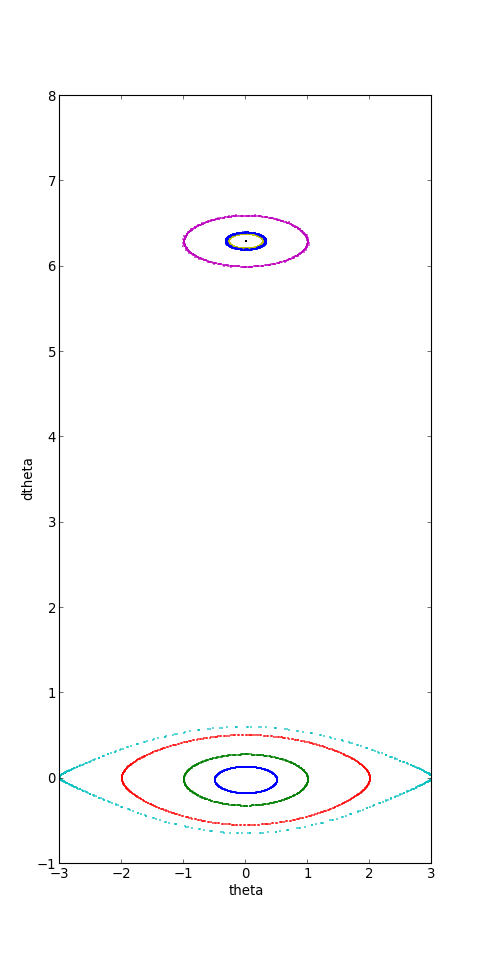plotG.pdf

Pour ce paramètre de stochasticité plus grand, on observe toujours des résonances soit autour du champ fixe, soit autour du champ tournant. Pour cette dernière, les tores sont plus étroits.

4. Résonances pour s=0.8

a1=0.2
a2=a1
solver.set_cst([(2*math.pi*a1)**2,(2*math.pi*a2)**2])
reltol=1e-5
abstol=1e-6
        

figure(figsize=(6,12))
xlabel('theta') 
ylabel('dtheta')
tmax=500
for y0 in init1:
    poincare(y0,tmax) 
for y0 in init2:
    poincare_tournant(y0,tmax)
axis([-3,3,-3,8])
        

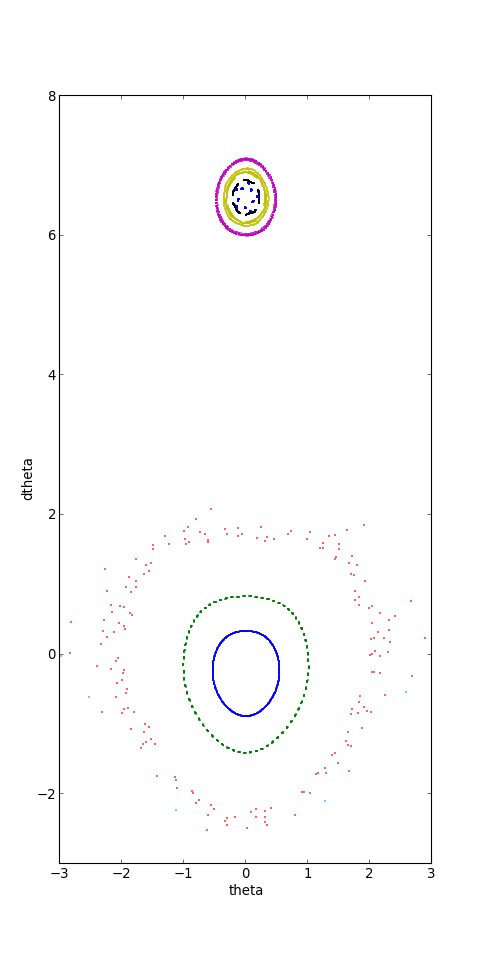plotI.pdf

Pour ce paramètre de stochasticité encore plus grand, on observe toujours des résonances mais une des trajectoires (angle initial de 2 radians) n'est plus périodique.