Télescope de Newton
1. Définition
Le télescope de Newton est le plus simple des télescopes à miroir. Les télescopes de petit diamètre (150 mm à 300 mm) sont souvent de ce type en raison de leur faible coût de fabrication. Il est constitué d'un miroir primaire parabolique et d'un miroir secondaire plan. Ce dernier sert à renvoyer la lumière sur le côté du tube et n'a pas d'effet sur les aberrations géométriques de l'image. Il a une influence sur le champ angulaire de l'image et modifie la figure de diffraction d'une étoile, ce qui a un effet sur la fonction de transfert optique du télescope. Dans un premier temps, on ne triendra pas compte du miroir secondaire.
On considère un miroir parabolique dont le rayon de courbure sur l'axe est 2000 mm, soit une distance focale de 1000 mm. Le diamètre du miroir est 200 mm, ce qui correspond à un rapport f/D de 5. Pour étudier les aberrations géométriques, on utilise le module Python décrit dans Dioptres centrés : optique géométrique. Voici tout d'abord la définition du miroir et le calcul des foyers et plans principaux :
from math import *
from IndiceVerre import *
from Dioptres import *
from pylab import *
n1 = Vide()
n2 = Vide()
n2.negatif()
r = 100
c = -1.0/2000
miroir = Conique(0,c,0.0,n1,n2,r)
sys = SystemeCentre()
sys.ajouter(miroir)
sys.ni.negatif()
sys.matriceTransfert('d')
[Fo,Fi,Ho,Hi] = sys.foyers('d')
focale = Hi.z-Fi.z
print([Fo.z,Fi.z,Ho.z,Hi.z]) --> [-1000.0, -1000.0, 0.0, 0.0]
On remarquera la nécessité de définir un indice négtif (-1) pour le milieu image.
2. Image primaire
On considère l'image primaire d'une étoile obtenue dans le plan focal du miroir. Le profil parabolique du miroir permet d'obtenir une image dénuée d'aberrations géométriques lorsque l'étoile est sur l'axe du miroir. Dans ce cas, le rayon de l'image est celui de la tache de diffraction d'Airy, calculé ci-dessous pour la raie d à 588 nm :
rAiry = 1.2*588e-6/(2*r)*focale
print(rAiry) --> 0.0035279999999999995
Ci dessous le tracé des rayons méridiens pour une étoile sur l'axe :
f = FaisceauParalleleMeridien(10,0.0,-2000,r)
sys.refractionFaisceau(f,'d')
figure()
for Rc in f.listeRayons:
XYZ = Rc.getXYZ(1200)
plot(XYZ[2],XYZ[0],color='y')
xlabel('z')
ylabel('x')
grid(True)
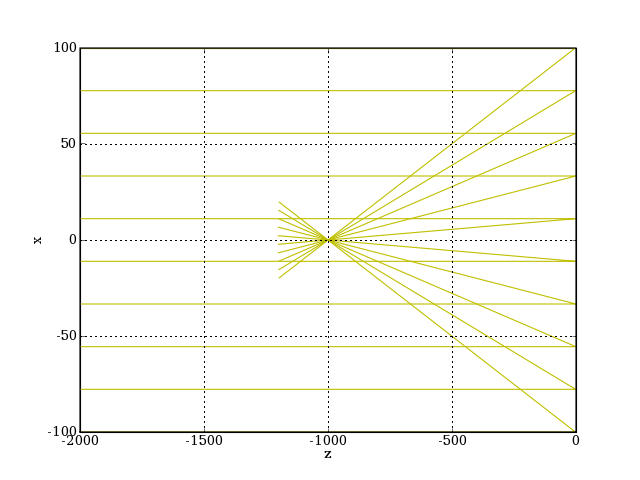plotA.pdf
On ajoute un plan image au système, contenant le foyer :
zi = Fi.z
planImage = PlanImage(zi,r)
sys.ajouter(planImage)
La fonction suivante effectue le tracé des points d'intersection d'un faisceau de rayon cylindrique avec le plan image. L'angle de position de l'étoile par rapport à l'axe est donné en argument. Un cercle représentant la tache de diffraction est tracé à l'abscisse xi.
from matplotlib.patches import Circle
def spotDiagram(sys,alpha,r,xi):
f = FaisceauParallele(20,alpha,-100,r)
sys.refractionFaisceau(f,'d')
for Rc in f.listeRayons:
P = Rc.getRayon().P
plot([P[0]],[P[1]],color='y',marker='.')
angles = linspace(0,2*pi,100)
plot(xi+rAiry*cos(angles),rAiry*sin(angles),color='k')
Voyons tout d'abord d'image sur l'axe :
figure(figsize=(6,6))
spotDiagram(sys,0.0,r,0)
xlabel('x')
ylabel('y')
grid(True)
scale = 0.04
axis([-scale,scale,-scale,scale])
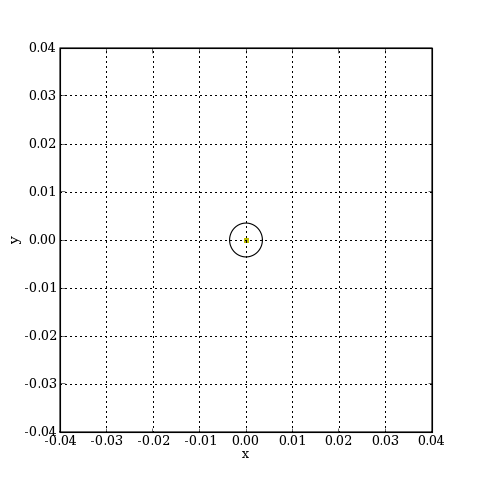plotB.pdf
Comme prévu, l'image de l'optique géométrique est ponctuelle. Le cercle indique la tache de diffraction d'Airy, qui limite la résolution dans ce cas.
Ci-dessous l'image d'une étoile à 0.005 radians de l'axe, soit à 5 mm de l'axe sur le plan image.
fig=figure(figsize=(6,6))
alpha = 0.005
x = alpha*focale
spotDiagram(sys,alpha,r,x)
xlabel('x')
ylabel('y')
grid(True)
axis([x-scale,x+scale,-scale,scale])
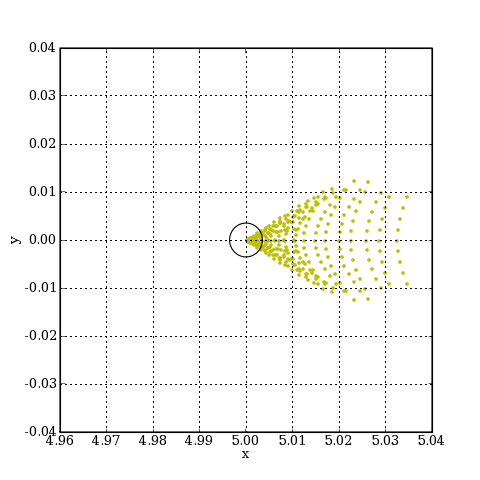plotC.pdf
L'image est altérée par l'aberration de coma et par l'astigmatisme. L'étalement de la lumière se fait bien au delà du rayon de la tache de diffraction.
Ci-dessous l'image d'une étoile à 0.001 radians de l'axe.
fig=figure(figsize=(6,6))
alpha = 0.001
x = alpha*focale
spotDiagram(sys,alpha,r,x)
xlabel('x')
ylabel('y')
grid(True)
axis([x-scale,x+scale,-scale,scale])
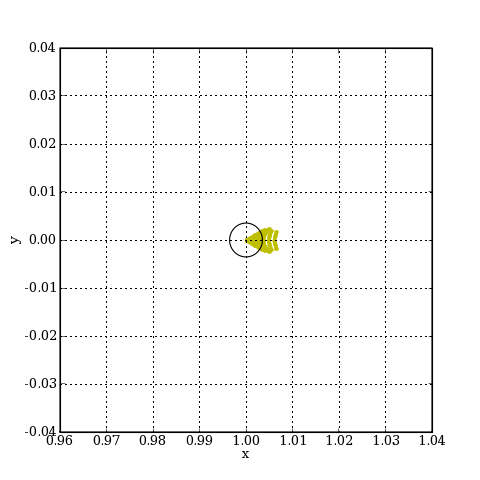plotD.pdf
Dans ce cas, l'image se forme à 1 mm de l'axe. L'effet de la coma est beaucoup plus faible mais elle conduit tout de même à une image plus grande que la tache de diffraction.
On peut en conclure que l'image primaire fournie par un miroir parabolique est fortement affectée par les aberrations dès qu'on s'éloigne de quelques milliradians de l'axe (1 mrad = 3.4 min d'arc). L'utilisation d'un télescope de Newton pour la photographie sur un champ important, par exemple 1 degré, nécessite l'ajout d'un correcteur de coma. L'observation ou la photographie des planètes, dont le diamètre est inférieur à 1 minute d'arc, peut se faire sans correction des aberrations, à condition que l'oculaire soit bien aligné avec l'axe du miroir.
3. Lentille de Barlow
Afin d'agrandir l'image fournie par le miroir parabolique, on ajoute une lentille de Barlow. Il s'agit d'une lentille divergente, qui a pour effet d'augmenter la focale effective du système. En pratique, il faut au minimum un doublet crown-flint pour limiter les aberrations sphériques et chromatiques. La lentille doit être placée en arrière du foyer primaire.
La fonction suivante fournit le système centré constitué du miroir parabolique et de la lentille de Barlow. Celle-ci est constituée d'une lentille biconvexe en verre flint accolée à une lentille biconcave en verre crown dont les rayons de courbure sont donnés en argument. La courbure de la face avant permet de réduire les aberrations sphériques. Le diamètre des lentilles est fixé à 20 mm. La distance d est celle de la lentille frontale par rapport au foyer primaire.
cat = CatalogueVerre()
def systemeBarlow(c1,c2,d):
nb = cat.verre['N-BK7']
na = cat.verre['F5']
na.negatif()
nb.negatif()
ra = 10.0
z = -1000.0+d
e1 = 3.0
e2 = 3.0
c0 = -5e-3
dioptreA = Spherique(z,c0,n2,na,ra)
dioptreB = Spherique(z-e1,c2,na,nb,ra)
dioptreC = Spherique(z-e1-e2,c1,nb,n2,ra)
sys = SystemeCentre()
sys.ajouter(miroir)
sys.ajouter(dioptreA)
sys.ajouter(dioptreB)
sys.ajouter(dioptreC)
barlow = SystemeCentre()
barlow.ajouter(dioptreA)
barlow.ajouter(dioptreB)
barlow.ajouter(dioptreC)
return [barlow,sys]
On fixe la courbure c1, la distance d avec le foyer primaire, puis on trace l'aberration chromatique longitudinale (raies F et C) du système en fonction de la courbure c2 :
c1 = -25e-3
d = 60
c2List = []
y = []
N=10
for k in range(N):
c2 = 10e-3+20e-3/N*k
c2List.append(c2)
[barlow,sys] = systemeBarlow(c1,c2,d)
sys.ni.negatif()
sys.matriceTransfert('F')
[Fo,Fi,Ho,Hi] = sys.foyers('F')
z = Fi.z
sys.matriceTransfert('C')
[Fo,Fi,Ho,Hi] = sys.foyers('C')
y.append(Fi.z-z)
figure()
plot(c2List,y,color='r')
xlabel('c2')
ylabel('ACL')
grid(True)
axis([0.013,0.015,-0.1,0.1])
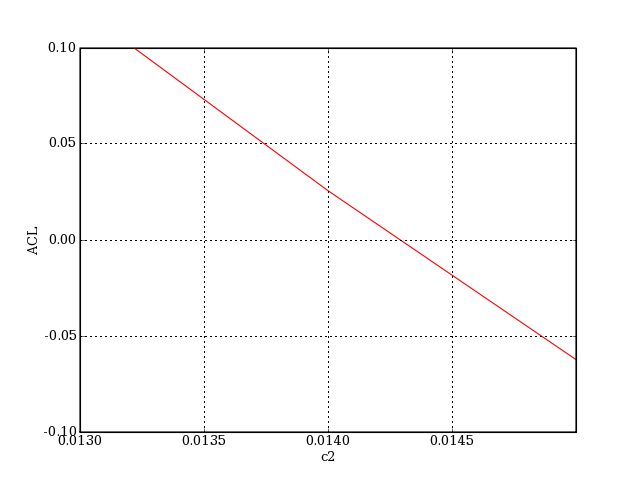plotE.pdf
Pour obtenir un système achromatique, on choisit la courbure qui annule l'aberration chromatique longitudinale des raies F et C :
c2 = 0.0143
On calcule la position des foyers pour la raie d :
[barlow,sys] = systemeBarlow(c1,c2,d)
sys.ni.negatif()
sys.matriceTransfert('d')
[Fo,Fi,Ho,Hi] = sys.foyers('d')
print([Fo.z,Fi.z,Ho.z,Hi.z]) --> [-16781.114198947918, -1048.8182336610339, -14922.264547035536, 810.03141825134662]
L'aberration chromatique secondaire est obtenu en considérant le décalage entre les foyers de la raie F et de la raie d :
sys.matriceTransfert('F')
[Fo,Fi,Ho,Hi] = sys.foyers('F')
z = Fi.z
sys.matriceTransfert('d')
[Fo,Fi,Ho,Hi] = sys.foyers('d')
acl2 = Fi.z - z
print(acl2) --> -0.048992529512361216
Le foyer bleu est donc décalé de 49 micromètres par rapport au foyer jaune. L'apparition de chromatisme est le premier inconvénient de la lentille de Barlow.
On détermine la distance focale de la lentille de Barlow et le grandissement réalisé sur l'image primaire. Les indices des milieux image et objet étant ceux du vide par défaut, il faut ici les rendre négatifs en raison du sens inverse de la lumière.
barlow.ni.negatif()
barlow.no.negatif()
barlow.matriceTransfert('d')
[Fo,Fi,Ho,Hi] = barlow.foyers('d')
focaleBarlow = Fi.z - Hi.z
PObjet = Position(-1000.0) # objet au foyer primaire
g = barlow.grandissement(PObjet,'d')
print(focaleBarlow) --> 117.78950639849654
print(g) --> 1.8588496519123825
La focale image est positive car le foyer image est à droite de la lentille : la lentille de Barlow est bien divergente.
Ci-dessous un tracé des rayons méridiens pour une étoile sur l'axe :
f = FaisceauParalleleMeridien(10,0.0,-500,r)
sys.refractionFaisceau(f,'d')
figure()
for Rc in f.listeRayons:
XYZ = Rc.getXYZ(1200)
plot(XYZ[2],XYZ[0],color='y')
sys.tracerProfils(20,'k')
xlabel('z')
ylabel('x')
grid(True)
axis([-1100,-900,-20,20])
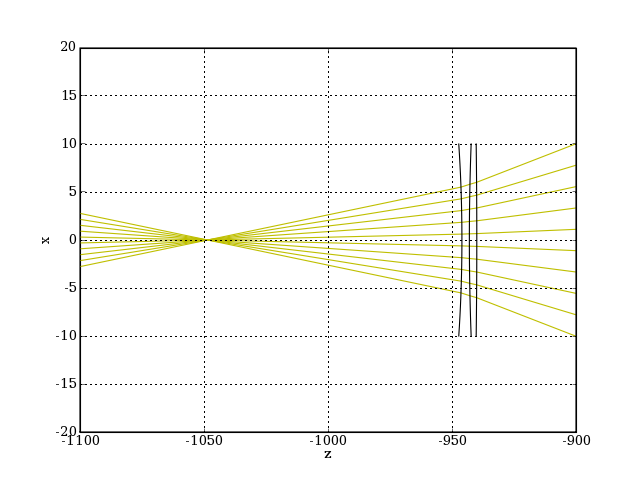plotF.pdf
La lentille de Barlow ainsi obtenue est optimisée pour une distance d=60 mm en arrière du foyer primaire. Si on augmente la distance d le grandissement augmente mais on perd le caractère achromatique.
Voyons en détail la zone de convergence des rayons vers le foyer :
axis([-1049,-1048,-0.1,0.1])
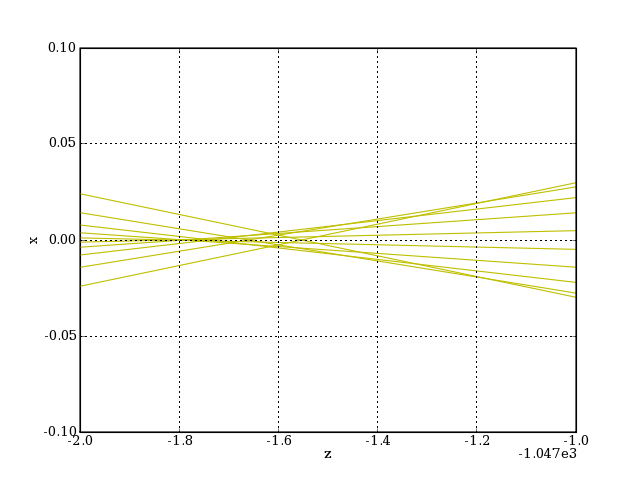plotG.pdf
On voit ici un autre inconvénient de la lentille de Barlow : une légère aberration sphérique qui se traduit par un décalage du point de convergence en fonction de l'angle des rayons. L'amplitude longitudinale du décalage est d'environ 1 mm. On placera le plan image pour obtenir le cercle de moindre confusion. En pratique, cela est obtenu lorsqu'on fait la mise au point sur l'axe.
zi = -1048.6
planImage = PlanImage(zi,r)
sys.ajouter(planImage)
figure(figsize=(6,6))
alpha = 0.0
spotDiagram(sys,alpha,r,0.0)
xlabel('x')
ylabel('y')
grid(True)
scale = 0.04
axis([-scale,scale,-scale,scale])
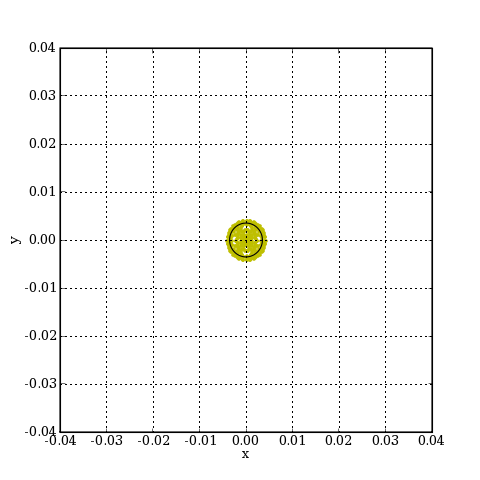plotH.pdf
Contrairement au miroir parabolique seul, l'image se formant sur l'axe est ici affectée d'une aberration sphérique. Néanmoins, celle-ci reste de l'ordre de la tache de diffraction. Voyons l'image à 0.005 radians :
figure(figsize=(6,6))
alpha = 0.005
x = 9.325
spotDiagram(sys,alpha,r,x)
xlabel('x')
ylabel('y')
grid(True)
scale = 0.04
axis([x-scale,x+scale,-scale,scale])
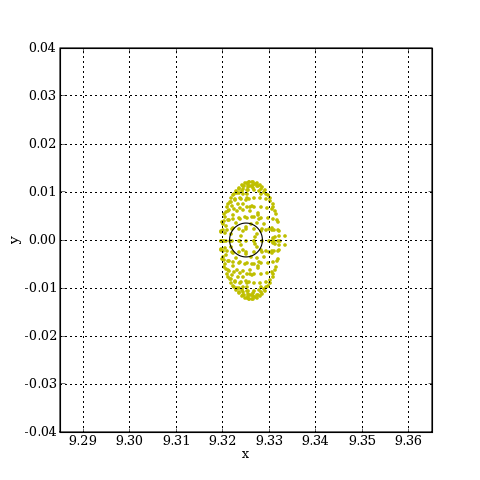plotI.pdf
L'image obtenue est à 9.3 mm de l'axe alors qu'elle était à 5 mm sans la lentille de Barlow. On remarque l'importance des aberrations, avec un étalement de la lumière au delà de la tache d'Airy. Néanmoins, l'aberration de coma est plus faible que sur l'image primaire obtenue pour le même angle, bien que l'image soit deux fois plus loin de l'axe. L'étalement de la lumière se fait plutôt dans la direction y, ce qui provient d'un astigmatisme.
Conclusion : la lentille de Barlow ajoute une aberration sphérique négligeable sur l'axe tout en réduisant l'aberration de coma hors de l'axe. Sur la version modélisée ici, il y a toutefois de l'astigmatisme hors de l'axe. Idéalement, cette lentille devrait être optimisée pour un miroir primaire donné et un grandissement fixé.
Une lentille de Barlow de grandissement 2 a pour effet de doubler le rapport f/D du système, ce qui n'est pas souhaitable pour la photographie des objets peu lumineux. De plus, le champ total visible est certainement réduit.
4. Correcteur de coma
Le correcteur de coma permet de réduire l'aberration de coma sans modifier de rapport f/D du système. On considère ici le cas du correcteur de Ross, constitué de deux lentilles. On reprend la description du correcteur de Ross donnée dans [1].
La fonction suivante construit le système complet formé du miroir parabolique et du correcteur de Ross, celui-ci étant placé à une distance d en arrière du foyer primaire. Les deux lentilles sont en verre crown BK7; leur diamètre est de 50 mm.
def systemeRoss(d):
n = cat.verre['N-BK7']
n.negatif()
r = 25
z = -1000.0+d
dioptreA = Spherique(z,-1.0/93.21,n2,n,r)
dioptreB = Spherique(z-2.01,-1.0/47.31,n,n2,r)
dioptreC = Spherique(z-2.01-5.70,-1.0/215.52,n2,n,r)
dioptreD = Spherique(z-2.01-5.70-5.28,1.0/173.50,n,n2,r)
sys = SystemeCentre()
sys.ajouterListe([miroir,dioptreA,dioptreB,dioptreC,dioptreD])
ross = SystemeCentre()
ross.ajouterListe([dioptreA,dioptreB,dioptreC,dioptreD])
return [ross,sys]
Voyons le tracé des rayons méridiens pour une étoile sur l'axe, le correcteur étant à 50 mm du foyer primaire :
[ross,sys] = systemeRoss(61.0)
f = FaisceauParalleleMeridien(10,0.0,-500,r)
sys.refractionFaisceau(f,'d')
figure()
for Rc in f.listeRayons:
XYZ = Rc.getXYZ(1200)
plot(XYZ[2],XYZ[0],color='y')
sys.tracerProfils(20,'k')
xlabel('z')
ylabel('x')
grid(True)
axis([-1050,-900,-20,20])
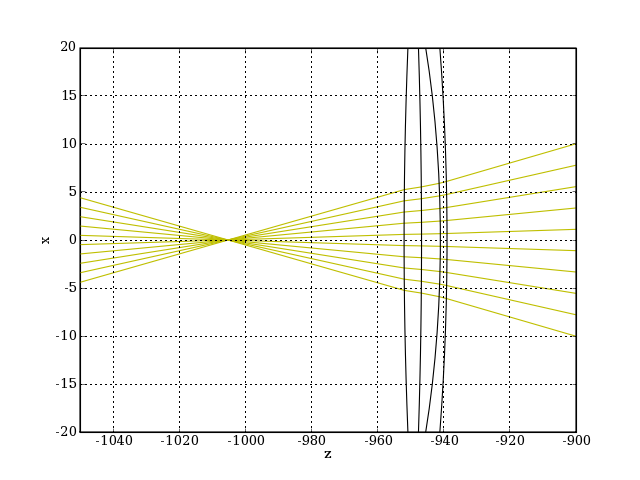plotJ.pdf
Le foyer est très légèrement reculé, ce qui montre que le grandissement est proche de 1. Ci-dessous le détail de la zone du foyer :
axis([-1005.5,-1004.5,-0.1,0.1])
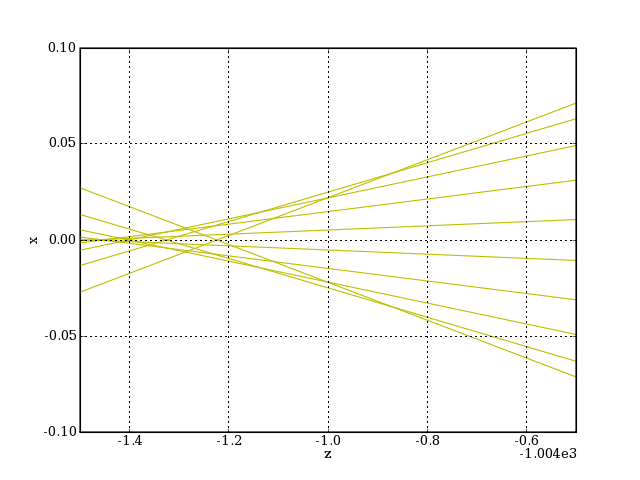plotK.pdf
On remarque la présence d'une aberration sphérique. Le plan image est choisi coïncidant avec le cercle de moindre confusion :
zi = -1005.29
planImage = PlanImage(zi,r)
sys.ajouter(planImage)
figure(figsize=(6,6))
alpha = 0.0
spotDiagram(sys,alpha,r,0.0)
xlabel('x')
ylabel('y')
grid(True)
scale = 0.04
axis([-scale,scale,-scale,scale])
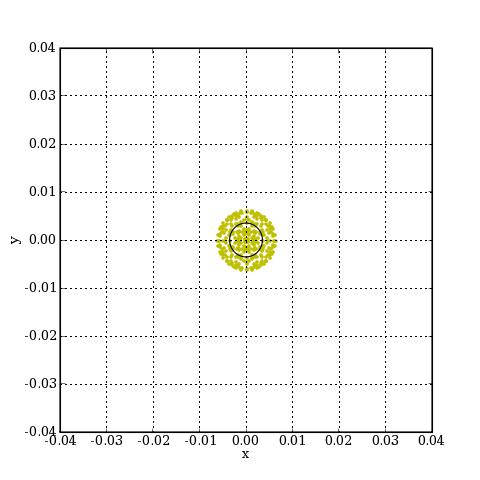plotL.pdf
L'image obtenue est très bonne, comparable à la tache de diffraction. Voyons l'image d'une étoile située à 0.005 radians de l'axe :
figure(figsize=(6,6))
alpha = 0.005
x = 5.11
spotDiagram(sys,alpha,r,x)
xlabel('x')
ylabel('y')
grid(True)
scale = 0.04
axis([x-scale,x+scale,-scale,scale])
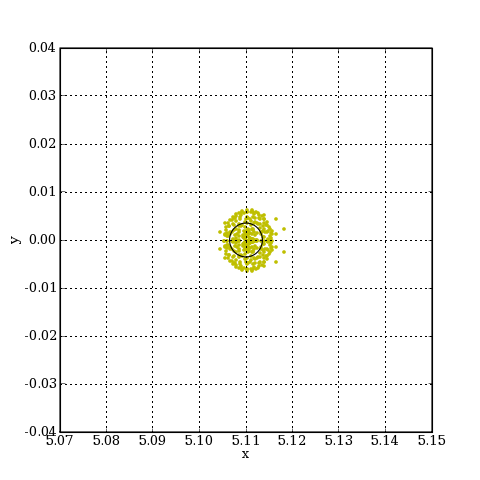plotM.pdf
On constate d'une part que l'image se forme pratiquement à 5 mm de l'axe; le correcteur ne modifie pas la taille de l'image et le rapport f/D est conservé. D'autre part, l'aberration de coma est bien réduite. Sans le correcteur, la queue de coma fait environ 30 micromètres. Le diamètre de l'image est ici comparable à celui de la tache de diffraction (10 micromètres).
