Profondeur de champ

1. Introduction

Pour un système optique centré formant l'image d'objets sur un plan, la profondeur de champ désigne la plage de distances des objets dont l'image sur ce plan peut être considérée comme suffisamment nette.

Dans ce document, on s'intéresse à la profondeur de champ dans le domaine de la photographie, dans le cas où le plan du capteur est perpendiculaire à l'axe optique de l'objectif (ce qui exclut le cas des chambres photographiques). La profondeur de champ dépend de la distance de l'objet sur lequel on fait la mise au point, de la distance focale de l'objectif et de son ouverture. Son calcul repose sur la notion de cercle de confusion.

Le problème est étudié dans le cadre de l'optique géométrique, c'est-à-dire que les phénomènes de diffraction sont négligeables. L'objectif photographique est assimilé à une lentille mince convergente étudiée dans le cadre de l'optique paraxiale (rayons proches de l'axe). La lentille est supposée parfaitement stigmatique, ce qui revient à supposer que les aberrations géométriques de l'objectif sont négligeables. En pratique, l'insuffisance de la profondeur de champ est en effet une cause de manque de netteté plus fréquente que l'astigmatisme de l'objectif.

2. Cercle de confusion

On emploiera le terme image pour désigner deux concepts différents :

• L'image au sens photographique est celle qui se forme sur le capteur. Cette image est transformée en image informatique puis visualisée sur un écran ou bien imprimée.
• L'image d'un point au sens de l'optique (géométrique) est son point conjugué par le système optique, dans la mesure où celui-ci est supposé parfaitement stigmatique.

Dans le cas de la photographie sur film (photographie argentique), il est possible de réaliser une image imprimée au moyen d'un agrandisseur, donc sans passer par une image informatique. Bien sûr, cela ne change rien au problème de la profondeur de champ.

L'image de la scène (au sens photographique) se forme sur le plan où se trouve le capteur (noté Σ). Soit P un point objet et P' son image (au sens optique) par la lentille. Comme l'illustre la figure suivante, si la mise au point n'est pas faite sur le plan transversal contenant P, le point P' ne se trouve pas sur le plan du capteur.

Figure pleine page

On note f la distance focale de la lentille et d son diamètre, qui est déterminé par le diaphragme. L'ouverture de l'objectif est définie par le rapport N=f/d. Les valeurs standards du rapport f/d sont 2.8, 4, 5.6, 8, 11, 16, 22. Par exemple, un rapport f/d de 11 signifie que le diamètre est 11 fois plus petit que la focale. Le rapport entre une valeur standard et la précédente (par exemple entre 4 et 2.8) est approximativement égal à $\sqrt{2}$, ce qui implique que la seconde collecte en principe deux fois plus de lumière que la première, donc que le temps d'exposition sera deux fois plus court. Il est bien sûr possible d'utiliser des valeurs intermédiaires entre les valeurs standards.

La distance entre la lentille et le point objet est notée p; celle entre la lentille et le point conjugué est notée p'. La relation de conjugaison s'écrit :

$$\frac{1}{p\text{'}}+\frac{1}{p}=\frac{1}{f}\text{(1)}$$

Les rayons lumineux qui proviennent du point P forment sur le plan Σ une image (au sens photographique) ayant la forme d'un disque de diamètre c. Le cercle qui limite cette image est le cercle image. Si le plan Σ est le plan conjugé du plan transversal où se trouve P, le diamètre du cercle image est nul.

Le cercle de confusion est le cercle image le plus grand dont le diamètre sur l'image photographique peut être considéré comme négligeable. Si le diamètre du cercle image est inférieur au diamètre du cercle de confusion, l'image photographique de P sera considérée comme ponctuelle. Autrement dit, l'image photographique d'un objet plan situé dans le plan transversal contenant P sera considérée comme nette.

L'évaluation du diamètre du cercle de confusion est délicate, car il dépend de la manière dont l'image finale (écran ou impression) est observée. Les valeurs communément utilisées reposent sur l'hypothèse que l'image finale est une image imprimée observée à une distance de vision telle que l'image dans son ensemble soit visible. Cette hypothèse correspond à un angle de vision de la diagonale de l'image d'environ 60 degrés. On fait aussi l'hypothèse que l'œil, lorsqu'il observe à 25 cm, ne peut discerner deux lignes dont la distance est inférieure à 0,2 mm. Avec ces hypothèses, on obtient la formule suivante pour le diamètre du cercle de confusion :

$$c_{max}=\frac{d_i}{1500}\text{(2)}$$

où d_i est la diagonale du capteur. Par exemple pour un capteur de taille $24\times 36$ mm, le diamètre du cercle de confusion est c_max=0,029 mm.

Il faut remarquer que les valeurs du diamètre de cercle de confusion communément admises sont très largement supérieures à la taille d'un photosite sur le capteur. Par exemple, pour un capteur 24x36 mm contenant 25 Mega-pixels, la taille des photosites est de 5 micromètres, soit environ 6 fois moins que le diamètre du cercle de confusion.

La détermination géométrique du cercle image n'a de sens que si l'optique géométrique s'applique. Le diamètre de la tache de diffraction (tache d'Airy) pour une source de lumière ponctuelle à l'infini est

$$\Phi =2,4\frac{\lambda }{d}f=2,4\lambda N\text{(3)}$$

La prise en compte du caractère ondulatoire de la lumière augmenterait le diamètre du cercle image mais nous ne pouvons savoir a priori quelle serait l'ampleur de cette augmentation. Nous pouvons cependant écrire un critère simple de validité de la théorie géométrique : le diamètre de la tache de diffraction doit être inférieur au diamètre du cercle de confusion. Cette condition conduit à :

$$N<\frac{c_{max}}{2,4\lambda }\text{(4)}$$

Avec une longueur d'onde moyenne de 500 nm et pour le format 24x36 mm, la condition est N<24. En pratique, il est rare qu'on emploie dans ce format un nombre d'ouverture supérieur à 16.

3. Profondeur de champ

Pour déterminer la profondeur de champ, il faut considérer les deux point images P'₁ et P'₂ (situés sur l'axe optique) dont les images photographiques ont un diamètre égal à celui du cercle de confusion (le premier étant le plus proche de la lentille). On notera P' le point image situé sur le plan Σ et sur l'axe.

Figure pleine page

Soient P₁,P₂,P les points conjugués de P'₁,P'₂,P'. Le point P a son image optique sur le plan Σ. La mise au point est donc faite sur ce point (ou sur tout point situé dans le même plan transversal). Le point P₁ est le point le plus éloigné dont l'image photographique a un diamètre inférieur ou égal au diamètre du cercle de confusion; le point P₂ est le plus proche. En conséquence, tous les plans compris entre P₁ et P₂ donnent une image photographique considérée comme nette. La profondeur de champ est en principe la différence des deux distances p₁-p₂ mais il est plus intéressant de donner l'intervalle [p₂,p₁]. Dans le cas où la construction précédente conduit à p'₁<f il faut prendre en fait p'₁=f et le point P₁ est à l'infini.

Le théorème de Thalès conduit aux deux relations suivantes :

$$\begin{array}{ccc}\hfill & \frac{p\text{'}-p{\text{'}}_1}{p{\text{'}}_1}=\frac{c_{max}}{d}\hfill & \hfill \text{(5)}\\ \hfill & \frac{p{\text{'}}_2-p\text{'}}{p{\text{'}}_2}=\frac{c_{max}}{d}\hfill & \hfill \text{(6)}\end{array}$$

qui conduisent à

$$\begin{array}{ccc}\hfill & p{\text{'}}_1=\frac{p\text{'}}{1+\frac{c_{max}}{d}}\hfill & \hfill \text{(7)}\\ \hfill & p{\text{'}}_2=\frac{p\text{'}}{1-\frac{c_{max}}{d}}\hfill & \hfill \text{(8)}\end{array}$$

Si $p{\text{'}}_1<f$ on prend $p{\text{'}}_1=f$.

L'utilisation de la relation de conjugaison permet d'obtenir :

$$\begin{array}{ccc}\hfill & \frac{1}{p_1}=\frac{1}{f}-(1+\frac{c_{max}}{d})(\frac{1}{f}-\frac{1}{p})\hfill & \hfill \text{(9)}\\ \hfill & \frac{1}{p_2}=\frac{1}{f}-(1-\frac{c_{max}}{d})(\frac{1}{f}-\frac{1}{p})\hfill & \hfill \text{(10)}\end{array}$$

où p est la distance du point conjugué de P', c'est-à-dire la distance de l'objet sur lequel la mise au point est faite (distance de mise au point). Ces relations peuvent se simplifier :

$$\begin{array}{ccc}\hfill & \frac{1}{p_1}=\frac{1}{p}-\frac{c_{max}}{d}(\frac{1}{f}-\frac{1}{p})\hfill & \hfill \text{(11)}\\ \hfill & \frac{1}{p_2}=\frac{1}{p}+\frac{c_{max}}{d}(\frac{1}{f}-\frac{1}{p})\hfill & \hfill \text{(12)}\end{array}$$

En introduisant le nombre d'ouverture $N=\frac{f}{d}$, on obtient :

$$\begin{array}{ccc}\hfill & \frac{1}{p_1}=\frac{1}{p}-\frac{c_{max}N}{f}(\frac{1}{f}-\frac{1}{p})\hfill & \hfill \text{(13)}\\ \hfill & \frac{1}{p_2}=\frac{1}{p}+\frac{c_{max}N}{f}(\frac{1}{f}-\frac{1}{p})\hfill & \hfill \text{(14)}\end{array}$$

Dans le cas où $p{\text{'}}_1<f$, on obtient $\frac{1}{p_1}<0$ et $\frac{1}{p_1}$ doit être pris égal à 0. Remarquons que p₁ est comme prévu plus grand que p₂.

La fonction suivante calcule les distances p₁ et p₂. La valeur par défaut du diamètre du cercle de confusion est celle du format 24x36 mm.

import numpy as np

def profondeur(p,f,N,cmax=29e-3):
    # f en mm
    # p en m
    p = p*1e3
    p1 = 1/(1/p-cmax*N/f*(1/f-1/p))
    p2 = 1/(1/p+cmax*N/f*(1/f-1/p))
    if p1<0: p1=float('inf')
    return (p1/1e3,p2/1e3)
                   

Voici un exemple :

f = 35 # focale en mm
N = 11
p = 10 # objet à 10 m
p1,p2 = profondeur(p,f,N)
                   

print((p1,p2))
--> (inf, 2.7816664339149857)

Pour cette distance de mise au point et cette ouverture, la profondeur de champ est donc l'intervalle de 2,8 mètres à l'infini. Voici le résultat avec une ouverture plus petite :

f = 35 # focale en mm
N = 2.8
p = 10 # objet à 10 m
p1,p2 = profondeur(p,f,N)
                   

print((p1,p2))
--> (29.458303875029458, 6.022147738769555)

La profondeur de champ s'étend de 6 à 29 mètres environ. Pour une focale et une distance de mise au point donnée, la profondeur de champ est d'autant plus petite que l'ouverture est grande. Voici le résultat pour la même ouverture et la même distance mais pour une focale plus grande :

f = 50 # focale en mm
N = 2.8
p = 10 # objet à 10 m
p1,p2 = profondeur(p,f,N)
                   

print((p1,p2))
--> (14.774889779322244, 7.557573595651674)

Une focale plus grande donne une profondeur de champ plus faible.

On peut faire une représentation graphique de p₁ et p₂ en fonction de p :

f = 50 # focale en mm
N = 8
p = np.linspace(1,10,100)
Np = len(p)
p1 = np.zeros(Np)
p2 = np.zeros(Np)
for i in range(Np):
    (p1[i],p2[i]) = profondeur(p[i],f,N)
    
from matplotlib.pyplot import *
figure(figsize=(16,8))
plot(p,p1,label=r"$p_1$")
plot(p,p2,label=r"$p_2$")
grid()
xlabel("p (m)",fontsize=16)
legend(loc='upper left',fontsize=16)
                   

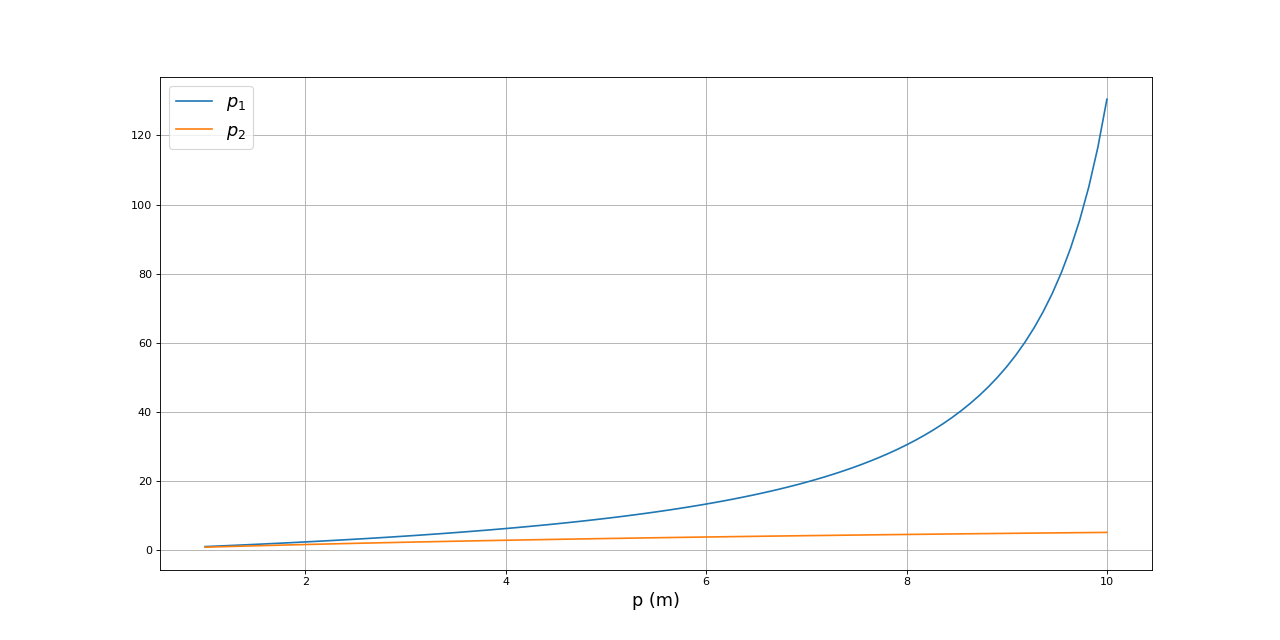fig1.pdf

4. Distance hyperfocale

La distance hyperfocale est la distance p de mise au point telle que $p_1=\infty$. On obtient cette distance en posant $\frac{1}{p_1}=0$ :

$$p_h=f\frac{1+\frac{c_{max}N}{f}}{\frac{c_{max}N}{f}}\text{(15)}$$

Même dans le cas extrême d'une focale très petite (16 mm) et d'une ouverture très petite (N=22), le rapport $\frac{c_{max}N}{f}$ est très petit donc on a :

$$p_h\approx \frac{f^2}{c_{max}N}\text{(16)}$$

La distance la plus proche correspondant à $p_1=\infty$ est :

$$p_2\approx \frac{p_h}{2}\text{(17)}$$

Lorsqu'on fait la mise au point à la distance hyperfocale, on a donc une profondeur de champ qui s'étend de la moitié de cette distance à l'infini. La distance hyperfocale peut être utilisée en photographie de paysage lorsque le premier plan est très proche et l'arrière plan à l'infini. La distance hyperfocale est la distance de mise au point optimale pour maximiser la profondeur de champ.

Supposons que l'on fasse la mise au point à l'infini : $p=\infty$. On a dans ce cas :

$$\begin{array}{ccc}\hfill & p_1=\infty \hfill & \hfill \text{(18)}\\ \hfill & p_2=\frac{f^2}{c_{max}N}\hfill & \hfill \text{(19)}\end{array}$$

La distance hyperfocale est donc aussi (approximativement) la distance du plan net le plus proche lorsque la mise au point est faite à l'infini.

La fonction suivante calcule l'hyperfocale (avec les relations exactes) :

def hyperfocale(f,N,cmax=29e-3):
    # f en mm
    p = f*(1+cmax*N/f)/(cmax*N/f)
    p2 = 1/(1/p+cmax*N/f*(1/f-1/p))
    return (p/1e3,p2/1e3)
               

Voici un exemple :

f = 35
N = 11
p,p2 = hyperfocale(f,N)
               

print((p,p2))
--> (3.8751253918495294, 1.937562695924765)

Pour une focale de 35 mm et une ouverture f/11, on a donc une profondeur de champ qui s'étend de 1,9 m à l'infini si l'on fait la mise au point sur un plan situé à 3,9 mètres environ. La mise au point sur un plan situé à une distance précise peut être difficile avec un objectif ne possédant pas d'indication de distance, comme c'est malheureusement le cas de la plupart des objectifs de dernière génération. Il faut alors repérer un objet dont la distance est à peu près la distance hyperfocale et faire la mise au point sur cet objet. Pour une focale de 35 mm et une ouverture f/11, si le premier plan se trouve à plus de 1,9 m, on peut aussi faire la mise au point à l'infini. Une manière pratique de faire la mise au point sur la distance hyperfocale (avec un appareil photo numérique) serait la suivante : prendre une photo avec la mise au point à l'infini, examiner la photo à la loupe pour repérer le plan le plus lointain dont l'image est floue; ce plan est à la distance hyperfocale donc on refait une photo en faisant la mise au point sur ce plan.

Voici des courbes représentant la distance hyperfocale en fonction du nombre d'ouverture, pour différentes distances focales (format 24x36 mm) :

N = np.linspace(2,16,100)
figure(figsize=(16,8))
(p,p2) = hyperfocale(24,N)
plot(N,p,label="f=24 mm")
(p,p2) = hyperfocale(35,N)
plot(N,p,label="f=35 mm")
(p,p2) = hyperfocale(50,N)
plot(N,p,label="f=50 mm")
xlabel("N",fontsize=16)
ylabel("p (m)",fontsize=16)
grid()
legend(loc='upper right',fontsize=16)
title('Hyperfocale 24x36 mm',fontsize=16)
                

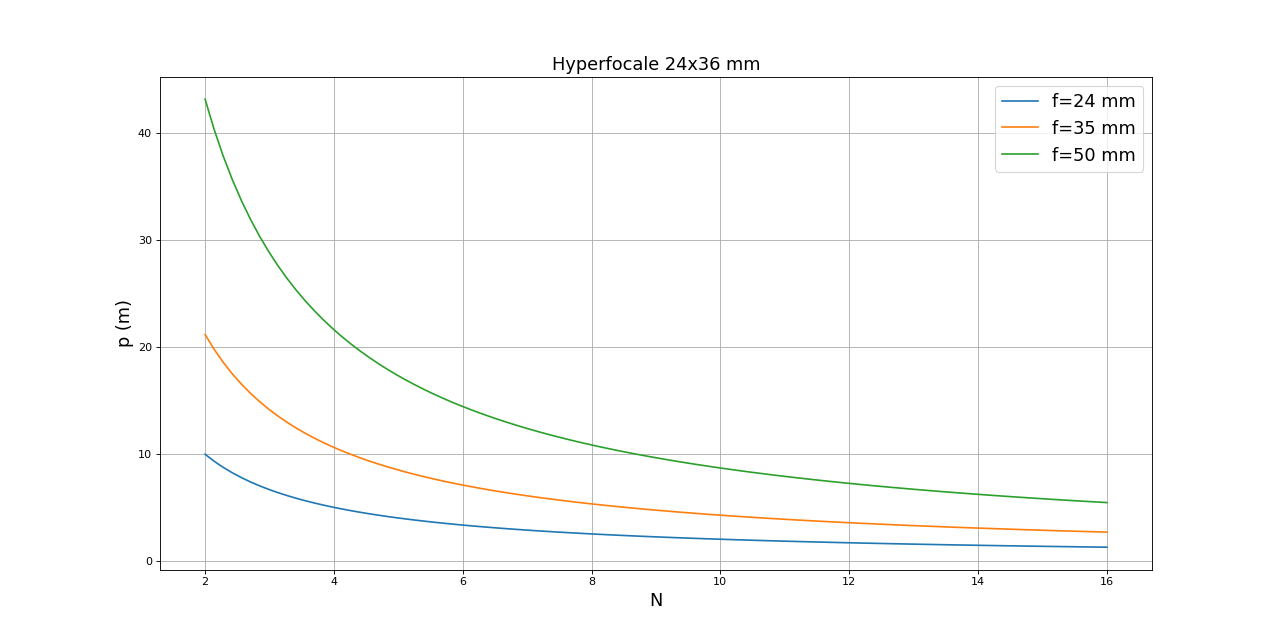fig2.pdf

Pour une utilisation à faible ouverture, l'échelle suivante est plus pertinente :

xlim(5.6,16)
ylim(0,15)
                

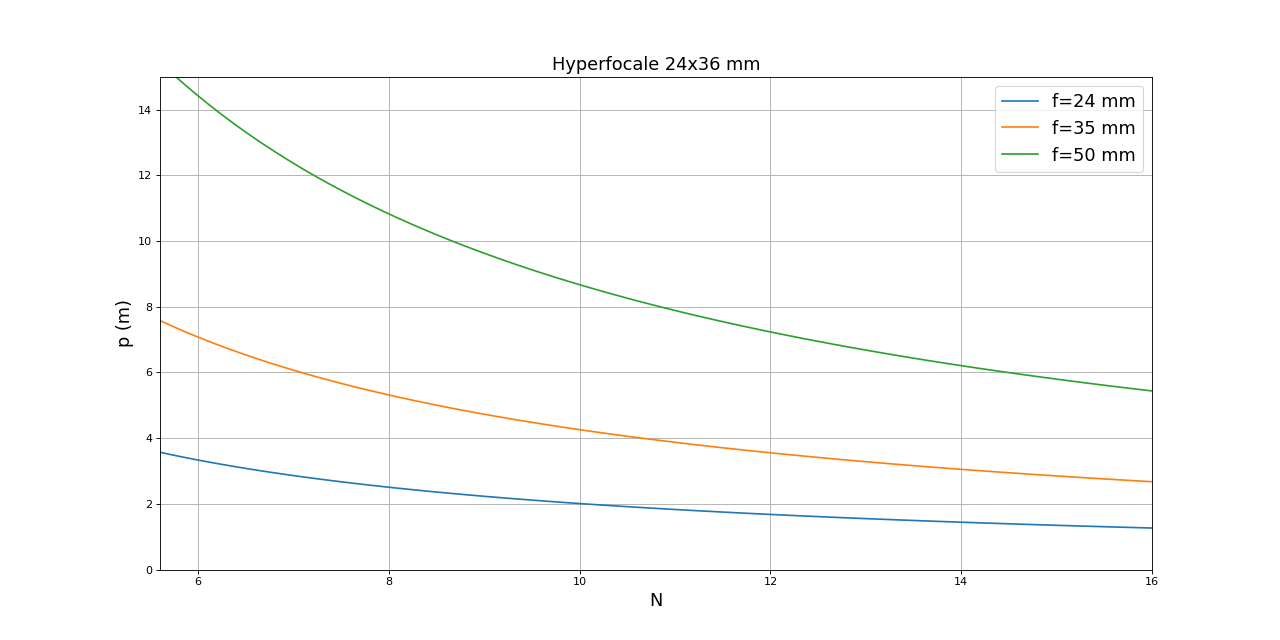fig3.pdf

Ces courbes permettent de choisir rapidement l'ouverture en fonction de la distance du premier plan (à supposer qu'on souhaite qu'il soit net). Par exemple, pour une focale de 24 mm, si le premier plan est à 1 mètre, la distance hyperfocale doit être égale à 2 mètres, donc N doit être égal à 10. Dans ce cas, il faut faire la mise au point sur un objet situé à 2 mètres puis fermer le diaphragme au moins à 10.

Il ne faut pas oublier que ces valeurs d'hyperfocale sont calculées avec une valeur du diamètre cercle de confusion qui correspond à une vision de la photographie imprimée à une certaine distance. Si l'on juge la netteté en observant la photo sur un écran à l'échelle 1 (1 pixel sur la photo = 1 pixel sur l'écran), ces valeurs d'hyperfocales sont sous-estimées (le diamètre du cercle de confusion est surestimé). Nous avons par exemple constaté, avec une focale de 35 mm et N=11 que la distance hyperfocale évaluée sur un écran à l'échelle 1 est plutôt de l'ordre de 8 m (soit le double de la valeur calculée). Si en revanche on regarde la photo dans son intégralité (sur un écran 24 pouces), une distance hyperfocale de 4 mètres convient. Si cela est possible, on a donc toujours intérêt à fermer le diaphragme un peu plus que ce prévoit le modèle avec le diamètre de cercle de confusion c_max=0,029 mm.

Remarque : les nombres d'ouverture plus grands que 16 sont rarement utilisés en format 24x36 car ils conduisent à une baisse de la netteté de l'image à cause de la diffraction. Cependant, il peut arriver qu'un nombre supérieur à 16 conduise tout de même à une image finale plus nette en raison de l'augmentation de profondeur de champ. L'insuffisance de la profondeur de champ est, avec le bougé du photographe ou du sujet, la cause la plus fréquente de manque de netteté d'une image photographique, loin devant la qualité de stigmatisme de l'objectif (qui est très bonne sur les objectifs récents). Si l'on veut obtenir le maximum de netteté pour un objet donné, il faut évidemment faire la mise au point sur cet objet.

5. Influence de la taille du capteur.

Pour une scène de largeur angulaire donnée, la profondeur de champ dépend de la taille du capteur. Comparons un capteur 24x36 à un capteur de taille 16x24 mm (format APS-C). Pour obtenir la même largeur angulaire, il faut utiliser une distance focale 1,5 fois plus grande pour le premier. Par exemple, une focale de 50 mm en format 24x36 est équivalente à une focale 35 mm en 16x24. Pour un capteur de cette taille, le diamètre du cercle de confusion est c_max=0,019 mm (il est 1,5 fois plus petit que pour le format 24x36).

Voici une comparaison des profondeurs de champ de ces deux capteurs pour un même angle de champ et une ouverture donnée :

fa = 50 # focale en mm
fb = 35
N = 5.6
p = np.linspace(1,10,100)
Np = len(p)
p1a = np.zeros(Np)
p2a = np.zeros(Np)
p1b = np.zeros(Np)
p2b = np.zeros(Np)
for i in range(Np):
    (p1a[i],p2a[i]) = profondeur(p[i],fa,N,cmax=29e-3)
    (p1b[i],p2b[i]) = profondeur(p[i],fb,N,cmax=19e-3)
    
from matplotlib.pyplot import *
figure(figsize=(16,8))
plot(p,p1a,'r-',label=r"$p_1,\ 24\times 36$")
plot(p,p2a,'r--',label=r"$p_2,\ 24\times 36$")
plot(p,p1b,'b-',label=r"$p_1,\ 16\times 24$")
plot(p,p2b,'b--',label=r"$p_2,\ 16\times 24$")
grid()
xlabel("p (m)",fontsize=16)
legend(loc='upper right')
                   

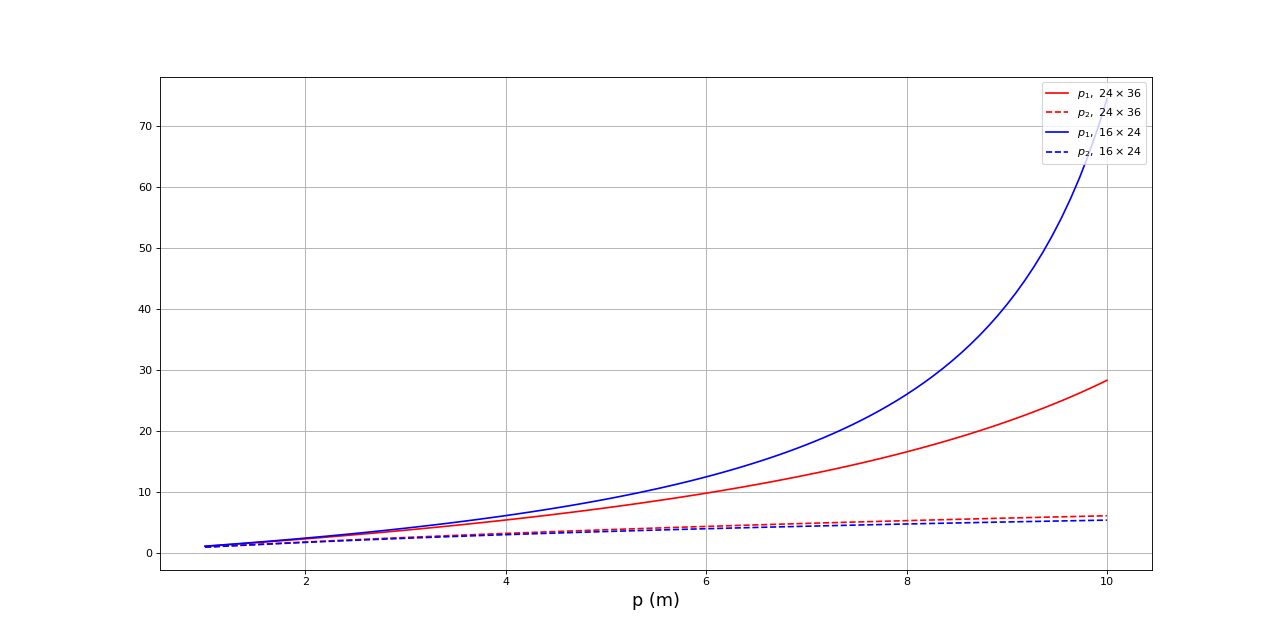fig4.pdf

La taille de capteur plus petite (en bleu) donne une profondeur de champ plus grande que le capteur plus grand (en rouge). La différence est plus marquée pour les grandes distances. Il s'en suit que maximiser la profondeur de champ est beaucoup plus facile avec un petit capteur. Voici les hyperfocales pour le capteur 16x24 mm, avec des focales équivalentes au précédentes :

N = np.linspace(2,16,100)
figure(figsize=(16,8))
(p,p2) = hyperfocale(13,N,cmax=19e-3)
plot(N,p,label="f=23 mm")
(p,p2) = hyperfocale(16,N,cmax=19e-3)
plot(N,p,label="f=16 mm")
(p,p2) = hyperfocale(23,N,cmax=19e-3)
plot(N,p,label="f=23 mm")
(p,p2) = hyperfocale(35,N,cmax=19e-3)
plot(N,p,label="f=35 mm")
xlabel("N",fontsize=16)
ylabel("p (m)",fontsize=16)
grid()
legend(loc='upper right',fontsize=16)
title('Hyperfocale 16x24 mm',fontsize=16)
                

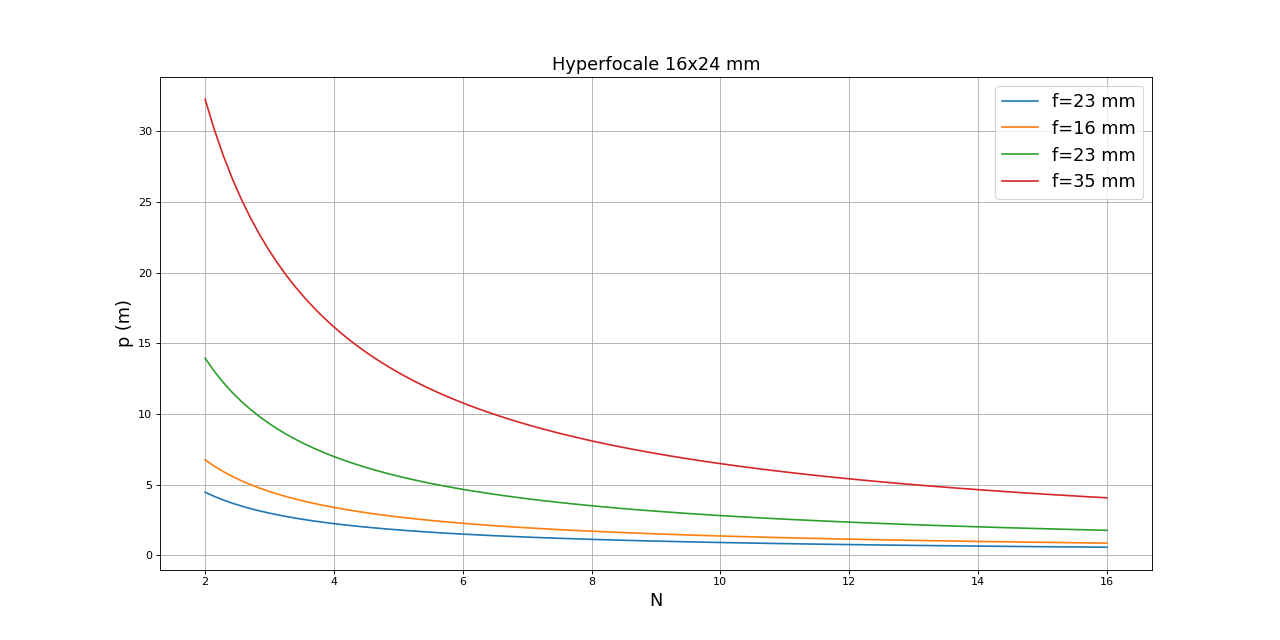fig5.pdf

Rappelons l'expression de la distance l'hyperfocale :

$$p_h\approx \frac{f^2}{c_{max}N}\text{(20)}$$

Augmenter la taille du capteur d'une facteur 1,5 fait augmenter le diamètre du cercle de confusion d'un facteur 1,5 et la focale du même facteur donc la distance l'hyperfocale augmente d'un facteur 1,5. Par exemple, si la profondeur de champ s'étend de 1,5 m à l'infini avec un capteur 24x36, elle s'étend de 1 m à l'infini avec un capteur 16x24 (même ouverture et focales équivalentes). Pour avoir la même profondeur de champ sur le capteur 24x36 mm, il faut augmenter N d'un facteur 1,5, ce qui oblige à augmenter le temps d'exposition de ${(1,5)}^2\approx 2,3$ ou bien à augmenter le gain électronique (sensibilité ISO) du même facteur.