Obstruction centrale des télescopes
1. Introduction
Les télescopes réflecteurs possèdent un miroir primaire de grand diamètre et un petit miroir secondaire. Dans le cas du télescope de Newton, ce miroir est plan et sert à former l'image sur le côté du tube. Dans les télescopes de la famille Cassegrain, le miroir secondaire et convexe; il renvoit la lumière en arrrière du miroir primaire tout en effectuant un grandissement de l'image primaire. Le miroir secondaire obstrue partiellement l'ouverture du télescope. On exprime le diamètre de l'obstruction en valeur relative au diamètre du miroir principal. Elle varie de 0.2 à 0.4 suivant le type de télescope. À l'inverse, les télescopes réfracteurs, appelés aussi lunettes astronomiques, n'ont pas d'obstruction centrale.
L'objectif du calcul présenté ici est de déterminer la fonction de transfert optique d'un télescope présentant une obstruction centrale. Le télescope est supposé parfaitement corrigé des aberrations géométriques (coma, aberrations chromatiques, courbure de champ, etc). Il s'agit donc de quantifier l'effet de la diffraction en présence d'une obstruction centrale.
2. Fonction de transfert optique
2.a. Image d'une étoile
Les calculs suivants font appel au module TfdImage.py présenté dans la page sur la transformée de Fourier d'une image.
from math import *
import Image
from TfdImage import *
from numpy.fft import fft2, ifft2
Une étoile est une source ponctuelle, supposée monochromatique, donnant au foyer de l'instrument une figure de diffraction de Fraunhofer. Celle-ci est obtenue par transformée de Fourier de la fonction de pupille du télescope. On commence par définir l'échantillonnage puis la fonction de pupille, pour un rayon et une obstruction fournis en argument:
Nx=400
Ny=400
def pupille(r,ob):
P = zeros((Ny,Nx),dtype=complex)
nx=Nx/2
ny=Ny/2
for k in range(Nx):
for m in range(Ny):
if pow((k-nx)*(k-nx)+(m-ny)*(m-ny),0.5) < r:
P[m,k] = 1.0
if pow((k-nx)*(k-nx)+(m-ny)*(m-ny),0.5) < r*ob:
P[m,k] = 0.0
return P
La fonction suivante calcule la réponse impulsionnelle (figure de diffraction), pour un rayon et une obstruction centrale donnés. Remarquer qu'à ce stade les dimensions réelles de l'ouverture ne sont pas précisées (le rayon est un nombre de points).
def diffraction(r,ob):
P=pupille(r,ob)
TFP=matriceCentre(fft2(P))
return matricePuissance(TFP)
Pour attribuer une échelle à la figure de diffraction (en secondes d'arc), il faut préciser le diamètre réel de l'ouverture (en millimètres). La fonction suivante fournit cette échelle :
def echelleDiffraction(D,r):
Lambda=500e-9
Lx=D*Nx/(2*r)*1e-3
Ly=D*Ny/(2*r)*1e-3
fxm = Nx/(2*Lx)*180/pi*3600*Lambda
fym = Ny/(2*Ly)*180/pi*3600*Lambda
return [-fxm,fxm,-fym,fym]
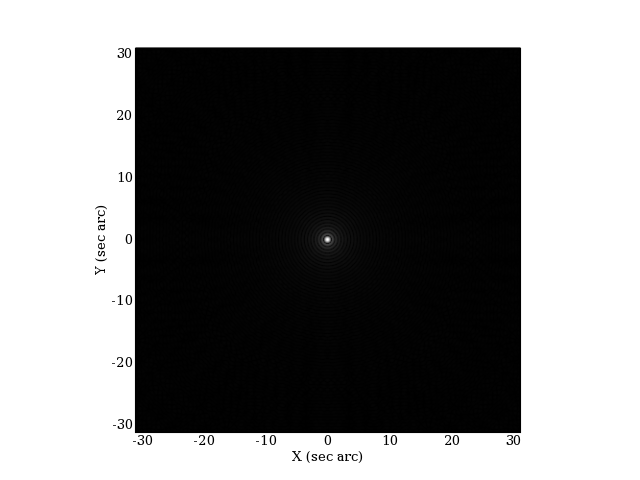
Voyons tout d'abord la figure de diffraction (réponse impulsionnelle), pour une lunette de diamètre 200 mm, sans obstruction centrale :
D=200
r=60
d1=diffraction(r,0.0)
imd1=matriceImage(d1,3.0,[1.0,1.0,1.0])
scale=echelleDiffraction(D,r)
figure()
imshow(imd1,extent=scale)
xlabel('X (sec arc)')
ylabel('Y (sec arc)')
 plotA.pdf
plotA.pdf
Une correction gamma de 3 a été appliquée pour renforcer la visibilité des anneaux de diffraction. En pratique, seul le premier anneau est visible à l'oculaire d'un télescope.
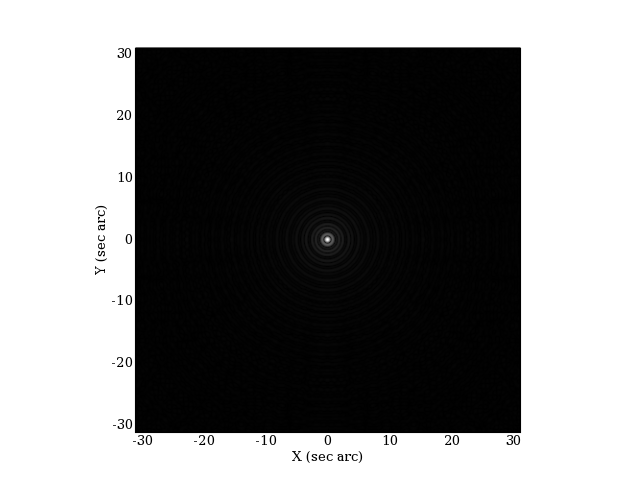
Voyons à présent l'image d'une étoile pour une obstruction centrale de 0.3 :
d2=diffraction(r,0.3)
imd2=matriceImage(d2,3.0,[1.0,1.0,1.0])
figure()
imshow(imd2,extent=scale)
xlabel('X (sec arc)')
ylabel('Y (sec arc)')
 plotB.pdf
plotB.pdf
On constate que le premier anneau est intensifié par la présence de l'obstruction centrale. En principe, cela n'affecte pas le pouvoir résolvant tel qu'il est défini par le critère de Rayleigh.
2.b. Fonction de transfert
La fonction de transfert optique (FTO) est la transformée de Fourier de la réponse impulsionnelle. La fonction de transfert de modulation (FTM) est le module de la FTO. La fonction suivante calcule le profil radial de la FTM pour une réponse impulsionnelle donnée en argument :
def transfertModulation(reponseI):
H=matriceCentre(fft2(reponseI))
imH=matriceImage(matriceModule(H),1.0,[1.0,1.0,1.0])
return imH[Ny/2]
FTM1=transfertModulation(d1)
FTM2=transfertModulation(d2)
figure()
fScale = Nx/(2*2*scale[0])
fx=arange(-fScale,fScale,2*fScale/Nx)
plot(fx,FTM1,color='r')
plot(fx,FTM2,color='b')
xlabel('fx (1/sec arc)')
ylabel('FTM')
 plotC.pdf
plotC.pdf
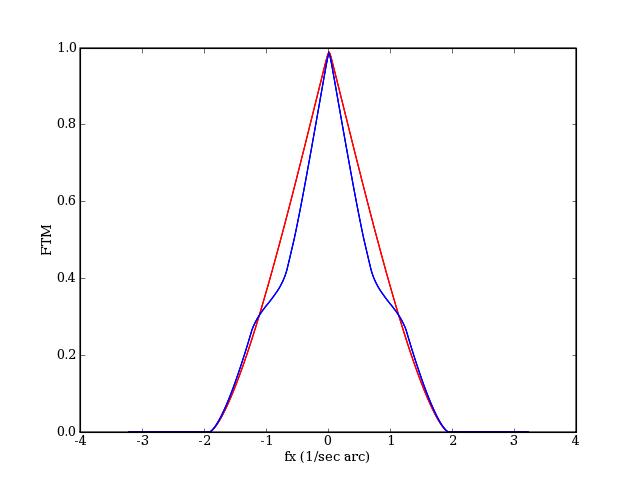
Le système optique est un filtre passe-bas. La fréquence de coupure ne dépend pas de l'obstruction; elle est d'environ 2 sec-1, ce qui signifie que les modulations sinusoïdales de période inférieure à 0.5 secondes d'arc n'apparaissent pas sur l'image. On peut comparer cette limite à la limite de résolution donnée par le critère de Rayleigh (demi-largeur de la tache centrale de diffraction) :
Lambda=500e-6
lim=1.2*Lambda/D*180/pi*3600
print(lim) --> 0.61879441874128904
L'effet de l'obstruction centrale est une réduction du contraste pour des fréquences inférieures à la moitié de la fréquence de coupure. Même si la fréquence de coupure n'est pas modifiée, l'obstruction a un effet notable sur le contraste des détails de l'image télescopique.
3. Comparaison réfracteur-réflecteur
La courbe précédente montre que, à diamètre égal, une lunette (réfracteur) fournit des images plus contrastées qu'un télescope (réflecteur). Il faut toutefois remarquer que cette conclusion ne tient pas compte des différentes aberrations géométriques et défauts de réglage du télescope. Pour le réfracteur, la principale aberration est l'aberration chromatique. Pour le réflecteur, il y a surtout une aberration de coma en dehors de l'axe optique. En pratique, la FTM peut aussi être modifiée par un défaut d'alignement de l'axe de symétrie du miroir avec celui du télescope (défaut de collimation).
Les lunettes astronomiques pour amateur de diamètre supérieur à 100 mm ayant un coût de fabrication considérablement plus élevé que celui d'un télescope réflecteur de même diamètre, on se pose la question suivante : pour une lunette de 100 mm, quel télescope ayant une obstruction centrale de 0.3 permet d'obtenir la même FTM pour des fréquences inférieures à la moitié de la fréquence de coupure ?
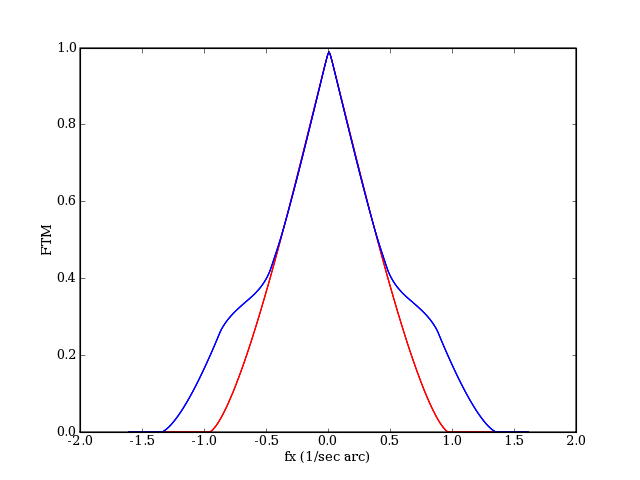
Pour la lunette, on reprend le calcul précédent en modifiant la valeur du diamètre réel. Pour une obstruction de 0.3 (télescope de Newton), l'ajustement des deux courbes de FTM aux basses fréquences est obtenu pour un diamètre de 140 mm :
D=100
scale=echelleDiffraction(D,r)
fScale = Nx/(2*2*scale[0])
fx=arange(-fScale,fScale,2*fScale/Nx)
d3=diffraction(r*1.4,0.3)
FTM3=transfertModulation(d3)
figure()
plot(fx,FTM1,color='r')
plot(fx,FTM3,color='b')
xlabel('fx (1/sec arc)')
ylabel('FTM')
 plotD.pdf
plotD.pdf
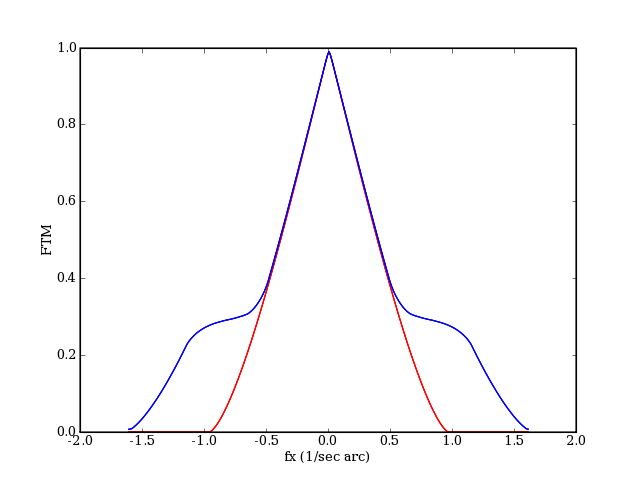
Pour les basses fréquences, la lunette de 100 mm est donc équivalente à un télescope de 140 mm obstrué à 30 % (toutes choses égales par ailleurs). Cependant, le télescope a un avantage sur les détails les plus fins, de période inférieure à 2 seconde d'arc. Bien entendu, cette conclusion est indépendante de la supériorité du télescope en terme de quantité de lumière collectée, 1.8 fois plus grande dans le cas présent.
Reprenons la même comparaison pour une obstruction centrale de 0.4. L'ajustement est obtenu pour un diamètre de 170 mm environ.
d4=diffraction(r*1.7,0.4)
FTM4=transfertModulation(d4)
figure()
plot(fx,FTM1,color='r')
plot(fx,FTM4,color='b')
xlabel('fx (1/sec arc)')
ylabel('FTM')
 plotE.pdf
plotE.pdf