Dioptres centrés : diffraction

1. Introduction

Le calcul des rayons traversant un système de dioptres centrés, selon les lois de l'optique géométrique, a été exposé dans Dioptres centrés : optique géométrique. Pour les systèmes dont les aberrations géométriques sont faibles, il est nécessaire de prendre en compte la diffraction de la lumière pour déterminer la structure de l'image. Dans cette page, on s'intéresse à l'image d'une source ponctuelle monochromatique. L'application du principe de Huygens-Fresnel sa fait avec la sphère de référence introduite dans Dioptres centrés : calcul des aberrations.

2. Principe de Huygens-Fresnel et sphère de référence

L'application du principe de Huygens-Fresnel nécessite le choix d'une surface (surface de Huygens) sur laquelle on connait l'amplitude et la phase de l'onde incidente. Dans le cas d'un système de dioptres, on choisit cette surface en sortie du système de telle sorte que les rayons diffractés ne traversent pas de dioptre. La méthode du tracé des rayons permet de calculer l'amplitude et la phase de l'onde en tout point de cette surface, comme expliqué dans Dioptres centrés : calcul des aberrations.

Une première idée consiste à choisir une surface plane, perpendiculaire à l'axe du système. Désignons par (x_P,y_P,z_P) les coordonnées d'un point P sur cette surface de Huygens. On note p(x_P,y_P) l'amplitude complexe de l'onde incidente sur cette surface. Le plan image est fixé arbitrairement à une position z, généralement au voisinage de l'image paraxiale. Soient (x,y) les coordonnées d'un point M du plan image. L'application du principe de Huygens-Fresnel, où plus précisément l'intégrale de Fresnel-Kirchhoff, permet d'exprimer l'amplitude complexe de l'onde au point M comme une intégrale sur la surface de Huygens :

$$A(x,y,z)=\frac{-1}{i\lambda }\int \int p(x_P,y_P)\frac{exp(-ikr)}{r}K({\theta }_i,\theta )dxdy$$

avec

$$\begin{array}{cc}\hfill & r=PM\hfill \\ \hfill & K({\theta }_i,\theta )=\frac{cos{\theta }_i+cos\theta }{2}\hfill \\ \hfill & \theta =(\overrightarrow{PM},\overrightarrow{n})\hfill \\ \hfill & {\theta }_i=(\overrightarrow{r_i},\overrightarrow{n})\hfill \\ \hfill & k=\frac{2\pi }{\lambda }\hfill \end{array}$$

Le vecteur $\overrightarrow{n}$ est normal à la surface, ici $\overrightarrow{n}=\overrightarrow{e_z}$, et $\overrightarrow{r_i}$ désigne la direction du rayon incident au point P. Si l'ouverture du faisceau de sortie est faible, le facteur d'obliquité K(θ_i,θ) est pratiquement égale à 1.

Un développement limité à l'ordre 2 de la distance PM permet d'écrire l'intégrale sous la forme suivante (approximation de Fresnel) :

$$A(x,y,z)=\frac{-i}{\lambda }\frac{exp(-ikR)}{R}exp(-ik\frac{x^2+y^2}{2R})\int \int p(x_P,y_P)exp(-ik\frac{x_P^2+y_P^2}{2R})exp(-ik\frac{x{x}_P+y{y}_P}{R})d{x}_{P}d{y}_P$$

où R=z-z_P est la distance entre la surface de Huygens et le plan image. L'approximation de Fraunhoffer est obtenue lorsque :

$$R\gg k(x_P^2+y_P^2)$$

condition qui sera vérifiée dans la très grande majorité des instruments d'optique. L'intégrale s'écrit alors :

$$A(x,y,z)=C\int \int p(x_P,y_P)exp(-ik\frac{x{x}_P+y{y}_P}{R})d{x}_{P}d{y}_P$$

On définit les fréquences spatiales :

$$f_x=\frac{x}{\lambda R}{f}_y=\frac{y}{\lambda R}$$

Exprimée en fonction de ces fréquences, l'amplitude complexe dans le plan image est la transformée de Fourier de l'amplitude complexe de l'onde sur la surface de Huygens. Si celle-ci est échantillonnée de manière régulière, le calcul de la transformée de Fourier discrète peut en principe se faire à l'aide de la FFT.

Cependant, le choix d'une surface de Huygens plane pose le problème pratique suivant. Lorsque le point objet est hors de l'axe, la fonction p(x_P,y_P) présente principalement une forme liée à la position hors axe de l'image, à laquelle se superpose des petites variations liées aux aberrations du système. Supposons pour simplifier que l'objet soit sur l'axe X. Si on néglige les aberrations, on a :

$$p(x_P,y_P)=exp\left(ik\frac{x_i{x}_P}{R}\right)$$

où x_i désigne la position de l'image, c'est-à-dire précisément la position du centre de la figure de diffraction.

Lorsque x_P varie à travers le diamètre de la pupille de sortie, ce terme varie très rapidement. Il faudra donc échantillonner la pupille de sortie très finement, pratiquement à l'échelle de la longueur d'onde pour utiliser cette information sur la position de l'image. Cela est tout à fait impraticable en raison du temps nécessaire au tracé des rayons et à l'application de la FFT. C'est la raison pour laquelle le calcul doit être mené avec une surface de Huygens sphérique, appelée sphère de référence ([1]).

La sphère de référence est en principe centrée sur l'image. Celle-ci n'étant pas connue a priori, une première estimation consiste à utiliser la position de l'image obtenue par l'approximation paraxiale. On verra plus loin que le centrage exacte de la sphère n'est pas nécessaire. En l'absence d'aberrations, les chemins optiques des rayons issus de la source sont égaux sur cette surface, avec éventuellement des petites variations dues à une erreur de centrage de la sphère. La présence d'aberrations se traduit par une variation de la phase sur la sphère de référence, qui est calculée par le tracé de rayons, comme expliqué dans Dioptres centrés : calcul des aberrations. Le rayon de la sphère de référence, noté R, est choisi de telle sorte que la sphère passe à peu près par la pupille de sortie. Si le centre est bien choisi, il suffit d'un échantillonnage qui permette d'obtenir les variations de la phase dues aux aberrations. D'autre part, les angles θ et θ_i apparaissant dans l'intégrale de Fresnel-Kirchhoff sont très faibles car les rayons coupent la sphère presque en incidence normale.

Figure pleine page

3. Objet sur l'axe

On commence par le cas où l'objet est sur l'axe du système. Dans ce cas, le centre de la sphère de référence est l'intersection du plan image avec l'axe.

Si on suppose que la distance $z-z_P\simeq R$, l'intégrale de Fraunhoffer donnée plus haut reste valable, à condition d'effectuer l'intégration sur la sphère de référence.

Pour montrer le principe du calcul, on considère l'exemple d'une lentille mince convergente, avec un objet à l'infini.

from CalculImage import * 
cat = CatalogueVerre() 
n1 = Vide() 
n2 = cat.verre['N-BK7'] 
rc = 1033.0
r = 30.0
dioptre1 = Spherique(0,1.0/rc,n1,n2,r)
dioptre2 = Spherique(2,-1.0/rc,n2,n1,r)
sys = SystemeCentre()
sys.ajouterListe([dioptre1,dioptre2])
PObjet = Position(0)
PObjet.infini = True
sys.matriceTransfert('d')
PImage = sys.image(PObjet,'d')
zi = PImage.z
            

print(zi)
--> 1001.0897545313436

La sphère de référence est centrée sur l'image paraxiale. Son sommet est placé juste après la face de sortie de la lentille :

zs = dioptre2.z+0.1
R = zi-zs 
sphereImage = SphereImage(zs,[0,0,zi])
sys.ajouter(sphereImage)
            

L'échantillonnage de la sphère de référence doit être assez fin pour enregistrer les variations de phase dues aux aberrations et le caractère net des bords du diaphragme d'ouverture (hautes fréquences). D'autre part, il faut aussi élargir le domaine au delà du diamètre de la pupille de sortie (basses fréquences).

cal = CalculImage(sys)
Nx = Ny = 400
np = 200
r = 200.0
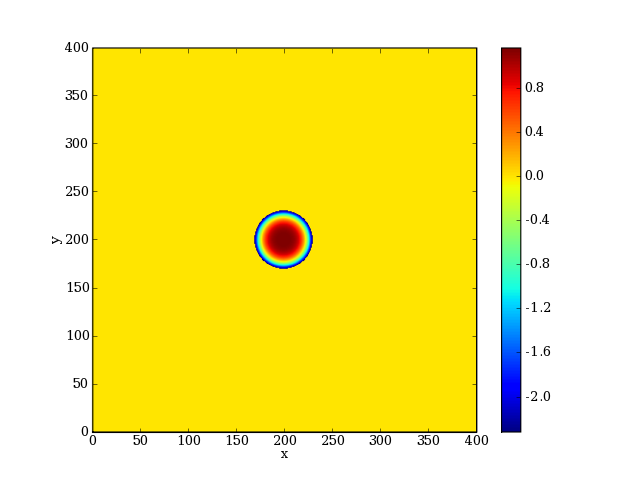
[P,M,Phi] = cal.surfacePhase(PObjet,0,'d',r,0,np,Nx)
clf()
xlabel('x')
ylabel('y')
imshow(Phi)
colorbar()
            

plotA.pdf

La matrice P contient l'amplitude complexe. La référence de la phase est ajustée pour obtenir une valeur moyenne nulle.

On calcule l'amplitude complexe dans le plan image au moyen de la transformée de Fourier discrète puis l'éclairement :

from TfdImage import *
from numpy.fft import fft2, ifft2
TFP=matriceCentre(fft2(P))
I=matricePuissance(TFP)
Lambda = cal.Lambda['d']
imI = matriceImage(I,2.0,[1.0,1.0,1.0])
figure()
xScale = Nx/(2*r)*0.5*Lambda*1e-6*R
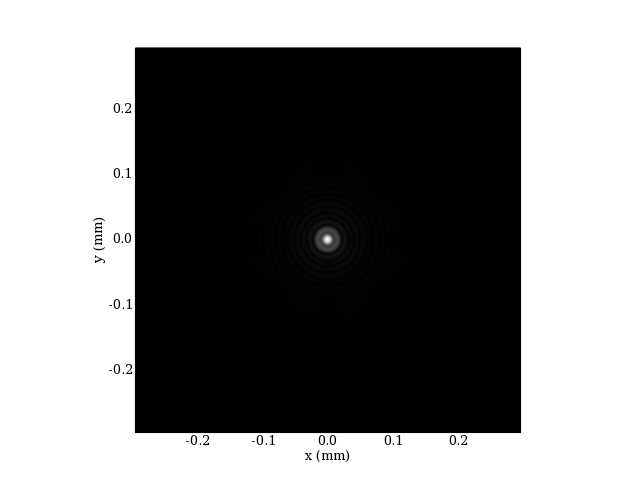
imshow(imI,extent=[-xScale,xScale,-xScale,xScale])
xlabel('x (mm)')
ylabel('y (mm)')
            

plotB.pdf

En l'absence d'aberrations, la figure d'Airy aurait un diamètre de 23 micromètres. La tache centrale est ici notablement plus grande.

La figure obtenue ne dépend pas du rayon de la sphère de référence, pourvu que son sommet gauche soit à l'extérieur du système. Pour cette lentille, le diagramme de spots montre un minimum de l'étalement des spots pour zi=1000.0, soit à environ 1 mm en avant du plan conjugué paraxial. Voyons l'image pour cette nouvelle position :

zi=1000
sphereImage.PC = [0,0,zi]
[P,M,Phi] = cal.surfacePhase(PObjet,0,'d',r,0,np,Nx)
TFP=matriceCentre(fft2(P))
I=matricePuissance(TFP)
Lambda = cal.Lambda['d']
imI = matriceImage(I,2.0,[1.0,1.0,1.0])
figure()
xScale = Nx/(2*r)*0.5*Lambda*1e-6*R
imshow(imI,extent=[-xScale,xScale,-xScale,xScale])
xlabel('x (mm)')
ylabel('y (mm)')
            

plotC.pdf

4. Objet hors axe

Dans ce cas, il faut choisir le centre de la sphère de référence au plus proche de l'image. Considérons comme exemple le miroir parabolique (télescope de Newton), qui a la particularité de fournir une image axiale sans aberrations et une forte aberration de coma hors axe.

n1 = Vide()
n2 = Vide()
n2.negatif()
r = 100.0
c = -1.0/2000
miroir = Conique(0,c,0.0,n1,n2,r)
sys = SystemeCentre()
sys.ajouter(miroir)
sys.ni.negatif()
             

Définition du plan objet à l'infini et du plan image au foyer :

PObjet = Position(0)
PObjet.infini = True
zi = -1000.0
             

On ajoute une sphère de référence dont le sommet se trouve juste après le miroir et dont le centre est encore inconnu. On ajoute aussi un plan image pour le diagramme de spots.

zs = -10.0
R = abs(zi-zs)
sphereImage = SphereImage(zs,[0,0,zi])
sys.ajouter(sphereImage)
planImage = PlanImage(zi,200)
sys.ajouter(planImage)
             

Considérons un objet ponctuel à 10 minutes d'arc de l'axe et voyons son diagramme de spots :

cal = CalculImage(sys)
angle = 10
figure(figsize=(6,6))
xlabel('x')
ylabel('y')
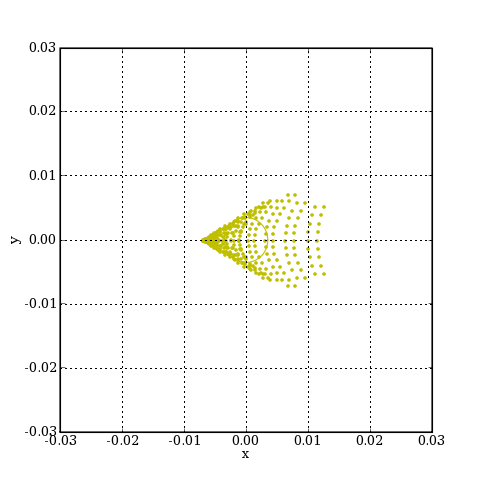
xCentre = cal.diagrammeSpots(PObjet,angle,['d'],0,20)
rAiry = cal.airy(PObjet,'d')
grid(True)
scale=0.03
axis([-scale,scale,-scale,scale])
             

plotD.pdf

L'aberration de coma dépasse nettement le cercle de la tache d'Airy. Le diagramme de spots est centré sur le barycentre, dont la position est :

print(xCentre)
--> 2.91596493047

Cette position peut être adoptée pour centre de la sphère de référence. On calcule l'amplitude complexe de l'onde sur cette sphère :

sphereImage.PC = [xCentre,0,zi]
Nx = Ny = 400
np = 200
r = 500.0
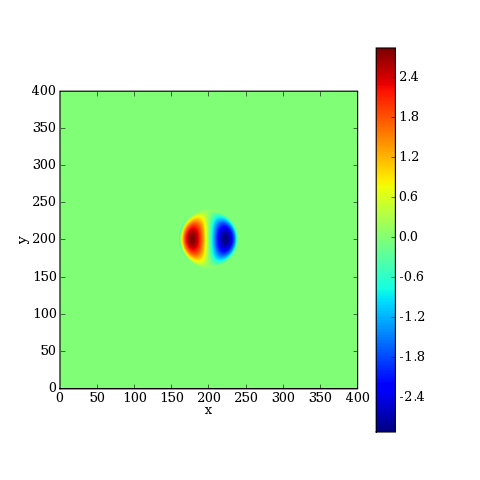
[P,M,Phi] = cal.surfacePhase(PObjet,angle,'d',r,1,np,Nx)
clf()
xlabel('x')
ylabel('y')
imshow(Phi)
colorbar()
             

plotE.pdf

Enfin on calcule la figure de diffraction :

TFP=matriceCentre(fft2(P))
I=matricePuissance(TFP)
Lambda = cal.Lambda['d']
imI = matriceImage(I,2.0,[1.0,1.0,1.0])
figure()
xScale = Nx/(2*r)*0.5*Lambda*1e-6*R
imshow(imI,extent=[-xScale,xScale,-xScale,xScale])
xlabel('x (mm)')
ylabel('y (mm)')
             

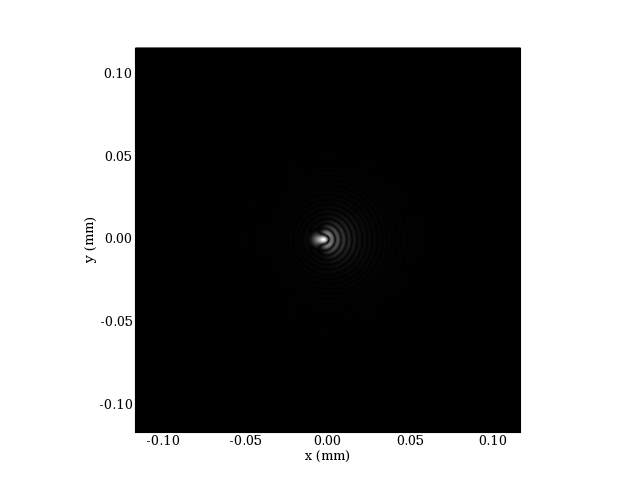plotF.pdf

Voyons l'effet d'un léger décalage du centre de la sphère de référence :

sphereImage.PC = [xCentre+0.05,0,zi]
[P,M,Phi] = cal.surfacePhase(PObjet,angle,'d',r,1,np,Nx)
TFP=matriceCentre(fft2(P))
I=matricePuissance(TFP)
imI = matriceImage(I,2.0,[1.0,1.0,1.0])
figure()
imshow(imI,extent=[-xScale,xScale,-xScale,xScale])
xlabel('x (mm)')
ylabel('y (mm)')
             

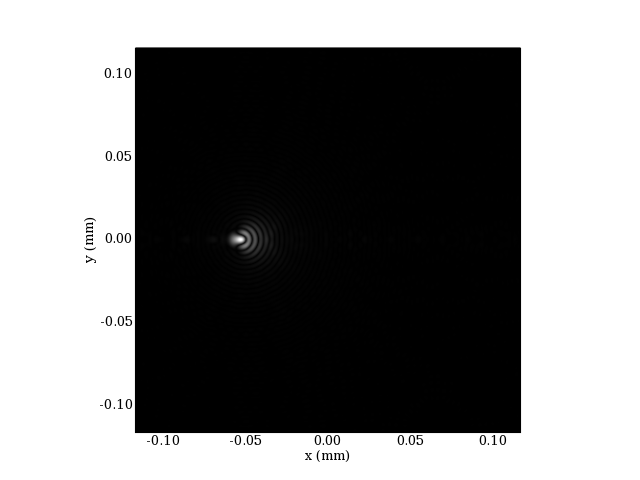plotG.pdf

La figure de diffraction n'est pratiquement pas modifiée, avec tout au plus une petite altération des anneaux périphériques. On retrouve l'image à sa position correcte par rapport au centre. Cela montre qu'une petite erreur de centrage de la sphère de référence est sans conséquence sur le résultat. L'estimation du centre au moyen du barycentre des spots est largement suffisante.