Dioptres centrés : calcul des aberrations

1. Introduction

La calcul des rayons traversant un système de dioptres centrés est exposé dans Dioptres centrés : optique géométrique. La présente partie développe des fonctions permettant une étude sytématique des aberrations et différents calculs complémentaires. Ces fonctions sont regroupées dans le module CalculImage.py. Il contient une seule classe, dont le constructeur prend en argument le système centré à utiliser pour les calculs :

from Dioptres import *
from IndiceVerre import *
from math import *
from pylab import *
from numpy import *

class CalculImage:
    def __init__(self,systeme):
        self.systeme = systeme
        self.min2rad = pi/180/60
        self.Lambda = {'d':587,'F':486,'C':656}
        self.couleurs = {'d':'y','F':'b','C':'r'}
            

2. Grandissement paraxial

On définit le grandissement comme le rapport de la position transversale de l'image sur la position transversale de l'objet. La position transversale est soit un angle en minutes d'arc, si le point est à l'infini, soit une distance en millimètres. La méthode suivante fournit ce rapport dans le cadre de l'approximation paraxiale :

    def grandissementParaxial(self,PObjet,raie):
        self.systeme.matriceTransfert(raie)
        PImage = self.systeme.image(PObjet,raie)
        g = self.systeme.grandissement(PObjet,raie)
        if PObjet.infini:
            g = g*self.min2rad
        if PImage.infini:
            g = g/self.min2rad
        return g
            

3. Faisceau émis par un objet ponctuel

Le premier cas est celui d'un faisceau de rayons parallèles émis par un point objet situé à l'infini. La méthode suivante prend en arguments l'angle de position de l'objet par rapport à l'axe (en minutes d'arc), le nom de la raie spectrale et le nombre de rayons à calculer :

    def faisceauInfini(self,angle,raie,nRayons):
        r1 = self.systeme.listeD[0].r
        dz = self.systeme.listeD[0].dzBord()
        zf = self.systeme.listeD[0].z-10-abs(angle*self.min2rad*r1)
        if dz < 0:
            zf += dz
        faisceau = FaisceauParallele(nRayons,angle*self.min2rad,zf,r1)
        self.systeme.refractionFaisceau(faisceau,raie)
        return faisceau
            

Le deuxième cas est celui d'un faisceau émis par un point objet situé à distance finie dont la position transversale x0 est donnée. La position du plan objet PObjet est une instance de la classe Position.

    def faisceauFini(self,PObjet,x0,raie,nRayons):
        r1 = self.systeme.listeD[0].r
        dz = self.systeme.listeD[0].dzBord()-10
        if dz < 0:
            zf += dz
        faisceau = FaisceauDivergent(PObjet,x0,raie,nRayons)
        self.systeme.refractionFaisceau(faisceau,raie)
        return faisceau
            

La méthode suivante calcule le faisceau de rayons pour un objet quelconque. L'argument x0 désigne soit une distance transversale soit un angle en minutes d'arc.

    def faisceau(self,PObjet,x0,raie,nRayons):
        if PObjet.infini:
            return self.faisceauInfini(x0,raie,nRayons)
        else:
            return self.faisceauFini(PObjet,x0,raie,nRayons)
            

4. Diagramme de spots

Un diagramme de spots représente les points d'intersection des rayons issus d'un point objet avec un dioptre. Si le dioptre est un plan image, on obtient une représentation de l'image. La méthode suivante fournit les points sous forme de deux listes. L'argument entier last désigne l'indice du dioptre en partant du dernier. Généralement, le plan image étant le dernier dioptre, cet argument sera nul. L'argument xCentre est la position du centre de l'image.

    def spots(self,faisceau,xCentre,last):
        x = []
        y = []
        for Rc in faisceau.listeRayons:
            if Rc.listeR[Rc.n-1].actif:
                R = Rc.listeR[Rc.n-1-last]
                x.append(R.P[0]-xCentre)
                y.append(R.P[1])
        return [x,y]
            

Un diagramme de spots complet est obtenu en traçant les rayons pour plusieurs raies spectrales, afin de mettre en évidence les aberrations chromatiques transversales. Le diagramme est centré sur le barycentre des spots de la raie d. La méthode suivante trace le diagramme de spots sur le dioptre dont la position à partir du dernier (0 pour celui-ci) est donnée par last. En principe, il s'agit d'un dioptre de type PlanImage, mais tous les dioptres sont possibles.

    def diagrammeSpots(self,PObjet,x0,raies,last,nRayons):
        faisceau_d = self.faisceau(PObjet,x0,'d',nRayons)
        xCentre = faisceau_d.barycentre()[0]
        for raie in raies:
            if raie=='d':
                xy = self.spots(faisceau_d,xCentre,last)
                plot(xy[0],xy[1],linestyle=' ',marker='.',color=self.couleurs[raie])
            if raie=='F':
                xy = self.spots(self.faisceau(PObjet,x0,'F',nRayons),xCentre,last)
                plot(xy[0],xy[1],linestyle=' ',marker='.',color=self.couleurs[raie])
            if raie=='C':
                xy = self.spots(self.faisceau(PObjet,x0,'C',nRayons),xCentre,last)
                plot(xy[0],xy[1],linestyle=' ',marker='.',color=self.couleurs[raie])
        return xCentre
            

5. Ouverture du faisceau de sortie

Le rapport d'ouverture (f/D) du faisceau de sortie est calculé pour un point situé sur l'axe. L'ouverture est obtenue en considérant le rayon du bord d'un faisceau de rayons méridiens.

    def ouvertureImage(self,PObjet,raie,nr):
        z0 = self.systeme.listeD[0].z
        dz = self.systeme.listeD[0].dzBord()
        if dz < 0:
            z0 += dz
        if PObjet.infini:
            faisceau = FaisceauParalleleMeridien(nr,0,z0-10,self.systeme.listeD[0].r)
        else:
            faisceau = FaisceauDivergentMeridien(nr,PObjet.z,0,z0-0.001,self.systeme.listeD[0].r)
        self.systeme.refractionFaisceau(faisceau,raie)
        for Rc in faisceau.listeRayons:
            R = Rc.getRayon()
            if R.actif:
                return abs(2*R.U[0]/R.U[2]) 
           
            

La connaissance de l'ouverture permet de calculer le rayon de la tache de diffraction (tache d'Airy) qu'il y aurait en l'absence d'aberrations. La méthode suivante trace le cercle représentant la tache d'Airy, à superposer au diagramme de spots :

    def airy(self,PObjet,raie):
        rAiry = 1.2*self.Lambda[raie]*1e-6/self.ouvertureImage(PObjet,raie,100)
        angles = linspace(0,2*pi,100)
        plot(rAiry*cos(angles),rAiry*sin(angles),color=self.couleurs[raie])
        return rAiry
            

6. Aberrations longitudinales

Pour étudier les aberrations sphériques et chromatiques longitudinales, on considère un point objet situé sur l'axe du système. Un rayon issu de l'objet entre par le dioptre frontal à une distance r de l'axe. La méthode suivante calcule le point d'intersection avec l'axe de ce rayon en sortie du système.

    def intersectionRayonAxe(self,PObjet,r,raie):
        if r==0:
            self.systeme.matriceTransfert(raie)
            image = self.systeme.image(PObjet,raie)
            if image.infini:
                return [False,0]
            return [True,image.z]
        z0 = self.systeme.listeD[0].z
        dz = self.systeme.listeD[0].dzBord()
        if dz < 0:
            z0 += dz
        if PObjet.infini:
            R = Rayon([r,0,z0-10],[0,0,1.0])
        else:
            R = Rayon([0,0,PObjet.z],[r,0,z0-0.001-PObjet.z])
        Rc = RayonComplet()
        Rc.ajouter(R)
        self.systeme.refraction(Rc,raie)
        if Rc.getRayon().actif==False:
            return [False,0]
        R2 = Rc.getRayon()
        if R2.U[0]==0:
            return [False,0]
        return [True,R2.P[2]+R2.U[2]*(-R2.P[0]/R2.U[0])]
            

La méthode suivante trace, pour les raies demandées, la position z du point d'intersection en fonction de la distance r à l'axe sur le dioptre d'entrée.

    def aberrationsLongitudinales(self,PObjet,raies,npts):
        for raie in raies:
            rr = []
            zz = []
            rmax = self.systeme.listeD[0].r
            dr = rmax/float((npts-1))
            for k in range(npts):
                r = dr*k
                a = self.intersectionRayonAxe(PObjet,r,raie)
                if a[0]:
                    rr.append(r)
                    zz.append(a[1])
            plot(zz,rr,color=self.couleurs[raie])
        

7. Chemins optique et front d'onde

Pour un système optique sans aberrations, la surface d'onde en sortie est sphérique (pour un objet ponctuel). Afin de caractériser le front d'onde en présence d'aberrations, on calcule le chemin optique des rayons lorsqu'ils coupent une sphère de référence.

On considère d'abord le cas où l'objet est sur l'axe. La sphère de référence est centrée sur l'axe, par exemple sur l'image paraxiale, et sa surface se trouve juste en sortie du système. Cette surface sphérique est ajoutée au système sous la forme d'une instance de la classe SphereImage.

La méthode suivante trace la phase en fonction de la distance à l'axe, pour les points d'intersection sur le dioptre dont la position à partie du dernier est donnée par last (en principe de type SphereImage). Pour faciliter la lecture des courbes, on retranche la valeur moyenne à la phase.

    def courbePhase(self,PObjet,raies,last,npts):
        for raie in raies:
            z0 = self.systeme.listeD[0].z
            dz = self.systeme.listeD[0].dzBord()
            if dz < 0:
                z0 += dz
            if PObjet.infini:
                faisceau = FaisceauParalleleMeridien(npts,0,z0-10,self.systeme.listeD[0].r)
            else:
                faisceau = FaisceauDivergentMeridien(npts,PObjet.z,0,z0-0.001,self.systeme.listeD[0].r)
            self.systeme.refractionFaisceau(faisceau,raie)
            r = []
            phi = []
            moyenne = 0.0
            n = 0
            for Rc in faisceau.listeRayons:
                if Rc.getRayon().actif:
                    rayon = Rc.listeR[Rc.n-1-last] 
                    l = Rc.longueurOptique(last)
                    r.append(rayon.P[0])
                    phi.append(l)
                    n += 1
                    moyenne += l
            moyenne = moyenne/n
            for k in range(n):
                phi[k] = 2*pi*(phi[k]-moyenne)*1e6/self.Lambda[raie]
            plot(r,phi,color=self.couleurs[raie])
            

Lorsque l'objet ponctuel est hors de l'axe, la position transversale du centre de la sphère de référence n'est pas connue a priori, car on ne sait pas exactement où se situe le centre de la tache de diffraction. Seule sa position longitudinale est imposée par le choix du plan image.

Pour obtenir un échantillonnage régulier de la phase sur la sphère de référence, on définit un maillage carré sur les coordonnées (x,y). La phase attribuée à un noeud est la phase moyenne des rayons passant dans le carré voisin. On suppose de plus que l'éclairement de la pupille de sortie est pratiquement uniforme sur son diamètre. L'amplitude complexe de l'onde sur la zone éclairée a donc un module de 1.

La méthode suivante effectue l'échantillonnage de la phase sur le dioptre dont l'indice à partir du dernier est donné par last (0 pour le dernier dioptre). L'argument r est le rayon de la zone échantillonnée, qui doit impérativement excéder le rayon du faisceau sur le dioptre. npts au carré est le nombre de rayons tracés. nx est la largeur du maillage.

    def surfacePhase(self,PObjet,x0,raie,r,last,npts,nx):
        faisceau = self.faisceau(PObjet,x0,raie,npts)
        M = zeros([nx,nx],dtype=float)
        Phi = zeros([nx,nx],dtype=float)
        moyPhi = 0.0
        n = 0.0
        for Rc in faisceau.listeRayons:
            if Rc.getRayon().actif:
                rayon = Rc.listeR[Rc.n-1-last]
                l = Rc.longueurOptique(last)
                x = rayon.P[0]
                y = rayon.P[1]
                j = int((x/r+1)/2.0*float(nx-1))
                i = int((y/r+1)/2.0*float(nx-1))
                M[i,j] = M[i,j]+1.0
                phi = 2*pi*l*1e6/self.Lambda[raie]
                Phi[i,j] = Phi[i,j] + phi
                moyPhi += phi
                n += 1
        moyPhi = moyPhi/n
        P = zeros([nx,nx],dtype=complex)
        for i in range(nx):
            for j in range(nx):
                if M[i,j] != 0:
                    Phi[i,j] = Phi[i,j]/M[i,j]-moyPhi
                    P[i,j] = (cos(Phi[i,j])+1.0j*sin(Phi[i,j]))
        return [P,M,Phi]
            

8. Exemple : lentille biconvexe

from CalculImage import * 
cat = CatalogueVerre() 
n1 = Vide() 
n2 = cat.verre['N-BK7'] 
rc = 1033.0  
dioptre1 = Spherique(0,1.0/rc,n1,n2,30.0)
dioptre2 = Spherique(2,-1.0/rc,n2,n1,30.0)
sys = SystemeCentre()
sys.ajouterListe([dioptre1,dioptre2])
            

L'objet étant à l'infini, on détermine la position de son image paraxiale pour la raie d:

PObjet = Position(0)
PObjet.infini = True
sys.matriceTransfert('d')
PImage = sys.image(PObjet,'d')
zi = PImage.z
            

print(zi)
--> 1001.0897545313436

Pour les calculs de front d'onde, on ajoute au système une sphère centrée sur l'image paraxiale dont la surface se trouve à droite de la face de sortie de la lentille :

sphereImage = SphereImage(dioptre2.z+0.1,[0,0,zi])
sys.ajouter(sphereImage)
            

On place aussi un plan image :

planImage = PlanImage(zi,100)
sys.ajouter(planImage) 
            

Voyons le diagramme de spots pour un point objet situé sur l'axe.

cal = CalculImage(sys)
figure(figsize=(6,6))
xlabel('x')
ylabel('y')
cal.diagrammeSpots(PObjet,0,['d'],0,20)
rAiry = cal.airy(PObjet,'d')
grid(True)
scale=0.05
axis([-scale,scale,-scale,scale])
            

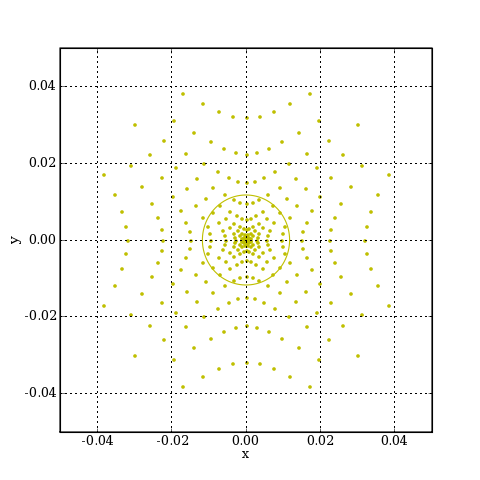plotA.pdf

On trace la position du point d'intersection sur l'axe en fonction du point d'entrée du rayon sur le dioptre frontal :

clf()
xlabel('z')
ylabel('r')
cal.aberrationsLongitudinales(PObjet,['d','F','C'],50)
grid(True)
            

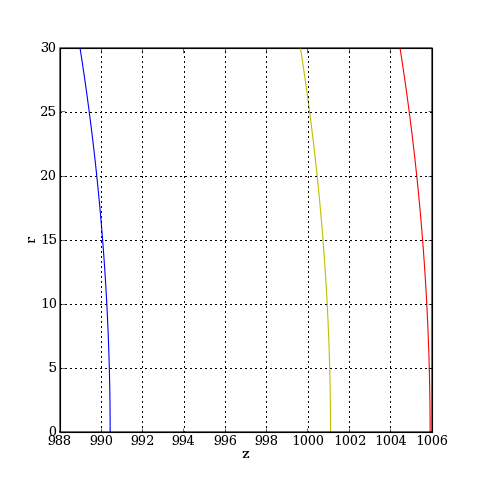plotB.pdf

Ci-dessous la courbe donnant la phase des rayons sur la sphère de référence définie plus haut, centrée sur l'image paraxiale de la raie d. Cette courbe quantifie la déformation du front d'onde par rapport à une sphère.

clf()
xlabel('r')
ylabel('phi')
cal.courbePhase(PObjet,['d'],1,50)
grid(True)
            

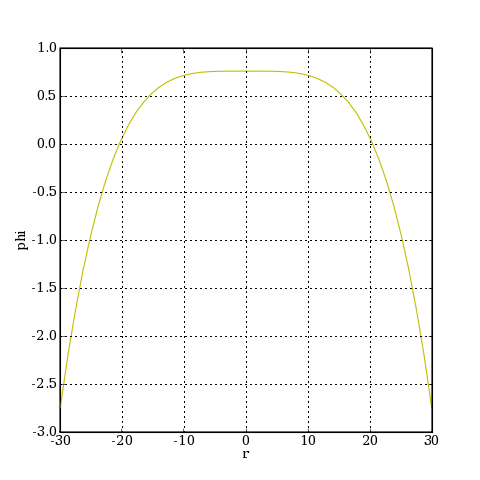plotC.pdf

Voyons la phase de l'onde lumineuse sur la sphère de référence placée en sortie :

[P,M,Phi] = cal.surfacePhase(PObjet,0,'d',40.0,1,80,40)
clf()
xlabel('x')
ylabel('y')
imshow(Phi)
colorbar()
            

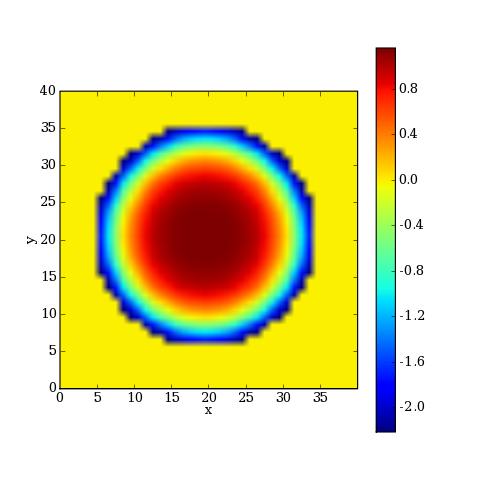plotD.pdf

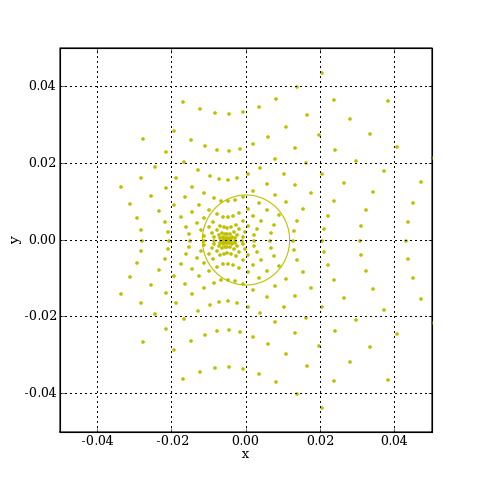
Voyons à présent le cas d'un point objet à l'infini hors axe, par exemple à 30 minutes d'arc de l'axe.

angle = 30.0
figure(figsize=(6,6))
xlabel('x')
ylabel('y')
xCentre = cal.diagrammeSpots(PObjet,angle,['d'],0,20)
rAiry = cal.airy(PObjet,'d')
grid(True)
scale=0.05
axis([-scale,scale,-scale,scale])
            

plotE.pdf

La position du barycentre des spots est :

print(xCentre)
--> 8.72960730977

Celle-ci donne une première indication de la position transversale du centre de la sphère de référence. Pour comparaison, voici la position obtenue à l'aide du grandissement paraxial :

xGauss = angle*cal.grandissementParaxial(PObjet,'d')
            

print(xGauss)
--> 8.72445809493097

Dans le cas présent, cette dernière position correspond bien au centre de la zone de plus forte densité des points. Cependant, cela est dû au fait que le plan image coïncide ici avec le plan conjugué donné par l'approximation paraxiale. Si on déplace le plan image pour parfaire la mise au point, le grandissement paraxial n'est plus nécessairement valable.

On choisit la position du centre de la sphère de référence et on calcule la phase de l'onde sur cette sphère :

sphereImage.PC = [xGauss,0,zi]
[P,M,Phi] = cal.surfacePhase(PObjet,angle,'d',40.0,1,80,40)
clf()
xlabel('x')
ylabel('y')
imshow(Phi)
colorbar()
            

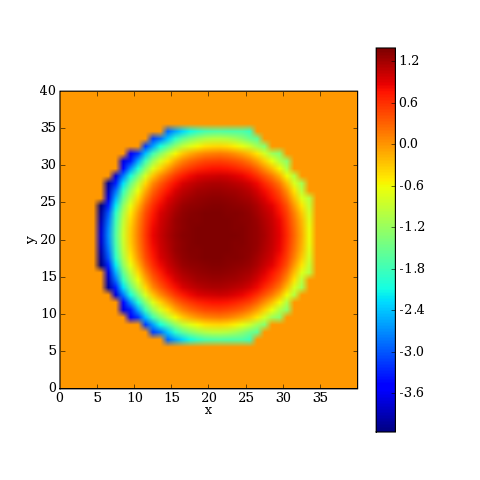plotF.pdf