Synthèse numérique d'un signal périodique

2.a. Principe

Cette méthode consiste à calculer au préalable les échantillons du signal et à les stocker dans une table. C'est la méthode utilisée dans la centrale Sysam SP5, qui possède une mémoire RAM pour la table d'échantillons.

Dans un circuit d'électronique numérique, l'échantillonnage se fait avec une horloge (un oscillateur à quartz), qui délivre des impulsions à intervalle de temps régulier. La période d'échantillonnage T_e est nécessairement multiple de la période τ de l'horloge :

$$T_e=q\tau \text{(1)}$$

Par exemple, le convertisseur numérique-analogique de la centrale SP5 a une période d'horloge τ=0.2μs. Les périodes d'échantillonnage possibles sont donc 0.4, 0.6, 0.8, etc. Cela signifie que la fréquence d'échantillonnage ne peut pas être choisie arbitrairement, et c'est une contrainte très importante pour la conception des méthodes de synthèse numérique.

Notons u la fonction périodique à échantillonner, qui peut être une fonction sinusoïdale, une somme de fonctions sinusoïdales, ou toute autre fonction. Il est commode d'utiliser la phase comme variable pour cette fonction, que l'on notera θ, et qui varie de 0 à 2π. Par exemple pour une sinusoïde on écrit u(θ)=Asin(θ).

Une première idée simple est de considérer N valeurs de phase régulièrement réparties sur l'intervalle [0,2π], et de stocker dans la table des valeurs de u correspondantes. Si la mémoire à une faible capacité, c'est effectivement la méthode utilisée. Par exemple, avec N=256 (mémoire adressée sur 8 bits), on peut donner une bonne définition de la forme d'une sinusoïde. Avec cette valeur, le théorème de Shannon nous dit même que l'on peut ajouter des harmoniques jusqu'au rang 128.

Supposons qu'une valeur de T_e (multiple de la période d'horloge) ait été choisie. On peut lire les éléments de la table avec cette période pour en faire la conversion N/A. Lorsque la fin de la table est atteinte, on revient au début. De cette manière, les N éléments de la table sont parcourus en une durée NT_e. La fréquence du signal obtenu est ainsi :

$$f=\frac{1}{Nq\tau }\text{(2)}$$

Les grandes fréquences sont obtenues pour les valeurs faibles de q. Les fréquences par ordre décroissant sont donc dans les proportions 1, 1/2, 1/3, etc. Cela signifie que les valeurs possibles de la fréquence sont très limitées, du moins pour les fréquences élevées. Par exemple, si l'horloge fonctionnne à 256 MHz et si N=256, il est possible de générer un signal à 1 MHz, à 0.5 MHz, mais les valeurs intermédiaires sont impossibles. Nous allons voir deux manières de résoudre ce problème.

2.b. Échantillonnage sur plusieurs périodes

Cette méthode consiste à stocker dans la table plusieurs périodes du signal, si possible un grand nombre. C'est la méthode qui peut être utilisée avec la centrale SP5, car elle possède une mémoire importante, pouvant stocker jusqu'à 2¹⁸=262142 échantillons. Les éléments de la table sont toujours lus avec une période T_e.

Soit N_p le nombre de périodes, qui doit être entier pour ne pas avoir de saut de phase lorqu'on passe de la fin au début de la table. Si N est le nombre de points total que l'on décide de stocker et T la période du signal, on a :

$$N{T}_e=N_{p}T\text{(3)}$$

La fréquence du signal obtenu est donc :

$$f=\frac{N_p}{N}\frac{1}{T_e}=\frac{N_p}{Nq\tau }\text{(4)}$$

On peut donc jouer sur le rapport N/N_p pour ajuster finement la fréquence. Contrairement au cas précédent, ce rapport, qui représente le nombre d'échantillons par période, n'est pas nécessairement entier.

Pour déterminer N_p et N, on peut suivre l'algorithme suivant. On commence par choisir la période d'échantillonnage la plus petite, soit T_e=τ. Soit N la taille de la table (approximative) que l'on souhaite utiliser. On calcule le nombre de périodes par :

$$N_p=E\left(Nf{T}_e\right)\text{(5)}$$

où E(x) désigne le plus grand entier inférieur ou égal à x. Si ce nombre est strictement inférieur à 1, on doit augmenter la période d'échantillonnage et recalculer N_p.

Le nombre exact d'échantillons est alors calculé par :

$$N=E\left(N_p\frac{T}{T_e}\right)\text{(6)}$$

La phase utilisée pour calculer les échantillons est alors :

$${\theta }_k=2\pi k\frac{N_p}{N}\text{(7)}$$

où k est l'indice d'accès aux éléments de la table.

Voyons à présent quelle est la résolution fréquentielle obtenue avec cette méthode. Pour faire varier finement la fréquence, il n'est pas nécessaire de faire varier q. On joue plutôt sur N_p. Une variation d'une unité du nombre de périodes nous donne donc la résolution fréquentielle :

$$\Delta f=\frac{1}{Nq\tau }=\frac{f_e}{N}\text{(8)}$$

Si la mémoire est grande, la résolution fréquentielle est très bonne. Par exemple, pour une mémoire de 100000 échantillons, une fréquence d'échantillonnage de 1 MHz donne une résolution de 10 Hz. Pour des signaux de basse fréquence, il faudra bien sûr réduire la fréquence déchantillonnage, et la résolution sera réduite dans les mêmes proportions.

Voyons un exemple, avec utilisation de la centrale SysamSP5 pour la conversion numérique-analogique. On souhaite produire une sinusoïde de fréquence inférieure à 1000 Hz. On choisit une fréquence d'échantillonnage f_e=100 kHz, possible puisque la fréquence d'horloge est 5 MHz. On aura alors au moins 100 échantillons par période. On souhaite fixer la fréquence au Hertz près, ce qui nécessite environ 100000 échantillons (la mémoire peut en contenir 262142).

fe = 10000.0
f = 365.0
N = 100000
Np = int(N*f/fe)
N = int(Np*fe/f)
                     

print(Np)
--> 3650

print(N)
--> 100000

Voici le calcul de la table des échantillons, pour une sinusoïde (attention à la division des deux entiers qui doit donner un flottant) :

import math
import numpy

u = numpy.zeros(N)
a = 2*math.pi*Np*1.0/N
for k in range(N):
    u[k] = math.sin(k*a)
                     

Voici comment programmer la sortie SA1 de la centrale Sysam SP5 :

import pycan.main as pycan
sys = pycan.Sysam("SP5")
sys.ouvrir()
te = 1.0/fe
sys.config_sortie(1,te*10**6,u,-1)
                     

La sortie 1 est configurée, avec un temps d'échantillonnage donné en microsecondes (il est arrondi à la valeur multiple de 0.2μs la plus proche). Le troisième argument est le tableau des échantillons, qui est recopié dans la mémoire interne de la centrale. Le dernier argument est le nombre de répétitions du tableau. S'il vaut -1, la répétition se fait sans fin. Pour déclencher la conversion, il faut exécuter :

 sys.declencher_sorties(1,0)
                     

Cette fonction retourne immédiatement (elle est bloquante sur Sysam PCI). Il faut donc prévoir soit une attente avec time.sleep, soit une autre fonction bloquante, par exemple la fonction matplotlib.pyplot.show.

Voici ce qu'il faut faire pour émettre le signal pendant 60 s :

 import time
 time.sleep(60)
 sys.fermer()
                     

On déduit de ce qui précède qu'une mémoire de 100000 échantillons nous permet d'avoir une résolution de fréquence au millième tout en ayant 100 échantillons par période. Pour un signal de fréquence inférieure à 100 Hz, il suffira de réduire la fréquence d'échantillonnage d'un facteur 10.

2.c. Accumulateur de phase

Les circuits de génération de signaux numériques (Direct Digital Synthesis ou DDS) ont généralement une mémoire de faible taille, par exemple 256 échantillons. On se contente alors de stocker les échantillons correspondant à des phases régulièrement réparties sur l'intervalle [0,2π] (une période).

Au lieu de lire les échantillons avec une période égale à la période d'échantillonnage, on se sert de la période d'échantillonnage pour incrémenter un accumulateur de phase dont nous allons expliquer le fonctionnement.

Supposons que la table soit adressée sur 8 bits, et contienne donc 256 échantillons. L'accumulateur, noté A, contient un entier (non signé) codé sur 32 bits. On utilise un entier I pour fixer la fréquence, qui doit être codé sur 32-8=24 bits. La valeur de I est utilisée comme incrément de l'accumulateur à chaque période d'échantillonnage :

$$A\leftarrow A+I\text{(9)}$$

Le résultat de cette somme est compris entre 0 et 2³²-1 (modulo 2³²). L'adressage de la table se fait avec les 8 bits de poids fort de A. La lecture complète de la table, qui correspond à une période du signal, se fait après un nombre d'incréments égal à

$$M=E\left(\frac{2^{32}}{I}\right)\text{(10)}$$

La durée de lecture de la table, qui correspond à une période du signal, est :

$$T=M{T}_e\text{(11)}$$

La plus grande valeur possible de l'incrément est I=2²⁴-1. Elle donne M=256, ce qui signifie que les éléments de la table sont lus avec la période T_e. Pour une valeur plus petite de I, certains échantillons seront lus plusieurs fois de suite. Dans tous les cas, chaque échantillon de la table est utilisé au moins une fois.

La plus petite valeur de l'incrément (I=1) donne la résolution fréquentielle :

$$\Delta f=\frac{f_e}{2^{32}}\text{(12)}$$

La résolution obtenue est incomparablement meilleure que celle de la méthode précédente. Par exemple, pour une fréquence d'échantillonnage de 100 MHz, qui permet de générer des signaux jusqu'à au moins 1 MHz (avec 100 points par période au moins), la résolution est de 2 centièmes de Hertz.

La phase s'écrit :

$$\theta =2\pi \frac{k}{256}\text{(13)}$$

où k est l'entier codé par les 8 bits de poids fort de l'accumulateur. On remarque que l'accumulateur A représente en fait un nombre réel dont la partie entière est égale à k, les 24 autres bits codant la partie fractionnaire. La technique de calcul utilisée est appelée calcul en virgule fixe (fixed point arithmetic), car le nombre de chiffres avant et après la virgule est fixe. Elle est utilisée sur les processeurs qui n'ont pas d'unité de calcul en virgule flottante.

k/256 peut donc être vu comme un nombre réel compris entre 0 et 1, défini même lorsque k n'est pas entier. En comparant à la relation $\mathrm{(7)}$ de la méthode précédente, on établit la correspondance avec kN/N_p. Or N_p/N est justement le nombre de points moyen par périodes. On en conclue que les deux méthodes sont équivalentes. La première utilise une mémoire de grande capacité pour stocker plusieurs périodes, la seconde utilise un accumulateur de phase pour accéder à une table limité à une période.

Finalement, le choix de I en fonction de la fréquence f souhaité se fait de la manière suivante :

$$I=E\left(2^{32}\frac{f}{f_e}\right)\text{(14)}$$

Voyons une simulation sur python. On commence par créer la table des échantillons d'une sinusoïde :

tab = numpy.zeros(256)
for k in range(256):
    tab[k] = math.sin(2*math.pi*k/256)
                    

Nous allons stocker les échantillons obtenus sur plusieurs périodes afin de les tracer et de faire leur analyse spectrale par transformée de Fourier discrète.

fe = 1.0e6
f = 1123.354
A = numpy.int32(0)
I = numpy.int32(2**32*f/fe) # pas de type int24 dans numpy
T = 0.1 # duree d'acquisition
N = int(T*fe)
u = numpy.zeros(N)
for i in range(N):
    A = numpy.uint32(A+I)
    k = int(numpy.uint8(A>>24)) # k = 8 bits de poids fort de A
    u[i] = tab[k]
                    

Voyons les échantillons obtenus sur quelques périodes :

from matplotlib.pyplot import *
n = 3000
t = numpy.arange(n)*1.0/fe
figure(figsize=(8,4))
plot(t,u[0:n])
xlabel('t (s)')
ylabel('u')
grid()
                    

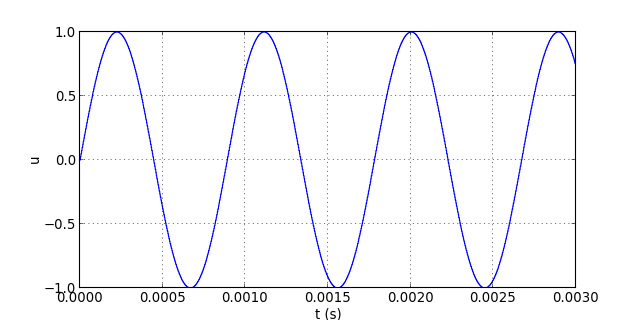figA.pdf

On peut regarder une petite zone en détail :

figure(figsize=(8,4))
plot(t,u[0:n],'.')
xlabel('t (s)')
ylabel('u')
axis([0,1e-4,-1,1])
grid()                    
                    

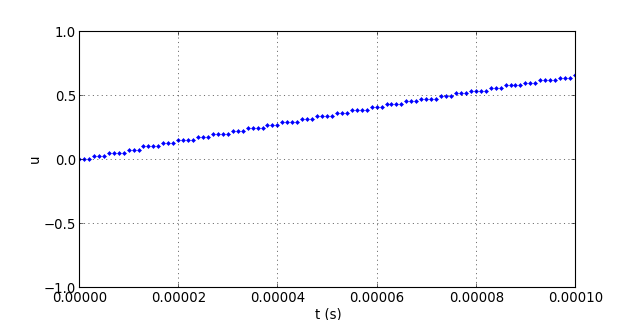figB.pdf

On voit que chaque élément de la table est lu plusieurs fois de suite, ici 3 ou 4 fois.

Voici le spectre :

import numpy.fft
a = numpy.absolute(numpy.fft.fft(u)/N)
freq = numpy.arange(N)*1.0/T
figure(figsize=(8,4))
plot(freq,a,'.-')
xlabel('f (Hz)')
ylabel('A')
axis([1000,1500,0,a.max()])
xticks([1000,f,1500])
grid()
                    

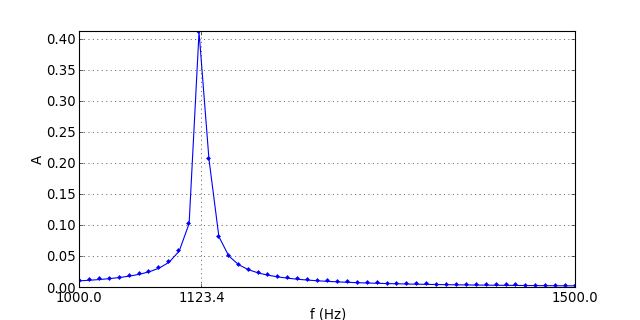figC.pdf

Ici la résolution du spectre est de 10 Hz car T=0.1 s. Elle est très inférieure à la précision de l'oscillateur, qui de l'ordre du milli-Hertz.

Une application de ce type d'oscillateur est la modulation de fréquence. Il suffit en effet de modifier la valeur de l'incrément I pour que la fréquence du signal généré soit instantanément modifiée. Voici par exemple la génération d'un signal comportant deux fréquences. Des bits aléatoires sont transmis (modulation FSK) : un bit 0 donne la première fréquence, un bit 1 la seconde. Chaque bit est transmis pendant une durée égale à nT_e. La durée de l'acquisition est multipliée par 10 pour augmenter la résolution de l'analyse spectrale.

import random
fe = 1.0e6
f1 = 1000.0
f2 = 900.0
A = numpy.int32(0)
I1 = numpy.int32(2**32*f1/fe)
I2 = numpy.int32(2**32*f2/fe)
listI = [I1,I2]
T = 1.0 # duree d'acquisition
N = int(T*fe)
u = numpy.zeros(N)
s = 0
n = 10000
for i in range(N):
    if s==0:
        I = listI[random.getrandbits(1)]
    s = (s+1)%n
    A = numpy.uint32(A+I)
    k = int(numpy.uint8(A>>24)) # k = 8 bits de poids fort de A
    u[i] = tab[k]
                      

On trace le spectre du signal :

a = numpy.absolute(numpy.fft.fft(u)/N)
freq = numpy.arange(N)*1.0/T
figure(figsize=(8,4))
plot(freq,a,'-')
xlabel('f (Hz)')
ylabel('A')
axis([800,1200,0,a.max()])
xticks([800,900,1000,1100,1200]) 
grid()
                    

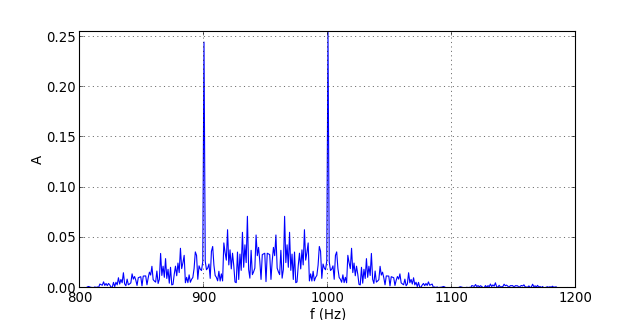figD.pdf

3.a. Principe

La synthèse par recursion ([1]) consiste à générer les échantillons avec une relation de récurrence de la forme :

$$y_n=a_1{y}_{n-1}+a_2{y}_{n-2}+a_3{y}_{n-3}+\mathrm{.}\mathrm{.}\mathrm{.}\text{(15)}$$

Il s'agit d'un cas particulier de filtre à réponse impulsionnelle infinie (ou filtre récursif), dans lequel le signal d'entrée est nul.

Ce type de synthèse a l'avantage de nécessiter très peu de mémoire de stockage. En contrepartie, l'application de la relation de récurrence nécessite généralement des calculs en virgule flottante, ou en virgule fixe.

3.b. Sinusoïdes en quadrature

La synthèse de deux sinusoïdes déphasées de π/2 (un cosinus et un sinus) est utile pour certaines opérations de traitement du signal, comme la détection de phase. Soit f_e la fréquence d'échantillonnage et f la fréquence des sinusoïdes à générer. On considère la pulsation (sans dimensions) suivante :

$$\Omega =2\pi \frac{f}{f_e}\text{(16)}$$

Les signaux numériques x et y sont générés par les relations de récurrence suivantes :

$$\begin{array}{ccc}\hfill & x_n=cos\left(\Omega \right)x_{n-1}+sin\left(\Omega \right)y_{n-1}\hfill & \hfill \text{(17)}\\ \hfill & y_n=cos\left(\Omega \right)y_{n-1}-sin\left(\Omega \right)x_{n-1}\hfill & \hfill \text{(18)}\end{array}$$

Pour démarrer la récursion, il faut une condition initiale. Celle-ci est donnée par :

$$x_0=0,y_0=1\text{(19)}$$

Pour comprendre la relation ci-dessus, il suffit de remarquer qu'elle s'interprète géométriquement comme une rotation d'angle Ω autour du centre, appliquée au point de coordonnées (x_n-1,y_n-1) : le point se déplace ainsi sur le cercle unité, ce qui donne bien des oscillations sinusoïdales en quadrature pour ses coordonnées.

Dans un oscillateur temps-réel, les échantillons sont calculés et utilisés au fur et à mesure (éventuellement convertis en analogique). Dans un calcul sur python, nous allons stocker les échantillons dans une table pour les tracer et effectuer leur analyse spectrale par transformée de Fourier discrète.

La condition de Nyquist-Shannon impose une fréquence d'échantillonnage au moins deux fois supérieure à la fréquence des sinusoïdes. Le paramètre Ω est donc compris entre 0 et π. La fonction suivante calcule N échantillons pour un rapport a=f/f_e donné. La condition initiale est fournie en argument.

import math
import numpy
from matplotlib.pyplot import *

def oscillation(N,a,x0,y0):
    c = math.cos(2*math.pi*a)
    s = math.sin(2*math.pi*a)
    x = numpy.zeros(N)
    y = numpy.zeros(N)
    x[0] = x0
    y[0] = y0
    for k in range(1,N):
        x[k] = c*x[k-1]+s*y[k-1]
        y[k] = c*y[k-1]-s*x[k-1]
    return (x,y)
                    

Pour obtenir une forme d'onde bien définie, il faut se placer en sur-échantillonnage, c'est-à-dire avec une valeur de a faible :

N=1000
a=0.01
(x,y)=oscillation(N,a,0,1)
figure(figsize=(10,4))
plot(x,'b')
plot(y,'r')
xlabel('n')
ylabel('x,y')
grid()

                     

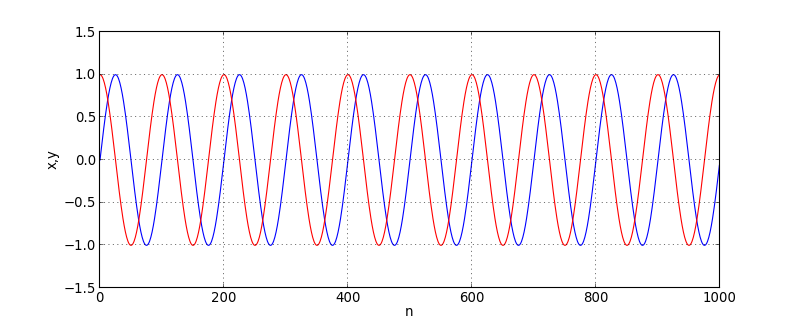figE.pdf

Dans certains cas, on peut avoir besoin d'une oscillation dont la fréquence n'est pas petite devant celle d'échantillonnage. Voyons le cas a=0.2 :

N=100
a=0.2
(x,y)=oscillation(N,a,0,1)
figure(figsize=(10,4))
plot(x,'b')
plot(y,'r')
xlabel('n')
ylabel('x,y')
grid()

                     

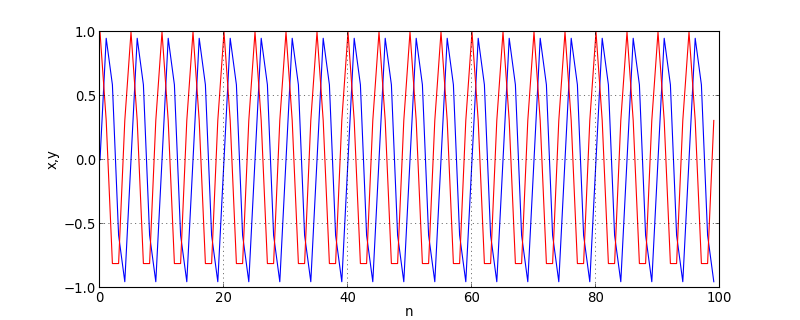figF.pdf

Faison une analyse spectrale :

import numpy.fft
A = numpy.absolute(numpy.fft.fft(x/N))
f = numpy.arange(N)*1.0/N
figure(figsize=(10,4))
plot(f,A)
grid()
                     

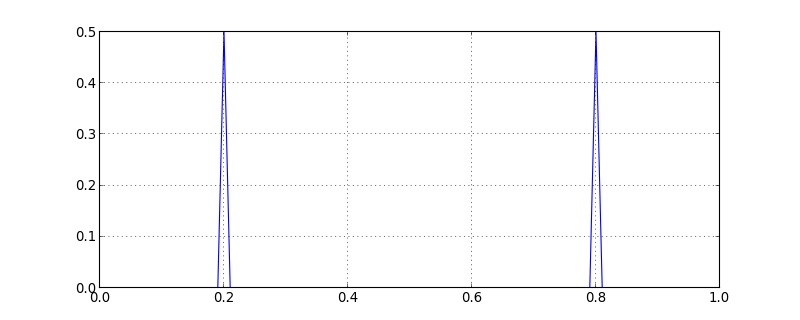figG.pdf

La condition de Nyquist-Shannon est respectée, donc le spectre est correct.

Lorsqu'on dispose d'une unité de calcul en virgule flottante, pourquoi ne pas calculer directement les échantillons avec la relation suivante ?

$$\begin{array}{ccc}\hfill & x_n=cos\left(n\Omega \right)\hfill & \hfill \text{(20)}\\ \hfill & y_n=sin\left(n\Omega \right)\hfill & \hfill \text{(21)}\end{array}$$

La première raison est que cette dernière méthode fait appel au calcul d'un cosinus et d'un sinus, bien plus coûteux en nombre d'opérations que les multiplications et additions de la méthode par récurrence. Même si l'on dispose d'une vitesse de calcul suffisante, la méthode récursive est plus adaptée aux changements instantanés de fréquence qui peuvent se produire, par exemple dans l'oscillateur d'une boucle à verrouillage de phase.

Pour voir cela, considérons la génération de N échantillons à une fréquence donnée, suivie d'une augmentation de la fréquence de 50 pour cent pour les N échantillons suivants :

N = 300
a=0.01
(x,y) = oscillation(N,a,0,1)
(x1,y1)=oscillation(N,a*1.5,x[N-1],y[N-1])
x = numpy.concatenate((x,x1[1:N-1]))
y = numpy.concatenate((y,y1[1:N-1]))
figure(figsize=(10,4))
plot(x,'b')
plot(y,'r')
xlabel('n')
ylabel('x,y')
grid()

                        

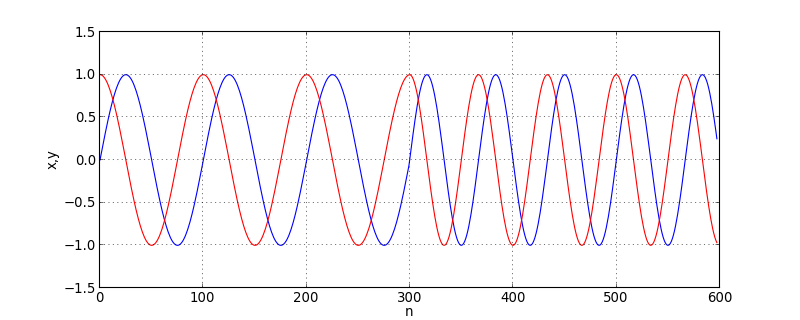figH.pdf

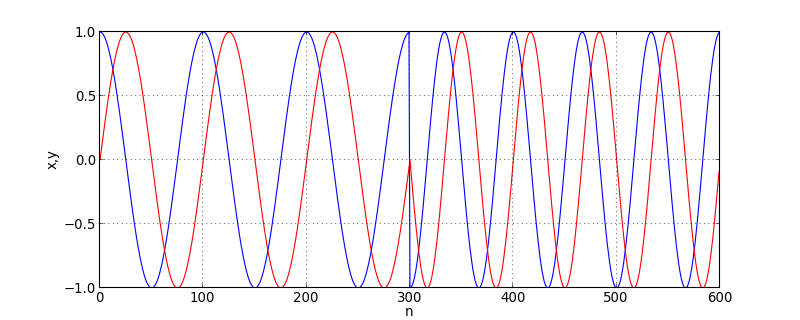
Le changement de fréquence se fait sans discontinuité de la phase. La méthode de l'accumulateur de phase exposée plus haut permet d'arriver au même résultat. Voyons ce qu'il arrive avec le calcul par la relation directe :

N = 600
a = 0.01
x = numpy.zeros(N)
y = numpy.zeros(N)
for k in range(0,300):
    x[k] = math.cos(2*math.pi*a*k)
    y[k] = math.sin(2*math.pi*a*k)
a = a*1.5
for k in range(300,N):
    x[k] = math.cos(2*math.pi*a*k)
    y[k] = math.sin(2*math.pi*a*k)
figure(figsize=(10,4))
plot(x,'b')
plot(y,'r')
xlabel('n')
ylabel('x,y')
grid()
                         

figI.pdf

Il se produit un saut de phase au moment où la fréquence est modifiée.