Boucle à verrouillage de phase
1. Introduction
La boucle à verrouillage de phase (Phase Locked Loop) est un dispositif permettant de générer un signal périodique dont la phase est verrouillée sur celle d'un autre signal. Plus précisément, pour un signal quasi périodique u1(t), la boucle génère un signal u2(t) de même fréquence que u1(t), qui présente donc un déphasage constant par rapport au premier (à fréquence donnée). Les applications de la boucle à verrouillage de phase (B.V.P.) sont très nombreuses. On peut citer :
- Génération d'un signal synchrone avec un signal un autre.
- Démodulation de fréquence.
- Détection synchrone.
- Synthèse de signaux d'horloge.
2. Schéma général
Figure pleine pageLe signal constituant l'entrée de la B.V.P. est u1(t). On notera T1 la durée d'un cycle de ce signal. Celui-ci est quasi périodique, ce qui signifie que la durée T1 peut évoluer au cours du temps. Sa phase est comparée à celle du signal u2(t) au moyen d'un comparateur de phase, qui est constitué de deux parties : un détecteur de phase et un filtre passe-bas. Le signal en sortie du détecteur (entrée du filtre) est noté ud(t). Le signal en sortie du filtre est noté uf(t). Le détecteur de phase fournit un signal dont la valeur moyenne (sur la durée T1) est proportionnelle à la différence de phase entre u1 et u2, qui est constante lorsque ces deux signaux sont synchrones (boucle verrouillée). Lorsque le filtre passe-bas a une fréquence de coupure beaucoup plus basse que 1/T1, la sortie du filtre est une tension constante, dont la valeur est proportionnelle à la différence de phase. Cette tension fournit une information sur la fréquence de u1(t), c'est-à-dire sur 1/T1.
Nous définissons le bloc comparateur de phase, incluant le filtre, afin de rendre plus aisée la compréhension du fonctionnement de la boucle.
Le signal uf(t) constitue l'entrée d'un oscillateur commandé en tension, c'est-à-dire un oscillateur générant un signal u2(t) (le plus souvent de forme carrée) dont la fréquence est commandée par la tension uf(t). La pulsation de ce signal est supposée dépendre de la tension de commande en suivant une relation affine :
est la pulsation de référence de l'oscillateur et une constante s'exprimant en . est la tension de référence de l'OCT, c.a.d. la tension de commande pour laquelle l'OCT a la pulsation .
La pulsation est la dérivée par rapport au temps de la phase. La phase du signal u2(t) est donc reliée à la tension en sortie du filtre par l'équation :
Le signal u2(t) généré par l'OCT constitue la seconde entrée du détecteur de phase, ce qui permet de fermer la boucle.
3. Modélisation des signaux
On suppose que u1(t) est un signal quasi périodique : la durée T1 n'est pas parfaitement constante. Tout signal périodique présente en réalité des petites fluctuations de sa période. Le signal u1(t) peut aussi être constitué d'une porteuse à haute fréquence dont la fréquence est lentement modulée, auquel cas les variations de T1 sont très grandes. Par souci de simplification, nous ne considérons que l'harmonique fondamental de ce signal (et le décalage) car, comme nous le justifierons plus loin, les harmoniques de rang supérieur ou égal à 2 jouent un rôle négligeable dans le fonctionnement de la boucle. On a donc :
est la valeur moyenne. La pulsation de ce signal est, par définition :
L'écriture suppose que la fréquence de base de ce signal (sa fréquence lorsque la phase est constante) soit identique à la fréquence centrale de l'OCT. Cette hypothèse, dont l'intérêt apparaîtra plus loin, ne nuit pas à la généralité car si la pulsation du signal est différente de (elle le sera en général), la différence peut être incorporée dans la phase .
Le signal en sortie de l'OCT est le plus souvent de forme carrée mais on peut là encore limiter l'étude en considérant seulement le fondamental :
On remarquera que cette écriture fait intervenir un cosinus alors que la relation fait intervenir un sinus. En effet, le déphasage entre les deux signaux est proche de lorsque la boucle est verrouillée (pour les deux détecteurs de phase étudiés ici) et cette convention d'écriture permet d'avoir alors une différence de phase petite lorsque ω1 est proche de ωo..
Nous supposons que le détecteur de phase a une réponse linéaire, c'est-à-dire qu'il fournit un signal dont la valeur moyenne est proportionnelle à la différence de phase.
Le signal v(t) comporte des variations de pulsation ω1 ou plus. En première approche, on fait l'hypothèse que le filtre passe-bas est idéal, avec une pulsation de coupure ω0, un gain unité et un déphasage nul dans la bande passante. La tension en sortie du filtre s'écrit donc :
est une constante qui dépend du détecteur de phase utilisé (le gain du filtre vaut 1 dans la bande passante). Il faut noter que cette relation n'est valable que si la différence de phase est assez petite et que son domaine de validité dépend du détecteur de phase utilisé.
4. Filtre passe-bas
Le filtre passe-bas considéré sur le schéma ci-dessus est caractérisé par la fonction de transfert suivante :
avec et . Voici le diagramme de Bode ce filtre :
Figure pleine pageLa pulsation de coupure doit être inférieure à . La pulsation doit être plus grande que .
Dans ce document, le filtre passe-bas sera désigné R1C ou R1R2C suivant que R2 est nulle ou pas. Si R2 est nulle, le déphasage à haute fréquence est -π/2, ce qui, combiné au déphasage de -π/2 introduit par l'OCT, peut nuire à la stabilité de la boucle. L'intérêt de la résistance R2 vient de l'annulation du déphasage à haute fréquence.
En première approche, le fonctionnement de la boucle peut être décrit avec un filtre passe-bas idéal, défini comme un filtre de pulsation de coupure strictement inférieure à ωo, de gain unité et de déphasage nul dans la bande passante. On notera ufi(t) la tension en sortie du filtre dans l'hypothèse où il est idéal. Même pour un filtre réel, le signal ufi(t) intervient encore dans les équations car c'est en fait ce signal qui détermine la phase du signal en sortie de l'OCT.
5. Détecteur de phase
5.a. Multiplicateur
Un multiplicateur permet de réaliser la détection de phase. Le signal en sortie du détecteur est :
Pour un filtre idéal, la tension en sortie du filtre s'écrit :
La valeur de tension de référence de l'OCT est , ce qui revient à considérer que est en fait la pulsation de l'OCT lorsque la tension de commande est . Lorsque la différence des phases est petite, nous avons une relation linéaire :
Notons que lorsque est petit les deux signaux ont en fait un déphasage proche de .
En réalité, le filtre passe-bas est très loin d'un filtre idéal. Cependant, il s'en approche à condition que et . Ces deux conditions sur les caractéristiques du filtre ne sont pas indispensables pour faire fonctionner la boucle mais elles assurent une tension quasi constante en sortie du comparateur de phase lorsque la boucle est verrouillée, ce qui permet d'utiliser la boucle pour déterminer la fréquence du signal u1. Si 1/(τ1+τ2) n'est pas petit devant ωo, la tension uf(t) présente des oscillations de pulsation ω1 non négligeables, mais celles-ci n'ont qu'un effet négligeable sur le signal u2(t) généré par l'OCT (voir explication ci-dessous avec le comparateur XOR). Seules les variations de uf(t) plus lentes que ω1 sont significatives pour le fonctionnement de la boucle et ces variations sont représentées par le signal ufi(t).
5.b. Porte OU-exclusif
Une porte logique OU-exclusif (XOR) est un meilleur choix de détecteur de phase car sa plage de fonctionnement linéaire est plus grande (et beaucoup moins coûteux que le multiplicateur) mais il ne fonctionne qu'avec des signaux binaires (typiquement des signaux en créneau 0 et 5 V). Lorsque le signal est analogique (non binaire), il peut être aisément converti en signal binaire au moyen d'un comparateur de tensions.
Figure pleine pagePour un filtre passe-bas idéal qui annulerait les oscillations de pulsation supérieure à ω0, la tension en sortie du filtre est la valeur moyenne de . Dans ce cas, la tension ufi reste constante lorsque la boucle est verrouillée, mais elle varie (lentement) lorsque les deux signaux u1(t) et u2(t) ne sont plus synchrones. En réalité, le filtre n'est pas idéal et la tension ud(t) présente des oscillations de période T1/2 (en dents de scie si la fréquence de coupure du filtre est assez basse). Cette tension est utilisée pour commander la fréquence de l'OCT (relation ). Si l'OCT génère un signal de forme carrée, la demi-période de celui-ci est déterminée par la variation de la phase pendant la durée T1/2. Or la variation de la phase est égale à l'intégrale de la fréquence donc finalement à l'intégrale de la tension uf(t) :
Le signal en sortie du filtre idéal est la valeur moyenne :
On a donc :
Il s'en suit que les oscillations de période T1/2 de uf(t) n'ont aucun effet sur la phase effective de u2(t). Pour cette raison, on s'intéresse seulement à la valeur moyenne de uf (moyenne sur la durée T1), qui est bien constante lorsque la boucle est verrouillée et qui correspond à la sortie du filtre lorsqu'il est idéal. Finalement, on peut donc dire que la fréquence de l'OCT est pilotée par la valeur de tension en sortie du filtre idéal, ce qui justifie la relation . Cette relation devra tout de même être modifiée pour tenir de la réponse du filtre non idéal (voir l'étude linéaire plus loin).
Lorsque les deux signaux sont déphasés de , la tension en sortie du filtre est . Notons l'avance de par rapport à . C'est aussi la durée pendant laquelle la tension est au niveau haut. On a donc :
Or est le déphasage de par rapport à (tant que ). La tension de référence de l'OCT est . Lorsque les deux signaux sont en quadrature , et en conséquence :
avec :
La tension ufi(t) dépend du temps lorsque la différence de phase dépend du temps, c'est-à-dire lorsque les deux signaux ne sont pas synchrones. Pour un filtre idéal, les variations de la différence de phase dont la fréquence est dans la bande passante sont en effet transmises au signal ufi(t).
La figure suivante montre la sortie du comparateur de phase en fonction du déphasage.
Figure pleine pageLa relation linéaire est donc valable pour compris entre et . Avec la porte XOR, le domaine de validité de la relation est nettement plus large que dans le cas de l'utilisation d'un multiplicateur, puisque pour ce dernier il se limite aux différences de phase petites.
6. Fonctionnement de la boucle
6.a. Boucle verrouillée
La boucle est dite verrouillée lorsque les signaux et sont synchrones, c'est-à-dire lorsque le déphasage est constant, ce qui implique que ces deux signaux ont exactement la même fréquence. Cela n'exclue pas que cette fréquence puisse être différente de . En effet si désigne la fréquence des deux signaux, on a :
Lorsque la boucle est verrouillée, la tension en sortie du filtre idéal est donc constante (tant que le signal ne change pas de fréquence) :
Dans cette écriture (et dans toute cette partie) nous avons posé , ce qui revient simplement à considérer que désigne l'écart de la tension en sortie du filtre par rapport à la tension de référence . Par ailleurs, la tension n'est vraiment constante que si le filtre est idéal. En réalité, ufi désigne la valeur moyenne pendant un cycle de la tension uf(t).
Il s'en suit que la tension de commande de l'OCT est constante donc que la pulsation de est constante, égale à :
Cette pulsation est précisément celle du signal puisque le déphasage est constant. Ainsi, lorsque la boucle est verrouillée, l'OCT produit un signal périodique (de forme carrée) parfaitement synchrone avec le signal , c'est-à-dire de même fréquence. Le déphasage réel entre et est constant, égal à :
La valeur absolue est donc d'autant plus grande que est éloignée de . Sachant que doit être inférieur à (pour les deux comparateurs étudiés ci-dessus), le verrouillage n'est possible que si :
Si on note la plage de fréquences balayée par l'O.C.T. lorsque sa tension varie de 0 à sa tension d'alimentation (5 V), on a :
et cette plage de fréquence correspond en principe à la plage de fréquences verrouillées par la boucle, du moins pour le comparateur XOR et si la fréquence minimale fo-Δf/2 est positive. Lorsque le gain de l'OCT (Kd) est très grand, cette plage de fréquence peut être beaucoup plus grande que la plage de variation de fréquence du signal u1(t), et la fréquence minimale peut être négative.
Il faut remarquer que le déphasage change lorsque la pulsation ω1 change, mais que ce changement peut être rendu négligeable si Δf est très grand, c'est-à-dire si le gain de l'OCT Kd est très grand. Un telle boucle est qualifiée de boucle à fort gain et se caractérise aussi par une très faible variation de ufi lorsque la fréquence change. Comme nous le verrons plus loin, une boucle à fort gain réagit plus vite lorsque la fréquence change.
La tension qui pilote effectivement la phase du signal en sortie de l'OCT est la tension en sortie du filtre qui serait idéal :
Elle contient l'information sur la fréquence du signal d'entrée; la B.V.P. peut donc être utilisée pour effectuer une démodulation de fréquence.
Lorsque l'OCT délivre un signal de pulsation , on a , ce qui signifie que les deux signaux et sont déphasés de . En effet, l'intervalle de déphasage permettant d'avoir verrouillage de la boucle est centré sur . Le choix d'un déphasage de lorsque la pulsation est permet donc une excursion de pulsation symétrique autour de . Cependant, ce choix n'est qu'une convention adoptée pour le calcul : la seule chose qui importe en réalité est que la boucle reste verrouillée sur toute la plage de fréquence du signal .
Une B.V.P. bien réglée doit rester verrouillée, ou du moins très proche du verrouillage, lorsque la fréquence du signal change. Elle doit avoir un comportement stable, c'est-à-dire qu'elle peut éventuellement s'éloigner notablement du verrouillage à condition d'y retourner très vite, à une échelle de temps de l'ordre de quelques périodes de . Il faut donc étudier le comportement du système bouclé lorsque la fréquence de change.
6.b. Étude linéaire
On suppose que la relation est valable, ce qui dans le cas du détecteur XOR est vrai pour un déphasage dans l'intervalle . Dans ce cas, toutes les équations sont linéaires. Par ailleurs, l'effet des harmoniques de rang supérieur ou égal à 2 est supposé négligeable grace au filtre passe-bas et au filtrage accompli par l'OCT. Il est donc possible d'étudier la réponse du système en régime sinusoïdal. Il faut remarquer que la pertinence de cette étude n'est pas a priori évidente, car du point de vue des tensions, la multiplication et la fonction OU-exclusif sont des fonctions hautement non linéaires.
Pour définir une fonction de transfert, nous devons définir une grandeur d'entrée et une grandeur de sortie. Le plus souvent, la grandeur d'entrée qui nous intéresse est la fréquence du signal , ou bien sa pulsation . Plus précisement, la grandeur d'entrée est , l'écart entre la pulsation et la pulsation de base de l'OCT, que l'on notera . On a la relation :
La phase est donc obtenue par intégration de . En régime sinusoïdal, nous avons :
est la pulsation de modulation de fréquence, c'est-à-dire la pulsation de variation de la pulsation . Posons . En notation complexe, la relation entre et s'écrit :
Dans le cas d'une analyse du signal , la grandeur de sortie qui nous intéresse est .
Afin de tenir compte de la caractéristique du filtre, nous devons modifier la relation en la multipliant par la fonction de transfert du filtre :
Rappellons que ufi désigne la tension en sortie du filtre si celui-ci est idéal, c'est-à-dire la tension en sortie du filtre moyennée sur un cycle. Ce modèle, qui suppose que tous les signaux sont sinusoïdaux, ne peut pas rendre compte des oscillations de uf(t), qui sont non sinusoïdales. La pertinence du modèle linéaire provient du fait que l'OCT réalise, par son caractère intégrateur, une élimination des oscillations de uf(t), ce qui revient formellement à s'intéresser à ufi(t).
La relation s'écrit aussi :
Nous avons donc :
La fonction de transfert (sans dimensions) qui nous intéresse est :
Il s'agit donc de la fonction de transfert qui permet d'exprimer la phase en sortie de l'OCT par rapport à la phase du signal d'entrée. La relation s'écrit :
La fonction de transfert s'en déduit et, après simplification, on obtient :
La fréquence Fn=Ωn/(2π) est la fréquence naturelle de la boucle. ξ est le facteur d'amortissement.
Voici un schéma bloc du modèle linéaire de la boucle à verrouillage de phase, avec la phase comme entrée :
Figure pleine pageIl faut remarquer que ce modèle permet de décrire le comportement de la boucle tant que la différence de phase reste dans l'intervalle de linéarité du comparateur de phase. Si elle sort de ce domaine, le retour de la boucle à un état verrouillé ne peut pas être décrit par ce modèle. En particulier, il ne permet pas de décrire le démarrage de la boucle. Lorsqu'on sort du domaine de linéarité de la porte XOR, la boucle décroche et son comportement doit être décrit par des équations non linéaires. Dans le cas du multiplicateur, il y a des effets non linéaires bien avant que la boucle décroche puisque le domaine linéaire n'est qu'une approximation pour les déphasages petits.
Ce modèle permet d'obtenir la réponse indicielle de la boucle, c'est-à-dire comment la boucle retourne à l'état verrouillé lorsque le signal u1(t) subit une variation très rapide de sa phase ou de sa fréquence (par ex. dans le cas d'une modulation de fréquence FSK). La boucle doit retourner à l'état verrouillé rapidement et sans oscillations de ufi. Il ne faut pas confondre les oscillations amorties de la réponse indicielle, qu'il faudra absolument éviter, avec les oscillations permanentes en sortie du filtre lorsque la boucle est verrouillée, qui ne sont pas nuisibles au verrouillage bien qu'elles soient indésirables pour certaines applications.
Les pôles de la fonction de transfert sont :
La fonction de transfert permet de déterminer la réponse indicielle de la boucle, c'est-à-dire la réponse à un échelon de phase sur u1(t) ou à un échelon de fréquence. L'annexe A expose le calcul de la réponse indicielle. La fonction suivante calcule la réponse à un échelon de phase en temps réduit (t'=Ωnt ) :
import numpy as np
from matplotlib.pyplot import *
def echelonPhase(t,xi,tau2,Wn):
if xi >1:
r = np.sqrt(xi**2-1)
B = (xi-tau2*Wn+r)/(-2*r)
C = (xi-tau2*Wn-r)/(2*r)
s1 = -xi+r
s2 = -xi-r
phi2 = 1+B*np.exp(s1*t)+C*np.exp(s2*t)
elif xi<1:
r = np.sqrt(1-xi**2)
B = (xi-tau2*Wn+1j*r)/(-2*1j*r)
s1 = -xi+1j*r
phi2 = 1+2*np.real(B*np.exp(s1*t))
else:
phi2 = 1+((tau2*Wn-1)*t-1)*np.exp(-t)
return phi2
La fonction suivante calcule la réponse à un échelon de fréquence (variation de fréquence d'une unité) :
def echelonFrequence(t,xi,tau2,Wn):
if xi==1:
xi += 1e-2
A = tau2*Wn-2*xi
if xi > 1:
r = np.sqrt(xi**2-1)
B = (1+A*(xi+r))/(-2*r)
C = (1+A*(xi-r))/(2*r)
s1 = -xi+r
s2 = -xi-r
Dphi = A+B*np.exp(s1*t)+C*np.exp(s2*t)
else:
r = np.sqrt(1-xi**2)
B = (1+A*(xi+1j*r))/(-2*1j*r)
s1 = -xi+1j*r
Dphi = A+2*np.real(B*np.exp(s1*t))
return Dphi
La partie réelle des pôles est négative donc la boucle est théoriquement stable. Il faut néanmoins prévoir une marge de sécurité par rapport à la condition d'instabilité. Pour ce faire, on considère la fonction de transfert en boucle ouverte :
La boucle serait instable s'il existait une valeur de s pour laquelle on aurait un gain en boucle ouverte unité et un déphasage de π. Pour évaluer la marge, on trace le gain en décibel et le déphasage de la fonction de transfert en boucle ouverte puis on repère la fréquence pour laquelle le gain vaut 0 dB. La méthode de la marge de phase consiste à lire le déphasage à cette fréquence et à s'assurer qu'il diffère de π d'une valeur assez grande, typiquement π/4. Une valeur trop proche de π pourrait en effet rendre le système réel instable car le modèle linéaire ne correspond pas exactement au comportement du système réel (qui dépend des composants utilisés).
Nous verrons cependant qu'en pratique il n'est pas nécessaire de faire l'étude de la marge de stabilité car celle-ci est en fait déterminée par le coefficient d'mortissement ξ. Le choix d'une valeur de ξ supérieure à 1/2 garantit une marge de stabilité suffisante.
Filtre R1C
Supposons tout d'abord que , c'est-à-dire R2=0. Les équations s'écrivent :
Voici le tracé du gain en décibel et du déphasage pour différentes valeurs de :
import numpy as np
from matplotlib.pyplot import *
from conceptionPLL import *
x = np.logspace(-1,1,500)
def H(x,xi):
return 1/(1+2*1j*xi*x-x**2)
xi = [3,2,1,1/np.sqrt(2),0.5,0.2]
HH,GdB,phi = [],[],[]
for i in range(len(xi)):
HH = H(x,xi[i])
GdB.append(20*np.log10(np.absolute(HH)))
phi.append(np.angle(HH))
figure()
for i in range(len(xi)):
plot(x,GdB[i],label=r"$\xi = %0.2f$"%xi[i])
xscale('log')
xlabel(r"$\Omega/\Omega_n$")
ylabel(r"$G_{\rm dB}$")
legend(loc='upper right')
grid()
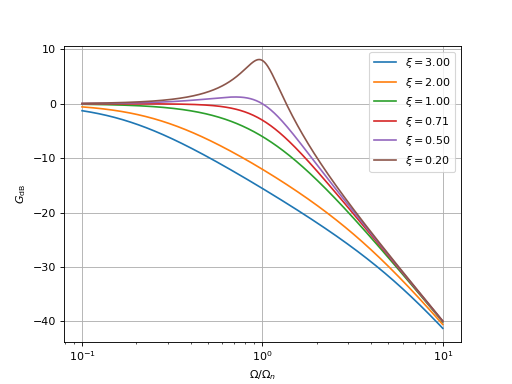 BodePLL-1.pdf
BodePLL-1.pdf
figure()
for i in range(len(xi)):
plot(x,phi[i]/np.pi,label=r"$\xi = %0.2f$"%xi[i])
xscale('log')
xlabel(r"$\Omega/\Omega_n$")
ylabel(r"$\phi/\pi$")
legend(loc='upper right')
grid()
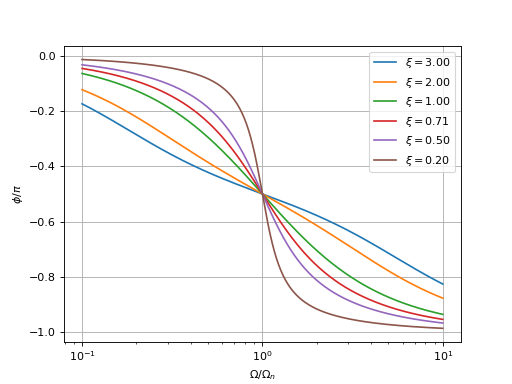 PhasePLL-1.pdf
PhasePLL-1.pdf
Nous pouvons aussi tracer la réponse indicielle :
t = np.linspace(0,15,1000)
figure(figsize=(12,5))
for i in range(len(xi)):
plot(t,echelonPhase(t,xi[i],0,0),label=r"$\xi = %0.2f$"%xi[i])
grid()
xlabel(r"$\Omega_nt$")
ylabel(r"$\phi_2/\delta\phi$")
legend(loc='lower right')
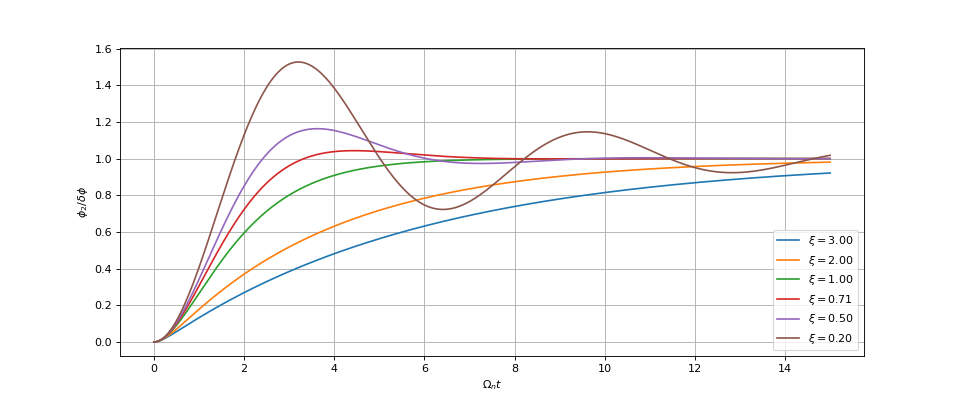 echelonPLL-1.pdf
echelonPLL-1.pdf
t = np.linspace(0,15,1000)
figure(figsize=(12,5))
for i in range(len(xi)):
plot(t,echelonFrequence(t,xi[i],0,0),label=r"$\xi = %0.2f$"%xi[i])
grid()
xlabel(r"$\Omega_nt$")
ylabel(r"$(\phi_2-\phi_1)/(\delta\omega/\Omega_n)$")
legend(loc='lower right')
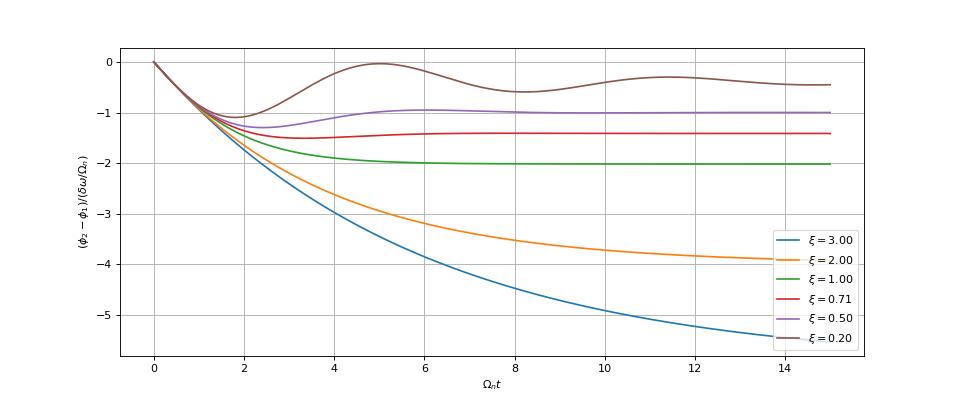 echelonFreqPLL-1.pdf
echelonFreqPLL-1.pdf
La valeur optimale est car elle conduit à une réponse indicielle la plus rapide et sans oscillations. La pulsation de coupure pour cette valeur est . Sachant que , la pulsation de coupure s'écrit :
Pour le coefficient d'amortissement optimal, le temps de réponse de la boucle (en cas de changement soudain de la phase ou de la fréquence) est environ . En conséquence, la plage de fréquence balayée par l'OCT doit être d'autant plus grande que l'on souhaite une réponse rapide. Cependant, plus la plage de fréquence est grande, plus il est difficile de détecter une petite variation de fréquence en sortie du filtre. Si la boucle est utilisée pour une mesure de variation de fréquence, il faut donc trouver un compromis entre la sensibilité à la variation de fréquence et la rapidité de la réponse.
Une valeur de ξ un peu plus grande que est tolérable. En revanche, il faudra éviter absolument les valeurs faibles de ξ car elles conduisent à des oscillations de la réponse impulsionnelle. La présence de ces oscillations est liée au fait que la partie réelle des pôles se rapproche de zéro, ce qui réduit la marge par rapport à la condition de stabilité.
Filtre R1R2C
La constante apporte un degré de liberté supplémentaire permettant d'augmenter , c'est-à-dire , indépendamment de la valeur de . Lorsque est très grand, le filtre R1C conduit en effet à une valeur trop faible du coefficient d'amortissement, d'autant plus que l'on choisit une valeur de faible. Le filtre R1R2C permet de réaliser une boucle à fort gain d'OCT avec une pulsation relativement faible.
Considérons le cas où est prépondérant dans l'expression de :
Une telle boucle est dite à gain fort. Le filtre R1R2C est intéressant pour les boucles à gain fort.
On obtient alors :
Cette dernière relation montre que ce filtre permet d'ajuster le coefficient d'amortissement pour un choix quelconque de .
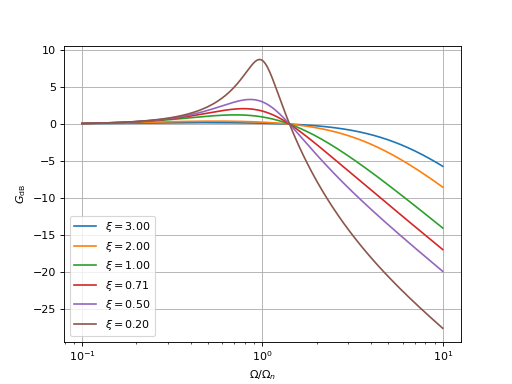
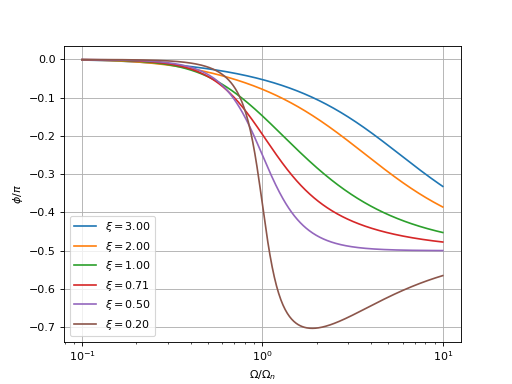
Voici le tracé du gain en décibel et du déphasage pour différentes valeurs de :
x = np.logspace(-1,1,500)
def H(x,xi):
return (1+2*1j*xi*x)/(1+2*1j*xi*x-x**2)
xi = [3,2,1,1/np.sqrt(2),0.5,0.2]
HH,GdB,phi = [],[],[]
for i in range(len(xi)):
HH = H(x,xi[i])
GdB.append(20*np.log10(np.absolute(HH)))
phi.append(np.angle(HH))
figure()
for i in range(len(xi)):
plot(x,GdB[i],label=r"$\xi = %0.2f$"%xi[i])
xscale('log')
xlabel(r"$\Omega/\Omega_n$")
ylabel(r"$G_{\rm dB}$")
legend(loc='lower left')
grid()
 BodePLL-2.pdf
BodePLL-2.pdf
figure()
for i in range(len(xi)):
plot(x,phi[i]/np.pi,label=r"$\xi = %0.2f$"%xi[i])
xscale('log')
xlabel(r"$\Omega/\Omega_n$")
ylabel(r"$\phi/\pi$")
legend(loc='lower left')
grid()
 PhasePLL-2.pdf
PhasePLL-2.pdf
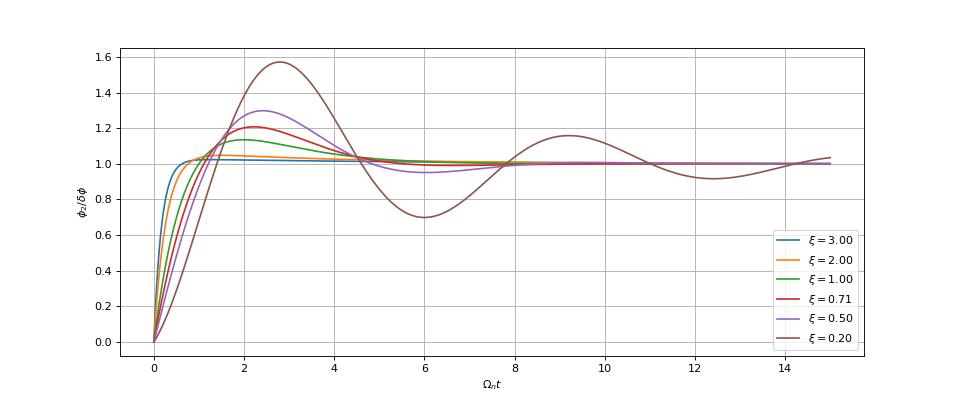
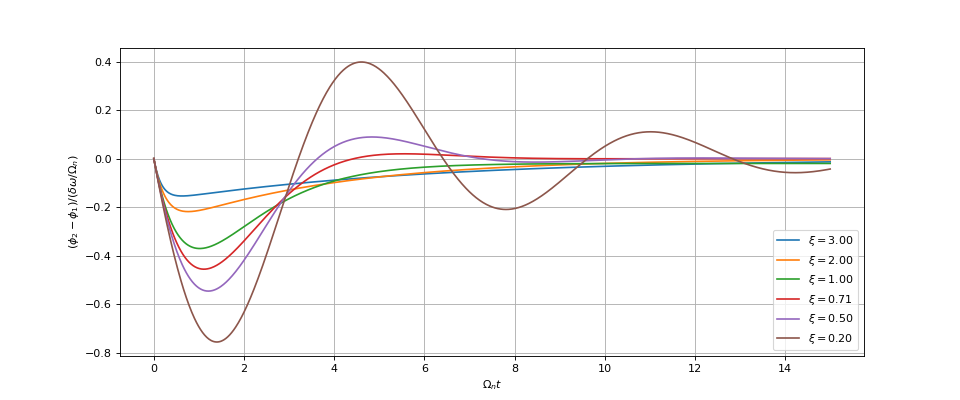
Voici la réponse indicielle en fonction du temps réduit t'=Ωnt, qui ne dépend que de ξ pour une boucle à gain fort :
t = np.linspace(0,15,1000)
tau2 = 1
figure(figsize=(12,5))
for i in range(len(xi)):
Wn=2*xi[i]/tau2
plot(t,echelonPhase(t,xi[i],tau2,Wn),label=r"$\xi = %0.2f$"%xi[i])
grid()
xlabel(r"$\Omega_nt$")
ylabel(r"$\phi_2/\delta\phi$")
legend(loc='lower right')
 echelonPLL-2.pdf
echelonPLL-2.pdf
t = np.linspace(0,15,1000)
tau2 = 1
figure(figsize=(12,5))
for i in range(len(xi)):
Wn=2*xi[i]/tau2
plot(t,echelonFrequence(t,xi[i],tau2,Wn),label=r"$\xi = %0.2f$"%xi[i])
grid()
xlabel(r"$\Omega_nt$")
ylabel(r"$(\phi_2-\phi_1)/(\delta\omega/\Omega_n)$")
legend(loc='lower right')
 echelonFreqPLL-2.pdf
echelonFreqPLL-2.pdf
Pour ce filtre, le temps de réponse diminue toujours lorsque le facteur d'amortissement augmente. Cependant, un facteur d'amortissement trop grand a aussi pour conséquence une pente dans la bande atténuante de la réponse fréquentielle plus faible, ce qui peut rendre la boucle trop sensible aux perturbations de haute fréquence. On considère, dans le cas général, que la valeur optimale est ou une valeur légèrement plus grande, comme pour le filtre R1C, mais la valeur de permet de satisfaire la condition sans imposer . On a en effet pour cette valeur optimale :
et la condition s'écrit :
Cette relation montre que le cas étudié (boucle à fort gain, condition ) correspond à une plage de fréquences très grande par rapport à la bande passante de la boucle. Pour résumer, on peut dire qu'il s'agit d'une boucle à fort gain d'OCT et à bande passante faible.
La pulsation Ωn est la pulsation de coupure du filtre, du moins lorsque le taux d'amortissement est proche de la valeur optimale. La boucle est donc capable de suivre des variations de fréquence de u1(t) dont la pulsation est inférieure à Ωn. Le choix de Ωn se fait en fonction de l'application, en limitant la bande passante aux signaux utiles, de manière à minimiser l'influence du bruit. Le temps de réponse de la boucle est environ τn=10/Ωn. Si la fréquence de u1(t) varie soudainement, la boucle mettra environ une durée τn pour verrouiller à nouveau. D'après l'étude linéaire précédente :
En conséquence, plus la fréquence de coupure du filtre est basse, plus τ1+τ2 est grand et plus le temps de réponse de la boucle est grand. Si l'on souhaite que la boucle réagisse très rapidement, il faudra donc se contenter d'une fréquence de coupure du filtre plus haute, ce qui peut avoir pour conséquence la présence d'oscillations en sortie du filtre. Par ailleurs, plus la plage de fréquence balayée par l'OCT (Δf) est grande, plus le temps de réponse est faible. Cependant, une grande plage de fréquence a aussi pour conséquence une moindre sensibilité de la tension de sortie du filtre par rapport à une variation de fréquence. Si la boucle est utilisée pour faire de la démodulation FM, il faut trouver un compromis entre la sensibilité et le temps de réponse. Si la boucle est utilisée pour générer un signal synchrone avec u1(t), il faut privilégier un temps de réponse faible, c'est-à-dire une plage de fréquence large et/ou une bande passante de filtre large.
6.c. Méthode de calcul
Il s'agit de déterminer une méthode de calcul permettant d'obtenir un filtre optimal pour ce qui est du fonctionnement en régime linéaire, c'est-à-dire la réponse de la boucle verrrouillée lorsque le signal u1(t) subit une variation de fréquence qui ne fait pas sortir du domaine linéaire. Le comportement de la B.V.P. lorsqu'elle sort du domaine linéaire (par une excursion trop grande de la fréquence) est abordée en partie 8.
La fréquence fo et la plage Δf sont supposées données. Le choix de ces deux paramètres dépend de l'application envisagée. La plage de fréquence est définie par le produit du gain du détecteur de phase par celui de l'OCT puisque KoKd=2Δf.
Il reste à choisir la valeur de Ωn (en respectant les contraintes de l'application) tout en maintenant une valeur de ξ proche de la valeur optimale, ou en tout cas éviter les valeurs petites qui allongeraient considérablement le temps de réponse et pourraient nuire à la stabilité de la boucle.
Il faut aussi remarquer que Δf pourra aussi être ajusté si le premier choix ne donne pas un résultat satisfaisant. En effet, cette plage de fréquence doit être au minimum égale à la plage de fréquence balayée par le signal u1(t) (avec bien sûr une marge de sécurité) mais elle peut être en fait beaucoup plus grande si l'on souhaite obtenir une boucle à fort gain.
Dans la pratique, on préfère utiliser la fréquence au lieu de la pulsation. Le temps de réponse de la boucle pour un coefficient d'amortissement optimale est alors :
On ne sait pas a priori quelle est la plage de valeurs pertinentes de Fn (qui définit la bande passante de la B.V.P.). On considère donc cette fréquence comme une variable et on trace les autres paramètres en fonction de Fn.
On cherche tout d'abord à savoir si le filtre peut être le filtre R1C, c'est-à-dire τ2=0. La réponse linéaire est alors définie par :
Dans ce cas, le coefficient d'amortissement ne peut être choisi librement si Ωn est fixée. On calcule :
La valeur minimale de τ1 qui permet d'éliminer pratiquement les oscillations en sortie du filtre est :
Il est cependant possible de choisir une valeur inférieure à , à condition d'accepter une tension uf non constante pendant le verrouillage (oscillations en sortie du filtre). Ces variations ne sont gênantes que si le but est d'extraire de la tension uf(t) la fréquence du signal u1(t), mais elles ne nuisent pas du tout au bon verrouillage de la boucle (comme nous l'avons démontré plus haut).
On trace ξ et τ1 en fonction de Fn, ce qui permet de repérer la plage de valeurs de Fn pour laquelle τ1>τ1min. Si la plage de valeurs de Fn possible avec un coefficient d'amortissement par trop faible est satisfaisante, on peut utiliser ce filtre. Sinon, on doit envisager le cas suivant.
Si le filtre possède un temps τ2 non nul (filtre R1R2C), la réponse linéaire est définie par :
Dans ce cas, le degré de liberté supplémentaire apporté par τ2 permet de fixer la valeur du coefficient d'amortissement. On choisit donc la valeur optimale , qui permet d'avoir une réponse indicielle rapide et sans oscillations. Un choix légèrement différent sera bien sûr possible selon les exigences de l'application envisagée. Les caractéristiques du filtre sont calculées par les formules suivantes :
Pour une boucle à gain fort, le temps τ2 est défini par :
On trace τ1, τ2 (qui doit être positif) et τ2' en fonction de Fn. La valeur de τ1min aussi tracée.
Voici les deux fonctions Python permettant de tracer ces courbes. Si une valeur non nulle de Fn est fournie en argument, la première renvoie les valeurs de τ1 et ξ correspondantes, la seconde renvoie les valeurs de τ1 et τ2.
def filtreR1C(f0,Df,Fn=0):
log = np.log10(f0)
if Fn==0:
Fn = np.logspace(log-3,log,500)
xi = 2*np.pi*Fn/(4*Df)
tau1 = 2*Df/(2*np.pi*Fn)**2
else:
xi = 2*np.pi*Fn/(4*Df)
tau1 = 2*Df/(2*np.pi*Fn)**2
return (tau1,xi)
tau1_min = np.ones(len(Fn))*100/(2*np.pi*f0)
figure()
subplot(211)
plot(Fn,tau1,'r',label=r"$\tau_1$")
plot(Fn,tau1_min,'g',label=r"$\tau_1^{\rm min}$")
grid()
legend(loc='upper right')
xscale('log')
yscale('log')
subplot(212)
plot(Fn,xi,'k')
xscale('log')
xlabel(r"$F_n\ (\rm Hz)$")
ylabel(r"$\xi$")
ylim(0,2)
grid()
def filtreR1R2C(f0,Df,xi,Fn=0):
log = np.log10(f0)
if Fn==0:
Fn = np.logspace(log-3,log,10000)
tau2 = 2*xi/(2*np.pi*Fn)-1/(2*Df)
tau2p = 2*xi/(2*np.pi*Fn)
tau1 = 2*Df/(2*np.pi*Fn)**2-tau2
else:
tau2 = 2*xi/(2*np.pi*Fn)-1/(2*Df)
tau1 = 2*Df/(2*np.pi*Fn)**2-tau2
return (tau1,tau2)
tau1_min = np.ones(len(Fn))*100/(2*np.pi*f0)
n = len(tau2)-1
for i in range(len(tau2)):
if tau2[i]<0:
n = i
break
figure()
Fn = Fn[0:n]
tau1 = tau1[0:n]
tau2 = tau2[0:n]
tau2p = tau2p[0:n]
tau1_min = tau1_min[0:n]
plot(Fn,tau1,'r',label=r"$\tau_1$")
plot(Fn,tau2,'b',label=r"$\tau_2$")
plot(Fn,tau2p,'b--',label=r"$\tau_2'$")
plot(Fn,tau1_min,'g',label=r"$\tau_1^{\rm min}$")
grid()
xlabel(r"$F_n\ (\rm Hz)$")
legend(loc='upper right')
xscale('log')
yscale('log')
Pour un choix donné de τ1 et τ2, il faut aussi évaluer la marge par rapport à la condition d'instabilité. La fonction suivante trace la réponse fréquentielle de la boucle ouverte et repère la fréquence pour laquelle le gain en décibel est nul :
def boucle_ouverte(Df,tau1,tau2,lgmin,lgmax):
f = np.logspace(lgmin,lgmax,500)
s = 1j*2*np.pi*f
Hbo = 2*Df*(1+tau2*s)/(s*(1+(tau1+tau2)*s))
GdB = 20*np.log10(np.absolute(Hbo))
j = -1
for i in range(len(f)-1):
if GdB[i]*GdB[i+1] < 0:
j = i
break
phi = np.angle(Hbo)
figure()
suptitle('Boucle ouverte')
subplot(211)
plot(f,GdB)
if j!=-1:
plot([f[j]],[GdB[j]],'ro')
xscale('log')
ylabel('GdB')
grid()
subplot(212)
plot(f,phi/np.pi)
if j!=-1:
plot(f[j],phi[j]/np.pi,'ro')
ylim(-1,0)
xscale('log')
ylabel(r"$\phi/\pi$")
xlabel('f (Hz)')
grid()
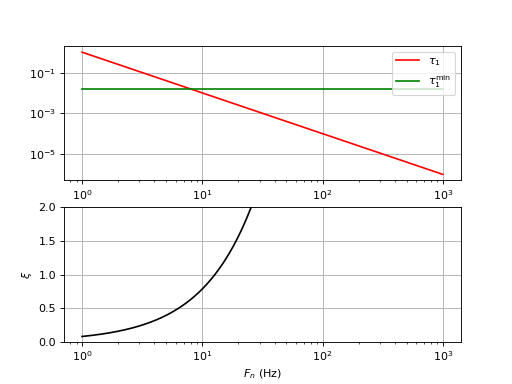
Considérons le cas suivant : et . Il s'agit d'une bande de fréquence très étroite (faible gain d'OCT), qui permet de détecter des faibles variations de fréquence avec une grande sensibilité. L'objectif de ce type de BVP est d'exploiter la tension en sortie du filtre pour suivre les variations de fréquences. Les oscillations en sortie du filtre doivent donc être de faible amplitude.
f0 = 1000
Df = 20
filtreR1C(f0,Df)
 filtreR1C-1.pdf
filtreR1C-1.pdf
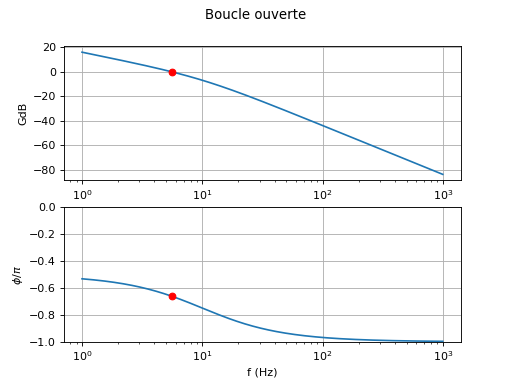
La valeur , correspondant à τ1=τ1min, donne un coefficient d'amortissement proche de la valeur optimale (0,62). Voici la réponse fréquentielle de la boucle ouverte :
(tau1,xi)=filtreR1C(f0,Df,8)
boucle_ouverte(Df,tau1,0,0,3)
print(1/tau1) --> 63.16546816697189
 filtreR1C-BO-1.pdf
filtreR1C-BO-1.pdf
Le déphasage lorsque GdB=0 est d'environ -0,63π. Il n'est pas très éloigné de π mais la marge est satisfaisante. On remarque que la pente de GdB lorsqu'il s'annule est d'environ -20 dB par décade (et pas -40 dB par décade), ce qui est un critère rapide souvent utilisé par les électroniciens pour évaluer la marge de stabilité simplement à partir de la courbe de gain. Ce critère repose sur le fait qu'un déphasage de -π est toujours associé à une fonction de transfert du deuxième ordre et donc à un gain décroissant de -40 dB par décade (comme le confirme la figure ci-dessus).
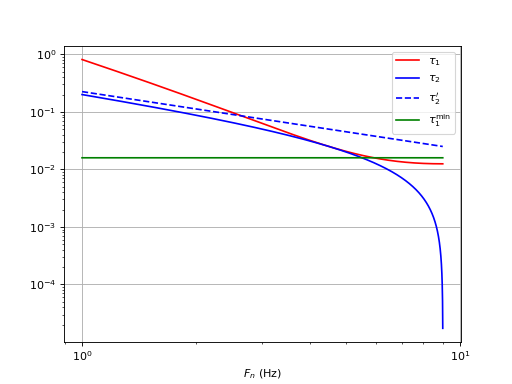
Voyons le filtre R1R2C pour la valeur optimale de ξ :
xi = 1/np.sqrt(2)
filtreR1R2C(f0,Df,xi)
 filtreR1R2C-1.pdf
filtreR1R2C-1.pdf
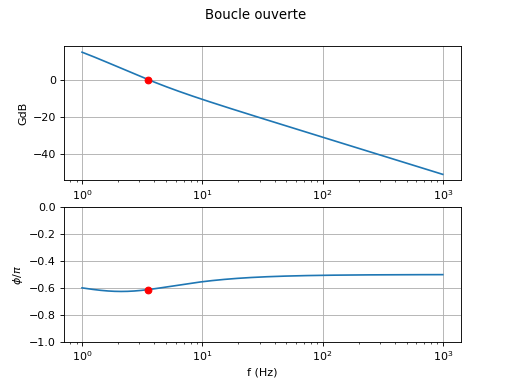
Tout à droite de ce graphique, la constante τ2 tend vers zéro et on retrouve donc le filtre R1C. L'intérêt du filtre R1R2C et de permettre un abaissement de la fréquence Fn tout en gardant la valeur de ξ optimale. Par exemple pour Fn=3 Hz, voici la réponse fréquentielle de la boucle ouverte :
Fn=3.0
(tau1,tau2)=filtreR1R2C(f0,Df,xi,Fn)
boucle_ouverte(Df,tau1,tau2,0,3)
print(1/(tau1+tau2)) --> 8.882643960980424
 filtreR1R2C-BO-1.pdf
filtreR1R2C-BO-1.pdf
La marge de sécurité de la phase lorsque GdB=0 est la même que précédemment. Ce filtre n'a donc pas d'avantage en terme de stabilité mais il sera moins sensible aux fluctuations de haute fréquence du signal u1. En revanche, l'abaissement de Fn a pour conséquence une augmentation des oscillations en sortie du filtre (puisque τ1 devient supérieur à τ1min).
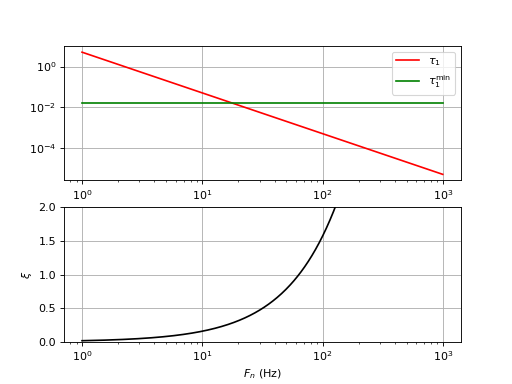
Voici un deuxième exemple, où la plage de fréquence est relativement plus élevée (gain de l'OCT plus grand) : et .
f0 = 1000
Df = 100
filtreR1C(f0,Df)
 filtreR1C-2.pdf
filtreR1C-2.pdf
Avec τ2=0, on peux choisir mais le coefficient d'amortissement est un peu faible. On peut tout de même augmenter un peu Fn, ce qui aura l'avantage de rapprocher ξ de sa valeur optimale, mais il faudra alors tolérer des oscillations en sortie du filtre.
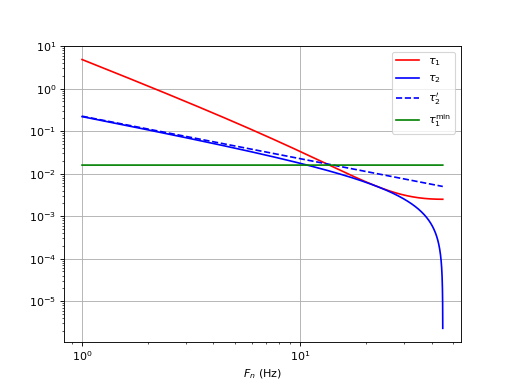
Voyons le filtre R1R2C avec la valeur optimale de ξ :
xi = 1/np.sqrt(2)
filtreR1R2C(f0,Df,xi)
 filtreR1R2C-2.pdf
filtreR1R2C-2.pdf
Pour ce coefficient d'amortissement optimal, ce filtre permet d'abaisser Fn. Par exemple, on peut choisir Fn=10 Hz si l'application envisagée le permet. Dans ce cas, on est à la limite d'une boucle à gain fort puisque τ2' est légèrement supérieur à τ2.
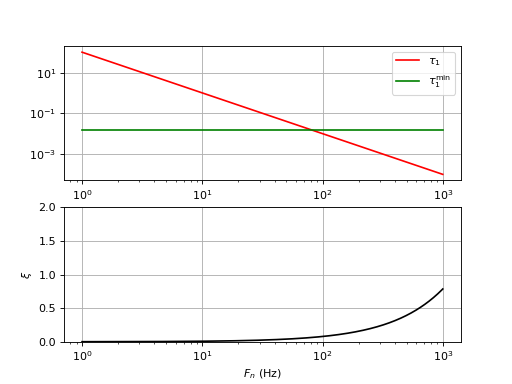
Voici un troisième exemple avec une plage de fréquence balayée beaucoup plus large (boucle à gain fort) : et . Même si les variations de fréquence du signal sont beaucoup plus faible que Δf, ce type de boucle est intéressant car le gain élevé (KoKd=Δf/2) permet d'obtenir une grande rapidité de suivi des variations de fréquence. L'intervalle Δf/2 peut d'ailleurs théoriquement dépasser la fréquence fo.
f0 = 1000
Df = 2000
filtreR1C(f0,Df)
 filtreR1C-3.pdf
filtreR1C-3.pdf
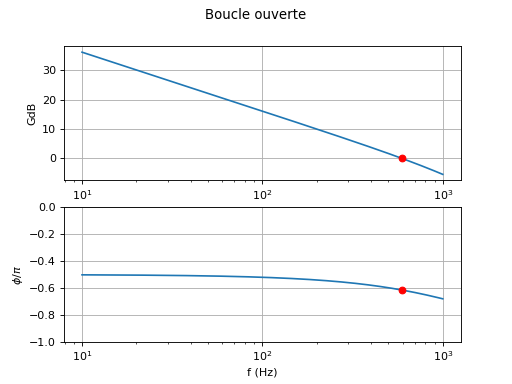
Pour ce filtre R1C, le choix τ1=τ1min donnera beaucoup trop d'oscillations dans la réponse indicielle car ξ est trop faible. Il est possible de choisir , ce qui conduit à une boucle très rapide puisque sa fréquence de coupure Fn est égale à la fréquence fo. Cette boucle s'adapte instantanément (c.a.d. à chaque cycle) aux variations de fréquence. Cette bande passante très large risque de rendre la boucle très sensible au bruit et il peut être souhaitable de l'abaisser (aussi pour diminuer les oscillations en sortie du filtre), ce qui n'est pas possible avec le filtre R1C car le facteur d'amortissement serait trop faible. Voyons la réponse en boucle ouverte pour ce choix de Fn :
Fn=1000
(tau1,xi)=filtreR1C(f0,Df,Fn)
tau2=0
boucle_ouverte(Df,tau1,tau2,1,3)
print(1/tau1) --> 9869.604401089357
print(xi) --> 0.7853981633974483
 filtreR1C-BO-3.pdf
filtreR1C-BO-3.pdf
Pour un gain de 0 dB, le déphasage est environ -0,62π, ce qui fait une différence avec π inférieure à π/4 mais la marge est satisfaisante. On peut souhaiter abaisser la fréquence Fn, soit pour que la boucle soit moins senseible au bruit de phase, soit pour réduire les oscillations en sortie du filtre. Par exemple :
Fn=200
(tau1,xi)=filtreR1C(f0,Df,Fn)
tau2=0
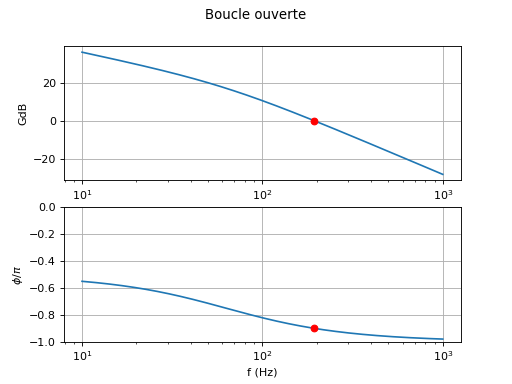
boucle_ouverte(Df,tau1,tau2,1,3)
print(1/tau1) --> 394.78417604357435
print(xi) --> 0.15707963267948966
 filtreR1C-BO-4.pdf
filtreR1C-BO-4.pdf
Le déphasage en boucle ouverte pour un gain de 0 dB est très proche de π, ce qui expose la boucle à un risque d'instabilité. Le coefficient d'amortissement est faible, ce qui conduit à des oscillations assez longues lors de la réponse indicielle, qui font que la boucle met trop longtemps à se verrouiller après une changement de fréquence. Comme nous le verron plus loin, la faible valeur du coefficient d'amortissement est liée à une faible marge de stabilité.
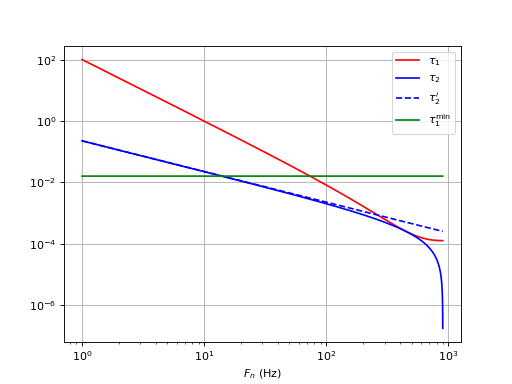
xi = 1/np.sqrt(2)
filtreR1R2C(f0,Df,xi)
 filtreR1R2C-3.pdf
filtreR1R2C-3.pdf
Le filtre R1R2C avec la valeur optimale de ξ est ici intéressant si on souhaite avoir une bande passante plus petite, par exemple Fn=100 Hz. Voyons la réponse fréquentielle de la boucle ouverte pour ce choix :
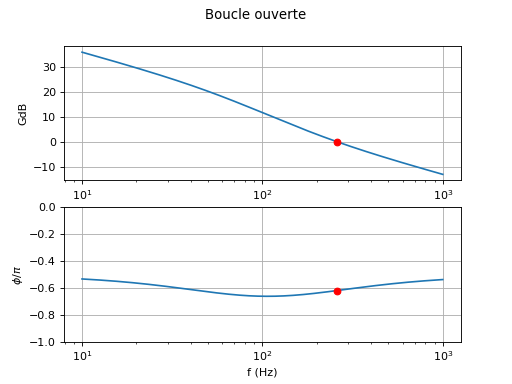
Fn=200
(tau1,tau2)=filtreR1R2C(f0,Df,xi,Fn)
boucle_ouverte(Df,tau1,tau2,1,3)
print(1/(tau1+tau2)) --> 394.78417604357435
 filtreR1R2C-BO-3.pdf
filtreR1R2C-BO-3.pdf
Le déphasage lorsque GdB=0 est environ -0,62π. Avec ce filtre, on a pu abaisser la fréquence Fn tout en gardant une marge de sécurité assez grande par rapport à l'instabilité et en gardant un facteur d'amortissement optimal. Il semble par ailleurs que la diminution de la marge de phase soit toujours associée à une diminution de ξ, ce qui implique que l'étude de la marge de phase ne soit pas nécessaire et qu'il suffit d'examiner la valeur de ξ pour le filtre R1C. D'un point de vue théorique, cette relation se comprend aisément puisque la diminution de ξ implique que la partie réelle des pôles de la fonction de transfert (qui est négative) se rapproche de zéro et donc se rapproche d'une valeur positive.
Pour confirmer et préciser le lien entre marge de stabilité et coefficient d'amortissement, nous pouvons tracer ces deux grandeurs en fonction de Fn :
def stabilite_R1C(Df,lgmin,lgmax):
Fn = np.logspace(lgmin,lgmax,500)
xi = 2*np.pi*Fn/(4*Df)
tau1 = 2*Df/(2*np.pi*Fn)**2
Dphi = np.zeros(len(Fn))
for k in range(len(Dphi)):
f = np.logspace(lgmin,lgmax,1000)
s = 1j*2*np.pi*f
Hbo = 2*Df*1/(s*(1+(tau1[k])*s))
GdB = 20*np.log10(np.absolute(Hbo))
phi = np.angle(Hbo)
j = -1
for i in range(len(f)-1):
if GdB[i]*GdB[i+1] < 0:
j = i
break
if j!=-1:
Dphi[k] = np.pi+phi[j]
else:
Dphi[k] = np.pi
figure()
subplot(211)
plot(Fn,xi)
xscale('log')
ylabel(r"$\xi$")
grid()
subplot(212)
plot(Fn,Dphi)
ylim(0,1)
xscale('log')
ylabel(r"$\Delta\phi$")
xlabel(r"$F_n$")
grid()
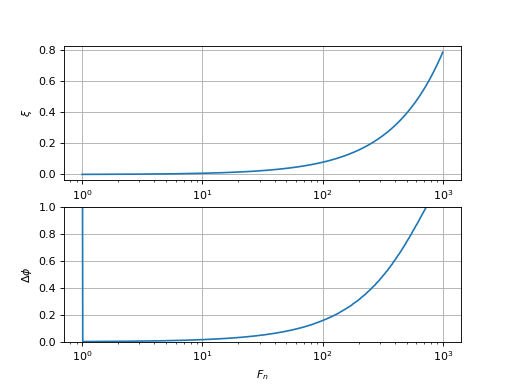
Df = 2000
stabilite_R1C(Df,0,3)
 filtreR1C-stabilite-3.pdf
filtreR1C-stabilite-3.pdf
Pour le filtre R1C avec Δf=2000 Hz, si on considère que ξ doit être supérieur à 0,5, le respect de cette condition implique une marge de phase supérieure à 0,8π, très largement suffisante. Voyons ce qu'il en est pour un gain d'OCT moins grand :
Df = 200
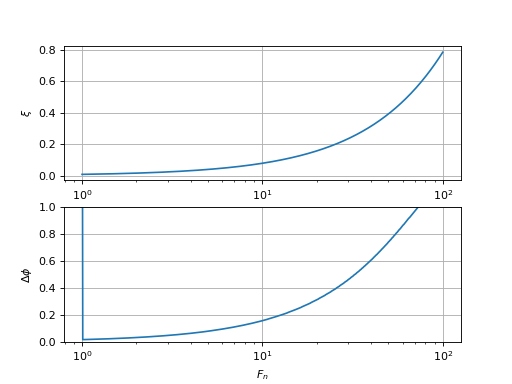
stabilite_R1C(Df,0,2)
 filtreR1C-stabilite-4.pdf
filtreR1C-stabilite-4.pdf
Cette courbe montre là encore que si ξ est supérieur à 0,5 la marge de phase par rapport à la condition d'instabilité est largement assez grande. En conclusion, pour le filtre R1C, il suffit d'imposer la condition ξ>0,5.
La fonction suivante trace la marge de phase pour le filtre R1R2C avec une valeur imposée de ξ (la valeur optimale) :
def stabilite_R1R2C(Df,xi,lgmin,lgmax):
Fn = np.logspace(lgmin,lgmax,500)
tau2 = 2*xi/(2*np.pi*Fn)-1/(2*Df)
tau1 = 2*Df/(2*np.pi*Fn)**2-tau2
Dphi = np.zeros(len(Fn))
for k in range(len(Dphi)):
f = np.logspace(lgmin,lgmax,1000)
s = 1j*2*np.pi*f
Hbo = 2*Df*1/(s*(1+(tau1[k])*s))
GdB = 20*np.log10(np.absolute(Hbo))
phi = np.angle(Hbo)
j = -1
for i in range(len(f)-1):
if GdB[i]*GdB[i+1] < 0:
j = i
break
if j!=-1:
Dphi[k] = np.pi+phi[j]
else:
Dphi[k] = np.pi
figure()
plot(Fn,Dphi)
ylim(0,1)
xscale('log')
ylabel(r"$\Delta\phi$")
xlabel(r"$F_n$")
grid()
Df = 2000
xi = 1/np.sqrt(2)
stabilite_R1R2C(Df,xi,1,3)
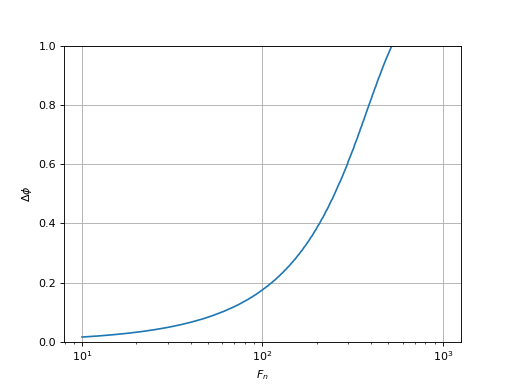 filtreRR21C-stabilite-3.pdf
filtreRR21C-stabilite-3.pdf
Cette courbe confirme que le filtre R1R2C permet d'abaisser la fréquence Fn tout en gardant la valeur optimale de ξ et une valeur raisonnable de marge de phase par rapport à la condition d'instabilité. Cependant, il ne faut pas trop diminuer Fn. Sur cet exemple, une valeur inférieure à 100 Hz conduit à une marge probablement trop faible.
7. Simulation numérique
7.a. Méthode
Une simulation numérique reposant sur des équations de différences finies permet d'étudier le comportement dynamique de la boucle lorsque le signal u1(t) change de fréquence. Contrairement à l'étude linéaire ci-dessus, elle permet d'observer les oscillations en sortie du filtre (qui sont éliminées par l'OCT) et devrait permettre de simuler la boucle lorsqu'elle sort du domaine de fonctionnement linéaire du détecteur de phase, en particulier le démarrage de la boucle. De plus, la simulation numérique permet de tester l'effet du bruit en ajoutant des variations aléatoires de la fréquence ou de la phase de u1(t).
Il faut cependant remarquer que des problèmes d'instabilité numériques peuvent provenir d'un mauvais choix de schéma de différence finie, plus particulièrement lorsque la boucle est en dehors du domaine de linéarité. Dans l'exemple qui suit, nous adoptons le schéma le plus simple (de type Euler) afin de tester son comportement.
La fonction de transfert du filtre conduit à l'équation différentielle suivante :
Notons h le pas de temps et t=nh. Soit udn=ud(tn) et ufn=uf(tn). L'équation différentielle précédente peut être remplacée par l'équation de différences finies suivante :
La phase du signal carré délivré par l'OCT est incrémentée de la manière suivante :
La sortie du détecteur de phase est donnée par l'opérateur OU exclusif :
qui est aisément implémenté au moyen de tests. Pour continuer, le calcul itératif reprend à l'étape .
Afin de suivre le verrouillage de la boucle, on détermine le retard entre le front montant de u2 et celui de u1 qui précède et (connaissant la fréquence) on génère un signal contenant le déphasage entre ces deux signaux.
La fonction suivante effectue le calcul :
def pll_xor(f0,Df,tau1,tau2,te,freq):
#f0 : fréquence centrale de l'OCT
#Df : plage de fréquence balayée
#tau1, tau2 : caractéristiques du filtre
#te : période d'échantillonnage (pas de temps h)
#freq : tableau contenant N fréquences pour le signal u1 où N est le nombre d'échantillons espacés de te à calculer
N = len(freq)
uf = np.zeros(N)
ud = np.zeros(N)
u1 = np.zeros(N)
u2 = np.zeros(N)
t = np.arange(N)*te
K0 = 2*Df*np.pi/5.0
phi1 = 0
for i in range(N):
phi1 += 2*np.pi*freq[i]*te
x = np.sin(phi1)
if x>=0:
u1[i] = 5.0
phi2 = 0
for i in range(1,N):
uf[i] = uf[i-1]+1/(tau1+tau2)*(ud[i-1]-uf[i-1]+tau2*(ud[i-1]-ud[i-2])/te)*te
phi2 += (2*np.pi*f0+K0*(uf[i]-2.5))*te
x = np.sin(phi2)
if x>=0:
x = 5.0
else:
x = 0
u2[i] = x
if (u1[i]>2.5 and u2[i]<2.5) or (u1[i]<2.5 and u2[i]>2.5):
ud[i] = 5.0
dephas = np.zeros(N)
i1 = 0
tau = 0
for i in range(1,N):
if u1[i-1]<2.5 and u1[i]>2.5:
i1 = i
if u2[i-1]<2.5 and u2[i]>2.5:
tau = (i-i1)*te
dephas[i] = tau*freq[i]*2*np.pi
dephas = np.unwrap(dephas)
return (t,u1,u2,uf,dephas)
7.b. Exemple
Boucle à gain faible
Reprenons l'exemple traité précédemment : et , avec τ2=0. Voyons tout d'abord le résultat avec τ1=100/(2πfo), qui est la valeur minimale pour que les oscillations en sortie du filtre soient négligeables. Nous ajoutons des petites variations de fréquence aléatoires (distribuées selon la loi normale) afin de simuler l'effet du bruit de fréquence. Bien sûr, la bande de fréquence de ce bruit est déterminée par la fréquence d'échantillonnage (1/h).
from numpy.random import normal
f0=1000
Df=20
fa=f0
fb=f0+5
fc=f0-5
fe = f0*500
te = 1/fe
tau1=100/(2*np.pi*f0)
tau2 = 0
Fn=np.sqrt(2*Df/(tau1+tau2))/(2*np.pi)
N=400000
freq = np.zeros(N)
freq[0:N//3] = fa
freq[N//3:2*N//3] = fb
freq[2*N//3:N] = fc
freq += normal(0,1) # bruit de fréquence
(t,u1,u2,uf,dephas) = pll_xor(f0,Df,tau1,tau2,te,freq)
fig=figure()
subplot(211)
plot(t,uf,'g')
grid()
ylim(0,5)
ylabel('uf')
subplot(212)
plot(t,dephas,'g')
grid()
ylabel('phi (rad)')
xlabel('t (s)')
print(Fn) --> 7.978845608028654
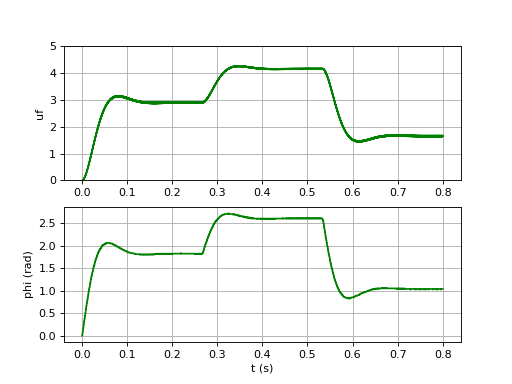 uf-1.pdf
uf-1.pdf
Voici les signaux lors du premier verrouillage, lorsque la fréquence de u1 est égale à fo :
fig=figure()
plot(t,u1,label='u1')
plot(t,u2,label='u2')
plot(t,uf,label='uf')
grid()
xlabel('t (s)')
ylim(-1,6)
xlim(0.2,0.205)
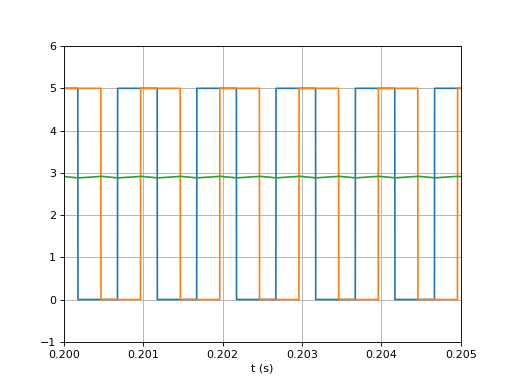 u1u2uf-1.pdf
u1u2uf-1.pdf
Les deux signaux u1 et u2 sont, comme prévu, synchrones et déphasés de π/2. Les oscillations en sortie du filtre (tension de commande de l'OCT) sont très faibles.
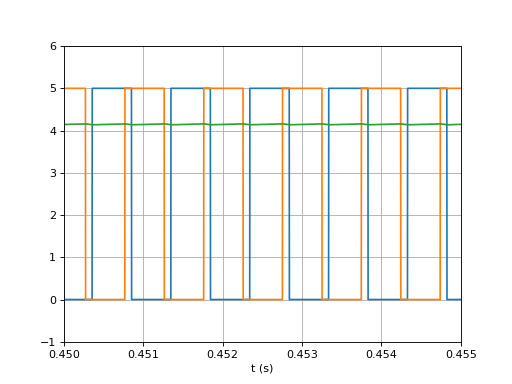
Voici les signaux lors du second verrouillage, lorsque la fréquence de u1 est égale à fo+5 :
fig=figure()
plot(t,u1,label='u1')
plot(t,u2,label='u2')
plot(t,uf,label='uf')
grid()
xlabel('t (s)')
ylim(-1,6)
xlim(0.45,0.455)
 u1u2uf-2.pdf
u1u2uf-2.pdf
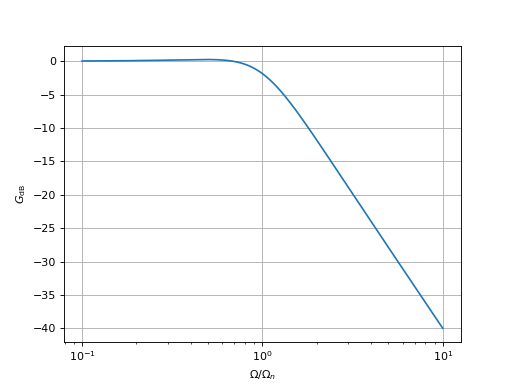
Le temps de réponse de la boucle est d'environ 0,15 s, ce qui est conforme à la valeur Fn=8 Hz. Le facteur d'amortissement est ξ=0,62, une valeur inférieure à la valeur optimale (0,71) mais tout à fait acceptable. Voici la réponse fréquentielle de la boucle :
x = np.logspace(-1,1,500)
def H(x,xi):
return 1/(1+2*1j*xi*x-x**2)
H1 = H(x,0.62)
GdB1 = 20*np.log10(np.absolute(H1))
figure()
plot(x,GdB1)
xscale('log')
xlabel(r"$\Omega/\Omega_n$")
ylabel(r"$G_{\rm dB}$")
grid()
 bode-1.pdf
bode-1.pdf
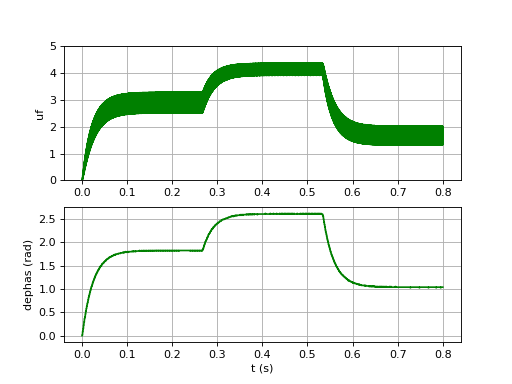
Il est intéressant de voir le comportement de la boucle pour un temps τ1 vingt fois plus petit (une bande passante 4,5 fois plus grande pour le filtre) :
tau1=5/(2*np.pi*f0)
Fn=np.sqrt(2*Df/(tau1+tau2))/(2*np.pi)
(t,u1,u2,uf,dephas) = pll_xor(f0,Df,tau1,tau2,te,freq)
fig=figure()
subplot(211)
subplot(211)
plot(t,uf,'g')
grid()
ylim(0,5)
ylabel('uf')
subplot(212)
plot(t,dephas,'g')
grid()
ylabel('dephas (rad)')
xlabel('t (s)')
print(Fn) --> 35.682482323055424
 uf-2.pdf
uf-2.pdf
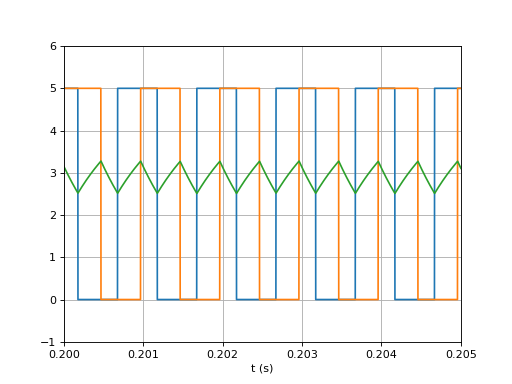
fig=figure()
plot(t,u1,label='u1')
plot(t,u2,label='u2')
plot(t,uf,label='uf')
grid()
xlabel('t (s)')
ylim(-1,6)
xlim(0.2,0.205)
 u1u2uf-3.pdf
u1u2uf-3.pdf
Comme prévu, le temps de réponse est plus petit. En revanche, les oscillations en sortie du filtre sont beaucoup plus grandes. Comme nous l'avons vu plus haut, ces oscillations n'ont aucun effet sur la phase du signal en sortie de l'OCT.
Une autre manière de réduire le temps de réponse serait d'augmenter la plage de fréquence balayée par l'OCT, c'est-à-dire le gain de l'OCT :
Df=100
fa=f0
fb=f0+20
fc=f0-20
freq = np.zeros(N)
freq[0:N//3] = fa
freq[N//3:2*N//3] = fb
freq[2*N//3:N] = fc
freq += normal(0,1) # bruit de fréquence
tau1=100/(2*np.pi*f0)
Fn=np.sqrt(2*Df/(tau1+tau2))/(2*np.pi)
(t,u1,u2,uf,dephas) = pll_xor(f0,Df,tau1,tau2,te,freq)
fig=figure()
subplot(211)
plot(t,uf,'g')
grid()
ylim(0,5)
ylabel('uf')
subplot(212)
plot(t,dephas,'g')
grid()
ylabel('dephas (rad)')
xlabel('t (s)')
print(Fn) --> 17.841241161527712
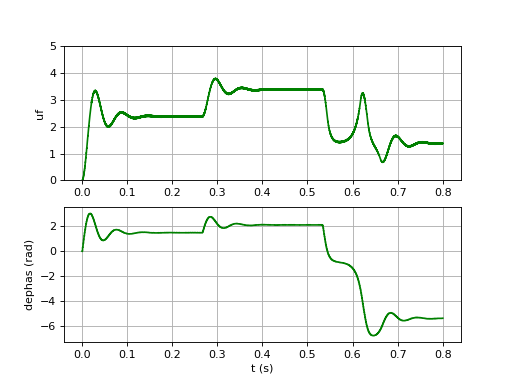 uf-3.pdf
uf-3.pdf
Le facteur ξ est plus petit, ce qui a pour conséquence un phénomène oscillatoire dans la réponse, qui détruit le bénéfice de l'augmentation de Fn. On a en effet :
La réponse la plus rapide est obtenue avec le filtre R1C et :
xi=1/np.sqrt(2)
tau1=1/(8*xi**2*Df*1.1)
tau2=0
Fn=np.sqrt(2*Df/(tau1+tau2))/(2*np.pi)
(t,u1,u2,uf,dephas) = pll_xor(f0,Df,tau1,tau2,te,freq)
fig=figure()
subplot(211)
plot(t,uf,'g')
grid()
ylim(0,5)
ylabel('uf')
subplot(212)
plot(t,dephas,'g')
grid()
ylabel('dephas (rad)')
xlabel('t (s)')
print(Fn) --> 47.212985926876414
 uf-4.pdf
uf-4.pdf
La fréquence de coupure de la boucle a augmenté, ce qui explique le temps de réponse plus court. De plus, le facteur d'amortissement est optimal. En contre-partie, il y a nettement plus d'oscillations en sortie du filtre. Si le but est de générer un signal synchrone au signal u1(t) et qui se synchronise au plus vite en cas de changement de fréquence, ce filtre convient bien. Si le but et de faire une mesure de fréquence avec une moindre exigence sur le temps de réponse, alors le filtre précédent convient mieux. Il faut cependant noter qu'il est possible d'appliquer un filtrage passe-bas du premier ordre au signal récupéré en sortie du filtre afin de lisser les oscillations (ce qui aura pour effet d'augmenter le temps de réponse mais sans l'inconvénient des oscillations).
Voyons le détail au voisinage d'un changement de fréquence :
fig=figure()
subplot(211)
plot(t,uf,'g')
grid()
ylim(0,5)
ylabel('uf')
xlim(0.25,0.3)
subplot(212)
plot(t,dephas,'g')
xlim(0.25,0.3)
grid()
ylabel('dephas (rad)')
xlabel('t (s)')
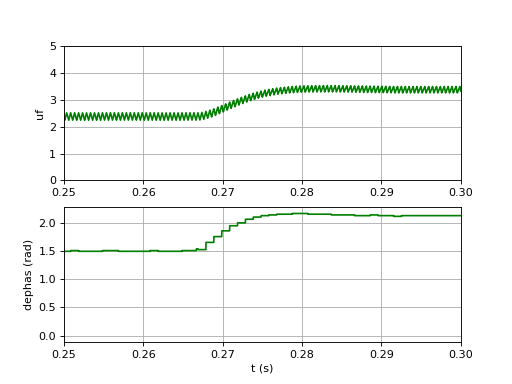 uf-5.pdf
uf-5.pdf
Boucle à gain fort
Considérons le cas fo=1000 Hz et Δf=2000 Hz déjà étudié avec le modèle linéaire. Supposons que l'on souhaite une fréquence de coupure de la boucle Fn=100 Hz. Voici le paramètre du filtre pour le fitre R1C1 :
f0 = 1000
Df = 2000
Fn = 100
(tau1,xi) = filtreR1C(f0,Df,Fn)
print((tau1,xi)) --> (0.010132118364233778, 0.07853981633974483)
Avec une valeur aussi faible de ξ, on doit s'attendre à un temps de réponse très long et à une marge de stabilité faible. Faisons tout de même la simulation :
freq = np.zeros(N)
fa = f0
fb=f0+100
fc=f0-100
freq[0:N//3] = fa
freq[N//3:2*N//3] = fb
freq[2*N//3:N] = fc
freq += normal(0,1) # bruit de fréquence
(t,u1,u2,uf,dephas) = pll_xor(f0,Df,tau1,tau2,te,freq)
fig=figure()
subplot(211)
plot(t,uf,'g')
grid()
ylim(0,5)
ylabel('uf')
subplot(212)
plot(t,dephas,'g')
grid()
ylabel('dephas (rad)')
xlabel('t (s)')
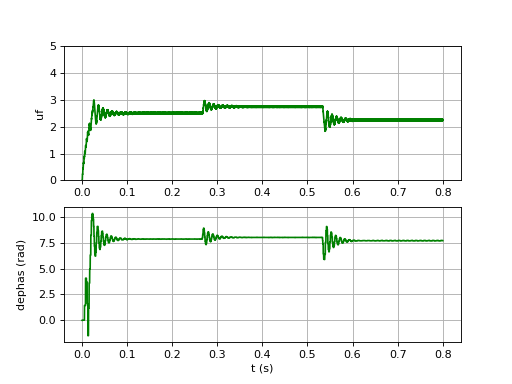 uf-6.pdf
uf-6.pdf
Comme prévu, les oscillations de la réponse indicielle sont trop longues, ce qui est associé à une marge de stabilité faible, qui risque de rendre la boucle réelle instable.
Voici les paramètres du filtre R1R2C (qui permet de choisir la valeur optimale de ξ) :
xi = 1/np.sqrt(2)
(tau1,tau2) = filtreR1R2C(f0,Df,xi,Fn)
print((tau1,tau2)) --> (0.008131327573841014, 0.002000790790392765)
et voici la simulation correspondante :
(t,u1,u2,uf,dephas) = pll_xor(f0,Df,tau1,tau2,te,freq)
figure()
subplot(211)
plot(t,uf,'g')
grid()
ylim(0,5)
ylabel('uf')
subplot(212)
plot(t,dephas,'g')
grid()
ylabel('dephas (rad)')
xlabel('t (s)')
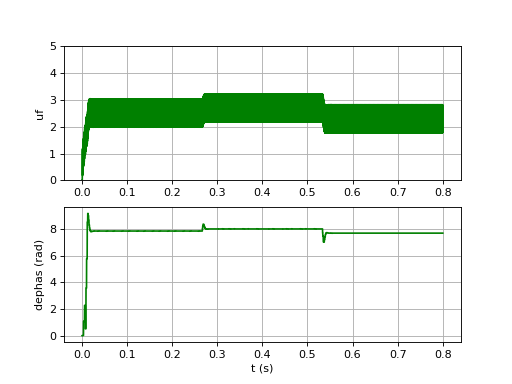 uf-7.pdf
uf-7.pdf
Le temps de réponse est beaucoup plus court et il n'y a plus d'oscillations dans la réponse indicielle. Comme prévu, les oscillations en sortie du filtre ont une amplitude beaucoup plus grande, ce qui est gênant si on veut exploiter le signal en sortie du filtre, mais sans importance si le but est la génération du signal u2(t) synchrone avec u1(t). Il est intéressant de voir la forme de ces oscillations :
fig=figure()
plot(t,u1,label='u1')
plot(t,u2,label='u2')
plot(t,uf,label='uf')
grid()
xlabel('t (s)')
ylim(-1,6)
xlim(0.6,0.605)
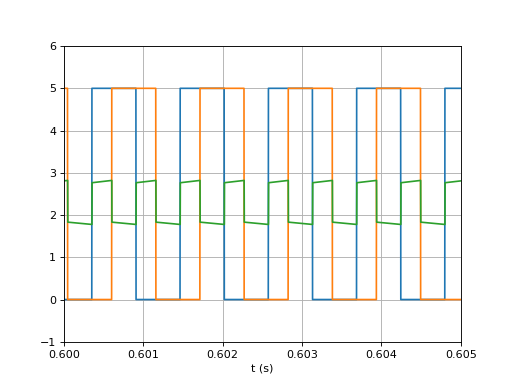 u1u2uf-7.pdf
u1u2uf-7.pdf
Avec le filtre R1R2C, il est possible d'augmenter le coefficient d'amortissement :
xi = 2
(tau1,tau2) = filtreR1R2C(f0,Df,xi,Fn)
print((tau1,tau2)) --> (0.004015920640557964, 0.006116197723675813)
(t,u1,u2,uf,dephas) = pll_xor(f0,Df,tau1,tau2,te,freq)
fig = figure()
subplot(211)
plot(t,uf,'g')
grid()
ylim(0,5)
ylabel('uf')
subplot(212)
plot(t,dephas,'g')
grid()
ylabel('dephas (rad)')
xlabel('t (s)')
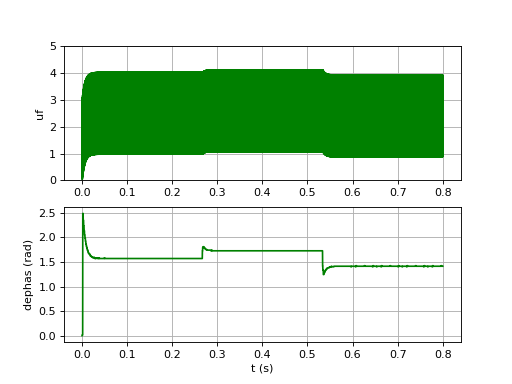 uf-8.pdf
uf-8.pdf
Le temps de réponse n'est pas réduit, contrairement à ce que pouvait faire penser les réponses impulsionnelles tracées plus haut. Les oscillations en sortie du filtre ont plus d'amplitude. On voit bien que l'augmentation de ξ ne peut pas se faire au delà de cette valeur, car les oscillations en sortie du filtre ne peuvent pas dépasser la plage [0,5] volts. Par ailleurs, l'augmentation du facteur d'amortissement a aussi pour conséquence une plus faible pente du gain dans la bande atténuante, ce qui rend la boucle plus sensible aux bruits de haute fréquence.
8. Accrochage de la boucle
8.a. Plage de fréquences d'accrochage
La boucle est dite verrouillée lorsque les signaux u1(t) et u2(t) sont synchrones, c'est-à-dire lorsque leur déphasage est constant. La plage de fréquence de verrouillage est donnée par la relation :
Si on pose comme précédemment, Δf désigne la plage de fréquences totale balayée par l'OCT (fréquence maximale moins fréquence minimale). Dans le cas d'un détecteur de phase OU-exclusif et d'après la relation , la plage de fréquences pouvant être verrouillées est . Il s'agit cependant d'une condition statique, qui ne tient pas compte de la réponse dynamique du filtre lorsque la fréquence change.
Au démarrage de la boucle, la fréquence de u1(t) est très différente de la fréquence de u2(t). En conséquence, le comparateur de phase n'est pas dans son domaine de fonctionnement linéaire. Avant que le verrouillage se produise, il faut tout d'abord que la boucle entre dans son domaine linéaire. Ce processus est appelé l'accrochage de la boucle. Même lorsque la boucle est verrouillée, une variation soudaine et trop grande de la fréquence de u1 peut conduire à un décrochage de la boucle et il faut alors savoir si l'accrochage peut se produire à nouveau et quel temps il faut pour l'obtenir.
On cherche à déterminer la plage de pulsations d'accrochage (appelée aussi plage de capture), qui est la plage de ω1 (centrée sur ω0) qui conduit à un accrochage si la boucle ne l'est pas initialement.
On se place dans le cas d'un détecteur de phase OU-exclusif, avec un signal u1 binaire, c'est-dire une forme d'onde donnée par la fonction rect, de période 2π et qui vaut soit -1 soit 1. Supposons que la pulsation de u1 soit ω1=ω0+Δω1 :
avec, pour un circuit alimenté en 5 V, U1m=2.5 V et U10=2.5 V. Supposons que la pulsation en sortie de l'OCT soit initialement ω0, c'est-à-dire qu'on a ufi=ufref. Rappellons que ufi est la tension en sortie du filtre lorsque celui-ci est idéal, c'est-à-dire la valeur moyenne de uf(t) sur un cycle complet. La pulsation de u2(t) évolue lorsque ufi change, l'évolution ne se faisant que tous les demi-cycles (puisque le signal est carré). Dans le raisonnement qui suit, on suppose néamoins que cette pulsation est constante :
avec U2m=2.5 V et U20=2.5 V.
La différence de phase entre les deux signaux est donc :
et la sortie du comparateur de phase (sortie du filtre idéal) est donc :
où tri est une forme d'onde triangulaire de période 2π variant de -1 à +1. Pour un circuit alimenté en 5 V on a uref=2.5 V et .
La tension qui commande la fréquence de l'OCT est en fait la tension moyenne ci-dessus mais multipliée par le gain du filtre à la pulsation Δω1. Il s'en suit que la pulsation en sortie de l'OCT est modifiée d'une valeur maximale égale à :
où G(Δω1) désigne le gain du filtre à la pulsation Δω1. Cette variation de pulsation est atteinte au bout d'une durée :
Plus l'écart de pulsation Δω1 est grand, plus cette évolution est rapide.
Pour que la boucle accroche, il faut que Δω2 soit supérieur à Δω1. La plage d'accrochage est donc définie implicitement par:
Le facteur 2 venant du fait qu'il s'agit de la plage totale (centrée sur ω0). Le raisonnement qui précède n'est pas exact car il suppose que la pulsation en sortie de l'OCT ne change pas, alors que justement elle s'approche de . En réalité, l'écart entre les deux fréquences se réduit au cours de l'accrochage. La plage donnée par l'équation est donc une surestimation de la plage réelle donc elle constitue une condition suffisante d'accrochage. Cette équation montre que la plage d'accrochage dépend des caractéristiques du filtre. Dans le cas du détecteur de phase OU-exclusif, Δf est la largeur de la plage de fréquences verrouillées (largeur de l'intervalle de fréquences). L'équation s'écrit aussi :
La plage Δfa peut être obtenue par résolution graphique. Si la bande passante du filtre est assez grande, la solution est :
On en déduit que si Δf est beaucoup plus petit que la fréquence de coupure du filtre alors c'est la plage d'accrochage et dans ce cas la condition est évidemment nécessaire. Si cette condition n'est pas vérifiée, Δfa peut être nettement plus petite que Δf. La figure suivante montre le principe d'une résolution graphique, dans le cas où le filtre à un gain unité dans la bande passante :
Figure pleine pageDans la situation montrée sur la figure, le point d'intersection correpond à un gain d'environ 1/2, ce qui fait que la plage d'accrochage est deux fois plus petite que la plage de verrouillage.
Plus le filtre à une fréquence de coupure basse, plus la plage d'accrochage est étroite. Il est intéressant de faire intervenir la fréquence Fn, qui correspond à la bande passante de la boucle. On a :
La condition s'écrit aussi . Pour maximiser la plage de fréquences d'accrochage afin qu'elle soit proche de Δf, il faut donc que la bande passante de la boucle soit beaucoup plus grande que Δf. On peut être amené à abaisser la bande passante de la boucle (avec le filtre R1R2C) pour que la boucle ne soit pas sensible aux bruits de haute fréquence, mais dans ce cas il faudra se contenter d'une plage d'accrochage plus étroite.
La fonction suivante calcule la plage d'accrochage :
def DeltaAccrochage(tau1,tau2,Df):
def H(f):
w = 2*np.pi*f
return (1+1j*w*tau2)/(1+1j*w*(tau1+tau2))
df = 1/tau1/1000
Dfa = 0
while np.absolute(H(Dfa)) > Dfa/Df:
Dfa += df
return Dfa
Voici un exemple :
f0 = 1000
Df = 2000
Fn = 100
xi = 1/np.sqrt(2)
(tau1,tau2) = filtreR1R2C(f0,Df,xi,Fn)
Dfa = DeltaAccrochage(tau1,tau2,Df)
print((tau1,tau2)) --> (0.008131327573841014, 0.002000790790392765)
print(Dfa) --> 402.3943163384679
Dans le cas d'une boucle à très fort gain (comme celle de cet exemple), on peut utiliser l'approximation suivante :
En utilisant les relations et (valables aussi pour une boucle à fort gain), on obtient :
8.b. Simulation
On reprend l'exemple précédent. Voici l'application d'un saut de fréquence qui est dans la plage d'accrochage :
N = 400000
fa=f0
fb=f0+380
freq = np.zeros(N)
freq[0:N//2] = fa
freq[N//2:N] = fb
freq += normal(0,1)
fe = f0*500
te = 1/fe
(t,u1,u2,uf,dephas) = pll_xor(f0,Df,tau1,tau2,te,freq)
fig=figure()
subplot(211)
plot(t,uf,'g')
grid()
ylim(0,5)
ylabel('uf')
subplot(212)
plot(t,dephas,'g')
grid()
ylabel('phi (rad)')
xlabel('t (s)')
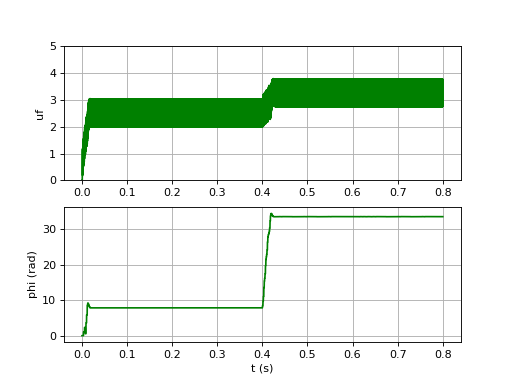 uf-9.pdf
uf-9.pdf
close(fig)
et un saut en dehors de la plage d'accrochage :
N = 400000
fa=f0
fb=f0+500
freq = np.zeros(N)
freq[0:N//2] = fa
freq[N//2:N] = fb
freq += normal(0,1)
fe = f0*500
te = 1/fe
(t,u1,u2,uf,dephas) = pll_xor(f0,Df,tau1,tau2,te,freq)
fig=figure()
subplot(211)
plot(t,uf,'g')
grid()
ylim(0,5)
ylabel('uf')
subplot(212)
plot(t,dephas,'g')
grid()
ylabel('phi (rad)')
xlabel('t (s)')
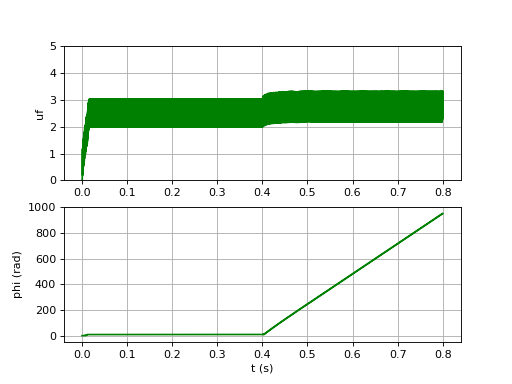 uf-10.pdf
uf-10.pdf
9. Annexe A : réponse indicielle
9.a. Échelon de phase
Considérons un saut de la phase de u1(t) d'amplitude .
La transformée de Laplace de la réponse à un échelon de phase en entrée est égale à la transformée de Laplace d'un échelon multipliée par la fonction de transfert du filtre :
Introduisons les pôles de la fonction de transfert de la boucle :
Le dénominateur de L(s) se factorise :
On recherche la décomposition en éléments simples pour :
Dans le cas ξ>1, on obtient :
Dans le cas ξ<1, on obtient :
La réponse indicielle est la transformée de Laplace inverse de :
Pour on a :
et la réponse indicielle est :
On tracera en fonction du temps réduit :
Pour le filtre R1C on a τ2=0 et la réponse en temps réduit ne dépend que du facteur d'amortissement ξ. Pour le filtre R1R2C la réponse ϕ2(t') dépend de Ωn et de τ2. Cependant, dans le cas d'une boucle à gain fort, on a :
ce qui fait que la réponse en temps réduit ne dépend finalement que de ξ.
9.b. Échelon de fréquence
Pour étudier la réponse de la boucle lorsque la fréquence de u1(t) change soudainement (échelon de fréquence), il suffit de considérer le passage d'une fréquence nulle à une fréquence δω/(2π), cette dernière état en fait le saut de fréquence. Dans ce cas, la phase appliquée en entrée est nulle pour t<0 et ϕ1(t)=δωt pour t>0. La transformée de Laplace de cette rampe de phase est . Il s'en suit que la transformée de Laplace de la sortie est :
En comparaison avec le cas de l'échelon de phase, nous avons un s2 au dénominateur à la place d'un s.
La décomposition en éléments simples conduit à :
On a d'une part :
D'autre part pour ξ>1 :
et pour ξ<1 :
La réponse qui nous intéresse est :
Il s'agit de la transformée de Laplace inverse de L(s) moins le premier terme :
On tracera en fonction de .