Boucles circulaires coaxiales

1. Introduction

Le calcul du champ magnétique créé par une spire circulaire de courant est effectué. Un programme python est présenté, qui effectue le calcul pour un ensemble de spires coaxiales et calcule les lignes de champ. Ce programme permet également de calculer la trajectoire d'une particule chargée en coordonnées cylindriques.

2. Champ magnétique

Afin de calculer le champ magnétique créé par des bobines de section circulaire, on s'intéresse tout d'abord au champ créé par une boucle de courant de rayon a, parcourue par un courant quasi stationnaire d'intensité I(t). Le calcul du potentiel vecteur en coordonnées sphériques est fait dans [1]. Afin de superposer facilement plusieurs boucles, le calcul doit être fait en coordonnées cartésiennes.

Soit Oxyz un repère orthogonal où O est le centre de la boucle et Oz un axe perpendiculaire au plan de la boucle.

Figure pleine page

Soit M(x,y,z) le point où on calcule le champ et P un point de la boucle repéré par son angle θ. La tangente unitaire en ce point est :

\vec{t} = - sin θ {\vec{e}}_{x} + cos θ {\vec{e}}_{y}

Le potentiel vecteur au point M est donné par l'intégrale :

\vec{A} (x, y, z) = \frac{μ_{0}}{4 π} \int_{- π}^{π} \frac{I \vec{t} a d θ}{P M}

Les composantes du potentiel vecteur sont donc :

\begin{matrix} A_{x} = \frac{μ_{0} I a}{4 π} \int_{- π}^{π} \frac{- sin θ d θ}{\sqrt{{(x - a cos θ)}^{2} + {(y - a sin θ)}^{2} + z^{2}}} \\ A_{y} = \frac{μ_{0} I a}{4 π} \int_{- π}^{π} \frac{cos θ d θ}{\sqrt{{(x - a cos θ)}^{2} + {(y - a sin θ)}^{2} + z^{2}}} \\ A_{z} = 0 \end{matrix}

Le champ magnétique est obtenu en calculant le rotationnel :

\begin{matrix} B_{x} = - \frac{\partial A_{y}}{\partial z} = \frac{μ_{0} I a}{4 π} \int_{- π}^{π} \frac{z cos θ d θ}{[{(x - a cos θ)}^{2} + {(y - a sin θ)}^{2} + z^{2}]^{3 / 2}} \\ B_{y} = \frac{\partial A_{x}}{\partial z} = \frac{μ_{0} I a}{4 π} \int_{- π}^{π} \frac{z sin θ d θ}{[{(x - a cos θ)}^{2} + {(y - a sin θ)}^{2} + z^{2}]^{3 / 2}} \\ B_{z} = \frac{\partial A_{y}}{\partial x} - \frac{\partial A_{x}}{\partial y} = \frac{μ_{0} I a}{4 π} \int_{- π}^{π} \frac{(- x cos θ - y sin θ + a) d θ}{[{(x - a cos θ)}^{2} + {(y - a sin θ)}^{2} + z^{2}]^{3 / 2}} \end{matrix}

Le vecteur $\vec{B}$ étant contenu dans le plan méridien (plan contenant M et l'axe Oz) et compte tenu de l'invariance par rotation, on peut se limiter à calculer le champ dans le plan y=0, ce qui donne :

\begin{matrix} B_{x} (x, 0, z) = \frac{μ_{0} I a}{2 π} \int_{0}^{π} \frac{z cos θ d θ}{[x^{2} + z^{2} + a^{2} - 2 a x cos θ]^{3 / 2}} \\ B_{y} (x, 0, z) = 0 \\ B_{z} (x, 0, z) = \frac{μ_{0} I a}{2 π} \int_{0}^{π} \frac{(- x cos θ + a) d θ}{[x^{2} + z^{2} + a^{2} - 2 a x cos θ]^{3 / 2}} \end{matrix}

Avec Mathematica, on peut évaluer les deux intégrales précédentes :

ibx=Integrate[z*Cos[theta]/(x^2+z^2+a^2-2*a*x*Cos[theta])^(3/2),theta];
bx=Evaluate[(ibx/.{theta->Pi})-(ibx/.{theta->0})]

\frac{z \sqrt{\frac{a^{2} + 2 a x + x^{2} + z^{2}}{a^{2} - 2 a x + x^{2} + z^{2}}} ((a^{2} + x^{2} + z^{2}) E (- \frac{4 a x}{a^{2} - 2 x a + x^{2} + z^{2}}) - (a^{2} + 2 a x + x^{2} + z^{2}) K (- \frac{4 a x}{a^{2} - 2 x a + x^{2} + z^{2}}))}{a x (a^{2} + 2 a x + x^{2} + z^{2})^{3 / 2}}

ibz=Integrate[(-x*Cos[theta]+a)/(x^2+z^2+a^2-2*a*x*Cos[theta])^(3/2),theta];
bz=Evaluate[(ibz/.{theta->Pi})-(ibz/.{theta->0})]

\frac{\sqrt{\frac{a^{2} + 2 a x + x^{2} + z^{2}}{a^{2} - 2 a x + x^{2} + z^{2}}} ((a^{2} + 2 a x + x^{2} + z^{2}) K (- \frac{4 a x}{a^{2} - 2 x a + x^{2} + z^{2}}) + (a^{2} - x^{2} - z^{2}) E (- \frac{4 a x}{a^{2} - 2 x a + x^{2} + z^{2}}))}{a (a^{2} + 2 a x + x^{2} + z^{2})^{3 / 2}}

Les expressions obtenues font intervenir les intégrales elliptiques complètes de première et seconde espèces. Voici la définition de ces intégrales :

\begin{matrix} K (x) = \int_{0}^{π / 2} \frac{d θ}{\sqrt{1 - x {sin}^{2} θ}} \\ E (x) = \int_{0}^{π / 2} \sqrt{1 - x {sin}^{2} θ} d θ \end{matrix}

Les lignes de champ magnétique sont obtenues par résolution numérique du système différentiel suivant :

\begin{matrix} \frac{d x}{d t} = \frac{B_{x} (x, z)}{\sqrt{B_{x} {(x, z)}^{2} + B_{z} {(x, z)}^{2}}} \\ \frac{d z}{d t} = \frac{B_{z} (x, z)}{\sqrt{B_{x} {(x, z)}^{2} + B_{z} {(x, z)}^{2}}} \end{matrix}

La variable t est l'abscisse curviligne le long de la ligne de champ.

Le potentiel vecteur en coordonnées cylindriques (r=x) est obtenu par l'intégrale suivante :

A_{θ} (x, z) = A_{y} (x, 0) = \frac{μ_{0} I a}{2 π} \int_{0}^{π} \frac{cos θ d θ}{\sqrt{x^{2} + z^{2} + a^{2} - 2 a x cos θ}}

On obtient avec Mathematica :

A=Integrate[Cos[theta]/(x^2+z^2+a^2-2*a*x*Cos[theta])^(1/2),theta];
Atheta=Evaluate[(A/.{theta->Pi})-(A/.{theta->0})]

\frac{\sqrt{\frac{a^{2} + 2 a x + x^{2} + z^{2}}{a^{2} - 2 a x + x^{2} + z^{2}}} ((a^{2} + x^{2} + z^{2}) K (- \frac{4 a x}{a^{2} - 2 x a + x^{2} + z^{2}}) - (a^{2} - 2 a x + x^{2} + z^{2}) E (- \frac{4 a x}{a^{2} - 2 x a + x^{2} + z^{2}}))}{a x \sqrt{a^{2} + 2 a x + x^{2} + z^{2}}}

Il peut être utile de calculer la dérivée suivante :

\frac{\partial A_{θ}}{\partial x} = \frac{\partial A_{y} (x, 0)}{\partial x} = \frac{μ_{0} I a}{2 π} \int_{0}^{π} \frac{(a cos θ - x) cos θ d θ}{[x^{2} + z^{2} + a^{2} - 2 a x cos θ]^{3 / 2}}

ADx=Integrate[(a*Cos[theta]-x)*Cos[theta]/(x^2+z^2+a^2-2*a*x*Cos[theta])^(3/2),theta];
ADx=Evaluate[(ADx/.{theta->Pi})-(ADx/.{theta->0})]

\frac{\sqrt{\frac{a^{2} + 2 a x + x^{2} + z^{2}}{a^{2} - 2 a x + x^{2} + z^{2}}} ((a^{4} - a^{2} (x^{2} - 2 z^{2}) + z^{2} (x^{2} + z^{2})) E (- \frac{4 a x}{a^{2} - 2 x a + x^{2} + z^{2}}) - (a^{2} + z^{2}) (a^{2} + 2 a x + x^{2} + z^{2}) K (- \frac{4 a x}{a^{2} - 2 x a + x^{2} + z^{2}}))}{a x^{2} (a^{2} + 2 a x + x^{2} + z^{2})^{3 / 2}}

3. Programme python

La classe Spire permet de calculer le champ créé par une spire. Le constructeur a pour arguments le rayon de la spire, sa position sur l'axe Oz et l'intensité du courant.

Le facteur $\frac{μ_{0}}{2 π}$ n'est pas pris en compte, ce qui signifie qu'il faudra multiplier le champ magnétique par $2 \cdot 1 0^{- 7}$ pour obtenir sa valeur en Tesla.

SpiresCoaxiales.py

import math 
import numpy
from scipy.integrate import odeint
from scipy.special import ellipk, ellipe
from matplotlib.pyplot import *

            
class Spire:
    def __init__(self,a,zs,i):
        self.a = a
        self.a2 = a*a
        self.a4 = self.a2*self.a2
        self.zs = zs
        self.i = i
    def champB(self,x,z):
        if abs(x) < 1e-8:
            x=0
        if x>0:
            sx = 1
            x = -x
        else:
            sx = -1
        z = z-self.zs
        x2 = x*x
        z2 = z*z
        r2 = x2+z2
        b1 = self.a2+ r2
        b2 = 2*x*self.a
        b3 = b1+b2
        b4 = b1-b2
        b5 = -2*b2/b4
        b6 = math.sqrt(b3/b4)*self.i 
        rb3 = math.sqrt(b3)
        b7 = b3*rb3
        b8 = self.a4-self.a2*(x2-2*z2)+z2*(x2+z2)
        b9 = (self.a2+z2)*b3
        e = ellipe(b5)
        k = ellipk(b5)
        bz = b6*((self.a2-r2)*e+b3*k)/b7
        if x==0:
            bx = 0.0
            Atheta = 0.0
            Adx = bz/2
        else:
            bx = -sx*z/x*b6*(b1*e-b3*k)/b7
            Atheta = -sx*b6/x*(-b4*e+(self.a2+r2)*k)/(self.a*rb3)
            Adx = b6/x2*(b8*e-b9*k)/b7
        return [bx,bz,Atheta,Adx]

La classe SystemeSpires effectue le calcul du champ et des lignes de champ pour plusieurs spires. Les arguments du constructeur sont les bornes du domaine utilisé pour le calcul des lignes de champ.

class SystemeSpires:
    def __init__(self,xmin,xmax,zmin,zmax):
        self.xmin = xmin
        self.xmax = xmax
        self.zmin = zmin
        self.zmax = zmax
        self.spires = []
        self.n = 0
    def bornes(self,xmin,xmax,zmin,zmax):
        self.xmin = xmin
        self.xmax = xmax
        self.zmin = zmin
        self.zmax = zmax
    def ajouter(self,spire):
        self.spires.append(spire)
        self.n += 1
    def champB(self,x,z):
        bx = 0.0
        bz = 0.0
        A = 0.0
        Adx = 0.0
        for spire in self.spires:
            b = spire.champB(x,z)
            bx += b[0]
            bz += b[1]
            A += b[2]
            Adx += b[3]
        return [bx,bz,A,Adx]

La fonction suivante calcul la composante axiale pour un tableau de valeurs de z

    def Bz_z(self,x,z):
        nz = len(z)
        bz = numpy.zeros(nz)
        for k in range(nz):
            b = self.champB(x,z[k])
            bz[k] = b[1]
        return bz

Voici des fonctions analogues pour d'autres composantes et coordonnées :

    def Bz_x(self,x,z):
        nx = len(x)
        bz = numpy.zeros(nx)
        for k in range(nx):
            b = self.champB(x[k],z)
            bz[k] = b[1]
        return bz
    def Bx_z(self,x,z):
        nz = len(z)
        bx = numpy.zeros(nz)
        for k in range(nz):
            b = self.champB(x,z[k])
            bx[k] = b[0]
        return bx
    def Bx_x(self,x,z):
        nx = len(x)
        bx = numpy.zeros(nx)
        for k in range(nx):
            b = self.champB(x[k],z)
            bx[k] = b[0]
        return bx
    def A_x(self,x,z):
        nx = len(x)
        A = numpy.zeros(nx)
        for k in range(nx):
            b = self.champB(x[k],z)
            A[k] = b[2]
        return A
    def Adx_x(self,x,z):
        nx = len(x)
        Adx = numpy.zeros(nx)
        for k in range(nx):
            b = self.champB(x[k],z)
            Adx[k] = b[3]
        return Adx

Les deux fonctions suivantes renvoient les composantes du champ (avec le potentiel vecteur) sur un domaine, sous forme de deux tableaux à deux dimensions :

    def B(self,x,z):
        nx = len(x)
        nz = len(z)
        bx = numpy.zeros((nx,nz))
        bz = numpy.zeros((nx,nz))
        A = numpy.zeros((nx,nz))
        for i in range(nz):
            for j in range(nx):
                b = self.champB(x[j],z[i])
                bx[j][i] = b[0]
                bz[j][i] = b[1]
                A[j][i] = b[2]
        return [bx,bz,A]

La fonction suivante calcule une ligne de champ en partant d'un point :

    def ligneB(self,x0,z0,sens):
        def equation(y,t):
            b = self.champB(y[0],y[1])
            nb = math.sqrt(b[0]*b[0]+b[1]*b[1])
            return [sens*b[0]/nb,sens*b[1]/nb]
        tmax = (self.xmax-self.xmin)
        te = 1.0*tmax/100
        xarray = numpy.array([x0])
        zarray = numpy.array([z0])
        x=x0
        z=z0
        t = 0.0
        while t < tmax:
            y = odeint(equation,[x,z],[0,te],rtol=1e-5,atol=1e-5)
            x = y[1][0]
            z = y[1][1]
            if x<self.xmin or x>self.xmax or z<self.zmin or z>self.zmax:
                break
            xarray = numpy.append(xarray,x)
            zarray = numpy.append(zarray,z)
            t += te
        return [xarray,zarray]

La fonction suivante trace des lignes de champ pour une liste de points initiaux. Pour chaque point, les deux lignes symétriques par rapport à l'axe sont tracées.

    def plot_lignes(self,points,style):
        for p in points:
            [x,z] = self.ligneB(p[0],p[1],1)
            plot(z,x,style)
            [x,z] = self.ligneB(p[0],p[1],-1)
            plot(z,x,style)
            [x,z] = self.ligneB(-p[0],p[1],1)
            plot(z,x,style)
            [x,z] = self.ligneB(-p[0],p[1],-1)
            plot(z,x,style)
            for s in self.spires:
                plot([s.zs,s.zs],[-s.a,s.a],linestyle=" ",marker="o",markersize=4,color="black")

La fonction suivante calcule la trajectoire d'une particule chargée en coordonnées cylindriques. Les équations du mouvement sont présentées dans Particule chargée dans un champ magnétique axial. Les arguments sont le rapport q/m de la particule, la position et la vitesse initiales (radiales et axiales), le temps maximal du calcul et la période d'échantillonnage. La vitesse angulaire initiale est nulle.

    def trajectoire(self,alpha,r0,z0,dr0,dz0,tmax,te):
        b = self.champB(r0,z0)
        ptheta = r0*alpha*b[2]
        def equation(y,t):
            r = y[0]
            theta = y[1]
            z = y[2]
            b = self.champB(r,z)
            if ptheta==0:
                u = -alpha*b[2]
                dpr = u*alpha*b[3]
                dpz = u*alpha*(-b[0])
                dtheta = -alpha*(b[1]-b[3])
            else:
                r2 = r*r
                u = ptheta/r-alpha*b[2]
                dpr = u*(ptheta/r2+alpha*b[3])
                dpz = u*alpha*(-b[0])
                dtheta = ptheta/r2-alpha*(b[1]-b[3])
            return [y[3],dtheta,y[4],dpr,dpz]
        rarray = numpy.array([r0])
        zarray = numpy.array([z0])
        thetarray = numpy.array([0.0])
        r = r0
        theta = 0.0
        z = z0
        dtheta = 0.0
        dr = dr0
        dz = dz0
        t = 0.0
        while t < tmax:
            y = odeint(equation,[r,theta,z,dr,dz],[0,te],rtol=1e-5,atol=1e-5)
            r = y[1][0]
            theta = y[1][1]
            z = y[1][2]
            dr = y[1][3]
            dz = y[1][4]
            if r<self.xmin or r>self.xmax or z<self.zmin or z>self.zmax:
                break
            rarray = numpy.append(rarray,r)
            zarray = numpy.append(zarray,z)
            thetarray = numpy.append(thetarray,theta)
        return [rarray,thetarray,zarray]

4. Exemple

On considère un exemple avec une spire. Il est intéressant de tracer des courbes universelles, valables quelles que soient le rayon de la spire et l'intensité du courant. Pour cela, on introduit les variables d'espace réduites définies par :

\begin{matrix} x' = \frac{x}{a} \\ z' = \frac{z}{a} \end{matrix}

Exprimons le vecteur $\vec{B}$ avec ces variables :

\begin{matrix} B_{x} (x', 0, z') = \frac{μ_{0} I}{2 π a} \int_{0}^{π} \frac{z' cos θ d θ}{[x'^{2} + z'^{2} + 1 - 2 x' cos θ]^{3 / 2}} \\ B_{z} (x', 0, z') = \frac{μ_{0} I}{2 π a} \int_{0}^{π} \frac{(- x' cos θ + 1) d θ}{[x'^{2} + z'^{2} + 1 - 2 x' cos θ]^{3 / 2}} \end{matrix}

Il s'en suit que les calculs peuvent être faits en posant a=1 et I=1. L'unité du champ magnétique ainsi calculé est donné par :

B_{0} = \frac{μ_{0} I}{2 π a} (1)

où a est le rayon réel de la spire et I l'intensité du courant réelle. Autrement dit, le calcul donne le champ divisé par cette constante.

from SpiresCoaxiales import *
import numpy
from matplotlib.pyplot import *

systeme = SystemeSpires(-5.0,5.0,-5.0,5.0)
systeme.ajouter(Spire(1.0,0.0,1.0))
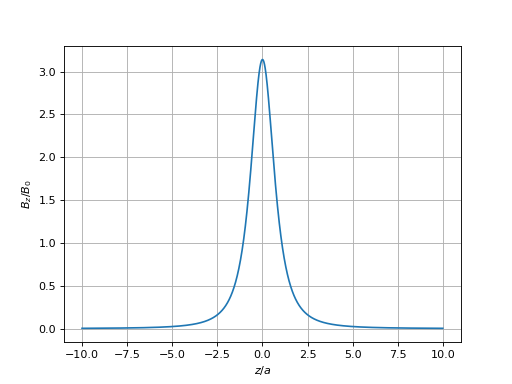
z = numpy.arange(-10.0,10.0,0.01)
bz = systeme.Bz_z(0.0,z)
figure()
plot(z,bz)
xlabel(r"$z/a$")
ylabel(r"$B_z/B_0$")
grid()

figA.pdf

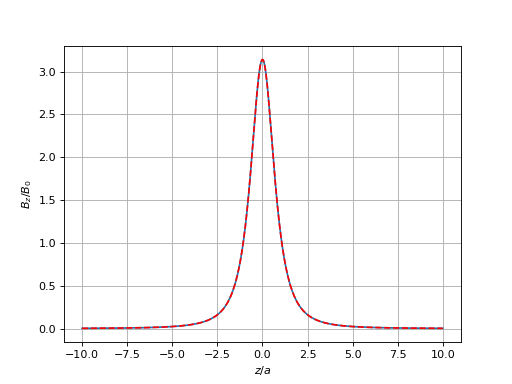
Pour valider ce résultat, faisons une comparaison avec l'expression du champ sur l'axe, qui peut être obtenu aisément avec la loi de Biot et Savart :

B_{z} (0, z') = \frac{μ_{0} I}{2 π a} \frac{π}{{(1 + z'^{2})}^{\frac{3}{2}}} (2)

bz_axe = numpy.pi/(1+z**2)**1.5
figure()
plot(z,bz)
plot(z,bz_axe,'r--')
xlabel(r"$z/a$")
ylabel(r"$B_z/B_0$")
grid()

figA1.pdf

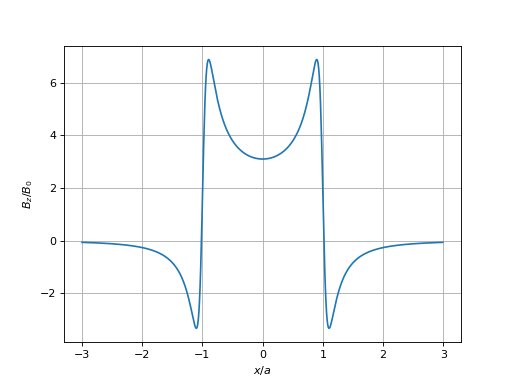
Voici la composante axiale du champ magnétique à une distance z' donnée :

x = numpy.arange(-3.0,3.0,0.01)
bz = systeme.Bz_x(x,0.1)
figure()
plot(x,bz)
xlabel(r"$x/a$")
ylabel(r"$B_z/B_0$")
grid()

figB.pdf

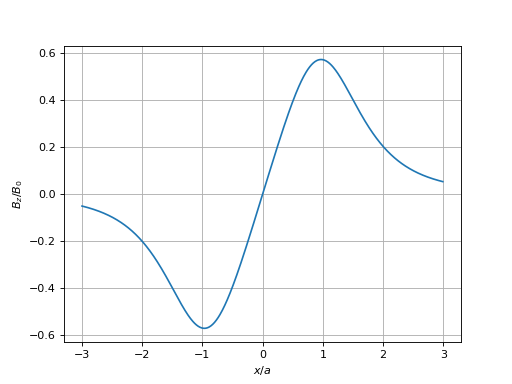
et la composante radiale à la même distance :

bx = systeme.Bx_x(x,1.0)
figure()
plot(x,bx)
xlabel(r"$x/a$")
ylabel(r"$B_z/B_0$")
grid()

figC.pdf

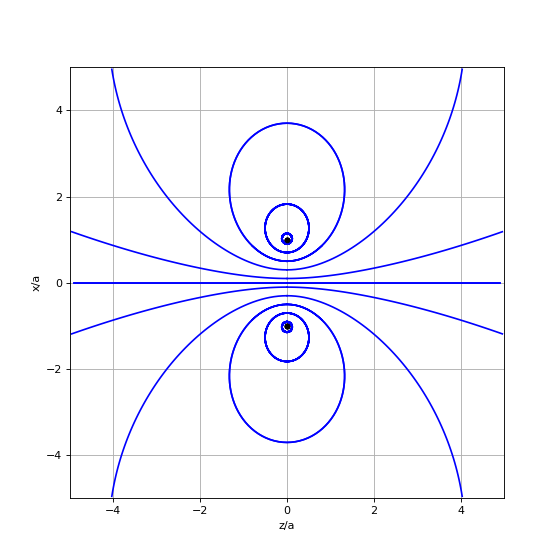
Tracé de lignes de champ :

figure(figsize=(7,7))
systeme.plot_lignes([[0.0,0.0],[0.1,0.0],[0.3,0.0],[0.5,0.0],[0.7,0.0],[0.9,0.0]],'b')
axis([-5.0,5.0,-5.0,5.0])
grid()
xlabel('z/a')
ylabel('x/a')

figD.pdf

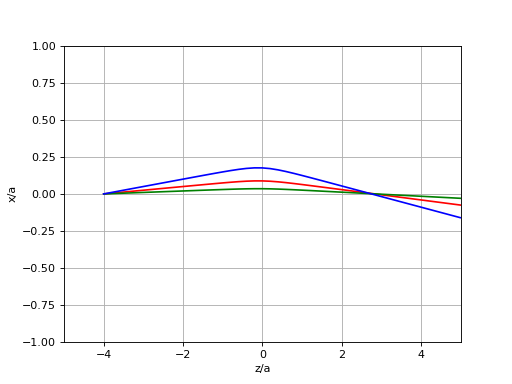
Trajectoires d'une particule chargée dans le plan méridien tournant :

figure()
tmax=200.0
te=0.1
alpha = 1.0
r0 = 0.00
z0 = -4.0
dz0 =2.0
[r,theta,z] = systeme.trajectoire(alpha,r0,z0,0.05,dz0,tmax,te)
plot(z,r,'r')
[r,theta,z] = systeme.trajectoire(alpha,r0,z0,0.02,dz0,tmax,te)
plot(z,r,'g')
[r,theta,z] = systeme.trajectoire(alpha,r0,z0,0.1,dz0,tmax,te)
plot(z,r,'b')
axis([-5.0,5.0,-1.0,1.0])
xlabel('z/a')
ylabel('x/a')
grid()

figE.pdf

Références

[1] J.D. Jackson, Classical Electrodynamics, (John Wiley Sons, 1975)