Freinage par courants induits

1. Introduction

Ce document décrit un modèle de freinage par courants induits. La figure suivante montre le dispositif étudié. Une plaque métallique (non magnétique) de largeur 2d, de longueur infinie et d'épaisseur e est en mouvement à vitesse constante $\overrightarrow{v}=v{\overrightarrow{u}}_x$. Un électro-aimant dont l'axe est perpendiculaire à la plaque et dont le noyau a une section de forme rectangulaire applique un champ magnétique $\overrightarrow{B}=B_0{\overrightarrow{u}}_z$ dans une zone rectangulaire de longueur 2a et de largeur 2b. Il peut aussi s'agir d'un aimant permanent de section droite rectangulaire. Ce champ magnétique est stationnaire dans le référentiel défini par le repère (Oxy), dans lequel l'aimant est fixe (référentiel fixe). On suppose que ce champ passe de manière discontinue de B₀ à zéro lorsqu'on sort de la zone rectangulaire en vis à vis du noyau (la plaque est très proche de celui-ci).

Figure pleine page

Le modèle repose aussi sur l'hypothèse que le champ magnétique créé par les courants induits est négligeable par rapport à celui créé par l'aimant, ce qui garantit la stationnarité du champ dans le référentiel fixe et implique que le champ magnétique $\overrightarrow{B}$ est bien présent dans la plaque sur toute son épaisseur. Le courant électrique dans la plaque est supposé bidimensionnel, c'est-à-dire :

$$\overrightarrow{J}=J_x(x,y){\overrightarrow{u}}_x+J_y(x,y){\overrightarrow{u}}_y\text{(1)}$$

Il faut remarquer qu'il s'agit de la densité de courant électrique dans le référentiel fixe (lié à (0xy)).

2. Mise en équation

Soit $\overrightarrow{E}$ le champ électrique dans la plaque et dans le référentiel fixe. Le champ électromoteur est $\overrightarrow{v}\wedge \overrightarrow{B}$. Si $\gamma$ est la conductivité électrique du métal de la plaque, la loi d'Ohm s'écrit :

$$\overrightarrow{J}=\gamma (\overrightarrow{E}+\overrightarrow{v}\wedge \overrightarrow{B})\text{(2)}$$

Le champ $\overrightarrow{E}\text{'}=\overrightarrow{E}+\overrightarrow{v}\wedge \overrightarrow{B}$ est le champ électrique dans le référentiel lié à la plaque, en translation rectiligne et uniforme par rapport au référentiel fixe.

En décomposant sur les axes on a :

$$\overrightarrow{J}=\gamma (E_x{\overrightarrow{u}}_x+E_y{\overrightarrow{e}}_y-v{B}_z{\overrightarrow{u}}_y)\text{(3)}$$

Comme on va le voir en détail, le champ électrique provient de la redistribution des charges causées par le champ électromoteur.

On commence par poser le problème pour un champ $B_z(x,y)$ quelconque et variant continûment. Le courant dans le référentiel fixe est stationnaire donc :

$$div\overrightarrow{J}=0\text{(4)}$$

Il s'en suit que :

$$div\overrightarrow{E}=-div\left(\overrightarrow{v}\wedge \overrightarrow{B}\right)\text{(5)}$$

D'après l'équation de Maxwell-Gauss, on a dans la plaque une densité de courant :

$$\rho (x,y)={\epsilon }_{0}div\overrightarrow{E}=-{\epsilon }_{0}div\left(\overrightarrow{v}\wedge \overrightarrow{B}\right)\text{(6)}$$

Le champ $\overrightarrow{E}$ est donc un champ électrostatique. Soit V(x,y) le potentiel électrostatique, qui vérifie l'équation de Poisson :

$$\Delta V=-\frac{\rho }{{\epsilon }_0}\text{(7)}$$

ou encore :

$$\Delta V=div\left(\overrightarrow{v}\wedge \overrightarrow{B}\right)\text{(8)}$$

Il faut préciser aussi les conditions limites sur les bords de la plaque, c'est-à-dire pour $y=\pm d$. Sur ces bords, la densité de courant n'a pas de composante selon ${\overrightarrow{u}}_y$. On a donc $E_y(x,\pm d)=0$ et le potentiel vérifie la condition limite suivante (de type Neumann) :

$$\frac{\partial V}{\partial y}(x,\pm d)=0\text{(9)}$$

Pour un champ $B_z(x,y)$ donné, la résolution de l'équation de Poisson avec cette condition limite permet de déterminer le potentiel puis le champ $\overrightarrow{E}$ et finalement la densité de courant. La force magnétique qui agit sur un volume élémentaire de la plaque (force de Laplace) est :

$$d\overrightarrow{F}=\left(\overrightarrow{J}\wedge \overrightarrow{B}\right)d\tau =(-E_x{B}_z{\overrightarrow{u}}_y+(E_y-v{B}_z){\overrightarrow{u}}_x)d\tau \text{(10)}$$

L'intégrale de cette densité de force sur le rectangle soumis au champ magnétique conduit à une force selon ${\overrightarrow{u}}_x$ (ce point sera à vérifier) qui s'écrit :

$$F_x=e\gamma B_0{\int }_a^{a}dx{\int }_{-b}^{b}dy(E_y(x,y)-v{B}_z(x,y))\text{(11)}$$

Revenons au modèle considéré ici où B_z est uniforme dans une zone rectangulaire est nul en dehors. La densité volumique de charge est :

$$\rho ={\epsilon }_{0}div\left(v{B}_z{\overrightarrow{u}}_y\right)={\epsilon }_{0}v\frac{\partial B_z}{\partial y}\text{(12)}$$

Elle est donc nulle partout mais il y a une charge surfacique sur les bords du rectangle parallèles à (Ox), là où la dérivée de B_z par rapport à y est infinie. Pour évaluer cette charge surfacique sur le côté en y=b, considérons que la charge volumique soit répartie dans une épaisseur ε qui tend vers zéro (pour donner une charge surfacique). On a alors :

$$\sigma \left(b\right)=\rho \epsilon ={\epsilon }_{0}v\frac{\partial B_z}{\partial y}(y=b)\epsilon =-{\epsilon }_{0}v{B}_0\text{(13)}$$

De même on obtient pour la densité de charge surfacique sur le côté opposé :

$$\sigma \left(b\right)=\rho \epsilon ={\epsilon }_{0}v\frac{\partial B_z}{\partial y}(y=-b)\epsilon ={\epsilon }_{0}v{B}_0\text{(14)}$$

Il y donc une accumulation de charges négatives sur le côté supérieur (x=b) et de charges positives sur le côté inférieure (x=-b), ce qui est en accord avec le fait que le champ électromoteur $\overrightarrow{v}\wedge \overrightarrow{B}$ est dirigé dans le sens de $-{\overrightarrow{u}}_y$.

On est donc ramené à un problème d'électrostatique avec une distribution de charges constituée de deux surfaces planes de largeur 2a parallèles, à une distance 2b l'une de l'autre et portant les densités $\pm \sigma$ avec $\sigma ={\epsilon }_{0}v{B}_0$. Le caractère bidimensionnel du problème implique que ces surfaces sont infinies dans la direction (Oz). Ce problème est analogue à celui d'une plaque d'électret d'épaisseur 2b, de largeur 2a et de longueur infinie, qui aurait une polarisation $\overrightarrow{P}=-\sigma {\overrightarrow{u}}_y$.

Figure pleine page

Sur chacune des surfaces chargées, le champ électromoteur présente une dicontinuité mais le champ électrique également. Écrivons la relation de passage pour ce dernier sur la surface chargée située en x=b :

$$E_y(y=b^{+})-E_y(y=b^{-})=-\frac{\sigma }{{\epsilon }_0}=-v{B}_0\text{(15)}$$

ce qui est précisément la discontinuité du champ électromoteur. On en déduit que le vecteur densité de courant est bien continu sur les surfaces chargées. Sur les côtés du rectangle parallèles à Oy il y a en revanche une discontinuité de la densité du courant due à la discontinuité du champ magnétique. En réalité, ce champ varie continûment mais sur une zone très étroite et il y a bien sûr continuité de la densité de courant.

Pour calculer le champ électrostatique généré par ces deux surfaces chargées, on commence par traiter le cas où la plaque a une largeur infinie.

3. Plaque de largeur infinie

La plaque a une largeur infinie, c'est-à-dire $d\to \infty$. Dans ce cas, les deux surfaces chargées sont dans un espace infini. Considérons un élément de largeur dx_p d'une de ces faces, situé au point P. Cet élément est équivalent à un fil infini parallèle à (Oz) portant une charge linéique $\lambda =\sigma d{x}_p$. Le champ électrique créé par ce fil en un point M :

$$d\overrightarrow{E}\left(M\right)=\frac{\sigma d{x}_p}{2\pi {\epsilon }_0}\frac{\overrightarrow{PM}}{P{M}^2}\text{(16)}$$

Notons (x,y) les coordonnées de M et (x_p,y_p) celles de P. Le champ électrique généré par une des deux faces, dont le signe de la densité est s et située en y_p est :

$$\begin{array}{ccc}\hfill & E_x(x,y)=\frac{s\sigma }{2\pi {\epsilon }_0}{\int }_{-a}^a\frac{x-x_p}{{(x-x_p)}^2+{(y-y_p)}^2}d{x}_p\hfill & \hfill \text{(17)}\\ \hfill & E_y(x,y)=\frac{s\sigma }{2\pi {\epsilon }_0}{\int }_{-a}^a\frac{y-y_p}{{(x-x_p)}^2+{(y-y_p)}^2}d{x}_p\hfill & \hfill \text{(18)}\end{array}$$

La première intégrale s'évalue sans difficulté :

$$E_x(x,y)=\frac{s\sigma }{4\pi {\epsilon }_0}(ln({(x+a)}^2+{(y-y_p)}^2)-ln({(x-a)}^2+{(y-y_p)}^2))\text{(19)}$$

La seconde intégrale se calcule au moyen de l'intégrale suivante :

$$\int \frac{du}{c^2+u^2}=\frac{1}{c}arctan\left(\frac{u}{c}\right)\text{(20)}$$

On obtient :

$$E_y(x,y)=\frac{s\sigma }{2\pi {\epsilon }_0}\left(arctan\right(\frac{a-x}{y-y_p})+arctan(\frac{a+x}{y-y_p}\left)\right)\text{(21)}$$

Il reste à sommer les champs créés par les deux surfaces. Pour celle située en y_p=b on a s=-1. Pour celle située en y_p=-b on a s=1. On obtient :

$$E_x(x,y)=\frac{v{B}_0}{4\pi }(-ln({(x+a)}^2+{(y-b)}^2)+ln({(x-a)}^2+{(y-b)}^2)+ln({(x+a)}^2+{(y+b)}^2)-ln({(x-a)}^2+{(y+b)}^2))\text{(22)}$$ $$E_y(x,y)=\frac{v{B}_0}{2\pi }(-arctan(\frac{a-x}{y-b})-arctan(\frac{a+x}{y-b})+arctan(\frac{a-x}{y+b})+arctan(\frac{a+x}{y+b}\left)\right)\text{(23)}$$

Le vecteur densité de courant s'écrit dans le rectangle ($\left|x\right|<a$ et $\left|y\right|<b$) :

$$\begin{array}{ccc}\hfill & J_x(x,y)=\gamma E_x(x,y)\hfill & \hfill \text{(24)}\\ \hfill & J_y(x,y)=\gamma (E_y(x,y)-v{B}_0)\hfill & \hfill \text{(25)}\end{array}$$

et hors du rectangle :

$$\begin{array}{ccc}\hfill & J_x(x,y)=\gamma E_x(x,y)\hfill & \hfill \text{(26)}\\ \hfill & J_y(x,y)=\gamma E_y(x,y)\hfill & \hfill \text{(27)}\end{array}$$

Afin de faire un tracé des lignes de courants, on attribue tout d'abord des valeurs aux dimensions du rectangles :

import numpy as np
from matplotlib.pyplot import *
a=2e-2 # en mètres
b=2e-2		
				

La fonction suivante calcule le champ électrique généré par une surface chargée (divisé par $v{B}_0$) :

def champEsurface(yp,s,x,y):
	Ex = s/(4*np.pi)*(np.log((x+a)**2+(y-yp)**2)-np.log((x-a)**2+(y-yp)**2))
	Ey = s/(2*np.pi)*(np.arctan((a-x)/(y-yp))+np.arctan((a+x)/(y-yp)))
	return [Ex,Ey]
				

La fonction suivante calcule le vecteur densité de courant divisé par $\gamma v{B}_0$ :

def courantJ(x,y):
	[Ex,Ey] = champEsurface(-b,1,x,y)
	Jx,Jy = Ex,Ey
	[Ex,Ey] = champEsurface(b,-1,x,y)
	Jx += Ex
	Jy += Ey
	if abs(x)<a and abs(y)<b:
		Jy -= 1
	return [Jx,Jy]
				

On définit aussi un vecteur unitaire colinéaire à la densité de courant :

def courantU(x,y):
	J = courantJ(x,y)
	norme = np.sqrt(J[0]**2+J[1]**2)
	return [J[0]/norme,J[1]/norme]
				

La fonction suivante calcule une ligne de champ (par la méthode d'Euler) à partir d'un point (x₀,y₀) :

def ligneChamp(x0,y0,longueur,h,sens=1):
    x = x0
    y = y0
    l = 0
    X = [x0]
    Y = [y0]
    while l<longueur:
        U = courantU(x,y)
        x += sens*U[0]*h
        y += sens*U[1]*h
        X.append(x)
        Y.append(y)
        l += h
    return np.array(X),np.array(Y)			
				

figure(figsize=(8,8))
L = 15e-2
xlim(-L,L)
ylim(-L,L)
y0 = 0
x0 = np.linspace(-L,L,21)
plot([-a,a],[-b,-b],'k-')
plot([-a,a],[b,b],'k-')
plot([-a,-a],[-b,b],'k--')
plot([a,a],[-b,b],'k--')
for k in range(len(x0)):
	X,Y = ligneChamp(x0[k],y0,L*2,L*1e-3,sens=1)
	plot(X,Y,'r-')
	X,Y = ligneChamp(x0[k],y0,L*2,L*1e-3,sens=-1)
	plot(X,Y,'r-')
grid()
xlabel('x (m)')
ylabel('y (m)')
				

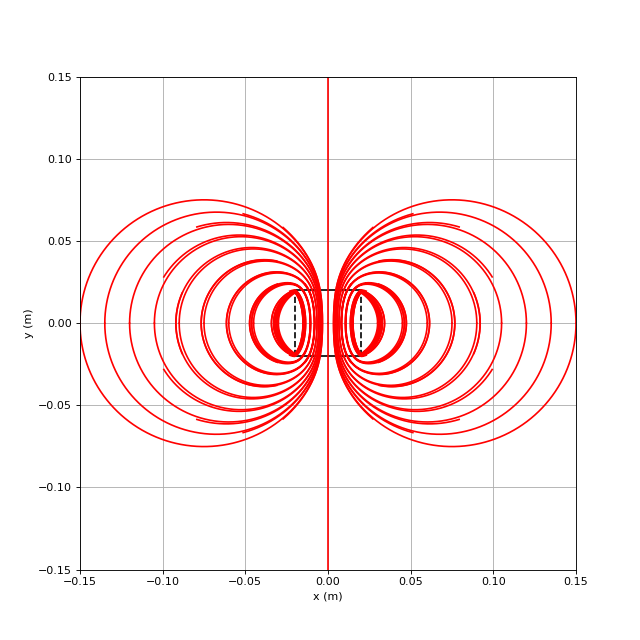figA.pdf

Les boucles de courant situées dans la partie droite (x>0) sont orientées dans le sens direct alors que les boucles situées dans la partie gauche sont orientés dans le sens horaire. Les lignes de courant dans la zone de champ magnétique rectangulaire sont donc orientées selon $-{\overrightarrow{u}}_y$, ce qui montre que la force de Laplace est vers la gauche, c'est-à-dire opposée au vecteur vitesse. Les boucles de courant qui traversent la zone de champ s'étendent sur une grande distance de part et d'autre de cette zone et cette distance (par rapport à la largeur du rectangle) ne dépend que du rapport b/a (pas de la vitesse ni du champ magnétique).

La force magnétique sur la plaque s'écrit :

$$F_x=-e\gamma B_0{\int }_{-a}^a{\int }_{-b}^b(v{B}_0-E_y(x,y))dxdy\text{(28)}$$

ou bien :

$$F_x=-4\alpha abe\gamma B_0^{2}v\text{(29)}$$

avec :

$$\alpha =1-\frac{1}{2\pi 4ab}{\int }_{-a}^a{\int }_{-b}^b(-arctan(\frac{a-x}{y-b})-arctan(\frac{a+x}{y-b})+arctan(\frac{a-x}{y+b})+arctan(\frac{a+x}{y+b}\left)\right)dxdy\text{(30)}$$

qu'on peut aussi écrire :

$$\alpha =1-\frac{1}{v{B}_{0}4ab}{\int }_{-a}^a{\int }_{-b}^b{E}_y(x,y)dxdy\text{(31)}$$

Le coefficient $\alpha$ est sans dimensions et ne dépend que du rapport b/a.

La force de freinage ne dépend que de la composante E_y du champ émectrique. Il est intéressant de tracer cette composante en fonction de x en y=0 et en y=b/2 :

def EySurface(yp,s,x,y):
	return s/(2*np.pi)*(np.arctan((a-x)/(y-yp))+np.arctan((a+x)/(y-yp)))
	
def EyComplet(x,y):
	E = EySurface(-b,1,x,y)
	E += EySurface(b,-1,x,y)
	return E

x = np.linspace(-L,L,1000)
figure(figsize=(12,8))
plot(x,EyComplet(x,0),label='y=0')
plot(x,EyComplet(x,b/2),label='y=b/2')
xlabel('x',fontsize=16)
ylabel(r"$E_y/(vB_0)$",fontsize=16)
plot([-a,-a],[0,0.5],'k--')
plot([a,a],[0,0.5],'k--')
grid()
legend(loc='upper right')
				

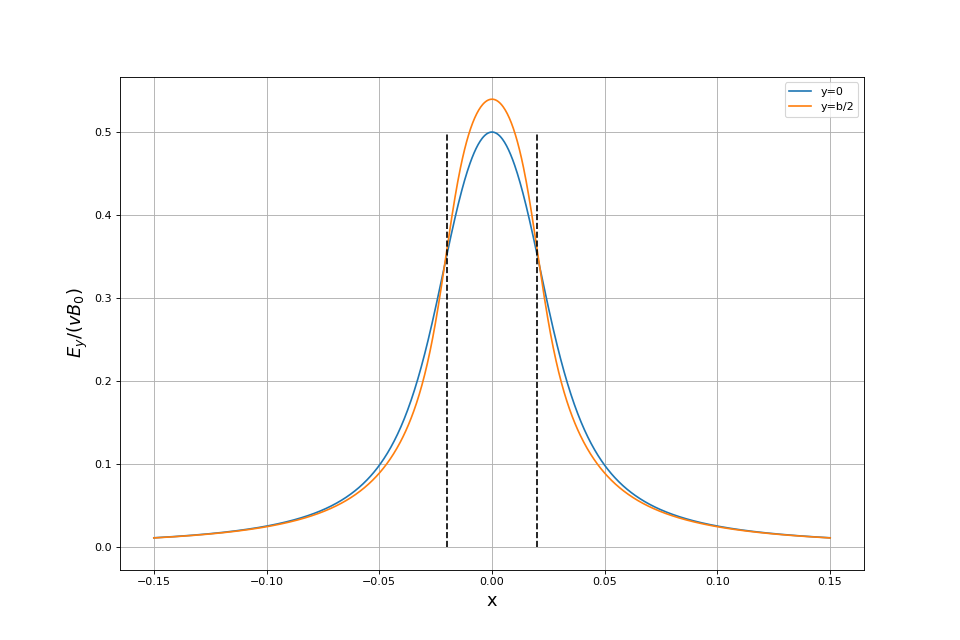figB.pdf

Le calcul formel de l'intégrale dans l'expression $\mathrm{(31)}$ est possible mais très laborieux. Nous allons plutôt procéder à une évaluation numérique par la méthode des rectangles :

	
def integraleEy(N):
	dx = 2*a/N 
	dy = 2*b/N 
	x = -a+np.arange(N)*dx 
	y = -b+np.arange(1,N)*dy 
	I = 0
	for j in range(N-1):
		Ey = EyComplet(x,y[j]) 
		I += np.sum(Ey) 
	return I*dx*dy
	
alpha = 1-integraleEy(200)/(4*a*b)
				

print(alpha)
--> 0.5031952843417509

Pour une zone de champ magnétique carrée, on obtient donc une force de freinage:

$$F_x=-\frac{S}{2}e\gamma B_0^{2}v\text{(32)}$$

où S est l'aire de la zone de champ magnétique (4ab).

On peut aussi remarquer que la valeur moyenne de E_y divisée par vB₀ est égale à $1-\alpha$. Dans la zone de champ magnétique, le champ électrique a donc une valeur moyenne égale à la moitié du champ électromoteur. Sachant cela, l'expression de la force ci-dessus s'obtient simplement en supposant que la densité de courant est pratiquement uniforme dans la zone de champ magnétique.

4. Plaque de largeur semi-finie

Lorsque la largeur 2d est finie, le vecteur densité de courant doit satisfaire la condition suivante sur les bords de la plaque :

$$J_y(y=\pm d)=0\text{(33)}$$

Puisque le champ électromoteur est nul en dehors du rectangle en vis à vis de l'aimant, cela implique pour le champ électrique :

$$E_y(y=\pm d)=0\text{(34)}$$

Dans cette partie, on considère le cas d'une plaque semi-finie, c'est-à-dire comportant un seul bord, par convention celui en y=d. Ce modèle correspond à une situation ou l'électro-aimant est proche d'un bord de la plaque. On a dans ce cas la condition limite suivante :

$$E_y(y=d)=0\text{(35)}$$

Ce problème peut être résolu par la méthode des images. On ajoute au système des deux surfaces chargées deux surfaces fictives images des deux surfaces réelles par le plan y=d, de telle manière que ce plan soit un plan de symétrie pour la distribution des charges.

Figure pleine page

Avec ces quatre surfaces chargées, la condition limite $\mathrm{(35)}$ est satisfaite. Le champ électrostatique créé par ces quatre surfaces dans la région x<d est précisément le champ électrostatique créé par les deux surfaces chargées réelles en présence du bord de la plaque. En effet, il n'existe qu'une solution de l'équation de Poisson avec cette condition limite et cette solution est donc nécessairement celle qui est obtenue en ajoutant les deux surfaces images. Remarquons bien que la solution obtenue ne sera pas valable en dehors de la plaque. Le calcul du champ électrostatique en dehors de la plaque sort du cadre de ce modèle.

Le calcul du champ électrostatique créé par ce système est immédiat. Il suffit d'ajouter une surface de densité de charge -σ en y=2d-b et une surface de densité de charge σ en y=2d+b.

On choisit une valeur pour d :

d = 4e-2
			 

puis on redéfinit la fonction qui calcule le vecteur densité de courant divisé par $\gamma v{B}_0$ :

def courantJ(x,y):
	[Ex,Ey] = champEsurface(-b,1,x,y)
	Jx,Jy = Ex,Ey
	[Ex,Ey] = champEsurface(b,-1,x,y)
	Jx += Ex
	Jy += Ey
	[Ex,Ey] = champEsurface(2*d-b,-1,x,y)
	Jx += Ex 
	Jy += Ey
	[Ex,Ey] = champEsurface(2*d+b,1,x,y)
	Jx += Ex 
	Jy += Ey
	if abs(x)<a and abs(y)<b:
		Jy -= 1
	return [Jx,Jy]
				

Voici les tracé des lignes de courant en présence du bord :

figure(figsize=(8,8))
L = 15e-2
xlim(-L,L)
ylim(-L,L)
y0 = 0
x0 = np.linspace(-L,L,21)
plot([-a,a],[-b,-b],'k-')
plot([-a,a],[b,b],'k-')
plot([-a,-a],[-b,b],'k--')
plot([a,a],[-b,b],'k--')
plot([-L,L],[d,d],'k-')
for k in range(len(x0)):
	X,Y = ligneChamp(x0[k],y0,L*2,L*1e-3,sens=1)
	plot(X,Y,'r-')
	X,Y = ligneChamp(x0[k],y0,L*2,L*1e-3,sens=-1)
	plot(X,Y,'r-')
grid()
xlabel('x (m)')
ylabel('y (m)')
				

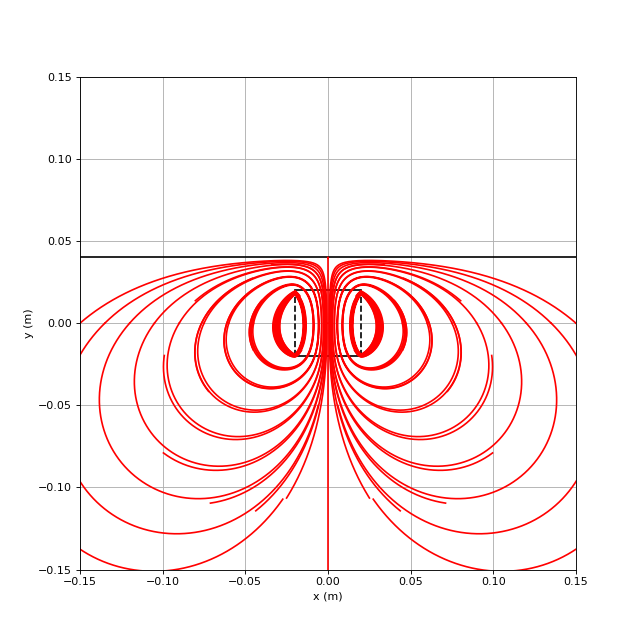figC.pdf

L'expression $\mathrm{(29)}$ de la force de freinage est toujours valable. Voici le tracé de E_y sur l'axe (Ox) :

def EyComplet(x,y):
	E = EySurface(-b,1,x,y)
	E += EySurface(b,-1,x,y)
	E += EySurface(2*d-b,-1,x,y)
	E += EySurface(2*d+b,1,x,y)
	return E
				
x = np.linspace(-L,L,1000)
figure(figsize=(12,8))
plot(x,EyComplet(x,0),label='y=0')
plot(x,EyComplet(x,b/2),label='y=b/2')
xlabel('x',fontsize=16)
ylabel(r"$E_y/(vB_0)$",fontsize=16)
plot([-a,-a],[0,0.5],'k--')
plot([a,a],[0,0.5],'k--')
grid()
legend(loc='upper right')
				

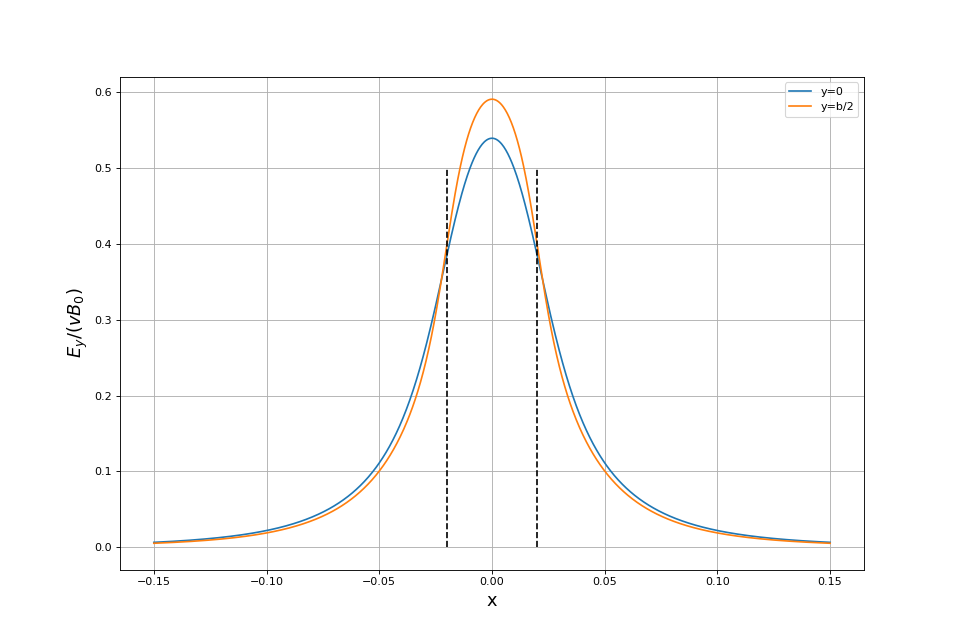figD.pdf

La composante E_y atteint une valeur plus grande en présence du bord. Voici la constante $\alpha$ :

alpha = 1-integraleEy(200)/(4*a*b)
				

print(alpha)
--> 0.4640114756799969

Le coefficient $\alpha$ est égale à 0,46 au lieu de 0,50 pour la plaque infinie. L'effet du bord est donc une petite réduction de la force de freinage.

5. Plaque de largeur finie

En présence de deux frontières à proximité de la zone de champ magnétique, la méthode des images ne permet plus de résoudre le problème. Une résolution numérique de l'équation de Poisson pour le potentiel $\mathrm{(7)}$ peut être faite par la méthode des différences finies. Nous utilisons pour cela le module présenté dans Équation de Poisson : module Python.

La distribution de charges comporte deux plans chargés de densité surfacique de charges $\pm \sigma$ avec $\sigma ={\epsilon }_{0}v{B}_0$. Pour introduire une source correspondant à une surface chargée, il faut définir une source sur la ligne du maillage correspondant à cette surface. Lorsqu'on définit une source avec la fonction poisson.source_polygon, il s'agit en fait d'une source volumique et non surfacique. Pour convertir la densité surfacique de charges en densité volumique, il suffit de la diviser par le pas Δy du maillage. Par ailleurs, on divisera la densité de charges par vB₀ afin d'obtenir le champ électrostatique divisé par cette constante. Finalement, le terme de source à introduire dans la résolution numérique est $\pm 1/\Delta y$ sur les deux lignes correspondant aux deux surfaces chargées.

Le domaine de calcul est rectangulaire, deux fois plus long dans la direction (Ox) que dans la direction (Oy). La condition limite en y=d et y=-d est une annulation de la composante du gradient sur (Oy), conformément à $\mathrm{(34)}$. Sur les bords du domaines parallèles à (Oy), il faut aussi définir une condition limite. Il est en effet impossible de simuler un milieu infini car le maillage a une taille finie : c'est le point faible de cette méthode comparée à une méthode de calcul direct du champ comme celle développée précédemment. Nous choisissons de définir sur ces bords une annulation du gradient du potentiel. Physiquement, cela revient à considérer une plaque dont la longueur est aussi finie (dans la direction (Ox)), mais dans ce cas le courant ne serait plus stationnaire.

Le maillage comporte un nombre de nœuds de 2ⁿ⁺¹ dans la direction (Ox) et 2ⁿ dans la direction (Oy). Les plans chargés sont définis sur un maillage réduit de taille 2^p+1 par 2^p. Les grilles intermédiaires entre la grille fine (indice n) et la grille grossière (indice p) sont utilisées par l'algorithme multigrille.

La fonction suivante effectue le calcul pour une taille donnée de la zone de champ magnétique, définie en nombre de nœud, la surface inférieure décalée de p1 nœuds vers le haut. Le maillage réduit contient 2⁶=64 nœuds dans la direction (Oy). Remarquons que le pas Δy utilisé pour définir le terme de source pour la surface chargée est le pas de la grille réduite.

from poisson.main import Poisson
				
def resolutionPoisson(a,b,p1):
	n=10
	p=6
	levels = n-p+1
	largeur = 2.0
	hauteur = 1.0
	poisson=Poisson(p+1,p,levels,largeur,hauteur,-largeur/2,-hauteur/2)
	poisson.laplacien()
	poisson.neumann_borders(0,0,0,0,0)
	w = 2**(p+1)
	h = 2**p
	i1 = w//2-a # indices sur le maillage réduit
	j1 = p1 + h//2-b
	poisson.source_polygon(i1,j1,[2*a],[0],-1/poisson.dy)
	poisson.source_polygon(i1,j1+2*b,[2*a],[0],1/poisson.dy)
	result = poisson.multigrid_full_norm(4,levels,50,2,1)
	V = poisson.get_array()
	Ex=-poisson.get_derivX()
	Ey=-poisson.get_derivY()
	Jx = Ex.copy()
	Jy = Ey.copy()
	ii1 = i1*2**(n-p) # indices sur le maillage fin
	jj1 = j1*2**(n-p)
	aa = a*2**(n-p)
	bb = b*2**(n-p)
	Jy[jj1:jj1+2*bb,ii1:ii1+2*aa]-=1
	I = 0
	for i in range(ii1,ii1+2*aa):
		for j in range(jj1,jj1+2*bb):
			I += Ey[j,i]
	I /= (4*aa*bb)
	alpha = 1-I
	return V,Ex,Ey,Jx,Jy,alpha,poisson.get_mask(),poisson.get_extent()
				

Voici un premier exemple, avec un domaine carré centré et assez loin des bords :

V,Ex,Ey,Jx,Jy,alpha,mask,extent =  resolutionPoisson(4,4,0)
figure(figsize=(12,6))
contour(V,20,extent=extent)
imshow(~mask,extent=extent,alpha=0.5, cmap=cm.gray)

				

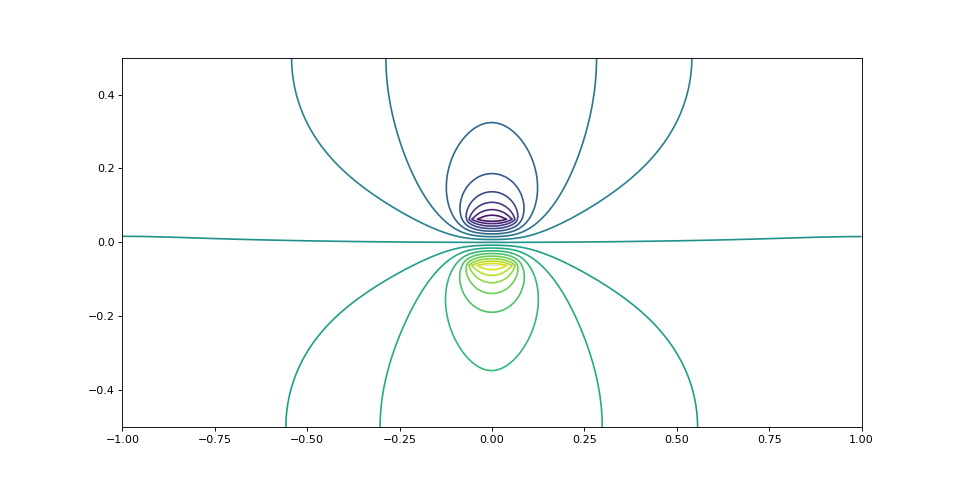figE.pdf

print(alpha)
--> 0.48642015626137436

figure(figsize=(12,6))
X,Y = np.meshgrid(np.linspace(-1,1,2**11+1),np.linspace(-0.5,0.5,2**10+1))
streamplot(X,Y,Jx,Jy,density=2)
imshow(~mask,extent=extent,alpha=0.5, cmap=cm.gray)
				 

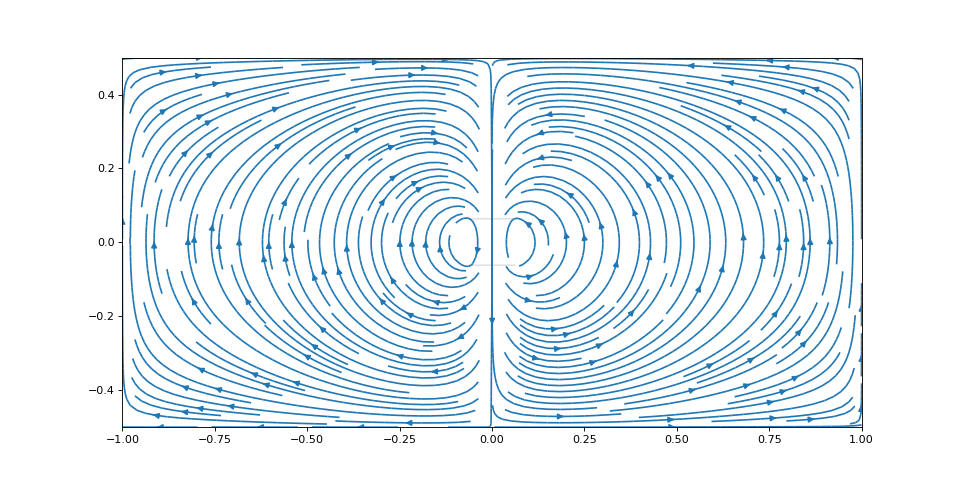figF.pdf

Voici un deuxième exemple, avec une zone de champ beaucoup plus grande (par rapport à la taille du domaine) :

V,Ex,Ey,Jx,Jy,alpha,mask,extent =  resolutionPoisson(10,10,0)
figure(figsize=(12,6))
contour(V,20,extent=extent)
imshow(~mask,extent=extent,alpha=0.5, cmap=cm.gray)

				

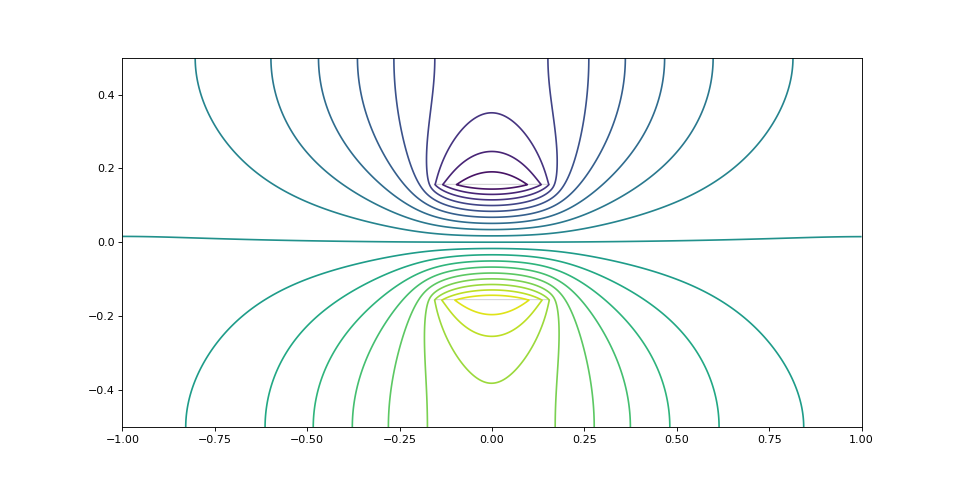figG.pdf

print(alpha)
--> 0.42093229067279025

figure(figsize=(12,6))
X,Y = np.meshgrid(np.linspace(-1,1,2**11+1),np.linspace(-0.5,0.5,2**10+1))
streamplot(X,Y,Jx,Jy,density=2)
imshow(~mask,extent=extent,alpha=1, cmap=cm.gray)
				 

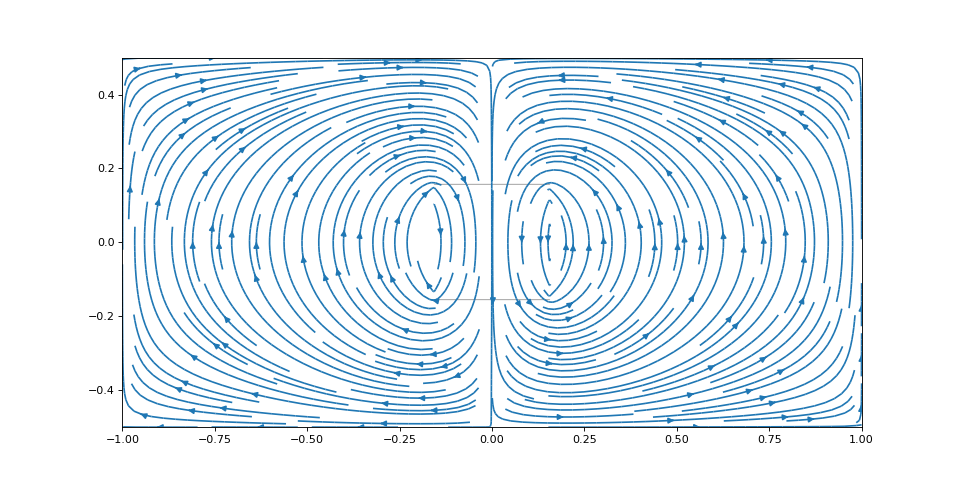figH.pdf

Le coefficient $\alpha$ vaut 0,41, ce qui fait une diminution de $16\%$ de la force de freinage par rapport à la situation où les bords sont très loins (pour la même taille réelle de la zone de champ magnétique).

Dernier exemple : on approche la zone de champ du bord supérieur :

V,Ex,Ey,Jx,Jy,alpha,mask,extent =  resolutionPoisson(10,10,20)
figure(figsize=(12,6))
contour(V,20,extent=extent)
imshow(~mask,extent=extent,alpha=0.5, cmap=cm.gray)

				

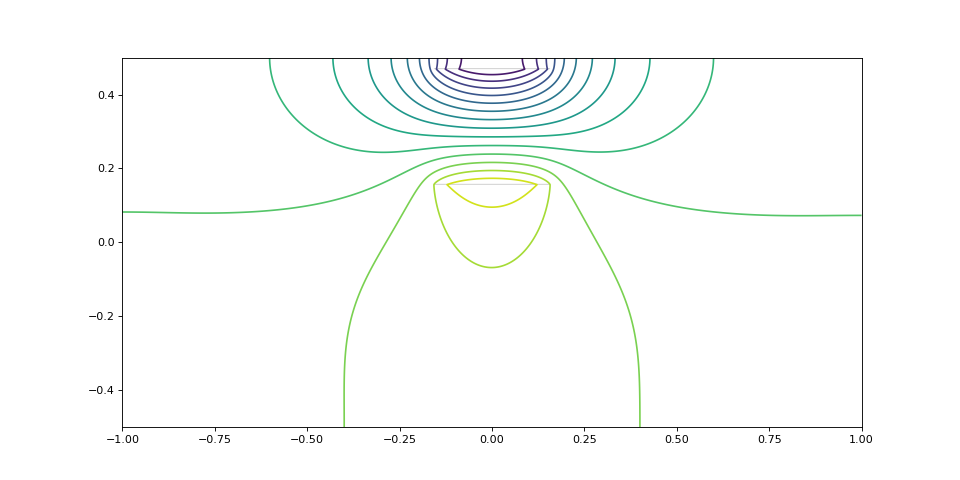figI.pdf

print(alpha)
--> 0.3639646003360394

figure(figsize=(12,6))
X,Y = np.meshgrid(np.linspace(-1,1,2**11+1),np.linspace(-0.5,0.5,2**10+1))
streamplot(X,Y,Jx,Jy,density=2)
imshow(~mask,extent=extent,alpha=1, cmap=cm.gray)
				 

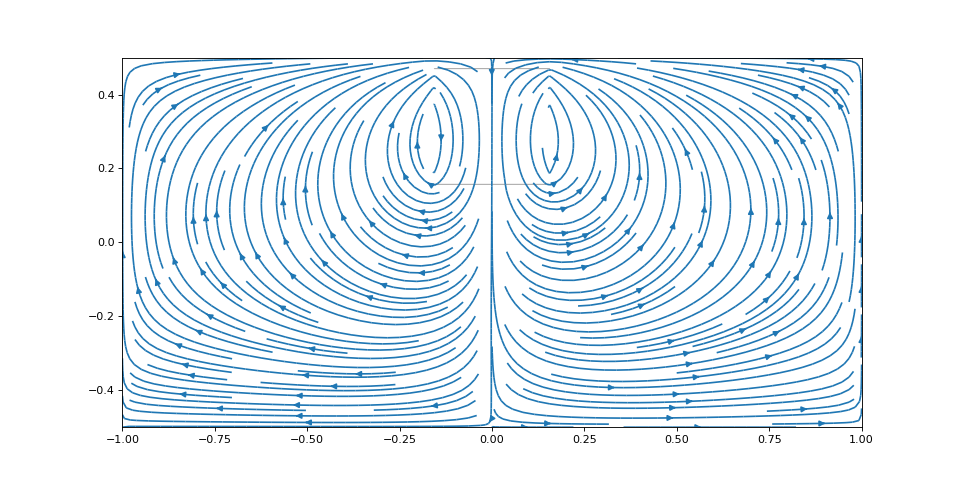figJ.pdf

On obtient $\alpha =0,36$, soit une réduction de $28\%$ de la force de freinage, par rapport à la situation où les bords sont très loins.