Fils chargés

1. Introduction

Cette page montre le calcul de la force électrostatique entre deux fils conducteurs portant deux charges linéiques opposées. Il s'agit de voir comment la redistribution des charges sur la surface des fils, lorsqu'il sont très proches l'un de l'autre, affecte la force.

Nous faisons la résolution par éléments finis avec le logiciel libre Finite Element Method Magnetic, au moyen de l'interface pour Python (pyfemm), qui permet de piloter le logiciel depuis un script Python (le logiciel doit être installé). Ce script permet de définir une géométrie complexe dépendant d'un ou de plusieurs paramètres et d'obtenir des tracés de champ sur des courbes particulières. Les commandes de l'interface Python sont des répliques des opérations que l'on effectue lorsqu'on utilise directement l'interface utilisateur. Il faut donc bien se familiariser avec cette interface avant d'aborder l'écriture des scripts Python.

Le logiciel FEMM permet d'effectuer la résolution numérique d'un problème d'électrostatique (ou de magnétostatique ou de diffusion thermique) par la méthode des éléments finis. Il résout les problèmes bidimensionnels, en géométrie plane ou axisymétrique. Contrairement au logiciel FreeFEM, dont l'utilisation pour un problème d'électrostatique est exposée dans Équation de Poisson : méthode des éléments finis, le logiciel FEMM peut être utilisé sans aucune connaissance sur la méthode des éléments finis ni même des équations de l'électrostatique. Le système électrostatique est en effet défini directement par ses caractéristiques physiques.

2. Définitions

On considère deux fils métalliques rectilignes de section droite de rayon R et de longueur infini.

Figure pleine page

Le fil 1, dont l'axe coupe le plan (0xy) en (x=0,y=h), porte sur sa surface une charge de densité linéique λ. Le fil 2, dont l'axe coupe le plan (Oxy) en (x=0,y=-h), porte sur sa surface une charge de densité linéique -λ. L'objectif est de calculer la répartition des charges sur la surface des fils et la force attractive en fonction de la distance Y=2h.

Si la distance entre les fils est grande devant leur rayon, les surfaces sont chargées uniformément avec une densité $σ_{0}$ et le champ électrique créé par un fil s'écrit (en coordonnée cylindrique par rapport à son axe) :

\vec{E} = \frac{σ_{0} a}{ε_{0}} \frac{1}{r} \vec{u_{r}} (1)

Soit C₂ le centre du fil 2 (dans le plan (Oxy)). La force élémentaire (par unité de longueur de fil) exercée par le fil 2 sur un élément du fil 1 centré au point M et de largeur angulaire $d θ$ s'écrit :

d \vec{F} = - \frac{σ_{0}^{2}}{ε_{0}} R^{2} d θ \frac{\vec{C_{2} M}}{C_{2} M^{2}} (2)

La résultante et dans la direction de l'axe (Oy) et s'écrit :

F_{y} = - \frac{σ_{0}^{2} R^{2}}{ε_{0}} \int_{0}^{2 π} \frac{d + R cos (θ)}{d^{2} + R^{2} + 2 d R cos (θ)} d θ (3)

Nous pouvons comparer cette force à celle qui serait exercée si le rayon du fil 1 était négligeable :

f_{y} = - \frac{2 π σ_{0}^{2}}{ε_{0}} \frac{R^{2}}{d} (4)

Si l'on pose $u = \frac{d}{R}$ , le rapport des deux forces est :

r = \frac{F_{y}}{f_{y}} = \frac{1}{2 π} \int_{0}^{2 π} \frac{u^{2} + u cos (θ)}{1 + u^{2} + 2 u cos (θ)} (5)

Nous pouvons calculer numérique l'intégrale pour différentes valeurs de u :

import numpy as np
from matplotlib.pyplot import *

N = 20
u=np.linspace(2,10,N)
r = np.zeros(N)
theta = np.linspace(0,2*np.pi,1000)
for i in range(N):
    df = (u[i]**2+u[i]*np.cos(theta))/(1+u[i]**2+2*u[i]*np.cos(theta))
    r[i] = df.sum()*(theta[1]-theta[0])/(2*np.pi)

figure() 
plot(u,r)
grid()
xlabel("u")
ylabel("r")
ylim(0,2)

fig1.pdf

L'intégrale vaut 1. On a donc :

F_{y} = - \frac{2 π σ_{0}^{2}}{ε_{0}} \frac{R^{2}}{d} (6)

3. Résolution par éléments finis

3.a. Lignes équipotentielles

On commence par ouvrir un document FEMM pour résoudre un problème d'électrostatique, en géométrie plane et avec le millimètre pour unité de longueur :

deuxFils.py

import femm
import numpy as np
import matplotlib.pyplot as plt

femm.openfemm()
femm.newdocument(1)
# 0 : magnetic, 1 : electrostatic, 2 ; heat flow, 3 : current flow
femm.ei_probdef('millimeters', 'planar', 1.0e-8, 0, 30);
# unit, type ('planar' ou 'axi'), precision, depth, minangle

Un matériau se définit par deux permittivités électriques (pour les deux axes) et une densité volumique de charge. On définit deux matériaux air et métal, de permittivité 1 :

femm.ei_addmaterial('air',1,1,0)
femm.ei_addmaterial('metal',1,1,0)

Deux conducteurs doivent être définis. Il y a deux types de conducteur : à potentiel imposé (type 1) et à charge imposée (type 2). On définit deux conducteurs à charge imposée. La charge définie est en fait la charge par unité de longueur λ :

lamb = 1e-14
femm.ei_addconductorprop('v1',0,lamb,0)
femm.ei_addconductorprop('v2',0,-lamb,0)

Voici la définition des deux conducteurs :

h = 10 
R = 5
R1 = 200

femm.ei_drawarc(R,h,-R,h,180,1)
femm.ei_drawarc(-R,h,R,h,180,1)
femm.ei_drawarc(R,-h,-R,-h,180,1)
femm.ei_drawarc(-R,-h,R,-h,180,1)

Il en résulte trois domaines, auquels il faut affecter un matériau :

femm.ei_addblocklabel(0,h)
femm.ei_addblocklabel(0,-h)
femm.ei_selectlabel(0,h)
femm.ei_selectlabel(0,-h)
femm.ei_setblockprop('metal',0,1,0)
femm.ei_clearselected()
femm.ei_addblocklabel(0,0)
femm.ei_selectlabel(0,0)
femm.ei_setblockprop('air',0,1,0)
femm.ei_clearselected()

Il faut aussi affecter les conducteurs définis plus hauts aux segments correspondants :

femm.ei_selectarcsegment(0,h-R)
femm.ei_selectarcsegment(0,h+R)
femm.ei_setarcsegmentprop(180,'<None>',0,0,'v1')
femm.ei_clearselected()

femm.ei_selectarcsegment(0,-h-R)
femm.ei_selectarcsegment(0,-h+R)
femm.ei_setarcsegmentprop(180,'<None>',0,0,'v2')
femm.ei_clearselected()

La frontière du domaine de calcul est définie par la fonction ei_makeABC, qui mermet de simuler un domaine infini au moyen de n couches (Improvised Asymptotic Boundary Condition). On choisit n=5 et une condition de type Dirichlet sur dernière couche :

femm.ei_makeABC(5,R1,0,0,0)

Pour finir, le document doit être enregistré dans un ficher avant de lancer le calcul : l'application FEMM s'ouvre avec le fichier et effectue le calcul.

femm.ei_zoomnatural()
femm.ei_saveas('deuxCylindres.fee')
femm.ei_analyze()
femm.ei_loadsolution()

Par défaut, le potentiel apparaît sous la forme d'une image en couleur. Voici comment obtenir un tracé de lignes équipotentielles :

femm.eo_hidedensityplot()
femm.eo_showcontourplot(30,-0.5,0.5)

Voici les lignes équipotentielles au voisinage des conducteurs, avec le tracé du maillage :

Pour ces deux fils relativement proches, la densité de charge sur un fil est plus forte du côté qui fait face à l'autre fil. Voici les lignes équipotentielles pour un espacement des fils cinq fois plus grand :

Les lignes équipotentielles au voisinage des fils sont quasi circulaires, ce qui montre que la densité surfacique de charge est quasi uniforme et que le modèle développé plus haut pour le calcul de la force (Définitions) est approximativement valable.

input("?")
femm.closefemm()

3.b. Force entre les deux fils

Pour calculer la force exercée par un fil sur l'autre (par unité de longueur), il y a deux méthodes différentes :

Calculer la densité surfacique de charge sur la surface du fil au moyen du champ électrique puis intégrer sur le contour du fil pour obtenir la force.
Utiliser la méthode des travaux virtuels.

Nous optons pour la seconde méthode, qui consiste à calculer l'énergie électrique :

W = ∭ \frac{1}{2} ε_{0} {\vec{E}}^{2} d v (7)

Soit F_y la force exercée par le fil 2 sur le fil 1. Si l'on éloigne le fil 2 du fil 1 de manière quasistatique d'une distance dY, c'est-à-dire en lui appliquant une force -F_y, on fournit un travail qui fait varier l'énergie électrique :

- F_{y} d Y = d W (8)

Il s'en suit que la force est l'opposée de la dérivée de l'énergie par rapport à la distance entre les deux fils :

F_{y} = - \frac{d W}{d Y} (9)

Il faut donc calculer l'énergie pour différentes distances puis calculer la force en dérivant par différence finie. Le script suivant effectue ce calcul :

deuxFils-force.py

import femm
import numpy as np
import matplotlib.pyplot as plt
femm.openfemm()

def energie(h,R,lamb=1e-14,R1=200):
    femm.newdocument(1)
    femm.ei_probdef('millimeters', 'planar', 1.0e-8, 0, 30);
    femm.ei_addmaterial('air',1,1,0)
    femm.ei_addmaterial('metal',1,1,0)
    femm.ei_addconductorprop('v1',0,lamb,0)
    femm.ei_addconductorprop('v2',0,-lamb,0)
    femm.ei_drawarc(R,h,-R,h,180,1)
    femm.ei_drawarc(-R,h,R,h,180,1)
    femm.ei_drawarc(R,-h,-R,-h,180,1)
    femm.ei_drawarc(-R,-h,R,-h,180,1)
    femm.ei_addblocklabel(0,h)
    femm.ei_addblocklabel(0,-h)
    femm.ei_selectlabel(0,h)
    femm.ei_selectlabel(0,-h)
    femm.ei_setblockprop('metal',0,1,0)
    femm.ei_clearselected()
    femm.ei_addblocklabel(0,0)
    femm.ei_selectlabel(0,0)
    femm.ei_setblockprop('air',0,1,0)
    femm.ei_clearselected()
    femm.ei_selectarcsegment(0,h-R)
    femm.ei_selectarcsegment(0,h+R)
    femm.ei_setarcsegmentprop(180,'<None>',0,0,'v1')
    femm.ei_clearselected()
    femm.ei_selectarcsegment(0,-h-R)
    femm.ei_selectarcsegment(0,-h+R)
    femm.ei_setarcsegmentprop(180,'<None>',0,0,'v2')
    femm.ei_clearselected()
    femm.ei_makeABC(5,R1,0,0,0)
    femm.ei_zoomnatural()
    femm.ei_saveas('deuxCylindres.fee')
    femm.ei_analyze()
    femm.ei_loadsolution()
    femm.eo_selectblock(0,0)
    W = femm.eo_blockintegral(0) # énergie par mm de longueur
    femm.eo_clearblock()
    return W[0]

R = 5
N = 100
Y = np.linspace(11,60,N)
deltaY = Y[1]-Y[0]
W = np.zeros(N)
for i in range(N):
    W[i] = energie(Y[i]/2,R)

np.savetxt("energie-R=5.txt",np.array([Y,W]).T)
plt.figure()
plt.plot(Y,W)
plt.grid()
plt.xlabel("Y")
plt.ylabel("W")

F = np.zeros(N-1)
for i in range(N-1):
    F[i] = -(W[i+1]-W[i])/deltaY
Y = Y[0:N-1]
plt.figure()
plt.plot(Y,F)
plt.grid()
plt.xlabel("Y")
plt.ylabel("F")
np.savetxt("force-R=5.txt",np.array([Y,F]).T)

plt.show()
femm.closefemm()

Voici le tracé de la force en fonction de Y/d, avec en pointillé celui correspondant à la relation $(6)$ :

[Y,F] = np.loadtxt("force-R=5.txt",unpack=True)
R=5
figure(figsize=(12,6))
plot(Y/R,F)
grid()
xlabel("Y/R",fontsize=16)
ylabel("Fy",fontsize=16)

lamb = 1e-14
eps0 = 8.85e-12
f = -lamb**2/(2*np.pi*eps0*Y*1e-3)
plot(Y/R,f,"k--")

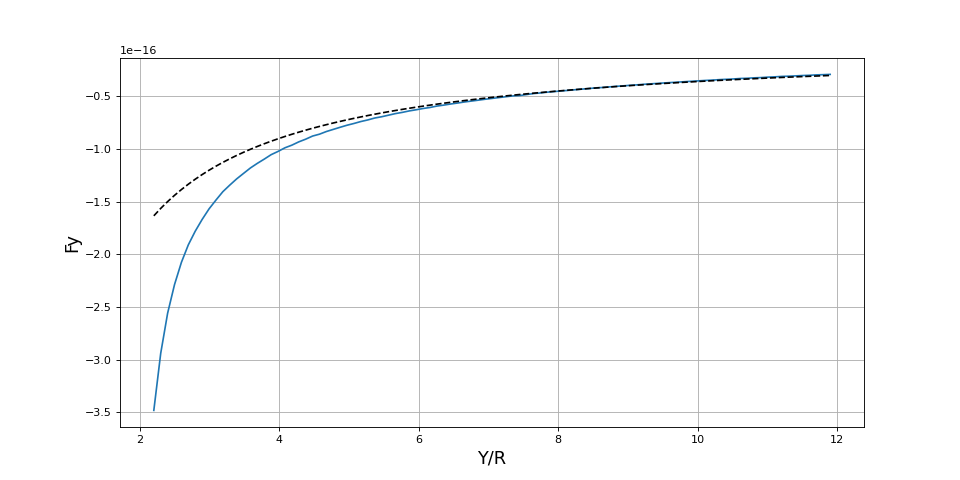fig2.pdf

On constate que pour Y/R > 6 (distance entre les fils au moins 6 fois leur rayon), la force suit la relation $(6)$ . À faible distance, la force est en valeur absolue plus grande que celle donnée par cette relation. Ce résultat s'explique par le fait que la redistribution des charges sur la surface des fils résulte en une diminution de la distance moyenne des charges qui s'attirent, comme le montre la figure suivante :