Effet de peau dans un fil rectiligne

1. Introduction

Ce document montre le calcul de l'effet de peau dans un fil rectiligne parcouru par un courant de fréquence donnée, dans le but de déterminer l'influence de la fréquence sur la résistance du fil.

Le modèle adopté est celui d'un fil rectiligne de longueur infinie, très loin de tout autre fil. Il ne s'applique pas à un fil qui serait à proximité d'autres fils.

2. Mise en équation

Un fil rectiligne de section circulaire et de rayon a est assimilé à un fil de longueur infinie. Soit (0z) l'axe de symétrie du fil. Un point de l'espace est repéré par ses coordonnées cylindriques (r,θ,z).

Figure pleine page

L'intensité de courant dans le fil varie à la pulsation ω :

$$I\left(t\right)=I_{0}cos\left(\omega t\right)\text{(1)}$$

Le métal a une perméabilité magnétique μ. Pour un métal non magnétique comme le cuivre, cette perméabilité est très proche de celle du vide (μ₀).

Si on se limite à une distance r petit devant la longueur d'onde du rayonnement électromagnétique de pulsation ω (300 mètres pour 100 kHz), on peut appliquer l'approximation des régimes quasi stationnaires.

Les équations de Maxwell (dans le métal et dans le vide) s'écrivent :

$$\begin{array}{ccc}\hfill & div\overrightarrow{E}=0\hfill & \hfill \text{(2)}\\ \hfill & \overrightarrow{rot}\overrightarrow{E}=-\frac{\partial \overrightarrow{B}}{\partial t}\hfill & \hfill \text{(3)}\\ \hfill & div\overrightarrow{B}=0\hfill & \hfill \text{(4)}\\ \hfill & \overrightarrow{rot}\overrightarrow{H}\approx \overrightarrow{J}\hfill & \hfill \text{(5)}\end{array}$$

Dans le vide, on a $\overrightarrow{J}=0$ et $\overrightarrow{H}=\overrightarrow{B}/{\mu }_0$. Dans le métal, on utilise la loi d'Ohm $\overrightarrow{J}=\gamma \overrightarrow{E}$. Si le métal est magnétique, on suppose que la courbe d'aimantation est linéaire (fer doux loin de la saturation), ce qui permet d'écrire $\overrightarrow{H}=\overrightarrow{B}/\mu$.

L'équation $div\overrightarrow{E}=0$ suppose que la densité de charge est nulle, ce qui est évidemment vrai dans le vide. Dans le métal, la dernière équation s'écrit $\overrightarrow{rot}\overrightarrow{H}=\gamma \overrightarrow{E}$, ce qui implique que $div\overrightarrow{E}=0$ donc que la densité de charge est nulle.

La symétrie axiale du problème implique que la densité de courant dans le métal est de la forme :

$$\overrightarrow{J}=J_z(r,t){\overrightarrow{u}}_z\text{(6)}$$

et le champ magnétique de la forme :

$$\overrightarrow{B}=B_{\theta }(r,t){\overrightarrow{u}}_{\theta }\text{(7)}$$

Des équations de Maxwell, on déduit une équation aux dérivées partielles pour le champ magnétique :

$$\overrightarrow{\Delta }\overrightarrow{B}=\mu \gamma \frac{\partial \overrightarrow{B}}{\partial t}\text{(8)}$$

Compte tenu de la forme du champ, l'équation s'écrit :

$$\frac{\partial }{\partial r}\left(\frac{1}{r}\frac{\partial }{\partial r}\right(r{B}_{\theta }\left)\right)=\mu \gamma \frac{\partial B_{\theta }}{\partial t}\text{(9)}$$

On se place en régime sinusoïdal de pulsation ω. Tous les champs sont complexes et proportionnels à $e^{i\omega t}$. L'équation à résoudre dans le métal est alors :

$$\frac{d}{dr}\left(\frac{1}{r}\frac{d}{dr}\right(r{B}_{\theta }\left)\right)=i\omega \mu \gamma B_{\theta }\text{(10)}$$

Une fois le champ magnétique dans le métal déterminé, on calcule la densité de courant par la relation $\overrightarrow{J}=\frac{1}{\mu }\overrightarrow{rot}\overrightarrow{B}$, qui s'écrit :

$$J_z\left(t\right)=\frac{1}{\mu }\frac{1}{r}\frac{d}{dr}\left(r{B}_{\theta }\right)\text{(11)}$$

En courant en continu (fréquence nulle), les équations $\mathrm{(10)}$ et $\mathrm{(11)}$ permettent de démontrer que la densité de courant est uniforme. Elle s'écrit :

$$J_z^{DC}=\frac{I}{\pi a^2}\text{(12)}$$

Le rapport des deux densités s'écrit :

$$A\left(r\right)=\frac{J_z}{J_z^{DC}}=\frac{\pi a^2}{\mu I}\frac{1}{r}\frac{d}{dr}\left(r{B}_{\theta }\right)\text{(13)}$$

L'équation $\mathrm{(10)}$ est une équation différentielle à conditions limites. L'intervalle de résolution est [0,a]. En r=0 on a B_θ=0. La condition limite en r=a (dans le métal) s'obtient aisément par application du théorème d'Ampère pour le cercle (C) de rayon a représenté sur la figure (cercle situé dans le métal) :

$${\oint }_C\overrightarrow{B}\cdot \overrightarrow{d}l=\mu I\text{(14)}$$

On obtient ainsi :

$$B_{\theta }^{metal}\left(a\right)=\frac{\mu I}{2\pi a}\text{(15)}$$

Il est important de remarquer que la possibilité d'obtenir la condition limite aussi simplement résulte de la symétrie axiale de ce problème. Le champ magnétique sur la surface du fil est indépendant de la distribution du courant dans le fil et ne dépend que de l'intensité I. Cette propriété ne serait évidemment pas vérifiée pour le problème de deux fils parallèles : dans ce cas, il serait impossible de trouver a priori le champ sur la surface des fils car celui-ci dépendrait de la distribution de courant, qui est inconnue.

Considérons la puissance moyenne dissipée dans une longueur $\ell$ de fil :

$$P_d=\frac{\ell }{2\gamma }{\int }_0^a|J_z\left(r\right){|}^{2}2\pi rdr\text{(16)}$$

Cette puissance moyenne permet d'obtenir la résistance R de la portion de fil car :

$$P_d=\frac{1}{2}R{I}^2\text{(17)}$$

La résistance R doit être comparée à la résistance en courant continu (résistance DC) :

$$R^{DC}=\frac{\ell }{\gamma \pi a^2}\text{(18)}$$

Le rapport des deux résistances s'écrit :

$$\frac{R}{R^{DC}}=\frac{\pi a^2}{I^2}{\int }_0^a|J_z\left(r\right){|}^{2}2\pi rdr\text{(19)}$$

La distance de pénétration dans le métal est définie par :

$$\delta =\sqrt{\frac{2}{\gamma \mu \omega }}$$

Si on introduit la variable réduite r'=r/a, l'équation $\mathrm{(10)}$ s'écrit, après développement des dérivées :

$$\frac{d^2{B}_{\theta }}{dr\text{'}}+\frac{1}{r\text{'}}\frac{d{B}_{\theta }}{dr\text{'}}-\frac{1}{{\left(r\text{'}\right)}^2}{B}_{\theta }=2i(\frac{a}{\delta }{)}^2{B}_{\theta }\text{(20)}$$

Posons :

$$B_0=\frac{\mu I}{2\pi a}\text{(21)}$$

et le champ réduit :

$$B_{\theta }\text{'}=\frac{B_{\theta }}{B_0}\text{(22)}$$

La condition limite en r=a s'écrit B'_θ=1 et le rapport des densités de courant s'écrit :

$$A\left(r\text{'}\right)=\frac{1}{2}\frac{1}{r\text{'}}\frac{d}{dr\text{'}}\left(r\text{'}B{\text{'}}_{\theta }\right)=\frac{1}{2}(\frac{dB{\text{'}}_{\theta }}{dr\text{'}}+\frac{B{\text{'}}_{\theta }}{r\text{'}})\text{(23)}$$

Lorsque $r\text{'}\to 0$, $B{\text{'}}_{\theta }\to 0$. Le terme $B{\text{'}}_{\theta }/r\text{'}$ est donc indéterminé en r'=0. La valeur de A(0) sera obtenu par continuité.

Le rapport des résistances s'écrit alors :

$$\frac{R}{R^{DC}}=2{\int }_0^1|A\left(r\text{'}\right){|}^{2}r\text{'}dr\text{'}\text{(24)}$$

3. Méthode numérique

L'équation diférentielle à conditions limites $\mathrm{(20)}$ est linéaire. Elle peut donc se résoudre numériquement par la méthode des différences finies.

On cherche les valeurs approchées de B'_θ pour r'=kh avec h=1/(N-1) et k=0,1,..N-1. Notons B_k ces valeurs approchées. L'écriture des dérivées sous forme de différence finie conduit à :

$$\frac{B_{k-1}+B_{k+1}-2B_k}{h^2}+\frac{1}{kh}\frac{B_{k+1}-B_{k-1}}{2h}-\frac{1}{{\left(kh\right)}^2}{B}_k=2i{u}^2{B}_k\text{(25)}$$

où u=a/δ. Cette équation s'applique pour k allant de 1 à N-2. Les conditions limites s'écrivent :

$$B_0=0,B_{N-1}=1\text{(26)}$$

L'équation s'écrit aussi :

$$(1-\frac{1}{2k})B_{k-1}+(-2-\frac{1}{k^2}-2i{u}^2{h}^2)B_k+(1+\frac{1}{2k})B_{k+1}=0\text{(27)}$$

Nous obtenons N-2 équations et 2 conditions limites, soit N équations linéaires pour N inconnues. Il s'agit d'un système tridiagonal, qui peut être résolu efficacement par un algorithme d'élimination spécifique (voir Équation de diffusion à une dimension). Si N n'est pas trop grand, nous pouvons néanmoins utiliser la fonction scipy.linalg.solve, qui implémente sans doute une méthode d'élimination de Gauss, non optimisée pour ce type de système. Le système linéaire étant mis sous la forme MB=P, il faut remplir les matrices M et P.

from scipy.linalg import solve
import numpy as np

def champB(N,u):
    M = np.zeros((N,N),dtype=np.complex64)
    P = np.zeros(N,dtype=np.complex64)
    h = 1/(N-1)
    M[0,0] = 1
    M[N-1,N-1] = 1
    P[N-1] = 1
    for k in range(1,N-1):
        M[k,k-1] = 1-1/(2*k)
        M[k,k] = -2-1/k**2-2*1j*u**2*h**2
        M[k,k+1] = 1+1/(2*k)
    B = solve(M,P)
    r = np.arange(N)*h
    return r,B
    
             

from matplotlib.pyplot import *

u=10
N=1000
r,B = champB(N,u)
figure()
plot(r,np.absolute(B))
grid()
xlabel(r"$r/a$")
ylabel(r"$|B_{\theta}|/B_0$")
             

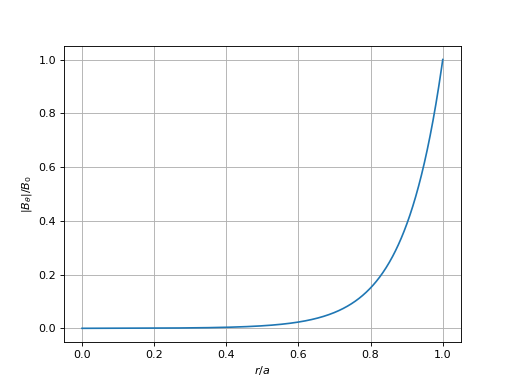champB-u10.pdf

Pour calculer le rapport de la densité de courant sur la densité en courant continu, donné par la relation $\mathrm{(23)}$, nous calculons la dérivée de B_θ(r') par la différence finie $(B_{k+1}-B_k)/h$. Cette différence ne permet pas de calculer la dérivée en r'=0 et l'expression $\mathrm{(23)}$ comporte r' au dénominateur. En conséquence, les tableaux renvoyés par cette fonction ne contiennent pas ce point et commencent donc à r'=h.

from scipy.signal import convolve
              
def rapportJ(B):
    N = len(B)
    h = 1/(N-1)
    r = np.arange(1,N)*h
    dB = convolve(B,[1,-1],mode='same')/h
    A = 0.5*(dB[1:N]+B[1:N]/r)
    return r,A
              

r,A = rapportJ(B)

figure()
grid()
plot(r,np.absolute(A))
xlabel(r"$r/a$")
ylabel(r"$|J_z|/J^{DC}$")
ylim(0,10)
              

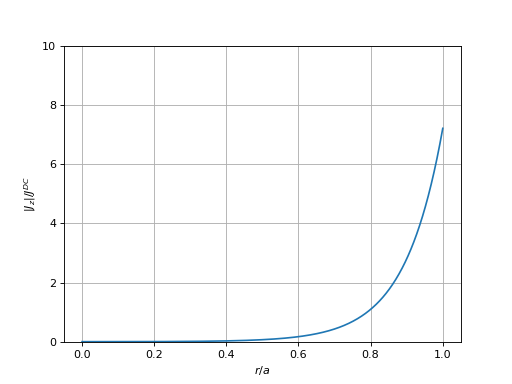rapportJ-u10.pdf

Pour calculer le rapport des résistances $\mathrm{(24)}$, nous évaluons l'intégrale avec la méthode des trapèzes :

def rapportR(r,A):
    N = len(A)
    h = 1/(N-1)
    y = r*np.absolute(A)**2
    S = np.sum(y[1:N-1])
    S += 0.5*(y[0]+y[N-1])
    return 2*S*h
    
K = rapportR(r,A)
              

print(K)
--> 5.219770203027197

4. Résultats

Voici le rapport de la résistance par la résistance en courant continu, en fonction de a/δ :

u = np.logspace(-1,2,100)
K = np.zeros(len(u))
N = 1000
for i in range(len(u)):
    r,B = champB(N,u[i])
    r,A = rapportJ(B)
    K[i] = rapportR(r,A)
    
figure(figsize=(8,6))
plot(u,K)
grid()
xlabel(r"$\frac{a}{\delta}$",fontsize=18)
ylabel(r"$\frac{R}{R^{DC}}$",fontsize=18)
xscale('log')
            

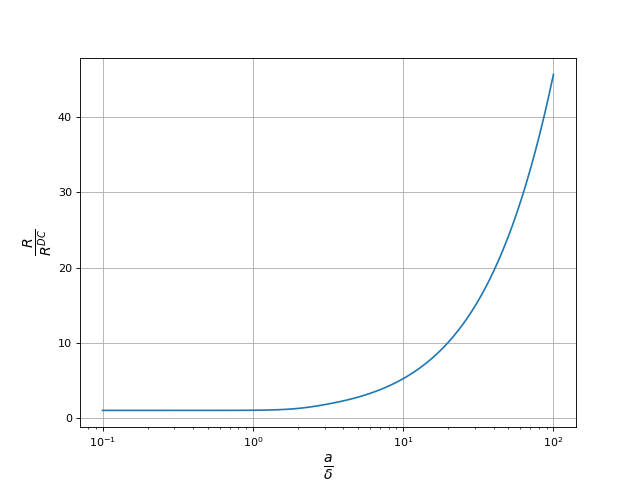rapportR.pdf

Pour un fil de cuivre de rayon a=0,5 mm, voici le rapport des résistances en fonction de la fréquence :

a = 0.5e-3
mu = 4*np.pi*1e-7
g = 6e7
f = np.logspace(3,7,500)
delta = np.sqrt(1/(np.pi*f*mu*g))
u = a/delta
K = np.zeros(len(u))
N = 1000
for i in range(len(u)):
    r,B = champB(N,u[i])
    r,A = rapportJ(B)
    K[i] = rapportR(r,A)
    
figure(figsize=(8,6))
plot(f,K)
grid()
xlabel(r"$f\ (\rm Hz)$",fontsize=18)
ylabel(r"$\frac{R}{R^{DC}}$",fontsize=18)
xscale('log')
title("a = 0,5 mm")
ylim(0,12)
            

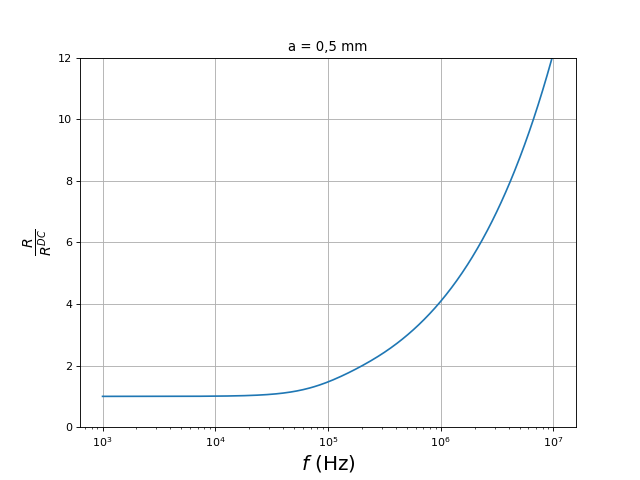rapportR-freq-1.pdf

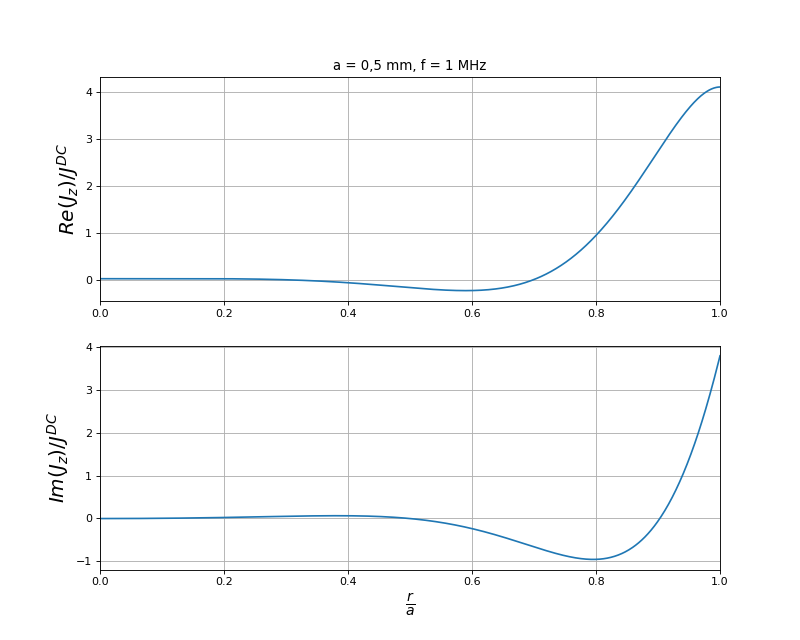
Pour une fréquence de 1 MHz, voici les parties réelle et imaginaire du rapport de la densité de courant dans le fil par la densité en courant continu :

f = 1e6
delta = np.sqrt(1/(np.pi*f*mu*g))
u = a/delta
r,B = champB(N,u)
r,A = rapportJ(B)
figure(figsize=(10,8))
subplot(211)
title("a = 0,5 mm, f = 1 MHz")
plot(r,np.real(A))
grid()
xlim(0,1)
ylabel(r"$Re(J_z)/J^{DC}$",fontsize=18)
subplot(212)
plot(r,np.imag(A))
ylabel(r"$Im(J_z)/J^{DC}$",fontsize=18)
xlabel(r"$\frac{r}{a}$",fontsize=18)
grid()
xlim(0,1)
            

rapportJ-1MHz.pdf

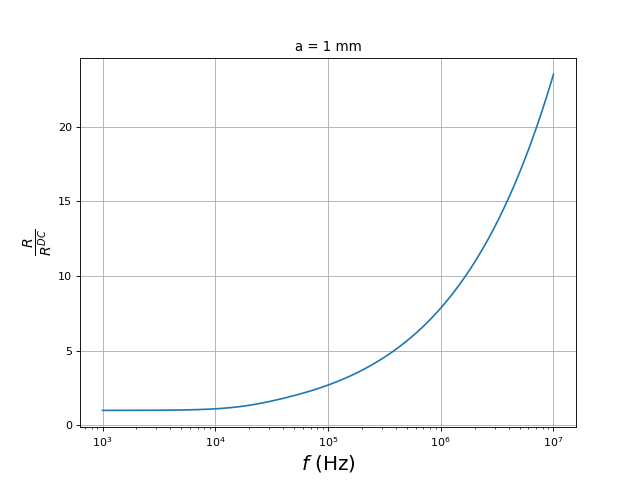
Pour un fil de cuivre de rayon a=1 mm, voici le rapport des résistances en fonction de la fréquence :

a = 1e-3
mu = 4*np.pi*1e-7
g = 6e7
f = np.logspace(3,7,500)
delta = np.sqrt(1/(np.pi*f*mu*g))
u = a/delta
K = np.zeros(len(u))
N = 1000
for i in range(len(u)):
    r,B = champB(N,u[i])
    r,A = rapportJ(B)
    K[i] = rapportR(r,A)
    
figure(figsize=(8,6))
plot(f,K)
grid()
xlabel(r"$f\ (\rm Hz)$",fontsize=18)
ylabel(r"$\frac{R}{R^{DC}}$",fontsize=18)
xscale('log')
title('a = 1 mm')
            

rapportR-freq-2.pdf

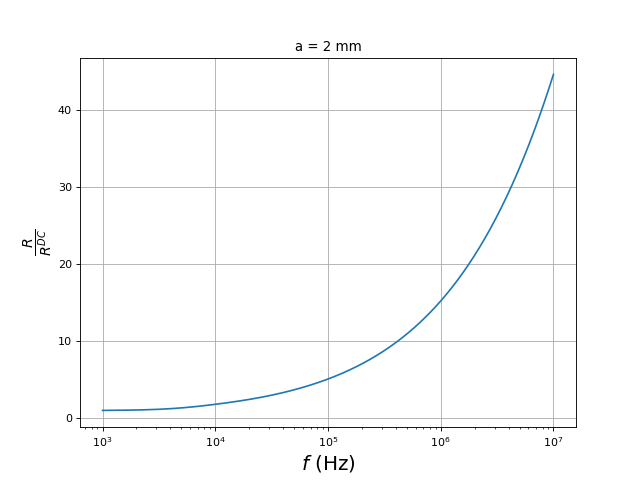
Pour un fil de cuivre de rayon a=2 mm, voici le rapport des résistances en fonction de la fréquence :

a = 2e-3
mu = 4*np.pi*1e-7
g = 6e7
f = np.logspace(3,7,500)
delta = np.sqrt(1/(np.pi*f*mu*g))
u = a/delta
K = np.zeros(len(u))
N = 1000
for i in range(len(u)):
    r,B = champB(N,u[i])
    r,A = rapportJ(B)
    K[i] = rapportR(r,A)
    
figure(figsize=(8,6))
plot(f,K)
grid()
xlabel(r"$f\ (\rm Hz)$",fontsize=18)
ylabel(r"$\frac{R}{R^{DC}}$",fontsize=18)
xscale('log')
title('a = 2 mm')
            

rapportR-freq-3.pdf