Chauffage par induction

1. Introduction

Ce document décrit un modèle de chauffage par induction. Le système étudié comporte une bobine inductrice d'axe (Oz), et une pièce métallique (l'induit) ayant la forme d'un cylindre de révolution de même axe.

Figure pleine page

Le matériau de l'induit est un métal non magnétique (cuivre ou aluminium par exemple) ou un métal ferromagnétique doux dont la relation constitutive est linéaire. On introduit donc une perméabilité magnétique relative μ_r pour le matériau de l'induit et la perméabilité magnétique μ=μ_rμ₀.

L'objectif est de déterminer le courant électrique dans l'induit en régime sinusoïdal puis la puissance dissipée.

2. Mise en équation

Le système est étudié en coordonnées cylindriques et les effets de bord aux extrémités sont négligés (inducteurs et induits de longueur infinie). Le vecteur densité de courant dans l'inducteur, d'épaisseur e, est de la forme :

$${\overrightarrow{J}}_i=J_i\left(t\right){\overrightarrow{u}}_{\theta }\text{(1)}$$

La densité de courant dans l'induit (cylindre de rayon a) est de la forme :

$$\overrightarrow{J}=J_{\theta }(r,t){\overrightarrow{u}}_{\theta }\text{(2)}$$

Dans celui-ci, la loi d'Ohm s'applique :

$$\overrightarrow{J}=\gamma \overrightarrow{E}\text{(3)}$$

Les plans perpendiculaires à l'axe étant des plans de symétrie du courant, on a pour le champ magnétique :

$$\overrightarrow{B}=B_z(r,t){\overrightarrow{u}}_z\text{(4)}$$

Par ailleurs, ce champ est nul à l'extérieur de la bobine. En conséquence, le champ magnétique dans l'espace qui sépare l'induit de l'inducteur (l'entrefer) est :

$$B_z\left(entrefer\right)={\mu }_{0}e{J}_i\left(t\right)\text{(5)}$$

Sur la surface de l'induit (en r=a), il y a continuité de la composante tangentielle de l'excitation magnétique $\overrightarrow{H}=\frac{\overrightarrow{B}}{\mu }$. On a donc la condition limite sur la surface de l'induit :

$$B_z(r=a^{-})=\mu e{J}_i\left(t\right)\text{(6)}$$

Les équations de Maxwell pour le champ électromagnétique dans l'induit sont :

$$\begin{array}{ccc}\hfill & div\overrightarrow{E}=0\hfill & \hfill \text{(7)}\\ \hfill & \overrightarrow{rot}\overrightarrow{E}=-\frac{\partial \overrightarrow{B}}{\partial t}\hfill & \hfill \text{(8)}\\ \hfill & div\overrightarrow{B}=0\hfill & \hfill \text{(9)}\\ \hfill & \overrightarrow{rot}\overrightarrow{B}=\mu \overrightarrow{J}\hfill & \hfill \text{(10)}\end{array}$$

La dernière s'écrit aussi $\overrightarrow{rot}\overrightarrow{B}=\mu \gamma \overrightarrow{E}$, ce qui implique que la divergence de $\overrightarrow{E}$ est nulle et montre que la densité de charge dans l'induit est nulle.

On obtient avec ces équations :

$$\begin{array}{ccc}\hfill & \Delta \overrightarrow{E}=\mu \gamma \frac{\partial \overrightarrow{E}}{\partial t}\hfill & \hfill \text{(11)}\\ \hfill & \Delta \overrightarrow{B}=\mu \gamma \frac{\partial \overrightarrow{B}}{\partial t}\hfill & \hfill \text{(12)}\end{array}$$

On peut chercher à déterminer en premier indifféremment le champ magnétique ou le champ électrique. Le passage de l'un à l'autre se fait avec la relation :

$$\overrightarrow{E}=\frac{1}{\mu \gamma }\overrightarrow{rot}\overrightarrow{B}=-\frac{1}{\mu \gamma }\frac{\partial B_z}{\partial r}{\overrightarrow{u}}_{\theta }\text{(13)}$$

Cette relation n'est valable que dans l'induit. Dans l'entrefer et dans l'induit, on a d'après l'équation de Maxwell-Faraday :

$$\frac{1}{r}\frac{\partial \left(r{E}_{\theta }\right)}{\partial r}=-\frac{d{B}_z}{dt}\text{(14)}$$

Pour le champ électrique nous devons cependant écrire la condition limite en r=a. Celle-ci est donnée par la relation ci-dessus appliquée en r=a :

$$\frac{1}{r}\frac{\partial \left(r{E}_{\theta }\right)}{\partial r}(r=a)=-\mu e\frac{d{J}_i}{dt}\text{(15)}$$

Il s'agit donc d'une condition de type Neumann. Lorsque le champ électrique dans l'induit est déterminé, cette même équation permettra de déterminer le champ électrique dans l'entrefer, sachant que la composante tangentielle de ce champ est continu à la surface de l'induit. Remarquons qu'il est impossible de déterminer le champ électrique dans l'entrefer dès le début car on ne sait rien a priori du flux magnétique dans l'induit.

Nous avons aussi besoin d'une condition limite en r=0. Pour le champ électrique, il s'agit de :

$$E_{\theta }(0,t)=0\text{(16)}$$

Pour le champ magnétique, si nous considérons que la fonction B_z(r) est définie sur un intervalle [-a,a], cette fonction est paire et dérivable en r=0, ce qui conduit à la condition limite suivante :

$$\frac{\partial B_z}{\partial r}(r=0)=0\text{(17)}$$

Finalement, les déterminations de $\overrightarrow{E}$ et de $\overrightarrow{B}$ sont similaires puisque l'équation aux dérivées partielles est la même et dans les deux cas il y a une condition limite de Dirichlet et une condition limite de Neumann. Nous préférons effectuer d'abord la détermination de $\overrightarrow{E}$ puisque la détermination du courant dans l'induit est l'objectif premier.

En explicitant l'opérateur laplacien, et en se plaçant en régime sinusoïdale de pulsation ω, l'équation différentielle à résoudre pour le champ complexe $\underline{E_{\theta }}\left(r\right)$ est :

$$\frac{d}{dr}\left(\frac{1}{r}\right(\frac{d\left(r\underline{E_{\theta }}\right)}{dr}\left)\right)=i\omega \mu \gamma \underline{E_{\theta }}\text{(18)}$$

étant convenu que les grandeurs complexes sont proportionnelles à $e^{i\omega t}$.

Les conditions limites sont :

$$\begin{array}{ccc}\hfill & \underline{E_{\theta }}\left(0\right)=0\hfill & \hfill \text{(19)}\\ \hfill & \frac{1}{r}\frac{\partial \left(r\underline{E_{\theta }}\right)}{\partial r}\left(a\right)=-i\omega \mu e{J}_0\hfill & \hfill \text{(20)}\end{array}$$

où J₀ est l'amplitude de la densité de courant dans l'inducteur.

Pour le champ magnétique, l'équation différentielle est :

$$\frac{1}{r}\frac{d}{dr}\left(r\frac{d\underline{B_z}}{dr}\right)=i\omega \mu \gamma \underline{B_z}\text{(21)}$$

On s'intéressera aussi à la puissance moyenne dissipée dans l'induit (par unité de longueur) :

$$P=\frac{1}{2}\iint \gamma \underline{E_{\theta }}{\underline{E_{\theta }}}^{*}ds=\frac{\gamma }{2}{\int }_0^R\underline{E_{\theta }}{\underline{E_{\theta }}}^{*}2\pi rdr\text{(22)}$$

L'intensité du courant dans l'induit (par unité de longueur) est :

$$\underline{I_2}={\int }_0^a\gamma \underline{E_{\theta }}dr\text{(23)}$$

L'intensité du courant dans l'inducteur (par unité de longueur) est :

$$I_1=J_{0}e\text{(24)}$$

Si L désigne le coefficient d'auto-inductance de l'induit, M le coefficient d'inductance mutuelle et R la résistance de l'induit, on a la relation :

$$\underline{I_2}=\frac{i\omega M{I}_1}{R+iL\omega }\text{(25)}$$

Remarque : il n'est pas attendu que L et M soient indépendants de la fréquence.

3. Modèle bidimensionnel rectiligne

Lorsque la profondeur de pénétration du champ dans le métal est faible devant le rayon de l'induit, une géométrie bidimensionnel rectiligne devrait donner une bonne approximation des champs. Celle-ci est constituée de deux plaques de courant de taille infinie et d'épaisseur e, disposées parallèlement. L'induit est une plaque d'épaisseur 2a. La figure suivante définit le système :

Figure pleine page

L'expression du champ magnétique dans l'entrefer $\mathrm{(5)}$ est inchangée.

Le champ électrique est dans la direction de ${\overrightarrow{u}}_y$ et obéit à l'équation :

$$\frac{d^2\underline{E_y}}{d{x}^2}=i\omega \mu \gamma \underline{E_y}\text{(26)}$$

avec les conditions limites :

$$\begin{array}{ccc}\hfill & \underline{E_y}\left(0\right)=0\hfill & \hfill \text{(27)}\\ \hfill & \frac{d\underline{E_y}}{dx}\left(a\right)=-i\omega \mu e{J}_0\hfill & \hfill \text{(28)}\end{array}$$

La résolution de cette équation se fait sans difficulté et conduit à :

$$\underline{E_y}\left(x\right)=-\frac{1+i}{2}\delta \omega \mu e{J}_0\frac{sinh\left(\frac{1+i}{\delta }x\right)}{cosh\left(\frac{1+i}{\delta }a\right)}\text{(29)}$$

avec :

$$\delta =\sqrt{\frac{2}{\omega \gamma \mu }}\text{(30)}$$

On peut aussi écrire $\mu e{J}_0={\mu }_r{B}_0$ où B₀ est l'intensité du champ magnétique à l'intérieur de l'inducteur en l'absence d'induit (égal au champ dans l'entrefer).

Cette solution devrait s'appliquer à la géométrie cyclindrique (en remplaçant x par r) lorsque $\delta \ll a$. Dans ce cas, on a :

$$\underline{E_y}\left(x\right)\approx -\frac{1+i}{2}\delta \omega \mu e{J}_{0}exp(-\frac{1+i}{\delta }(a-x))\text{(31)}$$

La puissance moyenne dissipée par unité de surface de l'induit est :

$$P=2{\int }_0^a\frac{1}{2}\gamma |\underline{E_y}\left(x\right){|}^{2}dx=\frac{1}{4}\gamma \delta {\left(\delta \omega \mu e{J}_0\right)}^2=\frac{1}{\sqrt{2}}{\omega }^{\frac{1}{2}}{\gamma }^{-\frac{1}{2}}{\mu }^{\frac{1}{2}}{e}^2{J}_0^2\text{(32)}$$

La puissance dissipée est donc proportionnelle à la racine carrée de la fréquence et à la racine carrée de la perméabilité magnétique.

L'équation de Maxwell-Faraday permet de calculer le champ magnétique dans l'induit :

$$\underline{B_z}=-\frac{1}{i\omega }\frac{d\underline{E_y}}{dx}=\mu e{J}_0\frac{cosh\left(\frac{1+i}{\delta }x\right)}{cosh\left(\frac{1+i}{\delta }a\right)}\text{(33)}$$

Lorsque $\delta \ll a$ on a :

$$\underline{B_z}\approx {\mu }_r{B}_{0}exp(-\frac{1+i}{\delta }(a-x))\text{(34)}$$

La pertinence de ce modèle peut sembler à première vue compromise par l'hypothèse d'une densité de courant uniforme dans l'inducteur. En réalité, la densité de courant dans l'inducteur ne peut être uniforme et présente évidemment un effet de peau similaire à celui qu'on obtient dans l'induit. Cependant, le champ magnétique dans l'entrefer

$$B_0={\mu }_{0}e{J}_0\text{(35)}$$

ne dépend que de l'intensité du courant dans l'inducteur et pas de la répartition du courant. En conséquence les résultats obtenus dans l'induit sont toujours valable si le vecteur densité de courant n'est pas uniforme dans l'inducteur. Il faut remarquer que cette conclusion est valable dans cette géométrie particulière et aussi dans la géométrie cylindrique (cylindre infini) mais qu'elle ne peut se généraliser à tout type de géométrie : dans le cas général, le champ magnétique créé par un courant dans un conducteur dépend, au moins au voisinage de celui-ci, de la répartition du courant dans le conducteur.

4. Résolution par différences finies

Développons le laplacien dans l'équation $\mathrm{(18)}$ :

$$\frac{1}{r}\frac{d{E}_{\theta }}{dr}-\frac{E_{\theta }}{r^2}+\frac{d^2{E}_{\theta }}{d{r}^2}=i\omega \mu \gamma E_{\theta }\text{(36)}$$

où la grandeur complexe est simplement notée E_θ.

L'introduction de la variable réduite r'=r/a conduit à :

$$\frac{1}{r\text{'}}\frac{d{E}_{\theta }}{dr\text{'}}-\frac{E_{\theta }}{r{\text{'}}^2}+\frac{d^2{E}_{\theta }}{dr{\text{'}}^2}=i\omega \mu \gamma a^2{E}_{\theta }\text{(37)}$$

Les conditions limites sont :

$$E_{\theta }\left(0\right)=0\text{(38)}$$

et, d'après $\mathrm{(15)}$ :

$$\frac{E_{\theta }\left(a\right)}{a}+\frac{d{E}_{\theta }}{dr}\left(a\right)=-i\omega \mu e{J}_0\text{(39)}$$

ou bien avec la variable réduite :

$$E_{\theta }\left(1\right)+\frac{d{E}_{\theta }}{dr\text{'}}\left(1\right)=-i\omega \mu ea{J}_0\text{(40)}$$

où J₀ désigne l'amplitude de la densité de courant dans l'inducteur.

On pose :

$$\begin{array}{ccc}\hfill & A=\omega \mu \gamma a^2\hfill & \hfill \text{(41)}\\ \hfill & C=\omega a{\mu }_r{\mu }_{0}e{J}_0=\omega a{\mu }_r{B}_0\hfill & \hfill \text{(42)}\end{array}$$

où B₀ est l'amplitude du champ magnétique dans l'entrefer, qui est aussi celle du champ dans la bobine en l'absence de l'induit.

La discrétisation de l'intervalle [0,1] est effectuée de la manière suivante :

$$\begin{array}{ccc}\hfill & r{\text{'}}_n=nh,n=0,1\dots N-1\hfill & \hfill \text{(43)}\\ \hfill & h=\frac{1}{N-1}\hfill & \hfill \text{(44)}\end{array}$$

L'écriture des dérivées sous forme de différences finies conduit à (pour $n=1,\dots N-2$) :

$$\frac{1}{nh}\frac{E_{n+1}-E_{n-1}}{2h}-\frac{E_n}{{\left(nh\right)}^2}+\frac{E_{n+1}+E_{n-1}-2E_n}{h^2}=iA{E}_n\text{(45)}$$

qui s'écrit aussi

$$(\frac{1}{h^2}-\frac{1}{2n{h}^2})E_{n-1}-(\frac{2}{h^2}+\frac{1}{{\left(nh\right)}^2}+iA)E_n+(\frac{1}{h^2}+\frac{1}{2n{h}^2})E_{n+1}=0\text{(46)}$$

ou encore :

$$a_n{E}_{n-1}+b_n{E}_n+c_n{E}_{n+1}=0\text{(47)}$$

avec :

$$\begin{array}{ccc}\hfill & a_n=1-\frac{1}{2n}\hfill & \hfill \text{(48)}\\ \hfill & b_n=-(2+\frac{1}{n^2}+iA{h}^2)\hfill & \hfill \text{(49)}\\ \hfill & c_n=1+\frac{1}{n^2}\hfill & \hfill \text{(50)}\end{array}$$

et les conditions limites s'écrivent :

$$\begin{array}{ccc}\hfill & E_0=0\hfill & \hfill \text{(51)}\\ \hfill & E_{N-1}+\frac{1}{h}(E_{N-1}-E_{N-2})=-iC\hfill & \hfill \text{(52)}\end{array}$$

Nous obtenons N-2 équations et 2 conditions limites, soit N équations linéaires pour N inconnues. Il s'agit d'un système tridiagonal :

$$\left(\begin{array}{cccccccc}\hfill 1\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill a_1\hfill & \hfill b_1\hfill & \hfill c_1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill a_2\hfill & \hfill b_2\hfill & \hfill c_2\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill a_{N-2}\hfill & \hfill b_{N-2}\hfill & \hfill c_{N-2}\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill -1\hfill & \hfill h+1\hfill \end{array}\right)\left(\begin{array}{c}\hfill E_0\hfill \\ \hfill E_1\hfill \\ \hfill E_2\hfill \\ \hfill \hfill \\ \hfill \hfill \\ \hfill E_{N-2}\hfill \\ \hfill E_{N-1}\hfill \end{array}\right)=\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill \hfill \\ \hfill \hfill \\ \hfill 0\hfill \\ \hfill -iCh\hfill \end{array}\right)\text{(53)}$$

Les trois triagonales sont :

$$\begin{array}{ccc}\hfill & 0,0,c_1,c_2,\dots c_{N-2}\hfill & \hfill \text{(54)}\\ \hfill & 1,b_1,b_2,\dots b_{N-2},h+1\hfill & \hfill \text{(55)}\\ \hfill & a_1,a_2,\dots a_{N-2},-1,0\hfill & \hfill \text{(56)}\end{array}$$

Afin que les trois diagonales aient N éléments, on a ajouté un zéro au début de la première et un zéro à la fin de la dernière.

Un système tridiagonal peut être résolu efficacement par un algorithme d'élimination spécifique en O(N) (voir Équation de diffusion à une dimension). La fonction scipy.linalg.solve_banded permet de résoudre efficacement un système avec une matrice bande, donc en particulier une matrice tridiagonale. La matrice doit être définie avec les trois diagonales comme écrites ci-dessus. On doit aussi préciser le nombre maximal de termes non nul au dessus de la diagonale principale (ici 1) et le nombre maximal en dessous (ici 1).

from scipy.linalg import solve_banded
import numpy as np
from matplotlib.pyplot import *
	
	
def champE(A,C,N,cyl=1):
	#cyl = 1 : géométrie cylindriques
	#cyl = 0 : géométrie rectiligne
	P = np.zeros(N,dtype=np.complex64)
	h = 1/(N-1)
	h2 = h**2
	P[N-1] = -1j*C*h
	D1 = np.zeros(N,dtype=np.complex64)
	D2 = np.zeros(N,dtype=np.complex64)
	D3 = np.zeros(N,dtype=np.complex64)
	for n in range(1,N-1):
		D1[n+1] = 1+cyl/(2*n)
	D2[0] = 1
	D2[N-1] = cyl*h+1
	for n in range(1,N-1):
		D2[n] = -2-1j*A*h2-cyl/(n**2)
	for n in range(1,N-1):
		D3[n-1] = 1-cyl/(2*n)
	D3[N-2] = -1
	M = np.array([D1,D2,D3])
	E = solve_banded((1,1),M,P)
	r = np.arange(N)*h
	dr = r[1]-r[0]
	p = 0.5*E*np.conjugate(E)
	P = np.sum(p*r)*dr*2*np.pi
	I2 = np.sum(E)*dr
	return r,E,np.real(p),np.real(P),I2
			

La fonction champE permet aussi de résoudre par différences finies le problème bidimensionnel rectiligne (avec cyl=0), ce qui permet de valider la méthode par comparaison avec la solution formelle.

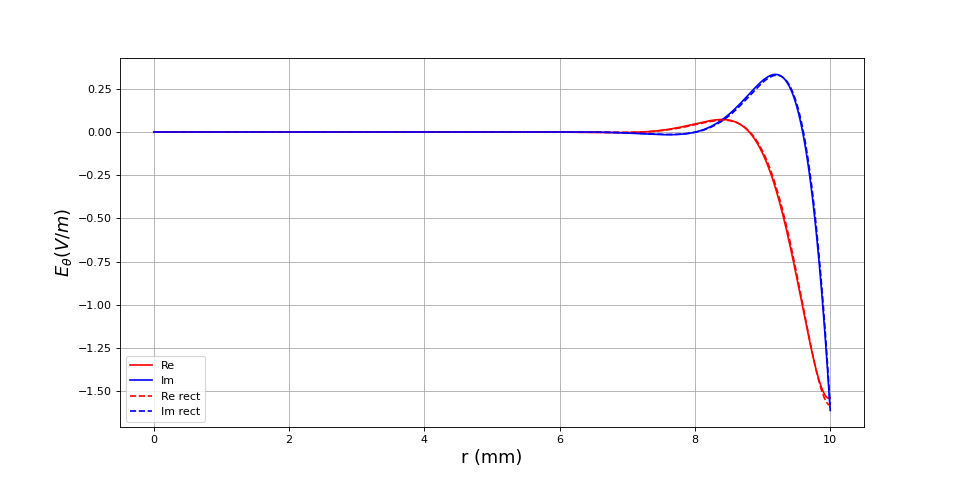
Voici un exemple : un tube en fer de rayon 1 cm, à la fréquence 100 Hz. Les parties réelle et imaginaire du champ électrique sont tracées pour la géométrie cylindrique résolue par différence finie et les mêmes grandeurs pour le modèle rectiligne.

a = 0.01
gamma = 1e7
mu0 = 4*np.pi*1e-7
mur=1000
mu = mur*mu0
B0 = 0.01
I1 = B0/mu0
f = 100
w = 2*np.pi*f 
A = w*mu*gamma*a**2
C = w*a*B0*mur
delta = np.sqrt(2/(mu*gamma*w))
N = 1000
r,E,p,P,I2 = champE(A,C,N)
P *= gamma
p*=gamma
E_rect = -(1+1j)/2*delta*w*mur*B0*np.sinh((1+1j)/delta*r*a)/np.cosh((1+1j)/delta*a)
figure(figsize=(12,6))
plot(r*a*1000,np.real(E),'r',label='Re')
plot(r*a*1000,np.imag(E),'b-',label='Im')
plot(r*a*1000,np.real(E_rect),'r--',label='Re rect')
plot(r*a*1000,np.imag(E_rect),'b--',label='Im rect')
xlabel("r (mm)",fontsize=16)
ylabel(r"$E_{\theta} (V/m)$",fontsize=16)
grid()
legend(loc='lower left')
		

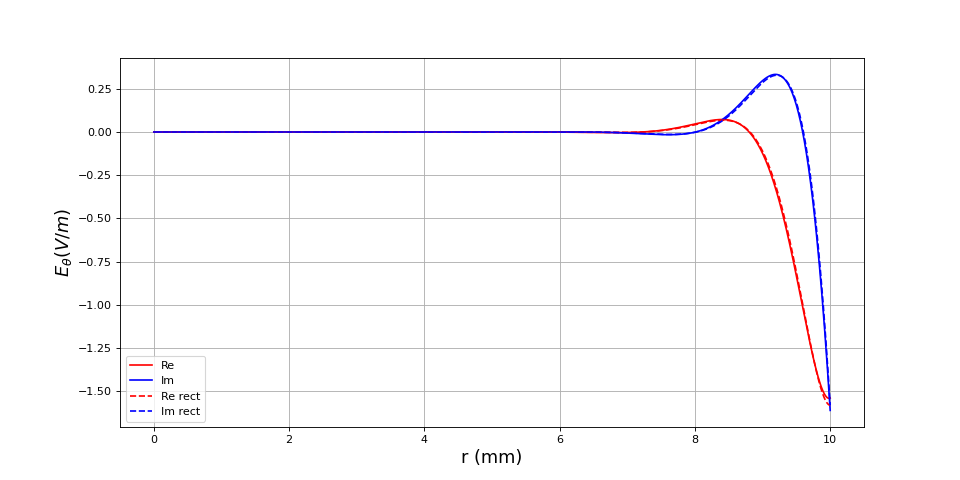figA.pdf

Les courbes obtenues sont quasi identiques à celles de la géométrie rectiligne.

La profondeur de pénétration (en mm) est :

print(delta*1e3)
--> 0.5032921210448703

Puissance dissipée par unité de longueur (en kW) :

print(P*1e-3)
--> 4003.0711510918636

print(I2/I1)
--> (-1.0189114214780407e-05-2.023209178338232e-07j)

Le rapport I₂/I₁ est quasi réel, ce qui montre que, à cette fréquence, $R\ll L\omega$. La valeur négative de la partie réelle indique que le courant dans l'induit est de sens opposé au courant dans l'inducteur, ce qui est bien attendu d'après la loi de Lenz.

Voici le résultat pour une fréquence de 10 kHz :

f = 10e3
w = 2*np.pi*f 
A = w*mu*gamma*a**2
C = w*a*B0*mur
delta = np.sqrt(2/(mu*gamma*w))
N=2000
r,E,p,P,I2 = champE(A,C,N)
P *= gamma
p*=gamma
I2 *=gamma
E_rect = -(1+1j)/2*delta*w*mur*B0*np.sinh((1+1j)/delta*r*a)/np.cosh((1+1j)/delta*a)
figure(figsize=(12,6))
plot(r*a*1000,np.real(E),'r',label='Re')
plot(r*a*1000,np.imag(E),'b-',label='Im')
plot(r*a*1000,np.real(E_rect),'r--',label='Re rect')
plot(r*a*1000,np.imag(E_rect),'b--',label='Im rect')
xlim(9.0,10)
xlabel("r (mm)",fontsize=16)
ylabel(r"$E_{\theta} (V/m)$",fontsize=16)
grid()
legend(loc='lower left')
		

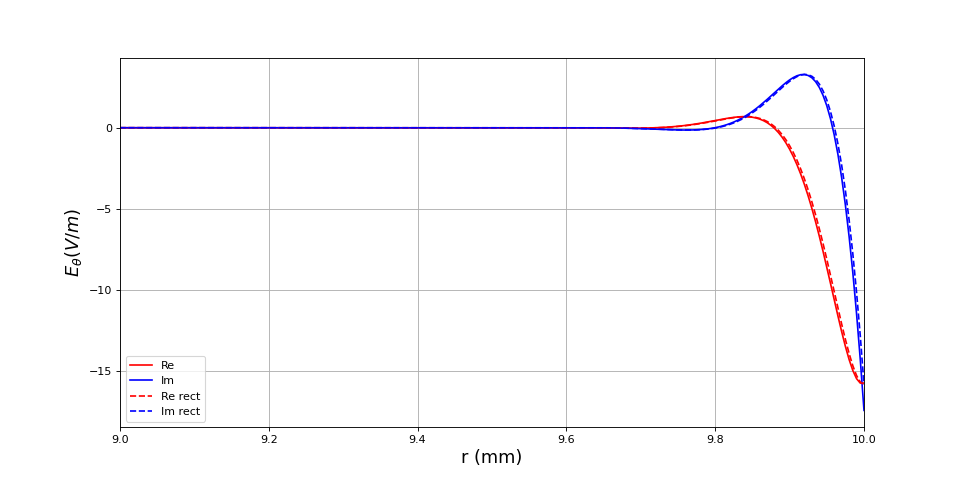figB.pdf

print(delta*1e3)
--> 0.05032921210448704

print(P*1e-3)
--> 47953.4184474598

print(I2/I1)
--> (-109.8601127176706-10.94645337769677j)

Le champ pénètre 10 fois moins dans le métal mais son amplitude est beaucoup plus grande. La puissance dissipée est environ 15 fois plus grande.

La résistance de l'induit a beaucoup augmenté puisque la partie imaginaire de I₂ n'est plus petite devant la partie réelle alors que $L\omega$ a été multiplié par 100. L'augmentation de la résistance avec la fréquence est une conséquence de la diminution de la profondeur de pénétration.

Voici la densité volumique de puissance en fonction de r au voisinage de la surface :

figure(figsize=(12,6))
plot(r*a*1000,p)
grid()
xlabel("r (mm)",fontsize=16)
ylabel(r"$p\ (\rm W\cdot m^{-3})$",fontsize=16)
xlim((a-3*delta)*1e3,a*1e3)
		

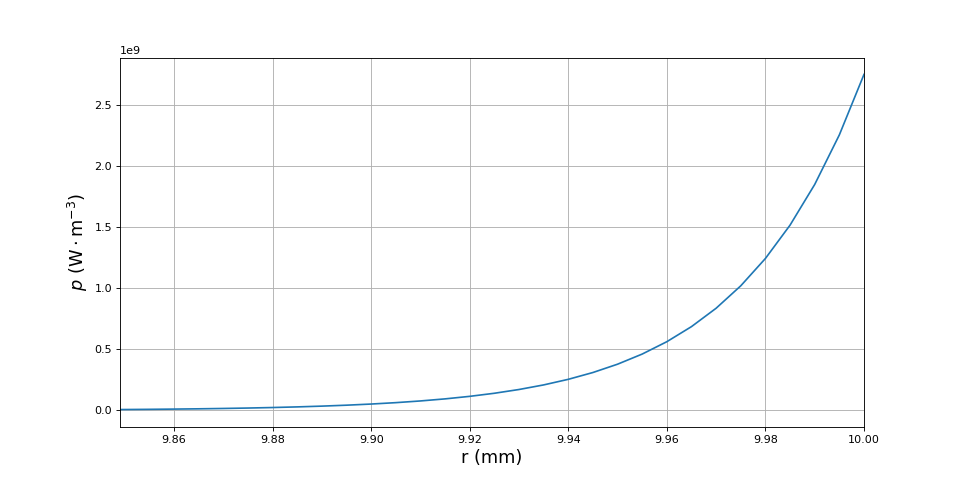figC.pdf

L'effet thermique de cette puissance doit être évalué au moyen de l'équation de diffusion thermique :

$$\rho c_p\frac{\partial T}{\partial t}=\lambda \frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial T}{\partial r}\right)+p\text{(57)}$$

Dans les deux exemples précédents, la profondeur de pénétration est beaucoup plus petite que le rayon de l'induit, ce qui fait que la solution bidimensionnelle rectiligne est valable (puisque le champ est non nul seulement au voisinage de la surface). Pour un matériau non magnétique à basse fréquence, voyons une situation où la profondeur de pénétration est du même ordre de grandeur que a :

a = 0.01
gamma = 1e7
mu0 = 4*np.pi*1e-7
mur=1
mu = mur*mu0
B0 = 0.01
I1 = B0/mu0
f = 100
w = 2*np.pi*f 
A = w*mu*gamma*a**2
C = w*a*B0*mur
delta = np.sqrt(2/(mu*gamma*w))
N = 1000
r,E,p,P,I2 = champE(A,C,N)
P *= gamma
p*=gamma
E_rect = -(1+1j)/2*delta*w*mur*B0*np.sinh((1+1j)/delta*r*a)/np.cosh((1+1j)/delta*a)
figure(figsize=(12,6))
plot(r*a*1000,np.real(E),'r',label='Re')
plot(r*a*1000,np.imag(E),'b-',label='Im')
plot(r*a*1000,np.real(E_rect),'r--',label='Re rect')
plot(r*a*1000,np.imag(E_rect),'b--',label='Im rect')
xlabel("r (mm)",fontsize=16)
ylabel(r"$E_{\theta} (V/m)$",fontsize=16)
grid()
legend(loc='lower left')
		

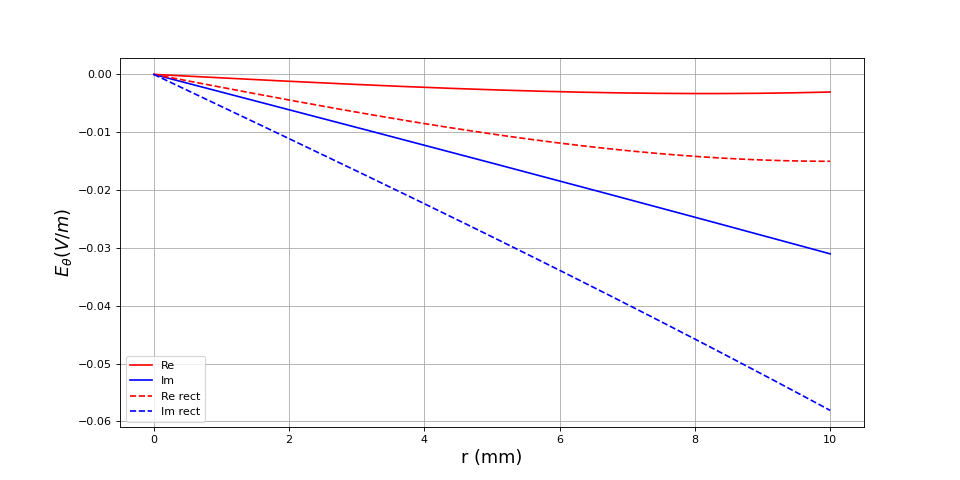figD.pdf

Dans ce cas, la solution en géométrie cylindrique est très différente de la solution en géométrie rectiligne.

print(delta*1e3)
--> 15.915494309189533

print(P*1e-3)
--> 7.634946679903085

La puissance dissipée est 500 fois moins grande que celle pour le matériau ferromagnétique (de perméabilité relative 1000) avec la même conductivité et la même fréquence (voir plus haut) et sa valeur est insuffisante pour obtenir un effet thermique notable. Pour chauffer un matériau non magnétique, il faut absolument utiliser une grande fréquence :

a = 0.01
gamma = 1e7
mu0 = 4*np.pi*1e-7
mur=1
mu = mur*mu0
B0 = 0.01
I1 = B0/mu0
f = 100e3
w = 2*np.pi*f 
A = w*mu*gamma*a**2
C = w*a*B0*mur
delta = np.sqrt(2/(mu*gamma*w))
N = 1000
r,E,p,P,I2 = champE(A,C,N)
P *= gamma
p*=gamma
E_rect = -(1+1j)/2*delta*w*mur*B0*np.sinh((1+1j)/delta*r*a)/np.cosh((1+1j)/delta*a)
figure(figsize=(12,6))
plot(r*a*1000,np.real(E),'r',label='Re')
plot(r*a*1000,np.imag(E),'b-',label='Im')
plot(r*a*1000,np.real(E_rect),'r--',label='Re rect')
plot(r*a*1000,np.imag(E_rect),'b--',label='Im rect')
xlabel("r (mm)",fontsize=16)
ylabel(r"$E_{\theta} (V/m)$",fontsize=16)
grid()
legend(loc='lower left')
		

figE.pdf

print(delta*1e3)
--> 0.5032921210448703

print(P*1e-3)
--> 4003.0711510918636

À cette fréquence de 100 kHz on obtient une puissance à peine plus grande que pour le matériau ferromagnétique à 100 Hz. D'après le modèle bidimensionnel rectiligne, lorsque $\delta \ll a$, La puissance dissipée devrait être proportionnelle à la racine carrée de la perméabilité relative et à la racine carrée de la fréquence. On retrouve bien cette dépendance (à peu près) : il faut multiplier la fréquence par 1000 afin de compenser une diminutation de la permabilité magnétique d'un facteur 1000.

5. Induit creux

On s'intéresse au cas où l'induit est un tube :

Figure pleine page

Dans l'induit (b<r<a), on a :

$$\begin{array}{ccc}\hfill & \Delta \overrightarrow{E}=\mu \gamma \frac{\partial \overrightarrow{E}}{\partial t}\hfill & \hfill \text{(58)}\\ \hfill & \Delta \overrightarrow{B}=\mu \gamma \frac{\partial \overrightarrow{B}}{\partial t}\hfill & \hfill \text{(59)}\end{array}$$

Dans le creux du tube (r<b), on a :

$$\begin{array}{ccc}\hfill & \Delta \overrightarrow{E}=\overrightarrow{0}\hfill & \hfill \text{(60)}\\ \hfill & \Delta \overrightarrow{B}=\overrightarrow{0}\hfill & \hfill \text{(61)}\end{array}$$

Il est impossible d'obtenir a priori une condition limite pour le champ électrique en r=b. En effet cette condition serait de la forme $\mathrm{(15)}$ et nécessiterait donc la connaissance du champ magnétique en r=b; or le champ magnétique dans le creux ne peut être calculé a priori. Il faut donc résoudre l'équation aux dérivées partielles sur l'intervalle [0,a], sachant que le champ électrique est partout continu.

La résolution du problème bidimensionnel rectiligne se fait sans difficulté. Dans le creux on a :

$$\underline{E_y}\left(x\right)=C_{1}x\text{(62)}$$

où C₁ est une constante. Dans l'induit, on a :

$$\underline{E_y}\left(x\right)=C_{2}exp\left(\frac{1+i}{\delta }x\right)+C_{3}exp(-\frac{1+i}{\delta }x)\text{(63)}$$

La fonction $\underline{E_y}$ est impaire donc C₂=-C₃ :

$$\underline{E_y}\left(x\right)=C_2\left(exp\right(\frac{1+i}{\delta }x)-exp(-\frac{1+i}{\delta }x\left)\right)\text{(64)}$$

En conséquence, il ne reste qu'une constante inconnue pour le champ dans le métal et celle-ci est déterminée, comme précédemment, avec la condition limite en r=a. Il s'en suit que la solution établie précédemment est encore valable lorsque l'induit est creux. On a donc pour b<r<a :

$$\underline{E_y}\left(x\right)=-\frac{1+i}{2}\delta \omega \mu b{J}_0\frac{sinh\left(\frac{1+i}{\delta }x\right)}{cosh\left(\frac{1+i}{\delta }a\right)}\text{(65)}$$

La continuité du champ électrique permet d'obtenir l'autre constante :

$$C_1=-\frac{1+i}{2}\frac{\delta \omega \mu e{J}_0}{b}\frac{sinh\left(\frac{1+i}{\delta }b\right)}{cosh\left(\frac{1+i}{\delta }a\right)}\text{(66)}$$

Dans le creux, l'équation de Maxwell-Faraday s'écrit :

$$\frac{d\underline{E_y}}{dx}=-i\omega \underline{B_z}\text{(67)}$$

Le champ magnétique dans le creux est donc uniforme :

$$\underline{B_z}=\frac{i{C}_1}{\omega }=\frac{1-i}{2}\frac{\delta \mu e{J}_0}{b}\frac{sinh\left(\frac{1+i}{\delta }b\right)}{cosh\left(\frac{1+i}{\delta }a\right)}\text{(68)}$$

L'amplitude du champ dans le creux est :

$$B_1=\frac{\delta {\mu }_r{B}_0}{b\sqrt{2}}{e}^{-\frac{a-b}{\delta }}\text{(69)}$$

où B₀ est l'amplitude en l'absence d'induit. Ce résultat est intéressant car il peut faire l'objet d'une vérification expérimentale. Il est en effet aisé de mesurer B₀ et B₁. Si la profondeur de pénétration est petite devant l'épaisseur du tube, le champ magnétique dans l'induit est négligeable (phénomène d'écrantage). L'étude expérimentale de B₁ en fonction de la fréquence devrait être un bon moyen de valider ce modèle.