Bobine épaisse : différences finies

1. Introduction

Ce document présente le calcul du champ magnétique créé par une bobine à symétrie axiale, par résolution numérique de l'équation de Poisson pour le potentiel vecteur.

Le calcul du coefficient d'auto-inductance de la bobine est aussi effectué.

La résolution numérique de l'équation de Poisson par la méthode des différences finies est expliquée dans Équation de Poisson à deux dimensions. La discrétisation de l'équation est expliquée dans Discrétisation de l'équation de Poisson vectorielle.

Le module python utilisé est présenté dans Équation de Poisson : programme Python.

Un calcul similaire par la méthode des éléments finis est présenté dans Bobine épaisse : éléments finis.

2. Mise en équation

On considère une bobine à symétrie axiale, modélisée par une densité de courant volumique orthoradiale.

Figure pleine page

La bobine est un tore de section rectangulaire, de longueur $\ell$, d'épaisseur e et de rayon moyen a.

Ce modèle peut aussi s'appliquer à un induit de forme torique, avec une densité de courant orthoradiale.

Le potentiel vecteur vérifie l'équation de Poisson en coordonnées cylindriques :

$${\nabla }^2\left(A_{\theta }\overrightarrow{e_{\theta }}\right)=-{\mu }_0{J}_{\theta }\overrightarrow{e_{\theta }}\text{(1)}$$ $$\frac{\partial }{\partial r}\left(\frac{1}{r}\frac{\partial \left(r{A}_{\theta }\right)}{\partial r}\right)+\frac{{\partial }^2{A}_{\theta }}{\partial z^2}=-{\mu }_0{J}_{\theta }\text{(2)}$$

Le champ magnétique (rotationnel du potentiel vecteur) est :

$$\begin{array}{ccc}\hfill & B_r=-\frac{\partial A_{\theta }}{\partial z}\hfill & \hfill \text{(3)}\\ \hfill & B_z=\frac{1}{r}\frac{\partial \left(r{A}_{\theta }\right)}{\partial r}\hfill & \hfill \text{(4)}\end{array}$$

La densité de courant $J_{\theta }$ est uniforme. L'intensité du courant à travers une section du tore est :

$$I=J_{\theta }e\ell \text{(5)}$$

La résolution numérique sera faite avec un terme de source égal à -1 et une largeur de domaine égale à 1. Soit L_d la largeur réelle du domaine. Le champ $A_{\theta }$ (sans dimensions) obtenu par ce calcul devra être multiplié par :

$$A_0={\mu }_0{J}_{\theta }{L}_d^2={\mu }_0\frac{I}{e\ell }{L}_d^2\text{(6)}$$

afin d'obtenir un potentiel vecteur en teslas mètres. Les champs $(B_r,B_z)$ devrons être multipliés par :

$$B_0=\frac{A_0}{L_d}={\mu }_0\frac{I}{e\ell }{L}_d\text{(7)}$$

afin d'obtenir des valeurs en teslas.

L'énergie magnétique (énergie à fournir pour établir le champ) s'écrit :

$$E_m=\frac{1}{2}{\iiint }_V\overrightarrow{J}\cdot \overrightarrow{A}dv=\frac{1}{2}{\iiint }_V{J}_{\theta }{A}_{\theta }dv\text{(8)}$$

où V désigne le volume de la bobine (volume du tore). L'énergie s'exprime aussi à l'aide du coefficient d'auto-inductance :

$$E_m=\frac{1}{2}L{I}_f^2\text{(9)}$$

où I_f est l'intensité du courant dans le fil de la bobine. Si celle-ci est constituée de N spires, on a I=NI_f.

Il s'en suit que l'auto-inductance L peut être calculée par :

$$L={\iiint }_V{J}_{\theta }{A}_{\theta }dv\text{(10)}$$

avec $J_{\theta }=\frac{N}{e\ell }$ (densité de courant si I_f=1 A). En toute rigueur, il s'agit d'un calcul d'auto-inductance en régime quasi stationnaire de très basse fréquence, où on suppose que la densité de courant est uniforme dans la section transversale des fils. L'auto-inductance s'écrit donc :

$$L=\frac{2\pi N}{e\ell }\iint A_{\theta }(z,r)rdrdz\text{(11)}$$

où l'intégrale est calculée sur une section rectangulaire du tore.

La discrétisation du domaine de calcul est définie par $z_i=i\Delta z$ et $r_j=j\Delta r$, comme expliqué dans Discrétisation de l'équation de Poisson vectorielle. Une approximation de l'intégrale peut être obtenue par la méthode des rectangles :

$$L\approx \frac{2\pi N}{e\ell }{\mu }_0\frac{N}{e\ell }{L}_d^2\sum _{i,j}{A}_{i,j}j{\left(\Delta r\right)}^2\Delta z\text{(12)}$$

où A_i,j sont les valeurs du potentiel vecteur obtenues avec un terme de source égal à -1 et une largeur de domaine égale à 1.

On obtient finalement :

$$L=2\pi {\mu }_0\frac{L_d^2}{{\left(e\ell \right)}^2}{\left(\Delta r\right)}^2\Delta z{N}^2\sum _{i,j}{A}_{i,j}j\text{(13)}$$

On calculera l'auto-inductance pour N=1, valeur qui ne dépend pas du diamètre du fil pour une bobine de taille donnée, puis on multipliera par N², qui dépend du diamètre du fil. Pour un fil de diamètre d, le nombre de spires est égal au nombre de spires par couche multiplié par le nombre de couches :

$$N=\frac{\ell }{d}\frac{e}{d}\text{(14)}$$

Ce calcul d'auto-inductance repose sur la modélisation du courant dans une section transversale du tore par un courant uniforme. Il ne tient pas compte du fait que la densité de courant et nulle de l'air entre les fils, qui a un effet à la fois sur la densité de courant et sur le potentiel vecteur dans les fils.

3. Bobine de faible longueur

from matplotlib.pyplot import *
import math
import numpy
import poisson.main
            

Le domaine de calcul (voir figure ci-dessus) comporte 2ⁿ⁺¹ mailles dans la direction de l'axe de symétrie z et 2ⁿ mailles dans la direction radiale. Pour définir les objets, on utilise un maillage réduit de 2^p+1 par 2^p. On commence par créer le maillage, discrétiser le laplacien et fixer des conditions limites de Dirichlet sur les bords du domaine (potentiel nul sur les bords). La largeur du domaine est 1 et on considère que c'est aussi sa largeur en mètres.

n=10
p=6
levels = n-p+1
width,height = 1.0,0.5 #taille du domaine en mètres
bobine=poisson.main.PoissonAxialVect(p+1,p,levels,width,height,x0=-0.5,y0=0.0)
bobine.laplacien()
bobine.dirichlet_borders(0.0)
echelle = width/2**(p+1) # echelle de la maille réduite en mètres
            

Pour définir le courant (la source), on se place sur le maillage réduit.

ci,cj = 2**(p+1)//2,2**(p+1)//16 # centre du rectangle
w = h = 2 # demi-largeur et demi-hauteur du rectangle
bobine.source_rect(ci,cj,w,h,-1.0)
e = 2*h*echelle
l = 2*w*echelle
a = cj*echelle
            

print(e)
--> 0.03125

print(a)
--> 0.0625

Compte tenu de la taille du domaine complet (1 par 1), une unité du maillage réduit correspond à une longueur de 1/128. Si on considère que la taille du domaine est donnée en mètres, on a donc pour ces valeurs : $e=\ell =1/32m$ et $a=1/16m$.

La taille du domaine doit être assez grande par rapport au rayon du tore pour que l'effet des bords du domaine soit négligeable dans la région qui nous intéresse (disons la moitié du domaine).

La discrétisation de l'équation de Poisson conduit à un système d'équations linéaires qui est résolu par la méthode itérative de Gauss-Seidel (avec sur-relaxation) ou bien par la méthode multigrilles avec itérations de Gauss-Seidel (beaucoup plus rapide).

#result=bobine.opencl_iterations_norm(100,60,omega=1.95)
result=bobine.multigrid_full_norm(2,levels,100,2,2)
            

Le tracé de la norme en fonction du nombre d'itérations permet de suivre la convergence :

figure(figsize=(8,5))
plot(result[0],result[1]) 
xlabel('niter')  
ylabel('norm')
grid() 
            

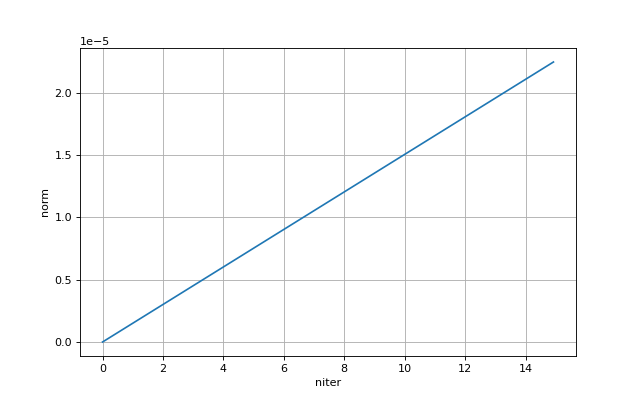plotA.pdf

On récupère le potentiel et les composantes du champ magnétique. L'argument symetry permet d'obtenir le champ sur un domaine comportant aussi les valeurs négatives de r (domaine complet). Lorsqu'il vaut 1, le champ obtenu est pair. Lorsqu'il vaut -1, le champ est impair.

Atheta=bobine.get_array(symetry=-1)
Br=-bobine.get_derivZ(symetry=-1)
Bz=bobine.get_derivRUR(symetry=1)
            

Tracé des lignes d'égale valeur de A_θ :

figure(figsize=(8,8))
extent=bobine.get_extent(symetry=1)
contour(Atheta,20,extent=extent)
imshow(~bobine.get_mask(symetry=1),extent=extent,alpha=0.5, cmap=cm.gray)
xlabel('z')
ylabel('r')
grid()
            

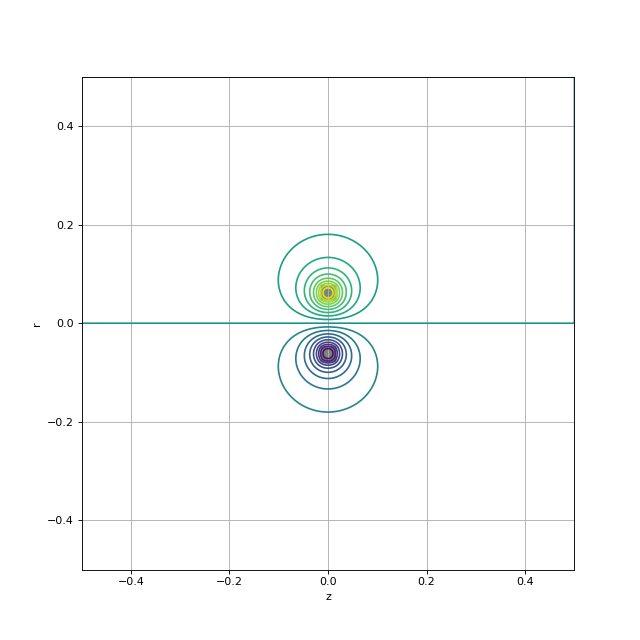plotB.pdf

Rermarque : ces lignes d'isovaleur de A_θ ne sont pas les lignes du champ magnétique.

Tracé du champ sur l'axe :

  
figure(figsize=(10,5))
z = bobine.get_z()
plot(z,Bz[2**n,:])
xlabel('z')
ylabel(r'$B_z/B_0$')
grid()
            

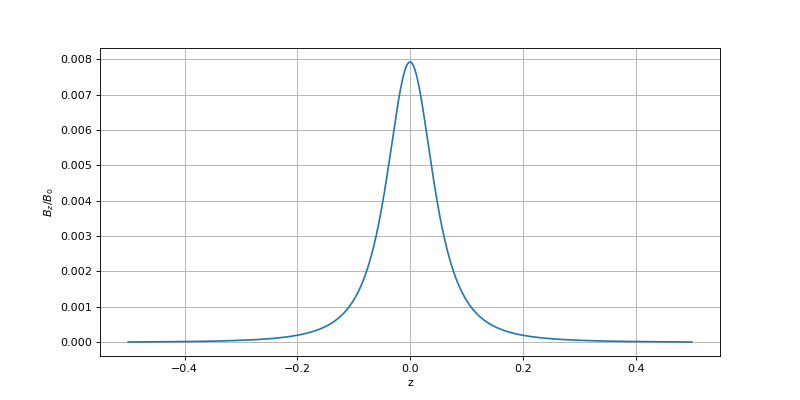plotC.pdf

print(numpy.max(Bz[2**n,:]))
--> 0.007927702

Pour donner une valeur à $B_0$, considérons un courant d'intensité I=1 A. La largeur du domaine complet est L_d=1 m. On a alors $B_0={\mu }_0{J}_{\theta }{L}_d=1,29\cdot 10^{-3}T$.

mu0 = 4*numpy.pi*1e-7
I = 1.0
J = I/(e*l)
B0 = mu0*J*width
A0 = mu0*J*width**2
			 

print(B0)
--> 0.0012867963509103793

La valeur du champ magnétique au centre de la bobine est donc (pour une intensité de 1 A) :

$$B_z\left(0\right)=0,00819\times 1,29\cdot 10^{-3}=1,06\cdot 10^{-5}T\text{(15)}$$

Comparons cette valeur à celle pour une boucle circulaire (fil de section nulle) :

$$B_z\left(0\right)=\frac{{\mu }_{0}I}{2a}=1,01\cdot 10^{-5}T\text{(16)}$$

La valeur du champ au centre est donc un peu plus grande pour cette bobine épaisse que pour une spire dont le rayon est égal au rayon moyen.

Voici la comparaison avec l'expression du champ sur l'axe d'une spire circulaire :

figure(figsize=(10,5))
z = bobine.get_z()
Bz_spire = mu0/2*I*a**2/(a**2+z**2)**1.5
plot(z,Bz[2**n,:])
plot(z,Bz_spire/B0,'r--')
xlabel('z')
ylabel(r'$B_z/B_0$')
grid()
			

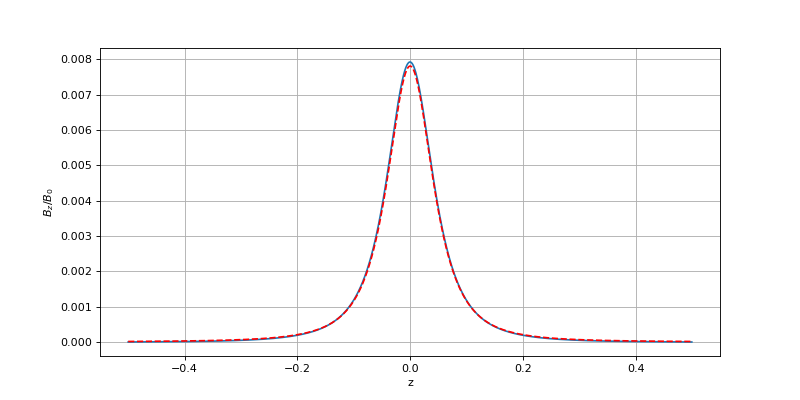plotC2.pdf

Tracé du champ dans le plan z=0 :

figure(figsize=(10,5))
plot(bobine.get_r(symetry=1),Bz[:,2**n])
xlabel('r')
ylabel(r'$B_z/B_0$')
grid()
            

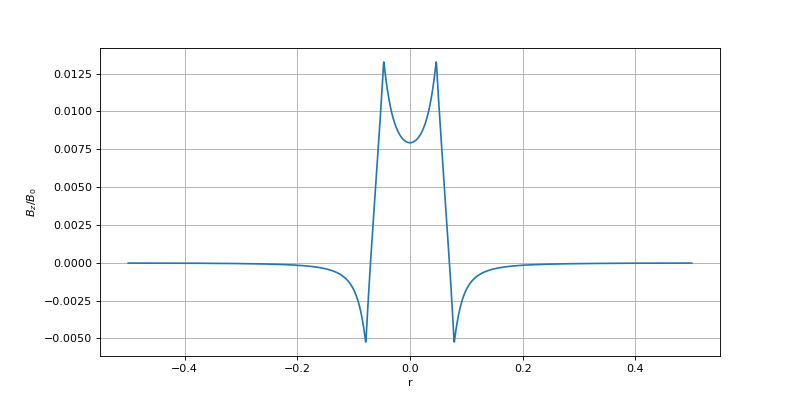plotD.pdf

Pour le calcul de l'auto-inductance (expression $\mathrm{(12)}$), on a besoin des indices de maille des sommets du rectangle qui définit la section du tore :

f = 2**(n-p)
i1 = (ci-w)*f
i2 = (ci+w)*f
j1 = (cj-h)*f
j2 = (cj+h)*f
			

La précision de ce calcul est déterminée par le nombre de nœuds dans le rectangle :

print((j2-j1)*(i2-i1))
--> 4096

Voici le calcul de l'auto-inductance :

A=bobine.get_array(symetry=0)
def autoInductance(A,i1,i2,j1,j2):
	(nj,ni) = A.shape
	L = 0
	for j in range(j1,j2):
		L += numpy.sum(A[j,i1:i2])*j
	Delta_r = height/(nj-1)
	Delta_z = width/(ni-1)
	L *= 2*numpy.pi/(e*l)**2*mu0*width**2*Delta_r**2*Delta_z
	return L

L = autoInductance(A,i1,i2,j1,j2)
			

print(L)
--> 1.294149588534613e-07

Cette valeur est l'auto-inductance par spire; il faut la multiplier par le nombre de spires au carré pour obtenir l'auto-inductance de la bobine. Si par exemple, le fil de la bobine a un diamètre d=1 mm :

d = 1e-3
N = (l/d)*(e/d)
			 

print(L*N**2)
--> 0.12341972241731768

4. Bobine longue

La bobine a toujours un rayon moyen $a=1/16m$ et une épaisseur $e=1/32m$. Sa longueur est 5 fois son épaisseur, soit $\ell =5/32m$.

n=10
p=6
levels = n-p+1
width,height = 1.0,0.5 #taille du domaine en mètres
echelle = width/2**(p+1) # echelle de la maille réduite en mètres
bobine=poisson.main.PoissonAxialVect(p+1,p,levels,width,height,x0=-0.5,y0=0.0)
bobine.laplacien()
bobine.dirichlet_borders(0.0)
ci,cj = 2**(p+1)//2,2**(p+1)//16 # centre du rectangle
w,h = 10,2 # demi-largeur et demi-hauteur du rectangle
bobine.source_rect(ci,cj,w,h,-1.0)
e = 2*h*echelle
l = 2*w*echelle
a = cj*echelle
			

print(e)
--> 0.03125

print(l)
--> 0.15625

print(a)
--> 0.0625

#result=bobine.opencl_iterations_norm(100,60,omega=1.95)
result=bobine.multigrid_full_norm(2,levels,100,2,2)
figure(figsize=(8,5))
plot(result[0],result[1]) 
xlabel('niter')  
ylabel('norm')
grid()  
            

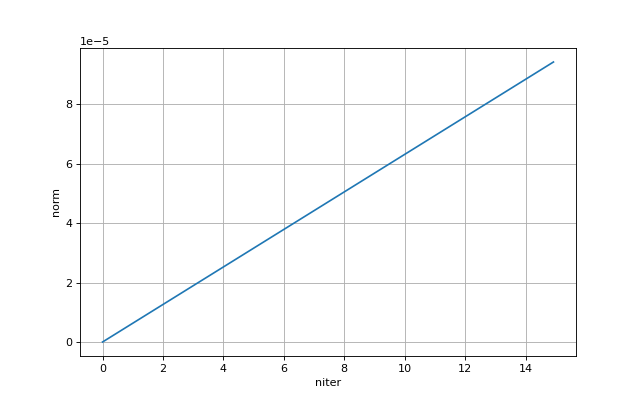plotE.pdf

Atheta=bobine.get_array(symetry=-1)
Br=-bobine.get_derivZ(symetry=-1)
Bz=bobine.get_derivRUR(symetry=1)
figure(figsize=(8,8))
extent=bobine.get_extent(symetry=1)
contour(Atheta,20,extent=extent)
imshow(~bobine.get_mask(symetry=1),extent=extent,alpha=0.5, cmap=cm.gray)
xlabel('z')
ylabel('r')
grid()
            

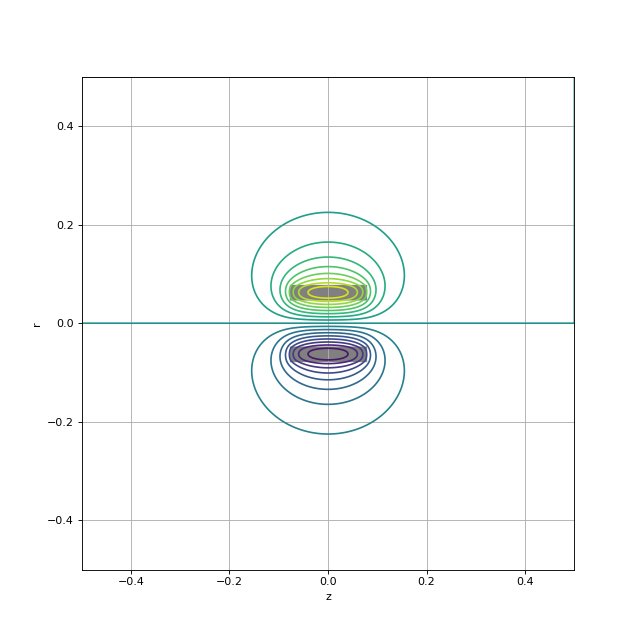plotF.pdf

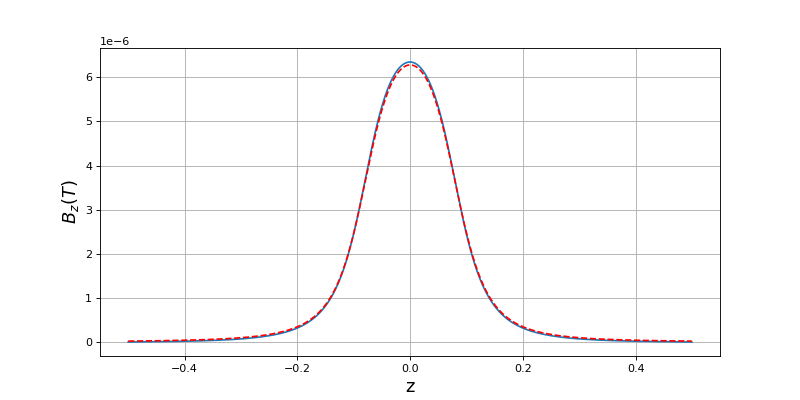
Voici le champ magnétique sur l'axe :

B0 = mu0*1/(e*l)            
figure(figsize=(10,5))
z = bobine.get_z()
plot(z,Bz[2**n,:]*B0)
xlabel('z',fontsize=16)
ylabel(r'$B_z (T)$',fontsize=16)
grid()
            

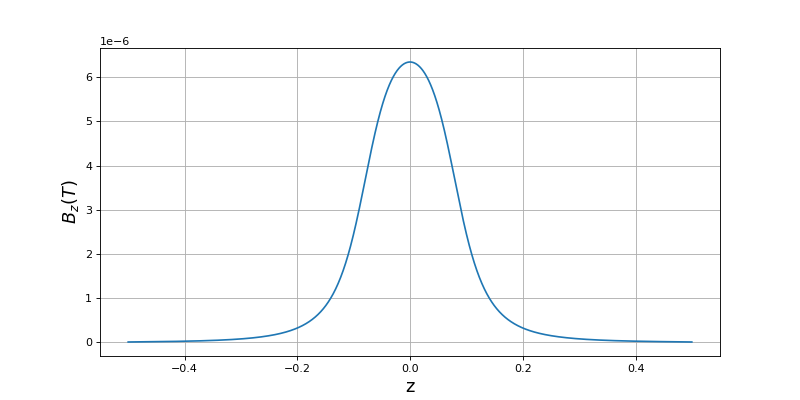plotG.pdf

print(numpy.max(Bz[2**n,:]))
--> 0.02466112

On a comme précédemment :

$$B_0={\mu }_0{J}_{\theta }{L}_d\text{(17)}$$

Il est intéressant de comparer ce résultat au champ magnétique à l'intérieur de la bobine lorsque $\ell \to \infty$, qui est :

$$B_{\infty }={\mu }_0{J}_{\theta }e\text{(18)}$$

Comparons la valeur obtenue au centre de la bobine à cette valeur :

$$\frac{0,025B_0}{B_{\infty }}=0,025\frac{L_d}{e}=0,80\text{(19)}$$

Le champ au centre est donc moins intense que celui créé par une bobine infinie de même rayon et de même épaisseur, ce qui est bien le résultat attendu.

On peut aussi comparer au champ sur l'axe d'une bobine constituée de spires de rayons a, dont l'expression analytique est connue :

$$B_z\left(z\right)=\frac{{\mu }_{0}I}{2\ell }(\frac{z+\frac{\ell }{2}}{{(a^2+{(a+\frac{\ell }{2})}^2)}^{\frac{1}{2}}}-\frac{z-\frac{\ell }{2}}{{(a^2+{(a-\frac{\ell }{2})}^2)}^{\frac{1}{2}}})\text{(20)}$$

mu0 = 4*numpy.pi*1e-7
I = 1.0
Bz_spires = mu0*I/(2*l)*((z+l/2)/(a**2+(z+l/2)**2)**(1/2)-(z-l/2)/(a**2+(z-l/2)**2)**(1/2))
figure(figsize=(10,5))
plot(z,Bz[2**n,:]*B0)
plot(z,Bz_spires,"r--")
xlabel('z',fontsize=16)
ylabel(r'$B_z (T)$',fontsize=16)
grid()  
            

plotG1.pdf

Les deux courbes sont très proches. Nous avons vérifié que la taille du domaine est assez grande : pour la même taille de bobine, augmenter la taille du domaine de calcul d'un facteur 2 a un effet négligeable sur le résultat. Il en est de même de la finesse du maillage (valeur de n).

figure(figsize=(10,5))
plot(bobine.get_r(symetry=1),Bz[:,2**n])
xlabel('r')
ylabel(r'$B_z/B_0$')
grid()
            

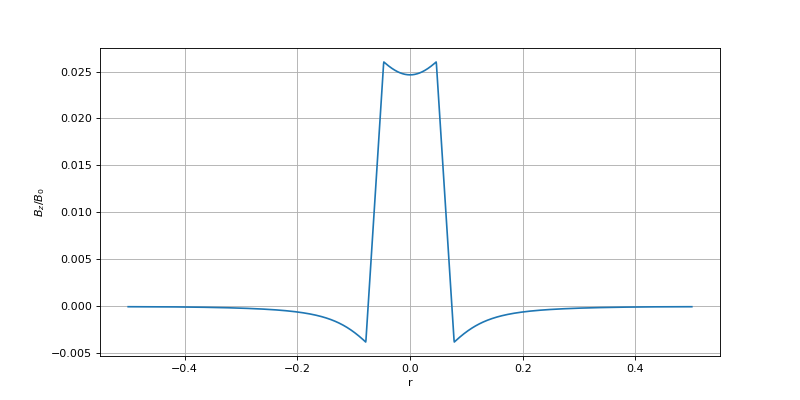plotH.pdf

Calcul de l'auto-inductance :

f = 2**(n-p)
i1 = (ci-w)*f
i2 = (ci+w)*f
j1 = (cj-h)*f
j2 = (cj+h)*f
A=bobine.get_array(symetry=0)
L=autoInductance(A,i1,i2,j1,j2)
			

print(L)
--> 5.907500933649765e-08

d = 1.0e-3
N = (l/d)*(e/d)
			 

print(N)
--> 4882.8125

print(L*N**2)
--> 1.408457978641931

Comparons cette valeur à celle qui est obtenue avec le modèle de solénoïde infini :

$$L_1={\mu }_0\frac{N^2}{\ell }\pi a^2\text{(21)}$$

L1 = mu0*N**2/l*numpy.pi*a**2
			

print(L1)
--> 2.3530970576022527

L'approximation du solénoïde infini donne une valeur d'auto-inductance plus grande.

Une formule empirique plus précise ([1]) est :

$$L_2=\frac{2,2\cdot 10^{-6}{\left(2a\right)}^2{N}^2}{2a+2,2\ell }\text{(22)}$$

L2 = 2.2e-6*(2*a)**2*N**2/(2*a+2.2*l)
			

print(L2)
--> 1.7484029134114583

Cette valeur est notablement plus grande que celle que nous obtenons ($23\%$ plus grande).

bobine.close()            
            

5. Bobine longue avec noyau

Un noyau cylindrique de fer doux (ou de ferrite doux) est placé dans la bobine. Le matériau de ce noyau est supposé linéaire, de perméabilité magnétique relative ${\mu }_r$. Dans le domaine correspondant, le potentiel vecteur vérifie l'équation de Poisson sans sources. La perméabilité magnétique apparaît dans la condition limite entre le domaine ferromagnétique doux et l'extérieur. D'après l'équation $\overrightarrow{rot}\overrightarrow{H}=\overrightarrow{J}$, il y a continuité de la composante tangentielle de $\overrightarrow{H}$, c'est-à-dire continuité de la composante tangentielle de $\overrightarrow{B}/{\mu }_r$. Pour une surface perpendiculaire à l'axe (Oz) séparant un milieu non magnétique (air ou cuivre) d'un milieu magnétique linéaire, on a :

$$(\frac{\partial A_{\theta }}{\partial z}{)}_{air}=(\frac{1}{{\mu }_r}\frac{\partial A_{\theta }}{\partial z}{)}_{fer}\text{(23)}$$

Pour une surface cylindrique de rayon r, la condition limite s'écrit :

$$(\frac{1}{r}\frac{\partial \left(r{A}_{\theta }\right)}{\partial r}{)}_{air}=(\frac{1}{{\mu }_r}\frac{1}{r}\frac{\partial \left(r{A}_{\theta }\right)}{\partial r}{)}_{fer}\text{(24)}$$

Une condition limite à l'interface entre deux milieux différents est introduite par la fonction interface_polygon. Voici le calcul avec un noyau de perméabilité relative égal à 1000 :

n=10
p=6
levels = n-p+1
width,height = 1.0,0.5
bobine=poisson.main.PoissonAxialVect(p+1,p,levels,width,height,x0=-0.5,y0=0.0)
bobine.laplacien()
bobine.dirichlet_borders(0.0)
ci,cj = 2**(p+1)//2,2**(p+1)//16 # centre du rectangle
w,h = 10,2 # demi-largeur et demi-hauteur du rectangle
R = cj-h
bobine.interface_polygon(ci-w,0,[0,2*w,0],[R,0,-R],0,1,1e-3)
bobine.source_rect(ci,cj,w,h,-1.0)
e = 2*h*echelle
l = 2*w*echelle
a = cj*echelle
			

#result=bobine.opencl_iterations_norm(100,60,omega=1.95)
result=bobine.multigrid_full_norm(2,levels,100,2,2)
figure(figsize=(8,5))
plot(result[0],result[1]) 
xlabel('niter')  
ylabel('norm')
grid()  
            

plotI.pdf

Atheta=bobine.get_array(symetry=-1)
Br=-bobine.get_derivZ(symetry=-1)
Bz=bobine.get_derivRUR(symetry=1)
figure(figsize=(8,8))
extent=bobine.get_extent(symetry=1)
contour(Atheta,20,extent=extent)
imshow(~bobine.get_mask(symetry=1),extent=extent,alpha=0.5, cmap=cm.gray)
xlabel('z')
ylabel('r')
grid()
            

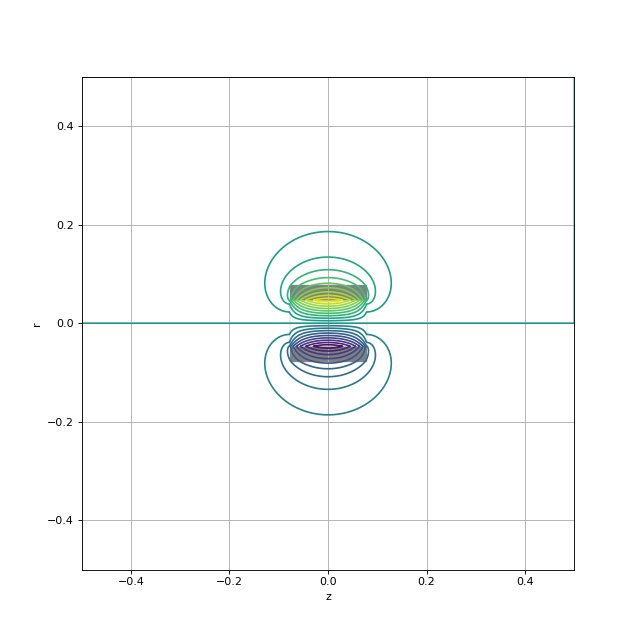plotJ.pdf

Calcul de l'auto-inductance :

f = 2**(n-p)
i1 = (ci-w)*f
i2 = (ci+w)*f
j1 = (cj-h)*f
j2 = (cj+h)*f
A=bobine.get_array(symetry=0)
L=autoInductance(A,i1,i2,j1,j2)
			

print(L)
--> 2.3700145897717245e-07

d = 1.0e-3
N = (l/d)*(e/d)
			 

print(N)
--> 4882.8125

print(L*N**2)
--> 5.650555109433471

Voici le champ magnétique sur l'axe :

  
figure(figsize=(10,5))
plot(bobine.get_z(),Bz[2**n,:])
xlabel('z')
ylabel(r'$B_z/B_0$')
grid()
            

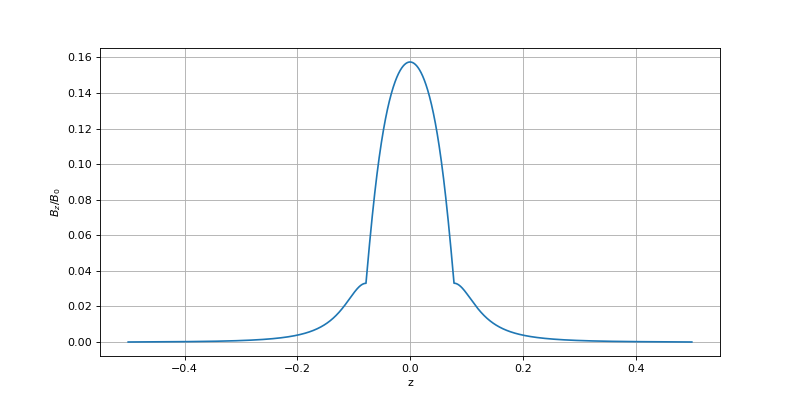plotK.pdf

et le champ magnétique en r=0 :

figure(figsize=(10,5))
plot(bobine.get_r(symetry=1),Bz[:,2**n])
xlabel('r')
ylabel(r'$B_z/B_0$')
grid()
            

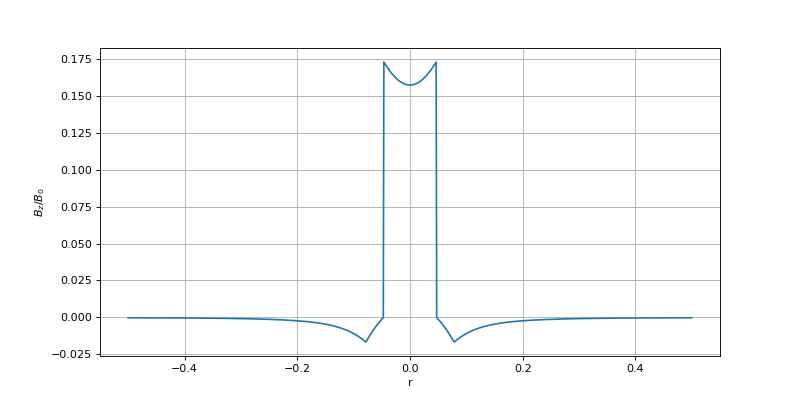plotL.pdf

bobine.close()