Aimant permanent : utilisation des intégrales elliptiques

1. Introduction

Ce document présente le calcul du champ magnétique créé par un ou plusieurs aimants permanents. La géométrie est axisymétrique et les aimants sont coaxiaux.

Chaque aimant, possédant une aimantation uniforme et constante, est équivalent à deux faces possédant chacune une charge magnétique surfacique uniforme. Le calcul de l'excitation magnétique $\overrightarrow{H}$ créé par une face d'un aimant se fait par une intégrale double sur cette face, comme expliqué dans Aimant permanent, où le calcul de cette intégrale double est fait entièrement de manière numérique, à partir d'un maillage de la face de l'aimant.

Nous présentons ici un calcul de l'intégrale reposant sur une expression de l'intégration par rapport à l'angle, qui fait intervenir des intégrales elliptiques complètes, ce qui permet de ramener le calcul de l'intégrale double à une intégrale simple. L'algorithme de Carlson [1] pour le calcul numérique des intégrales elliptiques permet réduire le temps de calcul par rapport au calcul numérique de l'intégrale double.

2. Calcul du champ magnétique

On considère un ou deux aimants en géométrie axisymétrique, chacun étant caractérisé par une aimantation uniforme. Un point P de l'espace est repéré par ses coordonnées cylindriques (r,z).

Figure pleine page

L'excitation magnétique en un point P est calculé par l'intégrale suivante pour chaque face des aimants :

$$\overrightarrow{H}\left(P\right)=\frac{{\sigma }_m}{4\pi }{\iint }_{disque}\frac{\overrightarrow{QP}}{\left|\right|\overrightarrow{QP}|{|}^3}dS\text{(1)}$$

où σ_m est la densité de charge magnétique de la face, égale à σ_m=M ou σ_m=-M selon qu'il s'agit de la face nord ou de la face sud de l'aimant d'aimantation M.

Pour expliciter cette intégrale, on peut considérer que θ=0. Notons (r₁,θ₁,z₁) les coordonnées cylindriques du point Q situé sur une face.

On a :

$$\overrightarrow{QP}=(r-r_{1}cos\left({\theta }_1\right)){\overrightarrow{u}}_x-r_{1}sin\left({\theta }_1\right){\overrightarrow{u}}_y+(z-z_1){\overrightarrow{u}}_z\text{(2)}$$

L'élément de surface s'écrit dS=r₁dθ₁dr₁. Les deux composantes de l'excitation magnétique s'écrivent donc :

$$\begin{array}{ccc}\hfill & H_r(r,z)=\frac{{\sigma }_m}{4\pi }{\int }_0^{a}d{r}_1{\int }_0^{2\pi }d{\theta }_1\frac{r_1(r-r_{1}cos\left({\theta }_1\right))}{(r^2+r_1^2-2r{r}_{1}cos\left({\theta }_1\right)+{(z-z_1)}^2{)}^{\frac{3}{2}}}\hfill & \hfill \text{(3)}\\ \hfill & H_z(r,z)=\frac{{\sigma }_m}{4\pi }{\int }_0^{a}d{r}_1{\int }_0^{2\pi }d{\theta }_1\frac{r_1(z-z_1)}{(r^2+r_1^2-2r{r}_{1}cos\left({\theta }_1\right)+{(z-z_1)}^2{)}^{\frac{3}{2}}}\hfill & \hfill \text{(4)}\end{array}$$

L'intégrale par rapport à l'angle θ₁ peut s'exprimer à l'aide des intégrales elliptiques de première et seconde espèces, définies par :

$$\begin{array}{cc}\hfill & K\left(x\right)={\int }_0^{\pi /2}\frac{d\theta }{\sqrt{1-x{sin}^2\theta }}\hfill \\ \hfill & E\left(x\right)={\int }_0^{\pi /2}\sqrt{1-x{sin}^2\theta }d\theta \hfill \end{array}$$

Pour exprimer ces intégrales, définissons les expressions suivantes :

$$\begin{array}{ccc}\hfill & b=z-z_1\hfill & \hfill \text{(5)}\\ \hfill & A={(r-r_1)}^2+b^2\hfill & \hfill \text{(6)}\\ \hfill & B={(r+r_1)}^2+b^2\hfill & \hfill \text{(7)}\\ \hfill & C=r^2-r_1^2-b^2\hfill & \hfill \text{(8)}\\ \hfill & x=-\frac{4r{r}_1}{A}\hfill & \hfill \text{(9)}\end{array}$$

Voici les expressions des intégrales sur la variable θ₁, obtenues grace au logiciel de calcul formel Mathematica :

$$\begin{array}{ccc}\hfill & f_r=\frac{2r_1}{r}\frac{CE\left(x\right)+BK\left(x\right))}{B\sqrt{A}}sir>0\hfill & \hfill \text{(10)}\\ \hfill & f_r=0sir=0\hfill & \hfill \text{(11)}\\ \hfill & f_z=\frac{4b{r}_{1}E\left(x\right)}{B\sqrt{A}}\hfill & \hfill \text{(12)}\end{array}$$

Les intégrales elliptiques sont calculées au moyen des fonctions ellipe et ellipk du module scipy.special. Ces deux fonctions implémentent l'algorithme itératif de Carlson, qui converge nettement plus vite qu'une méthode de calcul de type méthode des trapèzes.

import numpy as np
from scipy.special import ellipk, ellipe
from matplotlib.pyplot import *

def frfz(r,z,r1,z1):
    b = z-z1
    b2 = b*b
    A = (r-r1)**2+b2
    B = (r+r1)**2+b2
    C = r**2-r1**2-b2
    x = -4*r*r1/A
    E = ellipe(x)
    K = ellipk(x)
    D = B*np.sqrt(A)
    if r!=0:
        fr =  2*r1/r*(C*E+B*K)/D
    else:
        fr=0
    fz = 4*b*r1*E/D
    return fr,fz

frfz = np.frompyfunc(frfz,4,2)
                   

Voici un exemple :

z1 = 0
a = 1
z = 0.1
r = 0.1
N = 100
r1 = np.linspace(0,a,N)
fr,fz = frfz(r,z,r1,z1)
figure()
subplot(211)
plot(r1,fr)
ylabel('fr')
grid()
subplot(212)
plot(r1,fz)
ylabel('fz')
xlabel('r1')
grid()
                   

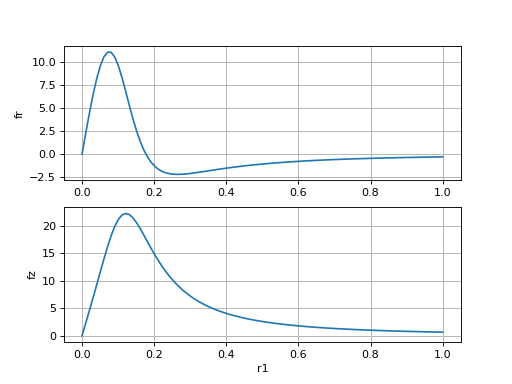frfz-1.pdf

et un autre à une distance plus petite du disque :

z1 = 0
a = 1
z = 0.01
r = 0.1
N = 500
r1 = np.linspace(0,a,N)
fr,fz = frfz(r,z,r1,z1)
figure()
subplot(211)
plot(r1,fr)
ylabel('fr')
grid()
subplot(212)
plot(r1,fz)
ylabel('fz')
xlabel('r1')
grid()
                   

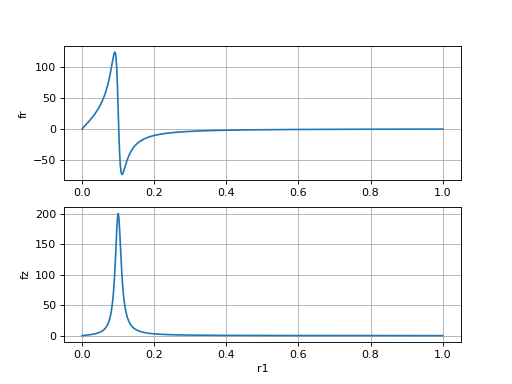frfz-2.pdf

Le calcul de l'intégrale sur la variable r₁ peut se faire par la méthode des trapèzes :

dr = r1[1]-r1[0]
Iz = (np.sum(fz[1:N-1])+0.5*(fz[0]+fz[N-1]))*dr
Ir = (np.sum(fr[1:N-1])+0.5*(fr[0]+fr[N-1]))*dr
M = 1
Hz = M/(4*np.pi)*Iz
Hr = M/(4*np.pi)*Ir
                   

print((Hz,Hr))
--> (0.49496075263083483, 0.02507405131733448)

Voici une fonction qui effectue le calcul du champ en un point de coordonnées (r,z) :

def HrHz(r,z,z1,a,M,N):
    r1 = np.linspace(0,a,N)
    dr = r1[1]-r1[0]
    fr,fz = frfz(r,z,r1,z1)
    Hz = M/(4*np.pi)*(np.sum(fz[1:N-1])+0.5*(fz[0]+fz[N-1]))*dr
    Hr = M/(4*np.pi)*(np.sum(fr[1:N-1])+0.5*(fr[0]+fr[N-1]))*dr
    return Hr,Hz
                   

Voici par exemple le tracé du champ sur l'axe, qui peut être comparé à l'expression exacte :

P = 100
z = np.linspace(1e-3,2,P)
Hz = np.zeros(P)
r = 0
z1 = 0
a = 1
M = 1
N = 500
for k in range(P):
    hr,hz = HrHz(r,z[k],z1,a,M,N)
    Hz[k] = hz
def Hz_axe(z,z1,a,M):
    return M/2*((z-z1)/abs(z-z1)-(z-z1)/(a**2+(z-z1)**2)**0.5)
Hz_exact = Hz_axe(z,z1,a,M)
figure()
plot(z,Hz,'b')
plot(z,Hz_exact,'r')
grid()
xlabel('z')
ylabel('Hz')
                   

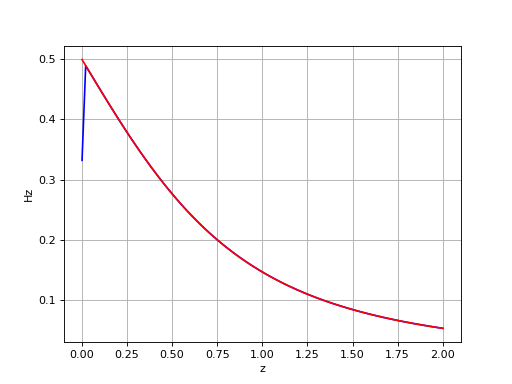Hz-1.pdf

Le calcul numérique de l'intégrale est incorrect lorsque le point est très proche du disque, car la fonction à intégrer présente dans ce cas des variations très rapides au voisinage de r₁=r. Dans le cas ci-dessus, la valeur N=500 n'est pas suffisante pour z-z₁=10^-3. À l'inverse, pour les points plus éloignés du disque il devrait être possible de réduire la valeur de N. Il est donc judicieux de mettre en place une méthode d'ajustement de N en fonction d'une tolérance. La fonction suivante répète le calcul en augmentant N d'un facteur deux jusqu'à ce que la variation relative de la norme du champ soit inférieure à la tolérance :

def HrHz_adapt(r,z,z1,a,M,Nmin,tol):
    N = Nmin
    Hr1,Hz1 = HrHz(r,z,z1,a,M,N)
    H1 = np.sqrt(Hr1*Hr1+Hz1*Hz1)
    N *= 2
    Hr,Hz = HrHz(r,z,z1,a,M,N)
    H = np.sqrt(Hr*Hr+Hz*Hz)
    while abs((H-H1)/H)>tol:
        H1 = H
        N *= 2
        Hr,Hz = HrHz(r,z,z1,a,M,N)
        H = np.sqrt(Hr*Hr+Hz*Hz)
    return Hr,Hz,N
                    

P = 100
z = np.linspace(1e-3,1,P)
Hz = np.zeros(P)
list_N = np.zeros(P)
r = 0
z1 = 0
a = 1
M = 1
Nmin = 10
tol=1e-2
for k in range(P):
    hr,hz,N = HrHz_adapt(r,z[k],z1,a,M,Nmin,tol)
    Hz[k] = hz
    list_N[k] = N
def Hz_axe(z,z1,a,M):
    return M/2*((z-z1)/abs(z-z1)-(z-z1)/(a**2+(z-z1)**2)**0.5)
Hz_exact = Hz_axe(z,z1,a,M)
figure()
plot(z,Hz,'b')
plot(z,Hz_exact,'r')
grid()
xlabel('z')
ylabel('Hz')
                   

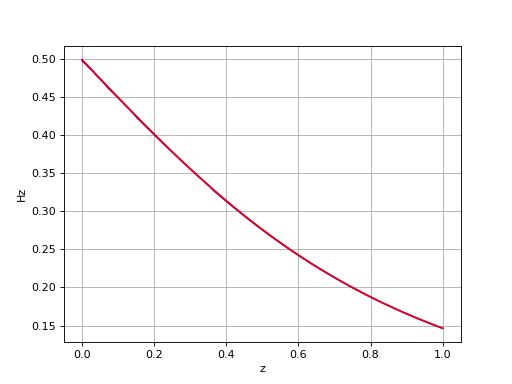Hz-2.pdf

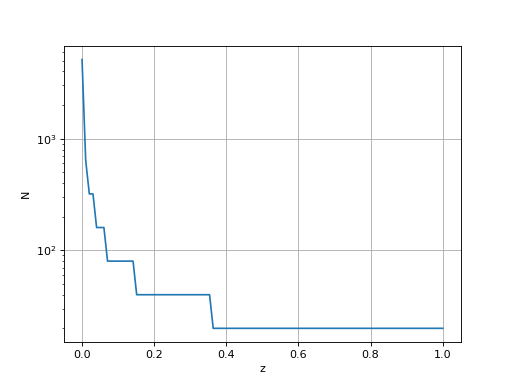
Voici les valeurs de N :

figure()
plot(z,list_N)
xlabel('z')
ylabel('N')
yscale('log')
grid()
                   

N-2.pdf

L'algorithme de calcul de l'intégrale peut être amélioré en remarquant que la somme des N-2 termes peut être réutilisée après avoir multiplié N par 2. Pour cela, il faut définir N comme étant le nombre de sous-intervalles de [0,a] (le nombre de points est N+1). On pose donc :

$$\begin{array}{ccc}\hfill & r_k^N=k\frac{a}{N}k=0,\dots N\hfill & \hfill \text{(13)}\\ \hfill & S^N=\sum _{k=1}^{N-1}f\left(r_k^N\right)\hfill & \hfill \text{(14)}\\ \hfill & I^N=\frac{a}{N}(\frac{1}{2}f\left(0\right)+\frac{1}{2}f\left(a\right)+S^N)\hfill & \hfill \text{(15)}\end{array}$$

I^N est l'approximation de l'intégralle pour N sous-intervalles. La somme pour 2N sous-intervalles s'écrit :

$$S^{2N}=S^N+\sum _{p=0}^{N-1}{r}_{2p+1}^{2N}\text{(16)}$$

Pour implémenter cet algorithme, il faut écrire une fonction qui prend en argument la somme S^N/2 et renvoie la somme S^N et l'approximation de l'intégrale I^N :

                     
def HrHz_partiel(r,z,z1,a,M,N,sum_fr,sum_fz):
    dr = a/N
    r1 = np.arange(1,N,2)*dr
    fr,fz = frfz(r,z,r1,z1)
    sum_fr += np.sum(fr)
    sum_fz += np.sum(fz)
    Hz = M/(4*np.pi)*(sum_fz*dr)
    Hr = M/(4*np.pi)*(sum_fr*dr)
    return Hr,Hz,sum_fr,sum_fz
                     

Pour démarrer l'itération à un N quelconque, il faut aussi une fonction qui fait le calcul complet de la somme :

def HrHz_complet(r,z,z1,a,M,N):
    fr0,fz0 = frfz(r,z,0,z1)
    fra,fza = frfz(r,z,a,z1)
    dr = a/N
    r1 = np.arange(1,N)*dr
    fr,fz = frfz(r,z,r1,z1)
    sum_fr = np.sum(fr)+0.5*(fr0+fra)
    sum_fz = np.sum(fz)+0.5*(fz0+fza)
    Hz = M/(4*np.pi)*(sum_fz*dr)
    Hr = M/(4*np.pi)*(sum_fr*dr)
    return Hr,Hz,sum_fr,sum_fz
                     

La fonction suivante effectue les calculs itératifs en partant de N=10.

def HrHz_iter(r,z,z1,a,M,tol):
    N = 10
    Hr1,Hz1,sum_fr,sum_fz = HrHz_complet(r,z,z1,a,M,N)
    H1 = np.sqrt(Hr1*Hr1+Hz1*Hz1)
    N *= 2
    Hr,Hz,sum_fr,sum_fz = HrHz_partiel(r,z,z1,a,M,N,sum_fr,sum_fz)
    H = np.sqrt(Hr*Hr+Hz*Hz)
    while abs((H-H1)/H)>tol:
        H1 = H
        N *= 2
        Hr,Hz,sum_fr,sum_fz = HrHz_partiel(r,z,z1,a,M,N,sum_fr,sum_fz)
        H = np.sqrt(Hr*Hr+Hz*Hz)
    return Hr,Hz,N
    
                     

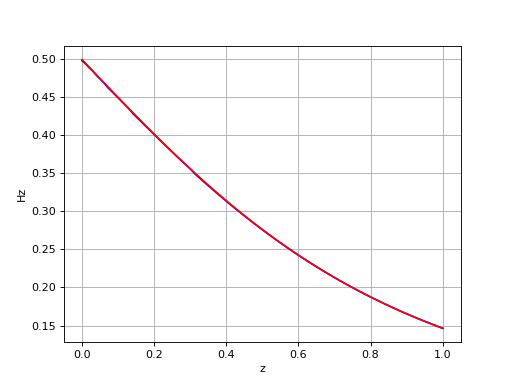
Voici la reprise du calcul précédent :

P = 100
z = np.linspace(1e-3,1,P)
Hz = np.zeros(P)
list_N = np.zeros(P)
r = 0
z1 = 0
a = 1
M = 1
Nmin = 10
tol=1e-2
for k in range(P):
    hr,hz,N = HrHz_iter(r,z[k],z1,a,M,tol)
    Hz[k] = hz
    list_N[k] = N
def Hz_axe(z,z1,a,M):
    return M/2*((z-z1)/abs(z-z1)-(z-z1)/(a**2+(z-z1)**2)**0.5)
Hz_exact = Hz_axe(z,z1,a,M)
figure()
plot(z,Hz,'b')
plot(z,Hz_exact,'r')
grid()
xlabel('z')
ylabel('Hz')
                   

Hz-3.pdf

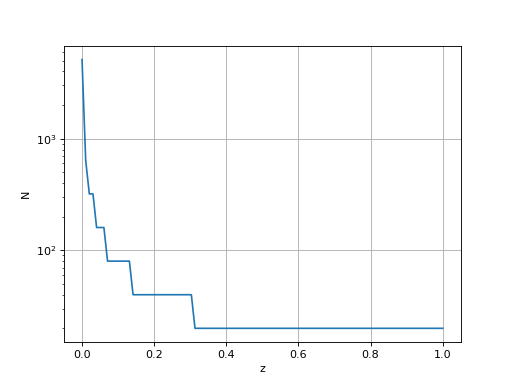
et les valeurs de N :

figure()
plot(z,list_N)
xlabel('z')
ylabel('N')
yscale('log')
grid()
                   

N-3.pdf

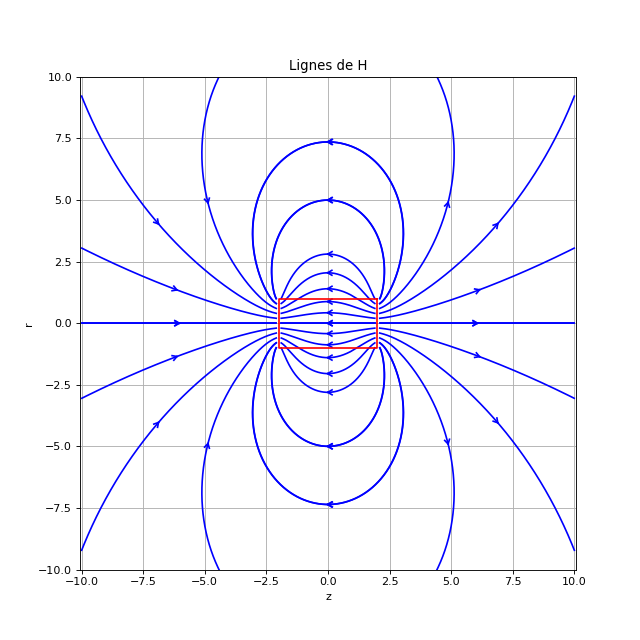
3. Lignes de champ d'un aimant

Le calcul du champ créé par un aimant est fait par la fonction suivante, qui renvoie les composantes de $\overrightarrow{H}$ et de $\overrightarrow{B}$. L'aimant est caractérisé par son rayon a, les côtes de ses faces z_s et z_n et son aimantation M.

def champAimant(r,z,a,zs,zn,M,mu0=1,tol=1e-2):
    Hr1,Hz1,N1 = HrHz_iter(r,z,zs,a,-M,tol)
    Hr2,Hz2,N2 = HrHz_iter(r,z,zn,a,M,tol)
    Br1 = mu0*Hr1
    Br2 = mu0*Hr2
    if abs(r)<a and z>min(zs,zn) and z<max(zs,zn):
        Bz1 = mu0*(Hz1+M)
        Bz2 = mu0*(Hz2+M)
    else:
        Bz1 = mu0*Hz1 
        Bz2 = mu0*Hz2
    return (Hr1+Hr2,Hz1+Hz2,Br1+Br2,Bz1+Bz2)

La fonction suivante permet de dessiner une flèche au milieu d'une ligne.

def fleche(x,y,sens,long,style='k-'):
    n = len(x)//2
    xa = x[n]
    xb = x[n+sens]
    ya = y[n]
    yb = y[n+sens]
    z = (xb-xa)+1j*(yb-ya)
    phi = np.angle(z)
    a = np.pi/2+np.pi/3
    xc = xb+long*np.cos(phi-a)
    yc = yb+long*np.sin(phi-a)
    xd = xb+long*np.cos(phi+a)
    yd = yb+long*np.sin(phi+a)
    plot([xb,xc],[yb,yc],style)
    plot([xb,xd],[yb,yd],style)
                    

Le tracé d'une ligne de champ de l'excitation magnétique se fait en partant d'un point à proximité d'une face, jusqu'à un point à proximité d'une face ou bien jusqu'à sortie d'un rectangle centré sur l'aimant. Il faut remarquer que le choix de la valeur de M et de μ₀ n'a aucune influence sur les lignes de champ.

def ligneH(a,zs,zn,M,ri,zi,sens,rmax,zmax,dmin):
    ds = 0.01*sens
    r = ri
    z = zi
    ligne_z = []
    ligne_r = []
    continuer = True
    while continuer:
        ligne_z.append(z)
        ligne_r.append(r)
        (Hr,Hz,Br,Bz) = champAimant(r,z,a,zs,zn,M)
        H = np.sqrt(Hr**2+Hz**2)
        r += Hr/H*ds                                    
        z += Hz/H*ds       
        if (abs(z-zs) < dmin and abs(r)<a) or (abs(z-zn)< dmin and abs(r)<a) or (abs(r)>rmax) or (abs(z)>zmax) : continuer=False
    return (np.array(ligne_r),np.array(ligne_z))
a=1
M = 1 
zs=-2
zn=2
ds = 0.05
figure(figsize=(8,8))
zmax = 10
rmax = 10
longfleche = 0.2
dmin = 0.1 # distance minimale d'approche des faces
for ri in np.array([0,0.2,0.4,0.6,0.8,1.0])*a: 
    sens = 1
    ligne_r,ligne_z = ligneH(a,zs,zn,M,ri,zn+dmin,sens,rmax,zmax,dmin)
    plot(ligne_z,ligne_r,'b-')
    fleche(ligne_z,ligne_r,sens,longfleche,style='b-')
    plot(ligne_z,-ligne_r,'b-')
    fleche(ligne_z,-ligne_r,sens,longfleche,style='b-')
    sens = -1
    ligne_r,ligne_z = ligneH(a,zs,zn,M,ri,zs-dmin,sens,rmax,zmax,dmin)
    plot(ligne_z,ligne_r,'b-')
    fleche(ligne_z,ligne_r,sens,longfleche,style='b-')
    plot(ligne_z,-ligne_r,'b-')
    fleche(ligne_z,-ligne_r,sens,longfleche,style='b-')
    sens = 1
    ligne_r,ligne_z = ligneH(a,zs,zn,M,ri,zn-dmin,sens,rmax,zmax,dmin)
    plot(ligne_z,ligne_r,'b-')
    fleche(ligne_z,ligne_r,sens,longfleche,style='b-')
    plot(ligne_z,-ligne_r,'b-')
    fleche(ligne_z,-ligne_r,sens,longfleche,style='b-')
axis('equal')
xlabel('z')
ylabel('r')
xlim(-zmax,zmax)
ylim(-rmax,rmax)
plot([-zs,zs,zs,-zs,-zs],[a,a,-a,-a,a],'r-')
grid()
title('Lignes de H')
                     

aimant-ligneH.pdf

def ligneB(a,zs,zn,M,ri,zi,sens,rmax,zmax,dmin):
    ds = 0.01*sens 
    r = ri
    z = zi
    ligne_z = []
    ligne_r = []
    continuer = True
    while continuer:
        ligne_z.append(z)
        ligne_r.append(r)
        (Hr,Hz,Br,Bz) = champAimant(r,z,a,zs,zn,M)
        B = np.sqrt(Br**2+Bz**2)
        r += Br/B*ds
        z += Bz/B*ds
        if (abs(z-zs) < dmin and abs(r)<a) or (abs(z-zn)< dmin and abs(r)<a) or (abs(r)>rmax) or (abs(z)>zmax) : continuer=False
    return (np.array(ligne_r),np.array(ligne_z))
    

figure(figsize=(8,8))
for ri in np.array([0,0.2,0.4,0.6,0.8,1.0])*a: 
    sens = 1
    ligne_r,ligne_z = ligneB(a,zs,zn,M,ri,zn+dmin,sens,rmax,zmax,dmin)
    plot(ligne_z,ligne_r,'b-')
    fleche(ligne_z,ligne_r,sens,longfleche,style='b-')
    plot(ligne_z,-ligne_r,'b-')
    fleche(ligne_z,-ligne_r,sens,longfleche,style='b-')
    sens = -1 
    ligne_r,ligne_z = ligneB(a,zs,zn,M,ri,zs-dmin,sens,rmax,zmax,dmin)
    plot(ligne_z,ligne_r,'b-')
    fleche(ligne_z,ligne_r,sens,longfleche,style='b-')
    plot(ligne_z,-ligne_r,'b-')
    fleche(ligne_z,-ligne_r,sens,longfleche,style='b-')
    sens = -1
    ligne_r,ligne_z = ligneB(a,zs,zn,M,ri,zn-dmin,sens,rmax,zmax,dmin)
    plot(ligne_z,ligne_r,'b-')
    fleche(ligne_z,ligne_r,sens,longfleche,style='b-')
    plot(ligne_z,-ligne_r,'b-')
    fleche(ligne_z,-ligne_r,sens,longfleche,style='b-')
axis('equal')
xlabel('z')
ylabel('r')
xlim(-zmax,zmax)
ylim(-rmax,rmax)
plot([-zs,zs,zs,-zs,-zs],[a,a,-a,-a,a],'r-')
grid()
title('Lignes de B')
                     

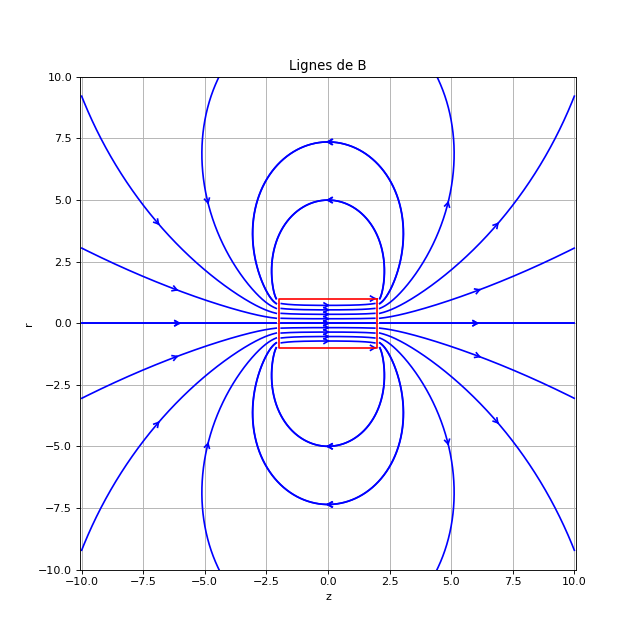aimant-ligneB.pdf

4. Force entre deux aimants

Comme démontré dans Aimant permanent, la force entre deux aimants coaxiaux s'écrit :

$$F_z=2\pi M{\int }_0^a{r}_1(B_z(r_1,z_n)-B_z(r_1,z_s))d{r}_1\text{(17)}$$

où $B_z$ est le champ créé par l'autre aimant.

Soit M l'unité dans laquelle les moments magnétiques sont exprimés. Si l'on pose ${\mu }_0=1$, le champ magnétique obtenu est sans dimensions et son unité est :

$$B_0={\mu }_{0}M\text{(18)}$$

Si L est l'unité de longueur, l'unité de la force est :

$$F_0=M{B}_0{L}^2=\frac{{\left({\mu }_{0}M\right)}^2}{{\mu }_0}{L}^2\text{(19)}$$

          
def force2Aimants(a1,zs1,zn1,a2,zs2,zn2,M1,M2,N,mu0=1):
    r1 = np.arange(N)*a1/N
    dr1 = r1[1]-r1[0]
    Fz = 0
    for k in range(N):
        (Hra,Hza,Bra,Bza) = champAimant(r1[k],zn1,a2,zs2,zn2,M2,mu0)
        (Hrb,Hzb,Brb,Bzb) = champAimant(r1[k],zs1,a2,zs2,zn2,M2,mu0)
        Fz += Bza-Bzb
    Fz *= 2*np.pi*M1*dr1*r1[k]
    return Fz
                

Voici la force entre deux aimants identiques, en fonction de la distance entre la face nord du premier et la face sud du second. Cette distance ne peut être nulle car le calcul de l'excitation magnétique créé par un disque ne peut se faire sur le disque lui-même. On prend donc une distance très petite comme point initial de la courbe.

a1 = a2 = 5 # en mm
L1 = L2 = 20 # en mm
mu0M = 1 # en teslas
F0 = (mu0M)**2/(4*np.pi*1e-7)*(1e-3)**2
zn1 = 0
zs1 = zn1-L1
zs2 = np.linspace(0.01,20,50) # en mm
zn2 = zs2+L2
Fz = np.zeros(len(zs2))
for k in range(len(zs2)):
    Fz[k] = force2Aimants(a1,zs1,zn1,a2,zs2[k],zn2[k],1,1,100) 
figure()
plot(zs2,Fz)
grid()
xlabel("distance (mm)")
ylabel(r"$F_z/F_0$",fontsize=18) 
                

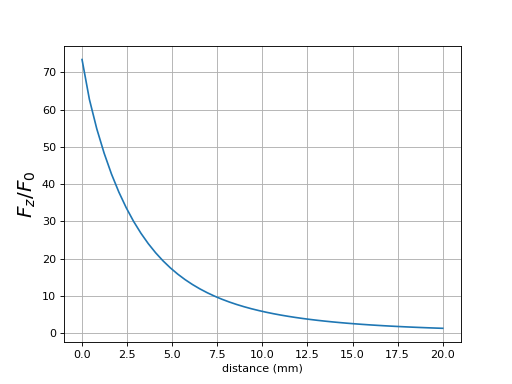fig10.pdf

print(F0)
--> 0.7957747154594766

Voici la force par unité de surface :

figure()
plot(zs2,Fz/(np.pi*a1**2))
grid()
xlabel("distance (mm)")
ylabel(r"$F_z/(F_0 \pi a^2)$",fontsize=18) 
                

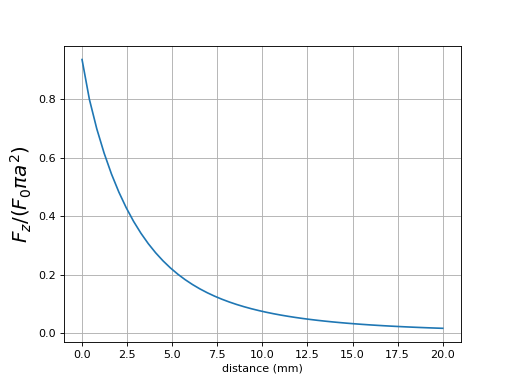fig11.pdf

Lorsque les aimants sont en contact, la force par unité de surface est environ $\frac{{\left({\mu }_{0}M\right)}^2}{{\mu }_0}$.

Voyons la force par unité de surface pour deux aimants plats :

a1 = a2 = 10 # en mm
L1 = L2 =  5# en mm
mu0M = 1 # en teslas
F0 = (mu0M)**2/(4*np.pi*1e-7)*(1e-3)**2
zn1 = 0
zs1 = zn1-L1
zs2 = np.linspace(0.01,20,50) # en mm
zn2 = zs2+L2
Fz = np.zeros(len(zs2))
for k in range(len(zs2)):
    Fz[k] = force2Aimants(a1,zs1,zn1,a2,zs2[k],zn2[k],1,1,100) 
figure()
plot(zs2,Fz/(np.pi*a1**2))
grid()
xlabel("distance (mm)")
ylabel(r"$F_z/(F_0 \pi a^2)$",fontsize=18) 
                

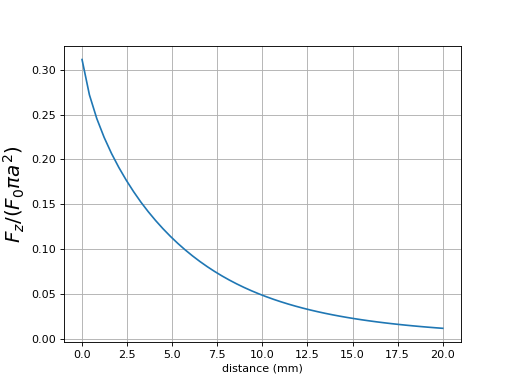fig12.pdf

La force par unité de surface est notablement moins grande pour un aimant plat que pour un aimant long mais elle décroit moins vite avec la distance.