Dynamique moléculaire : modèle des sphères molles à deux dimensions

1. Introduction

Ce document présente une introduction aux méthodes de la dynamique moléculaire ([1]). Le système considéré est constitué de sphères ne présentant aucune force attractive entre elles. La répulsion des sphères lorsqu'elles entrent en contact est modélisée par un potentiel répulsif. Contrairement au modèle des sphères dures où la force de répulsion est infinie, les sphères molles présentent une force finie au moment des collisions. Cela permet d'une part d'intégrer des équations différentielles du mouvement, d'autre part de calculer la pression à l'aide du viriel.

2. Mise en équation et méthode numérique

2.a. Forces intermoléculaires

Pour effectuer un calcul de dynamique moléculaire, il faut tout d'abord modéliser les forces intermoléculaires. Dans le cas du modèle des sphères molles, le potentiel intermoléculaire présente une symétrie sphérique. On adopte le potentiel suivant :

\begin{matrix} U (r) = ε [(\frac{d}{r})^{12} - 2 (\frac{d}{r})^{6}] + ε s i r < d & (1) \\ U (r) = 0 s i r \geq d & (2) \end{matrix}

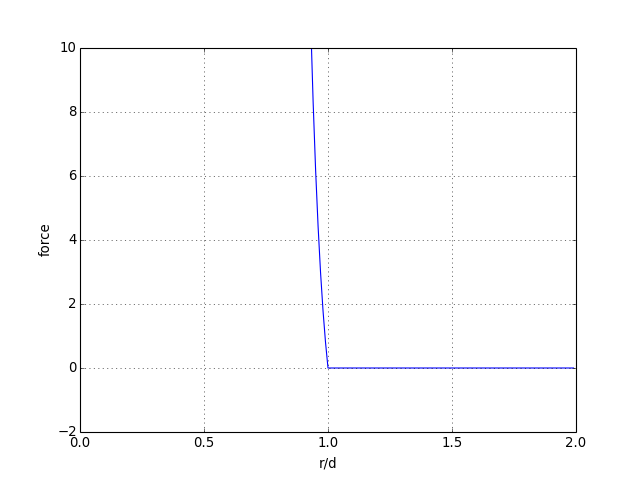
Il s'agit d'un potentiel de Lennard-Jones dont la partie attractive a été enlevée. La partie répulsive est dominée par le terme en puissance 12 : le potentiel augmente très rapidement lorsque r décroît en dessous de d. Le paramètre d peut être assimilé au diamètre des sphères. La force intermoléculaire obtenue en dérivant ce potentiel est, pour r<d :

\begin{matrix} \vec{f} (r) = 12 ε [(\frac{d}{r})^{13} - (\frac{d}{r})^{7}] \vec{u_{r}} & (3) \end{matrix}

Pour r>d, la force est nulle. Voyons un tracé de cette force :

from matplotlib.pyplot import *
import math
import numpy

def force(r):
    if r<1.0:
        return 12.0*(math.pow(r,-13)-math.pow(r,-7))
    else:
        return 0.0
r = numpy.arange(0.8,2.0,0.01)
f = r.copy()
for i in range(r.size):
    f[i] = force(r[i])
figure(figsize=(8,6))
plot(r,f)
xlabel("r/d")
ylabel("force")
axis([0,2,-2,10])
grid()

figA.pdf

2.b. Équations du mouvement

Les équations du mouvement des sphères sont obtenues dans le cadre de la mécanique classique (loi de Newton). Le système comporte N sphères de masse m. On note $\vec{r_{i}}$ la position de la sphère d'indice i (de son centre). Le système d'équations différentielles s'écrit :

m \frac{d^{2} \vec{r_{i}}}{d t^{2}} = \sum_{j \neq i} \vec{f} (\vec{r_{i}} - \vec{r_{i}}) (4)

où l'indice i varie de 0 à N-1. Pour obtenir une solution de ces équations, il faut fixer les positions et les vitesses initiales des sphères.

L'énergie du système s'écrit :

E = \frac{1}{2} m \sum_{i} v_{i}^{2} + ε \sum_{i < j} ({(d / r_{i j})}^{12} - 2 {(d / r_{i j})}^{6} + 1) (5)

où r_ij désigne la distance entre les sphères i et j. L'énergie du système est constante.

En pratique, les équations sont considérées sous leur forme adimensionnelle, obtenue en posant m=1, ε=1 et d=1.

2.c. Conditions limites périodiques

Le nombre N de sphères doit être le plus grand possible pour obtenir une modélisation convenable d'un système thermodynamique. Néanmoins, on est en pratique limité par les capacités de calcul disponibles. Avec un N de quelques milliers, on est très loin des nombres de molécules des systèmes macroscopiques (de l'ordre du nombre d'Avogadro).

Le mouvement des sphères est confiné à un carré de côté L. On pourrait limiter le carré par des parois, sur lesquelles les sphères subiraient des chocs élastiques. Compte tenu du nombre modeste de sphères dans le système, une telle approche conduirait à attribuer un rôle excessif aux parois, alors qu'on s'intéresse aux propriétés de volume du fluide (pour un volume infini). La solution à ce problème consiste à utiliser des conditions limites périodiques : lorsqu'une sphère quitte le domaine par un côté du carré, elle réapparaît par le côté opposé. La figure suivante montre une sphère A qui quitte le domaine par le bord droit pour y entrer par le bord gauche.

Figure pleine page

Cela revient à considérer que le domaine est bordé de répliques identiques de lui-même. Pourvu que la taille du carré soit beaucoup plus grande que les distances de corrélation du système, on obtient ainsi une assez bonne représentation d'un système infini.

2.d. Paires en interaction et subdivision d'espace

La force d'interaction entre deux sphères a une portée limitée à la distance r_c=d=1. Dans la somme des forces appliquées à une sphère (équation $(4)$ ), on peut donc se limiter aux sphères voisines, celles dont la distance est inférieure à r_c.

Pour obtenir rapidement le voisinage de chaque sphère, on utilise une subdivision du domaine carré sous forme de grille. Les cellules carrées doivent avoir une taille supérieure à la portée des interactions. Chaque sphère est associée à une cellule de la grille, celle qui contient son centre. Pour une sphère donnée, les interactions ne sont possibles qu'avec les sphères situées soit dans la même cellule, soit dans une des 8 cellules voisines.

On note L la largeur du domaine carré, N_c le nombre de cellules par dimension. La largeur des cellules est l_c=L/N_c. Elle doit être supérieure ou égale au diamètre d des sphères.

Sur la figure suivante, la largeur des cellules est égale au diamètre des sphères. Une sphère de centre C est représentée, avec les 9 cellules dans lesquelles il faut rechercher d'éventuelles voisines en interaction.

Figure pleine page

On remarque que pour une sphère située dans une cellule du bord du domaine, des cellules situées près du bord opposé font partie du voisinage à explorer. Une telle cellule est montrée sur la figure (en vert), avec ses 8 proches voisines. Les trois cellules voisines de droite ont un indice i=0, à cause des conditions limites périodiques. Pour ces cellules, les coordonnées des centres des sphères qu'elles contiennent doivent être décalées de la manière suivante :

x_{d} = x + L (6)

2.e. Intégration des équations différentielles

Pour intégrer les équations du mouvement $(4)$ , la méthode numérique doit présenter les propriétés suivantes :

Le moins possible d'évaluations des forces, très coûteuses en nombre d'opérations.
Une stabilité, qui permet d'effectuer des calculs sur des temps très longs.
Une énergie qui reste constante (aux fluctuations près).

La précision n'est pas recherchée pour ce type de calcul. Un système formé de N corps en interactions non linéaires se comporte de manière chaotique : la solution, qu'elle soit exacte ou approchée, est extrêmement sensible aux conditions initiales. Cela rend complètement illusoire la recherche d'une solution précise. Il n'est donc pas nécessaire d'utiliser des méthodes à ordre élevé, qui seraient très coûteuses en nombre d'évaluation des forces.

Une première idée est d'utiliser la méthode d'Euler explicite. Le pas de temps est fixé; on le note h. Les accélérations ayant été évaluées à l'instant t, on calcule les vitesses et les positions à l'instant t+h :

\begin{matrix} \vec{a_{i}} (t) = \sum_{j \neq i} \vec{f} (\vec{r_{i}} (t) - \vec{r_{j}} (t)) & (7) \\ \vec{r_{i}} (t + h) = \vec{r_{i}} (t) + h \vec{v_{i}} (t) & (8) \\ \vec{v_{i}} (t + h) = \vec{v_{i}} (t) + h \vec{a_{i}} (t) & (9) \end{matrix}

Comme nous le verrons plus loin, la méthode d'Euler est instable, et n'est donc pas adaptée à la dynamique moléculaire. Même si le pas de temps est choisi assez petit pour ne pas observer d'instabilité sur le temps de calcul, on observe une dérive de l'énergie.

Une modification de la méthode d'Euler permet de la rendre stable (pour les systèmes linéaires). La méthode symplectique Euler A est définie de la manière suivante :

\begin{matrix} \vec{r_{i}} (t + h) = \vec{r_{i}} (t) + h \vec{v_{i}} (t) & (10) \\ \vec{a_{i}} (t + h) = \sum_{j \neq i} \vec{f} (\vec{r_{i}} (t + h) - \vec{r_{j}} (t + h)) & (11) \\ \vec{v_{i}} (t + h) = \vec{v_{i}} (t) + h \vec{a_{i}} (t + h) & (12) \end{matrix}

Le calcul de la vitesse à l'instant t+h se fait avec l'accélération calculée à l'instant t+h (et non pas t comme dans la méthode d'Euler). Il faut donc effectuer un calcul des forces après avoir calculé la position à l'instant t+h. En dynamique moléculaire, cela se fait sans difficulté car les forces ne dépendent pas des vitesses.

Cette méthode fonctionne bien en dynamique moléculaire mais elle est d'ordre 1. Une variante, la méthode de Stormer-Verlet, est d'ordre 2. Elle consiste à calculer des vitesses intermédiaires, au temps t+h/2 :

\begin{matrix} \vec{v_{i}} (t + h / 2) = \vec{v_{i}} (t) + (h / 2) \vec{a_{i}} (t) & (13) \\ \vec{r_{i}} (t + h) = \vec{r_{i}} (t) + h \vec{v_{i}} (t + h / 2) & (14) \\ \vec{a_{i}} (t + h) = \sum_{j \neq i} \vec{f} (\vec{r_{i}} (t + h) - \vec{r_{j}} (t + h)) & (15) \\ \vec{v_{i}} (t + h) = \vec{v_{i}} (t + h / 2) + (h / 2) \vec{a_{i}} (t + h) & (16) \end{matrix}

La vitesse intermédiaire est utilisée pour calculer la position au temps t+h. L'accélération au temps t+h est calculée, puis la vitesse au temps t+h est calculée à partir de cette accélération. On voit qu'il y a un seul calcul des forces pour chaque pas de temps.

Ce schéma peut être reformulé sans faire intervenir la vitesse ([2]):

\vec{r_{i}} (t + h) = - \vec{r_{i}} (t - h) + 2 \vec{r_{i}} (t) + h^{2} \vec{a_{i}} (t) (17)

Il est toutefois intéressant de calculer aussi les vitesses, dans le but d'effectuer des calculs statistiques sur les vitesses.

Remarque : la stabilité de ces deux méthodes peut être démontrée pour un système linéaire. Pour un système non linéaire de dynamique moléculaire, l'expérience montre que ces méthodes sont stables en pratique.

2.f. Température et pression

La dynamique moléculaire permet d'obtenir facilement des moyennes temporelles (à la différence des méthodes de Monte-Carlo qui permettent d'obtenir des moyennes d'ensemble). Soit une grandeur A et A_n ses valeurs obtenues pour des configurations régulièrement espacées dans le temps. La moyenne temporelle sur P configurations est :

< A > = \frac{1}{P} \sum_{n = 1}^{P} A_{n} (18)

La température est définie avec le théorème d'équipartition de l'énergie. Les sphères ont ici deux degrés de liberté (en dimension 2). L'énergie cinétique moyenne (temporelle) est donc :

< E c > = N k_{B} T (19)

avec :

E c = \frac{1}{2} m \sum_{i} v_{i}^{2} (20)

Le viriel du système est défini par :

V = \sum_{i} \vec{r_{i}} \cdot \vec{f_{i}} (21)

où $\vec{f_{i}}$ est la somme des forces agissant sur la sphère i.

Le théorème du viriel ([3]) donne une relation entre la moyenne temporelle du viriel et celle de l'énergie cinétique :

< E_{c} > = - \frac{1}{2} < V > (22)

À deux dimensions, la pression est une force moyenne par unité de longueur. Considérons par exemple un cercle de rayon r centrée sur l'origine O. Le viriel des sphères situées à l'intérieur du cercle se décompose en deux parties : le viriel intérieur, qui fait intervenir les forces intérieures au cercle, et le viriel extérieur, qui s'exprime avec les forces exercées par les sphères situées en dehors du cercle. La moyenne du viriel extérieur s'exprime avec la pression par l'intégrale curviligne suivante sur le cercle :

< V_{e x t} > = - \oint \vec{r} \cdot P \vec{n} d l = - r P 2 π r = - 2 P A (23)

où A est l'aire du cercle. En utilisant le théorème du viriel, on obtient donc :

P A = N k_{B} T + \frac{1}{2} < \sum_{i} \vec{r_{i}} \cdot \vec{f_{i}} > (24)

Pour calculer la moyenne temporelle du viriel, il est préférable de regrouper les termes par paires de sphères. En utilisant le principe des actions réciproques, on obtient :

P A = N k_{B} T + \frac{1}{2} < \sum_{i < j} {\vec{r}}_{i j} \cdot \vec{f} ({\vec{r}}_{i j}) > (25)

Compte tenu de la forme adoptée pour la force, on obtient finalement :

P A = N k_{B} T + 6 ε < \sum_{i < j} ({(d / r_{i j})}^{12} - {(d / r_{i j})}^{6}) > (26)

On obtient ainsi la pression. Le calcul fait pour différentes densités permet d'obtenir l'équation d'état. L'échelle de température utilisée pour les calculs est choisie en posant k_B=1.

3. Implémentation Python

spheresMolles2d.py

import math
import numpy
import random
import pygame

Comme les sphères se déplacent sur un plan, elles sont représentées par des disques. La classe Disque contient les coordonnées du centre, la vitesse et l'accélérations :

class Disque:
    def __init__(self,x,y,vx,vy):
        self.x = x
        self.y = y
        self.vx  = vx
        self.vy = vy
        self.ax = 0.0
        self.ay = 0.0

Il s'agit d'une simple structure de données : on accédera directement aux données, pour les lire ou les modifier.

La classe suivante représente une cellule, qui contient une liste de disques. Le type set (ensemble) est utilisé pour cette liste. Ce type permet d'enlever et d'ajouter facilement un objet. Les disques seront référencés par un indice sur un tableau. On stocke donc cet indice dans la cellule.

class Cellule:
    def __init__(self):
        self.ensemble_disques = set()
        self.decal_x = 0.0
        self.decal_y = 0.0
    def ajouter(self,indice):
        self.ensemble_disques.add(indice)
    def enlever(self,indice):
        self.ensemble_disques.remove(indice)

La classe Grille contient un tableau bidimensionnel de cellules (une liste de listes). Le constructeur, qui prend en argument la largeur L de la grille, crée le tableau. La fonction obtenir_cellule(i,j) renvoit la cellule dont les indices sont donnés en argument. Lorsque les indices sortent des bornes de la grille, la condition limite périodique est appliquée. Dans ce cas, un décalage doit être appliqué aux coordonnées des disques. Ce décalage est stocké dans la cellule renvoyée.

class Grille:
    def __init__(self,Nc,L):
        self.L = L
        self.Nc = Nc
        self.tableau = []
        for i in range(self.Nc):
            ligne = []
            for j in range(self.Nc):
                ligne.append(Cellule())
            self.tableau.append(ligne)
    def obtenir_cellule(self,i,j):
            decal_x = 0.0
            decal_y = 0.0
            if i<0:
                i += self.Nc
                decal_x = -self.L
            elif i>=self.Nc:
                i -= self.Nc
                decal_x = self.L
            if j<0:
                j += self.Nc
                decal_y = -self.L
            elif j>=self.Nc:
                j -= self.Nc
                decal_y = self.L
            cellule = self.tableau[i][j]
            cellule.decal_x = decal_x
            cellule.decal_y = decal_y
            return cellule

La classe Systeme effectue les calculs. Le constructeur prend en argument le nombre de sphères par dimension (la racine du nombre total) et la densité.

class Systeme:
    def __init__(self,Nx,densite):
        self.Nx = Nx
        self.N = Nx*Nx
        self.rayon = 0.5
        self.diam = self.rayon*2
        self.diam2 = self.diam**2
        self.L = math.sqrt(math.pi/densite)*0.5*Nx
        self.aire = self.L*self.L
        self.demi_L = self.L*0.5
        self.Nc = int(self.L/self.diam)
        self.lc = self.L/self.Nc
        self.grille = Grille(self.Nc,self.L)
        self.liste_disques = []
        for d in range(self.N):
            self.liste_disques.append(Disque(0,0,0,0))
        self.energie = 0.0
        self.viriel = 0.0
        self.Ecinetique = 0.0
        self.Epotentielle = 0.0
        self.pression = 0.0

La fonction suivante permet d'initialiser un disque dont l'indice est donné, avec une position et une vitesse donnée. L'indice est ajouté dans la cellule qui contient le disque.

    def init_disque(self,indice,x,y,vx,vy):
        disque = self.liste_disques[indice]
        disque.x = x
        disque.y = y
        disque.vx = vx
        disque.vy = vy
        i = int(x/self.lc)
        j = int(y/self.lc)
        cellule = self.grille.obtenir_cellule(i,j)
        cellule.ajouter(indice)

Pour initialiser le système, on place les sphères régulièrement espacées avec une vitesse de direction aléatoire, dont la norme est donnée. En pratique, on pourra choisir cette vitesse en fonction de la température souhaitée.

    def initialiser(self,vitesse):
        dx = self.L*1.0/(self.Nx)
        print("distance initiale = %f"%dx)
        if dx < self.diam:
            raise Exception("densite trop forte")
        else:
            dy = dx
            x = dx/2
            y = x
            px = 0.0
            py = 0.0
            for k in range(self.N):
                a = random.random()*math.pi*2.0
                vx = vitesse*math.cos(a)
                vy = vitesse*math.sin(a)
                px += vx
                py += vy
                self.init_disque(k,x,y,vx,vy)
                x += dx
                if x > self.L:
                    x = dx/2
                    y += dy
            for k in range(self.N):
                disque = self.liste_disques[k]
                disque.vx -= px/self.N
                disque.vy -= py/self.N 
        self.calculer_forces()

La fonction suivante déplace un disque à une position donnée. Si le disque change de cellule, les deux cellules concernées sont mises à jour.

    def deplacer_disque(self,disque,indice,x1,y1):
        if x1<0:
            x1 %= self.L
        elif x1>=self.L:
            x1 %= self.L
        if y1<0:
            y1 %= self.L
        elif y1>=self.L:
            y1 %= self.L
        i = int(disque.x/self.lc)
        j = int(disque.y/self.lc)
        i1 = int(x1/self.lc)
        j1 = int(y1/self.lc)
        if i!=i1 or j!=j1:
            cellule = self.grille.obtenir_cellule(i,j)
            cellule.enlever(indice)
            cellule1 = self.grille.obtenir_cellule(i1,j1)
            cellule1.ajouter(indice)
        disque.x = x1
        disque.y = y1

La fonction suivante calcule les forces sur les disques et stocke le résultat dans les accélérations des disques. La boucle principale se fait sur les cellules de la grille. Pour chaque cellule, les cellules voisines sont explorées afin d'extraire les paires susceptibles d'interagir. Enfin si la distance entre les deux sphères est inférieure à la portée de l'interaction, on calcule la force et on affecte les valeurs des accélérations des deux disques. L'énergie potentielle et le viriel sont aussi calculés.

    def calculer_forces(self):
        for k in range(self.N):
            disque = self.liste_disques[k]
            disque.ax = 0.0
            disque.ay = 0.0
        self.Epotentielle = 0.0
        self.viriel = 0.0
        for i in range(self.Nc):
            for j in range(self.Nc):
                cellule = self.grille.obtenir_cellule(i,j)
                for k in range(-1,2):
                    for l in range(-1,2):
                        cellule1 = self.grille.obtenir_cellule(i+k,j+l)
                        for indice in cellule.ensemble_disques:
                                for indice1 in cellule1.ensemble_disques:
                                    if indice1<indice:
                                        disque = self.liste_disques[indice]
                                        disque1 = self.liste_disques[indice1]
                                        dx = disque1.x+cellule1.decal_x-disque.x
                                        dy = disque1.y+cellule1.decal_y-disque.y
                                        r2 = dx*dx+dy*dy
                                        if r2 < self.diam2:
                                            ir2 = 1.0/r2
                                            ir6 = ir2*ir2*ir2
                                            f = 12.0*ir6*(ir6-1.0)*ir2
                                            fx = f*dx
                                            fy = f*dy
                                            disque1.ax += fx
                                            disque1.ay += fy
                                            disque.ax -= fx
                                            disque.ay -= fy
                                            self.Epotentielle += ir6*(ir6-2.0)+1.0
                                            self.viriel += 6.0*ir6*(ir6-1.0)

La fonction suivante calcule l'énergie cinétique, la pression (instantanée), et l'énergie totale. Cette dernière est importante pour contrôler la stabilité du schéma numérique d'intégration, car elle doit en principe rester constante. Toutes ces grandeurs sont divisées par le nombre de sphères.

    def calculer_cinetique(self):
        self.Ecinetique = 0.0
        for k in range(self.N):
            disque = self.liste_disques[k]
            self.Ecinetique += 0.5*(disque.vx*disque.vx+disque.vy*disque.vy)
        self.pression = (self.Ecinetique+self.viriel)/self.aire
        self.Ecinetique /= self.N
        self.energie = self.Ecinetique+self.Epotentielle/self.N

Les trois fonctions suivantes effectuent un pas élémentaire pour respectivement, la méthode d'Euler, la méthode d'Euler symplectique (Euler A), et la méthode de Stormer-Verlet. Le pas de temps et sa moitié sont fournis en argument. Le calcul des forces devra être fait avant d'appeler ces fonctions pour la première fois.

    def euler(self,h,hd2):
        for k in range(self.N):
            disque = self.liste_disques[k]
            self.deplacer_disque(disque,k,disque.x+h*disque.vx,disque.y+h*disque.vy)
            disque.vx += h*disque.ax
            disque.vy += h*disque.ay
        self.calculer_forces()
    def eulerA(self,h,hd2):
        for k in range(self.N):
            disque = self.liste_disques[k]
            self.deplacer_disque(disque,k,disque.x+h*disque.vx,disque.y+h*disque.vy)
        self.calculer_forces()
        for k in range(self.N):
            disque = self.liste_disques[k]
            disque.vx += h*disque.ax
            disque.vy += h*disque.ay
    def verlet(self,h,hd2):
        for k in range(self.N):
            disque = self.liste_disques[k]
            disque.vx += hd2*disque.ax
            disque.vy += hd2*disque.ay
            self.deplacer_disque(disque,k,disque.x+h*disque.vx,disque.y+h*disque.vy)
        self.calculer_forces()
        for k in range(self.N):
            disque = self.liste_disques[k]
            disque.vx += hd2*disque.ax
            disque.vy += hd2*disque.ay

La fonction suivante effectue plusieurs pas d'intégration avec un pas de temps donné. La méthode est une des trois fonctions précédentes.

    def integration(self,methode,h,n):
        hd2 = h/2
        for i in range(n):
            methode(h,hd2)

La fonction suivante effectue le dessin des disques avec pygame.

    def dessiner_disques(self,screen,echelle,couleur):
        for k in range(self.N):
            disque = self.liste_disques[k]
            pygame.draw.ellipse(screen,couleur,[(disque.x-self.rayon)*echelle,(disque.y-self.rayon)*echelle,self.rayon*2*echelle,self.rayon*2*echelle],2)

4. Exemple

from spheresMolles2d import *
import pygame
from matplotlib.pyplot import *

On considère 400 disques avec une densité de 0.3. L'intégration se fait par paquet de 10 pas élémentaires. Une boucle permet de faire une animation pygame.

N = 20
densite = 0.3
h = 0.005
sys = Systeme(N,densite)
sys.initialiser(1.0)
pygame.init()
taille = 500
screen = pygame.display.set_mode([taille,taille])
echelle = taille*1.0/sys.L
clock = pygame.time.Clock()
done = False
pression = numpy.zeros(0)
ec = numpy.zeros(0)
energie = numpy.zeros(0)
iter = 500
while not done and iter > 0:
    iter -= 1
    clock.tick(30)
    screen.fill((255,255,255))
    for event in pygame.event.get():
        if event.type == pygame.QUIT:
            done = True
    sys.dessiner_disques(screen,echelle,(255,0,0))
    sys.integration(sys.verlet,h,10)
    sys.calculer_cinetique()
    print(sys.energie)
    pression = numpy.append(pression,sys.pression)
    ec = numpy.append(ec,sys.Ecinetique)
    energie = numpy.append(energie,sys.energie)
    pygame.display.flip()
pygame.image.save(screen,"../../../../figures/sciphys/dynmol/spheresmolles2d/disques.png")
pygame.quit()

Voici la dernière configuration obtenue, enregistrée sous forme d'image PNG :

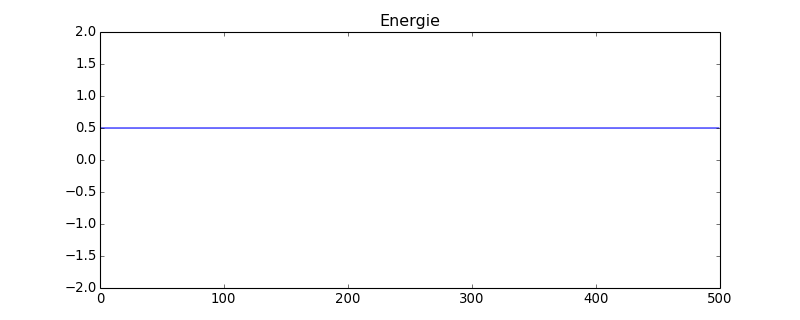
Lorsque la fenêtre graphique pygame est fermée, on procède au tracé de l'énergie, de l'énergie cinétique et de la pression instantanées.

figure(figsize=(10,4))
plot(energie)
title("Energie") 
axis([0,energie.size,-2,2])

figB.pdf

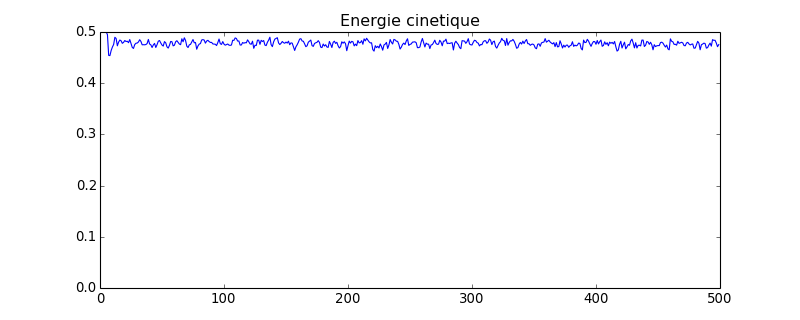
figure(figsize=(10,4))
plot(ec)
axis([0,ec.size,0,ec.max()])
title("Energie cinetique")

figC.pdf

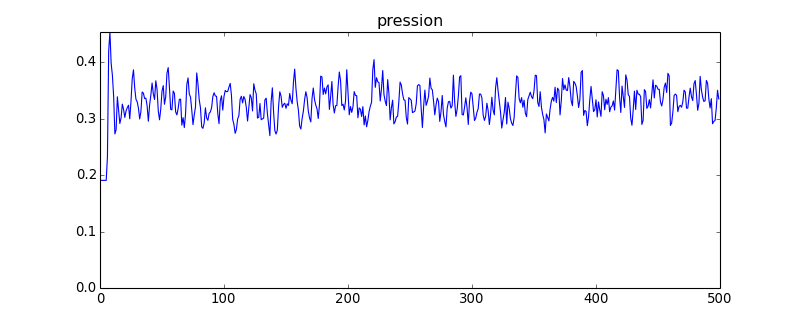
figure(figsize=(10,4))
plot(pression)
axis([0,pression.size,0,pression.max()])
title("pression")

figD.pdf

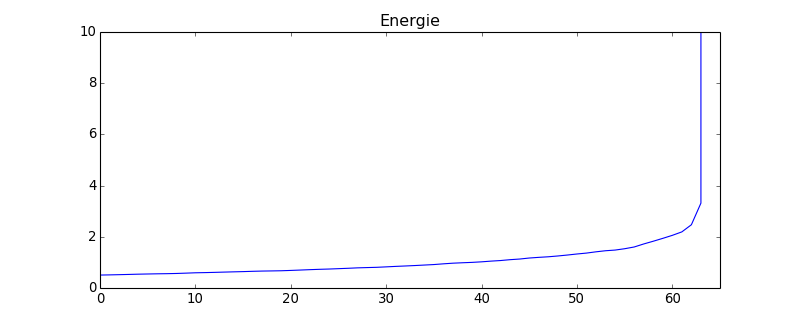
L'énergie mécanique est constante, ce qui montre que la méthode de Stormer-Verlet est bien adapté à ce problème. Voyons pour comparaison ce que donne la methode d'Euler. Comme l'énergie diverge, on place une énergie seuil pour arrêter la boucle :

energie = numpy.zeros(0)
while sys.energie < 10.0:
    sys.integration(sys.euler,h,10) 
    sys.calculer_cinetique()
    print(sys.energie)
    energie = numpy.append(energie,sys.energie)
figure(figsize=(10,4))
plot(energie)
title("Energie")
axis([0,energie.size,0,10.0])

figE.pdf

Dans un premier temps, l'énergie augmente lentement puis diverge très rapidement. La méthode d'Euler est donc instable pour ce problème. Si l'on abaisse le pas de temps, la divergence est retardée mais finit toujours par arriver.

Voyons l'influence du nombre de sphères, en augmentant Nx sans changer la densité

N = 40
densite = 0.3
h = 0.005
sys = Systeme(N,densite)
sys.initialiser(1.0)
pygame.init()
taille = 500
screen = pygame.display.set_mode([taille,taille])
echelle = taille*1.0/sys.L
clock = pygame.time.Clock()
done = False
pression = numpy.zeros(0)
ec = numpy.zeros(0)
energie = numpy.zeros(0)
iter = 500
while not done and iter > 0:
    iter -= 1
    clock.tick(30)
    screen.fill((255,255,255))
    for event in pygame.event.get():
        if event.type == pygame.QUIT:
            done = True
    sys.dessiner_disques(screen,echelle,(255,0,0))
    sys.integration(sys.verlet,h,10)
    sys.calculer_cinetique()
    print(sys.energie)
    pression = numpy.append(pression,sys.pression)
    ec = numpy.append(ec,sys.Ecinetique)
    energie = numpy.append(energie,sys.energie)
    pygame.display.flip()
pygame.quit()

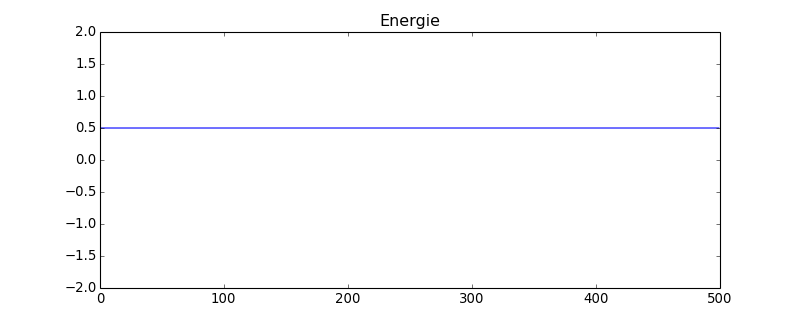
figure(figsize=(10,4))
plot(energie)
title("Energie") 
axis([0,energie.size,-2,2])

figF.pdf

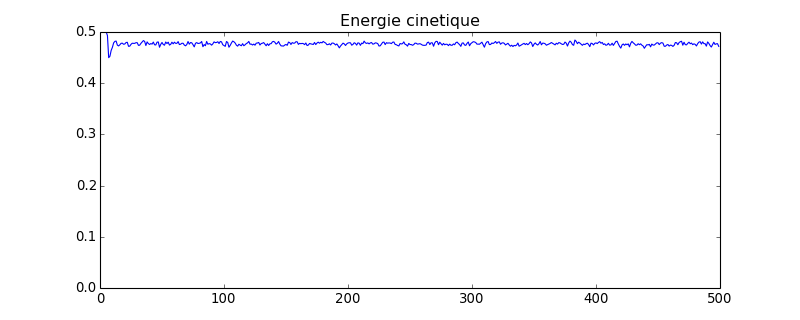
figure(figsize=(10,4))
plot(ec)
axis([0,ec.size,0,ec.max()])
title("Energie cinetique")

figG.pdf

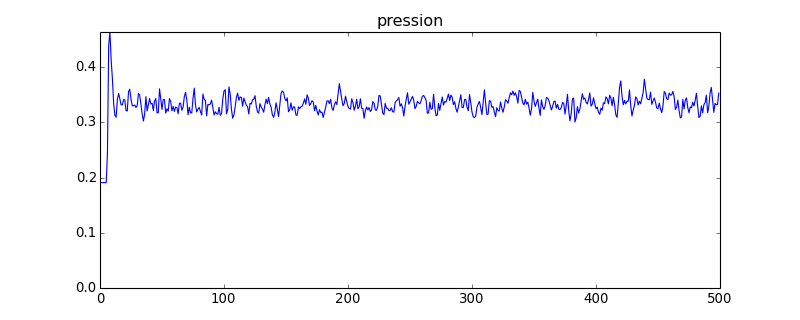
figure(figsize=(10,4))
plot(pression)
axis([0,pression.size,0,pression.max()])
title("pression")

figH.pdf

Avec ce système comportant 4 fois plus de sphères que le précédent, les fluctuations de la pression sont nettement réduites (en théorie d'un facteur 2). On constate aussi une légère diminution de la valeur moyenne, qui montre que la taille finie du système a une influence.

Un système macroscopique présente des fluctuations de température et de pression très faibles en raison du nombre gigantesque de molécules qu'il contient. Pour réduire les fluctuations à un niveau négligeable (disons un pour cent), il faut encore augmenter le nombre de sphères. Cela a bien sûr un coût en temps de calcul. Dans le meilleur des cas, le temps de calcul est proportionnel à N. Si les forces étaient calculées en considérant toutes les paires du système, on aurait une croissance en N². Dans notre cas, la méthode d'accélération consistant à explorer les cellules voisines conduit vraisemblablement à une croissance de la forme N^e, où l'exposant e est proche de 1. Des tests devront être fait pour déterminer cet exposant.

Références

[1] D.C. Rapaport, The art of molecular dynamics simulation, (Cambridge University Press, 2004)

[2] L. Verlet, Computer experiments on classical fluids. I. Thermodynamical properties of Lennard-Jones molecules, (Phys Rev 159 p 98, 1967)

[3] B. Diu, C. Guthmann, D. Lederer, B. Roulet, Physique statistique, (Hermann, 1989)