Mesure de déphasage

1. Introduction

Ce document montre comment déterminer le déphasage de deux signaux sinusoïdaux échantillonnés. Les expériences sont réalisées avec la carte Sysam SP5 mais les méthodes de traitement numérique du signal décrites sont utilisables avec tout système d'acquisition.

On considère deux signaux de forme sinusoïdale $e (t) = E cos (ω t)$ et $s (t) = S cos (ω t + φ)$ . Les signaux échantillonnés à la fréquence d'échantillonnage f_e sont notés e_n et s_n. Il s'agit de déterminer le déphasage $φ$ . On adoptera la convention d'un dépasage dans l'intervalle [0,2π]. Il sera aisé d'exprimer les déphasages dans l'intervalle [π,2π] sous la forme d'un déphasage négatif en leur retranchant 2π.

2. Méthodes de mesure du déphasage

2.a. Méthode du cosinus

Cette méthode repose sur le résultat suivant :

\frac{1}{T} \int_{0}^{T} e (t) s (t) d t = \frac{E S}{2} cos (φ) = E_{e f f} S_{e f f} cos (φ) (1)

Les valeurs efficaces sont définies par :

\begin{matrix} E_{e f f} = \sqrt{\frac{1}{T} \int_{0}^{T} e^{2} (t) d t} & (2) \\ S_{e f f} = \sqrt{\frac{1}{T} \int_{0}^{T} s^{2} (t) d t} & (3) \end{matrix}

L'intégrale $(1)$ est évaluée à partir des signaux échantillonnés comme étant la moyenne de e_ns_n sur la totalité de l'enregistrement, qui en général s'étend sur un grand nombre de cycles. Les valeurs efficaces sont les écart-types de e_n et s_n.

Ces calculs conduisent donc à la valeur de $cos (φ)$ . La fonction arccos fournit le déphasage mais cette méthode ne permet pas de savoir s'il est dans l'intervalle [0,π] ou dans l'intervalle [π,2π]. Elle est cependant intéressante si on sait a priori dans quel intervalle le déphasage se trouve, c'est-à-dire si s(t) est en avance ou en retard sur e(t).

L'avantage de cette méthode est qu'elle ne nécessite pas de connaître la fréquence du signal.

2.b. Méthode du cosinus et du sinus

Considérons la fonction suivante :

\begin{matrix} x (t) = & s (t) (e (t) - j e (t - \frac{T}{4})) \\ = & E S cos (ω t + φ) (cos (ω t) - j sin (ω t)) \\ = & \frac{E S}{2} (e^{j φ} + e^{- j (2 ω t + φ)}) \end{matrix}

Sa valeur moyenne est :

\bar{x} = \frac{E S}{2} e^{j φ} = E_{e f f} S_{e f f} e^{j φ} (4)

Le déphasage est donc l'argument de $\bar{x}$ . Cette méthode fournit à la fois le cosinus et le sinus du déphasage mais elle nécessite de disposer du signal e(t-T/4), c'est-à-dire le signal e(t) retardé d'un quart de période. Le signal échantillonné correspondant est accessible à condition de connaître la période T. Celle-ci peut être déterminée par analyse spectrale au moyen d'une transformée de Fourier discrète. Il est alors possible de déterminer le décalage d égal au nombre d'échantillons correspondant à un quart de période :

d = \frac{T}{4 T_{e}} (5)

On a alors

x_{n} = s_{n} (e_{n} - j e_{n - d}) (6)

La valeur de d n'est pas en général entière et on doit donc se contenter d'une approximation (nombre entier le plus proche). L'erreur qui résulte de cet arrondi peut être réduite en augmentant la fréquence d'échantillonnage grace à une méthode d'interpolation. On peut pour cela appliquer la méthode d'interpolation par transformée de Fourier. Cette méthode consiste à calculer la transformée de Fourier discrète (TFD) des N échantillons du signal e_n, à séparer ses deux parties conjugées de taille N/2 puis à ajouter kN zéro entre ces deux parties. On obtient ainsi la TFD d'un signal qui comporte (k+1)N échantillons et qui est obtenu par la transformée de Fourier inverse. L'ajout de zéro dans le domaine fréquentiel est équivalent à une interpolation dans le domaine temporel (et réciproquement). La fréquence d'échantillonnage du nouveau signal est (k+1)f_e donc la période d'échantillonnage est T_e/(k+1). Il s'en suit que :

d = \frac{(k + 1) T}{4 T_{e}} (7)

Plus k est grand, plus la valeur de d est grande et moins elle est sujette aux erreurs d'arrondi.

2.c. Méthode d'analyse temporelle

Cette méthode consiste à parcourir les valeurs s_n par indice n croissant et à détecter un passage par zéro par valeur croissante. On procède ensuite à la même recherche pour e_n. Le décalage temporel entre les deux passages par zéro par valeur croissante donne accès au déphasage, à condition de connaître la période. La recherche est répétée sur la totalité du signal échantillonné afin de calculer une moyenne des décalages temporels. Cette méthode a l'avantage de s'appliquer aussi aux signaux périodiques non sinusoïdaux, en particulier les signaux carrés. Il faut remarquer que la période peut être déterminée aussi par analyse temporelle, en déterminant le décalage entre deux passages par zéro par valeur croissante de e_n. Il n'est donc pas nécessaire de faire appel à la transformée de Fourier discrète.

Le passage par zéro de s est détecté lorsqu'on trouve un indice n tel que s_n<0 et s_n+1>0.

Cependant, cette méthode comporte une difficulté : lorsque les signaux sont bruités, ce qui doit être interprété comme un passage par zéro peut en réalité comporter plusieurs changements de signe très rapprochés. En électronique analogique, ce problème est résolu en ajoutant un hystérésis au comparateur. Il est possible de programmer un hystérésis numérique mais il est préférable d'appliquer un filtrage passe-bas numérique afin de lisser le signal et d'éliminer les passages multiples par zéro. Nous appliquons pour cela un filtre de convolution (filtre à réponse impulsionnelle finie). Bien sûr, il faut appliquer le même filtrage à s_n et à e_n car le filtrage introduit un retard.

Cette méthode nécessite a priori une fréquence d'échantillonnage beaucoup plus grande que celle du signal, sans quoi la détermination du retard est très imprécise. Il semble que ce soit la méthode mise en œuvre dans les oscilloscopes numériques, dont la fréquence d'échantillonnage de l'ordre du GHz est en effet très grande par rapport à la fréquence des signaux de basse fréquence (en dessous du MHz).

Cette méthode a aussi l'avantage de s'appliquer si le déphasage est amené à changer rapidement, par exemple en modulation de phase ou de fréquence.

3. Implémentation

Les deux signaux e(t) et s(t) sont numérisés avec la carte Sysam SP5 sur les entrées EA0 et EA1. Il est important de vérifier que les amplificateurs d'entrée sont bien calibrés (ils le sont en principe grace aux données de calibrage inscrites dans la carte et prises en compte par le logiciel). Ce qui importe en fait est que les deux entrées délivrent exactement les mêmes signaux échantillonnés si on leur fournit le même signal analogique. Il est facile de le vérifier.

Le script permet de tester les trois méthodes de détermination du déphasage au moyen d'un générateur DDS à deux sorties, le déphasage étant choisi sur le panneau du générateur. Pour chaque mesure, on entre la valeur du déphasage programmée, ou bien N pour arrêter les mesures et les enregistrer dans un fichier. Pour la méthode temporelle, nous déterminons la fréquence par analyse spectrale mais une détermination par analyse temporelle serait à adopter pour une détermination du déphasage en temps réel (cycle par cycle).

testMesureDephasage.py

import numpy as np
import matplotlib.pyplot as plt
import pycanum.main as pycan
from scipy.signal import blackman
from numpy.fft import fft,ifft
from scipy.signal import firwin,convolve

#mesure de déphasage phi entre 0 et 2pi

P = 40
filtre = firwin(numtaps=2*P+1,cutoff=[0.1],window='hann',nyq=0.5)

def frequence(t,x):
    # calcul de la fréquence par analyse spectrale
    N=len(x)
    te=t[1]-t[0]
    zeros=np.zeros(6*N)
    X = np.concatenate((x*blackman(N),zeros))
    NN=len(X)
    spectre = np.absolute(fft(X))*2.0/N/0.42
    freq = np.arange(NN)*1.0/(NN*te)
    k=np.argmax(spectre[0:NN//2])
    return freq[k]


def interpol(x,ninter):
    # interpolation par FFT
    # ninter est le paramètre noté k dans le texte
    N = len(x)
    tfd = fft(x)
    N1 = N//2
    tfd2 = np.concatenate((tfd[0:N1],np.zeros(N*ninter),tfd[N1:N]))
    y = np.real(ifft(tfd2))*(ninter+1)
    return y
    
def decalage(x1,x2):
    # calcul du décalage moyen de x2 par rapport à x1
    # la liste des décalages est aussi renvoyée
    x1 = convolve(x1,filtre,mode='valid')
    x2 = convolve(x2,filtre,mode='valid')
    N = len(x1)
    ia = 0
    decal = 0
    nd = 0
    liste_decal = []
    for i in range(1,N):
        if x1[i-1] < 0 and x1[i] > 0:
            ia = i
        if x2[i-1] <0 and x2[i] > 0:
            if ia!=0:
                decal += i-ia
                
                liste_decal.append(i-ia)
                nd += 1
                ia = 0
    decal /= nd
    return (np.array(liste_decal),decal)
    
def dephasageA(t,u0,u1):
    # méthode du cosinus
    cosphi = np.mean(u0*u1)/(u0.std()*u1.std())
    phiA = np.arccos(cosphi)
    return phiA
    
def dephasageB(t,u0,u1,ninter):
    # méthode du cosinus et du sinus
    # ninter est le paramètre k
    freq = frequence(t,u0)
    T = 1/freq
    te = t[1]-t[0]
    if ninter>0:
        v0 = interpol(u0,ninter)
        v1 = interpol(u1,ninter)
    d = int((ninter+1)*T/(4*te))
    N = len(v0)
    x = v1[d:N]*(v0[d:N]-1j*v0[0:N-d])
    phiB = np.angle(x.mean())
    if phiB<0:
        phiB = 2*np.pi+phiB
    return phiB
    
def dephasageC(t,u0,u1):
    # méthode d'analyse temporelle
    freq = frequence(t,u0)
    (decal,d) = decalage(u1,u0) # déphasage de u1 par rapport à u0
    te = t[1]-t[0]
    phiC = d*te*freq*2*np.pi
    return phiC
    
def mesure(can,techant,ninter,N=130000,plot=False):
    can.config_echantillon(techant*1e6,N)
    can.acquerir()
    t=can.temps()[0]
    signaux = can.entrees()
    u0=signaux[0]
    u1=signaux[1]
    u0=u0-u0.mean() #on élimine un éventuel décalage de tension
    u1=u1-u1.mean()
    phiA = dephasageA(t,u0,u1)
    phiB = dephasageB(t,u0,u1,ninter)
    phiC = dephasageC(t,u0,u1)
    if np.sin(phiC) <0:
        phiA = -phiA+np.pi*2
    if plot:
        plt.figure()
        plt.plot(t,u0,'b')
        plt.plot(t,u1,'r')
        plt.grid()
        plt.ylim(-10,10)
        plt.xlim(0,20/freq)
        plt.show()
    return (phiA*180/np.pi,phiB*180/np.pi,phiC*180/np.pi)
    
data = []
can = pycan.Sysam("SP5")
Vmax = 5
can.config_entrees([0,1],[Vmax,Vmax],diff=[0])
f = 10000 # fréquence
ninter = 4
techant = 1/f/1000 # période d'échantillonnage 
if techant < 1e-7:
    techant = 1e-7
while True:
    r = input("Déphasage (deg) ou N pour arrêter?")
    if r!='N':
        phi = float(r)
        (phiA,phiB,phiC) = mesure(can,techant,ninter,plot=False)
        print("phi = %f °, phiA = %f °, phiB = %f °, phiC = %f °"%(phi,phiA,phiB,phiC))
        
        data.append([f,phi,phiA,phiB,phiC])
    else:
        break
    
can.fermer()
data = np.array(data)
np.savetxt('testMesureDephasage-1000Hz-5.txt',data,header='f\t phi\t phiA\t phiB\t phiC')

phi = data[:,1]
phiA = data[:,2]
phiB = data[:,3]
phiC = data[:,4]

plt.figure()
plt.plot(phi,phiA,"ro")
plt.plot(phi,phiB,"bo")
plt.plot(phi,phiC,"go")
plt.grid()
plt.show()

4. Résultats

Le test est effectué avec un générateur DDS Siglent 1062X. Les signaux sinusoïdaux délivrés sur les deux voies sont programmés à la même fréquence et la même amplitude. Ils sont parfaitement synchrones et leur déphasage peut être ajusté au millième de degré près.

Voici les résultats pour une fréquence de 1000 Hz et une fréquence d'échantillonnage 1000 fois plus grande. Le déphasage est incrémenté de 10 degrés sauf au voisinage de 0 et 90 degrés où l'incrément est de 1 degré.

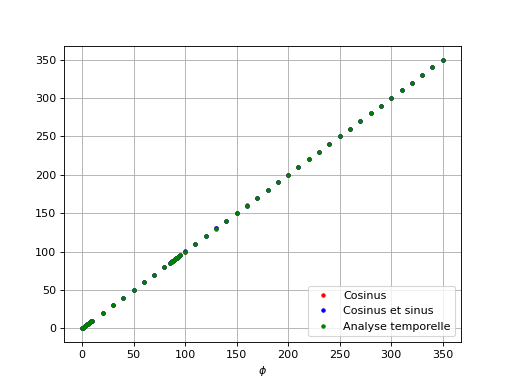dephasages-1.pdf

Pour tester la précision des méthodes, voici l'écart avec la valeur configurée sur le générateur :

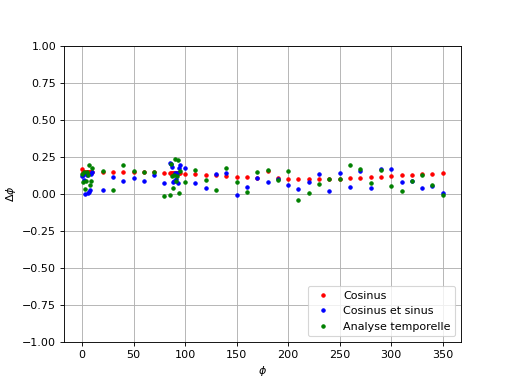dephasages-2.pdf

Les trois méthodes fournissent une valeur systématiquement plus grande que la valeur programmée sur le générateur. Il est possible que cette erreur systématique provienne d'une légère erreur de calibrage de la carte Sysam. Dans tous les cas, l'erreur est inférieure au quart de degré.

Voici les résultats pour la même fréquence mais pour une fréquence d'échantillonnage seulement 100 fois plus grande :

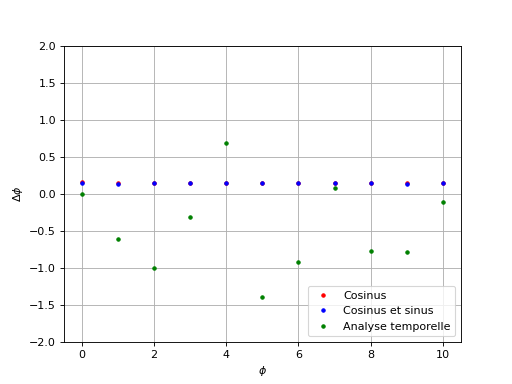dephasages-3.pdf

Dans ce cas, la méthode d'analyse temporelle est très mauvaise car l'écart dépasse parfois 1 degré. Comme prévu, cette méthode nécessite en effet une fréquence d'échantillonnage très grande par rapport à la fréquence du signal (au moins d'un facteur 1000). En revanche, on constate que les deux autres méthodes se comportent de manière plus régulière, ce qui est du au fait que le nombre de cycles analysés est 10 fois plus grand. Voyons les écarts de ces deux méthodes plus en détail :

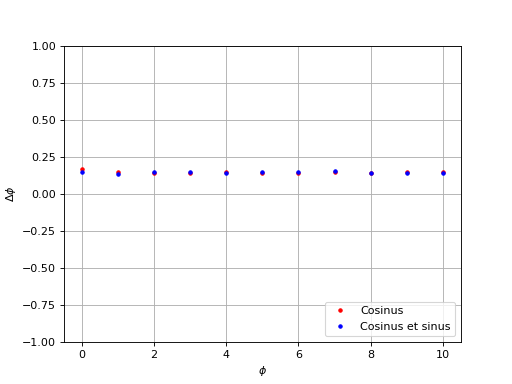dephasages-4.pdf

L'erreur est très faible, d'environ 0,15 degrés. Ces deux méthodes sont donc à privilégier lorsque la fréquence d'échantillonnage n'est pas au moins 1000 fois plus grand que la fréquence du signal, à condition de disposer d'un très grand nombre de cycles (ici 1300 cyles).

Voici les résultats pour une fréquence de 10 kHz, avec une fréquence d'échantillonnage 1000 fois plus grande :

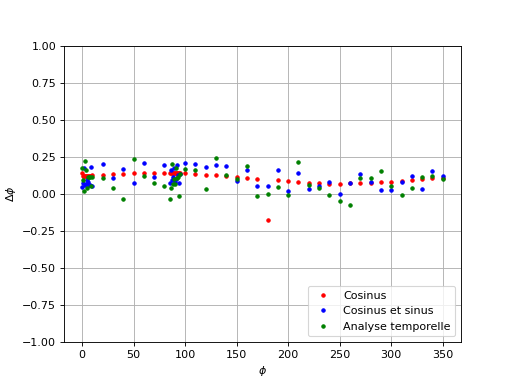dephasages-5.pdf

Le comportement des trois méthodes est similaire à celui obtenu à 1000 Hz. On remarque là aussi que l'erreur de la méthode de cosinus évolue de manière prévisible (en semblant suivre une courbe) alors que la méthode du cosinus et du sinus présente une erreur chaotique. Pour savoir si ces fluctuations sont dues aux fluctuations de la détermination de fréquence par transformée de Fourier, il faudrait faire le calcul en adoptant la valeur de fréquence programmée sur le générateur (qui est précise au micro-hertz près). Les fluctuations peuvent aussi provenir de la détermination du décalage d, qui fait aussi appel à la transformée de Fourier discrète.

Afin de vérifier que l'erreur systématiquement positive provient de la carte Sysam, nous avons inversé les entrées EA0 et EA1. Voici le résultat à 1000 Hz avec une fréquence d'échantillonnage 1000 fois plus grande.

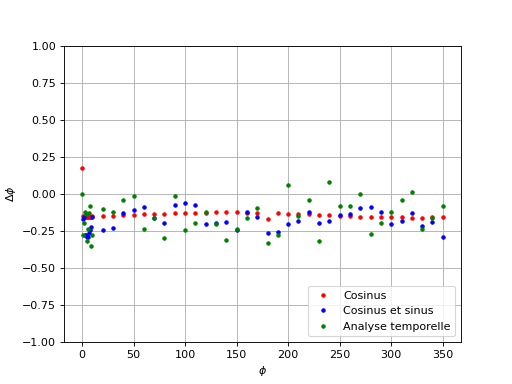dephasages-6.pdf

Il y a bien une erreur systématique négative. Cela confirme que l'erreur systématique est due à un déséquilibre entre les voies EA0 et EA1 de la carte, peut-être un léger décalage temporel dans l'échantillonnage (en principe, les deux voies ont chacune leur convertisseur A/N et fonctionnent simultanément). Le test de plusieurs cartes Sysam SP5 montre que l'erreur est systématiquement positive (déphasage légèrement surestimé) lorsqu'on fait l'acquisition de e(t) sur la voie EA0.