Analyse spectrale d'un signal numérique

1. TFD d'un signal échantillonné

Le spectre d'un signal analogique est obtenu avec sa transformée de Fourier. Le spectre d'un signal numérique est obtenu par sa transformée de Fourier discrète, selon la méthode décrite dans TFD appliquée à la transformée de Fourier.

Considérons comme exemple un signal périodique (de période 1) :

signal[t_]:=Cos[2*Pi*t]+0.5*Cos[2*2*Pi*t]+0.25*Sin[3*2*Pi*t]+0.125*Sin[4*2*Pi*t];

Pour échantillonner ce signal, on fixe un nombre de points et une durée totale qui ne coïncide pas avec une période du signal, comme c'est le cas dans les numérisations de signaux réels :

tmax=50.32563;
n=1000;
te=tmax/n;
fe=1/te (*frequence d'echantillonnage*)
            

19.870590790418323

echant=Table[signal[(k-1)*te],{k,n}];
            

On calcule la TFD et on construit l'échelle de fréquence correspondante :

tfd=Fourier[echant,FourierParameters->{-1,-1}];
spectre=Table[{(k-1)/tmax,Abs[tfd[[k]]]},{k,n}]; 
            

ListPlot[spectre,Filling->Axis,PlotRange->{{0,5},Full},AxesLabel->{"f","A"}]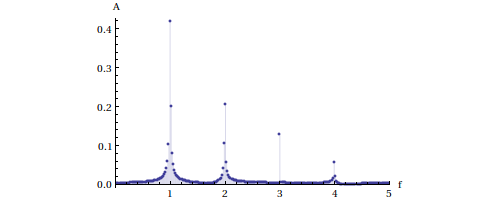

plotA.pdf

Si le signal était échantillonné sur une durée infinie, les raies seraient de largeur nulle (puisque le signal est périodique). L'élargissement de la base des raies est un effet de la durée finie de l'échantillon, c'est-à-dire de l'application d'une fenêtre rectangulaire au signal. On constate également des erreurs sur les hauteurs relatives des raies, qui viennent du fait que la résolution fréquentielle (inverse de la durée de l'échantillon) est insuffisante pour saisir le maximum des raies.

2. Fenêtres de troncature

Soit u(t) le signal analysé sur l'intervalle [0,T]. La fenêtre de troncature w(t) est une fonction nulle en dehors de cette intervalle. L'analyse spectrale consiste alors à calculer la transformée de Fourier suivante :

$$S\left(f\right)={\int }_0^{T}u\left(t\right)w\left(t\right)exp(-i2\pi ft)dt\text{(1)}$$

Dans l'exemple précédent, la fenêtre de troncature est rectangulaire (w(t)=1).

Si l'on note U(f) la transformée de Fourier de u(t) et W(f) celle de la fenêtre w(t), la transformée de Fourier calculée est le produit de convolution :

$$S\left(f\right)={\int }_{-\infty }^{+\infty }U(f-x)W\left(x\right)dx\text{(2)}$$

La transformée de Fourier de la fenêtre rectangulaire est :

$$W\left(f\right)=Texp(-i\pi fT)sinc\left(\pi fT\right)\text{(3)}$$

Pour caractériser l'effet de la fenêtre, on trace le module de sa transformée de Fourier en décibel (par convention T=1) :

Wr[f_]:=Sinc[Pi*f];
            

Plot[20*Log[10,Abs[Wr[f]]],{f,-10,10},AxesLabel->{"f","dB"},
            PlotRange->{Full,{-100,0}}]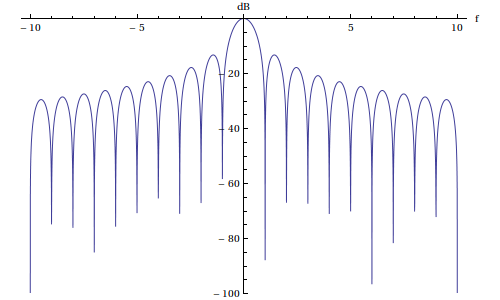

plotB.pdf

La fenêtre de Hamming est définie par :

$$w\left(t\right)=0,54-0,5cos\left(\frac{2\pi }{T}t\right)\text{(4)}$$

hamming[t_]:=Piecewise[{{0,t<0},{0,t>1}},0.54-0.5*Cos[2*Pi*t]];

Plot[hamming[t],{t,0,1}]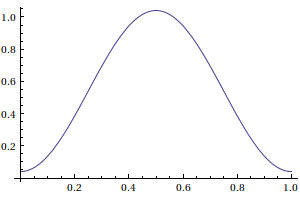

PlotC.pdf

On calcule sa transformée de Fourier puis on trace son module en décibel :

Wh=FourierTransform[hamming[t],t,f,FourierParameters->{0,-2*Pi}];

Plot[20*Log[10,Abs[Wh]],{f,-10,10},AxesLabel->{"f","dB"},PlotRange->{Full,{-100,0}}]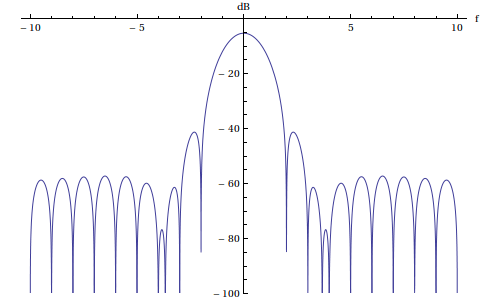

plotD.pdf

Le premier lobe secondaire de part et d'autre du maximum principal est beaucoup plus bas que pour la fenêtre rectangulaire. En revanche, le lobe principal a une largeur à -3dB plus grande. Voyons l'effet de cette fenêtre sur la TFD du signal :

echantHamming = Table[echant[[k]]*hamming[k/n],{k,n}];
tfd=Fourier[echantHamming,FourierParameters->{-1,-1}];
spectre=Table[{(k-1)/tmax,Abs[tfd[[k]]]},{k,n}]; 
            

ListPlot[spectre,Filling->Axis,PlotRange->{{0,5},Full},AxesLabel->{"f","A"}]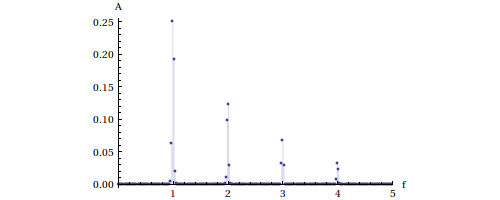

plotE.pdf

Les raies ne présentent plus l'élargissement de leur base observée avec une fenêtre rectangulaire. C'est une conséquence de la valeur beaucoup plus faible des lobes secondaires. Cette propriété est importante pour l'obtention de spectres continus. La hauteur des raies est mieux restituée car le lobe central est plus large : pour une durée totale donnée, il y a donc plus de points dans le lobe central. Lorsque c'est possible, on peut bien sûr augmenter la durée T pour affiner la précision des raies.

Par comparaison, la fenêtre rectangulaire a une bonne résolution fréquentielle (lobe central plus étroit) mais ne restitue pas correctement les spectres continus à cause des lobes secondaires trop intenses.

3. Fonction de calcul Mathematica

La fonction suivante effectue le calcul du spectre d'un signal discret. La fréquence d'échantillonnage est fournie en argument. Le type de fenêtre peut être précisé en option (hamming par défaut) :

Options[Spectre]={Fenetre->"hamming"};
Spectre[signal_,fe_,opts___]:=Module[{ne,fenetre,w,echant,tfd,spectre},
	fenetre = Fenetre/.{opts}/.Options[Spectre];
	ne=Length[signal];
	w["rectangulaire"][k_]:=1.0;
	w["hamming"][k_]:=0.54-0.46*Cos[2*Pi/ne*k];
	w["hanning"][k_]:=0.5-0.5*Cos[2*Pi/ne*k];
	w["blackman"][k_]:=0.42-0.5*Cos[2*Pi/ne*k]+0.08*Cos[4*Pi/ne*k];
	echant=Table[signal[[k+1]]*w[fenetre][k],{k,0,ne-1}];
	tfd=Fourier[echant,FourierParameters->{-1,-1}];
	spectre=Table[{fe*k/ne,Abs[tfd[[k]]]},{k,ne}];
	Return[spectre];
];
            

Exemple avec le signal défini plus haut :

spectre=Spectre[echant,fe,Fenetre->"hanning"];
            

ListPlot[spectre,Filling->Axis,PlotRange->{{0,5},Full},AxesLabel->{"f","A"}]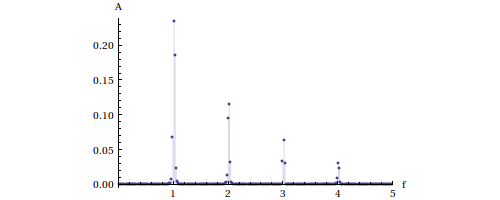

plotF.pdf