Introduction à l'analyse spectrale

3.a. Définition

La transformée de Fourier discrète (TFD) est la transformation qui permet de calculer le spectre d'un signal discret, obtenu par échantillonnage d'un signal continu. Considérons un échantillonnage de la fonction u sur l'intervalle [0,T], comportant N points et défini par :

$$\begin{array}{ccc}\hfill & t_k=k\frac{T}{N}(0\le k\le N-1)\hfill & \hfill \text{(12)}\\ \hfill & u_k=u\left(t_k\right)\hfill & \hfill \text{(13)}\end{array}$$

On définit la période d'échantillonnage et la fréquence d'échantillonnage par :

$$\begin{array}{ccc}\hfill & T_e=\frac{T}{N}\hfill & \hfill \text{(14)}\\ \hfill & f_e=\frac{1}{T_e}\hfill & \hfill \text{(15)}\end{array}$$

Une valeur approchée de l'intégrale $\mathrm{(6)}$ définissant les coefficients de Fourier peut être obtenue par la méthode des rectangles :

$$c_n\simeq \frac{1}{T}\sum _{k=0}^{N-1}\frac{T}{N}{u}_{k}exp(-i\frac{2\pi nk}{N})\text{(16)}$$

Par définition, la transformée de Fourier discrète ([1]) est l'application qui aux N nombres u_k associe les N nombres complexes suivants ($0\le n\le N-1$) :

$$\widetilde{U_n}=\frac{1}{N}\sum _{k=0}^{N-1}{u}_{k}exp(-i\frac{2\pi nk}{N})\text{(17)}$$

La TFD vérifie la propriété suivante (si u_k est réel) :

$${\tilde{U}}_n={\tilde{U}}_{N-n}^{*}\text{(18)}$$

La transformée de Fourier discrète est calculée numériquement avec l'algorithme dit de Transformée de Fourier rapide. La fonction qui effectue ce calcul (sur un oscilloscope ou dans un logiciel) est souvent désignée par FFT (Fast Fourier Transform).

3.b. Exemple : polynôme trigonométrique

Si u est un polynôme trigonométrique, il existe un rang P fini tel que $\forall n>P$ on a c_n=0. Autrement dit, la série de Fourier s'arrête à un rang fini. Il existe donc dans le spectre du signal une fréquence maximale :

$$f_{max}=\frac{P}{T}\text{(19)}$$

On suppose que la condition de Nyquist-Shannon est vérifiée : la fréquence d'échantillonnage est supérieure au double de la fréquence maximale du spectre

$$f_e>2f_{max}\text{(20)}$$

ou encore :

$$N>2P\text{(21)}$$

Si cette condition est vérifiée, alors les P+1 premières valeurs de la TFD sont exactement les coefficients de Fourier :

$$c_n={\tilde{U}}_n\text{pour}0\le n\le P\text{(22)}$$

Cette propriété est étonnante puisque la TFD est initialement définie pour donner des valeurs approchées des coefficients de Fourier. Sa démonstration est donnée plus loin (paragraphe 3.d).

Pour voir comment la TFD permet d'obtenir le spectre du signal, reprenons l'exemple précédent. Comme la période est égale à 1, l'indice n correspond exactement à la fréquence. La plus grande fréquence du spectre est P=3 (harmonique de rang 3). Pour respecter la condition, il faut donc échantillonner à au moins 6 points par période. Voyons le résultat pour N=10. La période du signal étant connue a priori, on peut échantillonner exactement 10 points sur une période :

N = 10
Tmax = 1.0
Te = Tmax/N
t = numpy.arange(0,N)*Te
x=u(t)
figure(figsize=(10,4))
stem(t,x)
xlabel('t')
ylabel('u')
grid()
                 

Figure pleine page

Voici le calcul de la transformée de Fourier discrète :

import numpy.fft
tfd = numpy.fft.fft(x)
                 

print(tfd)
--> array([4.00000000e+00+0.00000000e+00j, 5.00000000e+00+0.00000000e+00j,
       1.25000000e+00-2.16506351e+00j, 7.07106781e-01+7.07106781e-01j,
       1.94289029e-16-3.33066907e-16j, 3.88578059e-16-1.11022302e-16j,
       1.94289029e-16+3.33066907e-16j, 7.07106781e-01-7.07106781e-01j,
       1.25000000e+00+2.16506351e+00j, 5.00000000e+00+1.66533454e-16j])

On trace le module en fonction de la fréquence. On doit diviser par N car la fonction numpy.fft.fft calcule la TFD sans le facteur 1/N. Ici la fréquence est égale à l'indice n :

figure(figsize=(10,5))
f=numpy.arange(0,N,1)
stem(f,numpy.absolute(tfd)/N) 
xlabel("f")
ylabel("|cn|")
axis([-1,11,0,1])
grid()
                 

Figure pleine page

Les 4 premières valeurs de la TFD donnent bien les coefficients de Fourier de rang 0 à 3. Les éléments d'indice 4,5 et 6 sont nuls, aux erreurs d'arrondis près (erreurs de l'ordre de 1e-16). Les trois derniers éléments (indices 7 à 9) sont les conjugués des trois coefficients c₁, c₂ et c₃; ils ont donc le même module. Le terme d'indice 1 est conjugué du terme d'indice 9, celui d'indice 2 conjugué du terme d'indice 8, etc. La fréquence centrale du spectre est égale à la moitié de la fréquence d'échantillonnage; c'est la fréquence de Nyquist. Ici, la fréquence de Nyquist est f_n=5. Comme la condition de Nyquist-Shannon est respectée, cette fréquence est supérieure à P=3. La partie du spectre située à gauche de cette fréquence est le spectre du signal continu u(t). La totalité du spectre est celui du signal discret. La partie située à droite de la fréquence de Nyquist est l'image de la partie gauche (à l'exclusion de la composante de fréquence nulle). On voit que la condition de Nyquist-Shannon se traduit par le non chevauchement du spectre et de son image.

En fait, le spectre du signal discret est périodique, de période égale à la fréquence d'échantillonnage. La relation définissant la TFD vérifie en effet la relation :

$${\tilde{U}}_{N+n}=\widetilde{U_n}\text{(23)}$$

La TFD que nous avons calculée donne donc les valeurs de ce spectre sur une période. Cependant, ce qui nous intéresse en pratique est plutôt le spectre du signal continu u(t), qui est donné par la première moitié de la TFD.

En pratique, on s'intéresse aux amplitudes A_n des harmoniques plutôt qu'aux valeurs des coefficients de Fourier c_n. Il faut alors multiplier les coefficient par deux :

figure(figsize=(10,5))
f=numpy.arange(0,N,1)
stem(f,numpy.absolute(tfd)*2/N) 
xlabel("f")
ylabel("|cn|")
axis([-1,11,0,1.2])
grid()
                     

Figure pleine page

On remarque que la composante de fréquence nulle du spectre a une amplitude égale au double de la valeur moyenne. Dans le cas présent, on pourrait facilement diviser le terme d'indice 0 par deux pour obtenir directement la composante de fréquence nulle du signal, mais cette méthode n'est pas toujours applicable sur les spectres expérimentaux.

3.c. Transformée de Fourier discrète inverse

L'information présente dans le signal échantillonné est entièrement contenue dans sa TFD. On peut en effet calculer le signal à partir de sa TFD par la relation suivante (voir [1] pour la démonstration) :

$$u_k=\sum _{n=0}^{N-1}{\tilde{U}}_{n}exp\left(i\frac{2\pi nk}{N}\right)\text{(24)}$$

La transformation qui permet ainsi de retrouver le signal discret est la transformation de Fourier discrète inverse. Elle ressemble beaucoup à la TFD directe : on remarque le changement de signe dans l'exponentielle et l'absence du facteur 1/N. En ce qui concerne ce facteur, il existe d'ailleurs différentes conventions pour la définition de la TFD.

Comme exemple, calculons la TFD inverse de la TFD obtenue précédemment :

y = numpy.fft.ifft(tfd)
figure(figsize=(10,4))
stem(t,y)
xlabel('t')
ylabel('y')
grid()
                   

Figure pleine page

On retrouve bien le signal discret de départ.

Il est intéressant de modifier la TFD avant de calculer la TFD inverse. On peut par exemple enlever l'harmonique de rang 3. Pour cela, il faut annuler le coefficient d'indice 3 et son image, d'indice N-3=7 :

i=3
tfd[i] = 0
tfd[N-i] = 0
y = numpy.fft.ifft(tfd)
figure(figsize=(10,4))
stem(t,y)
xlabel('t')
ylabel('y')
grid()
                    

Figure pleine page

Le résultat est le signal discret qui serait obtenu par échantillonnage du signal u(t) auquel on aurait enlevé l'harmonique de rang 3. On a donc là une méthode de filtrage très sélective, appelée filtrage dans le domaine fréquentiel, ou filtrage par transformée de Fourier. Elle peut être utilisée lorsqu'on doit filtrer un signal discret dont la taille N est fixée à l'avance (et pas trop grand). Cependant, cette méthode est plus difficile à mettre en œuvre pour faire un filtrage temps-réel, pour lequel il y a un flux continu de données à traiter. Dans ce cas, on effectue plutôt un filtrage dans le domaine temporel, appelé aussi filtrage par convolution. Voir à ce sujet le document Introduction aux filtres numériques.

3.d. Relation entre la TFD et les coefficients de Fourier

Ce paragraphe donne la démonstration de l'égalité entre les coefficients de Fourier et la TFD.

On considère la série de Fourier pour l'instant t_k=kT/N :

$$u_k=\sum _{m=-\infty }^{+\infty }{c}_{m}exp\left(im\frac{2\pi }{T}\frac{kT}{N}\right)=\sum _{m=-\infty }^{+\infty }{c}_{m}exp\left(i\frac{2\pi mk}{N}\right)\text{(25)}$$

On se place pour l'instant dans le cas théorique général, où la somme doit être étendue à l'infini. Considérons la division entière de l'indice m par N :

$$m=qN+n\text{(26)}$$

q est l'entier résultat de cette division et n est le reste. La somme sur l'indice m peut s'écrire comme une double somme, sur n et sur q. En regroupant tous les termes qui ont le même reste, on obtient ainsi :

$$u_k=\sum _{n=0}^{N-1}\left(\sum _{q=-\infty }^{+\infty }{c}_{qN+n}\right)exp\left(i\frac{2\pi nk}{N}\right)\text{(27)}$$

En identifiant cette expression avec celle de la TFD inverse, on montre que :

$${\tilde{U}}_n=\sum _{q=-\infty }^{\infty }{c}_{qN+n}\text{(28)}$$

Pour le coefficient de Fourier de rang n, l'erreur de l'approximation par ${\tilde{U}}_n$ est donc :

$${\tilde{U}}_n-c_n=\sum _{q\ne 0}{c}_{qN+n}\text{(29)}$$

On se place à présent dans le cas où il existe un rang P tel que pour |k|>P on ait c_k=0. On suppose de plus que N>2P (condition de Nyquist-Shannon).

Soit un entier n tel que $0\le n\le P$. Pour q>0, on a qN+n>2qP+n>2P+n>P donc c_qN+n=0. De même pour q<0 on a qN+n<2qP+n<-2P+n<-P donc c_qN+n=0. Tous les termes de la somme sont donc nuls :

$${\tilde{U}}_n-c_n=0\text{pour}0\le n\le P\text{(30)}$$

Cela démontre l'égalité entre les P+1 premiers termes de la TFD et les coefficients de Fourier, pourvu que la condition de Nyquist-Shannon soit respectée.

4.a. Fenêtre d'analyse

Un signal périodique réel a une période qui, le plus souvent, n'est pas connue a priori. L'objectif de l'analyse spectrale est justement de déterminer les fréquences qu'il contient. Par ailleurs, sa périodicité peut être imparfaite, voire très grossière. On voit donc que l'approche précédente, qui consistait à échantillonner le signal sur sa période T, n'est pas applicable en pratique.

Au lieu de cherche à échantillonner sur une période, on considère une durée T grande devant la période supposée. Par exemple, pour un son de fréquence 400 Hz, on peut prendre T=1 s. On obtient ainsi un spectre dont les raies sont les coefficients de Fourier d'une fonction de période T. Les fréquences de ces raies sont donc multiples de 1/T. La durée T est la largeur de la fenêtre d'analyse. La résolution fréquentielle du spectre obtenu est 1/T.

4.b. Exemple : fonction échantillonnée

On reprend le signal déjà utilisé en modifiant sa fréquence :

f1 = 1.0324
                

On choisit une durée d'analyse T=20, qui donnera une résolution fréquentielle de 0,05. La fréquence d'échantillonnage doit respecter la condition de Nyquist-Shannon, c'est-à-dire f_e>7.

T=20.0
fe=10.0
N=int(T*fe)
t = numpy.arange(0,N)*Te
x=u(t)
tfd=numpy.fft.fft(x)
f=numpy.arange(0,N)*1.0/T
figure(figsize=(10,4))
vlines(f,[0],numpy.absolute(tfd)/N,'b')
xlabel('f')
ylabel('C')
axis([-1,10,0,0.5])
grid()
                 

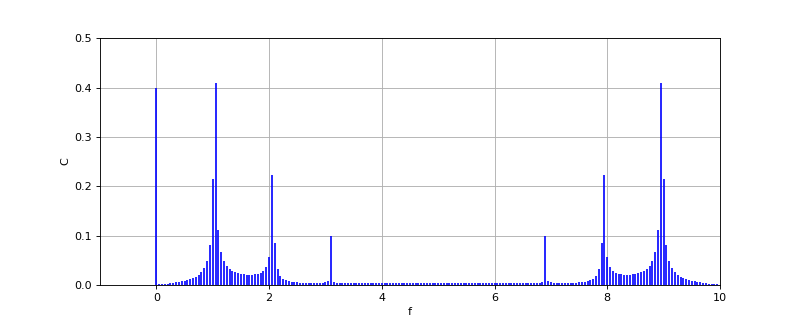figG.pdf

Le spectre obtenu est composé de raies très resserées, espacées de 1/T. Le spectre de la fonction apparaît comme la courbe dessinée par ces raies. La démonstration de cette propriété sort du cadre de cette introduction, car elle fait appel à la notion de transformée de Fourier.

On voit sur cet exemple que le spectre obtenu est imparfait : la position du maximum des raies est définie au mieux avec une précision de 1/T. Dans le cas présent, cela induit une erreur bien visible sur la hauteur des raies. Pour améliorer la précision, il faut augmenter la durée de la fenêtre d'analyse. Voyons le résultat avec T=10000 :

T=10000.0 
fe=10.0
N=int(T*fe)
t = numpy.arange(0,N)*Te
x=u(t)
tfd=numpy.fft.fft(x)
f=numpy.arange(0,N)*1.0/T
figure(figsize=(10,4))
plot(f,numpy.absolute(tfd)/N,'b')
xlabel('f')
ylabel('C')
axis([-1,10,0,0.5])
grid()
                 

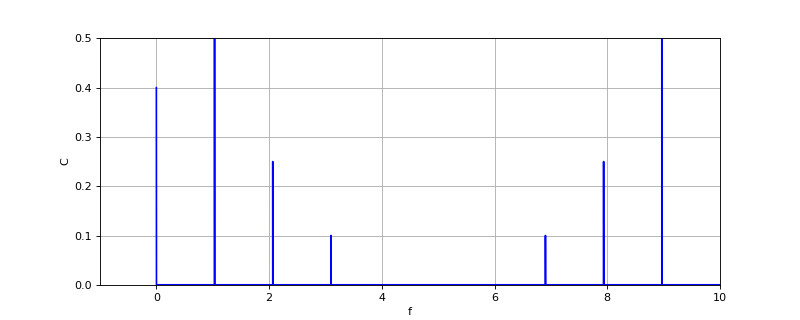figH.pdf

La résolution fréquentielle est bien meilleure. Les amplitudes des harmoniques attendues (d'après la définition du signal) sont correctes : c₀=0,4, c₁=0,5, c₂=0,25, c₃=0,1. Remarque : on a ici utilisé la fontion plot et non vlines car cette dernière n'est pas optimisée pour le traitement d'un gros volume de données.

Dans certains cas, l'augmentation de la durée de la fenêtre d'analyse n'est pas possible, ou bien n'est pas suffisante pour obtenir précisément la hauteur des raies. On peut alors utiliser la technique du remplissage par des zéros associée à un fenêtrage, expliquée dans Analyse spectrale d'un signal numérique.

4.c. Exemple : analyse d'un son

Voyons à présent un exemple plus réaliste, l'analyse du son émis par un instrument de musique. Il s'agit du son émis par une clarinette (note La₃) pendant une durée d'environ 3 secondes. Evidemment, la largeur de la fenêtre d'analyse est limitée par cette durée.

Le son est enregistré dans un fichier WAV. On commence par lire le fichier et on extrait la fréquence d'échantillonnage, le nombre d'échantillons et la durée du son :

import scipy.io.wavfile as wave
fe,data = wave.read("clarinette_la3.wav")
N = data.size
T = N*1.0/fe
data =data/data.max()
                 

print(fe)
--> 44100

print(T)
--> 2.8908843537414968

Pour obtenir une représentation temporelle du signal (la forme d'onde), il faut se limiter à une fenêtre comportant une dizaine d'oscillations, soit ici environ 0,02 s :

te = 1.0/fe
T = 0.02
N = int(T/te)
t = numpy.arange(N)*te
x = data[0:N]
figure(figsize=(10,4))
plot(t,x)
xlabel("t")
ylabel("A")
grid()
                 

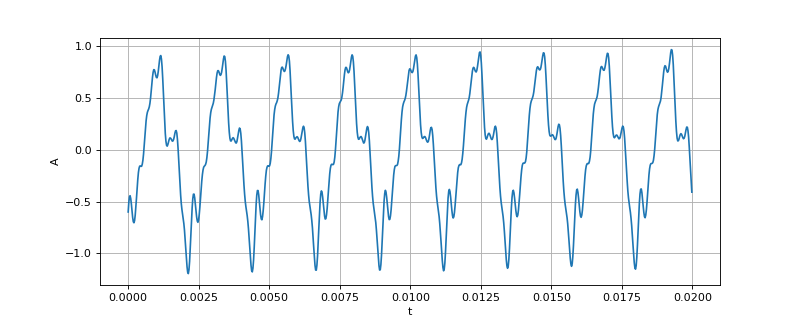figI.pdf

La forme d'onde laisse deviner un spectre très riche en harmoniques.

Pour faire l'analyse spectrale, on choisit une fenêtre de largeur T=1 Hz, qui donnera une précision de 1 Hz sur la fréquence :

T=1.0
N=int(T/te)
x = data[0:N]
tfd = numpy.fft.fft(x)
f = numpy.arange(N)*1.0/T
a = numpy.absolute(tfd)*2/N
figure(figsize=(10,4))
plot(f,a)
xlabel("f (Hz)")
ylabel("A")
grid()
                  

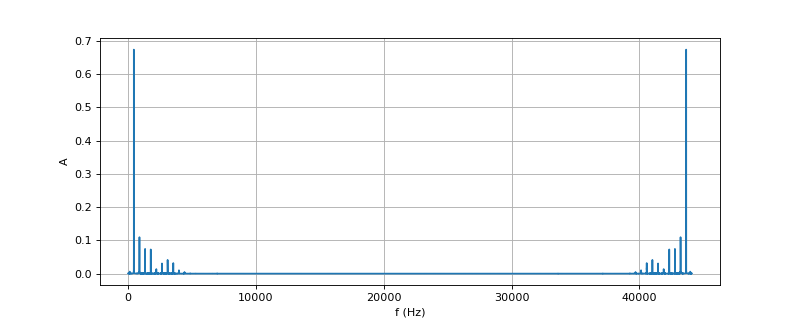figJ.pdf

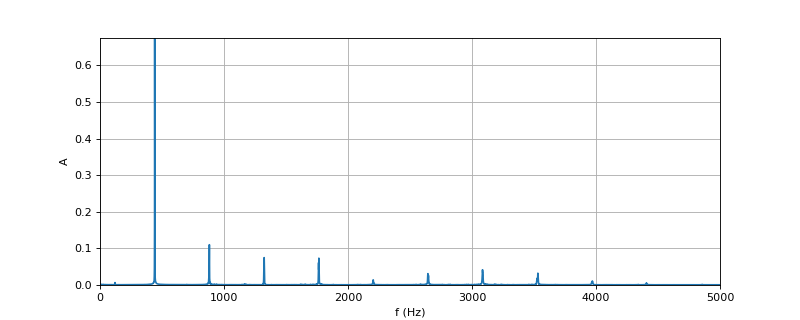
On s'intéresse au spectre du son en tant que signal continu, c'est-à-dire à la première moitié. Voyons le détail dans la bande [0,5 kHz] :

figure(figsize=(10,4))
plot(f,a)
xlabel("f (Hz)")
ylabel("A")
grid()
axis([0,5000,0,a.max()])
                   

figK.pdf

On repère sur ce spectre le fondamental (à 440 Hz) et des harmoniques de rang 2 à 8. Les harmoniques de rang élevé (par exemple 7) ont une fréquence très élevée (pour l'oreille). Bien que leur amplitude soit relativement faible, elles contribuent au timbre du son.