Analyse spectrale d'un signal aléatoire

1. Introduction

Ce document introduit la notion de signal aléatoire à travers un exemple et des simulations numériques. On verra comment calculer la fonction d'autocorrélation d'un signal aléatoire et sa densité spectrale de puissance.

2. Signaux aléatoires

La notion de signal aléatoire, qui s'oppose à celle de signal déterministe, est introduite pour définir mathématiquement un signal comportant une part plus ou moins grande d'imprévisibilité. Un signal aléatoire (ou processus stochastique) contient une ou plusieurs variables aléatoires dans sa définition.

Un exemple de signal déterministe est le signal sinusoïdal suivant :

$$x\left(t\right)=Acos(\omega t+\phi )\text{(1)}$$

où A, $\omega$ et $\phi$ sont des constantes (amplitude de crête, pulsation et phase à l'origine du temps). La valeur de x à tout instant est parfaitement déterminée. Les signaux réels, c'est-à-dire ceux qui sont obtenus avec des capteurs physiques, ne sont jamais parfaitement déterministes mais ils peuvent l'être approximativement sur une durée limitée.

Comme exemple de signal aléatoire (que nous allons étudier dans ce document), reprenons l'expression précédente de $x\left(t\right)$ mais avec une phase à l'origine $\phi$ qui est une variable aléatoire au lieu d'être une constante :

$$x_a\left(t\right)=Acos(\omega t+{\phi }_a)\text{(2)}$$

On suppose que ${\phi }_a$ reste constante pendant une durée Δt (constante) puis change de valeur aléatoirement. La densité de probabilité de $\phi$ est supposée uniforme sur l'intervalle [0,2π]. Notons x_a(t) ce signal. Remarquons que x_a n'est pas une fonction puisque sa valeur à l'instant t n'est pas déterminée, c'est-à-dire que x_a(t) est une variable aléatoire. L'espérance de x_a(t) est nulle pour ce signal :

$$E\left[x_a\left(t\right)\right]=0\text{(3)}$$

Une réalisation d'un signal aléatoire est une fonction x(t) correspondant à une valeur particulière de toutes les variables aléatoires qui entrent dans sa définition. On s'intéresse à une réalisation sur un intervalle de temps [0,T]. Numériquement, il s'agit d'un échantillonnage de la réalisation, qui constitue un signal aléatoire discret. Voici comment obtenir numériquement une réalisation du signal x_a :

import numpy as np
from numpy.random import uniform 
from matplotlib.pyplot import *
A = 1
f = 1
Delta_t = 10
Te = 1/50 # période d'échantillonnage

def realisation(T,Te):
    # T : durée
    # Te : période d'échantillonnage
    P = int(Delta_t/Te)
    xa = np.zeros(0)
    t = np.arange(P)*Te
    for k in range(int(T/Delta_t)):
        xa = np.append(xa,A*np.cos(2*np.pi*f*t+uniform(0,2*np.pi,1)))
    return xa

xa_1 = realisation(5*Delta_t,Te)
figure(figsize=(20,6))
t = np.arange(len(xa_1))*Te
plot(t,xa_1)
grid()
xlabel('t',fontsize=16)
ylabel(r"$x_a$",fontsize=16)      
                       

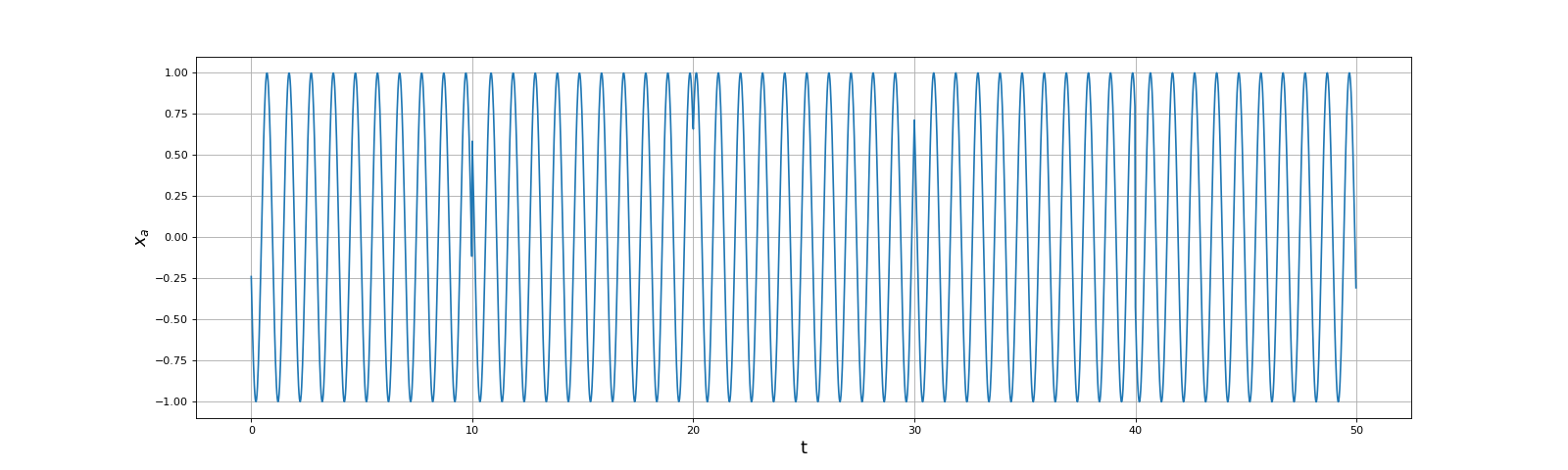fig1.pdf

L'ensemble des réalisations du signal définit entièrement le signal aléatoire. L'espérance d'une grandeur associée à ce signal est aussi appelée moyenne d'ensemble, terme couramment employé en physique statistique et que nous utiliserons. Quand on parle de moyenne il s'agit le plus souvent de moyenne d'ensemble. On peut dire aussi qu'une moyenne d'ensemble est une moyenne sur un nombre infini de réalisations du signal.

Un signal aléatoire est dit stationnaire lorsque la moyenne d'une grandeur à un instant t (quelle qu'elle soit) ne dépend pas de t.

Numériquement, on est évidemment limité à faire des calculs statistiques puisque le nombre de réalisations étudiées est fini. L'évaluation de moyennes par étude statistique d'un grand nombre de réalisations numériques est une simulation de Monte-Carlo.

Supposons que l'on cherche à évaluer numériquement la moyenne d'ensemble de x_a(t₁), où t₁ est un instant quelconque. Il faut pour cela générer un grand nombre de réalisations et calculer la moyenne de x_a(t₁) pour cet ensemble de réalisations. Cependant, ce signal aléatoire est stationnaire donc la moyenne cherchée peut être évaluée avec une réalisation très courte. À la limite, une réalisation ne comportant qu'un seul échantillon suffit. Pour bien montrer le principe d'un calcul de moyenne d'ensemble dans le cas général, faisons tout de même ce calcul pour un intervalle [0,T] :

Nr = 100 # nombre de réalisations 
P = 1
t1 = 0.0
i1 = int(t1/Te)
somme = 0.0
for r in range(Nr):
    xa = realisation(10*Delta_t,Te)
    somme += xa[i1]
x_moy = somme/Nr
                           

print(x_moy)
--> 0.052579346818184235

Bien évidemment, l'évaluation de la moyenne est elle-même une variable aléatoire. Voici une autre évaluation :

somme = 0.0
for r in range(Nr):
    xa = realisation(10*Delta_t,Te)
    somme += xa[i1]
x_moy = somme/Nr
                           

print(x_moy)
--> -0.04220039294063241

L'écart-type de la moyenne peut être évalué si on calcule aussi l'écart-type empirique (voir Principe des méthodes de Monte-Carlo). Le calcul de celui-ci nécessite le calcul de la somme des carrés :

somme = 0.0
somme2 = 0.0
for r in range(Nr):
    xa = realisation(10*Delta_t,Te)
    somme += xa[i1]
    somme2 += xa[i1]*xa[i1]
x_moy = somme/Nr
x_moy = somme/Nr
variance = somme2*1.0/Nr-x_moy**2
ecart_type = np.sqrt(variance/Nr)
                           

print((x_moy,ecart_type))
--> (0.08033172608598328, 0.0650394560553398)

Toute évaluation numérique d'une moyenne doit en principe être accompagnée de l'évaluation de l'écart-type de cette moyenne, qui indique le niveau de confiance qu'on peut accorder au résultat. Bien sûr, l'écart-type diminue si on augmente de nombre de réalisations.

On introduit aussi la notion de moyenne temporelle. La moyenne temporelle d'une grandeur f(t) est définie par :

$$<f\left(t\right)>=\underset{T\to \infty }{lim}\frac{1}{T}{\int }_0^{T}f\left(t\right)dt\text{(4)}$$

sous réserve que cette limite existe.

Un signal aléatoire est dit ergodique lorsque la moyenne d'ensemble de toute grandeur associée à ce signal est égale à sa moyenne temporelle. Autrement dit, une seule réalisation d'un signal ergodique de durée infinie contient toute l'information sur le signal.

Le signal aléatoire considéré en exemple est ergodique. On a donc en particulier :

$$E\left[x_a\left(t\right)\right]=\underset{T\to \infty }{lim}\frac{1}{T}{\int }_0^T{x}_a\left(t\right)dt\text{(5)}$$

L'évaluation numérique de la moyenne temporelle consiste à générer une réalisation très longue et à calculer la moyenne des valeurs des échantillons :

xa = realisation(1000*Delta_t,Te)
x_moy = xa.mean()

                        

print(x_moy)
--> 2.2435386881625164e-18

Si l'on compare les deux manières de calculer la moyenne du point de vue de la complexité, il apparaît que la seconde méthode (moyenne temporelle) est équivalente à la première à condition que cette dernière soit faite avec des réalisations ne comportant qu'un seul échantillon. L'évaluation de l'écart-type de la moyenne temporelle se fait exactement comme pour la moyenne d'ensemble. Cet écart-type est évidemment d'autant plus petit que T est grand.

3. Fonction d'autocorrélation

La fonction d'autocorrélation d'un signal aléatoire est définie par :

$$R(t_1,t_2)=E\left[x_a\left(t_1\right)x_a\left(t_2\right)\right]\text{(6)}$$

C'est donc la moyenne d'ensemble du produit de x_a à deux instants différents. Nous considérons le cas d'un signal stationnaire, pour lequel la fonction d'autocorrélation ne dépend que de l'écart τ=t₂-t₁. Dans ce cas, elle se définit par :

$$R\left(\tau \right)=E\left[x_a\left(t\right)x_a(t+\tau )\right]\text{(7)}$$

Si le signal est ergodique, cette moyenne est égale à la moyenne temporelle suivante :

$$R\left(\tau \right)=\underset{T\to \infty }{lim}\frac{1}{T}{\int }_0^T{x}_a\left(t\right)x_a(t+\tau )dt\text{(8)}$$

Voyons comment évaluer la fonction d'autocorrélation numériquement à partir de réalisations du signal. Pour chaque valeur de τ (sur un intervalle à définir), il faut calculer une moyenne. On a le choix entre faire le calcul de moyenne pour un nombre N_r de réalisations sur un intervalle [0,T] ou bien calculer une moyenne temporelle sur une seule réalisation dont la durée est T'=N_rT. Du point de vue de la complexité temporel, ces deux méthodes sont équivalentes. Nous choisissons la seconde méthode car elle nous semble plus facile à implémenter. Par ailleurs c'est la méthode qu'on applique dans la plupart des cas pour déterminer la fonction d'autocorrélation d'un signal expérimental, tout simplement parce qu'il est souvent plus simple de réaliser une seule longue expérience qu'un grand nombre d'expériences indépendantes. Soit [0,τ_m] l'intervalle de τ. τ_m est à choisir en fonction du signal considéré. Comme nous allons le voir, la fonction d'autocorrélation tend vers zéro lorsque τ tend vers l'infini et τ_m doit être assez grand pour que R(τ) soit négligeable pour tout τ>τ_m. Pour l'exemple considéré ici, τ_m devra probablement être plus grand que Δt. Posons T_m=N_rτ_m comme étant la durée de la réalisation avec N_r grand (au moins 1000). Remarquons qu'une seule réalisation est nécessaire pour calculer les moyennes pour différentes valeurs de τ. On pose τ=qtTe et τ_m=q_mT_e où T_e est la période d'échantillonnage. On doit calculer la somme suivante :

$$R\left(q\right)=\frac{1}{N}\sum _{n=0}^{N-1}{x}_n{x}_{n+q}\text{(9)}$$

pour q variant de 0 à q_m. En pratique, on choisit le nombre d'échantillons N_e de la réalisation et on a :

$${\tau }_m=\frac{N_e}{N_r}{T}_e\text{(10)}$$

Il faut que N-1+q<N_e pour la plus grande valeur de q, soit :

$$N-1+q_m<N_e\text{(11)}$$

on prendra donc :

$$N=N_e-q_m\text{(12)}$$

Dans une implémentation en Python, le calcul des sommes $\mathrm{(9)}$ au moyen d'une boucle conduit à un temps de calcul très long. Un moyen plus efficace est d'utiliser la fonction numpy.roll, qui effectue un décalage sur les éléments d'un tableau. On calcule en fait les sommes $\mathrm{(9)}$ avec N=N_e et l'indice n+q est considéré comme égal à n+q modulo N. Ce calcul correspond à celui d'une corrélation cyclique. Compte tenu du caractère stationnaire du signal, la différence entre la corrélation cyclique et la corrélation non cyclique est négligeable.

tau_m = 5*Delta_t
Nr = 10000
T = Nr*tau_m
Te = 1/20
xa = realisation(T,Te)
qm = int(tau_m/Te)
R = np.zeros(qm)
for q in range(qm):
    R[q] = 0.0
    R[q] = (xa*np.roll(xa,q)).sum()
R /= len(xa)
tau = np.arange(qm)*Te
np.save("autocor-1.npy",np.array([tau,R]))
                    

figure(figsize=(12,6))
[tau,R] = np.load("autocor-1.npy")
plot(tau,R)
grid()
xlabel(r"$\tau$",fontsize=16)
ylabel(r"$R$",fontsize=16)
                     

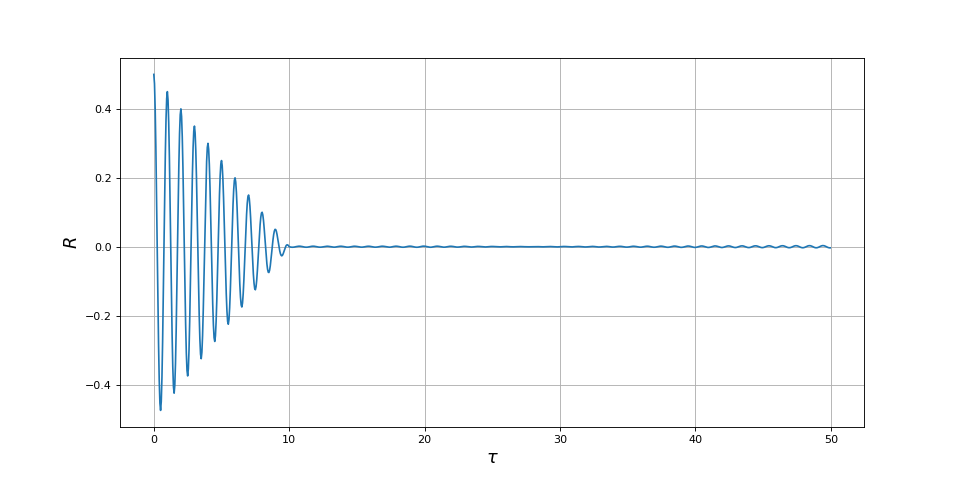fig2.pdf

Ce calcul est très long, c'est pourquoi nous sauvegardons le résultat dans un fichier, afin d'éviter de le refaire à chaque compilation de cette page.

On peut remarquer que la valeur de la fonction d'autocorrélation à τ=0 est :

$$R\left(0\right)=E\left[x_a^2\left(t\right)\right]\text{(13)}$$

Pour un signal sinusoïdal d'amplitude de crête A=1, cette moyenne vaut bien 1/2.

La forme de la fonction d'autocorrélation du signal étudié possède deux caractéristiques intéressantes :

• Une oscillation pseudo-périodique caractéristique de la sinusoïde.
• Une décroissance associée au temps Δt.

La durée Δt est la durée de cohérence de ce signal, c'est-à-dire la durée au delà de laquelle la fonction d'autocorrélation est pratiquement nulle.

4. Densité spectrale de puissance - théorème de Wiener-Khinchine

L'analyse spectrale des signaux repose sur la transformée de Fourier. La transformée de Fourier d'une fonction x(t) est définie par :

$$\tilde{X}\left(f\right)={\int }_{-\infty }^{\infty }x\left(t\right)exp(-i2\pi ft)dt\text{(14)}$$

Si x(t) est une fonction périodique, par exemple une fonction sinusoïdale, la transformée de Fourier n'est pas définie en tant que fonction mais elle l'est en tant que distribution. Pour un signal aléatoire, la transformée de Fourier a de bonnes chances de pas être définie du tout. On doit donc limiter l'intégrale à une durée T, pour une réalisation de cette durée :

$$F\left(f\right)={\int }_0^T{x}_a\left(t\right)exp(-i2\pi ft)dt\text{(15)}$$

Le périodogramme d'une réalisation du signal est le module au carré de cette intégrale divisée par la durée :

$$\frac{1}{T}|F\left(f\right){|}^2\text{(16)}$$

On définit la densité spectrale de puissance du signal aléatoire comme l'espérance (moyenne d'ensemble) du périodogramme :

$${\rho }_T\left(f\right)=E\left[\frac{1}{T}\right|F\left(f\right){|}^2]\text{(17)}$$

Le théorème de Wiener-Khinchine [1] établit que la limite de la densité spectrale de puissance lorsque $T\to \infty$ est la transformée de Fourier de la fonction d'autocorrélation :

$${\rho }_{\infty }\left(f\right)={\int }_{-\infty }^{\infty }R\left(\tau \right)exp(-i2\pi f\tau )d\tau \text{(18)}$$

En conséquence, la fonction d'autocorrélation est la transformée de Fourier inverse de la densité spectrale de puissance limite:

$$R\left(\tau \right)={\int }_{-\infty }^{\infty }{\rho }_{\infty }\left(f\right)exp\left(i2\pi f\tau \right)df\text{(19)}$$

La densité spectrale de puissance permet de faire l'analyse spectrale du signal aléatoire sur une durée T donnée. Pour la calculer numériquement sur un intervalle de durée T, on a intérêt à appliquer sa définition, c'est-à-dire à calculer le périodogramme d'un grand nombre de réalisations (par transformée de Fourier discrète) puis à faire la moyenne de ces périodogrammes.

Pour calculer l'intégrale $\mathrm{(15)}$, on utilise la transformée de Fourier discrète (TFD) comme expliqué en annexe. Celle-ci est calculée par l'algorithme de transformée de Fourier rapide. Pour déterminer le facteur de normalisation, il suffit de se souvenir que la TFD (telle qu'elle est calculée par numpy.fft.fft) donne une approximation de l'intégrale $\mathrm{(15)}$ par la méthode des rectangles mais sans le facteur $\frac{T}{N}$.

from numpy.fft import fft,ifft
from scipy.signal.windows import get_window
              
def periodogramme(T,Te):
    xa = realisation(T,Te)
    N = len(xa)
    nz = 1
    p = int(np.log(nz*N)/np.log(2))+1
    Np = 2**p
    u = np.concatenate((xa,np.zeros(Np-N)))
    F = fft(u)*T/N
    rho = 1/T*np.absolute(F)**2
    freq = np.arange(Np)*1/(Np*Te)
    return (freq,rho)
    
    


T = 100*Delta_t
Te = 1/20
(freq,rho) = periodogramme(T,Te)
figure(figsize=(12,6))
plot(freq,rho)
grid()
xlim(0,2)
xlabel("f",fontsize=16)
ylabel(r"$\rho$",fontsize=16)
              

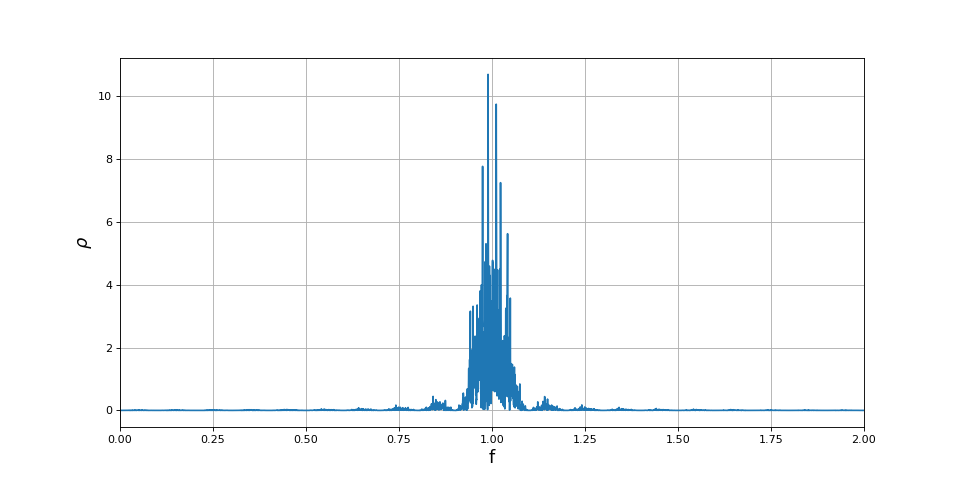fig3.pdf

Voici le calcul d'une moyenne de N_r périodogrammes, qui est une évaluation de la densité spectrale de puissance :

Nr = 2000
rho_m1 = np.zeros(len(rho))
for i in range(Nr):
    (freq1,rho) = periodogramme(T,Te)
    rho_m1 += rho
rho_m1 /= Nr
figure(figsize=(12,6))
plot(freq1,rho_m1)
grid()
xlim(0,2)
xlabel("f",fontsize=16)
ylabel(r"$\rho$",fontsize=16)
              

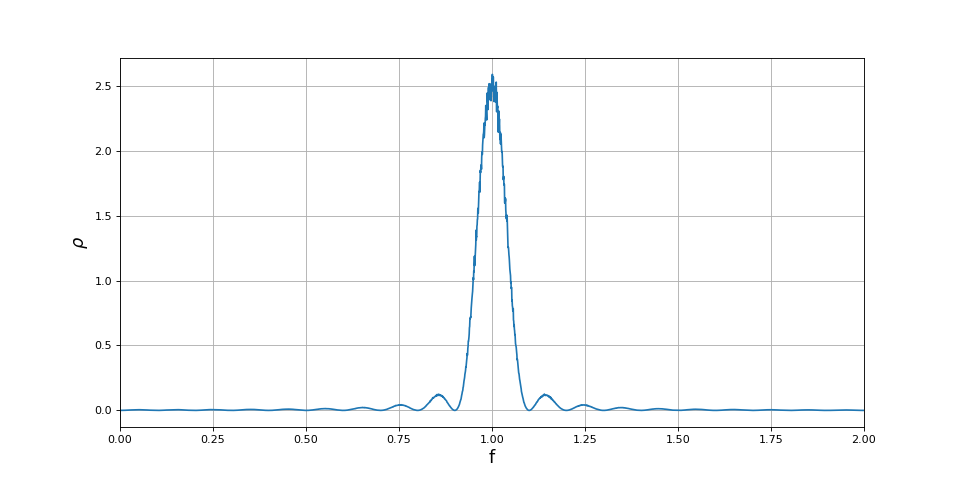fig4.pdf

La précision en fréquence de ce spectre est l'inverse de la durée T, soit dans le cas présent 1/1000 de la fréquence de la sinusoïde. Il est donc évident que la forme en sinus cardinal (au carré) obervée sur ce spectre n'est pas due à la fenêtre d'analyse mais aux sauts de phase qui se font par discontinuité. Multiplions par 2 la durée Δt entre sauts de phase :

Multiplions par 2 la durée T du signal analysé :

Delta_t = 20
T = 100*Delta_t
Te = 1/20
Nr = 500
(freq2,rho) = periodogramme(T,Te)
rho_m2 = np.zeros(len(rho))
for i in range(Nr):
    (freq2,rho) = periodogramme(T,Te)
    rho_m2 += rho
rho_m2 /= Nr
figure(figsize=(12,6))
plot(freq2,rho_m2)
grid()
xlim(0,2)
xlabel("f",fontsize=16)
ylabel(r"$\rho$",fontsize=16)
              

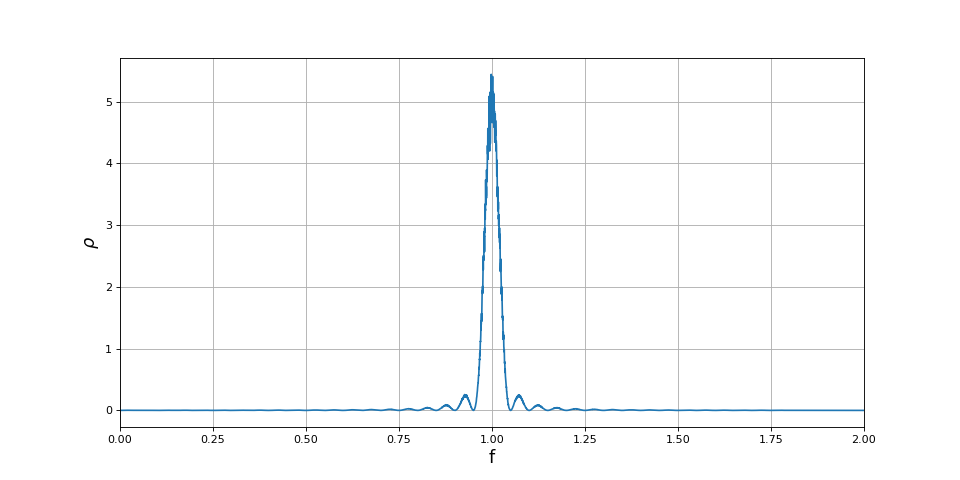fig5.pdf

Il est très vraisemblable que la largeur du lobe principal (entre deux annulations) soit :

$$\Delta f=\frac{2}{\Delta t}\text{(20)}$$

Nous pouvons à présent calculer la fonction d'autocorrélation au moyen de la transformée de Fourier inverse (relation $\mathrm{(19)}$). La densité spectrale de puissance a été calculée sur l'intervalle de fréquences [-f_e/2,f_e/2] où f_e est la fréquence d'échantillonnage. En conséquence, la fonction d'autocorrélation est calculée avec l'intégrale suivante :

$$R\text{'}\left(\tau \right)={\int }_{-f_e/2}^{f_e/2}{\rho }_{\infty }\left(f\right)exp\left(i2\pi f\tau \right)df\text{(21)}$$

Cette intégrale est calculée numériquement au moyen de la transformée de Fourier discrète inverse. L'échelle de τ se calcule sachant que la résolution temporelle est l'inverse de la fréquence d'échantillonnage, c'est-à-dire la période d'échantillonnage. En ce qui concerne le facteur de normalisation à appliquer, il faut tenir compte du fait que la TFD inverse comporte dans sa définition un facteur 1/N. Il suffit donc de la multiplier par la fréquence d'échantillonnage pour obtenir l'intégrale précédente.

Rp = np.real(ifft(rho_m1))*1/Te
taup = np.arange(len(Rp))*Te
figure(figsize=(12,6))
plot(taup,Rp)
grid()
xlabel(r"$\tau$",fontsize=16)
ylabel(r"$R$",fontsize=16)
              

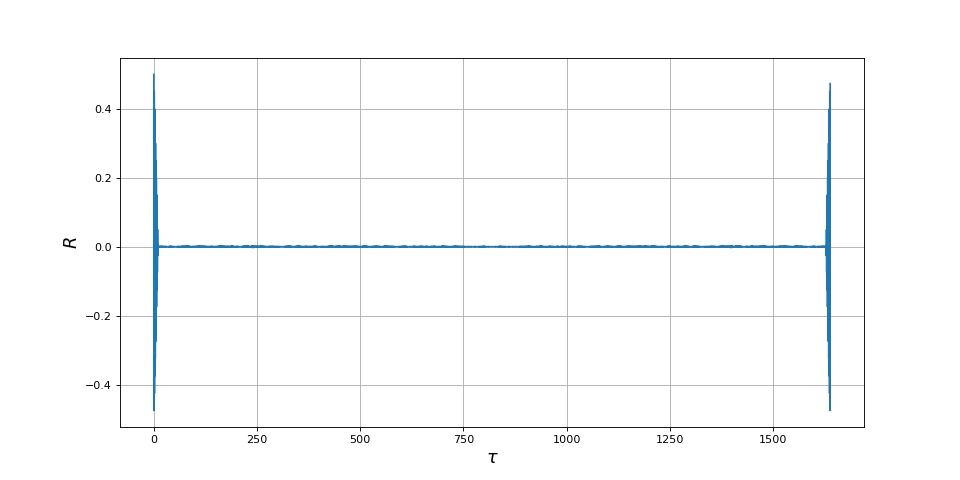fig6.pdf

xlim(0,50)

              

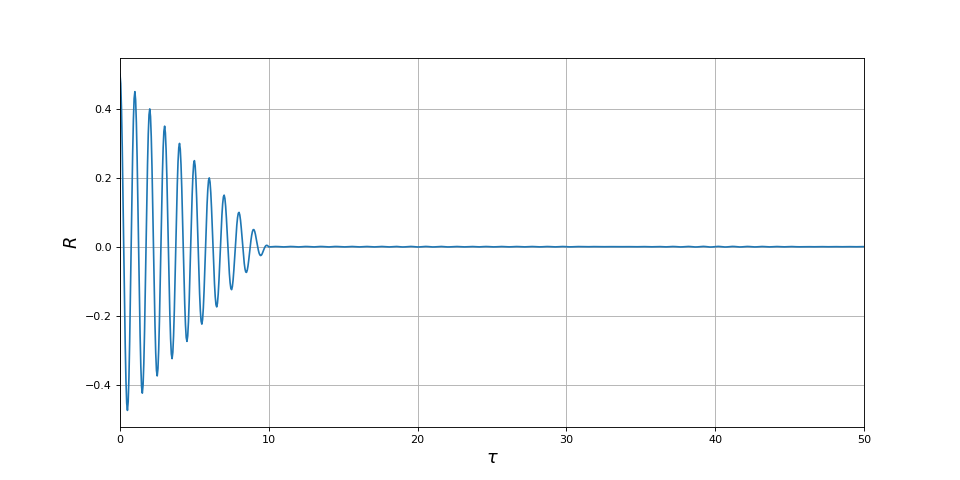fig7.pdf

Avec ce calcul où 2000 périodogrammes sont moyennés, nous obtenons une courbe d'autocorrélation très semblable à celle obtenue précédemment par calcul direct de l'autocorrélation. Cependant, le calcul par la densité spectrale de puissance est beaucoup plus rapide (quelques secondes contre plusieurs minutes). La raison de cette efficacité beaucoup plus grande réside dans l'algorithme de transformée de Fourier rapide. Lorsqu'on veut déterminer la fonction d'autocorrélation d'un signal expérimental ou bien d'un signal issu d'une simulation, on a intérêt à calculer d'abord le périodogramme moyen avant d'en déduire la fonction d'autocorrélation par transformée de Fourier inverse. Le périodogramme est lui-même intéressant puisqu'il constitue l'analyse spectrale du signal.

Pour revenir à l'exemple, les petites ondulations de l'autocorrélation qu'on observe pour t>Δt s'estompent lorsqu'on augmente N_r, ce qui montre qu'elles sont dues à un nombre insuffisant de périodogrammes pour le calcul de la moyenne. Augmenter N_r d'un facteur 2 ne fait que doubler le temps de calcul.

5. Annexe : calcul numérique d'une transformée de Fourier

Il s'agit de calculer numériquement l'intégrale suivante :

$$F\left(f\right)={\int }_0^{T}x\left(t\right)exp(-i2\pi ft)dt\text{(22)}$$

qui, dans la mesure où T est assez grand, est une approximation de la transformée de Fourier de x(t).

L'intervalle [0,T] est échantillonné de la manière suivante :

$$t_n=n\frac{T}{N}N=0,1\dots N-1\text{(23)}$$

et on définit le signal échantillonné $x_n=x\left(t_n\right)$. L'approximation de l'intégrale par la méthode des rectangles s'écrit :

$$F\left(f\right)\approx \frac{T}{N}\sum _{n=0}^{N-1}{x}_{n}exp(-i2\pi fn\frac{T}{N})\text{(24)}$$

On s'intéresse aux fréquences définies par :

$$f_k=\frac{k}{T}k=0,1,\dots N-1\text{(25)}$$

La transformée de Fourier discrète (TFD) de $(x_0,x_1,\dots N-1)$ est définie par :

$$X_k=\sum _{n=0}^{N-1}{x}_{n}exp(-i2\pi \frac{kn}{N})\text{(26)}$$

Il peut arriver que le facteur 1/N soit inclus dans la définition de la TFD. Nous optons ici pour la définition ci-dessus, qui correspond précisément à ce que calcule la fonction numpy.fft.fft. On a finalement :

$$F\left(f_k\right)\approx \frac{T}{N}{X}_k\text{(27)}$$

La TFD est calculée avec l'algorithme de transformée de Fourier rapide par la fonction numpy.fft.fft mais l'efficacité est optimale si N est une puissance de 2, c'est-à-dire N=2^p. Si le nombre de valeurs x_n n'est pas une puissance de 2, on ajoute des zéros afin d'obtenir un nombre d'échantillons puissance de 2.

La transformée de Fourier discrète inverse permet de calculer les x_n en fonction des X_k :

$$x_n=\frac{1}{N}\sum _{k=0}^{N-1}{X}_{k}exp\left(i2\pi \frac{kn}{N}\right)\text{(28)}$$

Il faut remarquer le facteur 1/N dans la TFD inverse (lorsqu'il est absent de la TFD) et le changement de signe de l'argument de l'exponentiel.

Lorsqu'on utilise la TFD inverse pour calculer une transformée de Fourier inverse, il faut tenir compte du facteur 1/N.