Gravitation

1. Introduction

L'objectif de ces travaux pratiques est l'application de la méthode d'Euler au problème gravitationnel à deux corps. On abordera la technique d'adaptation du pas de temps. On verra aussi la méthode du point milieu, plus précise que la méthode d'Euler.

2. Équations différentielles

Un point matériel de masse m est soumis, de la part d'un centre attracteur situé au point O, à une force centrale attractive de la forme K/r². Son équation du mouvement est :

m \frac{d^{2} \vec{O M}}{d t^{2}} = - K \frac{\vec{O M}}{O M^{3}} (1)

Pour le calcul numérique, on pose m=1 et K=1, ce qui revient à changer le système des unités. Le mouvement se fait dans un plan. La projection de l'équation du mouvement sur deux axes orthogonaux liés au référentiel et contenus dans ce plan donne :

\begin{matrix} \frac{d^{2} x}{d t^{2}} = - \frac{x}{{(x^{2} + y^{2})}^{3 / 2}} & (2) \\ \frac{d^{2} y}{d t^{2}} = - \frac{y}{{(x^{2} + y^{2})}^{3 / 2}} & (3) \end{matrix}

Les méthodes d'intégration des équations différentielles opèrent sur des équations du premier ordre. Il faut donc se ramener à un système du premier ordre en travaillant sur les variables de position et de vitesse (x,y,v_x,v_y). On opère ainsi dans un espace à 4 dimensions, appelé espace des phases. Le système différentiel du premier ordre s'écrit :

\begin{matrix} \frac{d x}{d t} = v_{x} & (4) \\ \frac{d y}{d t} = v_{y} & (5) \\ \frac{d v_{x}}{d t} = - \frac{x}{{(x^{2} + y^{2})}^{3 / 2}} & (6) \\ \frac{d v_{y}}{d t} = - \frac{y}{{(x^{2} + y^{2})}^{3 / 2}} & (7) \end{matrix}

Ces équations sont non linéaires et ne dépendent pas explicitement du temps. Elles sont intégrables mais on ne connaît pas de solution analytique exacte (mis à part le mouvement circulaire uniforme). On doit donc faire un calcul numérique afin d'obtenir une solution approchée.

La solution est unique à condition d'imposer les valeurs des 4 variables à l'instant t=0. On choisira la condition initiale simple suivante : le point matériel se trouve au point (1,0) avec une vitesse initiale orthoradiale (0,v₀). Avec ces conditions, un mouvement circulaire est obtenu pour v₀=1. La vitesse de libération est $v_{0} = \sqrt{2}$ .

Ce système admet une intégrale première, qui exprime la conservation de l'énergie mécanique au cours du temps :

E = \frac{1}{2} (v_{x}^{2} + v_{y}^{2}) - \frac{1}{{(x^{2} + y^{2})}^{1 / 2}} (8)

3. Méthode d'Euler

En notant Y la matrice colonne comportant les variables (les coordonnées et leur vitesse), le système différentiel s'écrit sous la forme :

\frac{d Y}{d t} = f (Y) (9)

Dans le cas présent, la variable indépendante temps n'intervient pas explicitement dans les équations.

La méthode d'Euler consiste à calculer une approximation de la solution à l'instant t_n+1=t_n+h à partir de l'approximation à l'instant t_n par la relation :

Y_{n + 1} = Y_{n} + h f (Y_{n}) (10)

L'approximation consiste donc à assimiler la courbe à un segment dont la pente est donnée par la dérivée à l'instant t_n.

Écrire une fonction pas_euler(x,y,vx,vy,h,tol) qui calcule Y_n+1 à partir de Y_n, pour le système différentiel étudié ici. Les valeurs de Y_n et le pas de temps h sont donnés en argument. L'argument tol n'est pas utilisé pour l'instant. La fonction renvoie (x,y,vx,vy,h), c'est-à-dire les valeurs de Y_n+1 et le pas de temps (qui n'est pas modifié pour l'instant). Cette fonction sera appelée des dizaines de milliers de fois. Les calculs qu'elle contient doivent donc être optimisés. En particulier, le calcul de ${(x^{2} + y^{2})}^{3 / 2}$ doit être fait une seule fois.

import numpy
from matplotlib.pyplot import *

def pas_euler(x,y,vx,vy,h,tol):
    r3 = numpy.power(x*x+y*y,1.5)
    ax = -x/r3
    ay = -y/r3
    return (x+h*vx,y+h*vy,vx+h*ax,vy+h*ay,h)

Pour réaliser l'intégration, on souhaite écrire une fonction générale, qui pourra être utilisée avec différentes méthodes numériques. On écrira pour cela une fonction integration qui prend en argument une fonction fonction_pas qui doit avoir les mêmes arguments et les mêmes variables renvoyées que la fonction pas_euler.

Écrire une fonction integration(fonction_pas,x0,y0,vx0,vy0,T,h,tol) dont les arguments sont la fonction de pas d'intégration, la condition initiale, l'instant final T de l'intégration, le pas de temps, et la tolérance (pas encore utilisée). La fonction doit renvoyer 5 tableaux ndarray : (tab_t,tab_x,tab_y,tab_vx,tab_vy,tab_h). Le dernier tableau contient les valeurs du pas de temps, qui pour l'instant est constant. La fonction devra aussi afficher le nombre de pas de temps calculés.

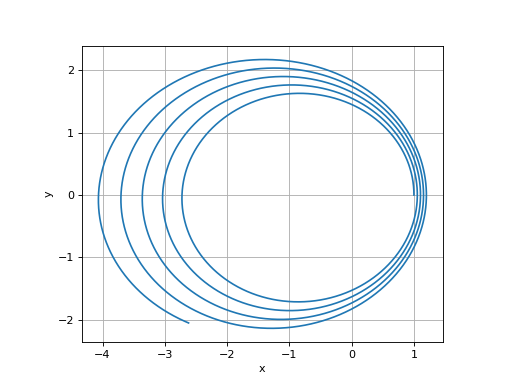
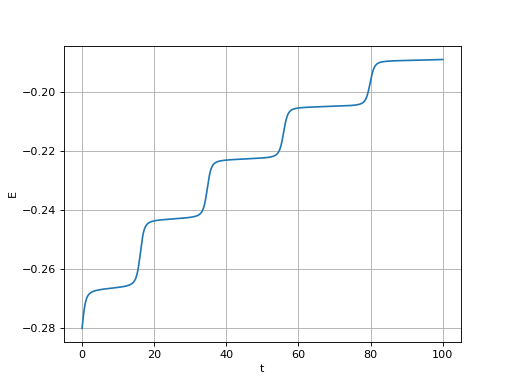
Tester la fonction integration avec la fonction pas_euler, la condition initiale v₀ = 1,2, l'instant final T = 100 et le pas de temps h = 0,01. Tracer la trajectoire puis l'énergie en fonction du temps.

Constater l'instabilité de la méthode d'Euler, qui se traduit pas une énergie mécanique croissante.

def integration(fonction_pas,x0,y0,vx0,vy0,T,h,tol):
    tab_x = numpy.zeros(1)
    tab_y = numpy.zeros(1)
    tab_vx = numpy.zeros(1)
    tab_vy = numpy.zeros(1)
    tab_t = numpy.zeros(1)
    tab_h = numpy.zeros(1)
    x = x0
    y = y0
    vx = vx0
    vy = vy0
    t = 0
    tab_x[0] = x
    tab_y[0] = y
    tab_vx[0] = vx
    tab_vy[0] = vy
    tab_t[0] = t
    tab_h[0] = h
    ni = 0
    while t<=T:
        (x,y,vx,vy,h)=fonction_pas(x,y,vx,vy,h,tol)
        tab_h = numpy.append(tab_h,h)
        t += h
        tab_x = numpy.append(tab_x,x)
        tab_y = numpy.append(tab_y,y)
        tab_vx = numpy.append(tab_vx,vx)
        tab_vy = numpy.append(tab_vy,vy)
        tab_t = numpy.append(tab_t,t)
        ni += 1
    print("Nombre de pas = %d"%ni)
    return (tab_t,tab_x,tab_y,tab_vx,tab_vy,tab_h,ni)

(t,x,y,vx,vy,h,ni)=integration(pas_euler,1,0,0,1.2,100,1e-2,0)
E=0.5*(vx**2+vy**2)-1/numpy.sqrt(x**2+y**2)
figure()
axes().set_aspect('equal')
plot(x,y)
xlabel("x")
ylabel("y")
grid()

figA.pdf

figure()
plot(t,E)
xlabel("t")
ylabel("E")
grid()

figB.pdf

print(ni)
--> 10000

La méthode d'Euler peut être rendue stable si l'on calcule séparément les positions et les vitesses (méthode d'Euler asymétrique). On calcule tout d'abord les nouvelles positions avec les vitesses à l'instant t_n :

x_{n + 1} = x_{n} + h v_{n} (11)

Ces positions à l'instant t_n+1 sont utilisées pour calculer les dérivées des vitesses à l'instant t_n+1, c'est-à-dire les accélérations :

a_{n + 1} = A (x_{n + 1}) (12)

Enfin les vitesses à l'instant t_n+1 sont calculées en utilisant ces accélérations :

v_{n + 1} = v_{n} + h a_{n + 1} (13)

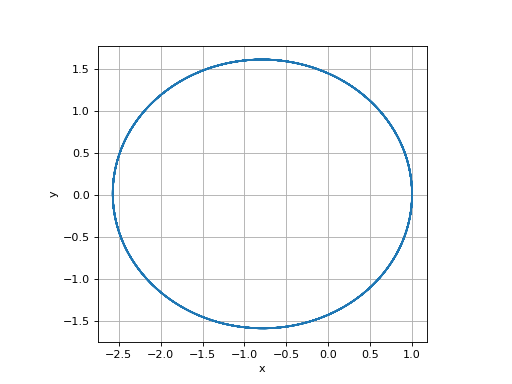
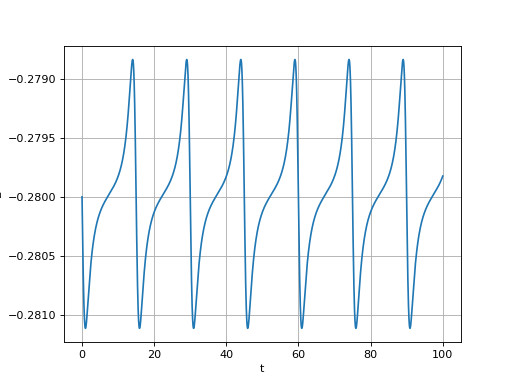
Écrire la fonction pas_euler_asym(x,y,vx,vy,h,tol).

Refaire le calcul précédent et comparer.

def pas_euler_asym(x,y,vx,vy,h,tol):
    x1 = x+h*vx
    y1 = y+h*vy
    r3 = numpy.power(x1*x1+y1*y1,1.5)
    ax = -x1/r3
    ay = -y1/r3
    return (x1,y1,vx+h*ax,vy+h*ay,h)
    
(t,x,y,vx,vy,h,ni)=integration(pas_euler_asym,1,0,0,1.2,100,1e-2,0)
E=0.5*(vx**2+vy**2)-1/numpy.sqrt(x**2+y**2)
figure()
axes().set_aspect('equal')
plot(x,y)
xlabel("x")
ylabel("y")
grid()

figC.pdf

figure()
plot(t,E)
xlabel("t")
ylabel("E")
grid()

figD.pdf

print(ni)
--> 10000

4. Adaptation du pas

Pour améliorer la précision de l'approximation obtenue, il faut réduire le pas de temps h. La méthode d'Euler est d'ordre 1, ce qui signifie qu'il faut réduire le pas de temps d'un facteur 10 pour obtenir un gain de précision d'un facteur 10 sur l'état du système à l'instant final T. Le coût en temps de calcul d'un gain en précision est donc très grand. Cependant, ce gain en précision peut être obtenu avec un pas de temps variable. Dans l'exemple étudié ici, le pas de temps peut être plus grand à l'apogée (loin du centre attracteur) et plus petit au périgée.

Pour mettre en place une adaptation du pas de temps, il faut pouvoir calculer, à chaque instant t_n, une estimation de l'erreur locale commise. Il ne s'agit bien sûr que d'une estimation, car l'erreur ne peut être déterminée si la solution exacte n'est pas connue. Une manière de faire cette estimation consiste à calculer $Y_{n + 1}^{h}$ avec un pas de temps h, puis $Y_{n + 1}^{h / 2}$ avec deux étapes chacune d'un pas h/2. Le seconde est plus précise et la différence entre les deux donne une estimation de l'erreur locale commise. Pour l'exemple traité ici, on pourra estimer l'erreur en calculant la distance entre les deux points :

e = \sqrt{{(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2}} (14)

où (x₁,y₁) sont les coordonnées obtenues à l'instant t_n+1 avec un pas h et (x₂,y₂) les coordonnées obtenues à l'instant t_n+1 avec deux pas de largeur h/2.

Cette estimation de l'erreur est comparée à une tolérance ε. Si l'erreur est supérieure à la tolérance, on doit réduire le pas et recommencer le calcul de Y_n+1 avec ce pas plus petit. Si à l'inverse l'erreur est inférieure à la tolérance, on augmente le pas pour le calcul de Y_n+2. Pour savoir comment réduire ou augmenter le pas, il faut tenir compte de l'ordre de la méthode. La méthode d'Euler est d'ordre 1 : l'erreur locale est donc asymptotiquement proportionnelle à h² (lorsque h tend vers zéro). On peut donc modifier le pas de temps de la manière suivante :

h' = h {(\frac{ε}{e})}^{\frac{1}{2}} (15)

Le calcul de Y_n+1 est refait avec ce nouveau pas seulement si le facteur correctif ${(\frac{ε}{e})}^{\frac{1}{2}}$ est inférieur à 0,9. Dans le cas contraire, on continue l'intégration avec le calcul de Y_n+2 pour t_n+1=t_n+h'.

Écrire une fonction pas_euler_adapt(x,y,vx,vy,h,tol) qui effectue le calcul de Y_n+1 à partir de Y_n avec un pas de temps h et en tenant compte de la tolérance tol. La fonction effectue l'estimation de l'erreur et corrige le pas de temps. Le calcul est refait tant que le facteur de correction est inférieur à 0,9. On prévoira un nombre maximal d'itérations (par exemple 10) pour éviter une boucle infinie et l'affichage d'un message si ce maximum est atteint. La fonction renvoie (x,y,vx,vy,h) où h est le nouveau pas de temps.

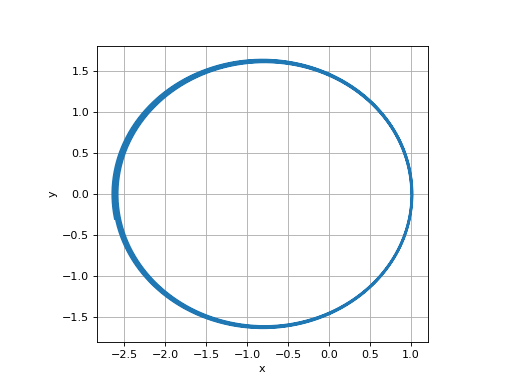
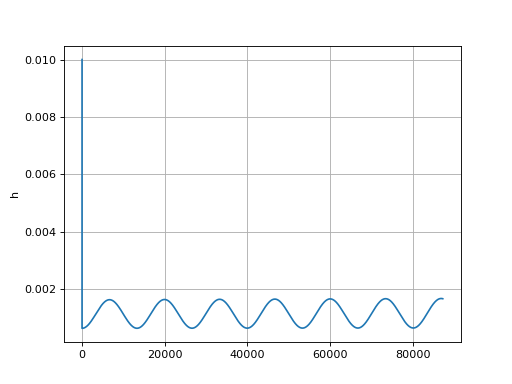
Tester avec un pas initial h = 0,01 et une tolérance 10^-6. Tracer l'évolution du pas de temps. Essayer d'obtenir un résultat similaire avec un pas de temps constant. Comparer les nombres de pas de temps calculés.

def pas_euler_adapt(x,y,vx,vy,h,tol):
    hh = h
    fh = 0.5
    n = 0
    while fh<=0.9 and n<10:
        (x1,y1,vx1,vy1,h) = pas_euler(x,y,vx,vy,hh,tol)
        (x2,y2,vx2,vy2,h) = pas_euler(x,y,vx,vy,hh*0.5,tol)
        (x2,y2,vx2,vy2,h) = pas_euler(x2,y2,vx2,vy2,hh*0.5,tol)
        dx = x2-x1
        dy = y2-y1
        e = numpy.sqrt(dx*dx+dy*dy)
        fh = numpy.sqrt(tol/e)
        hh *= fh
        n += 1
        if n==10:
            print("max n atteint")
    return (x2,y2,vx2,vy2,hh)
    
(t,x,y,vx,vy,h,ni)=integration(pas_euler_adapt,1,0,0,1.2,100,1e-2,1e-7)
E=0.5*(vx**2+vy**2)-1/numpy.sqrt(x**2+y**2)
figure()
axes().set_aspect('equal')
plot(x,y)
xlabel("x")
ylabel("y")
grid()

figE.pdf

figure()
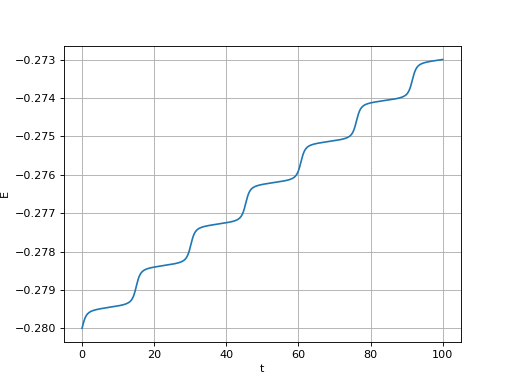
plot(t,E)
xlabel("t")
ylabel("E")
grid()

figF.pdf

figure()
plot(h)
ylabel("h")
grid()

figG.pdf

print(ni)
--> 87241

Une tolérance de plus en plus petite permet d'obtenir une approximation de plus en plus proche de la solution exacte. Cependant, le temps de calcul devient vite très grand. Il faut donc se tourner vers une méthode plus précise, c'est-à-dire qui donnera une meilleure précision pour le même pas de temps.

5. Méthode du point milieu

La méthode du point milieu (appelée aussi méthode de Runge-Kutta d'ordre 2) est une méthode plus précise que la méthode d'Euler puisqu'elle est d'ordre 2. Elle consiste à calculer tout d'abord une approximation au point milieu entre t_n et t_n+1=t_n+h, c'est-à-dire à l'instant t_n+h/2. On calcule donc tout d'abord :

Y_{n + 1 / 2} = Y_{n} + \frac{h}{2} f (Y_{n}) (16)

L'approximation Y_n+1 est calculée non pas avec la dérivée à l'instant t_n comme dans la méthode d'Euler, mais avec la dérivée évaluée au point milieu. On calcule donc :

Y_{n + 1} = Y_{n} + h f (Y_{n + 1 / 2}) (17)

Le calcul de Y_n+1 demande deux fois plus d'opérations que dans la méthode d'Euler. Cependant, l'erreur locale est proportionnelle à h³ (au lieu de h² pour la méthode d'Euler). On peut donc s'attendre, pour la même quantité de calcul, à une plus grande précision de la méthode du point milieu. C'est bien ce qu'on observe en pratique. D'une manière générale, les méthodes d'ordre plus élevé sont plus intéressantes même si le calcul d'un même pas de temps est plus coûteux.

Écrire une fonction pas_rk2(x,y,vx,vy,h,tol) qui effectue le calcul de Y_n+1 avec la méthode du point milieu (avec un pas de temps constant).

def pas_rk2(x,y,vx,vy,h,tol):
    r3 = numpy.power(x*x+y*y,1.5)
    ax = -x/r3
    ay = -y/r3
    x1 = x+0.5*h*vx
    y1 = y+0.5*h*vy
    vx1 = vx+0.5*h*ax
    vy1 = vy+0.5*h*ay
    r3 = numpy.power(x1*x1+y1*y1,1.5)
    ax1 = -x1/r3
    ay1 = -y1/r3
    return (x+h*vx1,y+h*vy1,vx+h*ax1,vy+h*ay1,h)
    
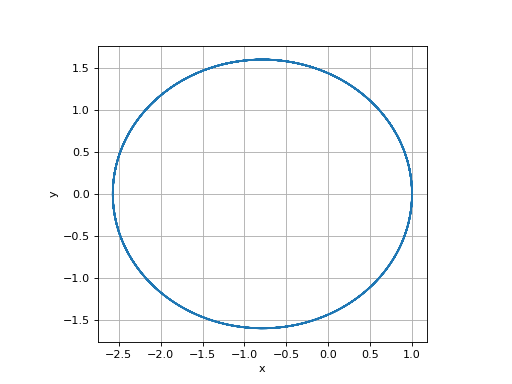
(t,x,y,vx,vy,h,ni)=integration(pas_rk2,1,0,0,1.2,100,1e-2,0)
E=0.5*(vx**2+vy**2)-1/numpy.sqrt(x**2+y**2)
figure()
axes().set_aspect('equal')
plot(x,y)
xlabel("x")
ylabel("y")
grid()

figH.pdf

 
figure()
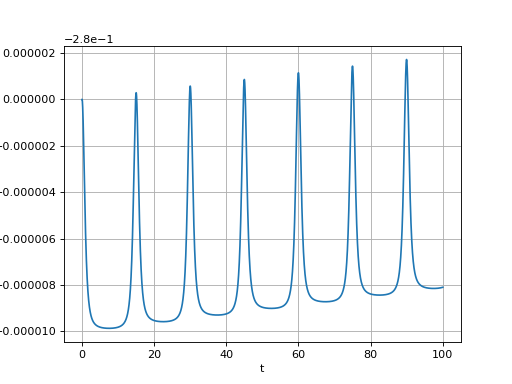
plot(t,E)
xlabel("t")
ylabel("E")
grid()

figI.pdf

print(ni)
--> 10000

La méthode d'adapation du pas pour la méthode du point milieu doit tenir compte de l'ordre de l'erreur local. On écrira donc :

h' = h {(\frac{ε}{e})}^{\frac{1}{3}} (18)

Écrire une fonction pas_rk2_adapt(x,y,vx,vy,h,tol) qui effectue le calcul de Y_n+1 avec la méthode du point milieu en adaptant le pas de temps.

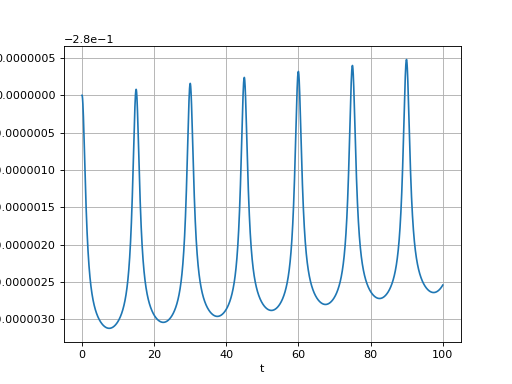
Comparer la méthode d'Euler avec adaptation du pas et la méthode du point milieu avec adaptation du pas. Remarquer que la même tolérance donne une erreur à l'instant T très différente dans les deux cas. Cela montre que le contrôle de l'erreur globale ne peut se faire par un paramètre fixé a priori.

def pas_rk2_adapt(x,y,vx,vy,h,tol):
    hh = h
    fh = 0.5
    n = 0
    while fh<=0.9 and n<10:
        (x1,y1,vx1,vy1,h) = pas_rk2(x,y,vx,vy,hh,tol)
        (x2,y2,vx2,vy2,h) = pas_rk2(x,y,vx,vy,hh*0.5,tol)
        (x2,y2,vx2,vy2,h) = pas_rk2(x2,y2,vx2,vy2,hh*0.5,tol)
        dx = x2-x1
        dy = y2-y1
        e = numpy.sqrt(dx*dx+dy*dy)
        fh = numpy.power(tol/e,0.33)
        hh *= fh
        n += 1
        if n==10:
            print("max n atteint")
    return (x2,y2,vx2,vy2,hh)
    
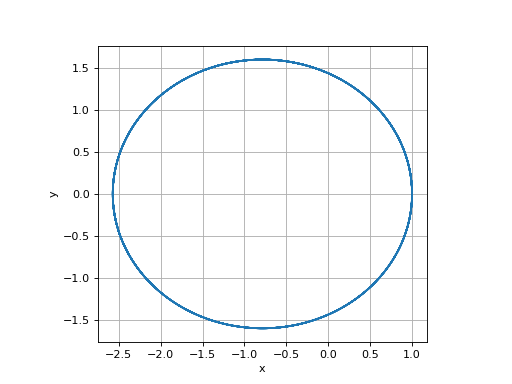
(t,x,y,vx,vy,h,ni)=integration(pas_rk2_adapt,1,0,0,1.2,100,1e-2,1e-7)
E=0.5*(vx**2+vy**2)-1/numpy.sqrt(x**2+y**2)
figure()
axes().set_aspect('equal')
plot(x,y)
xlabel("x")
ylabel("y")
grid()

figJ.pdf

figure()
plot(t,E)
xlabel("t")
ylabel("E")
grid()

figK.pdf

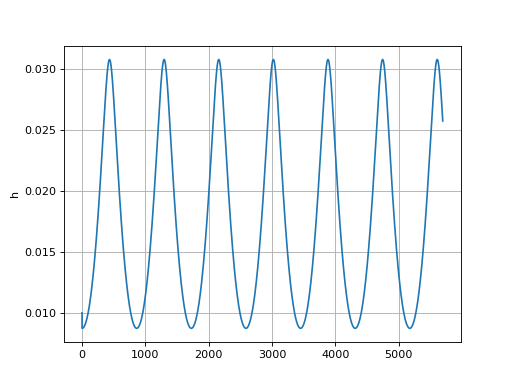
figure()
plot(h)
ylabel("h")
grid()

figL.pdf

print(ni)
--> 5693

Pour évaluer l'erreur globale à l'instant T, il faut refaire le calcul complet avec une tolérance plus faible et comparer. Supposons qu'on se fixe comme objectif de s'approcher de la solution exacte à l'instant T à moins de ε_g (tolérance globale). Si la réduction de la tolérance locale ε ne change pas l'état du système à l'instant T plus que la tolérance ε_g alors la tolérance locale ε est assez faible.

Méthode d'Euler : gravitation

1. Introduction

2. Équations différentielles

3. Méthode d'Euler

4. Adaptation du pas

5. Méthode du point milieu