Intégration des équations différentielles : méthode d'Euler
1. Introduction
En mécanique classique, les équations du mouvement d'un système mécanique (systèmes de points matériels, système de solides) sont des équations différentielles du second ordre par rapport au temps. La connaissance des positions et des vitesses des points à l'instant t=0 suffit à déterminer le mouvement pour t>0.
Ces équations sont souvent non linéaires car les forces elles-mêmes le sont (par exemple la force de gravitation) et car l'accélération est souvent une fonction non linéaire des degrés de liberté. Dans ce cas, il est fréquent que l'on ne connaisse pas de solution analytique exacte. On est alors amené à rechercher une solution approchée par une méthode numérique.
Ce document explique le principe de ce type d'intégration numérique. On prendra l'exemple de l'oscillateur harmonique (dont la solution exacte est connue) auquel on appliquera la méthode numérique d'Euler. On abordera les notions importantes de convergence et de stabilité.
2. Système différentiel du premier ordre
Considérons l'équation du mouvement d'un oscillateur harmonique :
Il s'agit d'une équation différentielle linéaire dont on connaît la solution exacte. En prenant une vitesse nulle à l'instant zéro, la solution est :
Les méthodes numériques n'ont d'intérêt que pour les équations dont on ne connaît pas la solution exacte, mais en appliquant la méthode d'Euler à l'oscillateur harmonique on pourra tester la méthode en comparant la solution approchée à la solution exacte.
Les méthodes d'intégration numériques opèrent sur des systèmes différentiels du premier ordre. Il faut donc transformer l'équation différentielle du second ordre en système du premier ordre. Dans le cas présent, cela se fait sans difficulté en introduisant la vitesse :
Les fonctions x(t) et v(t) vérifient le système différentiel du premier ordre suivant :
Pour raisonner de manière générale, on écrira ce système sous la forme suivante :
Y représente une liste de variables, qu'on peut représenter sous forme d'une matrice colonne. Dans le cas présent :
Pour l'oscillateur harmonique, la fonction f ne dépend pas explicitement du temps (le temps intervient implicitement dans y). Ce n'est pas toujours le cas, comme le montre l'exemple de l'oscillateur harmonique forcé.
Lorsque le système est linéaire, il peut s'écrire sous forme matricielle, par exemple pour l'oscillateur harmonique :
3. Méthode d'Euler explicite
3.a. Définition
L'intégration numérique de l'équation consiste à calculer des valeurs approchées de y sur un intervalle [0,T]. Pour cela, on divise cet intervalle en N sous-intervalles égaux de longueur h=T/N et on définit les instants :
où l'entier n varie de 0 à N. h est le pas de temps. La première valeur Y0 est la condition initiale.
Dans la méthode d'Euler explicite, la valeur approchée à l'instant tn+1 est obtenue à partir de la précédente par
La méthode d'Euler repose sur l'observation suivante. Supposons que la valeur exacte de Y à l'instant tn soit connue. La valeur de Y à l'instant tn+1=tn+h est donnée par le développement de Taylor :
La méthode d'Euler consiste à négliger dans ce développement tous les termes à partir du terme d'ordre 2 en h :
L'erreur commise par cette approximation (la somme des termes à partir du rang 2) est appelée erreur de troncature (ET), ou erreur locale. Pour la méthode d'Euler, l'ET est O(h2) car si h est assez petit il existe une constante K telle que .
Cela conduit à la relation de récurrence . Il faut remarquer que Yn est déjà une valeur approchée à l'instant tn et non pas la valeur exacte. La dérivée est évaluée avec cette valeur approchée; elle est donc en général légèrement différente de la dérivée exacte à l'instant tn.
Le système différentiel est défini dans une fonction python de la forme systeme(Y,t) où Y est un tableau contenant les variables (x et v dans l'exemple). Par convention, on utilise des lettres majuscules pour les tableaux. La fonction renvoie un tableau numpy.ndarray contenant les dérivées des variables par rapport au temps.
Voici par exemple la fonction définissant le système pour l'oscillateur harmonique (on pose ω=2π) :
import numpy
w2 = (2*numpy.pi)**2
def oscillateur(Y,t):
return numpy.array([Y[1],-w2*Y[0]])
Par convention, nous avons placé en premier paramètre le tableau Y, en second le temps t. Cette convention est aussi utilisée par la fonction scipy.integrate.odeint. En revanche, la fonction scipy.integrate.solve_ivp utilise la convention inverse (temps en premier, tableau des variables en second).
La fonction pas_euler(systeme,h,tn,Yn) effectue un pas élémentaire de la méthode d'Euler, c'est-à-dire le calcul de Yn+1 à partir de Yn. Ses arguments sont le système différentiel, le pas de temps h, le temps tn et le tableau Yn. La fonction renvoie Yn+1.
def pas_euler(systeme,h,tn,Yn):
deriv = systeme(Yn,tn)
return Yn+h*deriv
La fonction euler(systeme,Yi,T,h) effectue l'intégration numérique sur l'intervalle [0,T]. La condition initiale est Yi. Le pas de temps est h. La fonction stocke les valeurs de Y sous forme d'une liste (construite comme une pile). Une liste contenant le temps est aussi générée. Ces listes sont converties en tableau numpy avant d'être renvoyées. Voici par exemple la structure du tableau Y pour un système à 3 variables :
L'indice ajouté entre crochets permet de repérer la variable. Ainsi Yn[0] désigne la valeur de la variable d'indice 0 à l'instant n.
def euler(systeme,Yi,T,h):
Y = Yi
t = 0.0
liste_y = [Y]
liste_t = [t]
while t<T:
Y = pas_euler(systeme,h,t,Y)
t += h
liste_y.append(Y)
liste_t.append(t)
return (numpy.array(liste_t),numpy.array(liste_y))
Cette fonction utilise deux listes remplies au fur et à mesure avec append. Dans le cas présent, la longueur du tableau final est connue a priori (égale à T/h), mais ce n'est pas toujours le cas, par exemple si on met on place une adaptation du pas de temps, ou si le calcul doit s'arrêter lorsqu'une condition sur une des variables est remplie. Le résultat est renvoyé sous la forme de deux tableaux numpy.ndarray, ce qui facilite les manipulations ultérieures, par exemple pour le tracé des courbes. Il est possible d'écrire une version qui travaille entièrement sur ce type de tableaux :
def euler_bis(systeme,Yi,T,h):
Y = Yi
t = 0.0
tableau_y = numpy.array([Y])
tableau_t = numpy.array([t])
while t<T:
Y = pas_euler(systeme,h,t,Y)
t += h
tableau_y = numpy.append(tableau_y,[Y],axis=0)
tableau_t = numpy.append(tableau_t,t)
return (tableau_t,tableau_y)
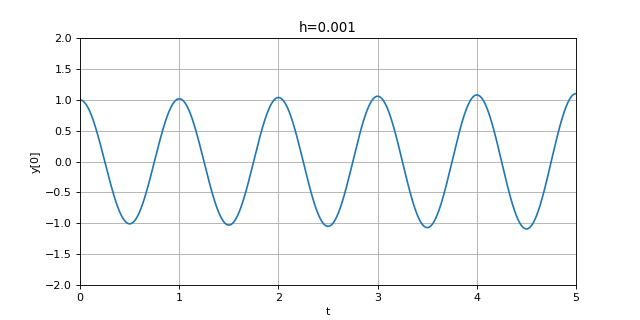
Voici le résultat avec l'oscillateur harmonique :
from matplotlib.pyplot import *
T = 5.0
h = 1.0e-3
Yi = [1.0,0]
(t,tab_y) = euler(oscillateur,Yi,T,h)
x = tab_y[:,0]
figure(figsize=(8,4))
plot(t,x)
xlabel('t')
ylabel('y[0]')
axis([0,T,-2,2])
title('h=0.001')
grid()
 figA.pdf
figA.pdf
3.b. Erreurs locale et globale
L'approximation consiste à négliger les termes d'ordre supérieur ou égal à 2 dans le développement de Taylor. L'erreur commise par cette approximation est appelée erreur locale de troncature. Lorsque h est assez petit, cette erreur est en valeur absolue inférieure à une constante multipliée par h2. Si le pas de temps h est divisé par deux, il y a une réduction d'un facteur 4 de l'erreur de troncature.
L'erreur globale (ou simplement l'erreur) à l'instant tn est l'écart entre la solution approchée et la solution exacte à cet instant :
L'erreur globale résulte de l'accumulation des erreurs locales commises sur les n pas précédents (ce qui ne signifie pas qu'elle soit toujours croissante). La figure suivante montre un exemple avec la solution exacte en trait plein et les valeurs approchées aux instants tn.
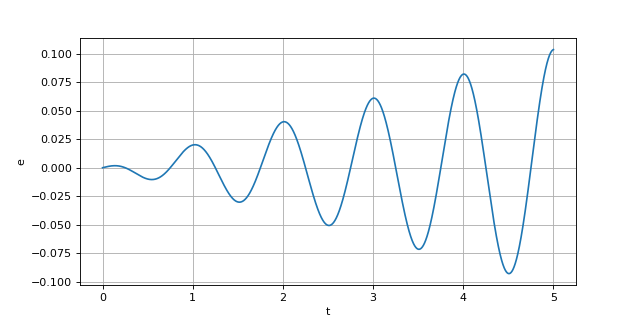
Figure pleine pageDans le cas de l'oscillateur harmonique, l'erreur peut être calculée puisque la solution exacte est connue. On trace donc l'erreur en fonction du temps :
erreur = x-numpy.cos(2*numpy.pi*t)
figure(figsize=(8,4))
plot(t,erreur,label='h=0.001')
xlabel('t')
ylabel('e')
grid()
 figB.pdf
figB.pdf
L'erreur présente ici une variation non monotone. Elle s'annule même périodiquement. Globalement, on constate néanmoins une augmentation de l'erreur.
3.c. Convergence
Une méthode numérique doit être convergente, c'est-à-dire que l'erreur globale doit, pour tout n, tendre vers zéro lorsque le pas h tend vers zéro. La méthode d'Euler est effectivement convergente.
La convergence nous garantit des valeurs approchées de plus en plus proches des valeurs exactes lorsqu'on réduit le pas de temps h.
Une question importante est celle de la vitesse de convergence, c'est-à-dire comment l'erreur globale évolue avec le pas h.
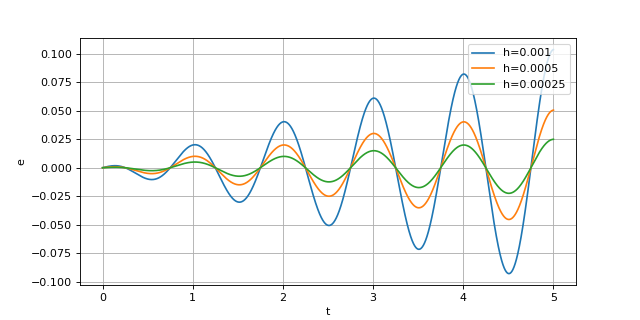
Divisons le pas par deux pour voir l'évolution de l'erreur :
h = h/2
(t2,tab_y) = euler(oscillateur,Yi,T,h)
yt = tab_y.transpose()
x = yt[0]
erreur2 = x-numpy.cos(2*numpy.pi*t2)
plot(t2,erreur2,label='h=0.0005')
h = h/2
(t3,tab_y) = euler(oscillateur,Yi,T,h)
x = tab_y[:,0]
erreur3 = x.copy()
for i in range(x.size):
erreur3[i] = x[i]-math.cos(2*math.pi*t3[i])
plot(t3,erreur3,label='h=0.00025')
legend(loc='upper right')
 figC.pdf
figC.pdf
L'erreur semble divisée par deux lorsque le pas est divisé par deux. Pour le confirmer, nous allons calculer l'erreur pour une valeur particulière de t, là ou elle présente un maximum relatif. Pour cela, il est inutile de stocker tous les points antérieurs. On écrit une fonction erreur_euler(systeme,solution,yi,T,h) qui calcule la valeur absolue de l'erreur à l'instant final T, pour la première variable. La solution exacte solution doit être fournie.
def erreur_euler(systeme,solution,Yi,T,h):
Y = Yi
t = 0.0
while t<T:
Y = pas_euler(systeme,h,t,Y)
t += h
return abs(Y[0]-solution(t))
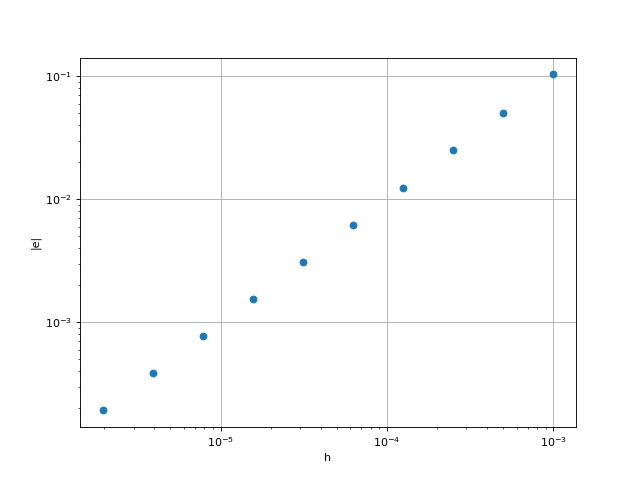
On trace l'erreur en t=5 en fonction de h, en échelle logarithmique. Pour cela, on génère une liste de valeurs de h et une liste contenant les erreurs correspondantes.
liste_h = []
liste_e = []
T = 5.0
h = 0.001
def solution(t):
return math.cos(2*math.pi*t)
for i in range(10):
liste_h.append(h)
liste_e.append(erreur_euler(oscillateur,solution,Yi,T,h))
h = h/2
figure(figsize=(8,6))
plot(liste_h,liste_e,'o')
xlabel('h')
ylabel('|e|')
xscale('log')
yscale('log')
grid()
 figD.pdf
figD.pdf
On obtient en échelle logarithmique une pente de 1, ce qui confirme que l'erreur globale est proportionnelle à la puissance 1 du pas h. La méthode d'Euler est donc d'ordre 1. Pour réduire l'erreur d'un facteur 10, il faut aussi réduire le pas d'un facteur 10, c'est-à-dire faire 10 fois plus de calculs. Une méthode d'ordre 1 est donc à éviter si l'on souhaite faire des calculs très précis. On utilisera d'autres méthodes d'ordre plus élevé, par exemple la méthode du point milieu (d'ordre 2), une méthode de Runge-Kutta d'ordre 4, ou la méthode de Bulirsch-Stoer.
3.d. Stabilité
On s'intéresse à présent à l'évolution de l'erreur avec le temps T, à h constant.
T = 100.0
h = 1.0e-3
(t,tab_y) = euler(oscillateur,Yi,T,h)
x = tab_y[:,0]
erreur = numpy.absolute(x-numpy.cos(2*numpy.pi*t))
figure(figsize=(8,5))
plot(t,erreur)
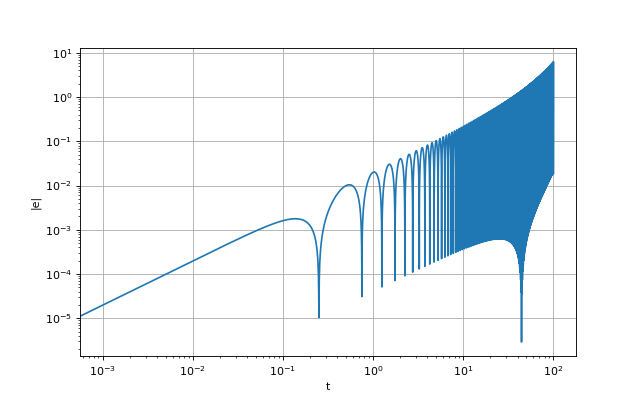
xlabel('t')
ylabel('|e|')
yscale('log')
xscale('log')
grid()
 figE.pdf
figE.pdf
Bien que l'erreur soit très faible au début, elle croît très rapidement. La méthode d'Euler est dite instable pour l'oscillateur harmonique car l'erreur est non bornée.
Voyons le tracé dans l'espace des phases :
v = tab_y[:,1]
figure(figsize=(6,6))
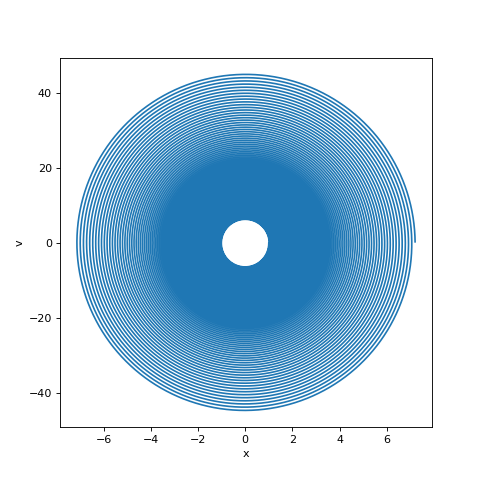
plot(x,v)
xlabel('x')
ylabel('v')
 figF.pdf
figF.pdf
On obtient une oscillation dont l'amplitude augmente sans fin, au lieu du mouvement périodique de la solution exacte. L'instabilité conduit dans ce cas à une solution physiquement inacceptable (l'énergie n'est pas conservée). On peut effectivement démontrer que la méthode d'Euler est instable pour l'oscillateur harmonique (voir paragraphe 6). L'expérience montre qu'elle l'est aussi pour des systèmes non linéaires en général. Pour la simulation des systèmes physiques sur des temps longs, c'est un inconvénient bien plus grave que la faible précision. Lorsqu'on simule un système physique complexe, on recherche plus la vraisemblance de la solution que sa précision. Dans le cas des systèmes chaotiques, la recherche de la précision est d'ailleurs vaine, en raison de l'extrême sensibilité aux conditions initiales.
Des méthodes plus précises comme les méthodes de Runge-Kutta (explicites) sont également instables pour les systèmes linéaires. La précision et la stabilité sont deux propriétés indépendantes.
Nous allons voir comment une modification de la méthode d'Euler permet de la rendre stable.
4. Méthode d'Euler asymétrique
4.a. Définition
Cette variante de la méthode d'Euler s'applique aux équations différentielles des systèmes mécaniques conservatifs (systèmes hamiltoniens). Elle consiste à traiter séparément les positions et les vitesses. Voyons comment cette méthode est définie dans le cas particulier d'une variable x et de sa vitesse v (la généralisation à un système quelconque est immédiate).
La première étape est le calcul de xn+1 comme pour la méthode d'Euler :
Avant de calculer la vitesse à l'instant tn+1, on calcule sa dérivée (c.a.d. l'accélération) en utilisant la valeur xn+1 de la position. Si on note a(x) la fonction qui permet de calculer l'accélération en fonction de la position, on calcule donc :
Cela est faisable pour les systèmes conservatifs car la force ne dépend pas de la vitesse. Enfin on calcule la vitesse à l'instant tn+1 en utilisant cette accélération :
Dans la méthode d'Euler classique, l'accélération utilisée pour calculer vn+1 est évaluée avec xn et non pas xn+1.
Cette méthode est asymétrique car elle traite de manière asymétrique les variables positions et les variables vitesses. Elle appartient à la classe des méthodes symplectiques (une propriété qui permet de conserver l'énergie). On la désignera sous le nom de méthode d'Euler-A (car il existe aussi une méthode Euler-B, où l'asymétrie est inversée).
Nous allons voir que ce changement modifie radicalement la stabilité de la méthode.Les équations sont définies par une fonction accel(X). La liste X contient les positions. Voici la fonction pour l'oscillateur harmonique :
def accel(X):
return numpy.array([-w2*X[0]])
La fonction pas_eulerA(accel,h,t,Xn,Vn) effectue un pas élémentaire de la méthode Euler-A. La fonction renvoie Xn+1 et Vn+1.
def pas_eulerA(accel,h,t,Xn,Vn):
X = Xn+h*Vn
A = accel(X)
V = Vn+h*A
return (X,V)
La fonction eulerA(accel,Xi,Vi,T,h) effectue l'intégration numérique sur l'intervalle [0,T] avec la condition initiale définie par les positions Xi et Vi et un pas de temps h.
def eulerA(accel,Xi,Vi,T,h):
X = numpy.array(Xi)
V = numpy.array(Vi)
t = 0.0
liste_t = [t]
liste_x = [X]
liste_v = [V]
while t<T:
(X,V) = pas_eulerA(accel,h,t,X,V)
t += h
liste_t.append(t)
liste_x.append(X)
liste_v.append(V)
return (numpy.array(liste_t),numpy.array(liste_x),numpy.array(liste_v))
4.b. Stabilité
Voyons l'application à l'oscillateur harmonique, en reprenant la valeur de h qui donnait une divergence très visible avec la méthode d'Euler.
T = 1000.0
h = 1.0e-3
Xi = [1]
Vi = [0]
(t,tab_x,tab_v) = eulerA(accel,Xi,Vi,T,h)
figure(figsize=(6,6))
plot(tab_x[:,0],tab_v[:,0])
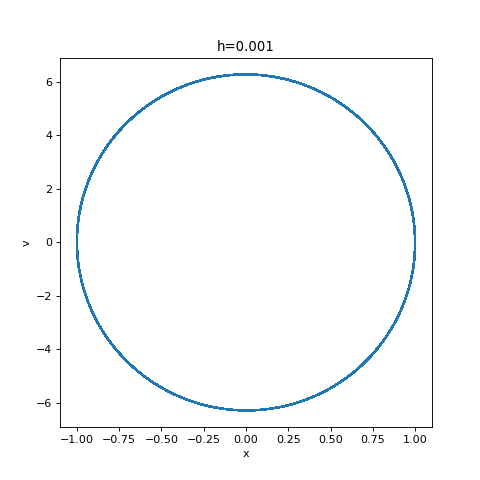
xlabel('x')
ylabel('v')
title('h=0.001')
 figG.pdf
figG.pdf
On obtient bien un mouvement périodique, même avec une durée T très longue.
Voyons le tracé de l'erreur :
x = tab_x[:,0]
erreur = x-numpy.cos(2*numpy.pi*t)
figure(figsize=(8,4))
plot(t,erreur)
xlabel('t')
ylabel('e')
title('h=0.001')
grid()
 figH.pdf
figH.pdf
L'erreur garde des valeurs très faibles même sur des temps très longs, là où la méthode d'Euler donnait une divergence catastrophique de l'erreur. On peut démontrer que cette méthode est stable pour l'oscillateur harmonique si h est inférieur à 2/ω (voir paragraphe 6 ci-dessous).
5. Méthodes d'ordre plus élevé
Lorsque une précision importante est requise, les méthodes d'Euler (d'ordre 1) sont insuffisantes. La fonction scipy.integrate.solve_ivp ( solve initial value problem) permet d'accéder à des méthodes d'ordre plus élevé et à des algorithmes dans lequel le pas de temps s'adapte automatiquement en fonction d'une tolérance choisie. Voici un exemple d'utilisation pour intégrer l'équation du pendule (équation non linéaire) :
from scipy.integrate import solve_ivp
def systeme(t,Y): # le temps en premier
return numpy.array([Y[1],-w2*numpy.sin(Y[0])])
T = 5
Y_init = [2,0]
t = numpy.linspace(0,T,1000)
solution = solve_ivp(systeme,[0,T],Y_init,method='RK45',t_eval=t,atol=1e-5,rtol=1e-5)
figure()
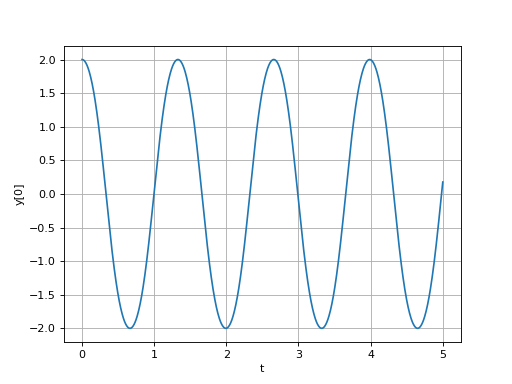
plot(solution.t,solution.y[0])
xlabel('t')
ylabel('y[0]')
grid()
 figH2.pdf
figH2.pdf
La méthode d'intégration fait appel à une adaptation du pas contrôlée par une tolérance absolue (atol) et une tolérance relative (rtol). La signification de ces deux tolérances est donnée dans l'annexe Adaptation du pas à la fin de ce document. Elles permettent de contrôler l'erreur locale mais ne donnent aucune information sur l'erreur globale obtenue. Pour évaluer l'erreur globale, il faut refaire plusieurs fois le calcul complet avec des tolérances différentes.
La fonction scipy.integrate.odeint peut aussi être utilisée, mais elle n'offre pas le choix de la méthode numérique :
from scipy.integrate import odeint
def systeme(Y,t): # le temps en second
return numpy.array([Y[1],-w2*numpy.sin(Y[0])])
T = 5
Y_init = [2,0]
t = numpy.linspace(0,T,1000)
y = odeint(systeme,Y_init,t,atol=1e-5,rtol=1e-5)
figure()
plot(t,y[:,0])
xlabel('t')
ylabel('y[0]')
grid()
6. Méthode de Verlet
La méthode d'Euler asymétrique étudiée ci-dessus possède une très bonne stabilité, qui la rend apte à intégrer des systèmes conservatifs comportant un grand nombre de degrés de liberté (problème des N corps, dynamique moléculaire, etc.). Néanmoins, elle est d'ordre 1 comme la méthode d'Euler. Verlet ([1]) a proposé une méthode d'ordre 2 (pour la position) afin d'effectuer des calculs de dynamique moléculaire, ce que la plupart des méthodes explicites sont incapables de faire en raison de leur instabilité. Il s'agissait d'établir une méthode à la fois stable et présentant un minimum de calculs afin de traiter des équations à plusieurs milliers d'inconnues.
Cette méthode consiste à introduire un temps intermédiaire entre tn et tn+1, que l'on notera tn+1/2 :
La vitesse intermédiaire est utilisée pour calculer la nouvelle position. La méthode est d'ordre 2 pour la position, d'ordre 1 pour la vitesse. Pour l'oscillateur harmonique, elle est stable si h est inférieur à 2/ω, une condition très peu contraignante ([2]) . D'une manière générale, l'expérience montre que cette méthode est stable pour les systèmes dynamiques conservatifs pourvu que le pas soit assez petit.
7. Étude de la stabilité
La lecture de cette partie nécessite des connaissances sur la diagonalisation des matrices et la résolution des équations différentielles linéaires à coefficients constants.
7.a. Principe
L'étude de la stabilité d'un schéma numérique peut se faire de manière générale dans le cas d'un système différentiel linéaire ([3]), qui s'écrit sous la forme :
On suppose que la matrice M est diagonalisable. On peut alors effectuer un changement de base qui conduit à résoudre le système suivant :
où la matrice est diagonale. On obtient ainsi des équations différentielles découplées, de la forme :
où q est une valeur propre de M. La solution de cette équation est :
Les fonctions y(t) solutions du système différentiel sont des combinaisons linéaires de ces fonctions.
Pour l'étude de la stabilité, on s'intéresse aux solutions bornées. Il faut pour cela que les valeurs propres q aient toutes une partie réelle négative ou nulle. Par exemple, pour l'oscillateur harmonique les valeurs propres sont q1=iω et q2=-iω et la solution est bornée.
Pour un système dont la solution est bornée, le schéma numérique est stable s'il donne également une solution bornée.
Considérons alors le schéma numérique sous forme matricielle :
La matrice P est le propagateur. Par exemple pour la méthode d'Euler appliquée à l'oscillateur harmonique :
La diagonalisation du propagateur (lorsqu'elle est possible), conduit par un changement de base à :
où la matrice est diagonale. On obtient ainsi des équations découplées de la forme :
où p est une valeur propre du propagateur. La solution du schéma numérique est donc :
La valeur propre p est en général un nombre complexe. Pour que la solution ci-dessus soit bornée, il faut et il suffit que son module soit inférieur ou égal à 1.
On arrive ainsi à la règle suivante : un schéma numérique linéaire est stable pour un système différentiel linéaire dont la solution est bornée si et seulement si toutes les valeurs propres du propagateur ont un module inférieur ou égal à 1.
7.b. Méthode d'Euler et oscillateur harmonique
Appliquons la règle précédente à la méthode d'Euler et à l'oscillateur harmonique. Le propagateur est :
Ses valeurs propres sont :
Elles ont un module toujours supérieur à 1. La méthode d'Euler conduit donc à une suite non bornée pour l'oscillateur harmonique, alors que la solution du système différentiel est bornée (fonction cosinus). On en déduit que la méthode d'Euler est instable pour l'oscillateur harmonique.
7.c. Méthode d'Euler asymétrique et oscillateur harmonique
Écrivons explicitement le schéma de la méthode d'Euler asymétrique (Euler-A) pour l'oscillateur harmonique :
Le propagateur est :
Les valeurs propres sont solutions de l'équation :
dont le discriminant est :
Si hω<2 on obient deux racines complexes conjuguées dont le module est égal à 1. Dans ce cas, le schéma est stable. Si hω>2, on obtient deux racines réelles dont le module au carré est :
Dans ce cas le module est donc strictement supérieur à 1 et le schéma est instable.
On en déduit que la méthode d'Euler asymétrique est stable pour l'oscillateur harmonique si hω<2.
8. Annexe : adaptation du pas
Pour contrôler l'erreur locale, il est intéressant de faire varier le pas de temps h au cours de l'intégration. Si l'erreur locale est trop grande, on réduit le pas, par exemple en le divisant par deux. Si l'erreur est faible, on augmente le pas d'un facteur deux. La difficulté est d'avoir une estimation de l'erreur. Une méthode d'estimation consiste à faire deux calculs de Yn+1, le premier avec le pas h, le second avec le pas h/2:
La différence de ces deux listes permet d'évaluer l'erreur :
Cela donne un vecteur dont il faut calculer une norme |Δ|. On peut prendre par exemple le maximum de la valeur absolue des composantes, qui correspond à l'écart absolu le plus grand.
On se fixe comme objectif de maintenir cette estimation de l'erreur inférieure à
où εa est une tolérance absolue et εr une tolérance relative, qui sont fixées au début de l'intégration. On peut alors adopter la règle suivante pour l'adaptation du pas :
- Si |Δ|>ε alors on divise h par deux et on refait le calcul de Yn+1 avec ce nouveau pas (et avec sa moitié).
- Si |Δ|<ε alors on multiplie le pas par deux et on passe directement au calcul de Yn+2.
L'adaptation du pas peut être effectuée avec profit sur la méthode d'Euler standard. Malheureusement, il faut l'éviter sur la méthode d'Euler asymétrique et la méthode de Verlet, car elle conduit à une altération significative de la conservation de l'énergie.