Équation de Poisson 1D : méthode des éléments finis

2.a. Formulation variationnelle

Soit v(x) une fonction continue et dérivable par morceaux sur [0,L], appelée fonction test. On considère l'intégrale suivante :

$${\int }_0^L\frac{d}{dx}\left(v\left(x\right)\frac{du}{dx}\right)dx=v\left(L\right)\frac{du}{dx}\left(L\right)-v\left(0\right)\frac{du}{dx}\left(0\right)\text{(3)}$$

Cette intégrale s'écrit aussi :

$${\int }_0^L\frac{d}{dx}\left(v\left(x\right)\frac{du}{dx}\right)dx={\int }_0^{L}v\left(x\right)\frac{d^{2}u}{d{x}^2}dx+{\int }_0^L\frac{dv}{dx}\frac{du}{dx}dx=-{\int }_0^{L}v\left(x\right)f\left(x\right)+{\int }_0^L\frac{dv}{dx}\frac{du}{dx}dx\text{(4)}$$

Au moyen de la condition limite de Robin ($\mathrm{(2)}$), on obtient l'égalité suivante :

$${\int }_0^{L}v\left(x\right)f\left(x\right)dx={\int }_0^L\frac{dv}{dx}\frac{du}{dx}dx+v\left(0\right)(K_0(u\left(0\right)-u_0)+g_0)-v\left(L\right)(K_L(u\left(L\right)-u_L)+g_L)\text{(5)}$$

où $K_0,u_0,g_0,K_L,u_L,g_L$ sont des constantes qui définissent les conditions limites.

Soit V l'ensemble des fonctions de carré sommable sur l'intervalle [0,L] et dont la dérivée est aussi de carré sommable. La formulation variationnelle du problème de Poisson [1][2] consiste à écrire que l'égalité $\mathrm{(5)}$ doit être vraie pour toute fonction test v appartenant à V. La fonction recherchée u, appelée aussi fonction d'essai, doit aussi appartenir à V. Si u(x) est solution de l'équation $\mathrm{(1)}$ avec les conditions limites $\mathrm{(2)}$ alors elle satisfait l'énoncé variationnel mais la réciproque n'est pas vraie.

2.b. Maillage de l'intervalle - Fonctions affines par morceaux

L'intervalle [0,L] est subdivisé en N sous-intervalles. On obtient ainsi un maillage (unidimensionnel) dont les N+1 nœuds sont :

$$x_0=0,x_1,x_2,\dots x_{N-1},x_N=L\text{(6)}$$

Remarquons que les sous-intervalles n'ont pas nécessairement la même largeur. On définit la largeur maximale :

$$h=max\left(\right|x_{i+1}-x_i\left|\right)\text{(7)}$$

Une solution u(x) du problème variationnel est recherchée sous la forme d'une fonction continue et affine par morceaux, c'est-à-dire affine sur chaque sous-intervalle [x_i,x_i+1]. La figure suivante en donne l'illustration dans le cas N=5.

Figure pleine page

Cette fonction est notée u_h. Bien que ses valeurs aux nœuds du maillage soient censées être des approximations de la fonction u(x) solution de l'équation de Poisson, elle n'est pas dérivable aux nœuds et sa dérivée seconde sur chaque sous-intervalle est nulle.

On note V_h l'ensemble des fonctions affines par morceaux pour le maillage choisi, qui est un sous-ensemble de V. Une fonction de V_h est entièrement définie par ses valeurs aux nœuds du maillage.

La formulation variationnelle dans V_h consiste à recherche une fonction $u_h\in V_h$ telle que pour toute fonction test $v\in V_h$ on ait :

$${\int }_0^{L}v\left(x\right)f\left(x\right)dx={\int }_0^L\frac{dv}{dx}\frac{d{u}_h}{dx}dx+v\left(0\right)(K_0(u_h\left(0\right)-u_0)+g_0)-v\left(L\right)(K_L(u_h\left(L\right)-u_L)+g_L)\text{(8)}$$

On introduit les N+1 fonctions de V_h notées ${\varphi }_n$ et définies par :

$$\begin{array}{ccc}\hfill & {\varphi }_n\left(x_i\right)=1sii=n\hfill & \hfill \text{(9)}\\ \hfill & {\varphi }_n\left(x_i\right)=0sii\ne n\hfill & \hfill \text{(10)}\end{array}$$

Les fonctions ${\varphi }_0$ et ${\varphi }_3$ sont tracées sur la figure ci-dessus. Ces fonctions sont appelées fonctions chapeaux en raison de leur forme. Le support de la fonction ${\varphi }_n$ est [x_n-1,x_n+1] pour $n=1,\dots N-1$. Le support de ${\varphi }_0$ est [x₀,x₁], celui de ${\varphi }_N$ est [x_N-1,x_N].

Il est facile de démontrer que ces N+1 fonctions chapeaux constituent une base de V_h. La fonction u_h peut donc s'écrire sous la forme suivante :

$$u_h\left(x\right)=\sum _{j=0}^N{\xi }_j{\varphi }_j\left(x\right)\text{(11)}$$

Le nombre réel ${\xi }_j$ est la valeur de u_h au nœud j, c'est-à-dire l'approximation de u(x_j). La fonction test v se décompose de la même manière puisqu'elle appartient aussi à V_h.

La formulation variationnelle dans le cas où u et v appartiennent à V_h (équation $\mathrm{(8)}$) se traduit par N+1 équations :

$${\int }_0^L{\varphi }_i\left(x\right)f\left(x\right)dx={\int }_0^L\frac{d{\varphi }_i}{dx}\frac{d{u}_h}{dx}dx+{\varphi }_i\left(0\right)(K_0(u_h\left(0\right)-u_0)+g_0)-{\varphi }_i\left(L\right)(K_L(u_h\left(L\right)-u_L)+g_L),i=0,1\dots N\text{(12)}$$

La formulation variationnelle pour les fonctions de V_h implique évidemment ces N+1 équations puisque les fonctions chapeaux sont dans V_h. Réciproquement, cette condition vérifiée pour $i=0,1,\dots N-1$ implique l'identité $\mathrm{(5)}$ pour toute fonction v de V_h.

2.c. Équations algébriques

Le report de l'expression $\mathrm{(11)}$ dans l'égalité $\mathrm{(12)}$ conduit à :

$${\int }_0^L{\varphi }_i\left(x\right)f\left(x\right)dx=\sum _{j=0}^N{\xi }_j{\int }_0^L\frac{d{\varphi }_i}{dx}\frac{d{\varphi }_j}{dx}dx+{\varphi }_i\left(0\right)(K_0({\xi }_0-u_0)+g_0)-{\varphi }_i\left(L\right)(K_L({\xi }_N-u_L)+g_L),i=0,1\dots N\text{(13)}$$

On obtient N+1 équations algébriques linéaires pour les n+1 nombres ${\xi }_i$.

Posons :

$$A_{ij}={\int }_0^L\frac{d{\varphi }_i}{dx}\frac{d{\varphi }_j}{dx}dx\text{(14)}$$ $$b_i={\int }_0^L{\varphi }_i\left(x\right)f\left(x\right)dx\text{(15)}$$

Les équations s'écrivent :

$$\sum _{j=0}^N{A}_{ij}{\xi }_j+{\varphi }_i\left(0\right)K_0{\xi }_0-{\varphi }_i\left(L\right)K_K{\xi }_N=b_i+{\varphi }_i\left(0\right)(K_0{u}_0-g_0)-{\varphi }_i\left(L\right)(K_L{u}_L-g_L),i=0,1\dots N\text{(16)}$$

Ce système d'équations peut être écrit en isolant la première et la dernière équations, qui font intervenir les conditions limites :

$$\begin{array}{ccc}\hfill & \sum _{j=0}^N{A}_{0j}{\xi }_j+K_0{\xi }_0=b_0+K_0{u}_0-g_0\hfill & \hfill \text{(17)}\\ \hfill & \sum _{j=0}^N{A}_{ij}{\xi }_j=b_i,i=1,\dots N-1\hfill & \hfill \text{(18)}\\ \hfill & \sum _{j=0}^N{A}_{Nj}{\xi }_j-K_L{\xi }_N=b_N-(K_L{u}_L-g_L)\hfill & \hfill \text{(19)}\end{array}$$

La condition limite de Dirichlet en x=0 s'obtient avec $K_0\to \infty$, ce qui revient à remplacer la première équation par ${\xi }_0=u_0$ (comme on pouvait s'y attendre). De même, une condition de Dirichlet en x=L consiste à remplacer la dernière équation par ${\xi }_N=u_L$. Une condition de Neumann en x=0 s'obtient en posant K₀=0.

Explicitons les coefficients $A_{ij}$. Seuls les coefficients $A_{i,i},A_{i-1i},A_{ii+1}$ sont non nuls. On pose $h_i=x_i-x_{i-1}$ pour $i=1,2,\dots N$.

$$A_{00}={\int }_0^L(\frac{d{\varphi }_0}{dx}{)}^{2}dx={\int }_{x_0}^{x_1}\frac{dx}{h_1^2}=\frac{1}{h_1}\text{(20)}$$ $$A_{NN}={\int }_0^L(\frac{d{\varphi }_N}{dx}{)}^{2}dx={\int }_{x_{N-1}}^{x_N}\frac{dx}{h_N^2}=\frac{1}{h_N}\text{(21)}$$ $$A_{ii}={\int }_0^L(\frac{d{\varphi }_i}{dx}{)}^{2}dx={\int }_{x_{i-1}}^{x_i}\frac{dx}{h_i^2}+{\int }_{x_i}^{x_{i+1}}\frac{dx}{h_{i+1}^2}=\frac{1}{h_i}+\frac{1}{h_{i+1}},i=1,\dots N-1\text{(22)}$$ $$A_{ii+1}={\int }_0^L\frac{d{\varphi }_i}{dx}\frac{{\varphi }_{i+1}}{dx}dx=-{\int }_{x_i}^{x_{i+1}}\frac{dx}{h_{i+1}^2}=-\frac{1}{h_{i+1}}\text{(23)}$$ $$A_{i-1i}=-\frac{1}{h_i}\text{(24)}$$

Les coefficients $b_i$ sont évalués avec la méthode des trapèzes. Pour $i=1,\dots N-1$ :

$$\begin{array}{ccc}\hfill b_i& ={\int }_{x_{i-1}}^{x_{i+1}}{\varphi }_i\left(x\right)f\left(x\right)dx\hfill & \hfill \text{(25)}\\ \hfill & \approx ({\varphi }_i\left(x_{i-1}\right)f\left(x_{i-1}\right)+{\varphi }_i\left(x_i\right)f\left(x_i\right))\frac{h_i}{2}+({\varphi }_i\left(x_i\right)f\left(x_i\right)+{\varphi }_i\left(x_{i+1}\right)f\left(x_{i+1}\right))\frac{h_{i+1}}{2}\hfill & \hfill \text{(26)}\\ \hfill & =f\left(x_i\right)\frac{h_i+h_{i+1}}{2}\hfill & \hfill \text{(27)}\\ \hfill b_0& =f\left(x_0\right)\frac{h_1}{2}\hfill & \hfill \text{(28)}\\ \hfill b_N& =f\left(x_N\right)\frac{h_N}{2}\hfill & \hfill \text{(29)}\end{array}$$

Pour $i=1,\dots N-1$, l'équation s'écrit :

$$-\frac{{\xi }_{i-1}}{h_i}+(\frac{1}{h_i}+\frac{1}{h_{i+1}}){\xi }_i-\frac{{\xi }_{i+1}}{h_{i+1}}=f\left(x_i\right)\frac{h_i+h_{i+1}}{2}\text{(30)}$$

Dans le cas d'un maillage uniforme $h_i=h\forall i$ et l'équation devient :

$$\frac{{\xi }_{i-1}-2{\xi }_i+{\xi }_{i+1}}{h^2}=-f\left(x_i\right)\text{(31)}$$

Il s'agit de l'équation qu'on obtient par discrétisation de la dérivée seconde (laplacien) par différence finie. Si le maillage n'est pas uniforme, l'équation de Poisson peut être discrétisée de la manière suivante :

$$\frac{2}{h_i+h_{i+1}}(\frac{{\xi }_{i+1}-{\xi }_i}{h_{i+1}}-\frac{{\xi }_{i+1}-{\xi }_i}{h_i})=-f\left(x_i\right)\text{(32)}$$

ce qui conduit à l'équation $\mathrm{(30)}$. Pour un problème de Poisson unidimensionnel, la méthode des éléments finis conduit donc aux mêmes équations algébriques que la méthode des différences finies. Bien entendu, on ne peut pas en dire autant pour un problème à deux dimensions puisque dans ce cas le maillage est triangulaire et la méthode des différences finies est tout simplement impossible à mettre en œuvre avec un maillage triangulaire.

Pour résumer, écrivons le système linéaire sous forme matricielle : $CX=D$ où X est une matrice colonne contenant les ${\xi }_i$. La matrice carrée C est tridiagonale :

$$\begin{array}{ccc}\hfill & C_{00}=\frac{1}{h_1}+K_0\hfill & \hfill \text{(33)}\\ \hfill & C_{01}=-\frac{1}{h_1}\hfill & \hfill \text{(34)}\\ \hfill & C_{ii}=\frac{1}{h_i}+\frac{1}{h_{i+1}},i=1,\dots N-1\hfill & \hfill \text{(35)}\\ \hfill & C_{ii+1}=-\frac{1}{h_{i+1}},i=1,\dots N-1\hfill & \hfill \text{(36)}\\ \hfill & C_{ii-1}=-\frac{1}{h_i},i=1,\dots N-1\hfill & \hfill \text{(37)}\\ \hfill & C_{NN-1}=-\frac{1}{h_N}\hfill & \hfill \text{(38)}\\ \hfill & C_{NN}=\frac{1}{h_N}-K_L\hfill & \hfill \text{(39)}\end{array}$$

Voici les coefficients de la matrice colonne D :

$$\begin{array}{ccc}\hfill & D_0=f\left(x_0\right)\frac{h_1}{2}+K_0{u}_0-g_0\hfill & \hfill \text{(40)}\\ \hfill & D_i=f\left(x_i\right)\frac{h_i+h_{i+1}}{2}i=1,\dots N-1\hfill & \hfill \text{(41)}\\ \hfill & D_N=f\left(x_N\right)\frac{h_N}{2}-K_L{u}_L+g_L\hfill & \hfill \text{(42)}\end{array}$$

2.d. Raffinement du maillage

Pour une fonction v de carré sommable sur l'intervale I=[0,L], on définit la norme L²(I) :

$$\parallel v{\parallel }_{L^2\left(I\right)}=\sqrt{{\int }_0^L{v}^2\left(x\right)dx}\text{(43)}$$

Pour une solution u_h, la norme de la dérivée de l'erreur satisfait l'inégalité suivante [1] :

$$\parallel (u-u_h)\text{'}{\parallel }_{L^2\left(I\right)}^2\le C\sum _{i=1}^N{\eta }_i^2\left(u_h\right)\text{(44)}$$

où ${\eta }_i$ est le résidu sur l'intervalle $I_i=[x_i,x_{i+1}]$, défini par :

$${\eta }_i\left(u_h\right)=h_i\parallel f+u\text{'}{\text{'}}_h{\parallel }_{L^2\left(I_i\right)}=h_i\parallel f{\parallel }_{L^2\left(I_i\right)}=h_i\sqrt{{\int }_{x_i}^{x_{i+1}}{f}^2\left(x\right)dx}\text{(45)}$$

Le raffinement du maillage consiste à réduire certains $h_i$, ceux des sous-intervalles où la norme de f est grande, afin de réduire globalement l'erreur sans augmenter de manière excessive le temps de calcul. Ce résultat se comprend aisément : les régions où la norme de f est grande sont les régions où la courbure de u est grande, donc les régions où la largeur h_i doit être la plus petite. Un maillage donné peut être raffiné au moyen de la stratégie suivante [1]. On fixe un paramètre $\alpha$ compris entre 0 et 1 puis on subdivise en deux parts égales tous les intervalles tels que :

$${\eta }_i>\alpha max{\eta }_i\text{(46)}$$

La possibilité de réduire la taille des mailles à certains endroits seulement est une propriété intéressante de la méthode des éléments finis. Avec la méthode des différences finies, on peut seulement réduire la taille de toutes les mailles.

2.e. Résolution du système linéaire

Il existe une méthode directe très efficace pour résoudre un système tridiagonal (voir Équation de diffusion à une dimension) qui conviendrait tout à fait pour le problème de Poisson unidimensionnel. Cependant, le problème bidimensionnel ne conduit évidemment pas à une matrice tridiagonale. Nous optons donc pour la méthode plus générale consistant à résoudre le système par une méthode itérative.

3.a. Fonction

Pour résoudre le système linéaire, nous utilisons la méthode itérative du gradient conjugué pour les matrices symétriques définies positives (fonction scipy.sparse.linalg.cg). La matrice D étant creuse, il est intéressant de la stocker sous la forme d'un type de matrice creuse de scipy.sparse (bien que cela ne s'impose pas pour un problème à une dimension). Nous optons pour le type Block Sparse Row, qui s'obtient à partir d'un tableau numpy.ndarray avec la fonction bsr_array.

import numpy as np
import scipy.sparse as sparse
import scipy.sparse.linalg as linalg
from scipy.linalg import solve

            

La fonction suivante effectue le calcul complet, pour des $x_i$ et une fonction f donnés, avec les paramètres définissant les conditions limites. Le tableau des ${\xi }_i$ est renvoyé.

def poisson(f,x,K0,u0,g0,KL,uL,gL,solver="iterative"):
    # f : fonction
    # x : tableau des x_i
    N = len(x)-1
    h = x-np.roll(x,1)
    C = np.zeros((N+1,N+1),dtype=np.float64)
    C[0,0] = 1/h[1]+K0
    C[0,1] = -1/h[1]
    C[N,N-1] = -1/h[N]
    C[N,N] = 1/h[N]-KL
    for i in range(1,N):
        C[i,i] = 1/h[i]+1/h[i+1]
        C[i,i+1] = -1/h[i+1]
        C[i,i-1] = -1/h[i]
    D = np.zeros((N+1),dtype=np.float64)
    D[0] = f(x[0])*h[1]*0.5+K0*u0-g0
    D[N] = f(x[N])*h[N]*0.5-KL*uL+gL
    for i in range(1,N):
        D[i] = f(x[i])*(h[i]+h[i+1])*0.5
    if solver=="iterative":
        C = sparse.bsr_array(C) # facultatif
        xi, exitCode = linalg.cg(C, D, atol=1e-5)
        print("exitCode : ",exitCode)
    else:
        xi = solve(C,D)
    
    return xi
            

La fonction suivante effectue un raffinement du maillage :

def raffinement(f,x,alpha):
    N = len(x)-1
    eta = np.zeros(N)
    for i in range(N):
        h = x[i+1]-x[i]
        eta[i] = h*np.sqrt((f(x[i])**2+f(x[i+1])**2)*h/2)
    mx = np.max(eta)
    xx = []
    for i in range(N):
        xx.append(x[i])
        if eta[i] > alpha*mx:
            xx.append((x[i]+x[i+1])/2)
    xx.append(x[N])
    return np.array(xx)
            

3.b. Exemples

Pour tester la fonction, on considère le cas $f\left(x\right)=1$ sur l'intervalle [0,1], avec les conditions limites de Dirichlet $u\left(0\right)=u\left(1\right)=0$, dont la solution exacte est :

$$u\left(x\right)=-\frac{1}{2}{x}^2+\frac{1}{2}x\text{(47)}$$

x = np.linspace(0,1,300)
def f(x):
    return 1.0
K0 = KL = 1e3
xi = poisson(f,x,K0,0,0,KL,0,0)
def u(x):
    return -0.5*x*x+0.5*x
from matplotlib.pyplot import *
figure(figsize=(12,6))
plot(x,xi,"r")
plot(x,u(x),"k--")
grid()
xlabel("x")
ylabel("u")
                

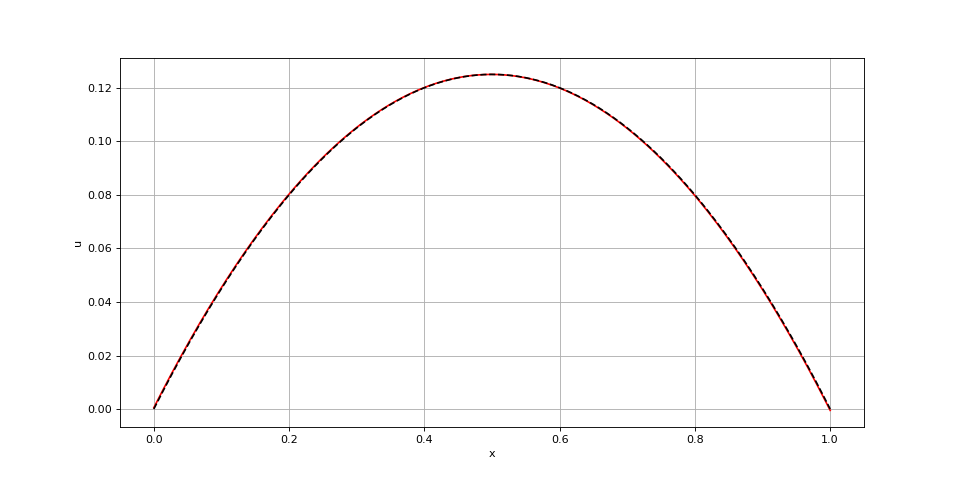fig1.pdf

Avec la condition de Neumann $u\text{'}\left(0\right)=0$ et de Dirichlet $u\left(1\right)=0$ la solution est :

$$u\left(x\right)=-\frac{1}{2}{x}^2+\frac{1}{2}\text{(48)}$$

x = np.linspace(0,1,300)
def f(x):
    return 1.0
K0 = 0
KL = 1e3
xi = poisson(f,x,K0,0,0,KL,0,0)
def u(x):
    return -0.5*x*x+0.5
figure(figsize=(12,6))
plot(x,xi,"r")
plot(x,u(x),"k--")
grid()
xlabel("x")
ylabel("u")
                

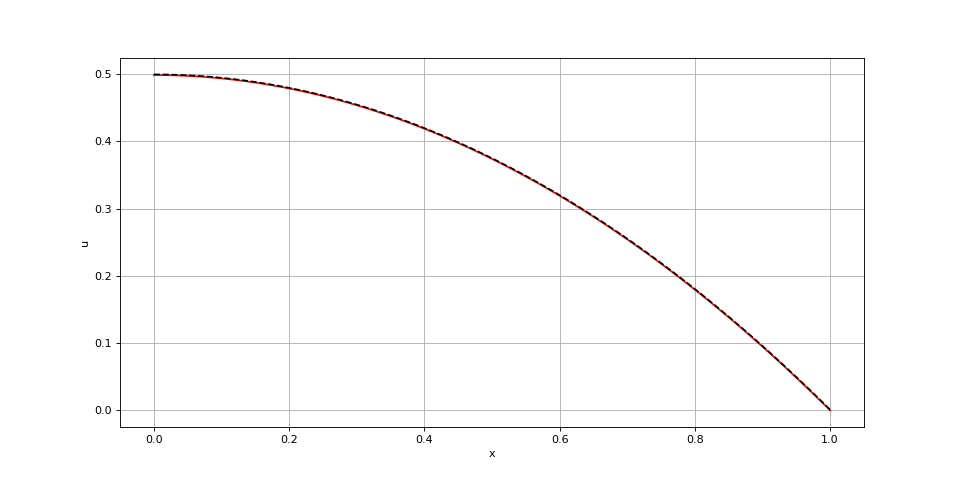fig2.pdf

Voici un autre exemple, correspondant à un problème thermique avec une source localisée au centre ou bien un problème d'électrostatique avec une charge au centre :

x = np.linspace(0,1,100)
def f(x):
    return np.exp(-200*(x-0.5)**2)
K0 = KL = 1e3
xi = poisson(f,x,K0,0,0,KL,0,0)
figure(figsize=(12,6))
plot(x,xi,"r")
grid()
xlabel("x")
ylabel("u")
                

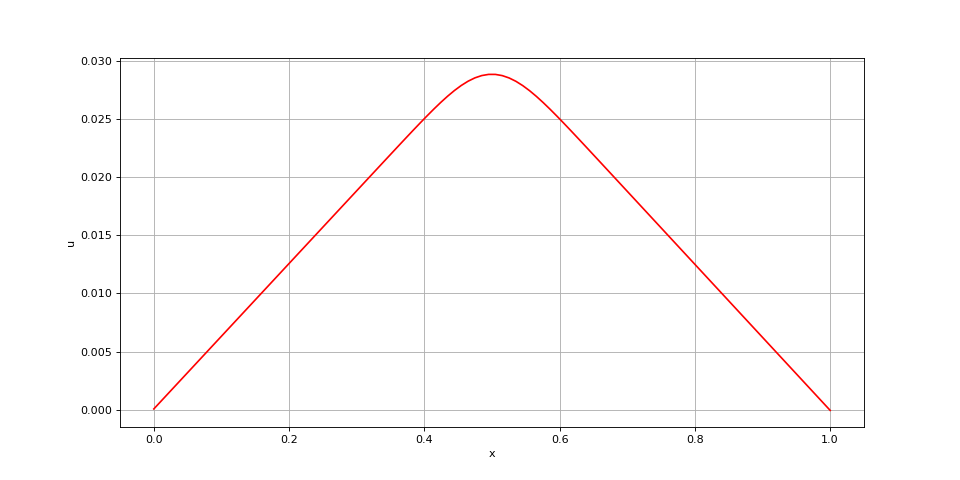fig3.pdf

Comme prévu, u(x) est une fonction affine dans les deux sous-intervalles où f(x)=0. Voici le même problème résolu avec un maillage moins fin :

x = np.linspace(0,1,20)
xi = poisson(f,x,K0,0,0,KL,0,0)
figure(figsize=(12,6))
plot(x,xi,"r.")
plot(x,xi,"r-")
grid()
xlabel("x")
ylabel("u")
                

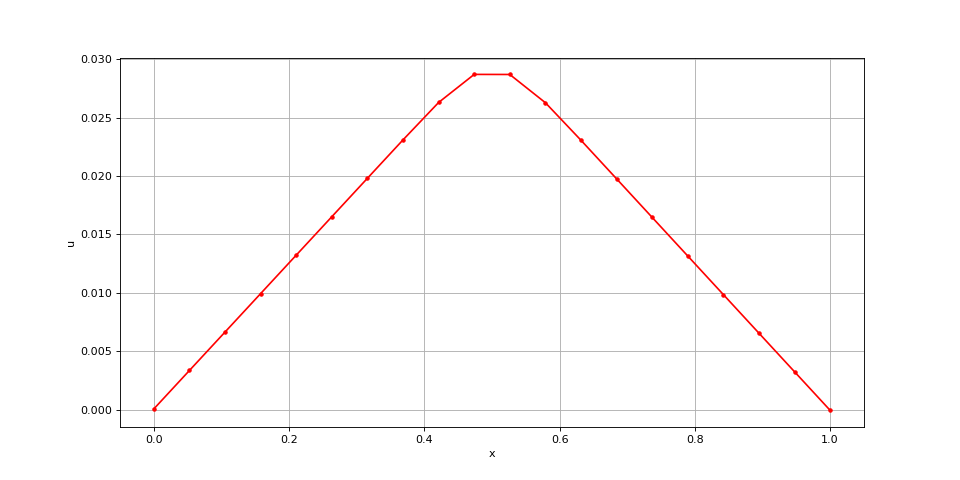fig4.pdf

Le résultat est globalement bon mais la courbe manque de précision dans la zone centrale, là où la fonction f a des grandes valeurs. On procède à un double raffinement du maillage :

x = raffinement(f,x,0.9)
x = raffinement(f,x,0.9)
xi = poisson(f,x,K0,0,0,KL,0,0)
figure(figsize=(12,6))
plot(x,xi,"r.")
plot(x,xi,"r-")
grid()
xlabel("x")
ylabel("u")
                

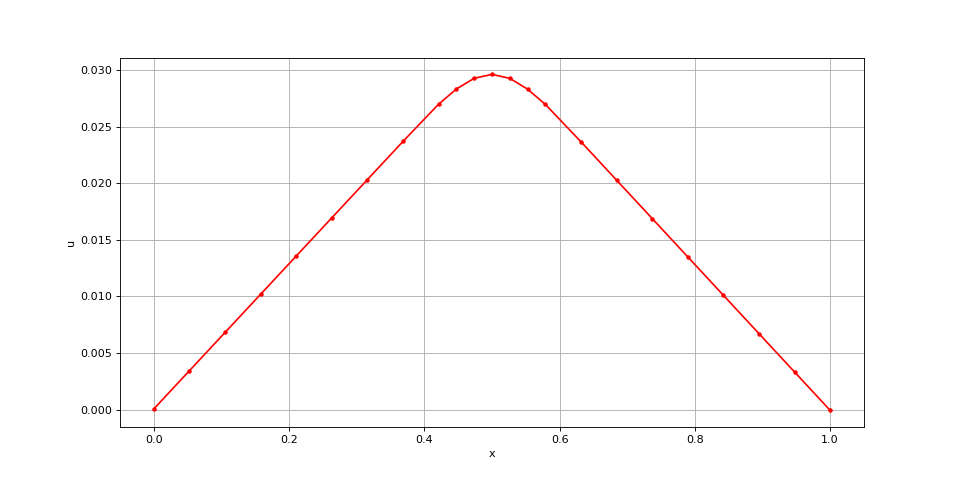fig5.pdf

Voici un exemple qui permet de tester la condition limite de Neumann : la conduction dans un milieu sans source thermique avec un température nulle en 0 et un flux imposé en L :

x = np.linspace(0,1,300)
def f(x):
    return 0
xi = poisson(f,x,1e9,0,0,0,0,1)
figure(figsize=(12,6))
plot(x,xi,"r")
grid()
xlabel("x")
ylabel("u")
                

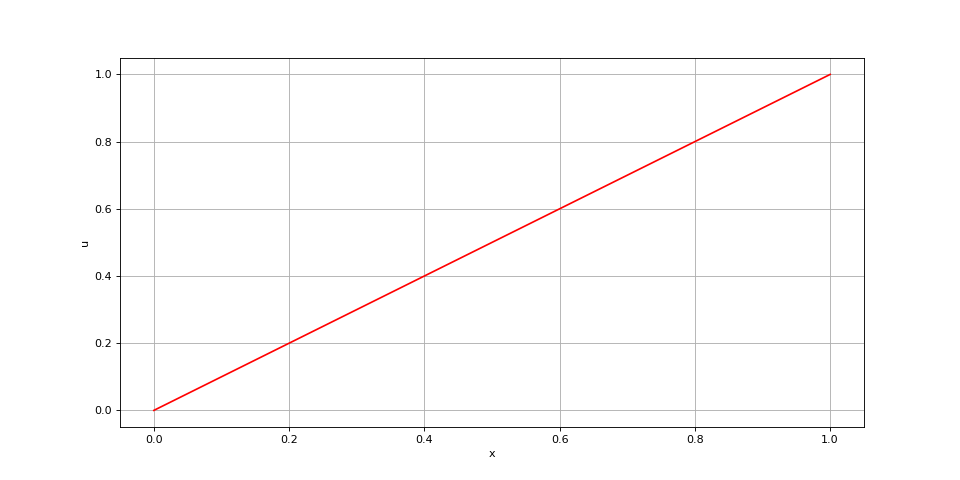fig6.pdf

Voici une conduction sans source avec deux conditions de Dirichlet :

x = np.linspace(0,1,300)
def f(x):
    return 0
xi = poisson(f,x,1e3,0,0,1e3,1,0)
figure(figsize=(12,6))
plot(x,xi,"r")
grid()
xlabel("x")
ylabel("u")
                

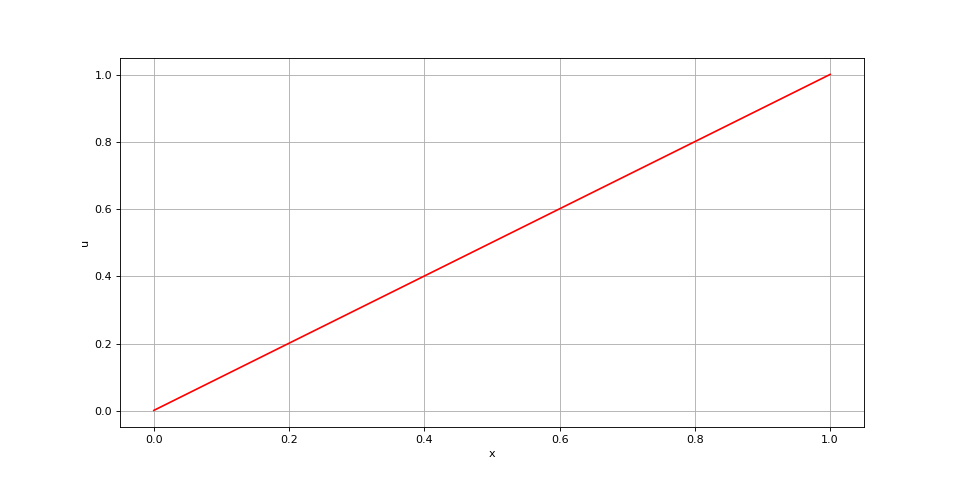fig7.pdf

Les conditions de Dirichlet sont obtenus avec des coefficients K₀ et K_L assez grands. Voici pourtant ce qu'il arrive si ces coefficients sont trop grands :

x = np.linspace(0,1,300)
def f(x):
    return 0
xi = poisson(f,x,1e6,0,0,1e6,1,0)
figure(figsize=(12,6))
plot(x,xi,"r")
grid()
xlabel("x")
ylabel("u")
                

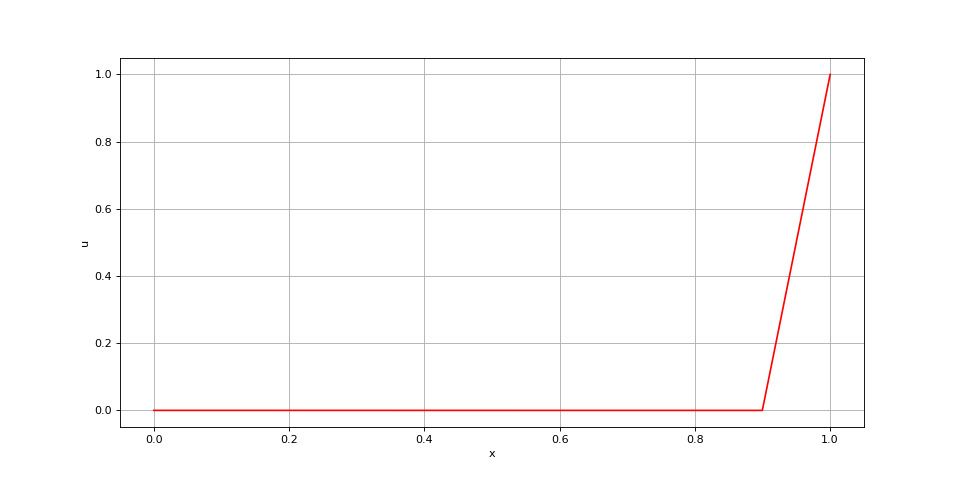fig8.pdf

Ce problème est lié à la méthode de résolution itérative puisque l'utilisation de la fonction scipy.linalg.solve (résolution par méthode directe) conduit à la bonne solution :

xi = poisson(f,x,1e6,0,0,1e6,1,0,solver="direct")
figure(figsize=(12,6))
plot(x,xi,"r")
grid()
xlabel("x")
ylabel("u")
                

fig9.pdf

3.c. Conditions limites de Dirichlet

Dans cette partie, on considère le cas où une condition de Dirichlet est appliquée en 0 et en L.

Dans le cas général de la condition de Robin, la condition limite de Dirichlet est introduite au moyen d'une valeur de K₀ ou K_L assez grande. Cependant, cette méthode pose problème (en tout cas pour la méthode itérative du gradient conjugué) car elle introduit des coefficients trop grands dans la matrice du système. Par ailleurs, le fait d'introduire commme a priori inconnues les valeurs ${\xi }_0$ et ${\xi }_N$ alors qu'elles sont connues est certainement une mauvaise idée lorsqu'une méthode de résolution itérative est utilisée. Il est donc préférable de définir un système d'équations pour les nœuds intérieurs seulement, c'est-à-dire en excluant les nœuds affectés par la condition de Dirichlet, les nœuds d'indices 0 et N.

La formulation variationnelle avec des conditions de Dirichlet consiste à considérer les fonctions test v dans l'ensemble des fonctions affines par morceaux (sur le maillage considéré) mais qui s'annulent en x=0 et en x=L. Cet ensemble est noté V_h,0. On a donc, pour toute fonction $v\in V_{h,0}$ :

$${\int }_0^{L}v\left(x\right)f\left(x\right)dx={\int }_0^L\frac{dv}{dx}\frac{d{u}_h}{dx}dx\text{(49)}$$

La fonction recherchée u_h peut être écrite comme la somme d'une fonction de V_h,0 et d'une fonction appartenant à l'ensemble des fonctions affines par morceaux qui vérifient les conditions de Dirichlet : u_h,d(0)=u₀ et u_h,d(L)=u_L, que l'on note V_h,d. On écrit donc :

$$u_h=u_{h,0}+u_{h,d}\text{(50)}$$

La fonction u_h,0 se décompose sur la base des fonctions chapeaux de la manière suivante :

$$u_{h,0}\left(x\right)=\sum _{j=1}^{N-1}{\xi }_v{\varphi }_j\left(x\right)\text{(51)}$$

puisque les fonctions ${\varphi }_1,\dots {\varphi }_{N-1}$ constituent une base de V_h,0. La formulation variationnelle s'écrit donc :

$${\int }_0^L{\varphi }_i\left(x\right)f\left(x\right)dx={\int }_0^L\frac{d{\varphi }_i}{dx}\frac{d{u}_{k,0}}{dx}dx+{\int }_0^L\frac{d{\varphi }_i}{dx}\frac{d{u}_{k,d}}{dx}dx,i=1,\dots N-1\text{(52)}$$

La fonction u_h,0 obtenue est indépendante de la fonction h_h,d [1]. On peut donc choisir une fonction particulière : celle qui vérifie les conditions de Dirichlet et qui est nulle sur tous les nœuds intérieurs. Cette fonction est représentée sur la figure suivante, avec les fonctions chapeaux qui interviennent dans l'intégrale ci-dessus :

Figure pleine page

On a :

$$\begin{array}{ccc}\hfill & {\int }_0^L\frac{d{\varphi }_1}{dx}\frac{d{u}_{k,d}}{dx}dx=-\frac{u_0}{h_1}\frac{1}{h_1}{h}_1=-\frac{u_0}{h_1}\hfill & \hfill \text{(53)}\\ \hfill & {\int }_0^L\frac{d{\varphi }_{N-1}}{dx}\frac{d{u}_{k,d}}{dx}dx=-\frac{u_L}{h_N}\frac{1}{h_N}{h}_N=-\frac{u_L}{h_N}\hfill & \hfill \text{(54)}\\ \hfill & {\int }_0^L\frac{d{\varphi }_i}{dx}\frac{d{u}_{k,d}}{dx}dx=0,i=2,\dots N-2\hfill & \hfill \text{(55)}\end{array}$$

On obtient finalement le système d'équations suivant, pour les inconnues ${\xi }_1,\dots N-1$ :

$$\begin{array}{ccc}\hfill & \sum _{j=1}^{N-1}{A}_{1j}{\xi }_j=b_1+\frac{u_0}{h_1}\hfill & \hfill \text{(56)}\\ \hfill & \sum _{j=1}^{N-1}{A}_{i,j}{\xi }_j=b_i,i=2,\dots N-2\hfill & \hfill \text{(57)}\\ \hfill & \sum _{j=1}^{N-1}{A}_{N-1j}{\xi }_j=b_1+\frac{u_L}{h_N}\hfill & \hfill \text{(58)}\\ \hfill & \hfill \text{(59)}\end{array}$$

Ce système est identique aux équations $i=1,\dots N-1$ du système établi plus haut (Équations algébrique) avec ${\xi }_0=u_0$ et ${\xi }_N=u_L$. Autrement dit, il s'agit du même système mais auquel on a enlevé les nœuds des bords dans les inconnues.

Les expressions de A_i,j et b_i établies plus haut sont inchangées. Afin de pourvoir transcrire directemenrt ces relations dans le code Python (sans changer les indices), on commence par créer une matrice A de taille (N+1)x(N+1) puis on extrait de celle-ci la matrice de taille (N-1)x(N-1) qui correspond au système précédent. On procède de manière similaire pour la matrice colonne B, à laquelle il faut ajouter les deux termes correpondant aux conditions limites.

def poissonDirichlet(f,x,u0,uL,solver="iterative"):
    # f : fonction
    # x : tableau des x_i
    N = len(x)-1
    h = x-np.roll(x,1)
    A = np.zeros((N+1,N+1),dtype=np.float64) 
    for i in range(1,N):
        A[i,i] = 1/h[i]+1/h[i+1]
        A[i,i+1] = -1/h[i+1]
        A[i,i-1] = -1/h[i]
    B = np.zeros((N+1),dtype=np.float64)
    for i in range(1,N):
        B[i] = f(x[i])*(h[i]+h[i+1])*0.5
    # extraction des matrice pour les noeuds intérieurs
    A = A[1:N,1:N]
    B = B[1:N]
    B[0] += u0/h[1] # conditions limites de Dirichlet
    B[N-2] += uL/h[N]
    if solver=="iterative":
        A = sparse.bsr_array(A) # facultatif
        xi, exitCode = linalg.cg(A, B, atol=1e-5)
        print("exitCode : ",exitCode)
    else:
        xi = solve(A,B)
        # xi contient les noeuds intérieurs
    xi = np.concatenate((np.array([u0]),xi,np.array([uL])))
    return xi
            

x = np.linspace(0,1,300)
def f(x):
    return 0
xi = poissonDirichlet(f,x,0,1)
figure(figsize=(12,6))
plot(x,xi,"r")
grid()
xlabel("x")
ylabel("u")
                

fig10.pdf

3.d. Conditions limites de Neumann

Une conditon de Neumann sur un bord se traite sans difficulté avec des fonctions tests dans V_h, c'est-à-dire des fonctions affines par morceaux qui ne s'annulent pas nécessairement sur le bord correspondant. Les équations sont celles établies plus haut (Équations algébriques) avec K₀=0 pour le bord x=0 ou bien K_L=0 pour le bord x=L.

3.e. Cas général

Nous pouvons à présent traiter correctement les conditions limites dans tous les cas : Dirichlet, Neumann ou Robin. On reprend le système d'équations obtenu dans (Équations algébriques) mais en enlevant les équations correspondant aux bords auquel une condition de Dirichlet est appliquée. Il s'agit d'enlever soit la première équation, soit la dernère, soit les deux.

def poissonGeneral(f,x,type0,K0,u0,g0,typeL,KL,uL,gL,solver="iterative"):
    # f : fonction
    # x : tableau des x_i
    # type0 et typeL : "dir","neu" ou "rob"
    if type0=="neu": K0 = 0
    if typeL=="neu": KL = 0
    N = len(x)-1
    h = x-np.roll(x,1)
    C = np.zeros((N+1,N+1),dtype=np.float64)
    C[0,0] = 1/h[1]+K0
    C[0,1] = -1/h[1]
    C[N,N-1] = -1/h[N]
    C[N,N] = 1/h[N]-KL
    for i in range(1,N):
        C[i,i] = 1/h[i]+1/h[i+1]
        C[i,i+1] = -1/h[i+1]
        C[i,i-1] = -1/h[i]
    D = np.zeros((N+1),dtype=np.float64)
    D[0] = f(x[0])*h[1]*0.5+K0*u0-g0
    D[N] = f(x[N])*h[N]*0.5-KL*uL+gL
    for i in range(1,N):
        D[i] = f(x[i])*(h[i]+h[i+1])*0.5
    if type0=="dir" and typeL=="dir":
        C = C[1:N,1:N]
        D = D[1:N]
        D[0] += u0/h[1] # conditions limites de Dirichlet
        D[N-2] += uL/h[N]
    elif type0=="dir" and typeL!="dir":
        C = C[1:N+1,1:N+1]
        D = D[1:N+1]
        D[0] += u0/h[1]
    elif type0!="dir" and typeL=="dir":
        C = C[0:N,0:N]
        D = D[0:N]
        D[N-1] += uL/h[N]
    if solver=="iterative":
        C = sparse.bsr_array(C) # facultatif
        xi, exitCode = linalg.cg(C, D, atol=1e-5)
        print("exitCode : ",exitCode)
    else:
        xi = solve(C,D)
    if type0=="dir" and typeL=="dir":
        xi = np.concatenate((np.array([u0]),xi,np.array([uL])))
    elif type0=="dir" and typeL!="dir":
        xi = np.concatenate((np.array([u0]),xi))
    elif type0!="dir" and typeL=="dir":
        xi = np.concatenate((xi,np.array([uL])))
    return xi
            

Voici une reprise d'exemples traités plus haut :

x = np.linspace(0,1,300)
def f(x):
    return 1.0
g0 = 0 # neumann en x=0
uL = 0 # dirichlet en x=L
xi = poissonGeneral(f,x,"neu",0,0,g0,"dir",0,uL,0)
def u(x):
    return -0.5*x*x+0.5
figure(figsize=(12,6))
plot(x,xi,"r")
plot(x,u(x),"k--")
grid()
xlabel("x")
ylabel("u")
                

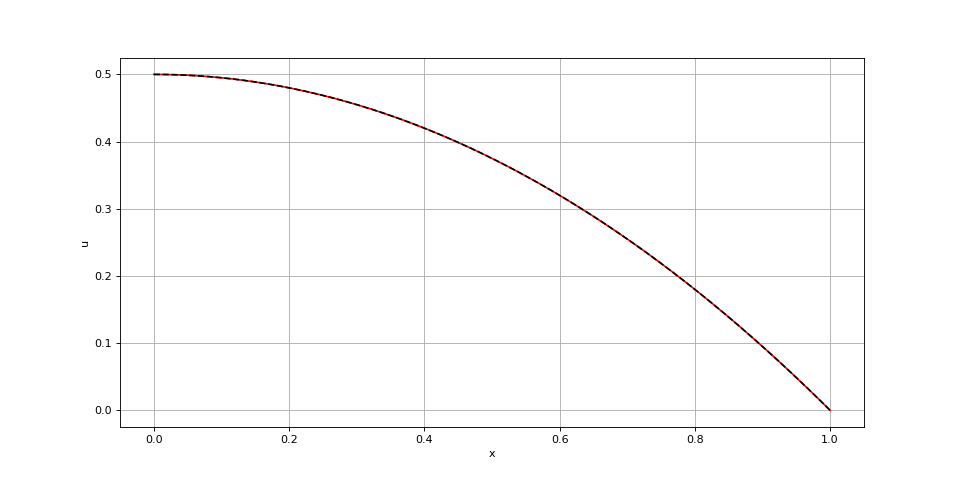fig11.pdf

x = np.linspace(0,1,300)
def f(x):
    return 0.0
u0 = 0 #dirichlet en x=0
uL = 1 # dirichlet en x=L
xi = poissonGeneral(f,x,"dir",0,u0,0,"dir",0,uL,0)
figure(figsize=(12,6))
plot(x,xi,"r")
grid()
xlabel("x")
ylabel("u")
                

fig12.pdf

4.a. Définition

Dans un problème de transfert thermique en régime stationnaire, il arrive qu'une frontière sépare deux milieux de conductivités thermiques différentes. L'équation de diffusion thermique dans un domaine où la conductivité thermique $\lambda$ n'est pas uniforme s'écrit :

$$\frac{d}{dx}\left(\lambda \frac{dT}{dx}\right)=-p\text{(60)}$$

où p est la densité volumique de puissance des sources thermiques.

Dans un problème d'électrostatique, si la permittivité électrique $\epsilon$ n'est pas uniforme, l'équation pour le potentiel s'écrit :

$$\frac{d}{dx}\left(\epsilon \frac{dV}{dx}\right)=-\rho \text{(61)}$$

où $\rho$ est la densité volumique de charge.

Considérons une frontière entre deux domaines dont les conductivités thermiques (où les permittivités électriques) sont différentes mais uniforme dans chacun. La dérivée de la conductivité n'est pas déifnie sur la frontière. La manière classique de traiter ce cas est de résoudre l'équation de Poisson dans les deux domaines avec une condition limite qui traduit la conservation du flux :

$${\lambda }_1\frac{dT}{dx}\left(x_0^{-}\right)={\lambda }_2\frac{dT}{dx}\left(x_0^{+}\right)\text{(62)}$$

pour une frontière située en $x=x_0$. Cette équation est appelée relation de passage entre les deux milieux. En électrostatique, une relation de passage similaire provient de la continuité de la composante normale de D_x=εE_x.

L'utilisation directe de la relation de passage se fait sans difficulté dans la méthode des différences finis (ou des volumes fini) : voir Équation de Poisson à deux dimensions.

Pour la méthode des éléments finis, il faut considérer l'équation de Poisson sous sa forme plus générale avec une propriété du milieu a(x) :

$$\frac{d}{dx}\left(a\left(x\right)\frac{du}{dx}\right)=-s\left(x\right)\text{(63)}$$

Lorsque le milieu est homogène, on a $f\left(x\right)=s\left(x\right)/a$.

4.b. Formulation variationnelle

Pour une fonction test v(x), on considère l'intégrale suivante :

$${\int }_0^L\frac{d}{dx}\left(v\left(x\right)a\left(x\right)\frac{du}{dx}\right)dx=v\left(L\right)a\left(L\right)\frac{du}{dx}\left(L\right)-v\left(0\right)a\left(0\right)\frac{du}{dx}\left(0\right)\text{(64)}$$

Cette intégrale s'écrit aussi :

$${\int }_0^L\frac{d}{dx}\left(v\left(x\right)a\left(x\right)\frac{du}{dx}\right)dx={\int }_0^{L}v\left(x\right)\frac{d}{dx}\left(a\left(x\right)\frac{du}{dx}\right)dx+{\int }_0^L\frac{dv}{dx}a\left(x\right)\frac{du}{dx}dx=-{\int }_0^{L}v\left(x\right)s\left(x\right)+{\int }_0^L\frac{dv}{dx}a\left(x\right)\frac{du}{dx}dx\text{(65)}$$

Au moyen de la condition limite de Robin (relation $\mathrm{(2)}$), on obtient l'égalité suivante :

$${\int }_0^{L}v\left(x\right)s\left(x\right)dx={\int }_0^L\frac{dv}{dx}a\left(x\right)\frac{du}{dx}dx+v\left(0\right)a\left(0\right)(K_0(u\left(0\right)-u_0)+g_0)-v\left(L\right)a\left(L\right)(K_L(u\left(L\right)-u_L)+g_L)\text{(66)}$$

La formulation variationnelle pour un fonction u_h et pour toute fonction v de V_h s'écrit :

$${\int }_0^L{\varphi }_i\left(x\right)s\left(x\right)dx={\int }_0^L\frac{d{\varphi }_i}{dx}a\left(x\right)\frac{d{u}_h}{dx}dx+{\varphi }_i\left(0\right)a\left(0\right)(K_0(u_h\left(0\right)-u_0)+g_0)-{\varphi }_i\left(L\right)a\left(L\right)(K_L(u_h\left(L\right)-u_L)+g_L),i=0,1\dots N\text{(67)}$$

4.c. Équations algébriques

Le report de l'expression $\mathrm{(11)}$ dans l'égalité $\mathrm{(12)}$ conduit à :

$${\int }_0^L{\varphi }_i\left(x\right)s\left(x\right)dx=\sum _{j=0}^N{\xi }_j{\int }_0^L\frac{d{\varphi }_i}{dx}a\left(x_j\right)\frac{d{\varphi }_j}{dx}dx+{\varphi }_i\left(0\right)a\left(0\right)(K_0({\xi }_0-u_0)+g_0)-{\varphi }_i\left(L\right)a\left(L\right)(K_L({\xi }_N-u_L)+g_L),i=0,1\dots N\text{(68)}$$

Nous pouvons ainsi traiter le cas général d'une propriété a(x) (conductivité ou permittivité) qui dépend de x. Le traitement du cas où a(x) présente une disconinuité en x=x₀ se fait sans problème à condition qu'il y ait un nœud en x=x₀. D'une manière générale, le maillage doit comporter des nœuds sur les frontières de discontinuité des propriétés (qui sont les frontières des différentes objets du problème).

Pour obtenir les matrices du système linéaire, il suffit de remplacer f(x) par s(x) et de multiplier par $a_j=a\left(\frac{x_{j-1}+x_j}{2}\right)$ le terme d'intégrale sur I_i dans l'expression de A_ij. On obtient :

$$\begin{array}{ccc}\hfill & C_{00}=\frac{a_1}{h_1}+K_0{a}_1\hfill & \hfill \text{(69)}\\ \hfill & C_{01}=-\frac{a_1}{h_1}\hfill & \hfill \text{(70)}\\ \hfill & C_{ii}=\frac{a_i}{h_i}+\frac{a_{i+1}}{h_{i+1}},i=1,\dots N-1\hfill & \hfill \text{(71)}\\ \hfill & C_{ii+1}=-\frac{a_{i+1}}{h_{i+1}},i=1,\dots N-1\hfill & \hfill \text{(72)}\\ \hfill & C_{ii-1}=-\frac{a_i}{h_i},i=1,\dots N-1\hfill & \hfill \text{(73)}\\ \hfill & C_{NN-1}=-\frac{a_N}{h_N}\hfill & \hfill \text{(74)}\\ \hfill & C_{NN}=\frac{a_N}{h_N}-K_L{a}_N\hfill & \hfill \text{(75)}\end{array}$$ $$\begin{array}{ccc}\hfill & D_0=s\left(x_0\right)\frac{h_1}{2}+K_0{a}_1{u}_0-a_1{g}_0\hfill & \hfill \text{(76)}\\ \hfill & D_i=s\left(x_i\right)\frac{h_i+h_{i+1}}{2}i=1,\dots N-1\hfill & \hfill \text{(77)}\\ \hfill & D_N=s\left(x_N\right)\frac{h_N}{2}-K_L{a}_N{u}_L+a_N{g}_L\hfill & \hfill \text{(78)}\end{array}$$

Le cas de la condition limite de Dirichlet sur un des bords se traite, comme expliqué plus haut (Conditions limites de Dirichlet), en enlevant du système d'équations le nœud correrspondant.

4.d. Implémentation

On fournit à la fonction de calcul le tableau des a_i, qui sont les valeurs de a aux milieux des sous-intervalles. Il y a N sous-intervalles. Il est convenu que le tableau contient N+1 élement (comme le tableau des x_i) mais que le premier élément, d'indice 0, n'est pas utilisé. Le coefficient a_i est ainsi l'élément d'indice i de ce tableau.

def poissonGeneral2(s,a,x,type0,K0,u0,g0,typeL,KL,uL,gL,solver="iterative"):
    # s : fonction
    # a : tableau des a_i
    # x : tableau des x_i
    # type0 et typeL : "dir","neu" ou "rob"
    if type0=="neu": K0 = 0
    if typeL=="neu": KL = 0
    N = len(x)-1
    h = x-np.roll(x,1)
    C = np.zeros((N+1,N+1),dtype=np.float64)
    C[0,0] = a[1]/h[1]+K0*a[1]
    C[0,1] = -a[1]/h[1]
    C[N,N-1] = -a[N]/h[N]
    C[N,N] = a[N]/h[N]-KL*a[N]
    for i in range(1,N):
        C[i,i] = a[i]/h[i]+a[i+1]/h[i+1]
        C[i,i+1] = -a[i+1]/h[i+1]
        C[i,i-1] = -a[i]/h[i]
    D = np.zeros((N+1),dtype=np.float64)
    D[0] = s(x[0])*h[1]*0.5+(K0*u0-g0)*a[1]
    D[N] = f(x[N])*h[N]*0.5+(gL-KL*uL)*a[N]
    for i in range(1,N):
        D[i] = s(x[i])*(h[i]+h[i+1])*0.5
    if type0=="dir" and typeL=="dir":
        C = C[1:N,1:N]
        D = D[1:N]
        D[0] += u0/h[1]*a[1] # conditions limites de Dirichlet
        D[N-2] += uL/h[N]*a[N]
    elif type0=="dir" and typeL!="dir":
        C = C[1:N+1,1:N+1]
        D = D[1:N+1]
        D[0] += u0/h[1]*a[1]
    elif type0!="dir" and typeL=="dir":
        C = C[0:N,0:N]
        D = D[0:N]
        D[N-1] += uL/h[N]*a[N]
    if solver=="iterative":
        C = sparse.bsr_array(C) # facultatif
        xi, exitCode = linalg.cg(C, D, atol=1e-5)
        print("exitCode : ",exitCode)
    else:
        xi = solve(C,D)
    if type0=="dir" and typeL=="dir":
        xi = np.concatenate((np.array([u0]),xi,np.array([uL])))
    elif type0=="dir" and typeL!="dir":
        xi = np.concatenate((np.array([u0]),xi))
    elif type0!="dir" and typeL=="dir":
        xi = np.concatenate((xi,np.array([uL])))
    return xi
            

4.e. Exemples

N = 300
x = np.linspace(0,1,N+1)
a = np.zeros(N+1)
a[1:N//2] = 1
a[N//2:N+1] = 2
def s(x):
    return 0
u0 = 0
uL = 1
xi = poissonGeneral2(s,a,x,"dir",0,u0,0,"dir",0,uL,0)
figure(figsize=(12,6))
plot(x,xi,"r-")
grid()
xlabel("x")
ylabel("u")
            

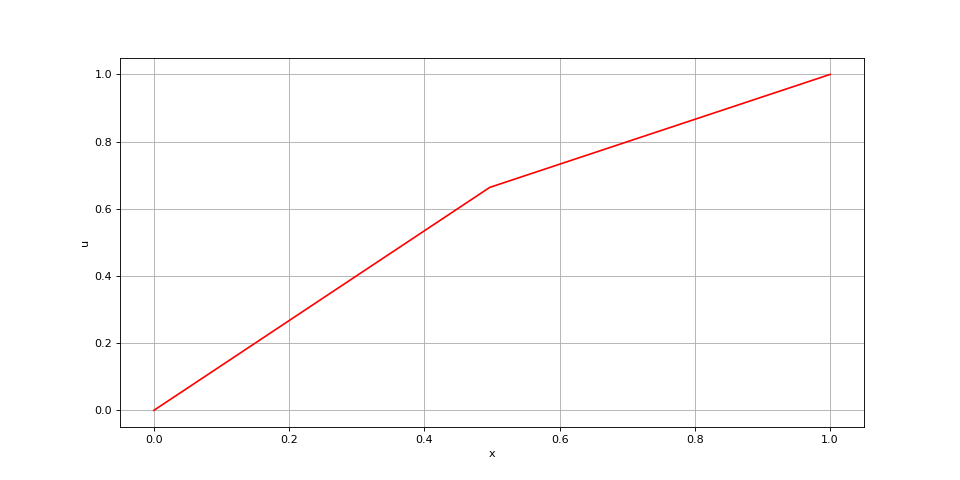fig13.pdf

u0 = 0
gL = 1
xi = poissonGeneral2(s,a,x,"dir",0,u0,0,"neu",0,0,gL)
figure(figsize=(12,6))
plot(x,xi,"r-")
grid()
xlabel("x")
ylabel("u")
            

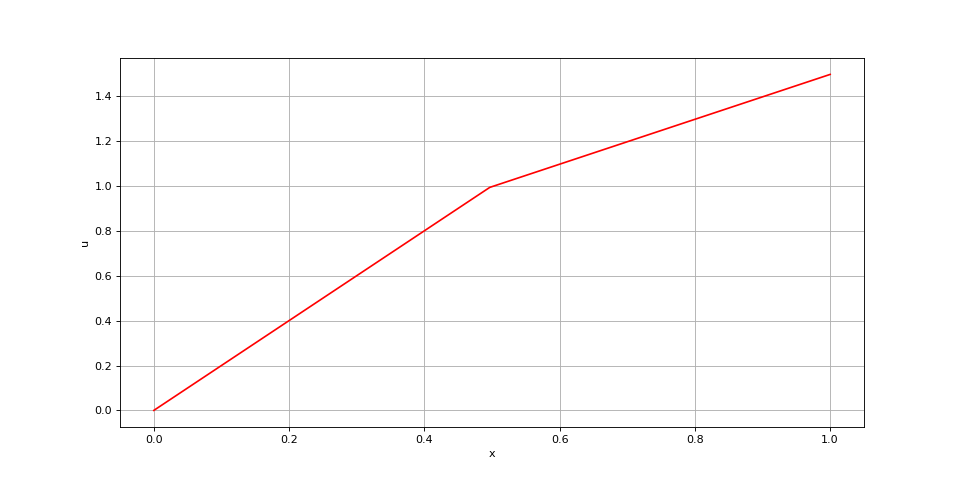fig14.pdf