Équation de Schrödinger à une dimension

3.a. Discrétisation

Soit N le nombre de points dans l'intervalle [0,L]. On définit le pas d'espace :

$$\Delta x=\frac{L}{N-1}\text{(8)}$$

Soit Δt le pas de temps. On pose :

$$\begin{array}{ccc}\hfill & {\psi }_j^n=\psi (j\Delta x,n\Delta t)\hfill & \hfill \text{(9)}\\ \hfill & V_j=V\left(j\Delta x\right)\hfill & \hfill \text{(10)}\end{array}$$

où n est un entier positif ou nul repésentant le temps.

La dérivée temporelle est discrétisée de la manière suivante :

$$\frac{\partial \psi }{\partial t}\to \frac{{\psi }_j^{n+1}-{\psi }_j^n}{\Delta t}\text{(11)}$$

La dérivée seconde par rapport à x est discrétisée par :

$$\frac{{\partial }^2\psi }{\partial x^2}\to \frac{{\psi }_{j+1}^n-2{\psi }_j^n+{\psi }_{j-1}^{n+1}}{{\left(\Delta x\right)}^2}\text{(12)}$$

Le schéma explicite qui en découle est :

$$i\frac{{\psi }_j^{n+1}-{\psi }_j^n}{\Delta t}=-\frac{{\psi }_{j+1}^n-2{\psi }_j^n+{\psi }_{j-1}^n}{{\left(\Delta x\right)}^2}+V_j{\psi }_j^n\text{(13)}$$

Comme pour l'équation de diffusion, ce schéma explicite a une condition de stabilité très contraignante. On lui préfère donc un schéma implicite.

Pour alléger les notations, on introduit l'opérateur hamiltonien discret défini par :

$$H{\psi }_j^n=-\frac{{\psi }_{j+1}^n-2{\psi }_j^n+{\psi }_{j-1}^n}{{\left(\Delta x\right)}^2}+V_j{\psi }_j^n\text{(14)}$$

3.b. Schéma implicite unitaire

En suivant la démarche adoptée pour l'équation de diffusion à une dimension, on est amené à considérer le schéma implicite suivant :

$$i\frac{{\psi }_j^{n+1}-{\psi }_j^n}{\Delta t}=H{\psi }_j^{n+1}\text{(15)}$$

ou encore :

$$(1+i\Delta tH){\psi }_j^{n+1}={\psi }_j^n\text{(16)}$$

Ce schéma conduit à la résolution, pour chaque pas de temps, d'un système linéaire tridiagonal, pour lequel il existe une méthode directe efficace. Il a toutefois l'inconvénient de ne pas conserver la norme de la fonction d'onde.

Pour un intervalle de temps, on a :

$$\psi (x,t+\Delta t)=e^{-iH\Delta t}\psi (x,t)\text{(17)}$$

Le schéma défini ci-dessus revient à utiliser l'approximation au premier ordre suivante :

$$e^{-iH\Delta t}\simeq 1-iH\Delta t\text{(18)}$$

Cette transformation n'est pas unitaire, c'est pourquoi la norme de la fonction d'onde n'est pas conservée. On la remplace par l'approximation de Cayley ([2]), qui est unitaire :

$$e^{-iH\Delta t}\simeq \frac{1-i\frac{1}{2}H\Delta t}{1+i\frac{1}{2}H\Delta t}\text{(19)}$$

Le schéma numérique s'écrit alors :

$$(1+i\frac{1}{2}\Delta tH){\psi }_j^{n+1}=(1-i\frac{1}{2}\Delta tH){\psi }_j^n\text{(20)}$$

On obtient ainsi le schéma implicite suivant :

$${\psi }_{j-1}^{n+1}+(i\alpha -{\left(\Delta x\right)}^2{V}_j-2){\psi }_j^{n+1}+{\psi }_{j+1}^{n+1}=-{\psi }_{j-1}^n+(i\alpha +{\left(\Delta x\right)}^2{V}_j+2){\psi }_j^n-{\psi }_{j+1}^n\text{(21)}$$

avec :

$$\alpha =\frac{2{\left(\Delta x\right)}^2}{\Delta t}\text{(22)}$$

On le met sous la forme générale suivante :

$$a_j{\psi }_{j-1}^{n+1}+b_j{\psi }_j^{n+1}+c_j{\psi }_{j+1}^{n+1}=d_j{\psi }_{j-1}^n+e_j{\psi }_j^n+f_j{\psi }_{j+1}^n+s_j^n\text{(23)}$$

Pour chaque pas de temps, le système tridiagonal est résolu par l'algorithme d'élimination décrit dans Équation de diffusion à une dimension.

Les conditions limites sont de type Dirichlet, puisqu'elles consistent à annuler la fonction d'onde sur les bords de l'intervalle :

$${\psi }_0^n={\psi }_{N-1}^n=0\text{(24)}$$

3.c. Paquet d'onde

Pour obtenir l'évolution d'un paquet d'onde, on considère comme condition initiale un paquet d'onde gaussien défini par :

$$\psi (x,0)=e^{i{k}_{0}x}{e}^{-\frac{{(x-x_0)}^2}{4{\sigma }_0^2}}\text{(25)}$$

Le paquet d'onde est initialement en x=x₀ et se déplace dans le sens de l'axe x. La densité de propabilité (non normée) associée à ce paquet est :

$$\rho (x,0)=\psi (x,0)\psi {(x,0)}^{*}=e^{-\frac{{(x-x_0)}^2}{2{\sigma }_0^2}}\text{(26)}$$

La variance de cette densité de probabilité est σ₀. Le spectre en nombre d'onde de ce paquet a une largeur donnée par :

$${\sigma }_0\Delta k=\frac{1}{2}\text{(27)}$$

Considérons l'évolution du paquet d'onde en l'absence de potentiel (particule libre). La largeur Δk reste constante au cours du temps. Notons σ la largeur du paquet à l'instant t. L'inégalité d'Heisenberg s'écrit :

$$\sigma \Delta k\ge \frac{1}{2}\text{(28)}$$

Pour ce paquet gaussien, l'égalité est réalisée à l'instant t=0. On peut calculer précisément la largeur du paquet à l'instant t ([3]) :

$$\sigma ={\sigma }_0\sqrt{1+\frac{{\hslash }^2{t}^2}{4m^2{\sigma }_0^4}}\text{(29)}$$

Cette relation montre l'étalement du paquet d'onde lorsqu'on s'éloigne de l'origine du temps.

La vitesse du paquet d'onde (la vitesse de groupe) est :

$$v_0=\frac{\hslash k_0}{m}\text{(30)}$$

Soit T la durée de la simulation. La distance parcourue par le paquet pendant cette durée doit être de l'ordre de la largeur L. Avec les unités utilisées (m=1/2 et ℏ=1), la condition s'écrit :

$$T\simeq \frac{L}{2k_0}\text{(31)}$$

Si l'on souhaite que l'étalement du paquet d'onde soit négligeable pendant cette durée, il faut respecter la condition suivante :

$$T\ll {\sigma }_0\text{(32)}$$

qui s'écrit aussi :

$$2{\sigma }_0^2{k}_0\gg L\text{(33)}$$

Par exemple, pour L=1 et σ₀=0.05, il faut que k₀>200.

Voyons comment choisir l'échantillonnage spatial et temporel. Le pas d'espace doit vérifier :

$$k_0\Delta x\ll 1\text{(34)}$$

La condition de Nyquist-Shannon impose une valeur maximale égale à π, mais il faut prévoir une marge à cause de la dispersion Δk. L'évolution dans le temps de la fonction d'onde se fait à la pulsation moyenne :

$$\omega =\frac{E}{\hslash }=\frac{\hslash k_0^2}{2m}\text{(35)}$$

Avec les unités utilisées, le pas de temps doit donc vérifier :

$$k_0^2\Delta t\ll 1\text{(36)}$$

Pour fixer les pas de temps et d'espace, on peut adopter la relation suivante :

$$\Delta t=2\Delta x^2\text{(37)}$$

Il suffit alors de vérifier la relation :

$$k_0\Delta x\ll 1\text{(38)}$$

Par exemple, pour k₀=200 et L=1, il faut N=2000 points. Le nombre de pas de temps nécessaire est :

$$P=\frac{T}{\Delta t}=\frac{L}{4k_0\Delta x^2}\text{(39)}$$

Avec les valeurs précédentes P=5000.

On voit donc que la simulation d'un paquet d'onde présentant un faible étalement est très exigeante en terme de quantité de calculs.

5.a. Diffusion de particules sur une marche de potentiel

import numpy
from Schrodinger1D import Schrodinger1D
from matplotlib.pyplot import *

N=2000
L=1.0
dx=L/(N-1)
x = numpy.arange(N)*dx
schrodinger = Schrodinger1D(L,N)
V = schrodinger.V_marche(1.0)
l0 = 2e-2
k0 = numpy.pi*2/l0
E=k0**2
x0 = 0.25
sigma0 = 0.04
psi = schrodinger.paquet(x0,k0,sigma0)

figure(figsize=(12,6))
plot(x,psi*numpy.conj(psi),'r')
plot(x,V,'b')
xlabel("x")
ylabel("|psi|^2")
grid()


                

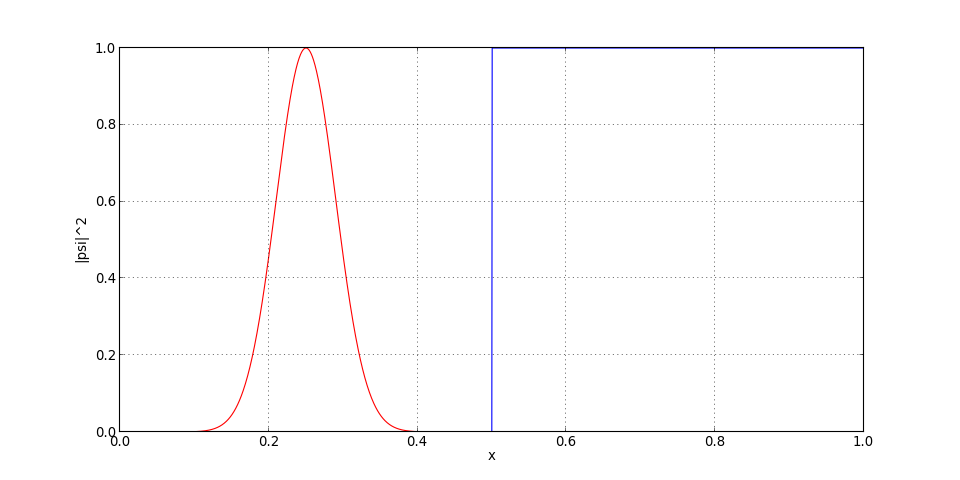figA.pdf

On trace le module de la fonction d'onde (densité de probabilité) pour différents instants.

t=0.0
dt=2*dx*dx
v=2*k0
T = 1.0/v
V0 = E
schrodinger.config(dt,V*V0)
[psi,t] = schrodinger.iterations(psi,t,T*0.2)

figure(figsize=(12,6))
plot(x,psi*numpy.conj(psi),'r')
plot(x,V,'b')
xlabel("x")
ylabel("|psi|^2")
grid()
                

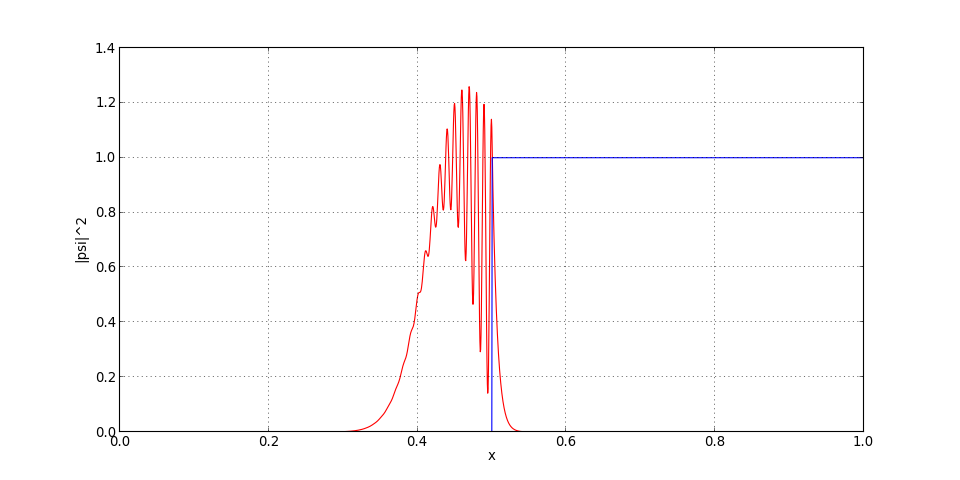figB.pdf

[psi,t] = schrodinger.iterations(psi,t,T*0.3)

figure(figsize=(12,6))
plot(x,psi*numpy.conj(psi),'r')
plot(x,V,'b')
xlabel("x")
ylabel("|psi|^2")
grid()
                

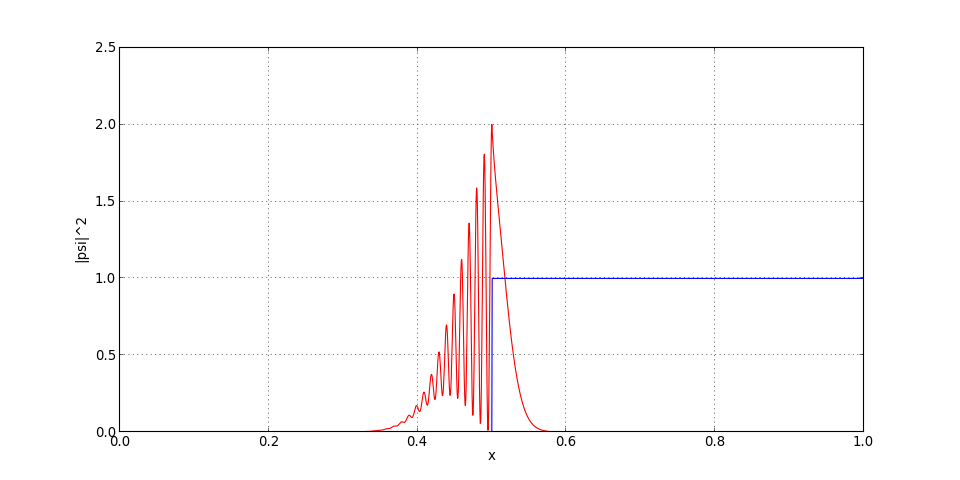figC.pdf

[psi,t] = schrodinger.iterations(psi,t,T*0.5)

figure(figsize=(12,6))
plot(x,psi*numpy.conj(psi),'r')
plot(x,V,'b')
xlabel("x")
ylabel("|psi|^2")
grid()
                

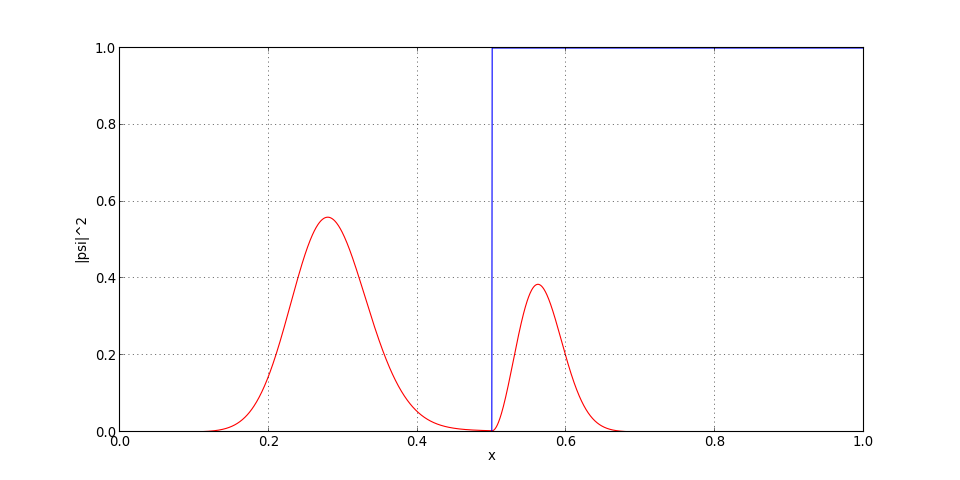figD.pdf

5.b. Diffusion de particules sur une barrière de potentiel

N=2000
L=1.0
dx=L/(N-1)
x = numpy.arange(N)*dx
schrodinger = Schrodinger1D(L,N)
V = schrodinger.V_barriere(1.0,0.05)
l0 = 2e-2
k0 = numpy.pi*2/l0
E=k0*k0
x0 = 0.25
sigma0 = 0.04
psi = schrodinger.paquet(x0,k0,sigma0)
                

On trace le module de la fonction d'onde (densité de probabilité) pour différents instants.

t=0.0
dt=2*dx*dx
v=2*k0
T = 1.0/v
V0=E
schrodinger.config(dt,V*V0)
[psi,t] = schrodinger.iterations(psi,t,T*0.2)

figure(figsize=(12,6))
plot(x,psi*numpy.conj(psi),'r')
plot(x,V,'b')
xlabel("x")
ylabel("|psi|^2")
grid()
                

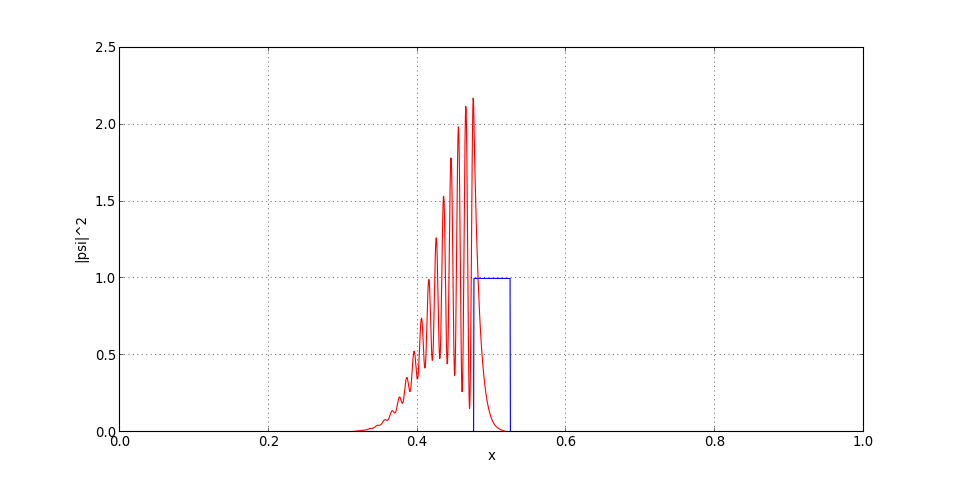figE.pdf

[psi,t] = schrodinger.iterations(psi,t,T*0.3)

figure(figsize=(12,6))
plot(x,psi*numpy.conj(psi),'r')
plot(x,V,'b')
xlabel("x")
ylabel("|psi|^2")
grid()
                

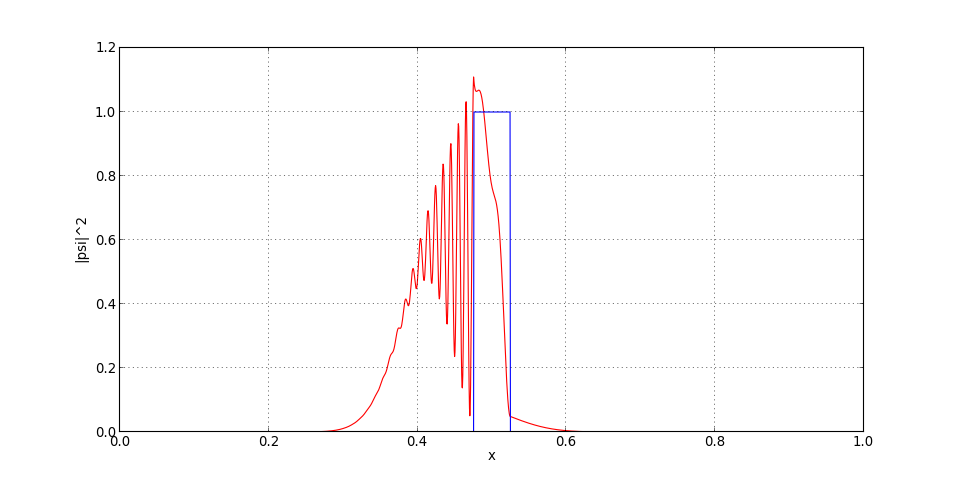figF.pdf

[psi,t] = schrodinger.iterations(psi,t,T*0.5)

figure(figsize=(12,6))
plot(x,psi*numpy.conj(psi),'r')
plot(x,V,'b')
xlabel("x")
ylabel("|psi|^2")
grid()
                

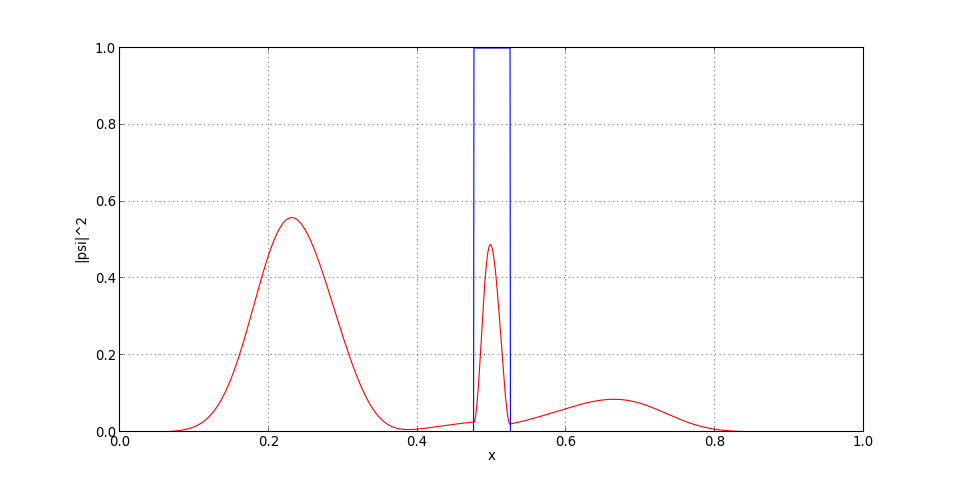figG.pdf

[psi,t] = schrodinger.iterations(psi,t,T*0.55)

figure(figsize=(12,6))
plot(x,psi*numpy.conj(psi),'r')
plot(x,V,'b')
xlabel("x")
ylabel("|psi|^2")
grid()
                

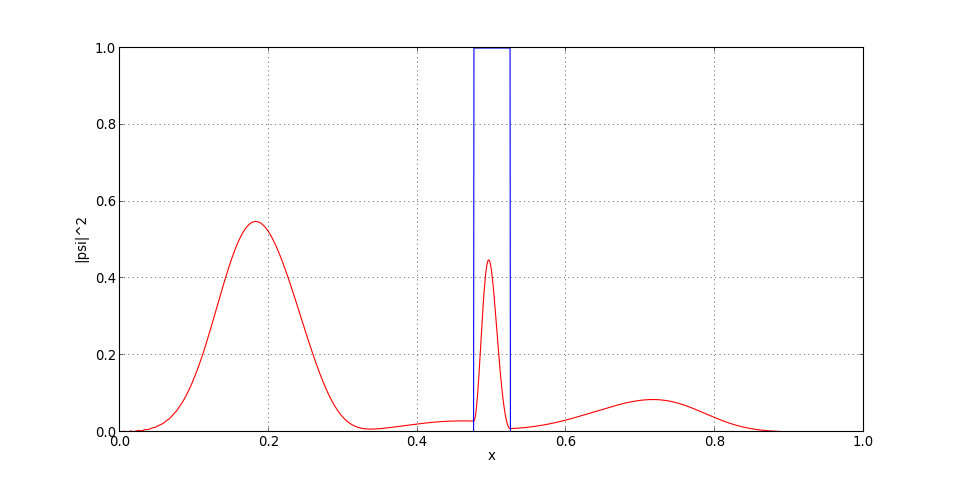figH.pdf