Thermodynamique statistique

1.a. Micro-états et état thermodynamique

L'objectif de la thermodynamique statistique est l'explication des propriétés thermodynamiques de la matière par sa structure et sa dynamique microscopique.

L'échelle microscopique est celle des atomes ou des molécules, de l'ordre de quelques nanomètres pour la matière condensée, quelques dizaines de nanomètres ou plus pour les gaz. L'échelle mésoscopique est l'échelle à partir de laquelle il est possible de définir des grandeurs thermodynamiques comme l'énergie interne ou la température. Un volume mésoscopique doit contenir un nombre d'atomes ou de molécules très grand (au moins 10⁶). Enfin l'échelle macroscopique, beaucoup plus grande que l'échelle mésoscopique, est celle des expériences ordinaires. À cette échelle, le nombre d'atomes ou de molécules est de l'ordre du nombre d'Avogadro, soit environ 10²³.

La thermodynamique statistique s'intéresse à un système mésoscopique ou macroscopique, c'est-à-dire contenant un nombre N de constituants élémentaires très grand. Le système étudié, qu'il soit mésoscopique ou macrosopique, est supposé être à l'équilibre thermodynamique.

Prenons l'exemple d'un gaz monoatomique, que l'on modélise par N atomes ponctuels, occupant un volume V et formant un système isolé d'énergie E. On suppose que ces atomes obéissent aux lois de Newton de la mécanique (gaz parfait classique). Chaque atome a donc une trajectoire : on peut à tout instant définir sa position dans l'espace et sa vitesse. Pour un gaz de faible pression, on peut utiliser le modèle du gaz parfait, pour lequel on néglige l'énergie potentielle d'interaction entre les atomes. L'énergie est alors la somme des énergies cinétiques des atomes :

$$E=\sum _{i=1}^N\frac{1}{2}m{\overrightarrow{v}}_i^2=\sum _{i=1}^N\frac{{\overrightarrow{p}}_i^2}{2m}\text{(1)}$$

L'état d'un atome à un instant donné est défini par sa position (x,y,z) et sa quantité de mouvement (p_x,p_y,p_z). Il peut être représenté par un point dans un espace à 6 dimensions, appelé espace des phases. La dénomination espace des phases vient de l'utilisation de cet espace pour l'étude des oscillateurs en mécanique. Une dénomination plus générale serait espace des états.

On appelle micro-état d'un système thermodynamique la donnée de l'état de tous ces constituants élémentaires, du moins ceux qui interviennent dans les propriétés auxquelles on s'intéresse. Dans le cas du gaz monoatomique, un micro-état est défini par la donnée des positions et des quantités de mouvement des N atomes. Il peut donc se représenter par un point dans un espace des phases à 6N dimensions.

Par exemple, les micro-états d'un système constitué d'une seule particule se déplaçant sur un axe Ox sont des points dans un domaine du plan (x,p_x) :

Figure pleine page

[0,L] est l'intervalle dans lequel se trouve la particule (L est le volume à une dimension). En principe, la composante p_x de la quantité de mouvement peut prendre toute valeur réelle (même si en réalité la vitesse doit être non relativiste). En mécanique classique, les micro-états sont non dénombrables car l'espace des phases est continu. Dans un volume fini de l'espace des phases, il existe une infinité de micro-états différentes. En mécanique quantique, les états d'une particule confinée sont au contraire dénombrables. Du fait de l'inégalité d'Heisenberg, on peut considérer que l'espace des phases est découpé en rectangles d'aire $\Delta x\Delta p_x\simeq \hslash$, chacun représentant un état de la particule. À l'échelle macroscopique (ou même mésoscopique), ces rectangles sont extrêmement petits, mais ils sont dénombrables, c'est-à-dire que le nombre d'états dans un volume fini de l'espace des phases est fini.

À l'échelle mésoscopique ou macroscopique, un gaz monoatomique à l'équilibre, comportant N atomes, est entièrement caractérisé par deux variables correspondant à des grandeurs observables à cette échelle. Par exemple, on peut choisir de le caractériser par la donnée de (E,V), mais d'autres choix de variables sont possibles, par exemple (P,T).

Un micro-état est défini par un nombre extrêmement grand de variables alors que l'état thermodynamique à l'échelle mésoscopique ou macroscopique est défini par un petit nombre de variables (2 pour un corps pur). Un système thermodynamique à l'équilibre parcourt un très grand nombre de micro-états, de manière très rapide. La simulation dynamique des micro-états est aujourd'hui possible grace à des algorithmes informatiques de dynamique moléculaire, mais seulement pour des nombres N de quelques millions et pour des temps de simulation relativement courts. La simulation dynamique d'un système macroscopique est impossible (de très loin).

L'approche probabiliste, inventée par Boltzmann (physicien autrichien 1844-1906), et développée par Gibbs (physicien américain 1839-1903), permet d'obtenir les propriétés macroscopiques d'un système à l'équilibre sans pour autant connaître le détail de la dynamique de ses micro-états.

1.b. Approche probabiliste

L'approche probabiliste adoptée en thermodynamique statistique consiste à considérer les micro-états du système de manière probabiliste, sans se préoccuper de la dynamique, c'est-à-dire de la manière dont le système passe d'un micro-état à un autre. Cette approche repose sur l'hypothèse fondamentale suivante, énoncée pour un système isolé, c'est-à-dire un système dont l'énergie E est constante :

Pour que l'approche probabiliste soit pertinente, il faut que le système occupe effectivement tous ces états accessibles lors de son évolution temporelle, en un temps de l'ordre du temps de mesure des grandeurs (typiquement quelques secondes). Un tel système est dit ergodique. Par exemple, un gaz occupant un volume de l'ordre du litre est effectivement ergodique à l'échelle de la seconde.

Considérons par exemple un gaz monoatomique comportant N atomes, occupant un volume V et d'énergie E, isolé de tout échange avec l'extérieur. Notons Ω(N,V,E) le nombre de micro-états compatibles avec les contraintes imposées au système ((N,V,E) fixés). Le calcul de ce nombre de micro-états ne pose pas de problème de principe lorsque les micro-états sont dénombrables. En revanche, si les états sont non dénombrables (comme c'est le cas en mécanique classique), il est nécessaire de découper l'espace des phases en volumes finis, une astuce inventée par Boltzmann bien avant la découverte de la mécanique quantique. En vertu du principe d'équiprobabilité, la probabilité d'un micro-état particulier est :

$$p=\frac{1}{\Omega }\text{(2)}$$

Boltzmann a réussi à relier cette probabilité aux grandeurs macroscopiques observables en définissant l'entropie de la manière suivante :

$$S=kln\left(\Omega \right)\text{(3)}$$

La constante k est connue aujourd'hui sous le nom de constante de Boltzmann, égale à $1,38\cdot 10^{-23}J\mathrm{.}{K}^{-1}$. L'entropie est donc d'autant plus grande que le nombre de micro-états (pour une énergie donnée) est grand. On dit aussi (de manière moins précise) que l'entropie quantifie le désordre du système. Cette définition de l'entropie de Boltzmann n'est pas à connaître car nous n'allons pas l'utiliser directement.

Si toutes les variables autres que l'énergie sont fixées, la variation d'entropie est reliée à la variation d'énergie par dE=TdS. On en déduit la définition suivante de la température :

$$\frac{1}{T}=(\frac{\partial S}{\partial E}{)}_X\text{(4)}$$

où X désigne l'ensemble des variables autres que E, par exemple le volume pour un gaz. Pour alléger les notations, on utilisera la variable suivante, homogène à l'inverse d'une énergie :

$$\beta =\frac{1}{kT}\text{(5)}$$

D'après l'entropie de Boltzmann, nous avons :

$$\beta =(\frac{\partial ln\left(\Omega \right)}{\partial E}{)}_X\text{(6)}$$

1.c. Exemple : système de particules à deux états

Considérons un système simple dans lequel les micro-états sont dénombrables, constitué de N particules indépendantes et identiques, chacunes ayant seulement deux états possibles, l'état 0 et l'état 1, d'énergie 0 et ε. Notons m_i l'état de la particule i, qui est un entier égal à 0 ou 1. L'indépendance des particules implique que l'énergie du système est simplement la somme des énergies des particules :

$$E=m_1\epsilon +m_2\epsilon +\cdots =(m_1+m_2+\cdots m_N)\epsilon =m\epsilon \text{(7)}$$

Un micro-état est défini par les N nombres $m_1,m_2,\cdots m_N$.

Le nombre de micro-états d'énergie E=mε est égal au nombre de parties à m éléments dans un ensemble à N éléments, soit :

$$\Omega (E,N)=\frac{N!}{(N-m)!m!}\text{(8)}$$

La figure suivante montre, pour N=4, les micro-états d'énergie $E=2\epsilon$. D'après le principe énoncé plus haut, ces 6 micro-états sont équiprobables.

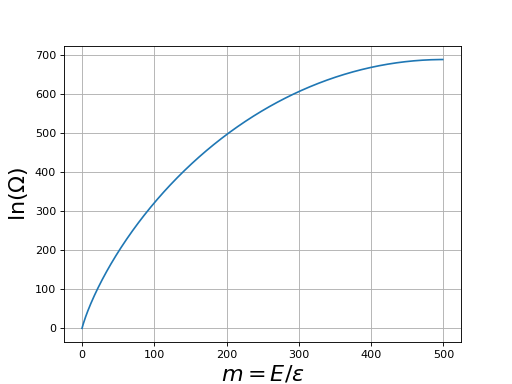
Figure pleine page

Voici, pour N=1000, le tracé de ln(Ω) (entropie divisée par k) en fonction de m :

import numpy
from matplotlib.pyplot import *
import math
   
def entropie(N,m):
    return math.log(math.factorial(N))-math.log(math.factorial(N-m))-math.log(math.factorial(m))
    
N=1000
M=500
m=numpy.arange(0,M)
S=numpy.zeros(M)
for i in range(M):
    S[i] = entropie(N,m[i])

figure()
plot(m,S)
grid()
xlabel("$m=E/\epsilon$",fontsize=20)
ylabel(r"$\ln(\Omega)$",fontsize=20)
                    

figA.pdf

Cette courbe montre que le nombre de micro-états est extrêmement grand, même pour un système comportant un nombre de particules modeste. Par exemple, pour une énergie m=100, le nombre de micro-états est e³⁰⁰. Ce nombre est si grand qu'il est bien sûr inenvisageable d'explorer tous ces états par un programme informatique. On voit de plus que le nombre de micro-états augmente avec l'énergie de manière spectaculaire. Calculons βε à l'aide de la relation $\mathrm{(6)}$, qui s'écrit aussi :

$$\beta \epsilon =(\frac{\partial ln\left(\Omega \right)}{\partial m}{)}_N\text{(9)}$$

beta=numpy.zeros(M-1)
m1=numpy.arange(M-1)
for i in range(M-1):
    beta[i] = S[i+1]-S[i]
figure()
plot(m1,1/beta)
ylim(0,50)
grid()
xlabel("$m=E/\epsilon$",fontsize=20)
ylabel(r"$kT/\epsilon$",fontsize=20)
                     

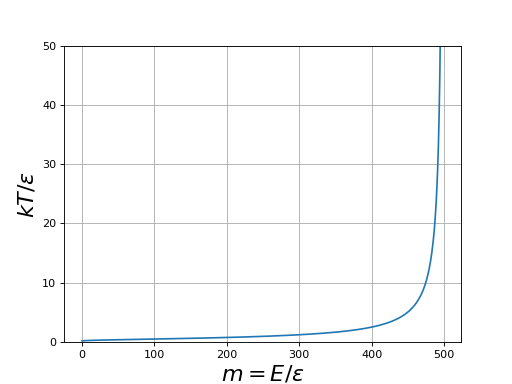figB.pdf

Cette courbe montre que la température augmente lorsque l'énergie augmente (et tend vers l'infini lorsque m tend vers N/2).

Portons à présent notre attention sur une particule. Notons p₀ la probabilité pour qu'elle soit dans l'état 0 et p₁ la probabilité pour qu'elle soit dans l'état 1. D'après l'hypothèse d'équiprobabilité des états de même énergie E, la probabilité p₀ est égale au nombre d'états pour lesquels la particule est dans l'état 0 divisé par le nombre total :

$$p_0=\frac{\Omega (N-1,m)}{\Omega (N,m)}\text{(10)}$$

En effet, si la particule se trouve dans l'état 0, alors les N-1 autres particules ont une énergie totale égale à mε.

Nous pouvons de même écrire la probabilité pour que la particule soit dans l'état 1 :

$$p_1=\frac{\Omega (N-1,m-1)}{\Omega (N,m)}\text{(11)}$$

car si la particule se trouve dans l'état 1 alors les N-1 autres particules ont une énergie (m-1)ε.

La figure suivante montre un exemple pour N=4 et une énergie $E=\epsilon$.

Figure pleine page

La probabilité que la particule 1 se trouve dans l'état 0 est 3/4 et la probabilité qu'elle se trouve dans l'état 1 est 1/4. Il en est évidemment de même pour toutes les autres particules.

On s'intéresse aux rapport des probabilités :

$$\frac{p_1}{p_0}=\frac{\Omega (N-1,m-1)}{\Omega (N-1,m)}\text{(12)}$$

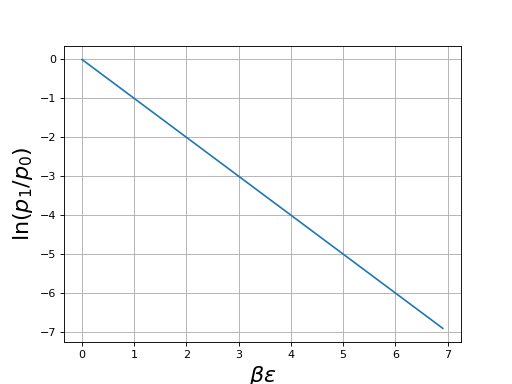
La courbe suivante montre le logarithme de ce rapport en fonction de βε :

log_rapport=numpy.zeros(M-1)
for i in range(0,M-1):
    log_rapport[i] = entropie(N-1,m[i+1]-1)-entropie(N-1,m[i+1])
figure()
plot(beta,log_rapport)
grid()
xlabel(r"$\beta\epsilon$",fontsize=20)
ylabel(r"$\ln(p_1/p_0)$",fontsize=20)
                        

figC.pdf

Ce logarithme du rapport des probabilités est égal à -βε donc :

$$\frac{p_1}{p_0}=exp(-\beta \epsilon )=exp(-\frac{\epsilon }{kT})\text{(13)}$$

Si la température est positive, la probabilité de l'état 1 est plus faible que celle de l'état 0. Le rapport de ces probabilités est d'autant plus faible que la température est basse et que l'énergie ε est grande. Si kT est très petit devant ε, la probabilité de l'état 1 est négligeable par rapport à celle de l'état 0. Inversement, si la température est très grande les deux états sont pratiquement équiprobables.

Le résultat $\mathrm{(13)}$ constitue la loi de Boltzmann, que nous allons généraliser.

2.a. Atmosphère isotherme

Nous allons tout d'abord retrouver la loi de Boltzmann en utilisant une autre approche. Nous considérons un gaz parfait en situation d'équilibre dans un champ de force, en utilisant l'équation d'état du gaz parfait.

Pour un gaz, il est possible de définir une densité locale n (nombre d'atomes par unité de volume), en se plaçant à l'échelle mésocopique. Lorsque le gaz n'est soumis à aucune force extérieure, cette densité est uniforme, égale à :

$$n=\frac{N}{V}\text{(14)}$$

Pour voir comment la densité est modifiée en présence d'un champ de force, considérons le cas du champ de pesanteur (uniforme). Le modèle utilisé est celui de l'atmosphère isotherme (l'atmosphère réelle n'est pas du tout isotherme). En raison de la pesanteur, la pression du gaz (parfait) dépend de l'altitude z. Considérons une couche de gaz mésoscopique comprise entre les altitudes z et z+dz, d'aire A. La figure suivante représente les trois forces qui agissent sur cette portion de gaz (ρ est la masse volumique).

Figure pleine page

L'équilibre mécanique s'écrit :

$$P\left(z\right)-P(z+dz)=\rho \left(z\right)gdz\text{(15)}$$

On introduit la densité locale n(z) et la masse m d'une molécule :

$$\rho \left(z\right)=mn\left(z\right)\text{(16)}$$

ce qui conduit à l'équation différentielle :

$$dP=-mn\left(z\right)gdz\text{(17)}$$

L'équation d'état du gaz parfait s'écrit :

$$P=n\frac{R}{N_a}T=nkT\text{(18)}$$

On a donc l'équation différentielle pour la densité :

$$\frac{dn}{n}=-\frac{mgdz}{kT}\text{(19)}$$

Si le gaz est à l'équilibre thermique (atmosphère isotherme), l'intégration de cette équation donne :

$$n\left(z\right)=n\left(0\right)exp(-\frac{mgz}{kT})\text{(20)}$$

L'argument de l'exponentielle est l'opposé du rapport de l'énergie potentielle d'un atome sur l'énergie thermique kT.

En l'absence de champ de force, un atome du gaz parfait a la même probabilité de se trouver dans tous les points du volume. Il n'en est plus de même en présence d'un champ de force extérieure. La densité obtenue dans le modèle de l'atmosphère isotherme nous suggère de définir la densité de probabilité par :

$$f\left(z\right)=Cexp(-\frac{E_p\left(z\right)}{kT})\text{(21)}$$

où E_p(z)=mgz est l'énergie potentielle de pesanteur. La probabilité pour un atome d'être entre z et z+dz est f(z)dz.

Le facteur exponentiel de cette expression est le facteur de Boltzmann. Il est caractéristique des systèmes en équilibre thermique à la température T.

La constante C est déterminée en écrivant la normalisation de la probabilité : la somme de toutes les probabilités doit être égale à 1. Pour une densité de probabilité, on écrit :

$${\int }_0^{H}f\left(z\right)dz=1\text{(22)}$$

où H est la hauteur du volume V. Si l'on considère que la hauteur de l'atmosphère est infinie, on a :

$${\int }_0^{\infty }f\left(z\right)dz=1\text{(23)}$$

Cette intégrale est bien définie, ce qui permet de calculer la constante C.

2.b. Loi de Boltzmann

La loi de Boltzmann s'applique à un système en équilibre thermodynamique à la température T, c'est-à-dire un système en équilibre avec un thermostat de température T. On rappelle qu'un thermostat est un autre système avec lequel le système considéré échange de l'énergie et qui est assez grand pour garder une température constante. Le système peut se réduire à une seule particule ou bien être constitué de plusieurs particules. Il n'est pas isolé, puisqu'il échange de l'énergie avec le thermostat. Insistons sur le fait que le système échange de l'énergie avec le thermostat même s'il est à l'équilibre (sans cela on ne pourrait parler d'équilibre avec le thermostat).

La constante C est déterminée en écrivant la condition de normalisation : la somme des probabilités de tous les micro-états du système doit être égale à 1 :

$$\sum _{\mu }{p}_{\mu }=1\text{(25)}$$

On obtient ainsi :

$$p_{\mu }=\frac{exp(-\beta E_{\mu })}{\sum _{\mu }exp(-\beta E_{\mu })}\text{(26)}$$

La somme qui apparaît au dénominateur, notée Z, est appelée fonction de partition :

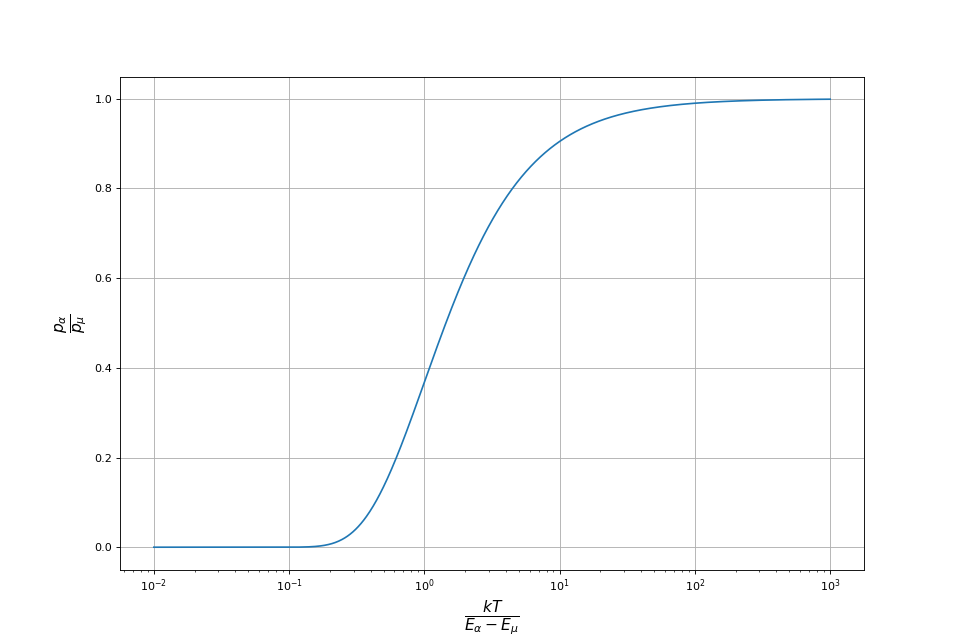
La fonction de partition est une somme sur tous les micro-états du système. Le calcul de cette somme peut être très difficile. Cependant, le rapport des probabilités de deux états peut se calculer sans la connaître :

$$\frac{p_{\alpha }}{p_{\mu }}=exp(-\beta (E_{\alpha }-E_{\mu }))\text{(28)}$$

Si E_α<E_μ alors p_α>p_μ. Ainsi un état d'énergie plus basse qu'un autre est plus probable et le rapport des probabilités est d'autant plus grand que la différence d'énergie est grande. Par ailleurs, ce rapport est d'autant plus grand que β est grand, c'est-à-dire que la température est basse. Plus la température est basse, plus le rapport de probabilité entre deux états d'énergies différentes est différent de 1. Plus précisément, si $kT\ll |E_{\alpha }-E_{\mu }|$ alors l'état de plus basse énergie a une probabilité beaucoup plus forte que l'autre. Inversement si $kT\gg |E_{\alpha }-E_{\mu }|$ alors les deux états ont quasiment la même probabilité.

x=numpy.logspace(-2,3,1000)
rapport = numpy.exp(-1/x)
figure(figsize=(12,8))
plot(x,rapport)
xscale('log')
xlabel(r"$\frac{kT}{E_{\alpha}-E_{\mu}}$",fontsize=20)
ylabel(r"$\frac{p_{\alpha}}{p_{\mu}}$",fontsize=20)
grid()
                         

figC1.pdf

La loi de Boltzmann s'applique à un système à l'équilibre thermique avec un thermostat, quelle que soit sa taille. Elle s'applique donc aussi bien à un système très petit, voire constitué d'une seule particule, qu'à un système comportant un grand nombre de particules. Elle ne s'applique pas à un système isolé puisque, comme nous l'avons vu, tous les micro-états d'un système isolé sont équiprobables. Considérons néanmoins une seule particule appartenant à un système isolé contenant un très grand nombre de particules. Les autres particules constituent un thermostat pour cette particule, ce qui fait qu'on peut lui appliquer la loi de Boltzmann, à condition de connaître la température du système.

2.c. Interprétation des probabilités

La loi de Boltzmann donne la probabilité pour qu'un système à l'équilibre thermique avec un thermostat soit dans un microt-état donné. Cette loi s'applique à tout système, quelle que soit sa taille.

Voyons comment interpréter physiquement une loi de probabilité sur les micro-états, en considérant le cas de la loi de Boltzmann.

La première approche, la plus générale, consiste à faire appel à la notion d'ensemble de micro-états associés à un état macroscopique donné. Pour un système mésoscopique ou macroscopique dans un état thermodynamique donné (par ex. P et T pour un gaz dans un volume V), on considère l'ensemble des micro-états que peut avoir ce système à un instant donné. La loi de Boltzmann définit les probabilités de ces micro-états, pourvu que le système considéré soit à l'équilibre thermique avec un thermostat. Pour réaliser physiquement cet ensemble, il faudrait préparer un très grand nombre de systèmes identiques et les observer à un instant donné (ce qui est irréalisable). L'instant d'observation n'a d'ailleurs pas d'importance car le système considéré est à l'équilibre thermodynamique.

Reprenons pour exemple le système de N particules indépendantes à deux états et considérons qu'il est à l'équilibre thermique avec un thermostat de température T. Tous les micro-états sont possibles (quelle que soit leur énergie) mais les micro-états de plus basse énergie sont plus probables. Le nombre de micro-états est 2^N. La figure suivante montre, pour N=10, un petit échantillon de ces micro-états, qui sont des micro-états possibles (mais pas équiprobables) du système à un instant donné. On a représenté le micro-état où toutes les particules sont dans l'état 0 et quelques uns des micro-états où une seule particule est dans l'état 1. Le premier est le plus probable, ceux où une seule particule est dans l'état 1 sont les seconds plus probables. Pour cet exemple, le nombre de micro-états de l'ensemble est 2¹⁰=1024 (chaque micro-état est représenté par un nombre entier codé sur 10 bits).

Figure pleine page

Cette notion d'ensemble est satisfaisante sur le plan théorique mais elle ne correpond pas à la réalité d'une mesure que l'on fait sur un système. Il faut alors considérer l'évolution temporelle du système. Supposons que l'on dispose d'un capteur permettant de mesurer l'énergie du système des particules à deux états (en réalité, on mesure la variation d'énergie lors d'une transformation entre deux états thermodynamiques). La mesure se fait pendant un intervalle de temps Δt. Pour interpréter les probabilités, on doit faire appel à l'hypothèse d'ergodicité, qui stipule que le système évolue au cours du temps en balayant les différents micro-états, chacun ayant une probabilité d'apparaître donnée par la loi de Boltzmann. Cela signifie que la probabilité de passer d'un micro-état à un autre est égale au rapport de probabilités de ces deux micro-états. L'hypothèse d'ergodicité doit être testée par l'expérience, car certains systèmes physiques ne la satisfons pas, ou la satisfons sur un intervalle de temps trop long. Si l'intervalle de temps Δt est assez grand pour que les micro-états explorés pendant cette durée représentent un échantillon significatif de tous les micro-états (en terme de probabilités), alors l'énergie mesurée correspond effectivement à l'énergie moyenne du système, au sens d'espérance de l'énergie sur l'ensemble des micro-états. Si Δt n'est pas assez grand, on observe des fluctuations au cours du temps de l'énergie mesurée. Ces fluctuations seront quantifiées par l'écart-type ΔE de l'énergie. Bien entendu, toutes ces considérations s'appliquent à toute autre grandeur physique mesurée. La figure suivante montre ce que pourrait être l'évolution temporelle du système de N=10 particules.

Figure pleine page

Au cours de l'évolution temporelle d'un système ergodique, la probabilité de survenu d'un micro-état est égale à sa probabilité dans la distribution de Boltzmann.

Lorsqu'on s'intéresse à une seule particule appartenant à un système comportant un très grand nombre de particules identiques, une autre interprétation de la probabilité de Boltzmann peut être donnée. Il s'agit de la probabilité pour que, si l'on prend au hasard une particule parmi toutes celles du système, elle soit dans un état donné. Pour reprendre l'exemple des particules à deux états, si l'on prend au hasard une particule dans le système, on a une probabilité p₀ qu'elle soit dans l'état 0 et une probabilité p₁ qu'elle soit dans l'état 1. Si on suivait l'évolution temporelle d'une seule particule (ce qui dans la réalité est infaisable), on la verrait passer aléatoirement de l'état 0 à l'état 1 mais elle passerait plus de temps dans l'état 0 puisque celui-ci est plus probable.

2.d. Valeurs moyennes et écart-types

La loi de probabilité de Boltzmann pemet de calculer la valeur moyenne (c'est-à-dire l'espérance) d'une grandeur physique X. Notons X_μ la valeur de cette grandeur lorsque le système se trouve dans le micro-état μ. La valeur moyenne est :

$$\overline{X}=\frac{\sum _{\mu }{X}_{\mu }exp(-\frac{E_{\mu }}{kT})}{\sum _{\mu }exp(-\frac{E_{\mu }}{kT})}\text{(29)}$$

On s'intéresse particulièrement à la valeur moyenne de l'énergie du système :

$$\overline{E}=\frac{\sum _{\mu }{E}_{\mu }exp(-\beta E_{\mu })}{\sum _{\mu }exp(-\beta E_{\mu })}\text{(30)}$$

Une autre grandeur importante est la variance, définie comme la moyenne du carré de l'écart entre X et sa valeur moyenne :

$$var\left(X\right)=\overline{{(X-\overline{X})}^2}\text{(31)}$$

L'expression de la variance se développe :

$$var\left(X\right)=\overline{X^2}+{\overline{X}}^2-2\overline{X}\overline{X}=\overline{X^2}-{\overline{X}}^2\text{(32)}$$

On appelle écart quadratique moyen (ou écart-type), la racine carrée de la variance :

$$\Delta X=\sqrt{var\left(X\right)}\text{(33)}$$

L'écart-type peut être comparé à la valeur moyenne, et donne une information sur la dispersion des valeurs autour de la moyenne.

Si l'on dispose d'une expression de la fonction de partition Z $\mathrm{(27)}$, on peut faire les calcul de valeur moyenne et d'écart-type. Considérons le logarithme népérien de la fonction de partition et dérivons le par rapport à β :

$$\frac{\partial }{\partial \beta }ln\left(\sum _{\mu }exp\right(-\beta E_{\mu }\left)\right)=\frac{\sum _{\mu }-E_{\mu }exp(-\beta E_{\mu })}{\sum _{\mu }exp(-\beta E_{\mu })}=-\overline{E}\text{(34)}$$

Nous pouvons donc calculer l'énergie moyenne de la manière suivante :

Dérivons deux fois le logarithme de la fonction de partition par rapport à β :

$$\frac{{\partial }^{2}lnZ}{\partial {\beta }^2}=\frac{\left(\sum _{\mu }{E}_{\mu }^{2}exp\right(-\beta E_{\mu }\left)\right)\left(\sum _{\mu }exp\right(-\beta E_{\mu }\left)\right)-\left(\sum _{\mu }{E}_{\mu }exp\right(-\beta E_{\mu }){)}^2}{\left(\sum _{\mu }exp\right(-\beta E_{\mu }){)}^2}\text{(36)}$$

Après simplification, on obtient :

$$\frac{{\partial }^{2}lnZ}{\partial {\beta }^2}=\overline{E^2}-{\overline{E}}^2={\left(\Delta E\right)}^2\text{(37)}$$

On a donc :

$${\left(\Delta E\right)}^2=-\left(\frac{\partial \overline{E}}{\partial \beta }\right)\text{(38)}$$

La capacité thermique à volume constant est la dérivée de l'énergie moyenne par rapport à la température :

$$C_v=\frac{\partial \overline{E}}{\partial T}=\frac{\partial \overline{E}}{\partial \beta }(\frac{\partial \beta }{\partial T}{)}_{}=-\frac{1}{k{T}^2}\frac{\partial \overline{E}}{\partial \beta }\text{(39)}$$

On a donc la relation suivante :

Ainsi la variance de l'énergie est proportionnelle à la capacité thermique à volume constant. Le rapport entre l'écart-type et la valeur moyenne est alors :

$$\frac{\Delta E}{\overline{E}}=\frac{\sqrt{k{T}^2{C}_v}}{\overline{E}}\text{(41)}$$

L'énergie moyenne et la capacité thermique sont deux grandeurs extensives proportionnelles à N. On en déduit la loi d'échelle :

$$\frac{\Delta E}{\overline{E}}\sim \frac{1}{\sqrt{N}}\text{(42)}$$

L'écart-type relatif de l'énergie est donc d'autant plus faible que le système est grand. Pour un système mésoscopique ou macroscopique, cet écart relatif est extrêmement faible, ce qui signifie que l'énergie du système reste très probablement très proche de son énergie moyenne. Ainsi un système thermodynamique en équilibre avec un thermostat est similaire à un système isolé d'énergie constante (tant qu'il reste à l'équilibre).

On remarque que cette loi est la même que celle qui donne l'écart-type de la moyenne empirique calculée avec N échantillons d'une variable aléatoire.

Bien évidemment, si le système ne comporte que quelques particules (voire une seule), la loi de Boltzmann s'applique à ce système mais l'écart-type de l'énergie n'est pas petit devant l'énergie moyenne. Pour une seule particule, l'écart-type est du même ordre de grandeur que l'énergie moyenne.

On appelle limite thermodynamique la limite obtenue lorsque $N\to \infty$. À la limite thermodynamique, le rapport de l'écart-type de l'énergie par l'énergie tend vers zéro : $\Delta E/\overline{E}\to 0$. La limite thermodynamique est cependant à manier avec précaution (comme toute limite) car l'écart-type lui-même tend vers l'infini, tout comme la capacité thermique. Lorsque le nombre de particules est très grand, le système échange bien de l'énergie avec le thermostat donc ΔE n'est pas nul, mais il devient négligeable devant l'énergie moyenne. Le système n'est jamais équivalent à un système isolé, car dans ce cas tous ces micro-états seraient équiprobables.

Remarque : l'écart-type d'une variable aléatoire est aussi appelée par les physiciens écart quadratique moyen. L'écart quadratique moyen au carré est la variance.

D'après la relation $\mathrm{(40)}$, la variance de l'énergie est une grandeur accessible expérimentalement par des mesures de capacité thermique.

Lorsqu'un système physique vérifie l'hypothèse d'ergodicité, des micro-états sont effectivement parcourus au cours du temps (pendant une durée variable suivant la taille du système). L'énergie interne, habituellement notée U, est égale à la valeur moyenne de l'énergie. L'écart-type ΔE représente l'amplitude des fluctuations d'énergie au cours du temps. Nous pouvons donc déduire de ce qui précède que les fluctuations d'énergie d'un système macroscopique à l'équilibre thermique avec un thermostat sont extrêmement faibles par rapport à l'énergie moyenne. Lorsque le système est à l'équilibre, les échanges d'énergie avec le thermostat sont donc extrêmement faibles.

3.a. Généralités

On considère un système formé de N particules indépendantes et discernables. Pour chaque particule, il y a M états possibles, numérotés de 0 à M-1. À chaque état m est associée une énergie ε_m. On suppose que ces niveaux d'énergie sont régulièrement espacés, et on note ε le quantum d'énergie.

La figure suivante montre les états de quelques particules du système.

Figure pleine page

Les particules sont indépendantes au sens où l'énergie d'interaction entre les particules est négligeable devant l'énergie des particules, ce qui implique que l'énergie du système est égale à la somme des énergies des particules :

$$E=\sum _{i=1}^N{m}_i\epsilon \text{(43)}$$

Il y a tout de même des petites interactions entre particules qui permettent au système d'atteindre l'équilibre thermodynamique. L'énergie d'une particule n'est pas constante puisque son état peut varier, ce qui signifie qu'une particule échange de l'énergie avec les autres particules du système. L'indépendance des particules ne signifie donc pas qu'elles n'échangent pas d'énergie entre elles; l'indépendance signifie seulement que l'énergie totale est la somme des énergies des particules.

Par convention, l'énergie de l'état fondamental (m=0) est supposée nulle : ε₀=0. Si elle n'est pas nulle, il suffira d'ajouter sa valeur à l'énergie moyenne par particule.

Le nombre moyen de particules dans l'état m, aussi appelé population de l'état, est :

$$N_m=\frac{Nexp(-\beta m\epsilon )}{\sum _{m=0}^{M-1}exp(-\beta m\epsilon )}\text{(44)}$$

L'énergie moyenne d'une particule est :

$$\overline{e}=\frac{\sum _{m=0}^{M-1}m\epsilon exp(-\beta m\epsilon )}{\sum _{m=0}^{M-1}exp(-\beta m\epsilon )}\text{(45)}$$

Pour la calculer, on fait appel à la fonction de partition d'une particule :

$$z=\sum _{m=0}^{M-1}exp(-\beta m\epsilon )\text{(46)}$$

La moyenne est alors :

$$\overline{e}=-(\frac{\partial ln\left(z\right)}{\partial \beta }{)}_{}\text{(47)}$$

La variance de l'énergie est :

$${\left(\Delta e\right)}^2=-(\frac{\partial \overline{e}}{\partial \beta }{)}_{}\text{(48)}$$

Pour calculer l'énergie moyenne du système tout entier, nous devons considérer la fonction de partition du système :

$$Z=\sum _{m_1,m_2,m_2,\mathrm{.}\mathrm{.}\mathrm{.}{m}_N}exp(-\beta (m_1\epsilon +m_2\epsilon +\mathrm{.}\mathrm{.}\mathrm{.}))\text{(49)}$$

On a utilisé l'indépendance des particules pour exprimer l'énergie totale comme la somme des énergies des particules. Cette somme se factorise de la manière suivante :

$$Z=\left(\sum _{m_1=0}^{M-1}exp(-\beta m_1\epsilon )\right)\left(\sum _{m_2=0}^{M-1}exp(-\beta m_2\epsilon )\right)\cdots \text{(50)}$$

La fonction de partition du système est simplement le produit des fonctions de partition des particules. Cette propriété vient du fait que les particules sont indépendantes. Puisque toutes les particules sont identiques, on a finalement :

$$Z=z^N\text{(51)}$$

L'énergie moyenne du système est donc :

$$\overline{E}=-\frac{\partial lnZ}{\partial \beta }=-N\frac{\partial lnz}{\partial \beta }=N\overline{e}\text{(52)}$$

Pour des particules indépendantes, l'énergie moyenne est donc égale au nombre de particules multipliée par l'énergie moyenne d'une particule.

La variance de l'énergie est :

$${\left(\Delta E\right)}^2=-(\frac{\partial \overline{E}}{\partial \beta }{)}_{N,V}=N{\left(\Delta e\right)}^2\text{(53)}$$

La variance pour le système est donc égale à la variance pour une particule multipliée par N. On en déduit le rapport de l'écart quadratique moyen sur la moyenne :

$$\frac{\Delta E}{\overline{E}}=\frac{1}{\sqrt{N}}\frac{\Delta e}{\overline{e}}\text{(54)}$$

L'écart relatif diminue comme l'inverse de la racine carrée du nombre de particules. Ce résultat n'est d'ailleurs pas spécifique à la distribution de Boltzmann. Il s'applique de manière générale à N variables aléatoires indépendantes.

Pour un système thermodynamique macroscopique, où N est de l'ordre du nombre d'Avogadro, l'écart relatif est infime. Autrement dit, l'énergie du système en équilibre avec un thermostat est pratiquement constante. D'une manière générale, les grandeurs physiques ont une très faible variance relative dans un système thermodynamique à l'équilibre.

La simulation de Monte-Carlo Distribution de Boltzmann : particules indépendantes montre des tirages aléatoires pour ce système à N particules.

3.b. Système à deux niveaux d'énergie

On s'intéresse au cas M=2.

Les populations des deux états sont :

$$\begin{array}{ccc}\hfill & N_0=\frac{N}{1+exp(-\beta \epsilon )}\hfill & \hfill \text{(55)}\\ \hfill & N_1=\frac{Nexp(-\beta \epsilon )}{1+exp(-\beta \epsilon )}\hfill & \hfill \text{(56)}\end{array}$$

Voici le tracé des populations en fonction de kT/ε :

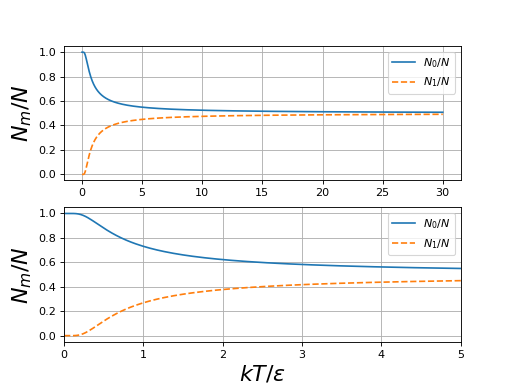figD1.pdf

L'énergie moyenne d'une particule est :

$$\overline{e}=\frac{\epsilon exp(-\beta \epsilon )}{1+exp(-\beta \epsilon )}\text{(57)}$$

On trace l'énergie moyenne en fonction de kT/ε :

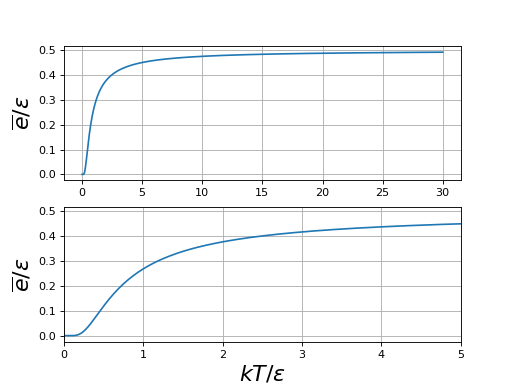figD.pdf

On peut distinguer trois domaines. À haute température ($kT\gg \epsilon$) les deux états sont pratiquement équiprobables. Il y a autant de particules dans un état que dans l'autre et donc :

$$\overline{e}\to \frac{\epsilon }{2}\text{(58)}$$

À basse température ($kT<\epsilon$), le premier niveau est beaucoup plus peuplé que le second et

$$\overline{e}=\epsilon e^{-\beta \epsilon }\text{(59)}$$

À très basse température ($kT\ll \epsilon$), seul le niveau fondamental est peuplé, car la probabilité pour une particule d'être dans l'autre état est négligeable.

L'énergie moyenne du système est :

$$\overline{E}=N\overline{e}\text{(60)}$$

Calculons sa capacité thermique :

$$C_v=\frac{d\overline{E}}{dT}=\frac{d\overline{E}}{d\beta }(\frac{\partial \beta }{\partial T}{)}_{}=-\frac{1}{k{T}^2}\frac{d\overline{E}}{d\beta }\text{(61)}$$

Le calcul conduit à :

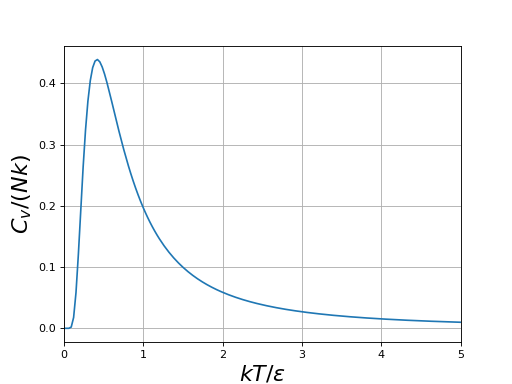$$\frac{C_v}{Nk}=\frac{{\epsilon }^2{\beta }^{2}exp(-\beta \epsilon )}{{(1+exp(-\beta \epsilon ))}^2}\text{(62)}$$ figE.pdf

La capacité thermique augmente avec la température, passe par un maximum puis décroît. Ce comportement peut sembler étrange mais il résulte simplement du fait qu'à haute température l'énergie du système n'augmente plus car les deux états sont équiprobables.

La capacité thermique est une grandeur thermodynamique directement accessible à l'expérience à l'échelle macroscopique. D'après la relation $\mathrm{(38)}$, elle est proportionnelle à la variance de l'énergie :

$$C_v=\frac{1}{k{T}^2}{\left(\Delta E\right)}^2\text{(63)}$$

On en déduit l'écart-type relatif de l'énergie du système :

$$\frac{\Delta E}{\overline{E}}=\frac{1}{\sqrt{N}}exp\left(\frac{1}{2}\beta \epsilon \right)\text{(64)}$$

On retrouve le résultat énoncé de manière générale plus haut : pour un grand système, l'écart-type de l'énergie est très faible. Cela signifie que les fluctuations d'énergie sont très faibles. Si N est de l'ordre du nombre d'Avogadro, elle sont complètement négligeables et l'énergie du système est donc pratiquement constante.

Il faut faire attention à ne pas confondre la probabilité d'un état avec la probabilité pour que le système ait l'énergie E. Cette dernière est égale à :

$$P\left(E\right)=C\Omega (E,N)exp(-\beta E)\text{(65)}$$

où C est une constante. On peut tracer son logarithme : $lnP\left(E\right)=ln\left(\Omega \right)-\beta E$ pour kT=ε :

N=1000
M=500
m=numpy.arange(M)
ln_P=numpy.zeros(M)
for i in range(M):
    ln_P[i] = entropie(N,m[i])-m[i]
figure()
subplot(211)
plot(m,ln_P)
ylabel(r"$\ln(P(E))$",fontsize=20)
grid()
subplot(212)
plot(m,numpy.exp(ln_P))
grid()
xlabel(r"$E/\epsilon$",fontsize=20)
ylabel(r"$P(E)$",fontsize=20)
                       

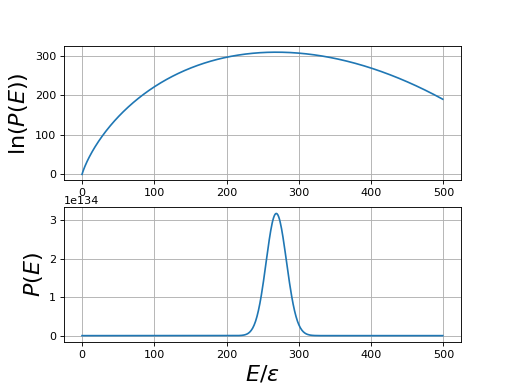figF.pdf

Ce calcul, effectué pour N=1000, montre la distribution des énergies autour de l'énergie moyenne. Lorsque N augmente, la dispersion des valeurs autour de la moyenne diminue. Il s'agit cependant d'une diminution lente, en $1/\sqrt{N}$.

3.c. Système à nombre de niveaux d'énergie infini

Lorsque le nombre de niveaux est infini ($M\to \infty$), la fonction de partition d'une particule est :

$$z=\sum _{m=0}^{\infty }exp{(-\beta \epsilon )}^m=\frac{1}{1-exp(-\beta \epsilon )}\text{(66)}$$

L'énergie moyenne d'une particule est alors :

$$\overline{e}=\frac{\epsilon exp(-\beta \epsilon )}{1-exp(-\beta \epsilon )}\text{(67)}$$

On trace l'énergie moyenne en fonction de kT/ε :

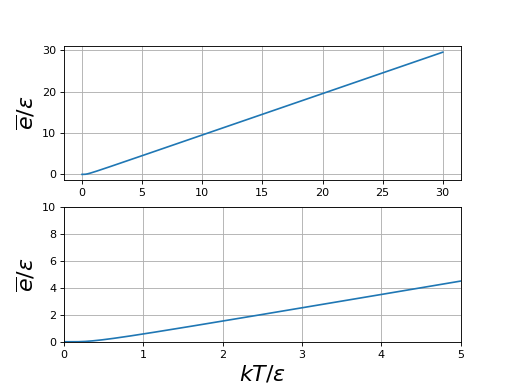figG.pdf

Lorsque $kT>\epsilon$ un développement limité conduit à :

$$\overline{e}\approx kT\text{(68)}$$

La capacité thermique du système est alors $C_v=Nk$.

À très basse température, c'est-à-dire $kT\ll \epsilon$, la probabilité de l'état fondamental est beaucoup plus forte que celle de l'état 1 et l'énergie moyenne est donc nulle.

La capacité thermique du système à N particules est :

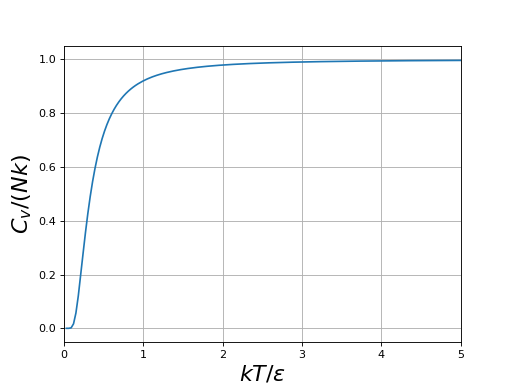$$C_v=-\frac{N}{k{T}^2}\frac{\partial \overline{e}}{\partial \beta }=Nk\frac{{\epsilon }^2{\beta }^{2}exp(-\beta \epsilon )}{{(1-exp(-\beta \epsilon ))}^2}\text{(69)}$$ figH.pdf

La capacité thermique est constante à haute température mais décroît et tend vers zéro lorsqu'on abaisse la température. À très basse température ($kT<\epsilon /10$), la capacité thermique est nulle car seul l'état fondamental est peuplé, les autres états ayant une probabilité négligeable.

4.a. Gaz parfait monoatomique classique

On reprend le modèle de gaz parfait monoatomique défini au début du chapitre. L'énergie d'un atome se limite à son énergie cinétique de translation :

$$e=\frac{{\overrightarrow{p}}^2}{2m}=\frac{p_x^2+p_y^2+p_z^2}{2m}\text{(70)}$$

où l'on a introduit les composantes de la quantité de mouvement sur trois axes.

Pour un gaz parfait, non seulement les atomes sont indépendants les uns des autres, mais les trois degrés de liberté des atomes sont eux même indépendants. On est donc amené à considérer un seul degré de liberté de translation, disons sur l'axe x, et à calculer la fonction de partition correspondant à l'énergie cinétique sur cet axe :

$$z={\int }_{-\infty }^{+\infty }exp(-\beta \frac{p_x^2}{2m})d{p}_x\text{(71)}$$

La quantité de mouvement étant une variable continue, nous avons une intégrale à la place d'une somme. La valeur moyenne de l'énergie cinétique associée à ce degré de liberté est :

$$\overline{\frac{p_x^2}{2m}}=\frac{1}{z}{\int }_{-\infty }^{+\infty }\frac{p_x^2}{2m}exp(-\beta \frac{p_x^2}{2m})=-(\frac{\partial lnz}{\partial \beta }{)}_{}\text{(72)}$$

En faisant le changement de variable $u={\beta }^{\frac{1}{2}}{p}_x$ on obtient :

$$z={\beta }^{-\frac{1}{2}}{\int }_{-\infty }^{\infty }exp(-\frac{u^2}{2m})du\text{(73)}$$

ce qui conduit à :

$$\overline{\frac{p_x^2}{2m}}=\frac{1}{2}{\beta }^{-1}=\frac{1}{2}kT\text{(74)}$$

L'énergie cinétique moyenne d'un atome, qui a trois degrés de liberté de translation, est donc 3/2kT. On en déduit l'énergie du gaz

$$\overline{E}=\frac{3}{2}NkT\text{(75)}$$

puis sa capacité thermique :

$$C_v=\frac{3}{2}Nk\text{(76)}$$

La capacité thermique à volume constant molaire est donc C_vm=3/2R, ce qui est conforme aux valeurs expérimentales pour les gaz monoatomiques (par ex. l'argon).

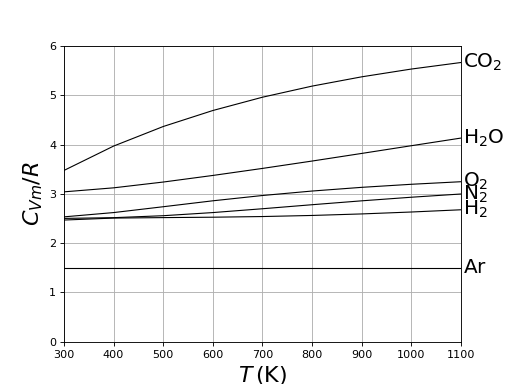figI.pdf

4.b. Théorème d'équipartition de l'énergie

Le résultat précédent se généralise à toute forme d'énergie qui est quadratique par rapport à un degré de liberté.

L'énergie considérée doit être proportionnelle au carré de la variable correspondant au degré de liberté et ne doit pas dépendre d'un autre degré de liberté.

Considérons comme exemple un gaz parfait formé de molécules diatomiques. L'énergie d'une molécule comporte son énergie cinétique de translation et son énergie cinétique de rotation. Pour la rotation, il y a 4 degrés de libertés, car il faut deux angles et leur dérivée temporelle (il y a invariance par rotation autour de son axe). L'énergie cinétique de rotation est quadratique par rapport à la vitesse angulaire. Par exemple, pour la rotation autour d'un axe fixe :

$$e_{rot}=\frac{1}{2}I{\omega }^2\text{(77)}$$

où I est le moment d'inertie de la molécule autour de l'axe de rotation. On admettra que pour deux angles de rotation, il y a bien deux énergies cinétiques quadratiques indépendantes pour les deux vitesses angulaires.

Pour un gaz parfait diatomique, il y a donc 5 degrés de liberté à énergie quadratique par molécule. Le théorème d'équipartition de l'énergie nous donne alors l'énergie moyenne par molécule :

$$\overline{e}=\frac{5}{2}kT\text{(78)}$$

On en déduit la capacité molaire 5/2R d'un gaz parfait diatomique classique.

Sur les courbes expérimentales données ci-dessus, on constate que cette valeur n'est réalisée qu'à 300 K. Lorsque la température augmente, il y une augmentation de la capacité thermique. Celle-ci est attribuable au degré de liberté interne à la molécule, associée à la distance entre les deux noyaux, autrement dit au mouvement de vibration interne de la molécule. L'aspect quantique des énergies de vibration des molécules ne peut être négligé, même à 300 K; le théorème d'équipartition de l'énergie ne s'applique pas aux degrés de liberté de vibration. D'une manière générale, une augmentation de la capacité thermique avec la température est l'indication d'une quantification des niveaux d'énergie.

4.c. Modèle classique des solides

Les solides non métalliques ont une capacité thermique qui augmente avec la température, avec une limite à haute température égale à 3R. Pour beaucoup de solides, cette limite est pratiquement déjà atteinte à 300 K.

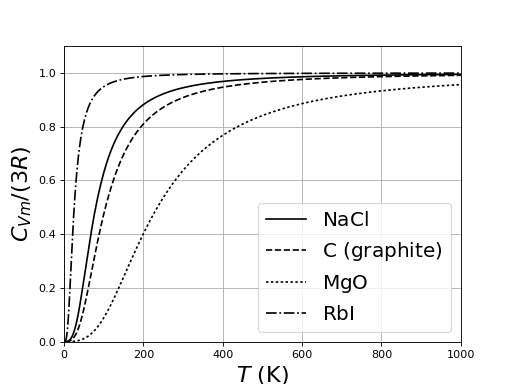figJ.pdf

Dans un solide, les atomes (ou les ions) du réseau cristallin ont une position moyenne fixe mais vibrent légèrement autour de cette position sous l'effet des forces exercées par les atomes voisins. Dans les solides non métalliques, ces mouvements sont la principale cause de l'énergie interne et permettent d'expliquer la capacité thermique. Les atomes d'un solide ne sont pas indépendants les uns des autres. Il faut au minimum tenir compte de l'interaction d'un atome avec ces plus proches voisins.

Considérons un cristal unidimensionnel, constitué d'atomes alignés sur un axe Ox. Soit x_i le déplacement de l'atome i par rapport à sa position d'équilibre.

Figure pleine page

L'énergie du cristal s'écrit :

$$E=\sum _i\frac{p_{xi}^2}{2m}+U(x_{i-1},x_i,x_{i+1})\text{(79)}$$

L'énergie potentielle U est une énergie d'interaction. Elle fait intervenir l'atome numéro i et ses deux plus proches voisins. On pourrait calculer cette énergie en considérant que chaque atome est relié à ces deux proches voisins par un ressort, comme sur la figure ci-dessus, ce qui conduit à :

$$U(x_{i-1},x_i,x_{i+1})=\frac{1}{2}K{(x_i-x_{i-1})}^2+\frac{1}{2}K{(x_{i+1}-x_i)}^2\text{(80)}$$

Cette fonction ne peut pas se mettre sous la forme d'une somme d'énergies pour chaque atome. Autrement dit, il est impossible de définir une énergie potentielle indépendante pour chaque degré de liberté. Une approche simplifiée, proposée par Einstein en 1907, consiste à considérer que chaque atome ressent un champ moyen, représenté par une énergie potentielle E_p(x_i). Comme les déplacements sont très petits (une petite fraction du paramètre de la maille), on peut utiliser un développement limité à l'ordre 2 de cette énergie potentielle moyenne, ce qui donne :

$$E=\sum _i\frac{p_{xi}^2}{2m}+\frac{1}{2}K{x}_i^2\text{(81)}$$

Avec cette approximation, on a une énergie cinétique quadratique pour le degré de liberté p_x et une énergie potentielle quadratique pour le degré de liberté x. D'après le théorème d'équipartition de l'énergie, l'énergie moyenne d'un atome est :

$$\overline{e}=kT\text{(82)}$$

Pour les trois dimensions de l'espace, cela fait une énergie moyenne 3kT, d'où l'on déduit la capacité thermique molaire du solide :

$$C_{vm}=3R\text{(83)}$$

Le fait que la plupart des solides ont à température ambiante la même capacité molaire est la loi de Dulong et Petit, qui a été constatée expérimentalement bien avant le développement de la thermodynamique statistique (en 1818). En fait, ce résultat n'est valable qu'à haute température, au dessus d'une température qui dépend du solide. Lorsque la température décroît, la capacité thermique diminue. Cette propriété ne peut être expliquée que par un modèle quantique, introduit par Einstein en 1907, qui s'est appuyé pour cela sur les découvertes de Planck à propos du rayonnement du corps noir. Le modèle de particules indépendantes à énergies quantifiées conduit en effet (voir courbes plus haut) à une capacité thermique tendant vers zéro à basse température. En reprenant l'hypothèse de Planck sur la quantification de l'énergie, Einstein a montré que les courbes de capacité thermique en fonction de la température pouvaient s'expliquer par l'introduction d'un quantum d'énergie :

$$\epsilon =\hslash \omega \text{(84)}$$

La pulsation de l'oscillateur est reliée aux paramètres classiques par :

$$\omega =\sqrt{\frac{K}{m}}\text{(85)}$$

C'est effectivement le résultat qui est obtenu pour un oscillateur harmonique en mécanique quantique : les niveaux d'énergie sont quantifiés, avec un espacement constant entre deux niveaux consécutifs.