Ising

1. Introduction

Le modèle d'Ising ([1]) a été introduit pour expliquer la physique des matériaux ferromagnétiques, en particulier la transition de phase ferromagnétique/paramagnétique se produisant à la température de Curie.

Ce document présente une simulation numérique du modèle d'Ising à deux dimensions, par la méthode de Monte-Carlo Metropolis. On se limite au modèle d'Ising sans champ magnétique extérieur. Comme la solution exacte est connue, une comparaison avec celle-ci pourra être faite.

Le modèle d'Ising permet d'aborder la technique du codage multispin, qui consiste à effectuer des calculs parallèles sur les bits d'un entier, en utilisant des opérations logiques bit à bit.

2. Modèle d'Ising

2.a. Définition

Le ferromagnétisme est causé par les moments magnétiques de spin des électrons. Dans le modèle d'Ising, ces moments magnétiques sont supposés tous alignés dans une direction. Soit S_i le spin d'un atome dans cette direction, qui peut prendre les valeurs -1/2 ou 1/2. Le spin d'un atome peut interagir avec les spins des atomes voisins du réseau cristallin. Il est par ailleurs sensible au champ magnétique extérieur dont la composante dans la direction des spins est notée B.

L'énergie du système de N spins s'écrit :

E = - g μ_{B} B \sum_{i = 0}^{N - 1} S_{i} - J \sum_{i, j} S_{i} S_{j} (1)

Le premier terme représente l'interaction entre les spins et le champ extérieur. μ_B est le magnéton de Bohr et g le facteur de Landé. Cette énergie est minimisée lorsque tous les spins sont alignés avec le champ, c'est-à-dire lorsqu'ils sont tous positifs.

Le second terme représente l'interaction entre les spins des atomes voisins. La somme porte sur les paires d'atomes voisins. J est une constante positive appelée constante de couplage. Cette énergie est minimisée lorsque les spins voisins sont dans le même sens, donc lorsque tous les spins sont dans le même sens. Ce terme de couplage entre spins explique la possibilité d'une aimantation dans le matériau ferromagnétique, en l'absence de champ extérieur.

Le moment magnétique total du système de spins est :

M = g μ_{B} \sum_{i = 0}^{N - 1} S_{i} (2)

Le système est en contact avec un thermostat de température T. La probabilité d'une configuration particulière des spins parmi toutes les configurations possibles est proportionnelle au facteur de Boltzmann :

exp (- \frac{E_{μ}}{k_{B} T}) = e^{- β E_{μ}} (3)

La valeur moyenne du moment magnétique est donc :

< M > = \frac{\sum_{μ} M_{μ} e^{- β E_{μ}}}{\sum_{μ} e^{- β E_{μ}}} (4)

où μ désigne une configuration des spins.

2.b. Modèle d'Ising à deux dimensions sans champ magnétique

Les spins sont disposés sur un réseau bidimensionnel NxN à mailles carrées. Soit S_i,j le spin situé sur la ligne j et la colonne i. Il interagit avec ses 4 plus proches voisins. La contribution à l'énergie des 4 paires est

- J (S_{i, j} S_{i - 1, j} + S_{i, j} S_{i + 1, j} + S_{i, j} S_{i, j - 1} + S_{i, j} S_{i, j + 1}) (5)

On applique une condition limite périodique, qui consiste à considérer que les spins de la colonne N-1 interagissent avec ceux de la colonne 0, et que ceux de la ligne N-1 interagissent avec ceux de la ligne 0.

On connait une solution exacte du modèle d'ising à deux dimensions, établie par L. Onsager en 1944 ([1]). On donne ici l'aimantation en fonction de la température pour T<T_c :

M (T) = M_{0} (1 - \frac{1}{{s h}^{4} (\frac{J}{2 k_{b} T})})^{1 / 8} (6)

La température de Curie est

T_{c} = \frac{J}{2 k_{b} a r c s h (1)} = 0, 567 \dots J / k_{b} (7)

3. Méthode de Monte-Carlo Metropolis

3.a. Algorithme

On applique l'algorithme de Metropolis au modèle d'Ising à deux dimensions. On commence par introduire des grandeurs réduites (sans dimensions). La constante de couplage est prise égale à 1; les valeurs possibles des spins sont -1 et 1 (au lieu de 1/2).

L'algorithme consiste à construire une chaîne d'états de spins. Un état est obtenu à partir du précédent de la manière suivante :

Sélection d'un spin au hasard et calcul de la variation d'énergie ΔE qui résulterait du changement de signe de ce spin.
Si ΔE<=0, le spin est changé de signe.
Si ΔE>0, un nombre aléatoire x est tiré avec une probabilité uniforme dans l'intervalle [0,1[. Si $x < e^{- β Δ E}$ , le spin est changé. Dans le cas contraire, le spin n'est pas changé.

Pour chaque nouvelle configuration, on calcule le moment magnétique totale M_k. Lorsque P configurations de spin ont été obtenues de cette manière, on calcule une estimation de la valeur moyenne par :

M_{P} = \frac{1}{P} \sum_{k = 1}^{P} M_{k} (8)

Voyons comme est modifiée l'énergie du système lorsqu'on change l'état d'un spin S_i,j. La variation d'énergie ΔE dépend du nombre de spins voisins qui sont de sens opposé au spin S_i,j. Le tableau suivant donne la variation d'énergie en fonction de ce nombre :

\begin{matrix} n & Δ E \\ 0 & 8 \\ 1 & 4 \\ 2 & 0 \\ 3 & - 4 \\ 4 & - 8 \end{matrix} (9)

Dans les trois derniers cas, le basculement du spin est accepté sans condition. Pour les deux premiers cas, il faut utiliser les facteurs de Boltzmann e^-8β et e^-4β.

3.b. Codage des spins

Le nombre n de voisins de sens opposés se détermine plus facilement si les spins sont codés par des valeurs 0 et 1, c'est-à-dire par des bits ([2]). Pour savoir si deux spins sont de sens opposé, il suffit alors d'appliquer l'opérateur logique OU exclusif, noté ⊕ :

S_{i, j} \oplus S_{i, j - 1} (10)

est égal à 1 si un seul des deux spins vaut 1, zéro sinon.

On considère alors les OU exclusifs formés avec les 4 proches voisins :

\begin{matrix} a_{1} = S_{i, j} \oplus S_{i - 1, j} \\ a_{2} = S_{i, j} \oplus S_{i + 1, j} \\ a_{3} = S_{i, j} \oplus S_{i, j - 1} \\ a_{4} = S_{i, j} \oplus S_{i, j + 1} \end{matrix} (11)

On note ∧ l'opération de ET logique et ∨ le OU logique. La présence d'au moins deux spins voisins de sens opposés au spin S_i,j peut être obtenu par le bit suivant :

R_{\geq 2} = [(a_{1} \lor a_{2}) \land (a_{3} \lor a_{4})] \land [(a_{1} \land a_{2}) \lor (a_{3} \land a_{4})] (12)

La présence d'au moins un spin de sens opposé est obtenu par :

R_{\geq 1} = a_{1} \lor a_{2} \lor a_{3} \lor a_{4} (13)

Finalement, on procède dans l'ordre aux tests suivants :

Si $R_{\geq 2}$ vaut 1, le spin est basculé sans condition.
Sinon, si $R_{\geq 1}$ vaut 1, la probabilité d'acceptation e^-4β est utilisée.
Sinon, la probabilité d'acceptation e^-8β est utilisée.

Le premier intérêt de ces opérations logiques sur les bits est la rapidité d'exécution des tests.

3.c. Codage multispin

Un entier codé sur 32 bits permet de stocker et de manipuler en parallèle 32 bits différents. Le codage multispin consiste à effectuer en parallèle 32 simulations, ce qui permet de réduire la variance des calculs statistiques. Chaque spin codé sur 32 bits représente alors 32 simulations parallèles et indépendantes. Les opérations logiques précédentes s'appliquent en effet bit à bit. Il faut cependant trouver un moyen d'appliquer en parallèle la troisième étape de l'algorithme de Metropolis, c'est-à-dire l'acceptation du basculement du spin avec une probabilité e^-βΔE.

La solution consiste à utiliser des entiers à bits aléatoires. Soit par exemple r₁ un entier 32 bits dont tous les bits ont une probabilité e^-4β d'avoir la valeur 1. Idéalement, les différents bits doivent être non corrélés. Si on note R₁ l'entier dont chaque bit prend la valeur 1 lorsque le spin correspondant a un seul voisin de sens opposé, alors le basculement de ce spin est effectué si le spin correspondant de R₁∧ r₁ vaut 1. Le basculement d'un spin se fait avec le OU exclusif. On a donc l'équation suivante pour l'actualisation d'un spin :

S_{i, j} \leftarrow S_{i, j} \oplus [R_{\geq 2} \lor (R_{1} \land r_{1}) \lor (R_{0} \land r_{0})] (14)

Les nombres $R_{\geq 1}$ et $R_{\geq 0}$ sont bien plus faciles à déterminer que R₁ et R₀. En effet, le premier est obtenu par l'équation (13), et le second a tous ses bits égaux à 1. La transformation (14) peut s'exprimer à l'aide de ces nombres ([2]) :

S_{i, j} \leftarrow S_{i, j} \oplus [R_{\geq 2} \lor (R_{\geq 1} \land r'_{1}) \lor r'_{0}] (15)

r'₀ et r'₁ sont deux entiers à bits aléatoires dont les bits ont les probabilités suivantes d'avoir la valeur 1 :

\begin{matrix} p_{0} = e^{- 8 β} & (16) \\ p_{1} = \frac{e^{- 4 β} - e^{- 8 β}}{1 - e^{- 8 β}} & (17) \end{matrix}

Voyons comment générer ces nombres à bits aléatoires, par exemple r'₀. Soit r_A un entier à bits aléatoires dont la probabilité pour ses bits d'être égaux à 1 est p_A< p₀. Soit aussi r_B un entier dont la probabilité pour ses bits d'être égaux à 1 est p_B>p₀. Si l'on choisit aléatoirement entre r_A et r_B avec une probabilité q pour le premier et 1-q pour le second, on obtient un entier dont les bits ont la probabilité qp_A+(1-q)p_B d'avoir la valeur 1. Pour que cette dernière probabilité ait la valeur souhaitée p₀, il suffit de poser :

q = \frac{p_{B} - p_{0}}{p_{B} - p_{A}} (18)

Un nombre entier dont les bits ont la probabilité 1/2 d'avoir la valeur 1 est obtenu avec des algorithmes standard de génération de nombres pseudo-aléatoires. Par exemple, la fonction python random.getrandbits le fait. À partir de ce type de nombre, on peut générer des nombres à bits aléatoires avec des probabilités s'exprimant comme fractions rationnelles simples, comme 2/3 ou 1/4 ([2]). Il faut donc choisir p_A et p_B sous cette forme.

Les probabilités p_A et p_B doivent encadrer p₀ au plus proche pour avoir le minimum de corrélation entre les bits obtenus. Dans le cas du modèle d'Ising, une certaine corrélation entre les bits traités en parallèle est acceptable. Nous pouvons alors choisir p_A=0 (tous les bits de r_A sont toujours nuls) et p_B=1/2 (r_B obtenu par un générateur standard). On a alors q=1-2p₀. Finalement, r'₀ est généré de la manière suivante :

Tirage d'un réel x aléatoirement dans l'intervalle [0,1[ avec une densité de probabilité uniforme.
Si x<2p₀ alors r'₀ est un nombre à bits aléatoires avec une probabilité 1/2 pour ses bits d'avoir la valeur 1.
Sinon, r'₀=0.

3.d. Implémentation

On définit une classe dont le constructeur prend en argument le nombre de spins sur chaque dimension du réseau. Le tableau de spins est constitué d'entiers codés sur 8 bits. On a donc 8 réseaux de NxN spins. Initialement, les spins sont tous alignés.

ising2D.py

import numpy
import random
import math

class Ising2D:
    def __init__(self,N):
        self.N = N
        self.Ns = N*N
        self.spin = numpy.zeros((N,N),dtype=numpy.uint8)
        self.nbits = 8
        self.Nspin = self.Ns*self.nbits

La première fonction affecte une valeur à la température et calcule les facteurs de Botzmann :

    def temperature(self,T):
        beta = 1.0/T
        p0 = math.exp(-8.0*beta)
        p1 = (math.exp(-4.0*beta)-p0)/(1.0-p0)
        self.deuxp0 = p0*2.0
        self.deuxp1 = p1*2.0

La fonction suivante renvoit l'état d'un spin voisin, en utilisant les conditions limites périodiques :

    def voisin(self,i,j):
        ii = i
        if ii<0:
            ii=self.N-1
        elif ii>=self.N:
            ii=0
        jj = j
        if jj<0:
            jj=self.N-1
        elif jj>=self.N:
            jj=0
        return self.spin[jj][ii]

La fonction suivante effectue le pas élémentaire de l'algorithme de Metropolis :

    def metropolis(self):
        i = random.randint(0,self.N-1)
        j = random.randint(0,self.N-1)
        s = self.spin[j][i]
        a1 = s^self.voisin(i-1,j)
        a2 = s^self.voisin(i+1,j)
        a3 = s^self.voisin(i,j-1)
        a4 = s^self.voisin(i,j+1)
        R1 = a1|a2|a3|a4
        R2 = ((a1|a2)&(a3|a4))|((a1&a2)|(a3&a4))
        if random.random() < self.deuxp0:
            r0 = random.getrandbits(self.nbits)
        else:
            r0 = 0
        if random.random() < self.deuxp1:
            r1 = random.getrandbits(self.nbits)
        else:
            r1 = 0
        self.spin[j][i] = s^(R2|(R1&r1)|r0)

La fonction suivante calcule la moyenne des moments magnétiques des 8 réseaux de spins.

    def moment(self):
        m = 0.0
        for i in range(self.N):
            for j in range(self.N):
                s = self.spin[j][i]
                for b in range(self.nbits):
                    m += 2*(s&1)-1
                    s = s >> 1
        return -m*1.0/self.Nspin

La fonction suivante effectue une boucle de calcul. Le nombre d'itérations est fourni en argument. Une itération est constituée d'autant de pas de Metropolis qu'il y a de spins dans chaque réseau. Ainsi à chaque itération tous les spins ont en moyenne été traités une fois. À chaque itération le moment magnétique est calculé et stocké dans un tableau. La valeur moyenne et l'écart type sont aussi calculés et renvoyés.

    def boucle(self,n):
        m = numpy.zeros(n,dtype=numpy.float32)
        for k in range(n):
            for l in range(self.Ns):
                self.metropolis()
            m[k] = self.moment()
        return (m,numpy.mean(m),numpy.std(m))

La fonction suivante renvoit un tableau comportant un des 8 réseaux de spins, pour l'affichage sous forme d'image :

    def couche(self,b):
        mask = numpy.ones((self.N,self.N),dtype=numpy.uint8)*2**b
        return numpy.bitwise_and(self.spin,mask)

4. Résultats

import numpy
import random
import math
from matplotlib.pyplot import *
import ising2D

La température critique est :

Tc = 2.0/(math.asinh(1.0))

print(Tc)
--> 2.269185314213022

On commence par une simulation à T=2.3, une température proche de la température critique, là où la convergence vers l'équilibre est la plus lente.

N = 30
ising = ising2D.Ising2D(N)
ising.temperature(2.3)
(m,M,dM)=ising.boucle(1000)
figure(figsize=(10,6))
plot(m,'r')
xlabel('iteration')
ylabel('M')
axis([0,1000,-1,1])
grid()

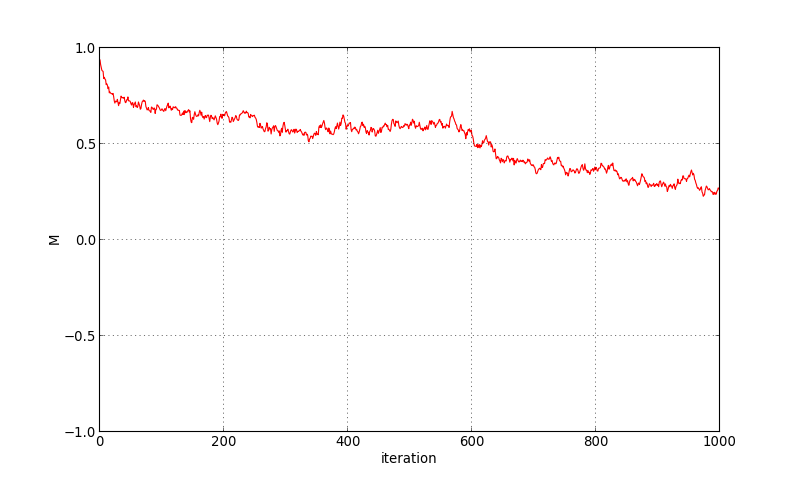figA.pdf

À cette température proche de la température critique, on tend vers un état d'équilibre où le moment magnétique est non nul. Voyons l'état des spins d'une des 8 couches :

figure(figsize=(6,6))
matshow(ising.couche(0))

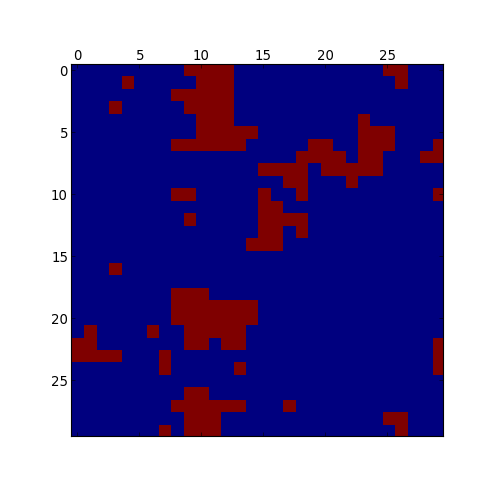figB.pdf

Il se forme des domaines comportant des spins orientés dans le même sens.

Une simulation complète est obtenue en faisant varier la température. Pour chaque température, on calcule le moment magnétique moyen et son écart-type sur un nombre suffisant d'itérations. Pour chaque température, l'état des spins obtenu à la température précédente est utilisé comme condition initiale, ce qui permet de réduire le temps nécessaire pour atteindre l'équilibre. On procède par température croissante, ce qui permet de commencer par un état où les spins sont presques tous alignés. On trace aussi la solution théorique (equation (6)).

 
ising = ising2D.Ising2D(N)
T = numpy.array([1.0,1.5,2.0,2.1,2.2,2.3,2.35,2.4,2.5,2.6,2.7,3.0])
T = numpy.array([2.0,2.1,2.2,2.3,2.4])
listM = numpy.zeros(T.size)
listDM = numpy.zeros(T.size)
for k in range(T.size):
    ising.temperature(T[k])
    (m,M,dM)=ising.boucle(200)
    (m,M,dM)=ising.boucle(1000)
    listM[k] = M
    listDM[k] = dM
figure(figsize=(8,6))
errorbar(T,listM,yerr=listDM,fmt=None)
xlabel("T")
ylabel("M")
grid()
axis([0,4.0,-1.0,1.0])
temp = numpy.arange(1.0,3.0,0.01)
moment = numpy.zeros(temp.size) 
for i in range(temp.size):
    if temp[i] >= Tc:
        moment[i] = 0.0
    else:
        moment[i]= math.pow((1.0-1.0/math.pow(math.sinh(2.0/temp[i]),4)),1/8.0)
plot(temp,moment,color='r')

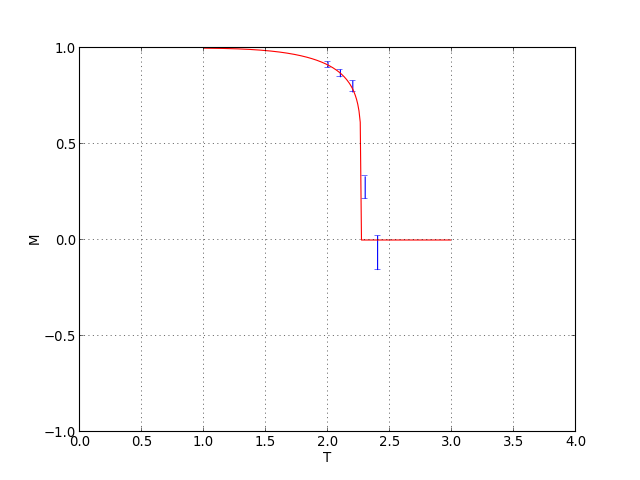figC.pdf

Modèle d'Ising à deux dimensions