Chaîne d'oscillateurs linéaires à bords fixes

1. Équations du mouvement

La chaîne d'oscillateurs est constituée de N points de masse m reliés par des ressorts identiques, de raideur a. Le déplacement du point k=1..N par rapport à sa position d'équilibre est noté q_k.

Pour un point autre que les bords (1<k<N), l'équation du mouvement est :

$$\frac{d^2{q}_k}{d{t}^2}=-{\omega }_0^2(2q_k-q_{k-1}-q_{k+1})\text{(1)}$$

avec :

$${\omega }_0=\sqrt{\frac{a}{m}}\text{(2)}$$

Les bords sont contitués d'un point fixe (points d'indice 0 et N+1), ce qui donne les deux équations différentielles :

$$\begin{array}{ccc}\hfill & \frac{d^2{q}_1}{d{t}^2}=-{\omega }_0^2(2q_1-q_2)\hfill & \hfill \text{(3)}\\ \hfill & \frac{d^2{q}_N}{d{t}^2}=-{\omega }_0^2(2q_N-q_{N-1})\hfill & \hfill \text{(4)}\end{array}$$

Si on note q le vecteur colonne des N déplacements, le système différentiel (équations 1, 3 et 4) s'écrit :

$$\begin{array}{cc}\hfill \frac{d^{2}q}{d{t}^2}=-{\omega }_0^{2}Vq& \hfill \text{(5)}\end{array}$$

où V est une matrice carrée (symétrique) définie par :

$$\begin{array}{ccc}\hfill & v_{1,1}=2,v_{1,2}=-1\hfill & \hfill \text{(6)}\\ \hfill (1<k<N)& v_{k,k-1}=-1,v_{k,k}=2,v_{k,k+1}=-1\hfill & \hfill \text{(7)}\\ \hfill & v_{N,N-1}=-1,v_{N,N}=2\hfill & \hfill \text{(8)}\end{array}$$

On définit les moments p_k comme les dérivées par rapport au temps des déplacements q_k. L'hamiltonien du système (énergie par unité de masse) s'écrit :

$$\begin{array}{ccc}\hfill H(p,q)& =\frac{1}{2}{p}^{T}p+\frac{1}{2}{\omega }_0^2{q}^{T}Vq\hfill & \hfill \text{(9)}\\ \hfill & =\frac{1}{2}\sum _k{p}_k^2+\frac{1}{2}{\omega }_0^2\sum _k\sum _l{q}_k{v}_{k,l}{q}_l\hfill & \hfill \text{(10)}\end{array}$$

Les équations du mouvement s'écrivent :

$$\begin{array}{ccc}\hfill & \frac{dq}{dt}=+\frac{\partial H}{\partial p}\hfill & \hfill \text{(11)}\\ \hfill & \frac{dp}{dt}=-\frac{\partial H}{\partial q}\hfill & \hfill \text{(12)}\end{array}$$

2. Approximation des milieux continus

Soit d la distance à l'équilibre entre deux points voisins. La longueur de la chaîne est L=Nd. L'approximation des milieux continus, valable pour N grand sur une échelle grande devant d, consiste à définir le déplacement des masses par une fonction continue u(x). L'équation (1) correspond à la discrétisation de l'équation différentielle suivante :

$$\frac{{\partial }^{2}u}{{\partial }^{2}t}={\omega }_0^2{d}^2\frac{{\partial }^{2}u}{\partial x^2}\text{(13)}$$

Il s'agit de l'équation des ondes (milieu non dispersif), avec une célérité :

$$c={\omega }_{0}d\text{(14)}$$

Les conditions aux limites du problème étudié sont :

$$\begin{array}{ccc}\hfill & u(0,t)=0\hfill & \hfill \text{(15)}\\ \hfill & u(L,t)=0\hfill & \hfill \text{(16)}\end{array}$$

Les modes propres du problème continu sont les solutions de la forme :

$$u(x,t)=U\left(x\right)e^{-i\omega t}\text{(17)}$$

La solution est :

$$U\left(x\right)=U_{0}sin\left(Kx\right)\text{(18)}$$

Les conditions limites imposent :

$$KNd=m\pi \text{(19)}$$

où m est un entier strictement positif. La pulsation du mode propre d'indice m est :

$${\omega }_m={\omega }_0\pi \frac{m}{N}\text{(20)}$$

La longueur d'onde du mode d'indice m est :

$$l_m=\frac{2Nd}{m}\text{(21)}$$

Les modes de basse fréquence, pour lesquels m est petit devant N, devraient se retrouver dans le problème discret.

3. Modes propres

Les modes propres sont les solutions de l'équation (5) de la forme :

$$q=a{e}^{-i\omega t}\text{(22)}$$

où a est un vecteur colonne à N éléments. Dans un mode propre, tous les points de la chaîne oscillent à la même pulsation.

En reportant dans l'équation différentielle, on obtient :

$$Va=\lambda a\text{(23)}$$

avec :

$$\lambda =\frac{{\omega }^2}{{\omega }_0^2}\text{(24)}$$

Il s'agit donc de déterminer les valeurs propres et les vecteurs propres de la matrice V. Celle-ci est réelle et symétrique; ces valeurs propres sont donc réelles et ses vecteurs propres sont orthogonaux.

Par analogie avec le problème continu traité ci-dessus, on recherche les vecteurs propres sous la forme :

$$a_k=sin\left(\alpha k\right)\text{(25)}$$

En reportant cette solution supposée dans (23), on obtient :

$$\begin{array}{ccc}\hfill & (2-2cos\alpha -\lambda )sin\left(\alpha k\right)=0(1\le k\le N-1)\hfill & \hfill \text{(26)}\\ \hfill & (2-2cos\alpha -\lambda )sin\left(N\alpha \right)=-sin\left((N+1)\alpha \right)\hfill & \hfill \text{(27)}\end{array}$$

On pose alors :

$$\begin{array}{ccc}\hfill & (N+1)\alpha =m\pi \left(1\le m\le N\right)\hfill & \hfill \text{(28)}\\ \hfill & \lambda =2(1-cos\alpha )=4{sin}^2\frac{\alpha }{2}\hfill & \hfill \text{(29)}\end{array}$$

La matrice V a donc N valeurs propres distinctes :

$${\lambda }_m=4{sin}^2\left(\frac{m\pi }{2(N+1)}\right)\text{(30)}$$

Le vecteur propre correspondant à la valeur propre d'indice m est :

$$a_{k,m}=\sqrt{\frac{2}{N+1}}sin\left(\frac{\pi mk}{N+1}\right)\text{(31)}$$

La constante multiplicative a été ajoutée pour obtenir des vecteurs propres normés.

Les pulsations propres sont :

$${\omega }_m=2{\omega }_{0}sin\left(\frac{m\pi }{2(N+1)}\right)\text{(32)}$$

On retrouve les pulsations propres du modèle continu lorsque N est grand et m petit devant N. Pour les modes dont la longueur d'onde est proche de d (m proche de N), la pulsation propre est très différente de celle prévue par le modèle continu, bien que les vecteurs propres aient une forme similaire.

4. Coordonnées normales

5. Exemple

L'exemple suivant (Mathematica) montre comment générer les déplacements à partir des coordonnées normales.

La fonction suivante calcule les pulsations propres :

omega[n_,m_]:=4*Pi*Sin[m*Pi/(2*(n+1))];

La solution est définie par la liste des constantes C_m. La fonction suivante génère les coordonnées normales :

xi[c_,t_]:=Module[{m},
            n=Length[c];
            Return[Table[c[[m]]*Cos[omega[n,m]*t],{m,1,n}]];
]

La transformée en sinus discret définie plus haut est calculée avec la fonction FourierDST (type 1). La fonction suivante calcule les déplacements :

p[c_,t_]:=FourierDST[xi[c,t],1];

Voyons par exemple une chaîne de 10 masses dans le mode fondamental :

c={1,0,0,0,0,0,0,0,0,0}
n=Length[c];
w1=omega[n,1];
T1=2*Pi/w1;

ListPlot[{p[c,0],p[c,T1*0.25],p[c,T1*0.5],p[c,T1*0.75]},PlotRange->{{0,n+1},{-1,1}},AxesLabel->{"k","pk"}]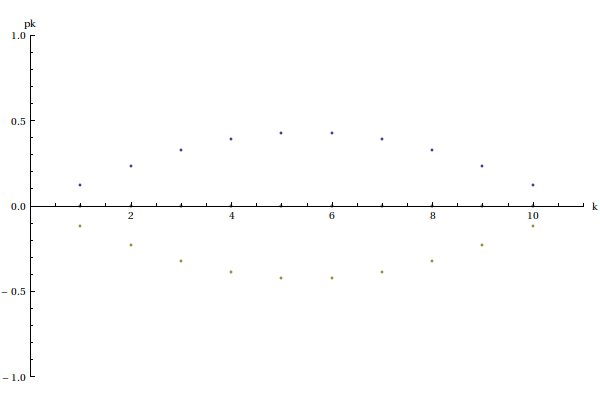

plot1.pdf

La même chaîne avec plusieurs modes :

c={1,0.8,0.7,0.5,0,0.3,0,0.1,0,0}

ListPlot[Table[p[c,T1*t/100],{t,0,10}],PlotRange->{{0,n+1},{-1,1}},AxesLabel->{"k","pk"}]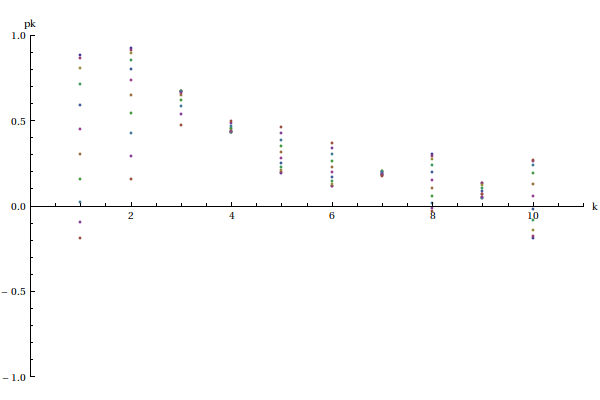

plot2.pdf