Système solaire : orbites képlériennes

2.a. L'orbite dans son plan

Lorsque la planète est soumise seulement à la force centrale attractive du Soleil, son mouvement se fait dans un plan. On commence donc par définir l'orbite dans son plan.

Le Soleil se trouve au foyer F de l'ellipse. Le repère Fxy est dans le plan de l'orbite, l'axe Fx pointant vers le périhélie. La planète se trouve au point M, repéré par ses coordonnées cartésiennes (x,y). Ses coordonnées polaires sont (r,f). L'angle f est l'anomalie vraie. L'équation polaire de la trajectoire s'écrit :

La distance entre le centre C de l'ellipse et le périhélie P est le demi-grand axe, noté a. La distance entre le centre de l'ellipse et son foyer F est CF=ae, où e est l'excentricité. Le paramètre de l'ellipse est p=FP=a(1-e). Le demi petit-axe b=CB est obtenu en utilisant la propriété FB=a.

L'équation $\mathrm{(1)}$ donne la trajectoire mais ne dit rien sur son parcours dans le temps. Il faut pour cela utiliser la loi des aires :

où T est la période de révolution. Bien qu'il soit possible d'intégrer numériquement cette équation différentielle pour obtenir l'anomalie vraie à l'instant t, il existe une méthode plus simple (développée bien avant l'invention des calculateurs électroniques) qui repose sur une construction géométrique donnée sur la figure ci-dessus.

On considère le cercle de rayon a qui circonscrit l'ellipse, et le point H, intersection de ce cercle avec la droite perpendiculaire au grand-axe et passant par M. L'angle E est l'anomalie excentrique. Les coordonnées de M s'expriment en fonction de cet angle :

L'anomalie excentrique s'exprime en fonction du temps par l'équation implicite suivante, appelée équation de Kepler :

$\tau$ est l'instant de passage de la planète au périhélie. n est le mouvement moyen, relié à la période par n=2π/T.

On définit aussi l'anomalie moyenne :

Si l'on souhaite simplement tracer l'ellipse complète, on échantillonne E dans l'intervalle [0,2π] puis on calcule les coordonnées. Pour obtenir le mouvement de la planète au cours du temps, ou sa position à un instant donné, il faut résoudre l'équation de Kepler.

2.b. Résolution de l'équation de Kepler

Pour obtenir l'anamolie excentrique E à l'instant t, on calcule tout d'abord l'anomalie moyenne M. Il faut ensuite résoudre l'équation de Kepler $\mathrm{(5)}$, une équation non linéaire qui ne peut être résolue que de manière approchée.

Parmi plusieurs méthodes de résolution, on peut utiliser la méthode de Newton-Raphson. Pour cela, on définit la fonction suivante :

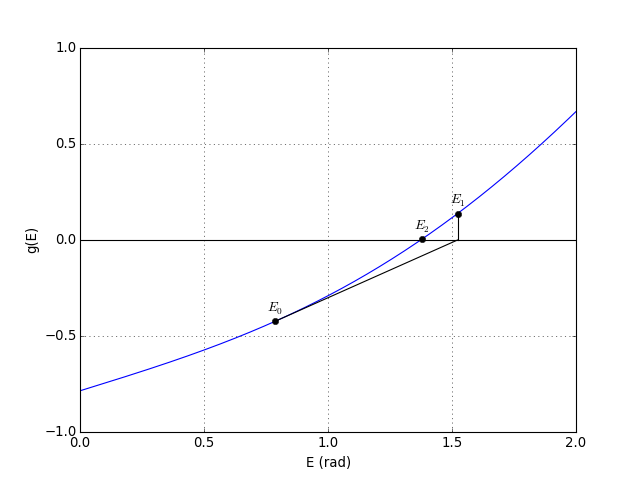
dont il s'agit de trouver la racine. Une première estimation de l'anomalie excentrique est $E_0=M$. La figure suivante montre le tracé de g(E) dans le cas M=π/4, pour une excentricité e=0,6 :

La méthode de Newton-Raphson consiste à calculer une suite d'approximations E_i qui converge vers la solution. Pour obtenir E_i+1 à partir de E_i, on calcule la dérivée $g\text{'}\left(E_i\right)$ et on trace l'intersection de la tangente en E_i avec l'axe des abscisses. La nouvelle estimation est donc donnée par :

En appliquant de manière récurrente cette relation, on obtient rapidement une estimation E_i très proche de la solution. Une tolérance ε est choisie. Lorsque |E_i+1-E_i|<ε, l'itération est stoppée.

2.c. L'orbite dans l'espace

Il faut à présent placer l'orbite de la planète dans l'espace. On utilise pour cela un repère héliocentrique FXYZ. Le plan de référence FXY est le plan orbital de la Terre (appelé aussi plan de l'écliptique) à la date J2000, l'axe X pointant vers la position de la Terre à l'équinoxe de printemps (point vernal) à la date J2000. La date J2000 est le 1 janvier 2000 (12h00).

L'orbite d'une planète est définie par les éléments suivants :

• Le demi-grand axe a.
• L'excentricité e.
• L'inclinaison I de l'orbite par rapport au plan de référence FXY.
• La longitude du nœud ascendant Ω.
• L'argument du périhélie ω.

Les trois derniers permettent de placer l'orbite dans le repère FXYZ.

Le nœud ascendant est le point N d'intersection de l'orbite avec le plan de référence FXY, lorsque la planète le franchit vers le nord (Z croissant).

On utilise aussi la longitude du périhélie, définie par la somme des deux angles non coplanaires suivante :

et la longitude moyenne définie par :

Remarque : les angles dénommés longitude sont tous définis avec l'axe FX pour référence, correspondant à l'équinoxe de printemps à la date J2000.

Un changement de repère permet de calculer les coordonnées de la planète (X,Y,Z) à partir de (x,y). Il s'exprime sous forme matricielle :

où R₁,R₂,R₃ sont trois matrices de rotation définies par :

2.d. Date julienne

Le temps est mesuré en secondes. On utilise aussi le jour julien (86400 s), l'année julienne (365,25 jours) et le siècle julien (36525 jours).

La date julienne (DJ) est le nombre de jours juliens depuis le 1er janvier de l'an 4713 avant J.C. à 12 h. La date julienne se calcule à partir de la date (A,M,J) de la manière suivante.

On calcule tout d'abord a et m définis par :

puis la quantité b défini par :

La fonction int(x) donne le plus grand entier inférieur ou égal à x.

La date julienne est alors donnée par la formule :

où UT est l'heure universelle.

La date julienne de J2000 est 2451545.

2.e. Utilisation des tables d'éléments

Le temps utilisé dans les tables d'éléments est le nombre de siècles juliens depuis la date J2000. Il se calcule à partir de la date julienne par :

Ce temps est bien sûr négatif pour une date antérieure à J2000.

Voici la table que nous utiliserons (obtenue au Jet Propulsion Laboratory) :

               a              e               I                L            long.peri.      long.node.
           AU, AU/Cy     rad, rad/Cy     deg, deg/Cy      deg, deg/Cy      deg, deg/Cy     deg, deg/Cy
-----------------------------------------------------------------------------------------------------------
Mercury   0.38709927      0.20563593      7.00497902      252.25032350     77.45779628     48.33076593
          0.00000037      0.00001906     -0.00594749   149472.67411175      0.16047689     -0.12534081
Venus     0.72333566      0.00677672      3.39467605      181.97909950    131.60246718     76.67984255
          0.00000390     -0.00004107     -0.00078890    58517.81538729      0.00268329     -0.27769418
Earth     1.00000261      0.01671123     -0.00001531      100.46457166    102.93768193      0.0
          0.00000562     -0.00004392     -0.01294668    35999.37244981      0.32327364      0.0
Mars      1.52371034      0.09339410      1.84969142       -4.55343205    -23.94362959     49.55953891
          0.00001847      0.00007882     -0.00813131    19140.30268499      0.44441088     -0.29257343
Jupiter   5.20288700      0.04838624      1.30439695       34.39644051     14.72847983    100.47390909
         -0.00011607     -0.00013253     -0.00183714     3034.74612775      0.21252668      0.20469106
Saturn    9.53667594      0.05386179      2.48599187       49.95424423     92.59887831    113.66242448
         -0.00125060     -0.00050991      0.00193609     1222.49362201     -0.41897216     -0.28867794
Uranus   19.18916464      0.04725744      0.77263783      313.23810451    170.95427630     74.01692503
         -0.00196176     -0.00004397     -0.00242939      428.48202785      0.40805281      0.04240589
Neptune  30.06992276      0.00859048      1.77004347      -55.12002969     44.96476227    131.78422574
          0.00026291      0.00005105      0.00035372      218.45945325     -0.32241464     -0.00508664
Pluto    39.48211675      0.24882730     17.14001206      238.92903833    224.06891629    110.30393684
         -0.00031596      0.00005170      0.00004818      145.20780515     -0.04062942     -0.01183482
                 

Cette table est valable entre les années 1800 et 2050.

Pour chaque planète, la première ligne donne le demi grand-axe a (en unité astronomique), l'excentricité, l'inclinaison de l'orbite I, la longitude moyenne L, la longitude du périhélie $\overline{\omega }$, la longitude du nœud ascendant Ω. Les angles sont donnés en degrés; ils devront être convertis en radian pour les calculs trigonométriques.

Toutes ces valeurs sont données à la date J2000. Elles varient lentement dans le temps, à cause des perturbations mutuelles entre planètes. Pour chaque planète, la seconde ligne donne les taux de variation par siècle. La longitude moyenne L varie rapidement en raison du mouvement orbital (variation de M avec le temps). Par exemple pour Mercure, la longitude moyenne s'écrit en fonction du temps t (en siècles juliens depuis J2000) :

L'anomalie moyenne se déduit de la longitude moyenne par la relation :

4.a. Trajectoires des planètes

Les données et les fonctions sont réunies dans une classe intitulée Kepler. Le constructeur de la classe effectue la lecture des fichiers de données (pour les planètes et les comètes) et remplit des dictionnaires. Voici les différents dictionnaires :

• a et a : demi grand axe (UA) et variation par siècle.
• e et de : excentricité et variation par siècle.
• I et dI : inclinaison de l'orbite (en degrés) et variation par siècle.
• L et dL : longitude moyenne (degrés) et variation par siècle.
• Lperi et dLperi : longitude du périhélie (degrés) et variation par siècle.
• Lnode et dLnode : longitude du nœud ascendant (degrés) et variation par siècle.

Pour accéder par exemple au demi grand-axe de Mercure à la date J2000, on écrira : self.a["Mercury"].

Les dictionnaires utilisés pour le calcul des trajectoires de comètes sont :

• masse : masse de la planète exprimée en masse solaire.
• comete_dj : date julienne des données de la comète.
• comete_Yi : condition initiale (positions et vitesses) pour la comète.
• comete_e : excentricité.
• comete_nom : nom du découvreur de la comète.

Les clefs pour les deux derniers dictionnaires sont les codes des comètes, que l'on peut consulter dans le fichier cometes.txt.

Les fichiers des données sont elementsPlanetes.txt et ELTNOM.TXT.

Voici la classe avec le constructeur complet et les entêtes des différentes fonctions :

import numpy
from matplotlib.pyplot import *
import re
import os
from scipy.integrate import odeint

class Kepler:
    def __init__(self):
        self.epsilon = 1e-6
        f=open("elementsPlanetes.txt","r")
        self.a={}
        self.e={}
        self.I={}
        self.L={}
        self.Lperi={}
        self.Lnode={}
        self.da={}
        self.de={}
        self.dI={}
        self.dL={}
        self.dLperi={}
        self.dLnode={}
        lines = f.readlines()
        n=3
        for p in range(9):
            ligne1 = re.split("[\s]+",lines[n])
            ligne2 = re.split("[\s]+",lines[n+1])
            n += 2
            nom = ligne1[0]
            print(nom)
            self.a[nom] = float(ligne1[1])
            self.e[nom] = float(ligne1[2])
            self.I[nom] = float(ligne1[3])
            self.L[nom] = float(ligne1[4])
            self.Lperi[nom] = float(ligne1[5])
            self.Lnode[nom] = float(ligne1[6])
            self.da[nom] = float(ligne2[1])
            self.de[nom] = float(ligne2[2])
            self.dI[nom] = float(ligne2[3])
            self.dL[nom] = float(ligne2[4])
            self.dLperi[nom] = float(ligne2[5])
            self.dLnode[nom] = float(ligne2[6])
            
        f.close()
        self.lettre = {'Mercury':'M','Venus':'V','Earth':'T','Mars':'Ma','Jupiter':'J','Saturn':'S','Uranus':'U','Neptune':'N','Pluto':'P'}
        self.deg2rad = numpy.pi/180
        self.rad2deg = 180/numpy.pi

        self.masse={}
        self.masse["Mercury"] = 1.0/6023600.0
        self.masse["Venus"] = 1.0/408523.5
        self.masse["Earth"] = 1.0/328900.5
        self.masse["Mars"] = 1.0/3098710.0
        self.masse["Jupiter"] = 1.0/1047.355
        self.masse["Saturn"] = 1.0/3498.5
        self.masse["Uranus"] = 1.0/22869.0
        self.masse["Neptune"] = 1.0/19314.0
        k = 0.01720209895 # constante de Gauss 
        self.k2 = k*k

        # cometes
        self.comete_dj={}
        self.comete_Yi={}
        self.comete_e={}
        self.comete_nom={}
        f = open("ELTNOM.TXT","r")
        #g = open("cometes.txt","w")
        lines = f.readlines()
        for n in range(0,len(lines),9):
            ligne1 = re.split("[\s]+",lines[n])
            ligne2 = re.split("[\s]+",lines[n+1])
            ligne3 = re.split("[\s]+",lines[n+2])
            ligne4 = re.split("[\s]+",lines[n+3])
            ligne6 = re.split("[\s]+",lines[n+5])
            code =lines[n][17:25]
            code=code.replace(" ","")
            dj = float(ligne2[0])
            self.comete_dj[code] = dj
            self.comete_Yi[code] = [float(ligne3[0]),float(ligne3[1]),float(ligne3[2]),float(ligne4[0]),float(ligne4[1]),float(ligne4[2])]
            nom = lines[n][27:56]
            nom=nom.replace(" ","")
            e = float(ligne6[2])
            self.comete_nom[code] = nom
            self.comete_e[code] = e
            #g.write("%s\t%s\t DJ=%0.1f\t e=%0.3f\n"%(code,nom,dj,e))
        #g.close()
        f.close()
    def dateJulienne(self,annee,mois,jour,heure):
        pass
    def t(self,DJ):
        pass
    def equationKepler(self,e,M,epsilon):
        pass
    def position_xy(self,planete,t):
        pass
    def ellipse_xy(self,planete,t,N=1000):
        pass
    def xy_XYZ(self,planete,t,x,y):
        pass
    def position_XYZ(self,planete,t):
        pass
    def ellipse_XYZ(self,planete,t,N=1000):
        pass
              

La fonction dateJulienne(self,annee,mois,jour,heure) renvoit la date julienne (en jours) pour une date et une heure données.

La fonction t(self,DJ) renvoit, pour une date julienne donnée, le temps écoulé depuis la date J2000, exprimé en siècles.

La fonction equationKepler(self,e,M,epsilon) résout l'équation de Kepler pour une excentricité, une anomalie moyenne et une tolérance donnés. Elle renvoit l'anomalie excentrique E.

La fonction position_xy(self,planete,t) calcule les coordonnées (x,y) d'une planète dans son plan orbital. Le nom et le temps (siècles depuis J2000) sont donnés.

La fonction ellipse_xy(self,planete,t,N=1000) renvoit la trajectoire elliptique d'une planète calculée à partir des éléments à un instant donné, sous la forme d'un n-uplet (x,y). Le nombre de points est N, égal à 1000 par défaut.

La fonction xy_XYZ(self,planete,t,x,y) effectue la conversion des coordonnées (x,y) en coordonnées (X,Y,Z) dans le repère héliocentrique J2000.

La fonction position_XYZ(self,planete,t) renvoit la position d'une planète à un instant donné.

La fonction ellipse_XYZ(self,planete,t,N=1000) renvoit la trajectoire elliptique d'une planète calculée à partir des éléments à un instant donné, sous la forme d'un n-uplet (X,Y,Z). Le nombre de points est N, égal à 1000 par défaut.

import numpy
from matplotlib.pyplot import *
import re
import os
from scipy.integrate import odeint

class Kepler:
    def __init__(self):
        self.epsilon = 1e-6
        f=open("elementsPlanetes.txt","r")
        self.a={}
        self.e={}
        self.I={}
        self.L={}
        self.Lperi={}
        self.Lnode={}
        self.da={}
        self.de={}
        self.dI={}
        self.dL={}
        self.dLperi={}
        self.dLnode={}
        lines = f.readlines()
        n=3
        for p in range(9):
            ligne1 = re.split("[\s]+",lines[n])
            ligne2 = re.split("[\s]+",lines[n+1])
            n += 2
            nom = ligne1[0]
            print(nom)
            self.a[nom] = float(ligne1[1])
            self.e[nom] = float(ligne1[2])
            self.I[nom] = float(ligne1[3])
            self.L[nom] = float(ligne1[4])
            self.Lperi[nom] = float(ligne1[5])
            self.Lnode[nom] = float(ligne1[6])
            self.da[nom] = float(ligne2[1])
            self.de[nom] = float(ligne2[2])
            self.dI[nom] = float(ligne2[3])
            self.dL[nom] = float(ligne2[4])
            self.dLperi[nom] = float(ligne2[5])
            self.dLnode[nom] = float(ligne2[6])
            
        f.close()
        self.lettre = {'Mercury':'M','Venus':'V','Earth':'T','Mars':'Ma','Jupiter':'J','Saturn':'S','Uranus':'U','Neptune':'N','Pluto':'P'}
        self.deg2rad = numpy.pi/180
        self.rad2deg = 180/numpy.pi

        self.masse={}
        self.masse["Mercury"] = 1.0/6023600.0
        self.masse["Venus"] = 1.0/408523.5
        self.masse["Earth"] = 1.0/328900.5
        self.masse["Mars"] = 1.0/3098710.0
        self.masse["Jupiter"] = 1.0/1047.355
        self.masse["Saturn"] = 1.0/3498.5
        self.masse["Uranus"] = 1.0/22869.0
        self.masse["Neptune"] = 1.0/19314.0
        k = 0.01720209895 # constante de Gauss 
        self.k2 = k*k

        # cometes
        self.comete_dj={}
        self.comete_Yi={}
        self.comete_e={}
        self.comete_nom={}
        f = open("ELTNOM.TXT","r")
        #g = open("cometes.txt","w")
        lines = f.readlines()
        for n in range(0,len(lines),9):
            ligne1 = re.split("[\s]+",lines[n])
            ligne2 = re.split("[\s]+",lines[n+1])
            ligne3 = re.split("[\s]+",lines[n+2])
            ligne4 = re.split("[\s]+",lines[n+3])
            ligne6 = re.split("[\s]+",lines[n+5])
            code =lines[n][17:25]
            code=code.replace(" ","")
            dj = float(ligne2[0])
            self.comete_dj[code] = dj
            self.comete_Yi[code] = [float(ligne3[0]),float(ligne3[1]),float(ligne3[2]),float(ligne4[0]),float(ligne4[1]),float(ligne4[2])]
            nom = lines[n][27:56]
            nom=nom.replace(" ","")
            e = float(ligne6[2])
            self.comete_nom[code] = nom
            self.comete_e[code] = e
            #g.write("%s\t%s\t DJ=%0.1f\t e=%0.3f\n"%(code,nom,dj,e))
        #g.close()
        f.close()
        
    def dateJulienne(self,annee,mois,jour,heure):
        if mois<=2:
            a=annee-1
            m=mois+12
        else:
            a=annee
            m=mois
        b=int(a/400)-int(a/100)
        DJ = int(365.25*a)+int(30.6001*(m+1))+b+1720996.5+jour+heure*1.0/24
        return DJ

    def t(self,DJ):
        return (DJ-2451545)*1.0/36525

    def equationKepler(self,e,M,epsilon):
        E = M
        delta = 1e6
        while delta > epsilon:
            new_E = E-(E-e*numpy.sin(E)-M)/(1-e*numpy.cos(E))
            delta = abs(new_E-E)
            E = new_E
        return E

    def position_xy(self,planete,t):
        L = self.L[planete]+self.dL[planete]*t
        Lperi = self.Lperi[planete]+ self.dLperi[planete]*t
        M = L-Lperi
        e = self.e[planete]+self.de[planete]
        E = self.equationKepler(e,M*self.deg2rad,self.epsilon)
        a = self.a[planete]+self.da[planete]*t
        x = a*(numpy.cos(E)-e)
        y = a*numpy.sqrt(1-e*e)*numpy.sin(E)
        return (x,y)

    def ellipse_xy(self,planete,t,N=1000):
        E = numpy.linspace(0,2*numpy.pi,N)
        a = self.a[planete]+self.da[planete]*t
        e = self.e[planete]+self.de[planete]
        x = a*(numpy.cos(E)-e)
        y = a*numpy.sqrt(1-e*e)*numpy.sin(E)
        return (x,y)

    def xy_XYZ(self,planete,t,x,y):
        I = self.I[planete]+self.dI[planete]*t
        Lperi = self.Lperi[planete]+self.dLperi[planete]*t
        Omega = self.Lnode[planete]+self.dLnode[planete]*t
        I *= self.deg2rad
        Omega *= self.deg2rad
        Lperi *= self.deg2rad
        omega = Lperi-Omega
        cos_omega = numpy.cos(omega)
        sin_omega = numpy.sin(omega)
        R1 = numpy.array([[cos_omega,-sin_omega,0],[sin_omega,cos_omega,0],[0,0,1]])
        cos_I = numpy.cos(I)
        sin_I = numpy.sin(I)
        R2 = numpy.array([[1,0,0],[0,cos_I,-sin_I],[0,sin_I,cos_I]])
        cos_Omega = numpy.cos(Omega)
        sin_Omega = numpy.sin(Omega)
        R3 = numpy.array([[cos_Omega,-sin_Omega,0],[sin_Omega,cos_Omega,0],[0,0,1]])
        R = numpy.dot(R3,numpy.dot(R2,R1))
        xyz = numpy.array([x,y,0])
        XYZ = numpy.dot(R,xyz)
        return XYZ

    def position_XYZ(self,planete,t):
        (x,y) = self.position_xy(planete,t)
        return self.xy_XYZ(planete,t,x,y)

    def ellipse_XYZ(self,planete,t,N=1000):
        (x,y) = self.ellipse_xy(planete,t,N)
        X = numpy.zeros(N)
        Y = numpy.zeros(N)
        Z = numpy.zeros(N)
        for k in range(N):
            XYZ = self.xy_XYZ(planete,t,x[k],y[k])
            X[k] = XYZ[0]
            Y[k] = XYZ[1]
            Z[k] = XYZ[2]
        return (X,Y,Z)

def systeme_comete(Y,dj,self,planetes):
    rs3 = numpy.power(Y[0]*Y[0]+Y[1]*Y[1]+Y[2]*Y[2],1.5)
    Fx = -Y[0]/rs3
    Fy = -Y[1]/rs3
    Fz = -Y[2]/rs3
    for planete in planetes:
        pos = self.position_XYZ(planete,self.t(dj))
        x = Y[0]-pos[0]
        y = Y[1]-pos[1]
        z = Y[2]-pos[2]
        r3 = numpy.power(x*x+y*y+z*z,1.5)
        Fx -= self.masse[planete]*x/r3
        Fy -= self.masse[planete]*y/r3
        Fz -= self.masse[planete]*z/r3
    return numpy.array([Y[3],Y[4],Y[5],Fx*self.k2,Fy*self.k2,Fz*self.k2])

                 

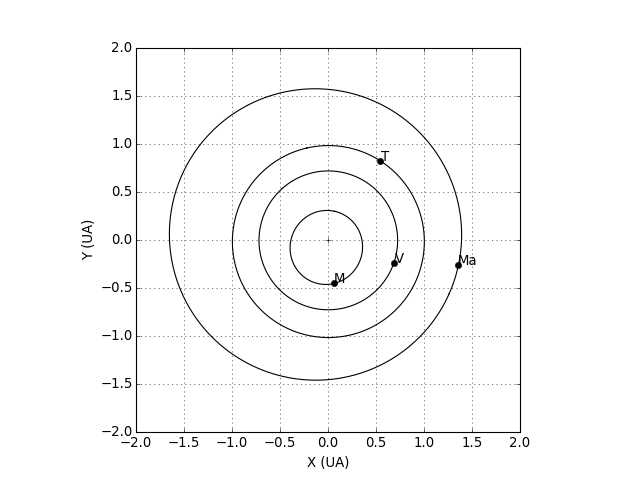
Voici un exemple avec les orbites des planètes internes :

kepler = Kepler()
t = kepler.t(kepler.dateJulienne(2016,11,19,0))
figure()
plot([0],[0],"k+")
for planete in ["Mercury","Venus","Earth","Mars"]:
    (X,Y,Z) = kepler.ellipse_XYZ(planete,t)
    plot(X,Y,"k-")
    (X,Y,Z) = kepler.position_XYZ(planete,t)
    plot([X],[Y],"ko")
    text(X+0.01,Y,kepler.lettre[planete])
    
axes().set_aspect('equal')
xlabel("X (UA)")
ylabel("Y (UA)")
axis([-2,2,-2,2])
grid()
                 

Pour évaluer la précision de ces positions, on pourra calculer et afficher les positions de la planète Mars pour 10 dates espacées de 1 jours, à partir de la date courante. Le service d'éphémérides de l'IMCCE permet de calculer ces positions, à partir de théories beaucoup plus précises que le modèle képlérien utilisé ici. On pourra ainsi évaluer la précision relative de nos résultats.

4.b. Trajectoire d'une comète

On doit tout d'abord définir le système différentiel sous forme d'une fonction de la forme :

def systeme_comete(Y,dj,self,planetes):
    pass
                        

Le tableau Y contient les coordonnées de la comète et les dérivées par rapport au temps. dj contient le temps sous forme de date julienne (en jours). Cette fonction sera transmise à la fonction scipy.integrate.odeint. Elle ne fait pas partie de la classe Kepler, mais elle doit néanmoins accéder aux données et fonctions de cette classe, c'est pourquoi nous avons ajouté un argument self en troisième position, qui servira à transmettre l'objet de la classe Kepler. L'argument planetes contient la liste des planètes qu'il faut prendre en compte pour le calcul de l'accélération de la comète.

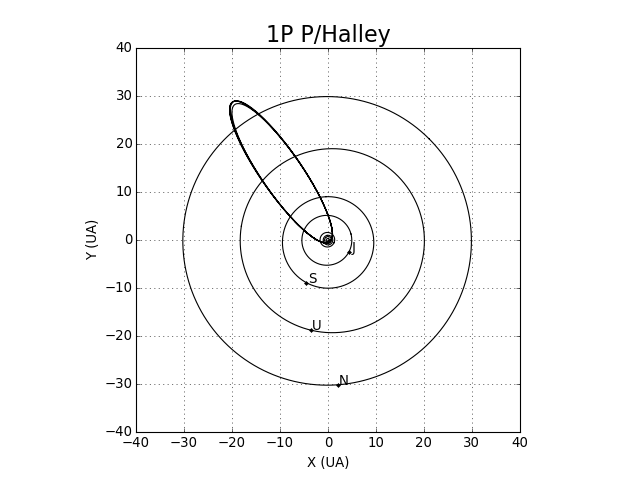
Voici par exemple le calcul de la trajectoire de la comète de Halley sur une durée de 300 ans :

code="1P"
DJ = kepler.comete_dj[code]
Yi = kepler.comete_Yi[code]
t = kepler.t(DJ)
duree=300
temps = numpy.linspace(DJ,DJ+365*duree,2000)
planetes=["Mercury","Venus","Earth","Mars","Jupiter","Saturn","Uranus","Neptune"]
Y = odeint(systeme_comete,Yi,temps,args=(kepler,planetes),atol=1e-12,rtol=1e-6)


figure()
plot([0],[0],"k+")
plot(Y[:,0],Y[:,1],"k-")

for planete in ["Mercury","Venus","Earth","Mars","Jupiter","Saturn","Uranus","Neptune"]:
    (X,Y,Z) = kepler.ellipse_XYZ(planete,t)
    plot(X,Y,"k-")
    (X,Y,Z) = kepler.position_XYZ(planete,t)
    if planete in ["Jupiter","Saturn","Uranus","Neptune"]:
        plot([X],[Y],"k.")
        text(X+0.5,Y,"%s"%kepler.lettre[planete])
    
axes().set_aspect('equal')
xlabel("X (UA)")
ylabel("Y (UA)")
title("%s %s"%(code,kepler.comete_nom[code]),fontsize=20)

axis([-40,40,-40,40])
grid()