Collision sans frottement entre deux disques

1. Introduction

On considère deux disques en mouvement sans frottement sur un plan horizontal (problème bi-dimentionnel). La collision entre les disques se fait sans frottement, avec un coefficient de restitution variable. Les équations obtenues sont valables aussi pour deux sphères en collision (sans frottement) dans l'espace à trois dimensions (modèle des sphères dures).

Lors d'un choc sans frottement, la vitesse de glissement entre les deux disques n'intervient pas dans les équations. C'est pourquoi il n'est pas nécessaire de tenir compte de la rotation des solides.

2. Mise en équation

2.a. Détermination géométrique du contact

À l'instant t=0, les positions et les vitesses des centres des deux disques sont données. Il s'agit de déterminer l'instant du contact et la position des deux centres à cet instant. Pour cela, on écrit le vecteur position relative des deux centres :

\vec{d} = \vec{x_{2}} (0) - \vec{x_{1}} (0) + (\vec{v_{2}} - \vec{v_{1}}) t (1)

Le contact a lieu lorsque la distance entre les deux centres est égale à la somme des rayons :

\vec{d} \cdot \vec{d} = {(r_{1} + r_{2})}^{2} (2)

On obtient ainsi une équation du second degré pour le temps $a t^{2} + 2 b t + c = 0$ . Les coefficients en fonction des composantes des vecteurs sur une base orthonormée sont :

\begin{matrix} a = \sum_{i} {(v_{2 i} - v_{1 i})}^{2} & (3) \\ b = \sum_{i} (x_{2 i} - x_{1 i}) (v_{2 i} - v_{1 i}) & (4) \\ c = \sum_{i} {(x_{2 i} - x_{1 i})}^{2} - {(r_{1} + r_{2})}^{2} & (5) \end{matrix}

où r₁ et r₁ sont les rayons des deux disques (ou sphères).

Lorsque l'équation a deux solutions réelles positives, il y a collision entre les deux disques à l'instant donné par la racine la plus petite. Le cas d'une racine double positive correspond à un contact rasant, que l'on peut considérer comme une absence de collision.

2.b. Résolution de la collision

Il s'agit de déterminer les vitesses des deux centres après la collision. Pour cela, on écrit la conservation de la quantité de mouvement sous la forme suivante :

\begin{matrix} m_{1} (\vec{v_{1}}' - \vec{v_{1}}) = {\vec{p}}_{12} & (6) \\ m_{2} (\vec{v_{2}}' - \vec{v_{2}}) = - {\vec{p}}_{12} & (7) \end{matrix}

où la notation prime a été introduite pour désigner les vitesses après la collision. Le vecteur $\vec{p}$ est la quantité de mouvement échangée entre les deux corps, appelée aussi impulsion; c'est l'intégrale de la force de contact sur la durée du choc. Ces deux équations peuvent se ramener immédiatement à une seule :

m_{1} \vec{v_{1}}' + m_{2} \vec{v_{2}}' = m_{1} \vec{v_{1}} + m_{2} \vec{v_{2}} (8)

Écrivons explicitement l'impulsion en fonction de la force exercée par le disque 2 sur le disque 1, de l'instant de contact t_c et de la durée τ du choc:

{\vec{p}}_{12} = \int_{t_{c}}^{t_{c} + τ} {\vec{F}}_{1 \leftarrow 2} d t (9)

Lorsque la collision se fait sans frottement, la force de contact est colinéaire à la normale au point de contact, c'est-à-dire au vecteur joignant les deux centres $\vec{N} = \vec{C_{1} C_{2}}$ . On en déduit que la variation de vitesse d'un disque n'a pas de composante sur la direction tangente $\vec{T}$ aux disques au point de contact. Il suffit d'écrire cette condition pour un des deux disques :

(\vec{v_{1}}' - \vec{v_{1}}) \cdot \vec{T} = 0 (10)

Pour deux disques (problème 2D) cela fait une équation scalaire. Pour deux sphères (problème 3D), il y a deux vecteurs tangents formant une base du plan tangent; on obtient donc deux équations scalaires.

La dernière équation est obtenue en introduisant le coefficient de restitution e dans la variation de la composante normale de la vitesse relative des deux disques (loi de Newton) :

(\vec{v_{1}}' - \vec{v_{2}}') \cdot \vec{N} = - e (\vec{v_{1}} - \vec{v_{2}}) \cdot \vec{N} (11)

La variation d'énergie cinétique du système des deux disques est (pour un choc sans frottement) :

Δ E_{c} = \frac{1}{2} {\vec{p}}_{12} \cdot (\vec{v_{1}} - \vec{v_{2}}) (1 - e) (12)

Le coefficient de restitution est égal à un 1 pour un choc élastique (sans perte d'énergie), inférieur à 1 sinon. L'introduction de ce coefficient pour quantifier la perte d'énergie permet de garder des équations linéaires (l'énergie cinétique n'est pas linéaire par rapport à la vitesse).

Les équations (8),(10) et (11) constituent un système de 4 équations linéaires pour les 4 inconnues suivantes (matrice colonne) :

U = {(\begin{matrix} v'_{1 x} & v'_{1 y} & v'_{2 x} & v_{2 x} \end{matrix})}^{T} (13)

où l'on a introduit les axes x et y. Pour une collision de sphères dans l'espace à trois dimensions, on a 6 équations. On écrit le système sous forme matricielle AU=B avec :

A = (\begin{matrix} m_{1} & 0 & m_{2} & 0 \\ 0 & m_{1} & 0 & m_{2} \\ T_{x} & T_{y} & 0 & 0 \\ N_{x} & N_{y} & - N_{x} & - N_{y} \end{matrix}) (14)

B = (\begin{matrix} m_{2} v_{2 x} + m_{1} v_{1 x} \\ m_{2} v_{2 y} + m_{1} v_{1 y} \\ \vec{v_{1}} \cdot \vec{T} \\ - e (\vec{v_{1}} - \vec{v_{2}}) \cdot \vec{N} \end{matrix}) (15)

Le système est résolu par la méthode d'élimination de Gauss-Jordan. On pourra pour cela utiliser une fonction générale d'une bibliothèque d'algèbre linéaire.

3. Fonctions de calcul python

import numpy
import numpy.linalg
import math
from pylab import *
from matplotlib.patches import Ellipse,Arrow

On commence par définir une classe pour représenter un disque :

class Disque:
    def __init__(self,r,m):
        self.r = r
        self.m = m
    def set_position(self,x,y):
        self.x = x
        self.y = y
    def set_vitesse(self,vx,vy):
        self.vx = vx
        self.vy = vy
    def deplacer(self,t):
        self.x += self.vx*t
        self.y += self.vy*t
    def tracer(self,color):
        return Ellipse([self.x,self.y],2*self.r,2*self.r,color=color,fill=False)
    def tracer_vitesse(self,color):
        return Arrow(self.x,self.y,self.vx,self.vy,width=0.2,color=color)

La fonction suivante recherche le contact entre deux disques et les place dans leur position de contact. La fonction renvoit True si un contact a lieu, False sinon.

def contact(d1,d2):
    Dvx = d1.vx-d2.vx
    Dvy = d1.vy-d2.vy
    Dx = d1.x-d2.x
    Dy = d1.y-d2.y
    a = Dvx*Dvx+Dvy*Dvy;
    b = Dx*Dvx+Dy*Dvy;
    dmin = d1.r+d2.r 
    c = Dx*Dx+Dy*Dy-dmin*dmin;
    delta = b*b-a*c
    if delta <=0 or a==0:
        return False
    rd = math.sqrt(delta)
    t = min((-b+rd)/a,(-b-rd)/a)
    if t<0:
        return False 
    d1.deplacer(t)  
    d2.deplacer(t)
    return True

La fonction suivante effectue le changement des vitesses des disques dû à la collision avec un coefficient de restitution e :

def collision(d1,d2,e):
    nx = d2.x-d1.x
    ny = d2.y-d1.y
    tx = ny
    ty = -nx
    A = numpy.array([[d1.m,0,d2.m,0],[0,d1.m,0,d2.m],[tx,ty,0,0],[nx,ny,-nx,-ny]])
    B = numpy.array([d1.m*d1.vx+d2.m*d2.vx,d1.m*d1.vy+d2.m*d2.vy,d1.vx*tx+d1.vy*ty,-e*((d1.vx-d2.vx)*nx+(d1.vy-d2.vy)*ny)])
    s = numpy.linalg.solve(A,B)
    d1.set_vitesse(s[0],s[1])
    d2.set_vitesse(s[2],s[3])

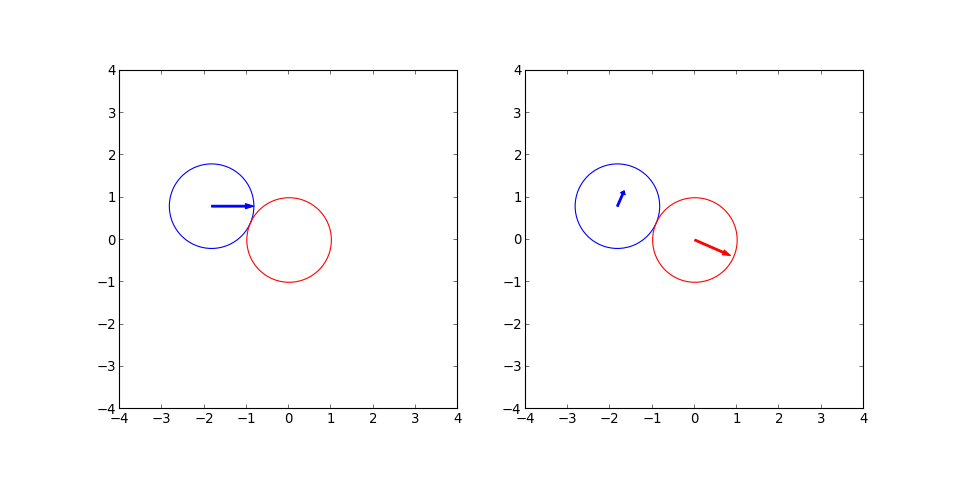
Voici un exemple :

d1 = Disque(1,1) 
d2 = Disque(1,1)
b = 0.8 # parametre d'impact
d1.set_position(-10,b)
d1.set_vitesse(1,0)
d2.set_position(0,0)
d2.set_vitesse(0,0) 
e = 1.0
fig = figure(figsize=(12,6))
ax1 = fig.add_subplot(121,aspect='equal')
ax2 = fig.add_subplot(122,aspect='equal')
ax1.set_xlim(-4,4)
ax1.set_ylim(-4,4)
ax2.set_xlim(-4,4)
ax2.set_ylim(-4,4)
contact(d1,d2)
ax1.add_artist(d1.tracer('b'))
ax1.add_artist(d1.tracer_vitesse('b'))
ax1.add_artist(d2.tracer('r'))
ax1.add_artist(d2.tracer_vitesse('r'))
collision(d1,d2,e)
ax2.add_artist(d1.tracer('b'))
ax2.add_artist(d1.tracer_vitesse('b'))
ax2.add_artist(d2.tracer('r'))
ax2.add_artist(d2.tracer_vitesse('r'))

plotA.pdf