Fonction de transfert optique
1. Introduction
La fonction de transfert optique (FTO) permet de décrire la formation d'une image par un système optique linéaire en terme de fréquences spatiales. En particulier, elle permet de savoir quels détails de l'objet sont visibles sur l'image. C'est l'analogue de la fonction de transfert des filtres électroniques linéaires. Dans cette page, on introduit la FTO dans le cas d'un système optique dénué d'aberrations géométriques.
2. Système optique limité par la diffraction
2.a. Définitions
On considère un système optique de symétrie axiale (système centré). Ce système est supposé corrigé de toutes les aberrations géométriques. Dans ce cas, son pouvoir résolvant est limité seulement par la diffraction.
Pour simplifier l'étude, on considère le cas d'une lentille mince convergente. Les plans objet et image (tous deux réels) sont définis par la relation de conjugaison :
On note (u,v) les coordonnées d'un point dans le plan objet et (x,y) celles d'un point du plan image.
L'étude suivante se limite à un éclairage monochromatique.
2.b. Image d'un point
Soit tout d'abord une source de lumière ponctuelle située dans le plan objet, de coordonnées (u,v). L'amplitude lumineuse obtenue pour ce point source dans le plan image est calculée par le principe de Huygens-Fresnel appliqué à la pupille de la lentille (en général un disque). De plus, le système est équivalent à une source ponctuelle placée au foyer objet d'une lentille de focale p0, avec un plan image situé au foyer image d'une lentille de focale pi. L'amplitude dans le plan image peut donc être obtenue dans le cadre de la diffraction à l'infini (approximation de Fraunhofer) :
Dans cette expression, l'intégration se fait sur la surface de la lentille.
On définit les variables sans dimensions suivantes :
Dans le cadre de l'approximation paraxiale, ces variables sont les angles par rapport au centre de la lentille. L'amplitude vérifie une invariance par translation :
Cela signifie qu'un déplacement de la source dans le plan objet ne fait que déplacer la réponse dans le plan image, sans affecter sa forme.
En introduisant les fréquences spatiales, on définit la transformée de Fourier de la pupille par :
La fonction pupillaire P(xL,yL) prend la valeur 1 sur l'ouverture de la lentille, 0 en dehors. Cette fonction permet également de prendre en compte les aberrations par une phase non nulle.
Finalement, l'amplitude de l'onde lumineuse dans le plan image est :
L'éclairement correspondant est :
2.c. Éclairage incohérent
On note la fonction définissant l'éclairement du plan objet.
Si l'éclairage de l'objet est incohérent, l'éclairement du plan image est obtenu en sommant les éclairements obtenus pour chaque point de l'objet :
où l'intégrale se fait sur le plan de l'objet. On définit la réponse impulsionnelle, ou fonction d'éclairement du point (point spread function) par :
C'est l'éclairement du plan image pour un point source situé au centre du plan objet. Finalement, l'éclairement du plan image est le produit de convolution de l'éclairement du plan objet par la réponse impulsionnelle :
La fonction de transfert optique (FTO) est par définition la transformée de Fourier de la réponse impulsionnelle :
Les fréquences spatiales sont des inverses d'angles.
Le théorème de convolution conduit au résultat suivant : la transformée de Fourier de l'éclairement du plan image est égale à la transformée de Fourier du plan objet multipliée par la fonction de transfert optique, soit
D'autre part, le théorème d'autocorrélation permet d'écrire la FTO comme l'autocorrélation de la fonction pupillaire :
Pour déterminer expérimentalement la fonction de transfert optique d'un système, on effectue l'image d'une modulation sinusoïdale, de manière similaire à l'étude des filtres électroniques en régime sinusoïdal. L'éclairement de l'objet est alors de la forme :
où ν est la fréquence spatiale de la modulation. On remarque la présence nécessaire d'une composante continue, de fréquence nulle. Le contraste, ou indice de modulation, est 1.
L'image obtenue est également sinusoïdale :
où ϕ est l'argument de la fonction de transfert. La fonction de transfert de modulation (MTF) est définie par :
C'est donc le contraste de la modulation de l'image pour la fréquence spatiale ν.
2.d. Éclairage cohérent
Un éclairage cohérent est obtenu pour un objet éclairé en transmission par une petite ouverture placé au foyer d'une lentille, ou bien au moyen d'un faisceau laser élargi. Dans ce cas, l'amplitude lumineuse dans le plan image est :
La réponse impulsionnelle est donc l'amplitude du plan image produite par un point source situé au centre du plan objet. La fonction de transfert optique est la transformée de Fourier de la réponse impulsionnelle. Le théorème de convolution permet de calculer la transformée de Fourier de l'amplitude dans le plan image. La transformée de Fourier inverse conduit à l'amplitude du plan image, dont le module au carré fournit l'éclairement.
3. Pupille circulaire en éclairage cohérent
Lorsque la fonction pupillaire présente une symétrie de révolution, la FTO présente la même symétrie et on peut se contenter de calculer
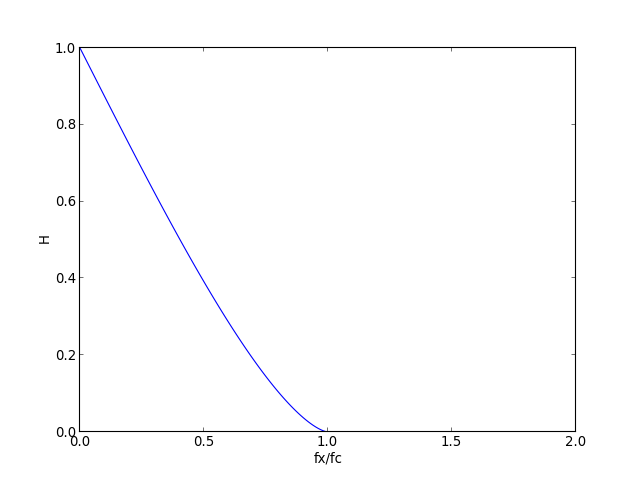
Si le système ne comporte pas d'aberrations géométriques, l'expression de la FTO comme autocorrélation de la fonction pupillaire conduit à une interprétation géométrique simple. Soit D le diamètre de la pupille (i.e. de la lentille). La FTO est l'aire de l'intersection de deux disques de rayons D dont les centres sont espacés de λfX.
Lorsque la distance entre les deux centres est supérieur au diamètre, la FTO est nulle. Cela permet de calculer la fréquence de coupure :
Le calcul de l'aire conduit au résultat suivant :
Ci-dessous le tracé de cette fonction :
from math import *
from numpy import *
from pylab import *
xa = []
H = []
for k in range(100):
x = 1.0/100*k
xa.append(x)
H.append(2/pi*(acos(x)-x*sqrt(1-x*x)))
clf()
plot(xa,H)
xlabel("fx/fc")
ylabel("H")
axis([0,2,0,1])
 plot1.pdf
plot1.pdf
4. Calcul numérique de la FTO
4.a. Objectif
La transformée de Fourier discrète permet d'effectuer les différents calculs sur des images échantillonnées. On se propose de simuler la formation de l'image par une lentille limitée par la diffraction, dans le cas d'un éclairage incohérent. D'autre part, l'utilisation de la transformée de Fourier discrète permet de calculer la réponse impulsionnelle et la FTO d'un système optique présentant une pupille avec obstruction ou des aberrations géométriques.
4.b. Réponse impulsionnelle et fonction de transfert
La réponse impulsionnelle est l'éclairement obtenu pour un point source situé au centre du plan objet. Pour une lentille sans aberrations géométriques, il s'agit de la figure de diffraction d'une ouverture circulaire, obtenue dans le cadre de la diffraction à l'infini.
On charge les différents modules puis on définit la taille de l'échantillonnage :
from math import *
import Image
from TfdImage import *
from numpy.fft import fft2, ifft2
Nx=400
Ny=400
La première fonction définit une matrice complexe représentant la fonction de transmission de la pupille :
def pupille(r):
P = zeros((Ny,Nx),dtype=complex)
nx=Nx/2
ny=Ny/2
for k in range(Nx):
for m in range(Ny):
if pow((k-nx)*(k-nx)+(m-ny)*(m-ny),0.5) < r:
P[m,k] = 1.0
return P
On fixe le diamètre de la lentille (en mètres) puis le nombre de points de ce diamètre, ce qui permet de calculer les dimensions réelles (en mètres) du domaine échantillonné, lequel doit dépasser largement la pupille :
D=0.01
np=80
Lx=D*Nx/np
Ly=D*Ny/np
On calcule la transformée de Fourier de la pupille, puis son spectre de puissance, qui correspond à l'éclairement, c'est-à-dire à la réponse impulsionnelle cherchée :
P=pupille(np/2)
TFP=matriceCentre(fft2(P))
h=matricePuissance(TFP)
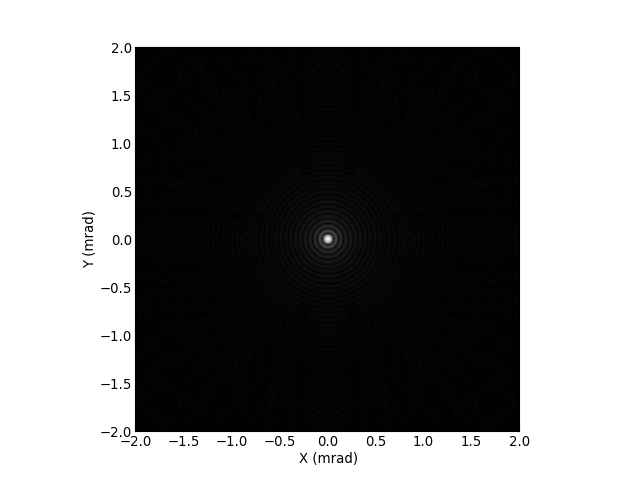
Voyons la représentation de cette réponse impulsionnelle. L'échelle des axes est en milliradians. L'échelle est établie sachant que la fréquence maximale obtenue par la FFT est la moitié de la fréquence d'échantillonnage :
Lambda=500e-9
imh = matriceImage(h,3.0,[1.0,1.0,1.0])
xmax = Nx/Lx*0.5*Lambda*1000
figure()
imshow(imh,extent=[-xmax,xmax,-xmax,xmax])
xlabel('X (mrad)')
ylabel('Y (mrad)')
 plotA.pdf
plotA.pdf
On reconnait la figure de diffraction d'Airy. La correction gamma permet de renforcer la visibilité des maxima secondaires.
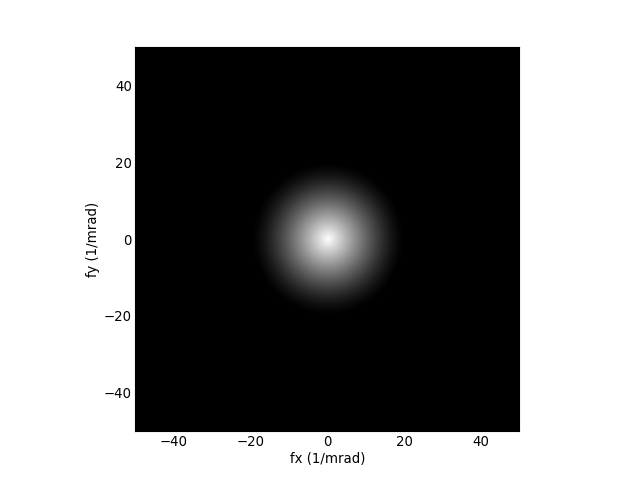
La fonction de transfert optique est la transformée de Fourier de la réponse impulsionnelle :
H=matriceCentre(fft2(h))
imH=matriceImage(matriceModule(H),1.0,[1.0,1.0,1.0])
figure()
fmax = Nx/(2*xmax)*0.5;
imshow(imH,extent=[-fmax,fmax,-fmax,fmax])
xlabel('fx (1/mrad)')
ylabel('fy (1/mrad)')
 plotB.pdf
plotB.pdf
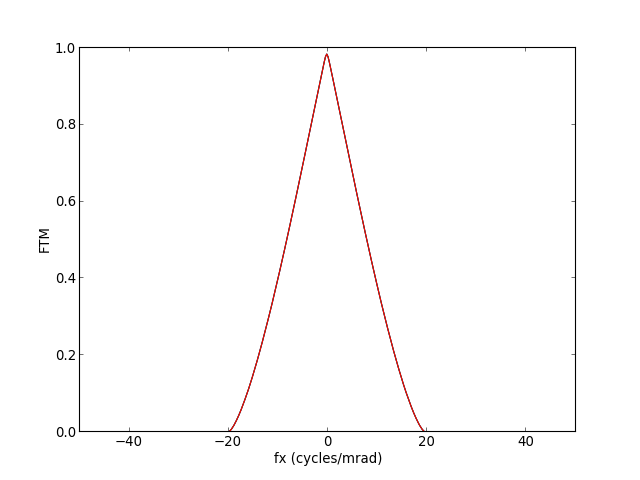
Cette dernière figure représente le module de la fonction de transfert, qui décroit continument lorsqu'on s'éloigne du centre. La fonction de transfert de modulation est obtenue pour Y=0 :
FTM=imH[Ny/2]
figure()
fx=arange(-fmax,fmax,2*fmax/Nx)
plot(fx,FTM)
xlabel('fx (cycles/mrad)')
ylabel('FTM')
axis([-fmax,fmax,0,1.0])
 plotD.pdf
plotD.pdf
On retrouve la FTM calculée plus haut. La fréquence de coupure est obtenue directement par la relation :
fc = D/Lambda/1000
print(fc) --> 20.0
4.c. Formation d'une image
La fonction suivante calcule l'image pour un éclairement donné du plan objet. La transformée de Fourier de l'image est obtenue en multipliant celle de l'objet par la fonction de transfert donnée en argument. L'image est ensuite obtenue par transformée de Fourier inverse. L'image fournie est normalisée (valeur maximale de 1).
def imageLentille(objet,H):
TFO = matriceCentre(fft2(objet))
TFI = zeros((Ny,Nx),dtype=complex)
for n in range(Nx):
for l in range(Ny):
TFI[l,n] = TFO[l,n]*H[l,n]
Im = matriceCentre(ifft2(matriceBords(TFI)))
norm=Im.max()
for n in range(Nx):
for l in range(Ny):
Im[l,n]=Im[l,n]/norm
return Im
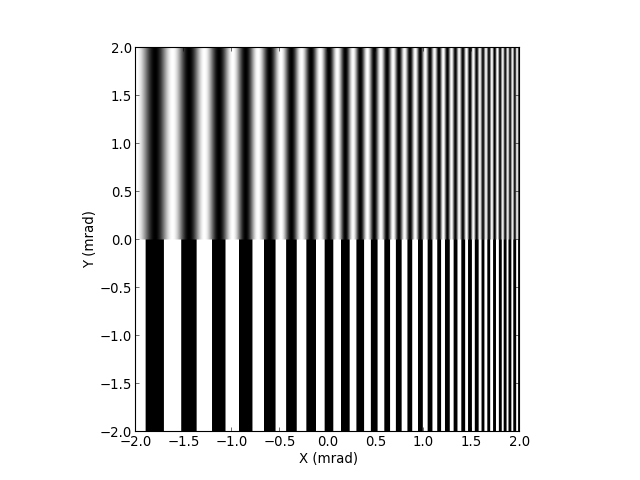
On génère un objet comportant une modulation sinusoïdale de fréquence variable et des bandes à bords nets :
A=zeros((Ny,Nx),dtype=float)
L0=40.0
ny=Ny/2
for k in range(Nx):
L=L0-L0/(float(Nx)*1.5)*float(k)
I=0.5*(1+cos(2*pi*k/L))
for m in range(ny):
A[m,k] = I
if I>0.5:
A[m+ny,k] = 1.0
figure()
scale = xmax
imshow(matriceImage(A,1.0,[1.0,1.0,1.0]),extent=[-scale,scale,-scale,scale])
xlabel('X (mrad)')
ylabel('Y (mrad)')
 plotE.pdf
plotE.pdf
L'échelle de cet objet (en milliradians) correspond à celle de la tache d'Airy obtenue plus haut, soit 4 mrad de large. Cela correspond à un objet de 4 mm de large situé à une distance de 1 m de la lentille.
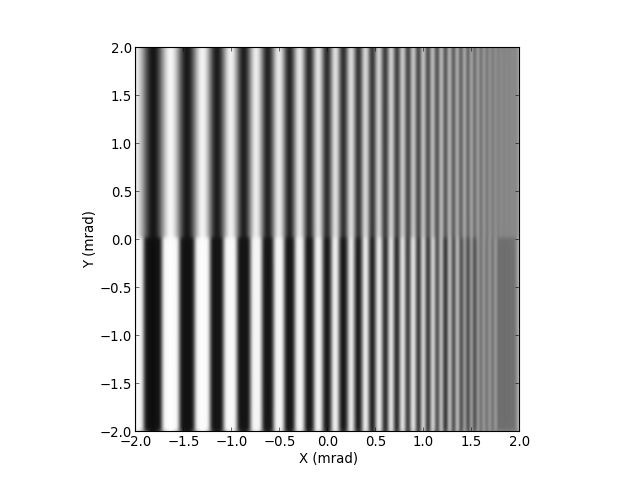
Calcul de l'image par la lentille et affichage
IA=imageLentille(A,H)
IA=matriceModule(IA)
imIA=matriceImage(IA,1.0,[1.0,1.0,1.0])
figure()
figure()
imshow(imIA,extent=[-scale,scale,-scale,scale])
xlabel('X (mrad)')
ylabel('Y (mrad)')
 plotC.pdf
plotC.pdf
On constate une réduction de la netteté des contours. Il y a aussi une réduction du contraste, qui se manifeste par une baisse du niveau lumineux des bandes horizontales les plus étroites.
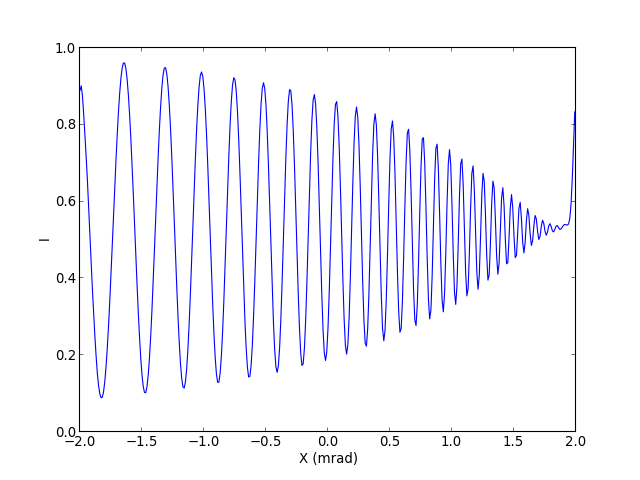
Voyons le profil de l'éclairement dans la zone de modulation sinusoïdale :
figure()
xlabel('X (mrad)')
ylabel('I')
x=arange(-scale,scale,2*scale/Nx)
plot(x,IA[50])
axis([-scale,scale,0,1])
 plotF.pdf
plotF.pdf
On remarque la réduction de contraste de la modulation lorsque la fréquence spatiale augmente, conformément à la courbe de MTF obtenue plus haut.